A non-homogeneous dynamic Bayesian network with a hidden Markov model dependency structure among the temporal data points

Abstract

In the topical field of systems biology there is considerable interest in learning regulatory networks, and various probabilistic machine learning methods have been proposed to this end. Popular approaches include non-homogeneous dynamic Bayesian networks (DBNs), which can be employed to model time-varying regulatory processes. Almost all non-homogeneous DBNs that have been proposed in the literature follow the same paradigm and relax the homogeneity assumption by complementing the standard homogeneous DBN with a multiple changepoint process. Each time series segment defined by two demarcating changepoints is associated with separate interactions, and in this way the regulatory relationships are allowed to vary over time. However, the configuration space of the data segmentations (allocations) that can be obtained by changepoints is restricted. A complementary paradigm is to combine DBNs with mixture models, which allow for free allocations of the data points to mixture components. But this extension of the configuration space comes with the disadvantage that the temporal order of the data points can no longer be taken into account. In this paper I present a novel non-homogeneous DBN model, which can be seen as a consensus between the free allocation mixture DBN model and the changepoint-segmented DBN model. The key idea is to assume that the underlying allocation of the temporal data points follows a Hidden Markov model (HMM). The novel HMM–DBN model takes the temporal structure of the time series into account without putting a restriction onto the configuration space of the data point allocations. I define the novel HMM–DBN model and the competing models such that the regulatory network structure is kept fixed among components, while the network interaction parameters are allowed to vary, and I show how the novel HMM–DBN model can be inferred with Markov Chain Monte Carlo (MCMC) simulations. For the new HMM–DBN model I also present two new pairs of MCMC moves, which can be incorporated into the recently proposed allocation sampler for mixture models to improve convergence of the MCMC simulations. In an extensive comparative evaluation study I systematically compare the performance of the proposed HMM–DBN model with the performances of the competing DBN models in a reverse engineering context, where the objective is to learn the structure of a network from temporal network data.

1 Introduction

In the topical field of systems biology there is considerable interest in learning regulatory networks, such as gene regulatory transcription networks (Friedman et al. 2000), protein signal transduction cascades (Sachs et al. 2005), neural information flow networks (Smith et al. 2006), or ecological networks (Aderhold et al. 2013). In the computational biology and machine learning literature a variety of powerful probabilistic machine learning methods based on graphical models, such as Bayesian networks (Friedman et al. 2000), have been proposed to learn these networks from data. The standard assumption underlying the conventional graphical models is that the observed time series are homogeneous so that potential changes in the regulatory interactions are not taken into account. That is, the standard graphical models, e.g. the conventional homogeneous Gaussian dynamic Bayesian network (DBN) model, describe a simple homogeneous linear dynamical system. Unfortunately, the assumptions of homogeneity and linearity are unrealistic for many applications in systems biology, and thus can cause erroneous and misleading inference results. Regulatory interactions in systems biology applications tend to be non-linear and adaptive so that they vary over time, e.g. in response to changing environmental and experimental conditions.

A more appropriate approach would therefore be the deduction of a detailed mathematical description of the entire network domain in terms of mechanistic models, e.g. in the form of coupled non-linear stochastic differential equations (DEs). Seminal examples have for example been presented in Vyshemirsky and Girolami (2008) and Toni et al. (2009). Since a proper Bayesian inference for those mechanistic models is computationally expensive, usually only very small network domains with typically only 3–4 nodes are considered (Vyshemirsky and Girolami 2008) or the inference is based on approximations (Toni et al. 2009). Therefore, in standard applications of mechanistic models only a limited amount of different hypotheses about the underlying network structure is compared, and the space of network structures is not systematically searched for those networks that are most consistent with the observed data. That is, mechanistic models cannot be used to learn regulatory networks from scratch (i.e. without any prior hypotheses about potential network structures). Therefore, there have been various efforts to relax the homogeneity assumption for undirected (see, e.g., Talih and Hengartner 2005 or Xuan and Murphy 2007) and directed (see, e.g., Ahmed and Xing 2009) graphical models, as well as for dynamic Bayesian networks (see references below). The key idea is to leave the class of homogeneous linear dynamic models, and to develop novel non-homogeneous graphical models that balance between two requirements: On the one hand, those models should offer enough flexibility so that they can appropriately capture the underlying non-homogeneous biological processes, and thus become competitive to the mechanistic models. On the other hand, from a computational perspective it must be possible to use these models to systematically search the space of network structures and to learn the underlying regulatory relationships from scratch (i.e. in the absence of any hypothesis about the underlying network structure). The focus of this paper is to propose a novel non-homogeneous dynamic Bayesian networks (DBN) model that fulfils both requirements.

Various DBN models have been proposed in the literature, and it can be distinguished between DBNs for which the parameters in the likelihood can be integrated out in closed-form, and DBNs for which the marginal likelihood is intractable. The latter DBNs tend to have a greater flexibility, but they are more susceptible to over-fitting, since the network structures and the interaction parameters have to be estimated simultaneously. Flexible DBNs with an intractable likelihood can, for example, be constructed along the lines proposed in Imoto et al. (2003), Rogers and Girolami (2005), or Ko et al. (2007).¹ Here, I concentrate on DBNs for which the network parameters can be integrated out in closed form. Although this requires certain regularity conditions, such as parameter independence and prior conjugacy, to be fulfilled, these DBNs have two attractive features: (i) The data-overfitting problem is intrinsically avoided, and (ii) “model-averaging” can be realised by efficient Reversible Jump Markov Chain Monte Carlo (RJMCMC) simulations in discrete configuration spaces (Green 1995).

To obtain a closed-form expression of the marginal likelihood in DBN models three models with their respective conjugate prior distributions have been proposed in the literature: (i) the multinomial distribution with the Dirichlet prior, leading to the BDe score (Cooper and Herskovits 1992), (ii) the linear Gaussian distribution with the normal-Wishart prior, leading to the BGe score (Geiger and Heckerman 1994), and (iii) a Bayesian linear regression model with a Gaussian prior on the regression coefficients (see, e.g., Lèbre et al. 2010). The former two approaches have originally been proposed for static Bayesian networks, but they can be extended straightforwardly to model homogeneous DBNs, as demonstrated in Friedman et al. (2000). Non-homogeneous DBNs with these two standard scores have for example been developed in Robinson and Hartemink (2009) and Robinson and Hartemink (2010) (with BDe), and in Grzegorczyk and Husmeier (2009) and Grzegorczyk and Husmeier (2011) (with BGe). The key idea behind these non-homogeneous DBNs is to relax the homogeneity assumption by complementing the standard homogeneous DBN with a Bayesian multiple changepoint process. Each time series segment defined by two demarcating changepoints is associated with separate interaction parameters, and in this way the regulatory relationships are allowed to vary over time.

Recently, the Bayesian regression model, described in Lèbre et al. (2010), has become a popular probabilistic model for non-homogeneous DBNs. A shortcoming of this “Bayesian regression” DBN (BR-DBN) model, as originally proposed by Lèbre et al. (2010), is potential model over-flexibility, as different time series segments are associated with different network structures, which for short time series will lead to over-fitting and inflated inference uncertainty. Various regularised variants of this BR-DBN model have been proposed (see, e.g., Dondelinger et al. 2010, 2012), and in other instantiations of the BR-DBN model, the authors follow Grzegorczyk and Husmeier (2011) or Grzegorczyk and Husmeier (2013) and keep the network structure fixed among segments so that only the interaction parameters vary from segment to segment. In this paper I follow the latter works and focus on applications where cellular processes take place on a short time scale so that it is not the network structure but rather the strength of the regulatory interactions that changes with time.² For those models, which do not allow for segment-wise network changes, various information coupling schemes with respect to the segment-specific network parameters have recently been proposed (Grzegorczyk and Husmeier 2012a, b, 2013).

All these non-homogeneous DBNs, mentioned above, follow the same paradigm and combine a classical homogeneous DBN model with a multiple changepoint process. However, the configuration space of the data segmentations that can be obtained by changepoints is restricted. Let us consider these changepoint processes in the broader context of mixture models, which are based on a free allocation of the data points to mixture components. From this perspective the changepoints divide the time series into disjunct temporal segments, and the segments (i.e. the data points within each segment) are assigned to disjunct (“mixture”) components. That is, there is a one-to-one mapping between the temporal segments and the mixture components, and hence, distant segments cannot be allocated to the same component; throughout the paper I will also say: “a component once left cannot be revisited”. For instance, if there are 10 temporal data points, then allocation schemes, such as [1112222211], are not part of the segmentation space of multiple changepoint processes and would have to be “approximated” by segmentations, such as [1112222233].

In earlier papers it has been proposed to combine Bayesian networks with classical mixture models (see, e.g., Ko et al. 2007 or Grzegorczyk et al. 2008). Unlike the DBNs with changepoints (CPS–DBNs), the proposed mixture DBN (MIX-DBN) allows for an unrestricted free allocation of the data points to (mixture) components, and, hence, substantially increases the configuration space of the possible data segmentations. However, for time series the temporal order of the data points is not taken into account, and this inevitably incurs an information loss, e.g. when a priori temporally neighbouring data points should be more likely to be assigned to the same component than distant ones.

In biological systems various examples for periodic gene regulatory processes can be found. E.g. plants, such as Arabidopsis thaliana, possess a circadian clock and the underlying molecular mechanisms depend on the presence/absence of light (see Sect. 3.3 for details and literature references). That is, the gene regulatory processes in Arabidopsis are diurnal and periodically depend on the daily dark:light (night:day) cycle. These daily alternations of darkness (“1”) and light (“2”) phases are caused by an external factor, namely the rotation of the earth, and they impose a periodic diurnal segmentation on the gene regulatory processes in the circadian clock, e.g. a segmentation of the form [111222111222].³ Apart from this plant biology example, described in more detail in Sect. 3.3, circadian rhythms also play an important role in the regulatory processes in mammalian cells (see, e.g., Yan et al. 2008). Another example are the periodic regulatory processes that can be observed during the cell cycle (see, e.g., Whitfield et al. 2002 or Rustici et al. 2004). As discussed above, neither the changepoint processes (CPS–DBN) nor the free allocation mixture models (MIX-DBN) are adequate for learning periodic segmentations; the CPS–DBN model cannot revisit states once left, while the MIX-DBN model completely ignores the temporal arrangement of the data points.

In this paper I present a novel non-homogeneous dynamic Bayesian network model, which can be seen as a consensus between the free allocation mixture DBN model (MIX-DBN) and the changepoint-process-segmented DBN model (CPS–DBN). The idea is to assume that the underlying allocation of the temporal data points follows a Hidden Markov model (HMM). The novel DBN model, which I will refer to as the HMM–DBN model, does take the temporal structure of the time series into account without putting any restriction onto the configuration space of the allocations. With the HMM–DBN model, periodic segmentations, such as [111222111222], can be inferred properly. In this paper I implement the novel model with a network structure that is kept fixed among segments and I only allow the network interaction parameters to vary in time. In a comparative evaluation study I demonstrate that the novel HMM–DBN model has the attractive feature that it is competitive to both (i) the CPS–DBN model for changepoint-segmented allocations and (ii) the MIX-DBN model for free mixture allocations. I also show how the allocation of the data points can be inferred with the allocation sampler (Nobile and Fearnside 2007). As the allocation sampler has been developed for classical Gaussian mixture models, it does not exploit the temporal information. I therefore propose to improve the allocation sampler by introducing two new pairs of complementary MCMC moves, which utilise the temporal arrangement of the data points. Although the key idea behind the proposed HMM–DBN model is generic, I present it in the context of the BR-DBN model (Lèbre et al. 2010). With regard to the real-world applications (see Sects. 3.2 and 3.3) I follow Grzegorczyk and Husmeier (2011) and Grzegorczyk and Husmeier (2013) and keep the network structure fixed among segments (components).

This paper is organized as follows: Sect. 2 provides a comprehensive exposition of the mathematical details behind the HMM–DBN model. I also present two new pairs of moves for the MCMC inference, and I briefly summarise the competing non-homogeneous DBN models. Section 3 gives an overview to the data on which I apply and cross-compare the models. I provide the details on how I implemented the HMM–DBN model for the comparative evaluation study in Sect. 4. The results of a study, in which I systematically compare the performances of the MIX-DBN, the CPS–DBN and the HMM–DBN model, are presented in Sect. 5. A discussion of the computational costs and a brief outlook to future work is provided in Sect. 6, before I draw my final conclusions in Sect. 7. Note that mathematical details from Sect. 2 have been relegated to the Appendices 1–4.

2 Methodology

2.1 Bayesian regression models

In this subsection I briefly summarise the non-homogeneous Bayesian regression DBN (BR-DBN) model, proposed by Lèbre et al. (2010). Recently, various different variants of the original BR-DBN model have been developed, proposed and applied in the literature. Here I consider the uncoupled BR-DBN variant, which has been recently used in Grzegorczyk and Husmeier (2012a) and Grzegorczyk and Husmeier (2012b). Unlike all BR-DBN model instantiations that have been developed so far, I combine the BR-DBN model with a free allocation model rather than a multiple changepoint process.⁴ The free allocation BR-DBN model, considered here, allows for more flexibility with respect to the configuration space of the possible data allocations.

Consider a set of $N$ nodes, $g\in \{1,\ldots ,N\}$, in a network, $\mathcal {M}=(\varvec{\pi }_1(\mathcal {M}),\ldots ,\varvec{\pi }_{N}(\mathcal {M}))$, where $\varvec{\pi }_{g}(\mathcal {M})$ denotes the parents of node $g$ in $\mathcal {M}$, that is the set of nodes with a directed edge pointing to node $g$. For notational convenience, I write $\varvec{\pi }_{g}=\varvec{\pi }_{g}(\mathcal {M})$ in the following representations; i.e. I do not indicate the dependency on $\mathcal {M}$ explicitly .

Given a $N$-by-$T$ data set matrix, $\mathcal {D}$, where the rows correspond to the $N$ nodes and the columns correspond to $T$ temporal observations, let $y_{g,t}$ denote the realisation of the random variable associated with node $g$ at time point $t \in \{1,\ldots ,T\}$, and let $\mathbf{x}_{\varvec{\pi }_{g},t}$ denote the vector of realisations of the random variables associated with the parent nodes of node $g$, $\pi _{g}$, at the previous time point, $(t-1)$, and including a constant element equal to 1 (for the intercept). With $|\varvec{\pi }_{g}|$ denoting the cardinality of the parent node set $\varvec{\pi }_{g}$, the vector $\mathbf{x}_{\varvec{\pi }_{g},t}$, which also includes the element 1 for the intercept, is of size $|\varvec{\pi }_{g}|+1$.

Unlike the mixture model DBN in Grzegorczyk et al. (2008) I here consider node-specific allocation vectors, ${\mathbf{V}}_{g}$ ($g=1,\ldots ,N$), where each vector ${\mathbf{V}}_{g}$ is of size $T$ and defines a free allocation of the last $T-1$ observations, $y_{g,2},\ldots ,y_{g,T}$, of node $g$ to $\mathcal {K}_{g}$ components. ${\mathbf{V}}_{g}(t)=k$ means that the observation $y_{g,t}$ is allocated to the $k$th component ($t=2,\ldots ,T$ and $k=1,\ldots ,\mathcal {K}_{g}$). Furthermore, I define $\mathbf{y}_{g,k}$ to be the vector of observations that have been allocated to component $k$ by ${\mathbf{V}}_{g}$ ($1\le k\le \mathcal {K}_{g}$). In the free allocation regression models, described below, the nodes $g=1,\ldots ,N$ are considered as target variables and their regressor variables are the variables in their parent sets, namely $\varvec{\pi }_{1},\ldots ,\varvec{\pi }_{N}$. More precisely, $\mathbf{y}_{g,k}$ is the target vector for component $k$, and I have to arrange the corresponding observations of the parent nodes, $\varvec{\pi }_{g}$, appropriately in a regressor (or design) matrix, which I denote $\mathbf{X}_{\varvec{\pi }_{g},k}$. Let the vector $\mathbf{y}_{g,k}$ be of size $n_k$, i.e. let $n_k$ observations have been allocated to component k, then $\mathbf{X}_{\varvec{\pi }_{g},k}$ is an $(|\varvec{\pi }_{g}|+1)$-by-$n_k$ matrix, and if the jth element of the target vector $\mathbf{y}_{g,k}$ is the observation $y_{g,t}$, then the jth column of the regressor matrix, $\mathbf{X}_{\varvec{\pi }_{g},k}$, has to be the vector $\mathbf{x}_{\varvec{\pi }_{g},t}$. As each vector $\mathbf{x}_{\varvec{\pi }_{g,t}}$ includes a constant element for the intercept, the first row of the design matrix, $\mathbf{X}_{\varvec{\pi }_{g},k}$, is a column vector of 1’s, which corresponds to the intercept.

Given a fixed graph topology $\mathcal {M}$, which implies the parent node sets, $\pi _{g}$, and thus the regressor variables for each node g, as well as fixed allocation vectors, ${\mathbf{V}}_{g}$, which imply the node-specific allocations, I follow Lèbre et al. (2010) and apply a linear Gaussian regression model to each target vector $\mathbf{y}_{g,k}$ using $\mathbf{X}_{\varvec{\pi }_{g},k}$ as regressor matrix:

$$\begin{aligned} \mathbf{y}_{g,k} = \mathbf{X}_{\varvec{\pi }_{g},k}^{\mathsf{T}}\mathbf{w}_{g,k}+\varepsilon _{g,k}, \end{aligned}$$

(1)

where $\mathbf{w}_{g,k}$ is the $(|\varvec{\pi }_{g}|+1)$-dimensional vector of regression parameters, $\varepsilon _{g,k}$ is the noise vector, and the superscript symbol “$\mathsf{T}$” denotes matrix transposition. I assume that the individual elements of the noise vectors, $\varepsilon _{g,k}$, are i.i.d. Gaussian distributed with zero mean and variance $\sigma _g^2$; i.e. the noise variances are node-specific but do not depend on the component $k$.⁵ The vectors $\varepsilon _{g,k}$ ($k=1,\ldots ,\mathcal {K}_{g}$) are then independently multivariate Gaussian distributed with zero mean vector and covariance matrix $\sigma _g^2 {\mathbf{I}}$, where $\mathbf{I}$ denotes the unit matrix. The likelihood of the regression model is given by:

$$\begin{aligned} P(\mathbf{y}_{g,k}|\mathbf{X}_{\varvec{\pi }_{g},k},\mathbf{w}_{g,k},\sigma _{g}) = \mathcal {N}\left( \mathbf{y}_{g,k}|\mathbf{X}_{\varvec{\pi }_{g},k}^{\mathsf{T}}\mathbf{w}_{g,k}, \sigma _g^2 \mathbf{I}\right) , \end{aligned}$$

On the component-specific regression parameter vectors, $\mathbf{w}_{g,k}$, I impose the following conjugate Gaussian priors:

$$\begin{aligned} P\left( \mathbf{w}_{g,k}|\sigma _{g}^2,\delta _{g}\right) \; = \; \mathcal {N}\left( \mathbf{w}_{g,k}|{\mathbf{0}},\delta _{g} \sigma ^2_{g} {\mathbf{I}}\right) \end{aligned}$$

(2)

where $\delta _{g}$ can be interpreted as a gene-specific “signal-to-noise” (SNR) hyperparameter (Lèbre et al. 2010). On the inverse noise variances, $\sigma ^{-2}_{g}$, and on the inverse SNR hyperparameters, $\delta _{g}^{-1}$, I also impose conjugate priors, i.e. Gamma priors:

$$\begin{aligned} P(\sigma ^{-2}_{g}|A_{\sigma },B_{\sigma })= & {} \mathrm {Gam}(\sigma ^{-2}_{g}|A_{\sigma },B_{\sigma }) = \frac{[B_{\sigma }]^{A_{\sigma }}}{\Gamma (A_{\sigma })} \left[ \sigma _{g}^{-2}\right] ^{A_{\sigma }-1} e^{-B_{\sigma }\sigma _{g}^{-2}}\end{aligned}$$

(3)

$$\begin{aligned} P(\delta _{g}^{-1}|A_{\delta },B_{\delta })= & {} \mathrm {Gam}(\delta _{g}^{-1}| A_{\delta },B_{\delta }) = \frac{[B_{\delta }]^{A_{\delta }}}{\Gamma (A_{\delta })} \left[ \delta _{g}^{-1}\right] ^{A_{\delta }-1} e^{-B_{\delta }\delta _{g}^{-1}} \end{aligned}$$

(4)

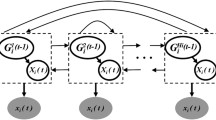
with the fixed level-2 hyperparameters $A_{\sigma }$, $B_{\sigma }$, $A_{\delta }$ and $B_{\delta }$. A compact representation of the relationships among the (hyper-)parameters of the Bayesian regression models, described above, can be found in Fig. 1. The free model parameters, indicated by white circles in Fig. 1, have to be sampled from the posterior distribution. Due to standard conjugacy arguments the full conditional distributions of the free parameters can be computed in closed form, and the Gibbs-sampling scheme from Grzegorczyk and Husmeier (2012b) can be applied to generate a sample from the posterior distribution $P(\mathbf{w}_{g,1},\ldots ,\mathbf{w}_{g,\mathcal {K}_{g}},\delta _{g},\sigma _{g}^2|\mathcal {D})$. ⁶

Fig. 1

Compact representation of the employed free allocation Bayesian regression model. The grey circles refer to fixed (hyper-)parameters and the data (${\mathbf{X}}_{\pi _g,k}$ and ${\mathbf{y}}_{g,k}$), while the white circles refer to free (hyper-)parameters. A detailed model description is provided in Sect. 2.1

To indicate the allocations implied by the allocation vector ${\mathbf{V}}_{g}$, I introduce the symbols:

$$\begin{aligned} \mathbf{y}_{g,{\mathbf{V}}_{g}}:= & {} \left\{ \mathbf{y}_{g,k}\right\} _{k=1,\ldots ,\mathcal {K}_g} \end{aligned}$$

(5)

$$\begin{aligned} \mathbf{X}_{\pi _g,{\mathbf{V}}_{g}}:= & {} \left\{ \mathbf{X}_{\pi _g,k}\right\} _{k=1,\ldots ,\mathcal {K}_g} \end{aligned}$$

(6)

$$\begin{aligned} \mathbf{w}_{g,{\mathbf{V}}_{g}}:= & {} \left\{ \mathbf{w}_{g,k}\right\} _{k=1,\ldots ,\mathcal {K}_g} \end{aligned}$$

(7)

The full conditional distributions of $\delta _{g}^{-1}$ and $\mathbf{w}_{g,k}$ are given by:

$$\begin{aligned}&\delta _{g}^{-1}|\left( \mathbf{w}_{g,{\mathbf{V}}_{g}},\sigma ^2_{g}\right) \sim \mathrm {Gam}\left( A_{\delta } + \frac{\mathcal {K}_{g}\left( |\varvec{\pi }_{g}|+1\right) }{2}, B_{\delta } + \frac{1}{2\sigma ^2_{g}} \sum _{k=1}^{\mathcal {K}_{g}} \mathbf{w}_{g,k}^{\mathsf{T}} \mathbf{w}_{g,k} \right) \end{aligned}$$

(8)

$$\begin{aligned}&\mathbf{w}_{g,k}|\left( \mathbf{y}_{g,k},\mathbf{X}_{\pi _g,k},\sigma ^2_{g},\delta _{g}\right) \sim \mathcal {N}\left( \mathbf{\Sigma }_{g,k}^{\star } \mathbf{X}_{\pi _g,k} \mathbf{y}_{g,k},\sigma ^2_{g}\mathbf{\Sigma }_{g,k}^{\star }\right) \end{aligned}$$

(9)

where $\mathcal {K}_{g}$ is the number of components for node $g$, $|\varvec{\pi }_{g}(\mathcal {M})|$ is the cardinality of the parent set, $\varvec{\pi }_{g}$, and $\mathbf{\Sigma }_{g,k}^{\star } = \left( \delta _{g}^{-1} {\mathbf{I}} + \mathbf{X}_{\pi _g,k} \mathbf{X}^{\mathsf{T}}_{\pi _g,k} \right) ^{-1}$.

The inverse variance hyperparameters, $\sigma ^{-2}_{g}$, could also be sampled from the full conditional distribution, but a computationally more efficient way is to to use a collapsed Gibbs sampling step, in which the regression parameter vectors, $\mathbf{w}_{g,k}$, have been integrated out. This marginalization yields:

$$\begin{aligned} \sigma ^{-2}_{g}|(\mathbf{y}_{g,{\mathbf{V}}_{g}},\mathbf{X}_{\pi _g,{\mathbf{V}}_{g}},\delta _{g}) \sim \mathrm {Gam}\left( A_{\sigma }+\frac{T-1}{2}, B_{\sigma }+\frac{\sum _{k=1}^{K_{g}} \Delta ^2_{g,k}}{2} \right) \end{aligned}$$

(10)

with the squared Mahalanobis distance $\Delta _{g,k}^2 = \mathbf{y}_{g,k}^{\mathsf{T}} \left( {\mathbf{I}} + \delta _{g} \mathbf{X}_{\pi _g,k}^{\mathsf{T}} \mathbf{X}_{\pi _g,k} \right) ^{-1} \mathbf{y}_{g,k}$.

If the parent node sets, $\varvec{\pi }_{g}$, and the allocation vectors, ${\mathbf{V}}_{g}$, are known and kept fixed, Eqs. (8–10) can be used, as indicated in Table 1, to generate a sample from the posterior distribution:

$$\begin{aligned} P\left( \mathbf{w}_{g,{\mathbf{V}}_{g}},\delta _{g},\sigma _{g}^2|\mathcal {D}\right) \propto \prod _{g} P\left( \delta _{g}\right) P\left( \sigma _{g}^2\right) \prod _{k} P\left( \mathbf{w}_{g,k}|\delta _{g},\sigma _{g}\right) P\left( \mathbf{y}_{g,k}|\mathbf{X}_{\pi _g,k},\sigma _g,\mathbf{w}_{g,k}\right) \nonumber \\ \end{aligned}$$

(11)

However, in real-wold applications the allocation vectors, ${\mathbf{V}}_{g}$, are usually unknown and the objective is to infer the parent node sets, $\varvec{\pi }_{g}$, which form the network structure, $\mathcal {M}=(\varvec{\pi }_{1},\ldots ,\varvec{\pi }_{N})$. Note that the regression model is defined such that the likelihood can be marginalized over both the regression parameters, $\mathbf{w}_{g,k}$, and the noise variance hyperparameters, $\sigma _{g,k}$. For each node g the marginal likelihood is given by:

$$\begin{aligned} P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{\pi _g,{\mathbf{V}}_{g}},\delta _{g}\right) = \frac{\Gamma \left( \frac{T-1}{2}+A_{\sigma }\right) \left( 2 B_{\sigma }\right) ^{A_{\sigma }}}{\Gamma (A_{\sigma })(\pi )^{(T-1)/2} \prod _{k=1}^{\mathcal {K}_{g}}|{\tilde{{\varvec{\Sigma }}}}_{g,k}|^{1/2}} \left( 2 B_{\sigma } + \Delta _{g}^2 \right) ^{-\left( \frac{T-1}{2}+A_{\sigma }\right) }\qquad \end{aligned}$$

(12)

where ${\tilde{{\varvec{\Sigma }}}}_{g,k} = \mathbf{I} + \delta _{g} \mathbf{X}_{\pi _g,k}^{\mathsf{T}} \mathbf{X}_{\pi _g,k}$, $\Delta _{g}^2 \; = \sum _{k=1}^{K_g} \Delta _{g,k}^2$, and the squared Mahalanobis distance terms, $\Delta _{g,k}^2$, were defined below Eq. (10); for a derivation see Grzegorczyk and Husmeier (2012b). Note that the marginal likelihood in Eq. (12) is invariant with respect to a permutation of the components’ labels, as I have imposed exchangeable (i.i.d.) priors on the component-specific regression parameter vectors [see Eq. (2)].

Table 1 The MCMC sampling scheme for the free allocation Bayesian regression model shown in Fig. 1

2.2 Network structure inference

I assume the allocation vectors, ${\mathbf{V}}_{g}$, still to be fixed, and I describe how the network structure, $\mathcal {M}$, can be inferred. For the prior on the network structures, $\mathcal {M}=(\pi _{1},\ldots ,\pi _{N})$, I assume a modular form:

$$\begin{aligned} P(\mathcal {M})=\prod _{g=1}^{N} P(\pi _{g}) \end{aligned}$$

(13)

and uniform distributions for $P(\pi _{g})$, subject to a fan-in restriction, $|\pi _{g}|\le \mathcal {F}$, for each $g$. The individual parent node sets, $\pi _{g}$, can then be inferred independently for each node g, and the collection of parent node sets forms the network structure, $\mathcal {M}=(\pi _{1},\ldots ,\pi _{N})$. For each node g the full conditional distribution is given by:

$$\begin{aligned} P\left( \pi _{g}|\mathcal {D},{\mathbf{V}}_{g},\delta _{g}\right) \propto P\left( \pi _{g}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{\pi _g,{\mathbf{V}}_{g}},\delta _g\right) \end{aligned}$$

(14)

where the expressions for $P(\mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{\pi _g,{\mathbf{V}}_{g}},\delta _g)$ can be computed with Eq. (12).

As the full conditional distribution of $\pi _g$ in Eq. (14) is not of closed form, I resort to Metropolis-Hastings sampling techniques. For each node g the MCMC algorithm keeps the SNR-hyperparameter, $\delta _{g}$, and the allocation vector, ${\mathbf{V}}_{g}$, fixed, and proposes to move from the current parent node set, $\pi _{g}^{(i-1)}$, to a new set $\pi _{g}^{(\diamond )}$, where $\pi _{g}^{(\diamond )}$ is randomly chosen from the system $\mathcal {S}(\pi _{g}^{(i-1)})$ of all parent sets which can be reached (i) either by removing a single parent node from $\pi _{g}^{(i-1)}$, (ii) or by adding a single parent node to $\pi _{g}^{(i-1)}$, unless the maximal fan-in, $\mathcal {F}$, is reached, (iii) or by a parent-node flip move.⁷ According to the Metropolis Hastings criterion, the move is accepted with probability

$$\begin{aligned} A\left( \pi _{g}^{(i-1)}\rightarrow \pi _{g}^{(\diamond )}\right) = \min \left\{ 1, \frac{P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{\pi _g^{(\diamond )},{\mathbf{V}}_{g}},\delta _{g}\right) }{P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{\pi _g^{(i-1)},{\mathbf{V}}_{g}},\delta _{g}\right) } \times \frac{P\left( \pi _{g}^{(\diamond )}\right) }{P\left( \pi _{g}^{(i-1)}\right) }\times \frac{|\mathcal {S}\left( \pi _{g}^{(i-1)}\right) |}{|\mathcal {S}\left( \pi _{g}^{\diamond }\right) |} \right\} \nonumber \\ \end{aligned}$$

(15)

where the likelihood-ratio can be computed with Eq. (12), the prior ratio is equal to 1, and the Hastings-ratio is the ratio of the cardinalities of the two parent node set systems $\mathcal {S}(\pi _{g}^{(i-1)})$ and $\mathcal {S}(\pi _{g}^{\diamond })$.⁸ If the move is accepted, set: $\pi _{g}^{(i)}=\pi _{g}^{(\diamond )}$, or otherwise leave the set unchanged, $\pi _{g}^{(i)}=\pi _{g}^{(i-1)}$. Pseudo code for this Metropolis-Hastings step is given in Table 2. Given the current network, $\mathcal {M}^{(i-1)}=(\pi _1^{(i-1)},\ldots ,\pi _{N}^{(i-1)})$, successively updating the parent node sets, symbolically $\pi _g^{(i-1)}\rightarrow \pi _g^{(i)}$ ($g=1,\ldots ,N$), yields the new network $\mathcal {M}^{(i)}=(\pi _1^{(i)},\ldots ,\pi _{N}^{(i)})$.

Table 2 Pseudo-code for the MCMC inference of the parent node sets, $\pi _g$, in the free allocation Bayesian regression model shown in Fig. 1

2.3 Modelling the allocation vectors

In the last two subsections I have assumed that the allocation vectors are known and fixed, although they will be unknown in many real-world applications. The focus of this subsection is on inferring the allocation vectors from the data. A common choice in the context of dynamic Bayesian networks (DBNs) is the application of (node-specific) multiple changepoint processes to infer the segmentations; see references in Sect. 1.

Another approach, presented in Ko et al. (2007) and Grzegorczyk et al. (2008), is to combine DBNs with a mixture model. The mixture approach is more flexible, as it allows for a free allocation of the data points. E.g. for 11 data points and 3 mixture components the allocation scheme $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,3,2,3,1,2,2,1,1]$ for the last 10 data points is valid. The changepoint approach imposes sets of changepoints to divide the temporal data points into disjunct segments. Since temporal observations follow a natural time ordering and a priori neighbouring time points should be more likely to be allocated to the same component than distant time points, the changepoint approach includes plausible prior knowledge. However, changepoint approaches have a restricted allocation space, since data points in different segments have to be allocated to different components; i.e. “a (segment) component once left cannot be revisited”. Consequently, certain allocation schemes can only be approximated by imposing additional changepoints, e.g. in this example the true allocation scheme $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,1,2,2,2,1,1,1,1]$ cannot be modelled properly with changepoints; the best changepoint set approximation might be: $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,1,2,2,2,3,3,3,3]$. The mixture model, on the other hand, can infer the correct allocation, but it ignores the temporal ordering of the data points. That is, it treats the temporal data points (time points) as interchangeable units. This information loss implies in this example that all ${10 \atopwithdelims ()3}$ allocation vectors, which allocate seven time points to component $k=1$ and three time points to component $k=2$, are a priori equally likely; including allocation schemes, such as $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,2,1,1,1,2,1,1,2,1]$, which might be very unlikely a priori.

A compromise between the mixture model and the changepoint process is a hidden Markov model (HMM). In HMMs there is a homogeneous Markovian dependency between the allocations of the data points. In a Markov chain of order $\tau =1$ the allocation (state) of the tth data point given the states of all earlier time points $2,3,4,\ldots ,t-1$ just depends on the state of the immediately preceding time point $t-1$. Moreover, in a homogeneous Markov chain these transition probabilities stay constant over time, i.e. they do not depend on t. The homogeneous state-transition probabilities can be chosen such that neighbouring points are likely to be allocated to the same state, and states once left can be revisited. In this subsection I show how to employ a HMM for the allocation vectors, ${\mathbf{V}}_{g}$.

I model the allocation vectors, ${\mathbf{V}}_{g}$, for each node, $g$, independently with a HMM. In a first step I impose a truncated Poisson distribution with parameter $\lambda$ on the number of states (components). For $\mathcal {K}_g=1,\ldots ,\mathcal {K}_{\textit{MAX}}$ this yields:

$$\begin{aligned} P\left( \mathcal {K}_g\right) = Poi\left( \mathcal {K}_g|\lambda ,1\le \mathcal {K}_g\le \mathcal {K}_{\textit{MAX}}\right) \propto \frac{ \lambda ^{\mathcal {K}_g} \cdot e^{-\lambda }}{\mathcal {K}_g !} \end{aligned}$$

(16)

Afterwards, I impose a HMM with $\mathcal {K}_g$ states on the allocation vector, ${\mathbf{V}}_{g}$. The allocation vector can be identified with the temporally ordered sequence $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(T)]$ and its probability is the probability of the sequence: $P({\mathbf{V}}_g|\mathcal {K}_g) = P({\mathbf{V}}_g(2),\ldots ,{\mathbf{V}}_g(T)|\mathcal {K}_g)$. Assuming a Markovian dependency of order $\tau =1$ for the state sequence, this leads to:

$$\begin{aligned} P\left( {\mathbf{V}}_g|\mathcal {K}_g\right) = P\left( {\mathbf{V}}_g(2)|\mathcal {K}_g\right) \prod _{t=3}^{T} P\left( {\mathbf{V}}_g(t)|{\mathbf{V}}_g(t-1),\mathcal {K}_g\right) \end{aligned}$$

(17)

For $t=3,\ldots ,T$ let $p^g_{k,j}$ denote the probability for a transition from state k to state j:

$$\begin{aligned} p^g_{k,j} = P\left( {\mathbf{V}}_{g}(t)=j|{\mathbf{V}}_{g}(t-1)=k,\mathcal {K}_g\right) \end{aligned}$$

(18)

This gives $\sum _{j=1}^{\mathcal {K}_g} p^g_{k,j}=1$ and the probability vectors ${\mathbf{p}}^g_k=(p^g_{k,1},\ldots ,p^g_{k,\mathcal {K}_g})^{\mathsf{T}}$ define categorical (or multinomial) random variables ($k=1,\ldots ,\mathcal {K}_g$). On ${{ \mathbf V}}_g(2)$ I impose a discrete uniform distribution with the possible outcomes $\{1,\ldots ,\mathcal {K}_g\}$. The probability of the sequence $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(T)]$ conditional on $\{{\mathbf{p}}^g_k \}_{k}=\{{\mathbf{p}}^g_k \}_{k=1,\ldots ,\mathcal {K}_g}$ is then given by:

$$\begin{aligned} P\left( {\mathbf{V}}_{g}|\left\{ {\mathbf{p}}^g_k\right\} _k\right) = \frac{1}{\mathcal {K}_g}\prod _{k=1}^{\mathcal {K}_g} \prod _{j=1}^{\mathcal {K}_g} \left( p^g_{k,j}\right) ^{n_{k,j}} \end{aligned}$$

(19)

where $n_{k,j} = | \{t| 3\le t\le T\wedge {\mathbf{V}}_{g}(t) = j \wedge {\mathbf{V}}_{g}(t-1) = k \}|$ is the number of transitions from state k to state j in the sequence $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(T)]$. For $k=1,\ldots \mathcal {K}_g$ I impose a Dirichlet distribution with hyperparameter vector ${\varvec{\alpha }}_k = (\alpha _{k,1},\ldots ,\alpha _{k,\mathcal {K}_g})^{\mathsf{T}}$ on ${\mathbf{p}}^g_k$:

$$\begin{aligned} P\left( {\mathbf{p}}^g_k\right) = Dir({\mathbf{p}}^g_k|{{\varvec{\alpha }}}_k) = \frac{\prod _{j=1}^{\mathcal {K}_g} \Gamma \left( \alpha _{k,j}\right) }{\Gamma \left( \sum _{j=1}^{\mathcal {K}_g} \alpha _{k,j}\right) }\prod _{j=1}^{\mathcal {K}_g} \left( p^g_{k,j}\right) ^{\alpha _{k,j}-1} \end{aligned}$$

(20)

Marginalizing over the set $\{{\mathbf{p}}^g_k\}_k$ in Eq. (19) gives the marginal distribution:

$$\begin{aligned} P\left( {\mathbf{V}}_{g}|\mathcal {K}_g\right) = \int _{\left\{ {\mathbf{p}}^g_k\right\} _k} P\left( {\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(T)|\left\{ {\mathbf{p}}^g_k\right\} \}_k\right) \cdot P\left( \left\{ {\mathbf{p}}^g_k\right\} _k\right) d\left\{ {\mathbf{p}}^g_k\right\} _k \end{aligned}$$

(21)

With independently distributed random vectors ${\mathbf{p}}^g_k$, $P(\{{\mathbf{p}}^g_k\}_k) = \prod _{k=1}^{\mathcal {K}_g} P({\mathbf{p}}^g_k)$, where $P({\mathbf{p}}^g_k)$ was defined in Eq. (20), the integral in Eq. (21) is effectively a product integral. Inserting Eq. (19) into Eq. (21) yields:

$$\begin{aligned} P({\mathbf{V}}_{g}|\mathcal {K}_g) = \frac{1}{\mathcal {K}_g} \prod _{k=1}^{\mathcal {K}_g} \left( \int _{{\mathbf{p}}^g_k} P({\mathbf{p}}^g_k) \prod _{j=1}^{\mathcal {K}_g} \left( p^g_{k,j}\right) ^{n_{k,j}}d{\mathbf{p}}^g_k\right) \end{aligned}$$

(22)

The inner integrals correspond to Dirichlet-multinomial distributions, which can be computed in closed form. This yields:

$$\begin{aligned} P\left( {\mathbf{V}}_g|\mathcal {K}_g\right) = \frac{1}{\mathcal {K}_g} \prod _{k=1}^{\mathcal {K}_g} \frac{\Gamma \left( \sum _{j=1}^{\mathcal {K}_g} \alpha _{k,j} \right) }{\Gamma \left( \sum _{j=1}^{\mathcal {K}_g} n_{k,j} + \alpha _{k,j}\right) } \prod _{j=1}^{\mathcal {K}_g} \frac{\Gamma \left( n_{k,j}+\alpha _{k,j}\right) }{\Gamma \left( \alpha _{k,j}\right) } \end{aligned}$$

(23)

In the absence of any genuine prior knowledge about the state-transition probabilities, $p_{k,j}^g$, I set $\alpha _{k,j}=\alpha$ in Eq. (20). The marginal distribution $P({\mathbf{V}}_g|\mathcal {K}_g)$ in Eq. (23) is then invariant to permutations of the states’ labels.

2.4 The proposed HMM–DBN model

The proposed Hidden Markov model (HMM) dynamic Bayesian network (DBN) model, which I refer to as the HMM–DBN model, is now fully specified. A compact representation of the relationships among the data and all (hyper-)parameters of the HMM–DBN model is given in Fig. 2. Figure 2 adds flexible parent node sets and allocation vectors along with their prior distributions to Fig. 1. Unlike the earlier Bayesian regression DBN model, shown in Fig. 1, the parent node sets and the allocation vectors are now flexible and have to be inferred. The joint posterior distribution of the HMM–DBN model is given by:

$$\begin{aligned} P\left( \mathcal {M},{\mathbf{V}}_1,\ldots ,{\mathbf{V}}_{N},\delta _1,\ldots ,\delta _{N},\mathcal {K}_1,\ldots ,\mathcal {K}_{N}|\mathcal {D}\right) = \prod _{g=1}^{N} P\left( \pi _g,{\mathbf{V}}_g,\mathcal {K}_g,\delta _g|\mathcal {D}\right) \end{aligned}$$

(24)

where $\mathcal {M}=(\pi _1,\ldots ,\pi _{N})$, and

$$\begin{aligned} P\left( \pi _g,{\mathbf{V}}_g,\mathcal {K}_g,\delta _g|\mathcal {D}\right) \propto P(\delta _g) P(\pi _g) P\left( \mathcal {K}_g\right) P\left( {\mathbf{V}}_g|\mathcal {K}_g\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{g,{\mathbf{V}}_{g}},\delta _g\right) \end{aligned}$$

(25)

In the latter equation $\mathcal {K}_g$ is the number of possible states (components) for the gth allocation vector, ${\mathbf{V}}_g$, which implies the target vector segmentation, $\mathbf{y}_{g,{\mathbf{V}}_{g}}=\{\mathbf{y}_{g,1},\ldots ,\mathbf{y}_{g,\mathcal {K}_g} \}$, and the segmentation of the regressor matrices, $\mathbf{X}_{\pi _g,{\mathbf{V}}_{g}} =\{\mathbf{X}_{\pi _g,1},\ldots ,\mathbf{X}_{\pi _g,\mathcal {K}_g}\}$. The marginal likelihood, $P(\mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{g,{\mathbf{V}}_{g}},\delta _g)$, can be computed with Eq. (12).

Fig. 2

Compact representation of the proposed HMM–DBN model. The graphical model in Fig. 1 has been extended by additional fixed (grey circles) and free (white circles) (hyper-)parameters. Detailed descriptions of the HMM–DBN model are provided in Sects. 2.1–2.3

With regard to the MCMC inference, described in Sect. 2.5, note that the posterior distribution in Eq. (24) is invariant (to permutations of the states’ labels), as the marginal likelihood in Eq. (12) and the priors on the allocation vector in Eq. (23) (if $\alpha _{k,j}=\alpha$) are invariant. For Bayesian mixture models with invariant posterior distributions it is challenging to infer the component-specific model parameters, since their marginal posterior distributions are identical. There is a so called “non-identifiability problem” with respect to the components’ labels (see, e.g., Nobile and Fearnside 2007). For the HMM–DBN model the problem of non-identifiability has not be tackled, as the interest is not on state-specific parameters. Here, I am interested in the network structure, $\mathcal {M}$, and in the co-allocation of data points.⁹

2.5 Allocation vector inference

For the allocation vector inference, in principle, two different RJMCMC sampling strategies (Green 1995) can be employed. The first technique is to implement a RJMCMC approach in a continuous configuration space, where concrete instantiations of all free parameters of the Bayesian regression model (i.e. the white circles in Fig. 1) are sampled, before the forward-backward simulation algorithm (Boys et al. 2000) is used to sample the allocation vector from its full conditional distribution via a Gibbs sampling step. This RJMCMC approach for hidden Markov models has been proposed by Robert et al. (2000) and has become popular in various fields of applications, such as DNA sequence analysis (see, e.g., Boys and Henderson 2004). However, the disadvantage of this approach is that the variation of the number of hidden states, $\mathcal {K}_g$, requires the implementation of efficient RJMCMC moves which switch between models with different dimensionalities in continuous parameter spaces. Otherwise, the RJMCMC simulations may become computationally inefficient (see, e.g., Nobile and Fearnside 2007).

The second sampling strategy is based on RJMCMC moves in the discrete allocation vector configuration space. In this approach the numbers of states and the allocation vectors are sampled from the posterior distribution. This strategy can be used when all state-specific parameters can be integrated out analytically so that the marginal likelihood does not depend on state-specific continuous parameters.¹⁰ The main advantage of this second RJMCMC strategy is that the resulting sampling scheme does not require any particular trans-dimensional jumping moves in continuous configuration spaces. In the present paper I resort to this second RJMCMC sampling strategy, and I employ the “allocation sampler” (Nobile and Fearnside 2007) for the allocation vector inference. The allocation sampler was proposed by Nobile and Fearnside (2007) and has already been utilised in the context of mixture dynamic Bayesian networks (MIX-DBNs) in Grzegorczyk et al. (2008). The allocation sampler consists of a simple Gibbs sampling move and various more involved Metropolis-Hastings moves. The mathematical details are briefly summarised in the “Appendix”. In Appendix 1 I describe a simple Gibbs sampling move, which re-samples the allocation state of one single data point from the full conditional distribution. Since this type of move yields very small steps in the configuration space, Nobile and Fearnside (2007) proposed a set of more involved allocation sampler moves. In Appendix 2 I describe these allocation sampler moves, namely the M1, the M2, and the Ejection-Absorption (EA) move. However, the allocation sampler moves have been developed for free allocation models, where data points are treated as interchangeable units without any natural (here: temporal) arrangement. These moves are sub-optimal when a Markovian dependency structure among the (temporal) data points is given. In Sects. 2.5.1 and 2.5.2 I therefore propose two new pairs of Metropolis-Hastings moves, which exploit the temporal structure and thus improve convergence and mixing for the HMM–DBN model. While the conceptualization of the ideas behind these moves is relatively simple and intuitive, the mathematical implementation is involved, due to the need to ensure that the sampling scheme satisfies the equations of detailed balance and converges to the proper posterior distribution. In Appendices 3 and 4 I rigorously formulate the mathematical details, and I show for both pairs of moves that the two moves are complementary to each other. Hence, the acceptance probabilities can be chosen according to the Metropolis-Hastings criterion, so as to guarantee that the equation of detailed balance is fulfilled. Combining the SNR hyperparameter inference (see Table 1) and the network inference (see Table 2) with the moves on the allocation vectors yields the MCMC sampling scheme for generating a sample from the posterior distribution in Eq. (24). Table 3 shows how the sampling steps can be combined.

Table 3 Pseudo code for the MCMC sampling scheme

2.5.1 First pair of new HMM moves: the inclusion and the exclusion move

In this subsection I propose and verbally describe the novel inclusion and the novel exclusion move for the HMM–DBN model. For each exclusion move there is a unique complementary inclusion move, and vice-versa. The introduction of this pair of moves can be best motivated by a simple example: Given 11 time points and the allocation $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,2,2,1,1,1,2,2,2]$ for the last 10 data points. If there is a Markovian dependency structure, it appears to be useful to propose to re-allocate the coherent time sequence $[{\mathbf{V}}_{g}(4),{\mathbf{V}}_{g}(5)]=[2,2]$ to state $k=1$, since the surrounding earlier (lower) and later (higher) time points ($[{\mathbf{V}}_{g}(2),{\mathbf{V}}_{g}(3)]$ and $[{\mathbf{V}}_{g}(6),{\mathbf{V}}_{g}(7),{\mathbf{V}}_{g}(8)]$) are allocated to $k=1$. The inclusion move proposes to “include” the surrounded sequence $[{\mathbf{V}}_{g}(4),{\mathbf{V}}_{g}(5)]$ into the state of the surrounding data points. This gives the new allocation $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,1,1,1,1,1,2,2,2]$. Given the new allocation, the complementary exclusion move has to cut the subsequence $[{\mathbf{V}}_{g}(4),{\mathbf{V}}_{g}(5)]$ out of the coherent sequence $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(8)]$ to move back to the original allocation. To this end, the exclusion move selects the coherent sequence $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(8)]$ of data points that are allocated to the same state ($k=1$). Subsequently, it proposes to cut out a randomly selected subsequence, which is then “excluded”, i.e. it is cut out and re-allocated to a new state (here: $k=2$). To guarantee that there is a complementary inclusion move for each exclusion move, it is important to impose a constraint: The randomly selected subsequence is not allowed to include the two limiting data points; i.e. the lower limit ${\mathbf{V}}_{g}(2)$ and the upper limit ${\mathbf{V}}_{g}(8)$ in the example. In Appendix 3 I rigorously formulate the mathematical details, and I show that there is a unique exclusion move for each inclusion move, and vice-versa.

2.5.2 Second pair of new HMM moves: the birth and the death move

In this subsection I propose and verbally describe the novel death and the novel birth move for the HMM–DBN model. For each birth move there is a unique complementary death move, and vice-versa. The introduction of this pair of novel Metropolis-Hastings moves can be best motivated by a simple example: Given 11 time points and the allocation vector $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,1,1,1,1,1,1,1,1]$ for the last 10 data points, then it appears to be useful to impose a changepoint, which re-allocates the last data points to a new state $k=2$. For example, re-allocating the last four data points yields the new allocation vector $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,1,1,1,1,2,2,2,2]$. The birth move randomly selects a state k and re-allocates the last data points that are allocated to k to a new state $k_{new}$. Thereby the novel birth move also allows for moves, such as $[1,1,2,2,1,1,2,2,1,1]\rightarrow [1,1,2,2,1,3,2,2,3,3]$, where the last two data points that were allocated to state $k=1$ have been re-allocated to a new state $k_{new}=3$.

Given the new allocation vector, $[{\mathbf{V}}_{g}(2),\ldots ,{\mathbf{V}}_{g}(11)]=[1,1,2,2,1,3,2,2,3,3]$ the complementary death move has to re-allocate all data points that are allocated to state $k=3$ back to state $k=1$. To this end the death move selects the two states $k=1$ and $k=3$, and then tests whether the data points allocated to state $k=1$ and the data points allocated to state $k=3$ are “separated” (do not “overlap”). Formally, I will say that the two sets $T_1=\{t:{\mathbf{V}}_g(t)=1\}$ and $T_3=\{t:{\mathbf{V}}_g(t)=3\}$ are separated if and only if: $\max (T_1)<\min (T_3)$ or $\min (T_1)>\max (T_3)$. If the “separation test” is successful, the death move is valid and can be performed. In the example, the highest time point allocated to $k=1$, namely $t=5$, precedes the lowest time point allocated to $k=3$, namely $t=6$, so that the “test for separation” is successful and the death move is valid. This formal test for separation is required, since otherwise the new allocation vector could not have been reached by the novel birth move, described above. In Appendix 4 I rigorously formulate the mathematical details, and I show that there is a unique novel death move for each novel birth move, and vice-versa.

2.6 Competing dynamic Bayesian network models

I will perform a systematic comparative evaluation, in which I compare the proposed HMM–DBN model with three competing DBN models. The traditional homogeneous DBN model (HOM-DBN) is described in Sect. 2.6.1, and in Sects. 2.6.2 and 2.6.3 the free allocation mixture DBN model (MIX-DBN) and the changepoint-segmented DBN model (CPS–DBN) are briefly summarised. An overview to the models is given in Table 4.

Table 4 Overview to the four (non-)homogeneous dynamic Bayesian network models

2.6.1 The conventional homogeneous DBN model (HOM-DBN)

In the homogeneous DBN model the network interactions do not vary over time. There is only one single state, $\mathcal {K}_g=1$, for each node g and the allocation vectors assign all data points to state 1, ${\mathbf{V}}_{g}=(1,\ldots ,1)^{\mathsf{T}}$. The HOM-DBN is a special case of the HMM–DBN model, where $\mathcal {K}_g$ and ${\mathbf{V}}_g$ are fixed and non-adaptable. In Fig. 2 the nodes ${\mathbf{V}}_{g}$ and $\mathcal {K}_g$ become fixed (grey), and the nodes for $\alpha ^g_k$, ${\mathbf{p}}^g_k$, $\mathcal {K}_g$, $\lambda$, and $\mathcal {K}_{\textit{MAX}}$ can be removed. The HOM-DBN model can be inferred with the MCMC sampling scheme in Table 3, but the allocation vector moves have to be left out, as $\mathcal {K}_g^{(i)}=1$ and ${\mathbf{V}}_g^{(i)}=(1,\ldots ,1)^{\mathsf{T}}$ for all i.

2.6.2 The non-homogeneous mixture DBN model (MIX-DBN)

The mixture DBN model (MIX-DBN) combines the traditional DBN model with a free allocation mixture model. As for the HMM–DBN model, I assume that the numbers of mixture components follow truncated Poisson distributions, $P(\mathcal {K}_g)\propto Poi(\lambda )$ for $1\le \mathcal {K}_g\le \mathcal {K}_{\textit{MAX}}$. And I impose a categorical (multinomial) distribution with hyperparameters ${\mathbf{p}}^g= (p^g_1,\ldots ,p^g_{\mathcal {K}_g})^{\mathsf{T}}$ on the components, $p^g_k := P({\mathbf{V}}_g(t)=k|\mathcal {K}_g)$ for all $t>2$. The probability of the allocation vector is then given by:

$$\begin{aligned} P\left( {\mathbf{V}}_{g}|{\mathbf{p}}^g\right) = \prod _{k=1}^{\mathcal {K}_g} \left( p^g_{k}\right) ^{n_{k}} \end{aligned}$$

(26)

where $n_{k} = |\{t| 2\le t\le T\wedge {\mathbf{V}}_{g}(t) = k \} |$ is the number of data points that are allocated to component k by ${\mathbf{V}}_g$. On ${\mathbf{p}}^g$ I impose a conjugate Dirichlet distribution with hyperparameters ${\varvec{\alpha }}=(\alpha _1,\ldots ,\alpha _{\mathcal {K}_g})^{\mathsf{T}}$, $P({\mathbf{p}}^g) = Dir({\mathbf{p}}^g|{\varvec{\alpha }})$. Marginalizing over ${\mathbf{p}}^g$ yields:

$$\begin{aligned} P\left( {\mathbf{V}}_g|\mathcal {K}_g\right) = \frac{\Gamma \left( \sum _{k=1}^{\mathcal {K}_g} \alpha _{k} \right) }{\Gamma \left( \sum _{k=1}^{\mathcal {K}_g} \left( n_{k} + \alpha _{k}\right) \right) } \prod _{k=1}^{\mathcal {K}_g} \frac{\Gamma \left( n_{k}+\alpha _{k}\right) }{\Gamma (\alpha _{k})} \end{aligned}$$

(27)

For $\alpha _k = \alpha$ the posterior distribution of the MIX-DBN model becomes invariant to permutations of the components’ labels. The MIX-DBN model can be inferred with the MCMC sampling scheme in Table 3, but exclusively allocation sampler moves can be performed on ${\mathbf{V}}_g$. The moves from Sects. 2.5.1 and 2.5.2 cannot be used, as the MIX-DBN model treats the data points as interchangeable units (without any ordering). If the allocation sampler moves, described in Appendix 2, are performed, the terms $P({\mathbf{V}}_g|\mathcal {K}_g)$ in the acceptance probabilities have to be computed with Eq. (27) instead of Eq. (23).

2.6.3 The non-homogeneous changepoint DBN model (CPS–DBN)

The changepoint DBN model (CPS–DBN) combines the traditional DBN model with a multiple changepoint process. As before, I assume that $\mathcal {K}_g$ follows a truncated Poisson distribution, $P(\mathcal {K}_g)\propto Poi(\lambda )$ for $1\le \mathcal {K}_g\le \mathcal {K}_{\textit{MAX}}$. I identify $\mathcal {K}_g$ with $\mathcal {K}_{g}-1$ changepoints $b_{g,1},\ldots ,b_{g,\mathcal {K}_{g}-1}$ on the set $\left\{ 2,\ldots ,T-1\right\}$. For node g this yields: ${\mathbf{V}}_g(t)=k$ if and only if $b_{g,k-1}< t \le b_{g,k}$, where $b_{g,0}:=1$ and $b_{g,\mathcal {K}_g}:=T$. Following Green (1995) I assume that the changepoints are distributed as the even-numbered order statistics of $\mathcal {L}:=2(\mathcal {K}_{g}-1)+1$ points uniformly and independently distributed on the set $\left\{ 2,\ldots ,T-1\right\}$. This induces the following prior distribution on the allocation vectors:

$$\begin{aligned} P\left( \mathbf{V}_{g}|\mathcal {K}_g\right) = \frac{1}{\left( \begin{array}{c} T-2 \\ 2\left( \mathcal {K}_{g}-1\right) +1 \end{array} \right) } \prod _{k=0}^{\mathcal {K}_g-1} \left( b_{g,k+1} - b_{g,k} -1\right) \end{aligned}$$

(28)

The allocation vectors can be inferred via changepoint birth, death and re-allocation moves along the lines of the RJMCMC algorithm of Green (1995).

The changepoint reallocation move from ${\mathbf{V}}_g^{(i-1)}$ to ${\mathbf{V}}_g^{\star }$ randomly selects one changepoint $b_{g,j}$ from the changepoint set, $\{b_{g,1},\ldots ,b_{g,\mathcal {K}_{g}^{(i-1)}-1}\}$, induced by ${\mathbf{V}}_g^{(i-1)}$. The replacement changepoint is randomly drawn from the set $\left\{ b_{g,j-1}+2,\ldots ,b_{g,j+1}-2\right\}$. This yields the new candidate allocation vector ${\mathbf{V}}_g^{\star }$, and $\mathcal {K}^{\star } = \mathcal {K}^{(i-1)}$.

The changepoint birth move from $[{\mathbf{V}}_g^{(i-1)},\mathcal {K}_{g}^{(i-1)}]$ to $[{\mathbf{V}}_g^{\star },\mathcal {K}_{g}^{\star }]$ randomly draws the location of one single new changepoint from the set of all valid new changepoint locations:

$$\begin{aligned} B^{\dagger } :=\left\{ b: 2\le b \le T-1 \wedge \forall j\in \left\{ 1,\ldots ,\mathcal {K}_{g}^{(i-1)}-1 \right\} : |b-b_{g,j}|>1 \right\} \end{aligned}$$

(29)

Adding the new changepoint to the changepoint set yields ${\mathbf{V}}_{g}^{\star }$, and $\mathcal {K}_g^{\star } = \mathcal {K}_g^{(i-1)}+1$.

The changepoint death move from $[{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_{g}^{(i-1)}]$ to $[{\mathbf{V}}_{g}^{\star },\mathcal {K}_{g}^{\star }]$ is complementary to the birth move. It randomly selects one of the changepoints induced by ${\mathbf{V}}_{g}^{(i-1)}$ and delets it. ${\mathbf{V}}_{g}^{\star }$ is the new candidate allocation vector after deletion, and $\mathcal {K}_g^{\star } = \mathcal {K}_g^{(i-1)}-1$.

The acceptance probabilities for these moves are given by $A=\min \{1,R\}$, with

$$\begin{aligned} R = \frac{P(\mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g)}{P(\mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g)} \cdot \frac{P({\mathbf{V}}_{g}^{\star }|\mathcal {K}_g^{\star })P(\mathcal {K}_g^{\star })}{P({\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}_g^{(i-1)}) P(\mathcal {K}_g^{(i-1)})} \cdot Q \end{aligned}$$

(30)

where Q is the Hastings ratio, which can be computed for each of the three changepoint move types (see, e.g., Green 1995). If the move is accepted, set ${\mathbf{V}}_{g}^{(i)}={\mathbf{V}}_{g}^{\star }$ and $\mathcal {K}_{g}^{(i)}=\mathcal {K}_{g}^{\star }$, or otherwise set: ${\mathbf{V}}_{g}^{(i)}={\mathbf{V}}_{g}^{(i-1)}$ and $\mathcal {K}_{g}^{(i)}=\mathcal {K}_{g}^{(i-1)}$.

The CPS–DBN model can be inferred with the MCMC sampling scheme described in Table 3, but the moves on the allocation vectors have to be replaced by the changepoint birth, death and re-allocation moves, described in this subsection.

I also include the globally coupled variant of the CPS–DBN model, proposed in Grzegorczyk and Husmeier (2012b) and Grzegorczyk and Husmeier (2013), in my comparative evaluation study. The key idea is to hierarchically couple the segment-specific regression parameter vectors, ${\mathbf{w}}_{g,k}$, in Eq. (2) to allow for information-sharing with respect to the regression parameters. In the coupled CPS–DBN model Eq. (2) is replaced by $P(\mathbf{w}_{g,k}|\sigma _{g}^2,\delta _{g}) = \mathcal {N}(\mathbf{w}_{g,k}|{\mathbf{m}}_{g},\delta _{g} \sigma ^2_{g} {\mathbf{I}})$, and the mean vector, ${\mathbf{m}}_{g}$, is now a flexible hyperparameter and has a multivariate standard Gaussian distribution, symbolically: ${\mathbf{m}}_{g,k}\sim \mathcal {N}({\mathbf{0}}, {\mathbf{I}})$; see, e.g., Grzegorczyk and Husmeier (2013) for the mathematical details. However, as the coupled CPS–DBN model is not in the primary scope of the present paper, I focus on the standard CPS–DBN model and discuss the results of the coupled CPS–DBN model only casually.

2.7 Network-wide (shared) allocation vectors

The non-homogeneous DBN models have been formulated with node-specific allocation vectors, ${\mathbf{V}}_g$ ($g=1,\ldots ,N$). That is, the allocations vary from node to node, and have to be inferred independently for each node g. This gives very flexible DBN models. For applications where all nodes are a priori expected to share the same segmentation the node-specific allocation vectors can be replaced by a network-wide allocation vector, which is then shared by all nodes, ${\mathbf{V}}_g = {\mathbf{V}}$ and $\mathcal {K}_g = \mathcal {K}$ for all g. For network-wide allocation vectors the moves from Sect. 2.5 have to be adapted. The probability terms $P(\mathcal {K}_g)$ and $P({\mathbf{V}}_g|\mathcal {K}_g)$ have to be replaced by $P(\mathcal {K})$ and $P({\mathbf{V}}|\mathcal {K})$, respectively. And each allocation vector change, ${\mathbf{V}}^{(i-1)}\rightarrow {\mathbf{V}}^{\star }$, applies to all nodes. The marginal likelihood terms (e.g. in the acceptance probabilities), $P(\mathbf{y}_{g,{\mathbf{V}}_{g}}|\mathbf{X}_{g,{\mathbf{V}}_{g}},\delta _g)$, have to be replaced by product terms: $\prod _{g=1}^{N}P(\mathbf{y}_{g,{\mathbf{V}}}|\mathbf{X}_{g,{\mathbf{V}}},\delta _g)$.

The usage of network-wide allocation vectors imposes a substantial restriction on the configuration space of the allocations. The underlying allocation vector can then be inferred more accurately, as conceptual problems associated with model over-flexibility (data-overfitting) are alleviated.

2.8 Marginal edge posterior probabilities

The MCMC sampling scheme for the HMM–DBN model is outlined in Table 3, and in Sects. 2.6.1–2.6.3 I provide details on how to modify this scheme for the competing models. I perform 200I iterations in total, and to avoid autocorrelations in the MCMC trajectories I take samples in equidistant intervals (every 100th iteration). From the sample of length 2I I withdraw the first I samples to allow for a “burn-in phase”, and I keep the remaining sample of length I: $\{\mathcal {M}^{(i)},{\mathbf{V}}_1^{(i)},\ldots ,{\mathbf{V}}_{N}^{(i)},\delta _1^{(i)},\ldots ,\delta _{N}^{(i)}\}_{i=I+1,\ldots ,2I}$. From the networks, $\mathcal {M}^{(I+1)},\ldots ,\mathcal {M}^{(2I)}$, I compute marginal edge posterior probabilities. The estimated marginal posterior probability of the edge from node n to node j ($n,j\in \{1,\ldots ,N$}) is:

$$\begin{aligned} e_{n,j} = \frac{1}{I} \sum _{i=I+1}^{2\cdot I} \mathcal {M}^{(i)}(n,j) \end{aligned}$$

(31)

where $\mathcal {M}^{(i)}(n,j)$ is 1 if $\mathcal {M}^{(i)}$ contains the edge $n\rightarrow j$, and 0 otherwise.

I also estimate the marginal posterior probabilities, $C_{s,t}^g$, of two data points s and t ($s,t\in \{2,\ldots ,T\}$) being assigned to the same state by the allocation ${\mathbf{V}}_g$:

$$\begin{aligned} \widehat{C}^g_{s,t} = \frac{1}{I} \cdot \left| \left\{ i: i\in \left\{ I+1,\ldots ,2I\right\} \wedge {\mathbf{V}}_g^{(i)}(s)={\mathbf{V}}_g^{(i)}(t) \right\} \right| \end{aligned}$$

I will refer to $\widehat{{\mathbf{C}}}^g = (\widehat{C}^g_{s,t})_{s,t\in \{2,\ldots ,T\}}$ as the estimated connectivity (co-allocation) matrix.

2.9 Criterions for quantifying the network reconstruction accuracy

If the true network, $\mathcal {M}^{\ddagger }$, is known, I evaluate the network reconstruction accuracy in terms of the areas under the precision recall curve. Let $\mathcal {M}^{\ddagger }(n,j)=1$ indicate that $\mathcal {M}^{\ddagger }$ possesses the edge from node n to node j, while $\mathcal {M}^{\ddagger }(n,j)=0$ indicates that the edge $n\rightarrow j$ is not in $\mathcal {M}^{\ddagger }$. The models yield marginal edge posterior probabilities $e_{n,j}\in [0,1]$ for every possible edge $n\rightarrow j$. For $\zeta \in [0,1]$ I define $E(\zeta )$ as the set of all edges whose posterior probabilities exceed the threshold $\zeta$. For each $E(\zeta )$ the number of true positive $TP[\zeta ]$, false positive $FP[\zeta ]$, and false negative $FN[\zeta ]$ edges can be counted, and the recall, $\mathcal {R}[\zeta ] = TP[\zeta ]/(TP[\zeta ]+FN[\zeta ])$, and the precision, $\mathcal {P}[\zeta ]=TP[\zeta ]/(TP[\zeta ]+FP[\zeta ])$, score can be computed.¹¹ Plotting the $\mathcal {P}[\zeta ]$ values (vertical axis) against the corresponding $\mathcal {R}[\zeta ]$ values (horizontal axis) and connecting neighbouring points by a nonlinear interpolation (Davis and Goadrich 2006) gives the Precision-Recall (PR) curve. The area under the PR curve (AUC-PR) is a quantitative measure, and can be obtained by numerically integrating the PR curve; larger AUC-PR values indicate a better network reconstruction accuracy. Another measure for the network reconstruction accuracy is the area under the receiver operator characteristic curve (AUC-ROC). I employ AUC-ROC values only to confirm that all trends in terms of the AUC-PR measure can also be obtained with the AUC-ROC measure; for details on AUC-ROC scores see Davis and Goadrich (2006).

2.10 Potential scale reduction factors (PSRFs) for network edges

The diagnostic that I apply to evaluate convergence, proposed in Grzegorczyk and Husmeier (2011), is based on the potential scale reduction factors (PSRFs); see Brooks and Gelman (1998) for details. I assume that H independent MCMC simulations, with 200I iterations each, have been performed on the same data set. I set $I=500$, and to monitor the PSRFs for the number of MCMC iterations I compute the marginal edge posterior probabilities for each simulation $h=1,\ldots ,H$ after 200s iterations ($s=1,2,\ldots ,I$). Let $e_{n,j}^{[h,s]}$ denote the probability of the edge $n\rightarrow j$ obtained with MCMC simulation h after 200s iterations, where s equidistant samples (every 100th iteration) are taken after the burn in phase of length 100s. For $s=1,\ldots ,I$ I compute the “between-chain” and the “within-chain” variance:

$$\begin{aligned} \mathcal {B}_{s}(n,j)= & {} \frac{1}{H-1} \sum _{h=1}^{H} \left( e_{n,j}^{[h,s]} - \overline{e}_{n,j}^{[.,s]}\right) ^2\end{aligned}$$

(32)

$$\begin{aligned} \mathcal {W}_{s}(n,j)= & {} \frac{1}{H(s-1)} \sum _{h=1}^{H} \sum _{i=1}^{s} \left( \mathcal {M}^{(i,h)}(n,j) - e_{n,j}^{[h,s]}\right) ^2 \end{aligned}$$

(33)

where $\overline{e}_{n,j}^{[.,s]}$ is the mean of $e_{n,j}^{[1,s]},\ldots ,e_{n,j}^{[H,s]}$, and $\mathcal {M}^{(i,h)}(n,j)$ is 1 if the ith network in the sample, taken from the hth simulation, contains the edge $n\rightarrow j$, and 0 otherwise. Following Brooks and Gelman (1998) the ${\textit{PSRF}}_{s}(n,j)$ of the edge $n\rightarrow j$ is given by:

$$\begin{aligned} {\textit{PSRF}}_{s}(n,j) =\frac{\left( 1-\frac{1}{s}\right) \mathcal {W}_{s}(n,j) +\left( 1+\frac{1}{H}\right) \mathcal {B}_{s}(n,j)}{\mathcal {W}_{s}(n,j)} \end{aligned}$$

(34)

where PSRF values near 1 indicate that the MCMC simulations are close to the stationary distribution. I use as a PSRF-based convergence diagnostic the fraction of edges $\mathcal {C}(\xi ,s)$ whose PSRF is lower than a threshold $\xi$ (e.g. $\xi =1.1$ and $\xi =1.01$). The fractions $\mathcal {C}(\xi ,s)$ can be monitored against the numbers of MCMC iterations 200s.

3 Data

3.1 Simulated data from the RAF pathway

For the RAF pathway, shown in Fig. 3, I generate synthetic network data. I employ a function V, which assigns a state $k\in \{1,\ldots ,\mathcal {K}_g\}$ to each temporal data point $t=2,\ldots ,T$. $V(t)=k$ means that data point t is assigned to the kth state. For each interaction between a node, g, and its parent nodes, which are defined by the RAF pathway, I require regression parameter vectors, which vary over time. Data points that are assigned to the same state k share the same regression parameter vectors, while the regression parameters differ among states. Let ${\mathbf{w}}_{g,k}$ denote the regression parameter vector (including the intercept) for the interaction between node g and its parent nodes for all time points that are assigned to state k. I distinguish two sampling scenarios for sampling random regression parameter vector instantiations. The first sampling strategy (scenario S1) has recently been employed in Grzegorczyk and Husmeier (2012b) and Grzegorczyk and Husmeier (2013) and guarantees that all regression parameter vectors, ${\mathbf{w}}_{g,k}$, share the same amplitude, $|{\mathbf{w}}_{g,k}|_2=1$. The second sampling strategy (scenario S2), which has for example been employed in Werhli et al. (2006), guarantees that the absolute value of each single element of the regression coefficient vector is in between 0.5 and 2.

Fig. 3

The topology of the RAF pathway, as reported in Sachs et al. (2005). The RAF protein signalling transduction pathway consists of 11 proteins (pip3, plcg, pip2, pkc, p38, raf, pka, jnk, mek, erk, and act) and the edges represent protein interactions

Sampling scenario (S1) For each node $g\in \{1,\ldots ,N\}$ and each state $k\in \{1,\ldots ,\mathcal {K}\}$, I sample random vectors from standard multivariate Gaussian distributed vectors, ${\mathbf{w}}_{g,k}^{\dagger }\sim \mathcal {N}({\mathbf{0}},{\mathbf{I}})$, and I normalize these random vectors to obtain regression parameter vectors, ${\mathbf{w}}_{g,k}$ of Euclidean norm (amplitude) one: ${\mathbf{w}}_{g,k}={\mathbf{w}}_{g,k}^{\dagger }/|{\mathbf{w}}_{g,k}^{\dagger }|_2$.

Sampling scenario (S2) For each node $g\in \{1,\ldots ,N\}$ and each state $k\in \{1,\ldots ,\mathcal {K}\}$, I sample each element of the regression parameter vector, ${\mathbf{w}}_{g,k}$, independently from a continuous uniform distribution on the interval [0.5, 2], and for each element (regression coefficient) I afterwards draw a coin to determine its sign.

As strategy (S2) yields higher amplitudes, $|{\mathbf{w}}_{g,k}|_2$, on average, I employ this sampling scenario when I compare the DBN models with node specific allocation vectors. For the DBN models with shared allocation vectors, ${\mathbf{V}}_g = {\mathbf{V}}$ for all g, I follow strategy (S1).¹²

Given the sampled regression parameter vectors, ${\mathbf{w}}_{g,k}$, which either stem from S1 or from S2, concrete data set instantiations, $\mathcal {D}$, can be generated. Let $\mathcal {D}_{g,t}$ denote the observation for node g at time point t. For the first time point, $t=1$, I sample the realisations of the $N=11$ nodes from independent univariate Gaussian distributions, $\mathcal {D}_{g,1}\sim \mathcal {N}(0,1)$ for all g. Afterwards, I generate realisations for $t=2,\ldots ,T$:

$$\begin{aligned} \mathcal {D}_{g,t} = \left( 1,\mathcal {D}_{\pi _g,t-1}^{\mathsf{T}}\right) {\mathbf{w}}_{g,V(t)} + \epsilon _{g,t} \end{aligned}$$

(35)

where $\mathcal {D}_{\pi _g,t-1}$ is the vector of the realisations of gth parent nodes at the previous time point $t-1$, the function V(.) assigns each data point t to a state $k\in \{1,\ldots ,\mathcal {K}_g\}$, and the noise variables $\epsilon _{g,t}$ are independently standard Gaussian distributed, $\epsilon _{g,t}\sim N(0,1)$. The element 1 is included for the intercept.

For each data set instantiation, $\mathcal {D}$, I add additive white noise in a gene-wise manner to vary the signal-to-noise ratio (SNR). For each node, g, I compute the standard deviation, $s_g$, of its $T$ realisations, $\mathcal {D}_{g,1},\ldots ,\mathcal {D}_{g,T}$, and I add i.i.d. Gaussian noise with zero mean and standard deviation SNR$^{-1}\cdot s_g$ to each data point, where SNR is the pre-defined signal-to-noise ratio level. That is, I substitute $\mathcal {D}_{g,t}$ for $\mathcal {D}_{g,t} + v_{g,t}$ ($t=1,\ldots ,T$), where $v_{g,1},\ldots ,v_{g,T}$ are realisations of i.i.d. $\mathcal {N}(0,(SNR^{-1}\cdot s_g)^2)$ variables. I distinguish five signal-to-noise ratio levels: SNR$\,=\,$16, SNR$\,=\,$8, SNR$\,=\,$4, SNR$\,=\,$2, and SNR$\,=\,$1.

The focus of my study is on different allocation schemes, i.e. different functions $V:\{1,\ldots ,T\}\rightarrow \{1,\ldots ,\mathcal {K}\}$. I assume that each data set consists of an initial first data point followed by H equidistant segments, $h=1,\ldots ,H$, and that each segment h comprises $T_{\star }=8$ coherent time points. For example, for $H=4$ the data set contains $T=1+H\cdot T_{\star }$=33 temporal data points, and the coherent time points in $\{2,\ldots ,9\}$, $\{10,\ldots ,17\}$, $\{18,\ldots ,25\}$, and $\{26,\ldots ,33\}$ correspond to the four segments $h=1,\ldots ,4$. The time points belonging to the same segment are always assigned to the same state k, while different segments can be assigned to different states. For notational convenience, I introduce boldface-symbols to indicate the true allocation scheme. Let $\mathbf{k}$ denote the row vector $(k,\ldots ,k)$ of length $H_{\star }=8$ ($k=1,\ldots ,\mathcal {K}$). For example, to indicate an allocation vector ${\mathbf{V}}_g$ that assigns the segments $h=1$ and $h=3$ to state $k=1$, and the segments $h=2$ and $h=4$ to state $k=2$, it can then be written compactly:

$$\begin{aligned} \left[ {\mathbf{V}_g(2),\ldots ,{\mathbf{V}}_g(33)}\right] = \left[ \underbrace{1,\ldots ,1}_{8 \times },\underbrace{2,\ldots ,2}_{8 \times },\underbrace{1,\ldots ,1}_{8 \times },\underbrace{2,\ldots ,2}_{8 \times }\right] =: \mathbf{1212}. \end{aligned}$$

Furthermore, let the symbol “MIX” indicate an allocation scheme that does not consist of segments, but assigns each of the states $k\in \{1,\ldots ,\mathcal {K}\}$ to $T_{\star }=(T-1)/\mathcal {K}$ randomly selected data points. For example, for $T=33$ and $\mathcal {K}=2$ I divide the time point set $\{2,\ldots ,T\}$ randomly into two disjunct subsets, consisting of $T_{\star }=16$ data points each. Then I assign the state $k=1$ to the data points in the first subset, and the state $k=2$ to the data points in the second subset. An overview to the allocation schemes that I employ in my study is given in Table 5. For each of the nine allocation schemes I distinguish five SNR levels, and I generate 20 independent data instantiations for each combination of allocation scheme and SNR level; i.e. $9\times 5\times 20=900$ data sets in total.

Table 5 Overview to the allocation scheme of the synthetic network data sets

3.2 Synthetic biology in Saccharomyces cerevisiae

A popular benchmark gene expression data set for non-homogeneous DBN models has been provided by Cantone et al. (2009). The authors synthetically designed a small network in Saccharomyces cerevisiae (yeast). This network, consisting of $N=5$ genes, is depicted in the right panel of Fig. 10. The authors measured expression levels of these genes in vivo with quantitative real-time Polymerase Chain Reaction at 37 time points over 8 h. During the experiment Cantone et al. (2009) changed the carbon source from galactose to glucose.¹³ As 16 measurements were taken in galactose and 21 measurements were taken in glucose, there are the following observations for each node g: $D_{g,1}^{gal},\ldots ,D_{g,16}^{gal},D_{g,1}^{glu},\ldots ,D_{g,21}^{glu}$. The first measurements in galactose and glucose, $D_{g,1}^{gal}$ and $D_{g,1}^{glu}$, were taken during washing steps, in which the extant glucose (galactose) was removed and new galactose (glucose) was added. Consequently, these two measurements were biased by external circumstances and have to be removed from the time series. After removal of these two measurements, the remaining time series was (i) standardized via a log transformation, before (ii) a z-score transformation over all measured expressions, $\{D_{g,2}^{gal},\ldots ,D_{g,16}^{gal},D_{g,2}^{glu},\ldots ,D_{g,21}^{glu}\}_{g=1,\ldots ,5}$, was performed to standardize the measured data to zero mean and a standard deviation of one. With respect to the data analysis it has to be taken into account that the measurement, $D_{g,2}^{glu}$ is not related to the last measurement, $D_{g,16}^{gal}$, in galactose, since the measurement in between (during the washing period), $D_{g,1}^{glu}$, had to be removed. That is, neither for $D_{g,2}^{gal}$ nor for $D_{g,2}^{glu}$ are there measurements of the preceding time point. Consequently, for each gene $g$ only the data points $D_{g,3}^{gal},\ldots ,D_{g,16}^{gal},D_{g,3}^{glu},\ldots ,D_{g,21}^{glu}$ can be used as targets in the DBN models; the corresponding values of the regressor variables (parent nodes) are given by: $D_{\pi _g,2}^{gal},\ldots ,D_{\pi _g,15}^{gal},D_{\pi _g,2}^{glu},\ldots ,D_{\pi _g,20}^{glu}$.

3.3 Circadian rhythms in Arabidopsis thaliana

Plants assimilate carbon via photosynthesis during the day, but have a negative carbon balance at night. The plants can buffer these daily carbon budget alternations by diurnal gene regulatory processes. They store some of the assimilated carbon as starch during the day (in the presence of light), and use the stored starch as a carbon supply during the night (in the absence of light). In order to synchronize this diurnal process with the external 24-h photo period, plants have a circadian clock that can potentially provide predictive, temporal regulation of metabolic processes over the day:night (light:dark) cycle. The molecular mechanisms behind this circadian regulation have not been fully elucidated yet.

I use four individual (independent) gene expression time series from Arabidopsis thaliana to study the diurnal gene regulatory processes among nine genes involved in the circadian clock.¹⁴ In the four experiments E1–E4 the Arabidopsis plants were entrained in different dark:light cycles: 12 h:12 h (E1 and E2), 10 h:10 h (E3), and 14 h:14 h (E4). In the experiments $T=12$ (E1) or $T=13$ (E2–E4) measurements were taken either in 4-h (E1 and E2) or in 2-h (E3 and E4) intervals. After the pre-experimental dark:light entrainment, the measurements were taken under experimentally generated constant light condition. RNA amounts were extracted with Affymetrix microarrays, and the data were background-corrected and RMA-normalized. The experimental protocols as well as more details on the time series can be found in Mockler et al. (2007) (E1), Edwards et al. (2006) (E2), and Grzegorczyk et al. (2008) (E3–E4).

For my data analysis I merge the four time series E1–E4 into one single data set by successively arranging them, symbolically: $E1,\ldots ,E4$. The expression values at the first time points of the time series are not related to the expression values at the last time point of the preceding time series; e.g. the value of gene g at the first time point in E2, $D_{g,1}^{E2}$, is not related to the values of the genes at the last time point of E1, $\{D_{g,T}^{E1}|g=1,\ldots ,N\}$. Therefore, the first time points, $D_{g,1}^{E1}$, $D_{g,1}^{E2}$, $D_{g,1}^{E3}$, and $D_{g,1}^{E4}$, have to be removed from the merged time series. That is, those four observations cannot be used as targets, as there are no measurements for their potential parent nodes (at the preceding time points).

My objective differs from the earlier studies. Neither do I assume the three boundaries between the four individual time series to be known (as in Grzegorczyk and Husmeier (2013)) nor do I try to infer them (as in Grzegorczyk and Husmeier (2011)). My focus is on capturing the diurnal nature (i.e. the alternating dark:light cycles) of the gene regulatory processes in the circadian clock.

4 Simulation study

4.1 The objectives of my empirical studies

First, I want to perform a comparative evaluation study to investigate under which circumstances the proposed HMM–DBN model achieves a higher network reconstruction accuracy than the competing DBN models. Second, I want to provide empirical evidence that the new MCMC moves, proposed in Sects. 2.5.1 and 2.5.2, improve convergence and mixing of the MCMC simulations. In Sect. 5.2 I employ data from the RAF pathway to systematically compare the network reconstruction accuracies of the DBN models, shown in Table 4, for various underlying segmentation schemes, shown in Table 5. The data are generated as explained in Sect. 3.1, and I distinguish five different SNR levels. I infer the DBN models with MCMC simulations and I compute marginal edge posterior probabilities to reverse-engineer the RAF pathway. As the RAF pathway does not possess self-feedback loops, i.e. edges, such as $g\rightarrow g$, I impose the constraint $g\notin \pi _g$ ($g=1,\ldots ,N$). Except for a first preliminary study in Sect. 5.1 I assume the segmentations to be unknown. That is, unlike related studies (see, e.g., Dondelinger et al. 2010; Husmeier et al. 2010; Dondelinger et al. 2012; Grzegorczyk and Husmeier 2012b, a, 2013), I here follow an unsupervised approach, in which the allocation vectors have to be inferred from the data. For the RAF pathway data I also compare the inferred segmentations with the true segmentations, and I show that the new MCMC moves substantially improve convergence and mixing. In Sect. 5.4 I employ the gene expression time series from Saccharomyces cerevisiae, described in Sect. 3.2, to extend my comparative evaluation by a real-world in vivo application from synthetic biology. Again I assume the segmentations to be unknown, and I exclude self-feedback loops, as the true network does not possess self-feedback loops. Although this application is quite small, the data have been measured in a true biological system, for which the true network is known. This study allows for an objective comparison of the performances of the DBN models on real biological data. In Sect. 5.5 I analyse the four gene expression time series from Arabidopsis thaliana, described in Sect. 3.3. For the Arabidopsis data a proper evaluation in terms of the network reconstruction accuracy is infeasible owing to the absence of a gold standard. My primary focus is thus on capturing the diurnal nature of the regulatory processes. Since the true Arabidopsis network is not known, I do not rule out self-feedback loops.

4.2 Hyperparameter settings

The HMM–DBN model is presented as a graphical model in Fig. 2, and values for the fix hyperparameters have to be chosen. In consistency with earlier studies on Bayesian networks I restrict the maximal cardinality of the parent node sets to $\mathcal {F}=3$.¹⁵ According to Eqs. (3–4) the inverse variance hyperparameters, $\sigma _{g}^{-2}$ ($g=1,\ldots ,N$), and the inverse SNR hyperparameters, $\delta _{g}^{-1}$ ($g=1,\ldots ,N$), are Gamma distributed with two hyperparameters each. I again follow earlier related studies, in which the Bayesian regression DBN model from Sect. 2.1 was used, and I set: $\sigma _g^{-2} \sim Gam(A_{\sigma }=0.005,B_{\sigma }=0.005)$ and $\delta _g^{-1} \sim Gam(A_{\delta }=2,B_{\delta }=0.2)$.¹⁶ Note that an extensive study in Grzegorczyk and Husmeier (2013) has shown that there is robustness with respect to different choices of these four hyperparameters. I also have to fix the hyperparameters of the Dirichlet priors for the MIX-DBN and the HMM–DBN model. In the absence of prior knowledge I follow Nobile and Fearnside (2007) and set $\alpha _i=1$ in Eq. (27) and $\alpha _{k,j}=1$ in Eq. (23). For the non-homogeneous DBN models I set $\mathcal {K}_{\textit{MAX}}=10$ and $\lambda =1$ in the truncated Poisson prior on the number of states (HMM) or components (MIX) or segments (CPS); see, e.g., Eq. (16).

4.3 MCMC simulation lengths and convergence diagnostics

I infer the DBN models with MCMC simulations, and for each simulation I perform 200I (with $I=500$) iterations. I take samples in equidistant intervals (every 100th iteration). From the resulting sample of length 1000 I withdraw the first 500 samples (“burn-in phase”), and I use the remaining sample of length 500 to compute the marginal edge posterior probabilities (see Sect. 2.8). To assess convergence and mixing I apply trace plot (Giudici and Castelo 2003) and potential scale reduction factor (Gelman and Rubin 1992) diagnostics. With respect to the PSRF based criterion, described in Sect. 2.10, I found that the PSRF’s of all edges were below 1.1 for the above mentioned simulation lengths. If the true network is known, I evaluate the network reconstruction accuracy in terms of the areas under the precision recall curve (AUC-PR), as described in Sect. 2.9.

5 Results

5.1 Pre-study: the supervised approach

I start with a pre-study, in which I cross-compare the network reconstruction accuracies of the proposed HMM–DBN model and the CPS–DBN model. I generate RAF pathway data for the segmentation $({\mathbf{V}}_g(2),\ldots ,{\mathbf{V}}_g(T)) = \mathbf{1212}$ and I employ strategy (S1) from Sect. 3.1 to sample the regression parameters. Unlike in the later studies (i), I here fix the noise level (SNR$=16$) and vary the numbers of data points instead, and (ii) I assume the segmentation to be known and fixed (“supervised approach”). For the proposed HMM–DBN model I can impose the true underlying allocation vectors. The CPS–DBN model employs changepoints to divide the data into disjunct segments with different states. Consequently, the true segmentation, $\mathbf{1212}$, is not a member of the allocation vector configuration space of the CPS–DBN model and has to be approximated by $\mathbf{1234}$. I vary the number of data points per segment, $T_{\star }\in \{2,4,8,16,32,64\}$, and the total number of data points is given by: $T=1+H\cdot T_{\star }$, where $H=4$ is the number of temporal segments. The results are shown in Fig. 4 and reveal a clear trend. The network reconstruction accuracy of both models increases in the number of data points, $T_{\star }$, and the proposed HMM–DBN model performs consistently better than the CPS–DBN model for $T_{\star }\le 32$. The difference in favour of the HMM–DBN model peaks at $T_{\star }=4$ and gets lower as $T_{\star }$ increases. Except for $T_{\star }=32$ ($T=129$) and $T_{\star }=64$ ($T=257$), where both models yield an almost perfect network reconstruction accuracy (AUC-PR$\approx 1$), the performance improvement of the HMM–DBN model is significant; see the t-test confidence intervals in the right panel of Fig. 4.

Fig. 4

Supervised approach: network reconstruction accuracy for RAF pathway data with the segmentation scheme 1212. Data were generated with the regression parameter sampling strategy (S1), and the allocations were assumed to be known and fixed (“supervised approach”). For the proposed HMM–DBN model the true allocation vectors, $({\mathbf{V}}_g(2),\ldots ,{\mathbf{V}}_g(T)) = \mathbf{1212}$, were imposed. For the CPS–DBN model the allocation vectors $({\mathbf{V}}_g(2),\ldots ,{\mathbf{V}}_g(T)) = \mathbf{1234}$ were used, as this model cannot revisit states once left. The left panel monitors the performances in terms of average AUC-PR scores. The horizontal axis refers to the segment sizes $T_{\star }$; the total number of data points is equal to $T=1+4\cdot T_{\star }$. The right panel monitors the average AUC-PR score difference between the HMM–DBN and the CPS–DBN model. The AUC-PR scores and score differences are averages over 20 data instantiations, with error bars indicating two-sided $95\%$ t-test confidence intervals

5.2 Network reconstruction and allocation vector accuracy for various segmentation schemes

In this subsection I cross-compare the performances of the four DBN models from Table 4. I generate RAF pathway data for various segmentations, as listed in Table 5, and I follow an unsupervised approach, i.e. I assume the segmentations to be unknown so that the allocation vectors have to be inferred from the data. I implement the models with node-specific and network-wide allocation vectors, and I distinguish the strategies (S1) and (S2) from Sect. 3.1 for sampling random instantiations of the regression parameters. I keep the numbers of data points per segment fixed ($T_{\star }=8$) and I vary the noise level (SNR$\in \{16,8,4,2,1\}$). The network reconstruction accuracy results for the models with network-wide allocations vectors, ${\mathbf{V}}_g = {\mathbf{V}}$, are shown in Figs. 5 and 6. The results obtained with node-specific allocation vectors, ${\mathbf{V}}_g$, are shown in Fig. 7. The results can be summarised as follows.

Fig. 5

Network reconstruction accuracy for the synthetic RAF pathway data for different segmentation schemes. Data were generated with the regression parameter sampling strategy (S1) for different allocation schemes; see Sect. 3.1 and Table 5 for details. The DBN models were implemented with network-wide allocation vectors, ${\mathbf{V}}_g = {\mathbf{V}}$. The three columns refer to three different segmentation schemes, 1111, 1122, and 112233. The panels in the top row monitor the network reconstruction accuracy in terms of average AUC-PR scores for the HOM-DBN, the CPS–DBN, the MIX-DBN, and the proposed HMM–DBN model. The horizontal axis refers to five different SNR levels. The following rows monitor the average AUC-PR differences between the proposed HMM–DBN model and the other three DBN models, HMM versus HOM (2nd row), HMM versus CPS (3rd row), and HMM versus MIX (4th row). The AUC-PR scores and AUC-PR score differences are averages over 20 independent data instantiations, with error bars indicating two-sided $95\%$ t-test confidence intervals. Note that identical plots with AUC-ROC scores (not provided) show very similar trends

Fig. 6

Network reconstruction accuracy for the synthetic RAF pathway data for different segmentation schemes. This figure is identical to Fig. 5 except that the three allocation schemes, 1212, 121212, and MIX are considered. Data were generated with the regression parameter sampling strategy (S1) and the DBN models were implemented with network-wide allocation vectors. See caption of Fig. 5 for further details

Fig. 7

Network reconstruction accuracy for the synthetic RAF pathway data for different segmentation schemes. This figure is similar to Figs. 5 and 6. Unlike the earlier figures, data were generated with the regression parameter sampling strategy (S2) and the DBN models were implemented with node-specific allocation vectors, ${\mathbf{V}}_g$. The three columns refer to three different segmentation schemes, 1122, 1212, and 121212. See caption of Fig. 5 for further details

5.2.1 Network reconstruction accuracies

(1) Homogeneous data: The segmentation 1111 in Fig. 5 refers to homogeneous data. As the number of states is equal to one, $\mathcal {K}=1$, the regression parameter vectors, ${\mathbf{w}}_{g,1}$ ($g=1,\ldots ,N$), do not vary over time. Fig. 5 shows that the models perform approximately equally well for this scenario. That is, the non-homogeneous models (CPS, MIX, and HMM) do not overfit the data by inferring spurious segmentations and are thus not inferior to the homogeneous DBN (HOM).

(2) Changepoint-segmented data: The segmentations 1122 and 112233 in Fig. 5 and the segmentation 1122 in Fig. 7 refer to classical changepoint-segmented time series. There are 2–3 different states, $\mathcal {K}_g$, and states once left are not revisited. Consequently, these segmentations can be easily inferred with the CPS–DBN model, which imposes changepoints to divide the data into disjunct segments with different states. The HOM-DBN model, which cannot segment these non-homogeneous time series, performs substantially worse than the other three models. For the MIX-DBN model, which ignores the temporal ordering of the data points, these segmentations are more difficult to learn than for the CPS–DBN and the HMM–DBN model. The latter models reach the highest network reconstruction accuracies and systematically outperform the MIX-DBN model. The CPS–DBN and the HMM–DBN model perform almost equally well with two exceptions: The CPS–DBN model outperforms the HMM–DBN model on segmentation 112233 in the right column of Fig. 5 for the two lowest SNR values (SNR$=2$ and SNR$=1$) and on segmentation 1212 in the left column of Fig. 7 for the noise levels SNR$=4$ and SNR$=2$. For noisy data, the CPS–DBN model benefits from its restricted allocation vector configuration space, which here includes the true segmentations.¹⁷

(3) Mixture data: The segmentation scheme MIX in Fig. 6 refers to mixture model data. As explained in Sect. 3.1, the data points are randomly assigned to two states ($k\in \{1,2\}$) with different regression parameter vectors. For the allocation the temporal ordering of the data points is not taken into account. For this scenario the HOM-DBN model and the CPS–DBN model both yield the lowest network reconstruction accuracies. The HOM-DBN model fails, as it cannot deal with non-homogeneity at all; the CPS–DBN model fails, as the true (mixture) allocation scheme is not included in its restricted allocation vector configuration space. The MIX-DBN model and the HMM–DBN model both perform systematically superior to the HOM-DBN and the CPS–DBN model. Only for SNR$=4$ and SNR$=2$ the MIX-DBN model performs slightly superior to the HMM–DBN model. For noisy data the MIX-DBN model benefits from its completely free allocation vectors. Unlike the HMM–DBN model, the MIX-DBN model employs a free allocation model, which is here in agreement with the data generating mechanism; i.e. a random free allocation of the data points. Although the HMM–DBN model can infer free allocations, it does take the temporal ordering into account by putting less prior weight onto (random) allocations (without any temporal dependencies). For noisy data the prior on the allocation vectors becomes important, and so the HMM–DBN model is disadvantaged compared to the MIX-DBN model, whose allocation vector prior ignores the temporal ordering of the data points altogether.

(4) Periodic data: The segmentations 1212 and 121212 in Figs. 6 and 7 have a temporal structure but do not correspond to changepoint-segmented data, since the states are revisited. The dependency structure behind these segmentations is compatible with a Hidden Markov model and I will refer to them as “periodic data”. As for the mixture data (MIX) the HOM-DBN and the CPS–DBN model cannot deal with these periodic segmentations and perform consistently and significantly worse than the HMM–DBN model unless the data are very noisy (SNR$=1$). Only for the simulations with network-wide allocation vectors on segmentation 1212 in Fig. 6 the difference between the HMM–DBN and the CPS–DBN model are moderate only.¹⁸ The MIX-DBN model also achieves consistently lower network reconstruction accuracies than the proposed HMM–DBN model, but the differences in favour of the HMM–DBN model are less pronounced. Form the left and middle column in Fig. 6 it appears that the MIX-DBN model is outperformed for the moderate noise levels, where the network reconstruction is neither perfect (AUC-PR $\ll 1$) nor impossible (AUC-PR $\gg 0.5$).

5.2.2 The estimated marginal connectivity matrices

For the non-homogeneous DBN models I estimate the marginal connectivity matrices, as described in Sect. 2.8. Figure 8 shows heatmap representations of the average connectivity matrices for the segmentations 1122, 112233, 1212, and 121212 of the simulations with network-wide allocation vectors and SNR$=16$. Figure 8 shows that the estimated connectivity matrices are consistent with my findings for the network reconstruction accuracy. The HMM–DBN model (bottom row in Fig. 8) infers the underlying segmentations (top row in Fig. 8) more accurately than the MIX-DBN model (2nd row in Fig. 8). That is, both models detect the underlying compartments, but the components are separated substantially stronger by the proposed HMM–DBN model. The CPS-model perfectly separates the segments only for those segmentations, 1122 and 112233, that are in agreement with its allocation vector configuration space. The segmentations 1212 and 121212 can only be approximated by 1234 and 123456, respectively, and the segments are then separated only weakly (last two panels in the 3rd row of Fig. 8).

Fig. 8

Graphical representation of the inferred temporal connectivity matrices for the RAF pathway data with SNR$\,=\,$16. The figure is arranged as a matrix, and the columns correspond to four different allocation schemes. The top row shows the true connectivity structures, and the following rows correspond to the non-homogeneous DBN models. Data were generated with sampling strategy (S2) from Sect. 3.1. The models were implemented with network-wide allocation vectors, ${\mathbf{V}}_g = {\mathbf{V}}$. The heatmaps in rows 2–4 indicate the estimated posterior probability of two data points being assigned to the same state. The probabilities are represented by a grey shading, where white corresponds to 1, and black corresponds to 0. The axes refer to the time points. In each heatmap the probabilities are averages over 20 data instantiations

5.2.3 Summary

The results shown in Figs. 5, 6, 7 and 8 demonstrate that the proposed HMM–DBN model is more robust than the competing DBN models with respect to a variation of the underlying allocation. The HOM-DBN model cannot deal with non-homogeneous data at all. The CPS–DBN model fails when the underlying segmentation cannot be approximated properly by changepoints. The MIX-DBN model fails when the underlying segmentation has a temporal structure, which cannot be taken into account. The proposed HMM–DBN model is always among the best-scoring models, and it significantly outperforms the competing models for periodic segmentations, such as $\mathbf{1212}$ and $\mathbf{121212}$.

Finally, note that I also applied the coupled variant of the CPS–DBN model from Grzegorczyk and Husmeier (2013); see Sect. 2.6.3 for a brief description of the coupling scheme. However, for the RAF-pathway data I have never observed a significant difference between the AUC-PR scores of the coupled CPS–DBN model and the AUC-PR scores of the standard CPS–DBN model. This finding is not surprising and consistent with the empirical results reported in Grzegorczyk and Husmeier (2013): As described in Sect. 3.1, I here sample independent state-specific regression parameters so that coupling the regression parameters is unlikely to yield any information gain.¹⁹

5.3 Convergence comparison for the HMM–DBN model

In this subsection I assess the degree of convergence and mixing of three different MCMC sampling schemes for the proposed HMM–DBN model. The MCMC sampling scheme for the HMM–DBN model is outlined in Table 3. I vary the 4th sampling step, i.e. the allocation vector inference part, to demonstrate that the adoption of the new moves, proposed in Sects. 2.5.1 and 2.5.2, improves convergence. The first MCMC sampling scheme, referred to as MIX and HMM moves, is the sampling scheme provided in Table 3. That is, a coin is drawn to decide randomly whether an allocation sampler (MIX) or a new (HMM) move is performed. Both move types are equally likely ($p_{MIX}=0.5$ and $p_{HMM}=0.5$). I consider two alternative schemes; each employing only one particular move-type. The second scheme, referred to as MIX moves only, performs exclusively allocation sampler (MIX) moves (i.e. I set $p_{MIX}=1$ and $p_{HMM}=0$). The third scheme, referred to as HMM moves only, performs only the new HMM moves (i.e. I set $p_{HMM}=1$ and $p_{MIX}=0$). I use the convergence criterion from Sect. 2.10, and I monitor the fractions of edges with a PSRF lower than the target values $\xi =1.1$ and $\xi =1.01$.²⁰ The average results for the simulations with node-specific allocation vectors for the segmentation schemes 1122 and 121212 are shown in Fig. 9.

Fig. 9

Convergence diagnostics based on potential scale reduction factors (PSRFs) of individual network edges—RAF network with SNR$\,=\,$16. I compare the performance of three MCMC sampling schemes for the proposed HMM–DBN model with node-specific allocation vectors. The MCMC sampling scheme was outlined in Table 3; here I vary the 4th sampling step, i.e. the allocation vector inference part: (i) MIX and HMM: Exactly as indicated in Table 3, randomly draw an unbiased coin to decide whether an allocation sampler (MIX) or a new move (HMM) is performed. Both move types are equally likely. (ii) MIX only: Perform the allocation sampler moves (MIX) with probability 1. (iii) HMM only: Perform the new HMM moves with probability 1. With the three sampling schemes I perform 5 independent MCMC simulations for one single data set instantiation. Afterwards, for each sampling scheme the 5 independent MCMC inference results were used to compute a PSRF for each edge, and the fractions of edges whose PSRF was lower than the thresholds $\xi =1.1$ (left panel) and $\xi =1.01$ (right panel) were computed. This procedure was repeated for five individual data set instantiations, and the panels show overlaid trace plots of the average fractions of edges whose PSRF was lower than the threshold $\xi$. The data sets were generated with sampling strategy (S2) for two segmentations, 1122 (top row) and 121212 (bottom row). Details on how I defined a PSRF for an edge are given in Sect. 2.10

A clear outcome of the convergence diagnostic is that the MCMC sampling scheme MIX and HMM moves, which combines both types of moves, yields the best convergence: About $100\%$ of the edges satisfy the standard convergence criterion (PSRF$<1.1$) already after 50k iterations. For the sampling scheme new HMM moves only scheme there is considerable scope for improvement. For the segmentation scheme 121212 on average only about $90\%$ of the edges satisfy the convergence criterion PSRF$<1.1$ after 50k iterations. The sampling scheme old MIX moves only fails to converge properly for the segmentation scheme 1122; only about $98\%$ ($92\%$) percent of the edges satisfy the criterion PSRF$<1.1$ (PSRF$<1.01$) after 50k iterations. Note that the same average percentage rates are reached with the MIX and HMM moves already after 10k (20k) iterations. This suggests that the inclusion of the new MCMC moves, proposed in Sects. 2.5.1 and 2.5.2, is advantageous. The novel moves are as straightforward to implement as the allocation sampler moves, described in Appendix 2, and yield a convergence improvement.

5.4 Network reconstruction in Saccharomyces cerevisiae (yeast)

In this subsection I cross-compare the network reconstruction accuracy of the DBN models on a small but topical data set from synthetic biology. The (true) yeast network, which was synthetically designed by Cantone et al. (2009), is depicted in the right panel of Fig. 10. Gene expression time series were measured in synthetically designed yeast cells, as described in Sect. 3.2. I apply each of the non-homogeneous DBN models (CPS, coupled CPS, HMM, and MIX) with node-specific, ${\mathbf{V}}_g$ and with network-wide, ${\mathbf{V}}_g = {\mathbf{V}}$, allocation vectors. Hence, I compare the performances of eight non-homogeneous DBN models and the conventional homogeneous DBN model. For each of the nine DBN models I run 5 independent MCMC simulations. The network reconstruction accuracy results (in terms of mean AUC-PR scores) are represented as histograms in Fig. 10. It can be seen that the non-homogeneous DBN models consistently achieve higher AUC-PR scores when they are implemented with node-specific allocation vectors. Two-sided Student’s t-tests show that the improvement achieved with node-specific allocation vectors is significant for the CPS–DBN model (p value 0.015), the coupled CPS–DBN model ($p=0.048$) and the HMM–DBN model (p value 0.011). For both allocation vector variants (node-specific and network wide) the proposed HMM–DBN reaches the highest average AUC-PR scores. In terms of the p values of two-sided t-tests the differences in favour of the proposed HMM–DBN model are significant except for the comparison with the coupled CPS–DBN model.²¹ When implemented with node-specific allocation vectors the coupled CPS–DBN model and the proposed HMM–DBN model perform approximately equally well ($p=0.517$).

Fig. 10

Network reconstruction accuracy in Saccharomyces cerevisiae (yeast). Cantone et al. (2009) synthetically designed the network and measured in vivo gene expression levels with real-time polymerase chain reaction. The histograms show the network reconstruction accuracies in terms of AUC-PR scores. The left (right) histogram refers to models with network-wide (node-specific) allocation vectors. Both histograms show bars of the average AUC-PR scores obtained with the HOM-DBN (white), the CPS–DBN (light grey), the coupled CPS–DBN (grey), the proposed HMM–DBN (black), and the MIX-DBN (dark grey) model. Average AUC-PR scores are computed from five independent MCMC simulations; the error bars indicate the standard deviations

This finding is in agreement with earlier results on the RAF-pathway data in Sect. 5.2. Because of the carbon source switch from galactose to glucose the true segmentation of the yeast time series should be roughly of the form $\mathbf{1122}$. For this segmentation it was found that the MIX-DBN model, which ignores the temporal order of the time points, performs substantially worse than the CPS–DBN and the HMM–DBN model; see, e.g., the middle column in Fig. 5 and the left column in Fig. 7. The improved network reconstruction accuracy of the coupled CPS–DBN model is in agreement with earlier reported results (see, e.g., Fig. 12 in Grzegorczyk and Husmeier 2013). The results in Fig. 10 suggest that the same improvement (i.e. the same “regularisation effect”) can also be reached by a more flexible data segmentation scheme, namely the proposed HMM–DBN model. Finally, I also applied the coupling scheme from Grzegorczyk and Husmeier (2013) to the proposed HMM–DBN model; see Sect. 2.6.3 for a brief description of this coupling scheme. For the “coupled” HMM–DBN model I have not observed further improvements, but a slight (non-significant) decrease of the average AUC-PR scores.

5.5 Network reconstruction in Arabidopsis thaliana

In this subsection I compare the performances of the non-homogeneous DBN models on a merged gene expression time series from Arabidopsis thaliana. One single long Arabidopsis time series has been obtained by successively arranging four individual short gene expression time series from different experiments, as explained in more detail in Sect. 3.3. In the four individual experiments (E1–E4) the gene expressions have been measured under constant light condition, but the plants were entrained in different experimentally controlled light-dark cycles. In the first two experiments E1 and E2 the plants were entrained in a 12 h:12 h light/dark-cycle and measurements were taken in 4 h intervals, and in E3 and E4 measurements were taken in 2 h intervals and the plants were entrained in the light/dark-cycles 10 h:10 h (E3) and 14 h:14 h (E4).

From a biological perspective the regulatory relationships among the circadian genes in Arabidopsis follow a two-stage process, which is related to the diurnal nature of the environmental dark-light cycle. Two groups of genes can be distinguished: Morning genes whose activities peak in the presence of light (i.e. in the morning), and evening genes whose activities peak in the absence of light (i.e. in the evening). Although all gene expression measurements in E1–E4 were taken under artificially generated constant light condition, the two-stage nature of the regulatory mechanisms will be preserved by the circadian clock (see, e.g., Johnson et al. 2003; McClung 2006). That is, even under constant light condition the regulatory processes (approximately) follow the diurnal dark:light cycle, in which the plants were entrained before the experiment. Since the dark:light cycle affects the activities of both the morning and the evening genes (i.e. the whole regulatory network) rather than specific genes only (Johnson et al. 2003; McClung 2006), I implement the non-homogeneous DBN models with network-wide allocation vectors, ${\mathbf{V}}_g = {\mathbf{V}}$; see Sect. 2.7 for details.

Heatmap representations of the inferred connectivity matrices are shown in Fig. 11a. All the non-homogeneous models (MIX-DBN, CPS–DBN, coupled CPS–DBN, and HMM–DBN) infer a two-stage process with the number of states (components) peaking at $\mathcal {K}=2$. The CPS–DBN model and the coupled CPS–DBN model (see Sect. 2.6.3) both infer the same segmentation with one single changepoint between E2 and E3 (see left panel in Fig. 11a). As the CPS–DBN models can only infer changepoint-divided segmentations, where the segments are assigned to disjunct components (i.e. a state once left cannot be revisited), they do not capture the true underlying segmentation of the Arabidopsis time series. The changepoint of the CPS–DBN models appears to be related to different experimental conditions in E1–E2 and E3–E4 (here: e.g. the distance between measurements). The inferred segmentation does not reflect the diurnal nature of the regulatory process. For the merged Arabidopsis time series the preservations of the entrained dark:light cycles corresponds to a segmentation scheme of the form “$\mathbf{121212\ldots }$”. Hence, the failure of the CPS–DBN model is in agreement with results observed for the synthetic RAF-pathway data. In Sect. 5.2 I found for segmentations, such as $\mathbf{1212}$ and $\mathbf{121212}$, that the CPS–DBN model cannot infer the correct segmentation; see, e.g., the last two panels in the third row of Fig. 8.

Fig. 11

Inference results on the Arabidopsis gene expression data. In the heatmaps in panels (a) and (b) the grey shading indicates the posterior probability of two data points being assigned to the same state, ranging from 0 (black) to 1 (white). a Heatmaps of the connectivity matrices inferred on the merged data set. The merged data set consists of four individual time series (E1–E4), which were arranged successively; see Sect. 3.3 for details. In the three panels the axes represent the indices of the data points, and the axes are ticked at the boundaries of the four individual time series. The CPS–DBN and the coupled CPS–DBN model both infer approximately the same segmentation (see left panel) with one single changepoint in between E2 and E3. b Sub-heatmaps extracted (“cut out”) from the heatmaps in panel (a). The extracted sub-heatmaps show the connectivity structures within the four individual time series E1–E4. Note that the temporal distance between neighbouring data points is 4 h in E1 and E2, while measurements in E3 and E4 have been taken in 2 h intervals. c Scatter plots of the marginal edge posterior probabilities inferred on the merged data set. In each panel the marginal edge posterior probabilities of two DBN models have been plotted against each other

From the middle and the right panel in Fig. 11a it can be seen that the inferred connectivity structures of the MIX-DBN model and the proposed HMM–DBN model are (also) very similar. I now have a closer look at the connectivity structures within the four individual time series. Figure 11b shows heatmap representations of the connectivity structures within E1–E4.²² The (sub-)heatmaps in Fig. 11b confirm the conjecture that the MIX-DBN and the HMM–DBN model infer very similar connectivities; i.e. the patterns in the top row are almost identical to the patterns in the bottom row. In particular, it can also be seen that the inferred segmentations are actually related to the dark:light cycles in which the Arabidopsis plants were entrained. In the heatmaps the “white windows around the diagonal” represent connected blocks, i.e. segments of data points that are assigned to the same state (component). The “white windows” in E3 (time points $26,\ldots ,30$) and in E4 (time points $38,\ldots ,44$) represent time intervals of length ($5\times 2\,\hbox {h}=$)10h and ($7\times 2\,\hbox {h}=$)14 h, and thus are in agreement with the entrainment cycles 10 h:10 h (E3) and 14 h:14 h (E4), respectively. In E1 and E2 there is at least a certain tendency towards segments (“white windows”) consisting of 3 data points. In E1 and E2, where measurements were taken in 4 h intervals, three neighbouring data points cover a time interval of length ($3\times 4\,\hbox {h}=$)12 h, what corresponds to the entrainment cycle 12 h:12 h of E1–E2. This suggests that the MIX-DBN model and the HMM–DBN model infer the same connectivity structure, which is related to the diurnal nature of the dark:light cycle and thus in agreement with biology.²³

Figure 11c shows scatter plots of the marginal edge posterior probabilities inferred with the non-homogeneous DBN models. As the MIX-DBN and the HMM–DBN model have inferred the same connectivity structure, it is not surprising that their marginal edge posterior probabilities are strongly correlated (see right panel of Fig. 11c). On the other hand, the CPS–DBN models, which could not capture the underlying dark:light cycle, yield deviating marginal edge posterior probabilities. That is, despite a certain correlation in the left and middle panel of Fig. 11c there are edges for which different marginal posterior probabilities have been inferred.

Finally, I use the inferred marginal edge posterior probabilities of the proposed HMM–DBN model to predict the regulatory relationships in the circadian clock. Figure 12 shows the predicted network possessing only those edges whose marginal posterior probability exceeds the threshold of 0.5. Unfortunately, there is no gold-standard network for the circadian clock in Arabidopsis so that the network reconstruction accuracy cannot be evaluated properly. However, the reconstructed network, shown in Fig. 12, possesses several edges that are consistent with the biological literature:

Fig. 12

Reconstructed gene regulatory network in Arabidopsis thaliana. The merged Arabidopsis data set was analysed with the proposed HMM–DBN model to reverse-engineer the interactions among the nine circadian genes. The graph shows all edges with a marginal posterior probability greater than 0.5; except for three self-feedback-loops ($LHY\rightarrow LHY$, $GI\rightarrow GI$ and $PRR9\rightarrow PRR9$) which have been left out. The morning (evening) genes are represented by white (grey) circles. Edges connecting either two morning genes or two evening genes with each other are represent by thin lines, while the bold edges refer to connections between the morning and the evening genes. Moreover, each individual edge is drawn either in black or in grey to distinguish whether it originates at the morning (black edge) or at the evening (grey edge) genes

According to the biological literature (see, e.g., McClung 2006) the morning genes activate the evening genes, and the evening genes inhibit the morning genes. In the predicted network there are six edges pointing from the morning genes to the evening genes and five edges pointing from the evening genes to the morning genes. McClung (2006) also reports that CCA1 and LHY are the central regulators among the morning genes.²⁴ From Fig. 12 it can be seen that four of the six edges pointing from the morning to the evening genes actually originate from LHY and CCA1 and that four of the five evening genes are regulated either by LHY or by CCA1. In particular, the regulation of the evening genes TOC1 and ELF4 by the central regulators CCA1/LHY has already been reported in Alabadi et al. (2001) and Kikis et al. (2005). Among the edges originating from the evening genes the two edges $ELF3\rightarrow CCA1$ and $ELF3 \rightarrow LHY$ are consistent with the biological finding in Kikis et al. (2005) that ELF3 is necessary for light-induced CCA1 and LHY expression. Moreover, the edges $ELF3\rightarrow TOC1$ and $GI\rightarrow TOC1$ are also in agreement with the literature, as Miwa et al. (2006) found that both genes ELF3 and GI are involved in the interaction between CCA1 and TOC1. Within the group of evening genes, the reconstructed network contains one single feedback loop $GI\leftrightarrow TOC1$ between GI and TOC1. Exactly this feedback loop has also been found in Locke et al. (2005).

6 Discussions

6.1 Computational costs of the MCMC inference

In this subsection I briefly discuss the computational costs of the required MCMC simulations. For the proposed HMM–DBN model I used the Matlab$^\circledR$ software to implement the MCMC algorithm, as outlined in the pseudo code, provided in Tables 1, 2 and 3, and I ran all MCMC simulations on a standard Desktop PC. For the three competing DBN models I modified the algorithm, as outlined in Sect. 2.6. Tables 6 and 7 show the measured computational costs for the MCMC simulations on the synthetic RAF network data, which were analysed in Sect. 5.2. As expected, the three non-homogeneous DBN models are associated with substantially higher computational costs than the traditional homogeneous DBN model (HOM-DBN). It can also be seen that the computational costs for the HOM-DBN model stay almost constant across all nine data scenarios. The MCMC simulations for the non-homogeneous changepoint DBN model (CPS–DBN) are consistently cheaper than the simulations for the two free allocation models, namely the MIX-DBN model and the proposed HMM–DBN model. This is due to the fact that the CPS–DBN model works on a restricted configuration space of the allocation vectors only; see Sect. 2.3 for details. The most interesting comparison is between the MIX-DBN model and the proposed HMM–DBN model, since both models allow for unrestricted free allocations and, hence, share the same (maximal) configuration space w.r.t. the allocation vectors. It can be seen the computational costs for the MCMC simulations are increased for the proposed MIX-DBN model. The difference is due to the fact that the new MCMC moves, proposed here, are slightly more expensive than the original allocation sampler moves. Although the difference appears to be irrelevant w.r.t. practical applications, it should be noted that the increase in the computational costs could be avoided by inferring the HMM–DBN model by allocation sampler moves only.

Table 6 Average computational costs (and standard deviations), measured for the MCMC simulations on the synthetic RAF network data with $N=11$ nodes

Table 7 Average computational costs (and standard deviations), measured for the MCMC simulations on the synthetic RAF network data with $N=11$ nodes

Since all MCMC simulations on a network with $N=11$ nodes could be finished within minutes on a standard Desktop PC, I would expect that the novel HMM–DBN model can also be applied to larger network domains (e.g. with $N=100$ nodes) in reasonable time. On the other hand, it certainly has to be taken into account that the number of possible parent sets grows at least polynomially in the number of network nodes N.²⁵ In this context it is worth mentioning that the MCMC simulations for the HMM–DBN model with network-specific allocation vectors can be run in parallel (e.g. on a computer cluster). That is, as there is no information-sharing among genes, the HMM–DBN model can be applied independently to each gene g to infer its particular parent set $\pi _g$ and its allocation vector ${\mathbf{V}}_g$. Given the increasing availability of high-performance computer clusters, I would thus argue that it is not the number of network nodes N but the number of observations T which restricts the applicability of the HMM–DBN model. E.g. in modern systems biology applications the number of measured observations T is usually substantially smaller than the number of variables (e.g. genes) N, symbolically $T<<N$, leading to diffuse posterior distributions. Hence, even if an MCMC sampling scheme guaranteed that the huge space of possible network structures could be systematically searched for those networks with “high” posterior probabilities, a lack of significance would have to be expected. I would then recommend reducing the size of the network by restricting on the most important variables (e.g. genes). Often biological prior knowledge can be exploited to reduce the network to a reasonable size; e.g. for the Arabidopsis thaliana data (see Sect. 3.3) the focus was set on the nine potentially “most important” circadian clock genes.

6.2 Outlook and future work

In this article I proposed a novel non-homogeneous DBN model, namely the HMM–DBN model, for which I assumed that the regulatory network structure, $\mathcal {G}$, is identical for all components (segments). Keeping the network structure constant allows for information-sharing among components (w.r.t. the network topology), and is certainly an appropriate assumption for the two presented real-world applications: (i) cellular response to fast environmental change in yeast (see Sect. 5.4) and (ii) the circadian clock network in Arabidopis thaliana (see Sect. 5.5). For certain other scenarios, e.g. morphogenesis, where the cellular processes take place on a longer time scale, the assumption of a fixed network structure might turn out to be too restrictive. For those applications it might be interesting to allow the network structure to vary with time and to implement the HMM–DBN model with component-specific network structures. This can, in principle, be accomplished straightforwardly, e.g. along the lines proposed and discussed in Lèbre et al. (2010) or Dondelinger et al. (2012).

An alternative extension of the proposed HMM–DBN model can be reached by incorporating the hierarchical global information-coupling scheme, proposed in Grzegorczyk and Husmeier (2013). The implementation of a coupled version of the HMM–DBN model is straightforward, and can be beneficial for applications where the component-specific network interaction parameters are similar to each other. For the yeast data (see Sect. 5.4) I incoporated the global information-coupling scheme into the changepoint-segmented DBN model (CPS–DBN) and the proposed HMM–DBN model, and I included these two new model variants into my cross-method comparison. In both cases the coupling did not yield substantially different results: For the coupled CPS–DBN model there was a slight (significant) improvement of the network reconstruction accuracy (see Fig. 10), and for the coupled HMM–DBN model I saw a slight (non-significant) decrease in the network reconstruction accuracy (see main text in Sect. 5.4). From a more general perspective, I would expect that the improvement through information-coupling, will be less pronounced for the HMM–DBN model than for the CPS–DBN model. With the CPS–DBN model, states once left cannot be revisited so that information-coupling is required for sharing information between distant time points. Unlike the CPS–DBN model, the proposed HMM–DBN model explicitly allows distant time points to be allocated to the same component and to share the same network interaction parameters.

7 Conclusion

I have proposed a novel non-homogeneous dynamic Bayesian network (DBN) model, which combines a conventional DBN with a Hidden Markov model (HMM). The key idea behind this HMM–DBN model is to assume that the temporal data points of a time series are allocated to different states (components) by a HMM. A graphical representation of the HMM–DBN model is provided in Table 2. My work complements earlier works which combined DBN models either with multiple changepoint processes (CPS–DBN) or with free allocation mixture (MIX-DBN) models; see Sect. 1 for various literature references. The CPS–DBN models, on the one hand, employ a multiple changepoint process to divide a time series into temporal segments with a one-to-one mapping between segments and states (components): All data points within a segment are assigned to the same state, but data points from different segments have to be allocated to different states; i.e. “a state (component) once left cannot be revisited”. This imposes a very strong restriction onto the configuration space of the possible data segmentations. The MIX-DBN model, on the other hand, allows for an unrestricted free allocation of the data points to states (mixture components) but loses important information about the data, since it cannot take the temporal ordering of the data points into account.

The novel HMM–DBN model is a consensus between the CPS–DBN and the MIX-DBN model, as it does take the temporal structure of the data into account without putting any restriction onto the configuration space of the data segmentations. The novel HMM–DBN model can be inferred with two different Reversible Jump Markov Chain Monte Carlo (RJMCMC) techniques, as briefly discussed in Sect. 2.5. In this paper I have shown how the allocation sampler from Nobile and Fearnside (2007) can be used for inference, and in Sects. 2.5.1–2.5.2 I have proposed two new pairs of complementary moves to improve mixing and convergence of the allocation sampler. Pseudo code of the proposed MCMC sampling scheme is provided in Table 3.

In Sect. 5.2 I have performed an extensive comparative evaluation study on synthetic RAF-pathway data to provide empirical evidence that the proposed HMM–DBN model is a consensus between the MIX-DBN and the CPS–DBN model. A brief overview to the four competing DBN models, which I cross-compared in my evaluation study, is given in Table 5. In my study I considered various segmentation scenarios, as listed in Table 4. For scenarios where the CPS–DBN model performed significantly better than the MIX-DBN model and vice-versa I found that the performance of the proposed HMM–DBN model was always very close (and only rarely significantly different) to the performance of the better-scoring DBN model. For scenarios with periodic segmentations the proposed HMM–DBN model outperformed the competing MIX-DBN model and the CPS–DBN models.

I have also cross-compared the learning performances of the four DBN models on two real-world applications from systems biology (see Sects. 5.4 and 5.5). My cross-method comparison for the real-world data also confirmed that the proposed HMM–DBN model is a consensus between the CPS–DBN and the MIX-DBN model. For a non-homogeneous yeast gene expression time series, which consists of two (“changepoint-divided”) temporal segments related to two different carbon sources, the free allocation MIX-DBN model has failed to reconstruct the underlying network, while the coupled CPS–DBN (Grzegorczyk and Husmeier 2013) and the proposed HMM–DBN model have performed substantially better; see Sect. 5.4 for details.

For a non-homogeneous Arabidopsis gene expression time series, in which the regulatory processes are diurnal and periodic, i.e. the processes follow recurrent entrained dark:light cycles, the CPS–DBN models have failed to capture the underlying data segmentation, while the MIX-DBN and the proposed HMM–DBN model both inferred a segmentation, which is in agreement with plant biology; see Sects. 3.3 and 5.5 for details. I have used the results of the HMM–DBN model to reconstruct the network among the circadian genes in Arabidopsis. As discussed in Sect. 5.5, the reconstructed network shows features that are consistent with the biological literature.

Appendices

Appendix 1: Sweep Gibbs move on the allocation vector

The Gibbs move keeps the network $\mathcal {M}=(\pi _1,\ldots ,\pi _{N})$ and the SNR hyperparameters fixed, and I describe the ith MCMC iteration, $(i-1)\rightarrow i$, for node g. The move re-allocates one single data point to a new state. If the number of states is currently equal to one, $\mathcal {K}_g^{(i-1)}=1$, skip the move. Otherwise randomly select one single observation $t\in \{2,\ldots ,T\}$. For $k=1,\ldots ,\mathcal {K}_g^{(i-1)}$ replace the tth element of the current allocation vector ${\mathbf{V}}_g^{(i-1)}$ by state k to obtain the vector ${\mathbf{V}}_{g,[t_k]}$. Sample the new allocation vector ${\mathbf{V}}_g^{(i)}$ from the full conditional distribution. For $k=1,\ldots ,\mathcal {K}_g^{(i-1)}$:

$$\begin{aligned} P\left( {\mathbf{V}}_g^{(i)}={\mathbf{V}}_{g,[t_k]}\right) = \frac{P\left( {\mathbf{V}}_{g,[t_k]}|\mathcal {K}_g^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g,[t_k]}}|\mathbf{X}_{g,{\mathbf{V}}_{g,[t_k]}},\delta _g\right) }{\sum _{u=1}^{\mathcal {K}_g^{(i-1)}} P\left( {\mathbf{V}}_{g,[t_u]}|\mathcal {K}_g^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g,[t_u]}}|\mathbf{X}_{g,{\mathbf{V}}_{{g},[t_u]},\delta _g}\right) } \end{aligned}$$

(36)

As this move does not change the number of states, it has to be set: $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

Appendix 2: The mixture model allocation sampler (MIX) moves

The MIX MCMC moves, presented in this appendix, have been developed by Nobile and Fearnside (2007) for Gaussian mixture models. Nobile and Fearnside (2007) proposed the resulting “allocation sampler” as an alternative to computationally expensive Reversible Jump Markov Chain Monte Carlo sampling schemes (Green 1995); see Nobile and Fearnside (2007) for details.

1.1 The M1 move

If the number of states is currently equal to one, $\mathcal {K}_g^{(i-1)}=1$, skip the move. Otherwise randomly select two states k and $\tilde{k}$ among the $\mathcal {K}_g^{(i-1)}$ available, and draw a random number $\tilde{p}$ from a Beta(a,a) distribution with $a=1$. Consider the set $H=\{t:{\mathbf{V}}_g^{(i-1)}(t)=k \vee {\mathbf{V}}_g^{(i-1)}(t)=\tilde{k} \}$ of all data points that are allocated either to state k or to state $\tilde{k}$ by ${\mathbf{V}}_g^{(i-1)}$. Re-allocate each point of the set H either to component k (with probability $\tilde{p}$) or to component $\tilde{k}$ (with probability, $1-\tilde{p}$). This gives a new allocation vector, ${\mathbf{V}}_{g}^{\star }$, which is accepted with probability:

$$\begin{aligned} A = \min \left\{ 1, \frac{P\left( {\mathbf{V}}_{g}^{\star }|\mathcal {K}_g^{(i-1)}\right) P(\mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g)}{P\left( {\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}_g^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g\right) } \cdot \frac{Q\left( {\mathbf{V}}_{g}^{(i-1)}|{\mathbf{V}}_{g}^{\star }\right) }{Q\left( {\mathbf{V}}_{g}^{\star }|{\mathbf{V}}_{g}^{(i-1)}\right) } \right\} \end{aligned}$$

(37)

The prior probabilities and the marginal likelihood terms can be computed with Eqs. (12), (23) and (16). Nobile and Fearnside (2007) show that the Hastings ratio is given by:

$$\begin{aligned} \frac{Q\left( {\mathbf{V}}_{g}^{(i-1)}|{\mathbf{V}}_{g}^{\star }\right) }{Q\left( {\mathbf{V}}_{g}^{\star }|{\mathbf{V}}_{g}^{(i-1)}\right) } = \frac{\Gamma (a + n_k)\Gamma (a + n_{\tilde{k}})}{\Gamma (a+n_k^{\star })\Gamma (a+n_{\tilde{k}}^{\star })} \end{aligned}$$

(38)

where $n_k$ and $n_{\tilde{k}}$ are the numbers of data points that are allocated to the states k and $\tilde{k}$ by ${\mathbf{V}}_g^{(i-1)}$, and $n_k^{\star }$ and $n_{\tilde{k}}^{\star }$ are the numbers of data points that are allocated to the states k and $\tilde{k}$ by ${\mathbf{V}}_g^{\star }$. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$, or otherwise set: ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$. As the move cannot change the number of states, set: $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

1.2 The M2 move

If the number of states is currently equal to one, $\mathcal {K}_g^{(i-1)}=1$, skip the move. Otherwise randomly select two states k and $\tilde{k}$ among the $\mathcal {K}_g^{(i-1)}$ available.

If the kth component is empty, the move fails outright. Otherwise draw a random number u from a uniform distribution on $\{1,\ldots ,n_{k}\}$, where $n_{k}$ is the number of data points t with ${\mathbf{V}}_g^{(i-1)}(t)=k$. Randomly select u observations from the $n_{k}$ data points and re-allocate them to state $\tilde{k}$ to obtain the new candidate allocation vector ${\mathbf{V}}_g^{\star }$. The new allocation vector is accepted with the probability given in Eq. (37), except that the Hastings Ratio is different. As shown in Nobile and Fearnside (2007), the Hastings ratio is:

$$\begin{aligned} \frac{Q\left( {\mathbf{V}}_{g}^{(i-1)}|{\mathbf{V}}_{g}^{\star }\right) }{Q\left( {\mathbf{V}}_{g}^{\star }|{\mathbf{V}}_{g}^{(i-1)}\right) } = \frac{n_{k}}{n_{\tilde{k}}+u} \cdot \frac{n_{k}! \cdot n_{\tilde{k}}!}{(n_{k}-u)! \cdot (n_{\tilde{k}}+u)!} \end{aligned}$$

(39)

where $n_{k}$ and $n_{\tilde{k}}$ are the numbers of data points allocated to the states k and $\tilde{k}$ by ${\mathbf{V}}_g^{(i-1)}$. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$, or otherwise set: ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$. As the M2 move cannot change the number of states, set: $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

1.3 The EA (ejection/absorption) moves

If $\mathcal {K}_g^{(i-1)}=1$, then an ejection move has to be performed. If $\mathcal {K}_g^{(i-1)}=\mathcal {K}_{\textit{MAX}}$, then an absorption move has to be performed. For $\mathcal {K}_g^{(i-1)}\in \{2,\ldots ,\mathcal {K}_{\textit{MAX}}-1\}$ the move type (ejection or absorption) is randomly drawn.

1.4 The ejection move

Randomly select a state $k\in \{1,\ldots ,\mathcal {K}_g^{(i-1)}\}$. Make a draw $p_{E}$ from a Beta(a, a) distribution and re-allocate each data point allocated to component k by ${\mathbf{V}}_g^{(i-1)}$ with probability $p_{E}$ to a new state with label $\mathcal {K}_g^{(i-1)}+1$ to obtain the new candidate allocation vector ${\mathbf{V}}_g^{\star }$. The new number of states, associated with ${\mathbf{V}}_g^{\star }$, is $\mathcal {K}_g^{\star }= \mathcal {K}_g^{(i-1)}+1$. The acceptance probability is $A=\min \{1,R\}$ where

$$\begin{aligned} R = \frac{P\left( {\mathbf{V}}_{g}^{\star }|\mathcal {K}_g^{\star }\right) P\left( \mathcal {K}_g^{\star }\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g\right) }{P\left( {\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}_g^{(i-1)}\right) P\left( \mathcal {K}_g^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g\right) } \cdot Q \end{aligned}$$

(40)

and Nobile and Fearnside (2007) show that the Hastings ratio is given by:

$$\begin{aligned} Q = \frac{Q\left( [{\mathbf{V}}_{g}^{(i-1)}, \mathcal {K}_g^{(i-1)}]|[{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]\right) }{Q\left( [{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}]\right) } = p_{E} \cdot \frac{\Gamma (a)^{2}}{\Gamma (2a)} \cdot \frac{ \Gamma (2a+n_{k})}{\Gamma (a+n_{\tilde{k}}^{*})\Gamma (a+n_{k}^{*})} \end{aligned}$$

(41)

where $n_{k}$ is the number of observations allocated to the kth state by ${\mathbf{V}}_g^{(i-1)}$, $n_{\tilde{k}}^{*}$ and $n_{k}^{*}$ are the numbers of data points allocated to the states $\tilde{k}$ and k by ${\mathbf{V}}_g^{\star }$. The factor $p_{E}$ is equal to one for $\mathcal {K}_g^{(i-1)}\in \{2,\ldots ,\mathcal {K}_{\textit{MAX}}-2\}$; while $p_E=0.5$ for $\mathcal {K}_g^{(i-1)}=1$, and $p_{E}=2$ for $\mathcal {K}_g^{(i-1)}=\mathcal {K}_{\textit{MAX}}-1$. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}+1$, or otherwise set: ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$. As suggested by Nobile and Fearnside (2007), I select the parameter a of the Beta(a,a) by numerically solving the equation:

$$\begin{aligned} \frac{\Gamma (2a)}{\Gamma (a)} \cdot \frac{\Gamma (a+n_k)}{\Gamma (2a+n_k)} = 0.1 \end{aligned}$$

where $n_k$ is the number of data points allocated to state k by ${\mathbf{V}}_g^{(i-1)}$, and I use a lookup table in my implementation. See Nobile and Fearnside (2007) for further details.

1.5 The absorption move

Randomly select two states $k,\tilde{k}\in \{1,\ldots ,\mathcal {K}_g^{(i-1)}\}$ with $\tilde{k}\ne k$. Re-allocate all data points allocated to state $\tilde{k}$ by the current allocation vector, ${\mathbf{V}}_g^{(i-1)}$, to state k to obtain the new allocation vector ${\mathbf{V}}_g^{\star }$. Then ${\mathbf{V}}_g^{\star }$ does not allocate data points to state $\tilde{k}$. If the (unemployed) state, $\tilde{k}$, is not equal to the maximal state, $\mathcal {K}_g^{(i-1)}$, swap the labels of the states $\tilde{k}$ and $\mathcal {K}_g^{(i-1)}$; i.e. set ${\mathbf{V}}_g^{\star }(t) = \tilde{k}$ for all t with ${\mathbf{V}}_g^{(i-1)}(t)=\mathcal {K}_g^{(i-1)}$. Afterwards delete the (unemployed) maximal state $\mathcal {K}_g^{(i-1)}$, and set $\mathcal {K}_g^{\star }=\mathcal {K}_g^{(i-1)}-1$. The acceptance probability is $A = \min \{1,R\}$, where R was specified in Eq. (40), and the Hastings ratio is now given by:

$$\begin{aligned} Q_A = \frac{Q\left( [{\mathbf{V}}_{g}^{(i-1)}, \mathcal {K}_g^{(i-1)}]|[{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]\right) }{Q\left( [{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}]\right) } = p_{A} \cdot \frac{\Gamma (2a)}{\Gamma (a)^{2}} \cdot \frac{\Gamma (a+n_{\tilde{k}})\Gamma (a+n_{k})}{ \Gamma (2a+n_{k}^{*})} \end{aligned}$$

where $n_{k}^{*}$ is the number of data points allocated to state k by the new candidate vector, ${\mathbf{V}}_g^{\star }$, $n_{k}$ and $n_{\tilde{k}}$ are the numbers of data points allocated to the states k and $\tilde{k}$ by ${\mathbf{V}}_g^{(i-1)}$, a is the parameter of the Beta(a,a) distribution in the ejection move, and $p_{A}=0.5$ for $\mathcal {K}_g^{(i-1)}=\mathcal {K}_{\textit{MAX}}$, $p_{A}=2$ for $\mathcal {K}_g^{(i-1)}=2$, while $p_{A}=1$ otherwise. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}-1$, or otherwise set: ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

Appendix 3: The novel inclusion and the novel exclusion move for the proposed HMM–DBN model

The novel inclusion move and the novel exclusion move both keep the network $\mathcal {M}=(\pi _1,\ldots ,\pi _{N})$ and the SNR hyperparameters fixed. I describe the ith MCMC iteration, $(i-1)\rightarrow i$, of this pair of moves for node g. If the current number of states is equal to one, $\mathcal {K}_g^{(i-1)}=1$, skip the move. Otherwise, draw an unbiased coin to decide, whether an inclusion or an exclusion move is performed. Given the current allocation vector, ${\mathbf{V}}_g^{(i-1)}$, both moves propose a new candidate allocation vector ${\mathbf{V}}_g^{\star }$. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$, or otherwise leave the allocation vector unchanged, ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$. Since neither the inclusion nor the exclusion move changes the number of states, set $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

1.1 The exclusion move

Randomly select one time point $t_0\in \{2,\ldots ,T\}$, and consider the state $k:={\mathbf{V}}_g^{(i-1)}(t_0)$ to which the selected time point is currently allocated to. Determine the highest time point $s_{E}\in \{2,\ldots ,t_0-1\}$ that is not allocated to state k:

$$\begin{aligned} s_{E} = \max \left\{ \tilde{t}\in \left\{ 2,\ldots ,t_0-1\right\} : {\mathbf{V}}_g^{(i-1)}(\tilde{t})\ne k\right\} \end{aligned}$$

(42)

If $s_{E}$ is not well-defined, set $s_{E}=1$ instead. Afterwards, determine the lowest time point $t_{E}\in \{t_0+1,\ldots ,T\}$ that is not allocated to state k:

$$\begin{aligned} t_{E} = \min \left\{ \tilde{t}\in \left\{ t_0+1,\ldots ,T\right\} : {\mathbf{V}}_g^{(i-1)}(\tilde{t})\ne k\right\} \end{aligned}$$

(43)

If $t_E$ is not well-defined, set $t_{E}=T+1$ instead.

Consider the sequence $s_E+1,\ldots ,t_E-1$. It follows from Eqs. (42–43) that all data points in the sequence are currently allocated to state k. The length of this sequence is $L_E=t_E-s_E-1$. If $L_E<3$, skip the move. Otherwise, draw a random number $u_1$ from the set $\{1,\ldots ,L_E-2\}$, and subsequently a random number $u_2$ from the set $\{0,\ldots ,L_E-2-u_1\}$. $u_1$ can be interpreted as the “subsequence length” and $u_2$ can be interpreted as the “lag”, since the exclusion move proposes to re-allocate the data points $s_E+u_2+2,\ldots ,s_E+u_2+1+u_1$ to a new state $\tilde{k}$, where $\tilde{k}\ne k$ is randomly drawn from all $\mathcal {K}_g^{(i-1)}-1$ states unequal to k. For the new candidate allocation vector, ${\mathbf{V}}_g^{\star }$, this yields: ${\mathbf{V}}_g^{\star }(t) = \tilde{k}$ if $t\in \{s_E+u_2+2,\ldots ,s_E+u_2+1+u_1\}$, and ${\mathbf{V}}_g^{\star }(t) = {\mathbf{V}}_g^{(i-1)}(t)$ for $t\notin \{s_E+u_2+2,\ldots ,s_E+u_2+1+u_1\}$. The Hastings is given by:

$$\begin{aligned} Q_E\left( {\mathbf{V}}_g^{\star }|{\mathbf{V}}_g^{(i-1)}\right) = \frac{L_E}{T-1} \cdot \frac{1}{L_E-2} \cdot \frac{1}{L_E-1-u_1} \cdot \frac{1}{\mathcal {K}_g^{(i-1)}-1} \end{aligned}$$

(44)

The first factor is the probability of selecting one point of the sequence $s_E+1,\ldots ,t_E-1$ of length $L_E$, the second and the third factor are the probabilities for selecting $u_1$ and $u_2$, respectively, and the last factor is the probability for selecting $\tilde{k}\ne k$.

1.2 The inclusion move

Randomly select one time point $t_0\in \{2,\ldots ,T\}$, and consider the state $k:={\mathbf{V}}_g^{(i-1)}(t_0)$ to which the selected time point is currently allocated to. Determine the highest time point $s_{I}\in \{2,\ldots ,t_0-1\}$ that is not allocated to state k:

$$\begin{aligned} s_{I} = \max \left\{ \tilde{t}\in \left\{ 2,\ldots ,t_0-1\right\} : {\mathbf{V}}_g^{(i-1)}(\tilde{t})\ne k\right\} \end{aligned}$$

(45)

If $s_{I}$ is not well-defined, skip the move. Otherwise, determine the lowest time point $t_{I}\in \{t_0+1,\ldots ,T\}$ that is not allocated to state k:

$$\begin{aligned} t_{I} = \min \left\{ \tilde{t}\in \left\{ t_0+1,\ldots ,T\right\} : {\mathbf{V}}_g^{(i-1)}(\tilde{t})\ne k\right\} \end{aligned}$$

(46)

If $t_I$ is not well-defined, skip the inclusion move.

Only if $s_I$ and $t_I$ are both well-defined, test whether ${\mathbf{V}}_g^{(i-1)}(s_I)$ is equal to ${\mathbf{V}}_g^{(i-1)}(t_I)$. If this ”equal boundaries“ test fails, skip the inclusion move. If the test is successful it holds: ${\mathbf{V}}_g^{(i-1)}(t)=k$ for $t\in \{s_I+1,\ldots ,t_I-1\}$ and ${\mathbf{V}}_g^{(i-1)}(s_I)={\mathbf{V}}_g^{(i-1)}(t_I)=:\tilde{k}$ where $\tilde{k}\ne k$. The inclusion move proposes to re-allocate all time points $t\in \{s_I+1,\ldots ,t_I-1\}$ to state $\tilde{k}$, i.e. to the state of the surrounding time points $s_I$ and $t_I$. This yields for the new candidate allocation vector, ${\mathbf{V}}_g^{\star }$: For $t=2,\ldots ,T$ set ${\mathbf{V}}_g^{\star }(t) = \tilde{k}$ if $t\in \{s_I+1,\ldots ,t_I-1\}$, or otherwise set ${\mathbf{V}}_g^{\star }(t) = {\mathbf{V}}_g^{(i-1)}(t)$. The proposal probability

$$\begin{aligned} Q_I\left( {\mathbf{V}}_g^{\star }|{\mathbf{V}}_g^{(i-1)}\right) = \frac{L_I}{T-1} \end{aligned}$$

(47)

is the probability of selecting one point $t_0$ of the sequence $s_I+1,\ldots ,t_I-1$ of length $L_I = t_I-s_I-1$.

1.3 Complementary inclusion move for the exclusion move

Consider the exclusion move from ${\mathbf{V}}_g^{(i-1)}$ to ${\mathbf{V}}_g^{\star }$, described above. The data points in the sequence $s_E+u_2+2,\ldots ,s_E+u_2+1+u_1$, which were originally allocated to state k, have been re-allocated to state $\tilde{k}$. The design of the exclusion move ensures that the new candidate vector, ${\mathbf{V}}_g^{\star }$, still allocates the two surrounding time points to state k, ${\mathbf{V}}_g^{\star }(s_E+u_2+1)=k={\mathbf{V}}_g^{\star }(s_E+u_2+2+u_1)$. The complementary move, which proposes to move back from ${\mathbf{V}}_g^{\star }$ to ${\mathbf{V}}_g^{(i-1)}$, is the inclusion move, which re-allocates the sequence $s_E+u_2+2,\ldots ,s_E+u_2+1+u_1$ back to state k. To this end, the complementary inclusion move has to select a point $t_0\in \{s_E+u_2+2,\ldots ,s_E+u_2+u_1+1\}$. It follows that $s_I=s_E+u_2+1$ and $t_I=s_E+u_2+u_1+2$ in Eqs. (45–46) are well-defined, and it is guaranteed that the “equal boundaries” test: ${\mathbf{V}}_g^{\star }(s_E+u_2+1)=\tilde{k}={\mathbf{V}}_g^{\star }(s_E+u_2+u_1+2)$ with $\tilde{k}\ne k$ is successful. Thus, the complementary inclusion move has the proposal probability:

$$\begin{aligned} Q_{I}^{C}\left( {\mathbf{V}}_g^{(i-1)}|{\mathbf{V}}_g^{\star }\right) = \frac{L_E}{T-1} \end{aligned}$$

(48)

where $L_E=u_1$ is the subsequence length parameter, which has been randomly drawn during the exclusion move. Hence, according to the Metropolis-Hastings criterion, the exclusion move, described above, is accepted with probability $A=\min \{1,R\}$, where

$$\begin{aligned} R = \frac{P\left( {\mathbf{V}}_{g}^{\star }|\mathcal {K}^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g\right) }{P\left( {\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g\right) } \cdot \frac{Q_I^{C}\left( {\mathbf{V}}_{g}^{(i-1)}|{\mathbf{V}}_{g}^{\star }\right) }{Q_E\left( {\mathbf{V}}_{g}^{\star }|{\mathbf{V}}_{g}^{(i-1)}\right) } \end{aligned}$$

(49)

The likelihood ratio can be computed with Eq. (12), and the Hastings ratio can be computed with Eqs. (44) and (48).

1.4 Complementary exclusion move for the inclusion move

Consider the inclusion move from ${\mathbf{V}}_g^{(i-1)}$ to ${\mathbf{V}}_g^{\star }$, described above. The data points in the sequence $s_I+1,\ldots ,t_I-1$, which were allocated to state k, have been re-allocated to state $\tilde{k}$, and the design of the inclusion move ensures that the new candidate vector, ${\mathbf{V}}_g^{\star }$, allocates the surrounding time points to state $\tilde{k}$ as well: ${\mathbf{V}}_g^{\star }(s_I)=\tilde{k}={\mathbf{V}}_g^{\star }(t_I)$.

The complementary move, which proposes to move back from ${\mathbf{V}}_g^{\star }$ to ${\mathbf{V}}_g^{(i-1)}$, is the exclusion move, which re-allocates the subsequence $s_I+1,\ldots ,t_I-1$ of length $L_I=t_I-s_I-1$ to state k. To this end, the complementary exclusion move has to select one single point $t_0$ out of the sequence $s_E^C+1,\ldots ,t_E^C-1$ where

$$\begin{aligned} s_{E}^C := \max \left\{ \tilde{t}\in \left\{ 2,\ldots ,s_I-1\right\} : {\mathbf{V}}_g^{\star }(\tilde{t})\ne \tilde{k}\right\} \end{aligned}$$

(50)

and $s_E^C=1$ if $s_E^C$ is not well-defined.

$$\begin{aligned} t_{E}^C := \min \left\{ \tilde{t}\in \left\{ t_I+1,\ldots ,T\right\} : {\mathbf{V}}_g^{(\star }(\tilde{t})\ne \tilde{k}\right\} \end{aligned}$$

(51)

and $t_E^C=T+1$ if $t_E^C$ is not well-defined.

Having selected $t_0$, the “subsequence length” $u_1:=L_I$ and the “lag” $u_2:=s_I-s_E^C-1$ have to be sampled out of the sets $\{1,\ldots ,L_E^C-2\}$ and $\{0,\ldots ,L_E^C-2-u_1\}$, respectively, where $L_E^C:=t_E^C-s_E^C-1$ is the length of the sequence $s_E^C+1,\ldots ,t_E^C-1$. Finally, the complementary exclusion move has to randomly draw the state k from all $\mathcal {K}_g^{(i-1)}-1$ states unequal to $\tilde{k}$. Thus, the complementary exclusion move has the proposal probability:

$$\begin{aligned} Q_E^{C}({\mathbf{V}}_g^{\star }|{\mathbf{V}}_g^{(i-1)}) = \frac{L_E^C}{T-1} \cdot \frac{1}{L_E^C-2} \cdot \frac{1}{L_E^C-1-u_1} \cdot \frac{1}{\mathcal {K}_g^{(i-1)}-1} \end{aligned}$$

(52)

Hence, according to the standard Metropolis-Hastings criterion, the inclusion move, described above, is accepted with probability $A=\min \{1,R\}$, where

$$\begin{aligned} R = \frac{P\left( {\mathbf{V}}_{g}^{\star }|\mathcal {K}^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g\right) }{P\left( {\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g\right) } \cdot \frac{ Q_E^{C}\left( {\mathbf{V}}_{g}^{(i-1)}|{\mathbf{V}}_{g}^{\star }\right) }{Q_I\left( {\mathbf{V}}_{g}^{\star }|{\mathbf{V}}_{g}^{(i-1)}\right) } \end{aligned}$$

(53)

The likelihood ratio can be computed with Eq. (12), and the Hastings ratio can be computed with Eqs. (47) and (52).

Appendix 4: The novel birth and the novel death move for the proposed HMM–DBN model

The novel birth and the novel death move both keep the network $\mathcal {M}=(\pi _1,\ldots ,\pi _{N})$ and the SNR hyperparameters fixed. I describe the ith MCMC iteration, $(i-1)\rightarrow i$, of the Metropolis-Hastings Birth/Death move for node g. Draw an unbiased coin to decide whether a birth or a death move is performed. Given the current allocation vector, ${\mathbf{V}}_g^{(i-1)}$, the birth move proposes to increase the number of states by 1, $\mathcal {K}_g^{\star }=\mathcal {K}_g^{(i-1)}+1$, while the death move proposes to decrease the number of states by 1, $\mathcal {K}_g^{\star }=\mathcal {K}_g^{(i-1)}-1$. Thereby both moves propose a new candidate allocation vector ${\mathbf{V}}_g^{\star }$. If the move is accepted, set ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{\star }$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{\star }$, or otherwise leave the allocation vector unchanged, i.e. set: ${\mathbf{V}}_g^{(i)}={\mathbf{V}}_g^{(i-1)}$ and $\mathcal {K}_g^{(i)}=\mathcal {K}_g^{(i-1)}$.

1.1 The novel birth move

If the current number of states has reached the maximum, $\mathcal {K}_g^{(i-1)}=\mathcal {K}_{\textit{MAX}}$, skip the move. Otherwise, randomly select one state $k_0\in \{1,\ldots ,\mathcal {K}^{(i-1)}_g\}$ and determine the set of all data points that are currently allocated to state $k_0$:

$$\begin{aligned} T_0 = \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{(i-1)}(t)=k_0 \right\} \end{aligned}$$

(54)

If the number of data points in the set $T_0$ is lower than 2, $|T_0|<2$, skip the birth move. Otherwise, draw a random number $b_1$ from the set $\{1,\ldots ,|T_0|-1\}$. Order the time points in the set $T_0$, and let $t_1,\ldots ,t_{|T_0|}$ denote the ordering of the data points in the set $T_0$. The birth move proposes to re-allocate the last $|T_0|-b_1$ data points, $t=t_{b_1+1},\ldots ,t_{|T_0|}$, with ${\mathbf{V}}_g^{(i-1)}(t)=k_0$ to a new state $k_{new}:=\mathcal {K}_g^{(i-1)}+1$. The new candidate allocation vector is given by: ${\mathbf{V}}_g^{\star }(t) = k_{new}$ for $t=t_{b_1+1},\ldots ,t_{|T_0|}$, and ${\mathbf{V}}_g^{\star }(t) = {\mathbf{V}}_g^{(i-1)}(t)$ for all other data points t. The proposal probability is given by:

$$\begin{aligned} Q_B\left( [{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]\right) = \frac{1}{\mathcal {K}_g^{(i-1)}} \cdot \frac{1}{|T_0|-1} \end{aligned}$$

(55)

1.2 The novel death move

If the number of states is equal to one, $\mathcal {K}_g^{(i-1)}=1$, skip the move. Otherwise, randomly select $k_1$ and $k_2$ with $k_1<k_2$ out of the set $\{1,\ldots ,\mathcal {K}_g^{(i-1)}\}$. Determine the sets of data points that are currently allocated to $k_1$ and $k_2$:

$$\begin{aligned} T_1= & {} \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{(i-1)}(t)=k_1 \right\} \end{aligned}$$

(56)

$$\begin{aligned} T_2= & {} \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{(i-1)}(t)=k_2 \right\} \end{aligned}$$

(57)

If one of the two sets is empty, skip the move. Otherwise, order the data points in $T_1$ and $T_2$, and let $t^{[1]}_{1},\ldots ,t^{[1]}_{|T_1|}$ and $t^{[2]}_{1},\ldots ,t^{[2]}_{|T_2|}$ denote the orders of the time points in $T_1$ and $T_2$, respectively. Check whether the time points in $T_1$ and $T_2$ are “separated” (not “overlapping”), i.e. check if either $t^{[1]}_1>t^{[2]}_{|T_2|}$ or $t^{[2]}_1>t^{[1]}_{|T_1|}$. If the test fails, skip the move. Otherwise, the birth move proposes to re-allocate all time points in the set $T_2$ to state $k_1$. The new candidate allocation vector is then given by: ${\mathbf{V}}_g^{\star }(t) = k_1$ for $t\in T_2$, and ${\mathbf{V}}_g^{\star }(t) = {\mathbf{V}}_g^{(i-1)}(t)$ for $t\notin T_2$, and the proposal probability is:

$$\begin{aligned} Q_D\left( [{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]\right) = \frac{2}{\mathcal {K}_g^{(i-1)}\cdot \left( \mathcal {K}_g^{(i-1)}-1\right) } \end{aligned}$$

(58)

The new candidate allocation vector, ${\mathbf{V}}_g^{\star }$, does not allocate time points to the state $k_2$ anymore. If $k_2\ne \mathcal {K}_g^{(i-1)}$, perform a swap move, i.e. set ${\mathbf{V}}_g^{\star }(t) = k_2$ for all t with ${\mathbf{V}}_g^{(i-1)}(t)=\mathcal {K}_g^{(i-1)}$. The last state is then obsolete and can be deleted, i.e. set: $\mathcal {K}_g^{\star }=\mathcal {K}_g^{(i-1)}-1$.

1.3 Complementary death move for the birth move

Consider the birth move from $[{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]$ to $[{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]$, described above. The data points $t_{b_1+1},\ldots ,t_{|T_0|}$, which were allocated to state $k_0$, have been re-allocated to the new state $k_{new}=\mathcal {K}_g^{(i-1)}+1$. The complementary death move has to select the states $k_{0}$ and $k_{new}$ out of the set $\{1,\ldots ,\mathcal {K}_g^{\star }\}$, where $\mathcal {K}_g^{\star }=\mathcal {K}_g^{(i-1)}+1$, and then has to re-allocate all data points in the set

$$\begin{aligned} T_0^C = \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{\star }(t)=k_{new}\right\} \end{aligned}$$

(59)

back to state $k_0$. The design of the birth move ensures that the two sets

$$\begin{aligned} T_1^C= & {} \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{\star }(t)=k_0 \right\} \end{aligned}$$

(60)

$$\begin{aligned} T_2^C= & {} \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{\star }(t)=k_{new} \right\} \end{aligned}$$

(61)

are non-empty, and that the highest time point in $T_1^C$ precedes the lowest time point in $T_2^C$, i.e. that the two sets are “separated” (non-overlapping). Hence, the complementary death move can be performed, i.e. will not be skipped, and has the proposal probability:

$$\begin{aligned} Q_D^C([{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]|]{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]) = \frac{2}{\left( \mathcal {K}_g^{(i-1)}+1\right) \cdot \mathcal {K}_g^{(i-1)}} \end{aligned}$$

(62)

According to the standard Metropolis-Hastings criterion, the birth move, described above, is accepted with probability $A=\min \{1,R\}$, where

$$\begin{aligned} R = \frac{P(\mathcal {K}_{g}^{\star }) P\left( {\mathbf{V}}_{g}^{\star }|\mathcal {K}_g^{\star }\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{\star }}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{\star }},\delta _g\right) }{P\left( \mathcal {K}_{g}^{(i-1)}\right) P\left( {\mathbf{V}}_{g}^{(i-1)}|\mathcal {K}_g^{(i-1)}\right) P\left( \mathbf{y}_{g,{\mathbf{V}}_{g}^{(i-1)}}|\mathbf{X}_{g,{\mathbf{V}}_{g}^{(i-1)}},\delta _g\right) } \cdot Q \end{aligned}$$

(63)

and

$$\begin{aligned} Q = \frac{ Q_D^{C}([{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}]|[{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]}{Q_B([{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}])} \end{aligned}$$

(64)

The likelihood ratio can be computed with Eq. (12), and the Hastings ratio, Q, can be computed with Eqs. (55) and (62).

1.4 Complementary birth move for the death move

Consider the death move from $[{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]$ to $[{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]$, described above. The birth move has proposed to re-allocate all time points of the set.

$$\begin{aligned} T_2 = \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{(i-1)}(t)=k_2 \right\} \end{aligned}$$

(65)

to state $k_1$. The complementary birth move has to select the state $k_1\in \{1,\ldots ,\mathcal {K}^{\star }_g\}$, and the design of the death move guarantees that the set:

$$\begin{aligned} T_0^C = \left\{ t\in \left\{ 2,\ldots ,T\right\} |{\mathbf{V}}_g^{\star }(t)=k_1\right\} \end{aligned}$$

(66)

has a cardinality greater than 2. Subsequently, the random number $b_1^C:=|T_0^C|-|T_2|$ has to be drawn from the set $\{1,\ldots ,|T_0^C|-1\}$. Ordering all the time points in the set $T_0^C$, yields the order $t_1,\ldots ,t_{|T_0^C|}$, and the complementary birth move proposes to re-allocate the last $|T_0^C|-b_1^C=|T_2|$ time points, $t=t_{b_1^C+1},\ldots ,t_{|T_0^C|}$ to a new state $k_{new}:=\mathcal {K}_g^{(i-1)}+1$.²⁶ The design of the death move, i.e. the successfully passed “separation” test, guarantees that the data points $t_{b_1^C+1},\ldots ,t_{|T_0^C|}$ correspond to the data points in the set $T_2$. The complementary birth move has the proposal probability:

$$\begin{aligned} Q_B^C([{\mathbf{V}}_g^{(i-1)},\mathcal {K}_g^{(i-1)}]|]{\mathbf{V}}_g^{\star },\mathcal {K}_g^{\star }]) = \frac{1}{\mathcal {K}_g^{\star }} \cdot \frac{1}{|T_0^C|-1} \end{aligned}$$

(67)

Hence, according to the standard Metropolis-Hastings criterion, the death move, described above, is accepted with probability $A=\min \{1,R\}$, where R was defined in Eq. (63) and the Hastings Ratio, Q, is now given by:

$$\begin{aligned} Q = \frac{ Q_B^{C}([{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}]|[{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]}{Q_D([{\mathbf{V}}_{g}^{\star },\mathcal {K}_g^{\star }]|[{\mathbf{V}}_{g}^{(i-1)},\mathcal {K}_g^{(i-1)}])} \end{aligned}$$

(68)

and can be computed with Eqs. (58) and (67).