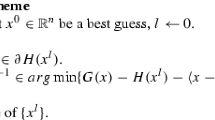Feature selection in machine learning: an exact penalty approach using a Difference of Convex function Algorithm

Abstract

We develop an exact penalty approach for feature selection in machine learning via the zero-norm $\ell _{0}$-regularization problem. Using a new result on exact penalty techniques we reformulate equivalently the original problem as a Difference of Convex (DC) functions program. This approach permits us to consider all the existing convex and nonconvex approximation approaches to treat the zero-norm in a unified view within DC programming and DCA framework. An efficient DCA scheme is investigated for the resulting DC program. The algorithm is implemented for feature selection in SVM, that requires solving one linear program at each iteration and enjoys interesting convergence properties. We perform an empirical comparison with some nonconvex approximation approaches, and show using several datasets from the UCI database/Challenging NIPS 2003 that the proposed algorithm is efficient in both feature selection and classification.

1 Introduction

Feature (or variable) selection, which consists of choosing a subset of available features that capture the relevant properties of the data, is one of fundamental problems in machine learning. Feature selection can help enhance accuracy in many machine learning problems, it can also improve the efficiency of training. Features can be divided into three categories: relevant, redundant and irrelevant features. An irrelevant feature does not apport any useful information while a redundant feature adds no new information to learning procedures (i.e. information already carried by other features). Ideally, the learning process should discard irrelevant/redundant features and use only a subset of relevant features that leads to the best performance.

Machine learning methods for feature selection can be divided into three classes (Rinaldi 2000): wrapper, filter, and embedded methods. Wrapper methods exploit a machine learning algorithm to evaluate the usefulness of features. Filter methods rank the features according to some discrimination measure and select features having higher ranks without using any learning algorithm (it utilizes the underlying characteristics of the training data to evaluate the relevance of the features or feature set by some independent measures such as distance measure, correlation measures, consistency measures (Chen et al. 2006). The wrapper approach is generally considered to produce better feature subsets but runs much more slowly than a filter. Embedded methods do not separate the learning from the feature selection part. It integrates the selection of features in the model building.

This paper concerns with an embedded approach for feature selection in machine learning. For a vector $x\in \mathbb {R}^{n}$, the support of $x$, denoted $supp(x)$, is the set of the indices of the non-zero components of $x$, say

$$\begin{aligned} supp(x)=\left\{ i\in \left\{ 1,\ldots ,n\right\} :\;x_{i}\ne 0\right\} , \end{aligned}$$

and the zero-norm of $x$, denoted $\ell _{0}$-norm is defined as

$$\begin{aligned} \left\| x\right\| _{0}{:=}\text {cardinality of }supp(x). \end{aligned}$$

The useful notation $\left| .\right| _{0}$ denoting the $\ell _{0}$-norm on $\mathbb {R},$ also called the step function ($\left| x\right| _{0}=1$ if $x\ne 0$, $0$ otherwise) allows for expressing the separability of $\Vert .\Vert _{0}$ on $\mathbb {R}^{n}$

$$\begin{aligned} \Vert x\Vert _{0}=\sum _{i=1}^{n}\left| x_{i}\right| _{0}. \end{aligned}$$

(1)

Given a training data $\left\{ \vartheta _{i},\delta _{i}\right\} _{i=1,\ldots ,m}$ where each $\vartheta _{i}\in \mathbb {R}^{n}$ corresponds to the observed value $\delta _{i}.$ Formally, a learning task can be defined as the following structural risk minimization problem (for a given $\lambda >0)$

$$\begin{aligned} \min _{x,y}\sum _{i=1}^{m}L(\vartheta _{i},\delta _{i};x,\mu )+\lambda \varOmega (x), \end{aligned}$$

(2)

where $L$ is a loss function defined on $\mathbb {R}^{n}\mathbb {\times R}^{p}$ and $\varOmega (\cdot )$ is the regularizer (or penalty) term. The loss function $L$ is the data fitting term measuring the discrepancy for all training examples $\left\{ \vartheta _{i},\delta _{i}\right\}$ between the predicted value and the observed value. The regularizer term $\varOmega (\cdot )$ is a penalty providing regularization and controlling generalization ability through model complexity.

A natural way to deal with feature selection in machine learning is using $\ell _{0}$-norm in the regularization term that leads to the following problem:

$$\begin{aligned} \min _{\ }\left\{ \sum _{i=1}^{m}L(\vartheta _{i},\delta _{i};x,\mu )+\lambda \left\| x\right\| _{0}:(x,\mu )\in \mathbb {R}^{n}\mathbb {\times R}^{p}\right\} . \end{aligned}$$

(3)

Let $K$ be a bounded polyhedral convex set in $\mathbb {R}^{n}\times \mathbb {R}^{p}.$ We consider in this paper a so called $\ell _{0}$-regularizer problem that takes the form

$$\begin{aligned} \min \left\{ f(x,\mu )+\lambda \left\| x\right\| _{0}:(x,\mu )\in K\right\} , \end{aligned}$$

(4)

where the function $f$ corresponding to a given convex criterion is assumed to be convex and the regularization parameter $\lambda$ makes the trade-off between the criterion $f$ and the sparsity of $x$. Here $\mu$ is the variable that does not deal with the sparsity. This problem is a common model that can be used in several learning contexts including feature selection in classification, feature selection in linear regression, sparse Fisher linear discriminant analysis, feature selection in learning to rank with sparse SVM, etc.

The function $\ell _{0}$, apparently very simple, is lower-semicontinuous on $\mathbb {R}^{n},$ but its discontinuity at the origin makes nonconvex programs involving $\Vert .\Vert _{0}$ challenging, they are known to be NP-hard (Amaldi and Kann 1998; Natarajan 1995) and actually intractable. To circumvent the discontinuity, continuous approaches are developed since many years.

During the last two decades, research is very active in models and methods optimization involving the zero-norm. Works can be divided into three categories according to the way to treat the zero-norm: convex approximation, nonconvex approximation, and nonconvex exact reformulation.

In the machine learning community, one of the best known approaches, belonging to the group “convex approximation”, is the $\ell _{1}$ regularization approach proposed in Tibshirani (1996) in the context of linear regression, called least absolute shrinkage and selection operator (LASSO), which consists in replacing the $\ell _{0}$ term $\left\| x\right\| _{0}$ by $\left\| x\right\| _{1}$, the $\ell _{1}$-norm of the vector $x$. In Gribonval and Nielsen (2003), the authors have proven that, under suitable assumptions, a solution of the $\ell _{0}$- regularizer problem over a polyhedral set can be obtained by solving the $\ell _{1}$- regularizer problem. However, these assumptions may not be satisfied in many cases. Since its introduction, several works have been developed to study the $\ell _{1}$-regularization technique, from the theoretical point of view to efficient computational methods (see Hastie et al. 2009, Chap. 18 for more discussions on $\ell _{1}$-regularized methods). Among the best approaches, it is worth to citing the Elastic net proposed by Zou and Hastie (2005) for variable selection in regression which is a combination between the ridge ($\ell _{2}$ norm) and the LASSO penalty. It has been shown that the elastic net not only dominates the LASSO in terms of prediction accuracy but also is a better variable selection procedure than the LASSO. The LASSO penalty has been shown to be, in certain cases, inconsistent for variable selection and biased (Zou 2006). Hence, the Adaptive LASSO is introduced in Zou (2006) in which adaptive weights are used for penalizing different coefficients in the $\ell _{1}$-penalty.

At the same time, nonconvex continuous approaches, belonging to the second group “nonconvex approximation” (the $\ell _{0}$ term $\left\| x\right\| _{0}$ is approximated by a nonconvex continuous function) were extensively developed. The first was concave exponential approximation with successive linear approximation (SLA) algorithm proposed in Bradley and Mangasarian (1998) for feature selection in SVM. Later, with the same approximation, an efficient Difference of Convex functions (DC) algorithm (DCA) was developed in Le Thi et al. (2008). Various other nonconvex regularizations have been developed in several works in different contexts, most of them are for feature selection in SVM or feature selection in regression. For example, hard-thresholding methods and/or DCA using the Smoothly Clipped Absolute Deviation (SCAD) (Fan and Li 2001; Kim et al. 2008; Le Thi et al. 2009; Ong and Le Thi 2013; Zou and Li 2008), the log penalty method (Candes et al. 2008) via the logarithmic approximation of Weston et al. (2003), the $\ell _{q}$, $0<q<1$ regularization with reweighted $\ell _{2}$ and/or DCA (Chartrand and Yin 2008; Fu 1998; Gasso et al. 2009; Huang et al. 2008; Knight and Fu 2000; Chen et al. 2010; Guan and Gray 2013; Gorodnitsky and Rao 1997; Rao and Kreutz-Delgado 1999; Rao et al. 2003). The common properties of these approaches are that the nonconvex regularization used for approximating the $\ell _{0}$ norm is a DC function, and the resulting optimization problem is a DC program for which DCA, an efficient approach in nonconvex programming framework (see e.g. Le Thi and Pham Dinh 2005; Pham Dinh and Le Thi 1998) has been investigated (Le Thi et al. 2008, 2009; Neumann et al. 2005; Ong and Le Thi 2013; Collober et al. 2006; Candes et al. 2008; Gasso et al. 2009; Guan and Gray 2013) (note also that the SLA (Bradley and Mangasarian 1998), the adaptive LASSO (Zou 2006) are special cases of DCA). These DCA based algorithms solve iteratively a sequence of convex programs (linear or quadratic programs in many cases) until the convergence and can be viewed as sequences of reweighted $\ell _{1}$ (see for example Candes et al. 2008) or reweighted $\ell _{2}$. For instance, Focal Underdetermined System Solver (FOCUSS) (Gorodnitsky and Rao 1997; Rao and Kreutz-Delgado 1999; Rao et al. 2003), Iteratively reweighted least squares (IRLS) (Chartrand and Yin 2008) introduced in the context of compressed sensing, via the $\ell _{q}$-regularizer with $0<q<1,$ can be viewed as a reweighted $\ell _{2}$ procedure. The Local Quadratic Approximation (LQA) algorithm in Fan and Li (2001) and Zhang et al. (2006) can be also regarded as reweighted $\ell _{2}$ applied on SCAD penalty. Overall, we can say that most of existing methods in nonconvex approximation approaches are DCA based algorithms. Besides, the relaxed Lasso, a generalization of both soft and hard thresholding, introducing a two-stage procedure has been proposed in Meinshausen (2007).

In the third category that we call nonconvex exact reformulation approaches, the $\ell _{0}$-regularized problem is reformulated as a continuous nonconvex program. There are few works in this category. In Mangasarian (1996), the author reformulated the problem (4) in the context of feature selection in SVM as a linear program with equilibrium constraints (LPEC). However, this reformulation is generally intractable for large-scale datasets. In Thiao et al. (2010) an exact penalty technique is used for Sparse Eigenvalue problem with $\ell _{0}$-norm in constraint functions

$$\begin{aligned} \max \{x^{T}Ax:x^{T}x=1,\left\| x\right\| _{0}\le k\}, \end{aligned}$$

(5)

where $A\in \mathbb {R}^{n\times n}$ is symmetric and $k$ an integer, and a DCA based algorithm was investigated for the resulting problem.

Convex regularization approaches involve convex optimization problems which are so far “easy” to solve, but they does not attain the solution of the $\ell _{0}$-regularizer problem. Nonconvex approximations are, in general, deeper than convex relaxations, and then can produce good sparsity, but the resulting optimization problems are still difficult since they are nonconvex and there are many local minima which are not global. Moreover, the consistency between the approximate problems and the original problem is an open question, i.e. it can not be guaranteed. The exact reformulation approaches can overcome these drawbacks if efficient methods for the reformulation problem are available.

Besides the three above categories, heuristic methods are developed to tackle directly the original problem (4) by greedy based algorithms, e.g. matching pursuit, orthogonal matching pursuit (Mallat and Zhang 1993; Bach et al. 2012), etc.

Our contributions. The above arguments suggest us to develop in this paper an exact reformulation approach for solving the original problem (4). Our main motivation is to exploit the efficiency of DCA to solve this hard problem in an equivalent formulation. A new result on exact penalty techniques recently developed in Le Thi et al. (2012) supports this idea. The $\ell _{0}$-regularization problem is first equivalently formulated as a combinatorial optimization problem by using the binary variables $u_{i}=0$ if $x_{i}=0$ and $u_{i}=1$ if $x_{i}\ne 0,$ and then the last problem is reformulated as a DC program via an exact penalty technique (Le Thi et al. 2012). These combinatorial and continuous formulations of (4) permit us to consider all the above convex and nonconvex approaches to treat the zero-norm in a unified view within DC programming and DCA framework. More precisely, we show that the $\ell _{1}$-approach is nothing else the linear relaxation of our combinatorial formulation of (4) while some nonconvex approximations can be regarded as our exact penalty reformulation with suitable parameters. This study is very useful to justify nonconvex approximation approaches. As an application of the proposed approach, we consider the problem of feature selection in SVM. We perform an empirical comparison with some nonconvex approximation approaches, and show using several datasets from the UCI database that the proposed algorithm is efficient in both feature selection and classification.

The rest of the paper is organized as follows. In the next section we present our exact penalty technique to equivalently reformulate the problem (4) as a DC program and discuss about the links between our approach with convex and/or nonconvex approximation approaches. The solution methods based on DC programming and DCA are developed in Sect. 3 while the implementation of the algorithm for feature selection in SVM and numerical experiments are presented in Sect. 4. Finally, some conclusions are provided in Sect. 5. In the appendix we describe the comparative DCA schemes considered in our experiments.

2 Exact penalty techniques related to the $\ell _{0}$-norm

In this section, we first consider the two following problems ($K$ being a bounded polyhedral convex set in $\mathbb {R}^{n}\times \mathbb {R}^{p}, \lambda$ a positive parameter and $k$ a positive integer)

$$\begin{aligned}&\alpha {{:=}}\inf \{f(x,\mu )+\lambda \Vert x\Vert _{0}:(x,\mu )\in K\},\end{aligned}$$

(6)

$$\begin{aligned}&\alpha {{:=}}\inf \{f(x,\mu ):(x,\mu )\in K,\},\Vert x\Vert _{0}\le k\} \end{aligned}$$

(7)

whose feasible sets are assumed to be nonempty.

2.1 Continuous reformulation via exact penalty techniques

We will present some main results concerning penalty techniques related to $\ell _{0}$-norm allowing for reformulation of (6 ) and (7) as nonconvex programs in the continuous framework, especially DC programs, that can be treated by DC programming and DCA.

Denote by $e$ the vector of ones in the appropriate vector space. We suppose that $K$ is bounded in the variable $x,$i.e. $K\subset \varPi _{i=1}^{n}[a_{i},b_{i}]\times \mathbb {R}^{m}$ where $a_{i},b_{i}\in \mathbb {R}$ such that $a_{i}\le 0<b_{i}$ for $i=1,\ldots ,n.$ Let $c_{i}{:=}\max \{\left| x_{i}\right| :x_{i}\in [a_{i},b_{i}]\}=\max \{\left| a_{i}\right| ,\left| b_{i}\right| \}$ for $i=1,\ldots ,n.$ Define the binary variable $u_{i}\in \left\{ 0,1\right\}$ as

$$\begin{aligned} u_{i}=\left| x_{i}\right| _{0}= {\left\{ \begin{array}{ll} 1\text { if }x_{i}\ne 0 \\ 0\text { if }x_{i}=0, \end{array}\right. } \qquad \forall i=1\ldots n. \end{aligned}$$

(8)

Then (6) and (7) can be reformulated as

$$\begin{aligned} \alpha {{:=}}\inf \{f(x,\mu )+\lambda e^{T}u:(x,\mu )\in K,u\in \{0,1\}^{n},\left| x_{i}\right| \le c_{i}u_{i},\text { }i=1,\ldots ,n\}, \end{aligned}$$

(9)

and

$$\begin{aligned} \alpha {{:=}}\inf \{f(x,\mu ):(x,\mu )\in K,u\in \{0,1\}^{n},\left| x_{i}\right| \le c_{i}u_{i},i=1,\ldots ,n,\text { }e^{T}u\le k\text { }\}, \end{aligned}$$

(10)

respectively.

Let $p(u)$ be the penalty function defined by

$$\begin{aligned} p(u){{:=}}\sum \limits _{i=1}^{n}\min \{u_{i},1-u_{i}\}\text { .} \end{aligned}$$

(11)

Then (6) and (7) can be rewritten respectively as

$$\begin{aligned} \alpha =\inf \{f(x,\mu )+\lambda e^{T}u:(x,\mu )\in K,u\in [0,1]^{n},\left| x_{i}\right| \le c_{i}u_{i},\text { }i=1,\ldots ,n,\text { }p(u)\le 0\}, \end{aligned}$$

(12)

and

$$\begin{aligned} \alpha {{:=}}\inf \{f(x,\mu ):(x,\mu )\in K,u\in [0,1]^{n},\left| x_{i}\right| \le c_{i}u_{i},i=1,\ldots ,n, e^{T}u\le k, p(u)\le 0\}. \end{aligned}$$

(13)

It leads to the corresponding penalized problems $(\tau$ being the positive penalty parameter)

$$\begin{aligned} \begin{array}{ll} \alpha (\tau ){{:=}}\inf \{f(x,\mu ){+}\lambda e^{T}u{+}\tau p(u):&(x,\mu )\in K,u\in [0,1]^{n}, \left| x_{i}\right| \le c_{i}u_{i},\text { }i=1,\ldots ,n\}, \end{array} \end{aligned}$$

(14)

and

$$\begin{aligned} \begin{array}{ll} \alpha (\tau ){{:=}}\inf \{f(x,\mu ){+}\tau p(u):&(x,\mu )\in K,u\in [0,1]^{n}, \left| x_{i}\right| {\le } c_{i}u_{i},i=1,\ldots ,n,e^{T}u\le k\}. \end{array} \end{aligned}$$

(15)

Proposition 1

There is $\tau _{0}\ge 0$ such that for every $\tau >\tau _{0}$ problems (6) (resp. (7)) and (14) (resp. (15)) are equivalent, in the sense that they have the same optimal value and $(x^{*},\mu ^{*})\in K$ is a solution of (6) (resp. (7)) iff there is $u^{*}\in \{0,1\}^{n}$ such that $(x^{*},\mu ^{*},u^{*})$ is a solution of (14) (resp. (15)).

Proof

Direct consequences of Theorem 8 in Le Thi et al. (2012).

It is clear that (14) and (15) are DC programs if the function $f(x,y)$ is a DC function on $K.$

Note that, in general, the minimal penalty parameter $\tau _{0}$, if any, is not computable. In practice, upper bounds for $\tau _{0}$ can be calculated in some cases, e.g. sparse eigenvalue problems (Thiao et al. 2010).

In the sequel, we will focus on the $\ell _{0}$-regularizer problem (6) and its penalized problem (14).

2.2 Link between (9) and the $\ell _{1}$-regularization problem

It is easy to see that the linear relaxation of Problem (9) is a $\ell _{1}$-regularization problem. Indeed, the linear relaxation of Problem (9) (which is in fact the penalized problem (14) when $\tau =0)$ takes the form

$$\begin{aligned} \inf \{f(x,\mu )+\lambda e^{T}u:(x,\mu )\in K,u\in [0,1]^{n},\left| x_{i}\right| \le c_{i}u_{i},i=1,\ldots ,n\}. \end{aligned}$$

(16)

Let $M=\max \{c_{i}:i=1,\dots ,n\}$, problem (16) becomes

$$\begin{aligned} \inf \{f(x,\mu )+\lambda e^{T}u:(x,\mu )\in K,u\in [0,1]^{n},|x_{i}|\le Mu_{i},~i=1,\dots ,n\} \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \inf \left\{ f(x,\mu )+\lambda e^{T}u\ :(x,\mu )\in K,u\in [0,1]^{n},\frac{ |x_{i}|}{M}\le u_{i}\le 1,~i=1,\dots ,n\right\} \end{aligned}$$

or again

$$\begin{aligned} \inf \left\{ f(x,\mu )+\ \frac{\lambda }{M}\sum _{i=1}^{n}|x_{i}|:(x,\mu )\in K\right\} =\inf \left\{ f(x,\mu )+\ \frac{\lambda }{M}\ \left\| x\right\| _{1}:(x,y)\in K\right\} . \end{aligned}$$

2.3 Link between (14) and a nonconvex approximate problem

Most existing approximations of $\ell _{0}$-norm are its DC minorants. We consider here the last (in chronological order) introduced approximation (Peleg and Meir 2008) which is among the best approximations of $\ell _{0}$-norm (Ong and Le Thi 2013). It is defined by:

$$\begin{aligned} \varPsi _{_{\theta }}(x){{:=}}\sum _{i=1}^{n}\psi _{_{\theta }}(x_{i}),\forall x=(x_{i})\in \mathbb {R}^{n},\text { with }\psi _{\theta }(t){{:=}}\min \{\theta \left| t\right| ,1\},\text { }t\in \mathbb {R}. \end{aligned}$$

(17)

Since $\psi _{\theta }(t)=\theta \left| t\right| +1-\max \{\theta \left| t\right| ,1\}$ is a polyhedral DC function, we name this approximation as polyhedral DC approximation. We will show that the resulting approximate problem of (4), namely

$$\begin{aligned} \beta (\theta ){{:=}}\inf \left\{ f(x,\mu )+\lambda \sum _{i=1}^{n}\psi _{\theta }\left( x_{i}\right) :(x,\mu )\in K\right\} \end{aligned}$$

(18)

is equivalent to the penalized problem (14) with suitable values of parameters $\lambda ,\tau$ and $\theta$.

Consider the problem (14) in the form

$$\begin{aligned} \alpha (\tau ){{:=}}\inf \{f(x,\mu )+\lambda e^{T}u+\tau p(u):(x,\mu )\in K,u\in [0,1]^{n},|x_{i}|\le Mu_{i},~i=1,\dots ,n\}. \end{aligned}$$

(19)

Let $r:\mathbb {R\rightarrow R}$ be the function defined by $r(t)=\min \{t,1-t\}.$ Then $p(u)=\sum _{i=1}^{n}r(u_{i})$ and the problem (19) can be rewritten as

$$\begin{aligned} \alpha (\tau ){{:=}}\inf \left\{ f(x,\mu )+\lambda \sum _{i=1}^{n}\left( u_{i}+\frac{\tau }{\lambda }r(u_{i})\right) :(x,\mu )\in K,\frac{|x_{i}|}{M}\le u_{i}\le 1,~i=1,\dots ,n\right\} , \end{aligned}$$

(20)

or again

$$\begin{aligned} \alpha (\tau ){{:=}}\inf \left\{ f(x,\mu )+\lambda \sum _{i=1}^{n}\pi \left( u_{i}\right) :(x,\mu )\in K,\frac{|x_{i}|}{M}\le u_{i}\le 1,~i=1,\dots ,n\right\} \end{aligned}$$

(21)

where $\pi :\mathbb {R\rightarrow R}$ be the function defined by $\pi (t){{:=}}t+ \frac{\tau }{\lambda }r(t).$

Proposition 2

Let $\theta {{:=}}\frac{\tau +\lambda }{\lambda M}.$ For all $\tau \ge \lambda$ problems (21) and (18) are equivalent in the following sense:

$(x^{*},\mu ^{*})$ is an optimal solution of (18) iff $(x^{*},\mu ^{*},u^{*})$ is an optimal solution of (21), where $u_{i}^{*}\in \left\{ \frac{|x_{i}^{*}|}{M} ,1\right\} \$such that $\pi (u_{i}^{*})=\psi _{\theta }(x_{i}^{*})$ for $i=1,\dots ,n.$.

Moreover, $\alpha (\tau )=\beta (\theta )$.

Proof

If $(x^{*},\mu ^{*},u^{*})$ is an optimal solution of (21), then $u_{i}^{*}$ is an optimal solution of the following problem, for every $i=1,\dots ,n$

$$\begin{aligned} \ \min \left\{ \pi (u_{i}):\frac{|x_{i}^{*}|}{M}\le u_{i}\le 1\right\} . \end{aligned}$$

(22)

Since $r$ is concave function, so is $\pi .$ Consequently

$$\begin{aligned} \begin{array}{ll} \min \left\{ \pi (u_{i}):\frac{|x_{i}^{*}|}{M}\le u_{i}\le 1\right\} &{} =\min \left\{ \pi \left( \frac{|x_{i}^{*}|}{M}\right) ,\pi (1)\right\} \\ &{} =\min \left\{ \left( 1+\frac{\tau }{\lambda }\right) \frac{|x_{i}^{*}| }{M},\frac{\tau }{\lambda }+\left( 1-\frac{\tau }{\lambda }\right) \frac{ |x_{i}^{*}|}{M},1\right\} . \end{array} \end{aligned}$$

If $\tau \ge \lambda$, then for any $|t|\le M$ there holds

$$\begin{aligned} \frac{\tau }{\lambda }+\left( 1-\frac{\tau }{\lambda }\right) \frac{|t|}{M} \ge 1. \end{aligned}$$

Thus, for $\tau \ge \lambda$ and $|x_{i}^{*}|\le M$, we have

$$\begin{aligned} \pi (u_{i}^{*})=\min \left\{ \pi (u_{i}):\frac{|x_{i}^{*}|}{M}\le u_{i}\le 1\right\} =\min \left\{ \left( 1+\frac{\tau }{\lambda }\right) \frac{|x_{i}^{*}|}{M},1\right\} =\psi _{\theta }(x_{i}^{*}). \end{aligned}$$

(23)

For an arbitrary $(x,\mu )\in K$, we will show that

$$\begin{aligned} f(x^{*},\mu ^{*})+\lambda \sum _{i=1}^{n}\psi _{\theta }(x_{i}^{*})\le f(x,\mu )+\lambda \sum _{i=1}^{n}\psi _{\theta }(x_{i}). \end{aligned}$$

(24)

By the assumption that $(x^{*},\mu ^{*},u^{*})$ is an optimal solution of (21), we have

$$\begin{aligned} f(x^{*},\mu ^{*})+\lambda \sum _{i=1}^{n}\pi (u_{i}^{*})\le f(x,\mu )+\lambda \sum _{i=1}^{n}\pi (u_{i}) \end{aligned}$$

(25)

for any feasible solution $(x,\mu ,u)$ of (21). Let

$$\begin{aligned} u_{i}^{x}\in \arg \min \left\{ \pi (\xi )\ :\xi \in \left\{ \frac{|x_{i}|}{M} ,1\right\} \right\} \subset \arg \min \left\{ \pi (\xi ):\frac{|x_{i}|}{M} \le \xi \le 1\right\} , \end{aligned}$$

for all $i=1,\dots ,n$. Then $(x,\mu ,u^{x})$ is a feasible solution of (19) and

$$\begin{aligned} \pi (u_{i}^{x})=\min \left\{ \pi (\xi ):\frac{|x_{i}|}{M}\le \xi \le 1\right\} \ =\psi _{\theta }(x_{i}),\quad \forall i=1,\dots ,n. \end{aligned}$$

Combining (25) in which $u_{i}$ is replaced by $u_{i}^{x}$ and the last equation we get (24), which implies that $(x^{*},\mu ^{*})$ is an optimal solution of (18).

Conversely, if $(x^{*},\mu ^{*})$ is a solution of (18), and let $u_{i}^{*}\in \left\{ \frac{|x_{i}^{*}|}{M},1\right\} \$such that $\pi (u_{i}^{*}){{:=}}u_{i}^{*}+\frac{\tau }{\lambda }r(u_{i}^{*})=\psi _{\theta }(x_{i}^{*})$ for $i=1,\dots ,n.$ Then $(x^{*},\mu ^{*},u^{*})$ is a feasible solution of (21) and for an arbitrary feasible solution $(x,\mu ,u)$ of (21), we have

$$\begin{aligned} \begin{array}{ll} f(x,\mu )+\lambda \sum _{i=1}^{n}\left( u_{i}+\frac{\tau }{\lambda } r(u_{i})\right) &{} \ge f(x,\mu )+\lambda \sum _{i=1}^{n}\psi _{\theta }(x_{i}) \ge f(x^{*},\mu ^{*})\\ &{}\quad \, +\,\lambda \sum _{i=1}^{n}\psi _{\theta }(x_{i}^{*}) \\ &{} =f(x^{*},\mu ^{*})+\lambda \sum _{i=1}^{n}\left( u_{i}^{*}+\frac{ \tau }{\lambda }r(u_{i}^{*})\right) . \end{array} \end{aligned}$$

Thus, $(x^{*},\mu ^{*},u^{*})$ is an optimal solution of (21). The equality $\alpha (\tau )=\beta (\theta )$ is immediately deduced from the equality $\pi (u_{i}^{*})=\psi _{\theta }(x_{i}^{*}).$

From the two previous propositions we see that for $\tau >\max \{\lambda ,\tau _{0}\}$ and $\theta =\frac{\tau +\lambda }{\lambda M},$ the approximate problem (18) is equivalent to the original problem (6). This result evidences the advantage of this polyhedral DC approximation of the zero-norm. It opens the door to other nonconvex approximation approaches which are consistent with the original problem.

We are going now to show how to solve the continuous exact reformulation of the $\ell _0$-regularization (6), say the penalized problem (14), by DC programming and DCA.

3 Solving the continuous exact reformulation problem by DCA

For the reader’s convenience we first give an brief introduction of DC programming and DCA.

3.1 Outline of DC programming and DCA

DC programming and DCA constitute the backbone of smooth/nonsmooth nonconvex programming and global optimization. They address general DC programs of the form:

$$\begin{aligned} \alpha =\inf \{f(x){{:=}}g(x)-h(x):x\in \mathrm {I\!R}^{n}\}\qquad \qquad (P_{dc}) \end{aligned}$$

where $g,h\in \Gamma _{0}$($\mathrm {I\!R}^{n})$, the convex cone of all lower semicontinuous proper convex functions defined on $\mathrm {I\!R}^{n}$ and taking values in $\mathrm {I\!R\cup \{+\infty \}.}$ Such a function $f$ is called a DC function, and $g-h$ a DC decomposition of $f$ while $g$ and $h$ are the DC components of $f.$ The convex constraint $x\in C$ can be incorporated in the objective function of $(P_{dc})$ by using the indicator function of $C$ denoted by $\chi _{C}$ which is defined by $\chi _{C}(x)=0$ if $x\in C$, and $+\infty$ otherwise :

$$\begin{aligned} \inf \{f(x){{:=}}g(x)-h(x):x\in C\mathrm {\ }\}=\inf \{\chi _{C}(x)+g(x)-h(x):x\in \mathrm {I\!R}^{n}\}. \end{aligned}$$

Polyhedral DC program is a DC program in which at least one of the functions $g$ and $h$ is polyhedral convex. The function $\varphi$ is polyhedral convex if it is a pointwise supremum of a finite collection of affine functions. Polyhedral DC programming, which plays a central role in nonconvex optimization and global optimization and is the foundation of DC programming and DCA, has interesting properties (from both a theoretical and an algorithmic point of view) on local optimality conditions and the finiteness of DCA’s convergence.

For a convex function $\varphi$, the subdifferential of $\varphi$ at $x_{0}\in$ dom $\varphi {:=}\{x\in \mathrm {I\!R}^{n}:\theta (x_{0})<+\infty \},$ denoted by $\partial \varphi (x_{0}),$ is defined by

$$\begin{aligned} \partial \varphi (x_{0}){:=}\{y\in \mathrm {I\!R}^{n}:\varphi (x)\ge \varphi (x_{0})+\langle x-x_{0},y\rangle ,\forall x\in \mathrm {I\!R}^{n}\}. \end{aligned}$$

(26)

The subdifferential $\partial \varphi (x_{0})$ generalizes the derivative in the sense that $\varphi$ is differentiable at $x_{0}$ if and only if $\partial \varphi (x_{0}) \equiv \{\bigtriangledown _{x}\varphi (x_{0})\}.$

The complexity of DC programs resides, of course, in the lack of practical optimal globality conditions. Local optimality conditions are then useful in DC programming.

A point $x^{*}$ is said to be a local minimizer of $g-h$ if $g(x^{*})-h(x^{*})$ is finite and there exists a neighborhood $\mathcal {U}$ of $x^{*}$ such that

$$\begin{aligned} g(x^{*})-h(x^{*})\le g(x)-h(x),\ \ \forall x\in \mathcal {U}. \end{aligned}$$

(27)

The necessary local optimality condition for (primal) DC program $(P_{dc})$ is given by

$$\begin{aligned} \emptyset \ne \partial h(x^{*})\subset \partial g(x^{*}). \end{aligned}$$

(28)

The condition (28) is also sufficient (for local optimality) in many important classes of DC programs, for instance when $(P_{dc})$ is a polyhedral DC program with $h$ being a convex polyhedral function (see Le Thi and Pham Dinh 1997; 2005).

A point $x^{*}$ is said to be a critical point of $g-h$ if

$$\begin{aligned} \partial h(x^{*})\cap \partial g(x^{*})\ne \emptyset . \end{aligned}$$

(29)

The relation (29) is in fact the generalized Karush-Kuhn-Tucker (KTT) condition for $(P_{dc})$ and $x^{*}$ is also called a generalized KKT point.

Philosophy of DCA: DCA is based on local optimality conditions and duality in DC programming. The main idea of DCA is simple: each iteration $l$ of DCA approximates the concave part $-h$ by its affine majorization (that corresponds to taking $y^{l}\in \partial h(x^{l}))$ and minimizes the resulting convex function.

The generic DCA scheme can be described as follows:

DCA scheme

Initialization: Let $x^{0}\in \mathrm {I\!R}^{n}$ be a guess, set $l{:=}0.$

Repeat

• Calculate some$\ y^{l}\in \partial h(x^{l})$

• Calculate $x^{l+1}\in \arg \min \{g(x)-[h(x^{l})+\langle x-x^{l},y^{l}\rangle ]:x\in \mathrm {I\!R}^{n}\}\quad (P_{l})$

• Increase $l$ by $1$

Until convergence of $\{x^{l}\}.$

Note that $(P_{l})$ is a convex optimization problem and is so far “easy” to solve.

Convergence properties of DCA and its theoretical basis can be found in (Le Thi 1997; Le Thi and Pham Dinh 1997, 2005; Pham Dinh and Le Thi 1998). For instance it is important to mention that (for the sake of simplicity we omit here the dual part of DCA).

• DCA is a descent method (the sequence $\{g(x^{l})-h(x^{l})\}$ is decreasing) without linesearch but with global convergence (i.e. convergence from every starting point).

• If $g(x^{l+1})-h(x^{l+1})=g(x^{l})-h(x^{l})$, then $x^{l}$ is a critical point of $g-h$. In such a case, DCA terminates at $l$-th iteration.

• If the optimal value $\alpha$ of problem $(P_{dc})$ is finite and the infinite sequence $\{x^{l}\}$is bounded, then every limit point $x^{*}$ of the sequence $\{x^{l}\}$ is a critical point of $g - h$.

• DCA has a linear convergence for DC programs.

• DCA has a finite convergence for polyhedral DC programs.

It is worth to noting that the construction of DCA involves DC components $g$ and $h$ but not the function $f$ itself. Hence, for a DC program, each DC decomposition corresponds to a different version of DCA. Since a DC function $f$ has an infinite number of DC decompositions which have crucial impacts on the qualities (speed of convergence, robustness, efficiency, globality of computed solutions,...) of DCA, the search of a “good” DC decomposition is important from an algorithmic point of view. How to develop an efficient algorithm based on the generic DCA scheme for a practical problem is thus a sensitive question to be studied. Generally, the answer depends on the specific structure of the problem being considered.The solution of a nonconvex program $(P_{dc})$ by DCA must be composed of two stages: the search of an appropriate DC decomposition of $f$ and that of a good initial point.

DCA has been successfully used for various nonconvex optimization models, in particular those in machine learning (see the list of references in Le Thi’s website and (Krause and Singer (2004); Le Thi et al. (2007); Liu et al. (2005)). It should be noted that

• (i) the convex concave procedure (CCCP) for constructing discrete time dynamical systems mentioned in Yuille and Rangarajan (2003) is a special case of DCA applied to smooth optimization;

• (ii) the SLA (Successive Linear Approximation) algorithm developed in Bradley and Mangasarian (1998) is a version of DCA for concave minimization;

• (iii) the EM algorithm, (Dempster et al. 1997) applied to the log-linear model is a special case of DCA.

Last but not least, with appropriate DC decomposition in DC reformulations, DCA generates most of standard algorithms in convex/nonconvex programming.

For a complete study of DC programming and DCA the reader is referred to (Le Thi 1997; Le Thi and Pham Dinh 1997, 2005; Pham Dinh and Le Thi 1998) and the references therein. We show below how the DCA can be applied on the penalized problem (12).

3.2 DCA for solving the continuous exact reformulation problem (14)

We consider in the sequel the problem with a sufficient large number $\tau >\tau _{0}:$

$$\begin{aligned} \alpha (\tau ){:=}\inf \{f(x,\mu )+\lambda e^{T}u+\tau p(u):(x,\mu )\in K,u\in [0,1]^{n},|x_{i}|\le Mu_{i},~i=1,\dots ,n\}. \end{aligned}$$

(30)

Let $\varDelta$ be the feasible set of Problem (12), i.e. $\varDelta {:=}\{(x,\mu ,u):(x,\mu )\in K,u\in [0,1]^{n},|x_{i}|\le Mu_{i},~i=1,\dots ,n\}.$ Since $f$ is convex and $p$ is concave, the following DC formulation of (12) seems to be natural:

$$\begin{aligned} \inf \{g(x,\mu ,u)-h(x,\mu ,u):(x,\mu ,u)\in \mathbb {R}^{n}\times \mathbb {R} ^{p}\times \mathbb {R}^{n}, \end{aligned}$$

(31)

where

$$\begin{aligned} g(x,\mu ,u){:=}\chi _{\varDelta }(x,\mu ,u)+f(x,\mu ), h(x,\mu ,u){:=}-\lambda e^{T}u-\tau p(u) \end{aligned}$$

are clearly convex functions. Moreover, since $h$ is a polyhedral convex function, (31) is a polyhedral DC program.

According to the general DCA scheme described above, applying DCA to (31) amounts to computing two sequences $\{(x^{l},\mu ^{l},u^{l})\}$ and $\{(y^{l},\upsilon ^{l},v^{l})\}$ in the way that $(z^{l},\upsilon ^{l},v^{l})\in \partial h(x^{l},\mu ^{l},u^{l})$ and $(x^{l+1},\mu ^{l+1},u^{l+1})$ solves the convex program of the form $(P_{l}).$ Since $(y^{l},\upsilon ^{l},v^{l})\in \partial h(x^{l},\mu ^{l},u^{l})\Leftrightarrow y^{l}=0,$ $\upsilon ^{l}=0$ and

$$\begin{aligned} \begin{array}{ll} v_{i}^{l} &{} = {\left\{ \begin{array}{ll} -\lambda +\tau \quad \text { if }u_{i}^{l}\ge 0.5 \\ -\lambda -\tau \quad \text { if }u_{i}^{l}<0.5 \end{array}\right. } ,i=1,\ldots n, \end{array} \end{aligned}$$

the algorithm can be described as follow.

DCAEP (DCA applied on Exact Penalty problem (30))

Initialization: Let $(x^{0},\mu ^{0},u^{0})\in \mathrm {I\!R} ^{n}\times \mathrm {I\!R}^{p}\times [0,1]^{n}$ be a guess, set $l{:=}0.$

Repeat

• Set $v^{l}=(v_{i}^{l})$ with $v_{i}^{l}=-\lambda +\tau$ if $u_{i}^{l}\ge 0.5,$ $-\lambda -\tau$ otherwise, for $i=1,\ldots n.$

• Solve the convex program

  $$\begin{aligned} \min \{f(x,\mu )-\langle u,v^{l}\rangle :(x,\mu ,u)\in \varDelta \} \end{aligned}$$

  (32)

  to obtain $(x^{l+1},\mu ^{l+1},u^{l+1})$.

• Increase $l$ by $1$.

Until convergence of $\{(x^{l},\mu ^{l},u^{l})\}.$

Note that (32) is a linear (resp. convex quadratic) program with $f$ is a linear (resp. quadratic) function. Note also that DCAEP has a finite convergence because that (30) with the DC decomposition (31) is a polyhedral DC program. The above exact penalty reformulation technique holds with another penalty function $p$, say $p(u){:=} \sum _{i=1}^{n}u_{i}(1-u_{i}).$ In this case DCA doesn’t have the finite convergence (if $f$ is not convex polyhedral function or $\varDelta$ is not a polytope) since this function $p$ is not polyhedral.

4 Application to feature selection in classification

4.1 DC formulation via exact penalty technique and DCA based algorithm

Feature selection is often applied to high-dimensional data prior to classification learning. The main goal is to select a subset of features of a given data set while preserving or improving the discriminative ability of the classifier.

Given a training data $\left\{ \vartheta _{i},\delta _{i}\right\} _{i=1,\ldots ,m}$ where each $\vartheta _{i}\in \mathbb {R}^{n}$ is labeled by its class $\delta _{i}\in Y$. The goal of classification learning is to construct a classifier function that discriminates the data points $\left\{ \vartheta _{i}\right\} _{i=1,\ldots ,m}$ with respect to their classes$\left\{ \delta _{i}\right\} _{i=1,\ldots ,m}$. The embedded feature selection in classification consists of determining a classifier which uses as few features as possible, that leads to the following optimization problem like (4). In this section we focus on the context of Support Vector Machines (SVMs) learning with two-class linear models (Cristianini and Shawe-Taylor 2000). Generally, the problem can be formulated as follows.

Given two finite point sets $\fancyscript{A}$ (with label $+1$) and $\fancyscript{B}$ (with label $-1$) in $\mathbb {R}^{n}$ represented by the matrices $A\in \mathbb {R}^{m\times n}$ and $B\in \mathbb {R}^{k\times n}$, respectively, we seek to discriminate these sets by a separating plane ($x\in \mathbb {R} ^{n},\gamma \in \mathbb {R)}$

$$\begin{aligned} P=\{w\in \mathbb {R}^{n}:w^{T}x=\gamma \} \end{aligned}$$

(33)

which uses as few features as possible. We adopt the notations introduced in Bradley and Mangasarian (1998) and consider the optimization problem proposed in Bradley and Mangasarian (1998) that takes the form:

$$\begin{aligned} \begin{array}{ll} \min \nolimits _{x,\gamma ,\xi ,\zeta } &{} (1-\lambda )(\frac{1}{m}e^{T}\xi +\frac{1}{k} e^{T}\zeta )+\lambda \left\| x\right\| _{0} \\ s.t. &{} -Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta ,\ \xi \ge 0,\ \zeta \ge 0. \end{array} \end{aligned}$$

(34)

The nonnegative slack variables $\xi _{j},j=1,\ldots m$ represent the errors of classification of $\vartheta _{j}\in \fancyscript{A}$ while $\zeta _{j},j=1,\ldots k$ represent the errors of classification of $\vartheta _{j}\in \fancyscript{B}$. More precisely, each positive value of $\xi _{j}$ determines the distance between a point $a_{j}\in \fancyscript{A}$ lying on the wrong side of the bounding plane $w^{T}x=\gamma +1$ for $\fancyscript{A}$. Similarly for $\zeta _{j}$, $\fancyscript{B}$ and $w^{T}x=\gamma -1$. The first term of the objective function of (34) is the average error of classification, and the second term is the number of nonzero components of the vector $x$, each of which corresponds to a representative feature. Further, if an element of $x$ is zero, the corresponding feature is removed from the dataset. Here $\lambda$ is a control parameter of the trade-off between the training error and the number of features.

Observe that the problem (34) is a special case of (4) where the function $f$ is given by

$$\begin{aligned} f(x,\gamma ,\xi ,\zeta ){:=}(1-\lambda )\left( \frac{1}{m}e^{T}\xi +\frac{1}{k} e^{T}\zeta \right) \end{aligned}$$

(35)

and $K$ is a polytope defined by

$$\begin{aligned} K{:=}\left\{ (x,\gamma ,\xi ,\zeta )\in \mathbb {R}^{n}\times \mathbb {R}\times \mathbb {R}_{+}^{m}\times \mathbb {R}_{+}^{k}:Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta \right\} . \end{aligned}$$

(36)

Applying the results developed in the previous section with $f$ and $K$ defined, respectively, in (35) and (36) we get the following DC formulation of (34):

$$\begin{aligned} \inf \{g(x,\gamma ,\xi ,\zeta ,u)-h(x,\gamma ,\xi ,\zeta ,u):(x,\gamma ,\xi ,\zeta ,u)\in \mathbb {R}^{n}\times \mathbb {R}^{1+m+k}\times \mathbb {R}^{n}\}, \end{aligned}$$

(37)

where

$$\begin{aligned} \begin{array}{l} g(x,\gamma ,\xi ,\zeta ,u){:=}\chi _{\varDelta }(x,\gamma ,\xi ,\zeta ,u)+(1-\lambda )(\frac{1}{m}e^{T}\xi +\frac{1}{k}e^{T}\zeta ),\\ h(x,\gamma ,\xi ,\zeta ,u){:=}-\lambda e^{T}u-\tau p(u). \end{array} \end{aligned}$$

Since $K$ is a polyhedral convex set, so is $\varDelta ,$ hence $\chi _{\varDelta }$ is a polyhedral convex function. Therefore (37) is a polyhedral DC program with both polyhedral DC components $g$ and $h$. In the algorithm DCAEP, the convex program (32) becomes now a linear program.

DCAEP-SVM (DCA applied on Exact Penalty problem (37))

Initialization: Let $(x^{0},\gamma ^{0},\xi ^{0},\zeta ^{0},u^{0}) \in \mathrm {I\!R}^{n}\times \mathbb {R}\times \mathbb {R} _{+}^{m}\times \mathbb {R}_{+}^{k}\times [0,1]^{n}$ be a guess, let $\epsilon >0$ be sufficiently small, set $l{:=}0.$

Repeat

• Set $v^{l}=(v_{i}^{l})$ with $v_{i}^{l}=-\lambda +\tau$ if $u_{i}^{l}\ge 0.5,$ $-\lambda -\tau$ otherwise, for $i=1,\ldots n.$

• Solve the linear program

  $$\begin{aligned} \min \{(1-\lambda )(\frac{1}{m}e^{T}\xi +\frac{1}{k}e^{T}\zeta )-\langle u,v^{l}\rangle :(x,\gamma ,\xi ,\zeta ,u)\in \varDelta \} \end{aligned}$$

  (38)

  to obtain $(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1},u^{l+1})$

• Increase $l$ by $1$

Until $\left\| (x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})-(x^{l-1},\gamma ^{l-1},\xi ^{l-1},\zeta ^{l-1},u^{l-1})\right\| \le \epsilon \left\| (x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l-1},u^{l})\right\| .$

Thanks to the very special structure of (37) ($f$ is a linear function and $\varDelta$ is a polytope), DCAEP-SVM enjoys interesting convergence properties.

Theorem 1

(Convergence properties of DCAEP-SVM)

• (i) DCAEP-SVM generates a sequence $\{(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})\}$ contained in $V(\varDelta )$ such that the sequence $\{f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\tau p(u^{l})\}$ is decreasing.

• (ii) For a number $\tau$ sufficiently large, if at an iteration $q$ we have $u^{q}\in \{0,1\}^{n}$, then $u^{l}\in \{0,1\}^{n}$ for all $l\ge q$.

• (iii) The sequence $\{(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})\}$ converges to $\{(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})\} \in V(\varDelta )$ after a finite number of iterations. The point $(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})$ is a critical point of Problem (37). Moreover if $u_{i}^{*}\ne \frac{1}{2}$ for all $i=1\ldots n$, then $\{(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})\}$ is a local solution to (37).

Proof

• (i) is consequence of DCA’s convergence Theorem for a general DC program.

• (ii) Let $\tau >\tau _{1}{:=}\max \left\{ \frac{f(x,\gamma ,\xi ,\zeta )+\lambda e^{T}u-\eta }{\delta }:(x,\gamma ,\xi ,\zeta ,u)\in V(\varDelta ),p(u)\le 0\right\}$ where $\eta {:=}\min \{f(x,\gamma ,\xi ,\zeta )+\lambda e^{T}u:(x,\gamma ,\xi ,\zeta ,u)\in V(\varDelta )\}$ and $\delta {:=}\min \{p(u):(x,\gamma ,\xi ,\zeta ,u)\in V(\varDelta )\}.$ Let $\{(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})\}\subset V(\varDelta )$ ($l\ge 1$) be generated by DCAEP-SVM. If $V(\varDelta )\subset \{\varDelta \cap u\in \{0,1\}^{n}\}$, then the assertion is trivial. Otherwise, let $(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})\in \{\varDelta \cap u\in \{0,1\}^{n}\}$ and $(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1},u^{l+1})\in V(\varDelta )$ be an optimal solution of the linear program ( 38). Then from (i) of this theorem we have

  $$\begin{aligned} f(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1})+\lambda e^{T}u^{l+1}+tp(u^{l+1})\le f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\lambda e^{T}u^{l}+tp(u^{l}). \end{aligned}$$

Since $p(u^{l})=0$, it follows

$$\begin{aligned} \begin{array}{ll} \tau p(u^{l+1}) &{} \le f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\lambda e^{T}u^{l}-f(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1})-\lambda e^{T}u^{l+1} \\ &{} \le f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\lambda e^{T}u^{l}-\eta . \end{array} \end{aligned}$$

If $p(u^{l+1})>0$, then

$$\begin{aligned} \tau \le \frac{f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\lambda e^{T}u^{l}-\eta }{p(u^{l+1})}\le \frac{f(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l})+\lambda e^{T}u^{l}-\eta }{\delta }\le \tau _{1} \end{aligned}$$

which contradicts the fact that $\tau >\tau _{1}$. Therefore we have $p(u^{l+1})=0.$

• (iii) Since (37) is a polyhedral DC program, DCAEP-SVM has a finite convergence, say, the sequence $\{(x^{l},\gamma ^{l},\xi ^{l},\zeta ^{l},u^{l})\}$ converges to a critical point $(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})\in V(\varDelta )$ after a finite number of iterations. If $u_{j}^{*}\ne 1/2,\forall j\in 1..n$, then the function $h$ is differentiable at $(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})$ and then the necessary local condition

  $$\begin{aligned} \partial h(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})\subset \partial g(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*}) \end{aligned}$$

  holds. Since $h$ is a polyhedral convex function, this subdifferential inclusion is also a sufficient local optimality condition, i.e. $(x^{*},\gamma ^{*},\xi ^{*},\zeta ^{*},u^{*})$ is a local minimizer of (37). The proof is then complete.

$\square$

4.2 Computational experiments

To study the performances of our approach, we perform it on several datasets. Our experiment is composed of two parts. In the first one we consider the synthetic data and in the second we test on a collection of real-world datasets.

4.2.1 Datasets

Synthetic datasets

We generate the datasets such that among $n$ features, there exists a subset of $n_i$ features that define a subspace in which two classes can be discriminated (i.e. only $n_i$ of $n$ features are informative while the others are irrelevant). Thus we are available to evaluate the performance of the algorithms in terms of feature selection, not only on the sparsity but also on the correctness of the selected features. The data are generated in a similar way given in Rakotomamonjy et al. (2011). First, we randomly drawn a mean vector $\nu \in \{-1,1\}^{n_i}$ and a $n_i \times n_i$ covariance matrix $\Sigma$ from Wishart distribution. Then, the $n_i$ informative features are generated from a multivariate Gaussian distribution $N(\nu ,\Sigma )$ and $N(-\nu ,\Sigma )$, respectively, for class $+1$ and $-1$. The $n - n_i$ remaining features (irrelevant features) follow an i.i.d Gaussian distribution $N(0,1)$.

Real-world datasets Real-word datasets are taken from well-known UCI data repository and from challenging feature-selection problems of the NIPS 2003 datasets. Datasets from UCI repository include several problems of gene selection for cancer classification with standard public microarray gene expression datasets. Challenging NIPS 2003 datasets are known to be difficult and are designed to test various feature-selection methods using an unbiased testing procedure without revealing the labels of the test set. They contain a huge number of features while the number of examples in both training sets and test sets is small. In Table 1, the number of features, the number of points in training and test set of each dataset are given. The full description of each dataset can be found on the web site of UCI repository and NIPS 2003.

Table 1 Datasets

4.2.2 Set up experiments and Parameters

All algorithms were implemented in the Visual C++ 2008, and performed on a PC Intel i5 CPU650, 3.2 GHz of 4GB RAM. CPLEX 12.2 was used for solving linear/quadratic programs. We stop all algorithms with the tolerance $\epsilon =10^{-4}$. The non-zero elements of $x$ are determined according to whether $|x_{i}|$ exceeds a small threshold ($10^{-5}$).

We used the following set of candidate values for the parameter $\lambda$ in our experiments $\{0.001,0.002,0.003,0.004,0.05,0.1,0.2,0.3,0.4,0.5\}$.

Concerning the parameter $\tau ,$ as $\tau _{0}$ is not computable, we take a quite large value $\tau _{0}$ at the beginning and use an adaptive procedure described in Pham Dinh and Le Thi (2014) for updating $\tau$ during the DCA scheme.

We compare the performance of algorithms in terms of the following three criteria: the percentage of well classified objects (PWCO), the number and percentage of selected features and CPU Time in seconds. $\hbox {POWC}_1$ (resp. $\hbox {POWC}_2$) denotes the POWC on training set (resp. test set). In addition, for the synthetic data we examine how the algorithms retrieve the informative features.

4.2.3 Comparative algorithms

We will compare our exact approach with some algorithms in convex and nonconvex approximation approaches. In convex regularization approaches we consider the well known $\ell _1$-regularization (Tibshirani 1996) and Elastic Net (Zou and Hastie 2005) ($\ell _1$-regularization and Elastic Net for SVM have been proposed, respectively in Bradley and Mangasarian (1998) (Appendix A) and Wang et al. (2006) (Appendix B)). Among usual sparse inducing functions in nonconvex approximation approaches the capped $\ell _{1}$ (Peleg and Meir 2008) (the polyhedral DC approximation discussed in Sect. 2), the piecewise concave exponential (Bradley and Mangasarian 1998) and SCAD (Fan and Li 2001) approximations have been proved to be the most efficient in several works of various authors. As we have proved in Sect. 2 that the capped $\ell _{1}$ is equivalent to our exact formulation with suitable parameters, we exclude it from our comparison and focus on the piecewise concave exponential and SCAD approximations. The first algorithm based on the piecewise concave exponential approximation is the SLA (Successive Linear Approximation) (Bradley and Mangasarian 1998) (which is in fact a version of DCA). The DCA based algorithm using this approximation (but with another DC decomposition) in Le Thi et al. (2008) (see Appendix C) has been shown to be more efficient than SLA, hence we consider it in our comparative experiments. Likewise, for the SCAD approximation we consider the DCA based algorithm developed in Le Thi et al. (2009) (Appendix D) which is less expensive than the LQA (Local Quadratic Approximation) algorithm proposed in Fan and Li (2001) and used for feature selection in SVM in Zhang et al. (2006) (subproblems are quadratic programs).

The comparative algorithms are named as follows:

• $\ell _1$ -SVM: SVM with $\ell _1$ regularization (Bradley and Mangasarian 1998);

• ElasticNet-SVM: SVM with Elastic net regularization (Wang et al. 2006);

• DCA-PiE-SVM: DCA for piecewise exponential approximation (Le Thi et al. 2008);

• DCA-SCAD-SVM: DCA for SCAD approximation (Le Thi et al. 2009);

• DCAEP-SVM: the algorithm proposed in this paper.

4.2.4 Experiment on synthetic data

We set the sample sizes of training and test set to $500$ and $10,000$, respectively. For each experimental setting $(n,n_i)$ (number total of features, number of informative features), $50$ training sets and $1$ test set are generated. For each training set, we performed $5$-folds cross-validation to choose the best parameters of each algorithm. Then, for each experimental setting $(n,n_i)$, we summarize in Table 2 the average of accuracy, the average of number of selected features,the average of CPU time as well as the percentage of success of $50$ runs over $50$ training sets. A success means the considered algorithm retrieves exactly the $n_i$ informative features and suppresses all irrelevant features.

Table 2 Comparative results on synthetic datasets

We observe from the Table 2 that

• In terms of feature selection, DCAEP-SVM and DCA-PiE-SVM give the best results on all three experimental settings $(n,n_i)$ (DCA-PiE-SVM is slightly better on the last dataset ($n=50,n_i=10$). Moreover, DCA based algorithms are more succes than the convex regularization approaches when retrieving the informative features. The percentage of success of DCA based algorithm varies from 84 to $94\%$, while that of $\ell _1$ -SVM (resp. ElasticNet-SVM) goes from $72\,\%$ to $81\,\%$ (resp. $68\,\%$ to $85\,\%$).

• As for the accuracy of classification, the results are comparable. All five algorithms furnish quite good accuracy, more than $85\,\%$ correctness.

4.2.5 Experiment on real-world data

For each algorithm, we first use a $10$-folds cross-validation to determine the best set of parameter values. Afterward, we perform, with these parameter values a $5$-folds cross-validation and report the average and the standard deviation of each evaluation criterion. The comparative results are given in Table 3.

Table 3 Comparative results on real-world datasets

Comments on numerical results:

• Concerning the sparsity of solution (the number of selected feature), as above, DCAEP-SVM and DCA-PiE-SVM are the best: averagely, only $5\,\%$ and $4.6\,\%$ of features are selected, respectively. All DCA based algorithms perform better than $\ell _1$ -SVM and ElasticNet-SVM, especially on Gisette and Breast. All DCA based algorithms suppress considerably the number of features (up to $99\,\%$ on large datasets such as Arcene and Leukemia) while the correctness of classification is quite good (from $77\,\%$ to $100\,\%$). For WPBC(60) and Prostate, DCAEP-SVM suppresses more features than the other algorithms while furnishing a better classification accuracy. On other datasets, DCAEP-SVM selects slightly more features than DCA-PiE-SVM ($1$ or $2$ features, except for Gisette). Overall, DCAEP-SVM realizes a better trade-off between accuracy and sparsity than other algorithms.

• As for the accuracy of classification, DCAEP-SVM is the best for $6$ out of $8$ training sets. The gain is important on $2$ datasets: WPBC(24) $10,4\,\%$ and Gisette $12,1\,\%$. The same conclusion goes for test sets, DCAEP-SVM is better on $6$ datasets (with a gain up to $17.1\,\%$ on Gisette dataset). ElasticNet-SVM is slightly better than DCA based algorithms ($1.1\,\%$ and $1.8\,\%$ on two datasets Breast and Ionosphere. This can be explained by the fact that ElasticNet-SVM selects $6$ (resp. $4$) times more features than DCA based algorithms on Breast (resp. Ionosphere) dataset.

• In terms of CPU time, not surprisingly, $\ell _1$ -SVM is the fastest algorithm, with an average of CPU time $11,1$ s, since it only requires solving one linear program. The CPU time of DCA based algorithms is quite small, less than $101$ s for the largest dataset (Gisette). DCAEP-SVM is somehow slightly faster with an average of CPU time $21,5$ s while that of DCA- PiE-SVM (resp. DCA-SCAD-SVM) is $24,6$ (resp. $22,6$) s.

5 Conclusion

We have proposed an exact reformulation approach based on DC programming and DCA for minimizing a class of functions involving the zero-norm and its application on feature selection in classification. Using a recent result on exact penalty in DC programming we show that the original problem (4) can be equivalently reformulated as a continuous optimization problem which is a DC program. By this result we can unify all nonconvex approaches for treating the zero-norm into the DC programming and DCA. The link between the exact reformulation and convex/nonconvex approximations stated in this paper allows to analyze / justify the performance of these approximations approaches. Numerical experiments on feature selection in SVM show that our algorithm is efficient on both feature selection and classification. The advantage of this approach is that it solves directly an equivalent model of the original problem. Several issues arise from this work. Firstly, the choice of a good exact penalty parameter is still open. Secondly, the link between the exact reformulation and the polyhedral approximation suggests us to study new approximations such that the exact penalty reformulation are equivalent to the approximate problem for which efficient DCA schemes can be investigated. Thirdly, we should extend our exact penalty approaches for larger classes of problems (when $f$ nonconvex for example) as well as other applications including regression, sparse Fisher linear discriminant analysis, feature selection in learning to rank with sparse SVM, compressed sensing, etc. Works in these directions are in progress.

Appendices

Appendix:

$\ell _1$ regularization for SVM (Bradley and Mangasarian (1998))

$\ell _1$ -SVM formulation:

$$\begin{aligned} \begin{array}{ll} \min _{x,\gamma ,\xi ,\zeta } &{} (1-\lambda )(\frac{1}{m}e^{T}\xi +\frac{1}{k} e^{T}\zeta )+\lambda \left\| x\right\| _{1} \\ s.t. &{} -Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta ,\ \xi \ge 0,\ \zeta \ge 0. \end{array} \end{aligned}$$

(39)

By adding a new variable $z \in \mathrm{I\!R }_+^n$, we obtain the following equivalent linear program:

$$\begin{aligned} \begin{array}{l@{\quad }l} \min _{x,\gamma ,\xi ,\zeta ,z } &{} (1-\lambda )\Big (\frac{1}{m}e^{T}\xi +\frac{1}{k} e^{T}\zeta \Big )+\lambda e^{T}z \\ s.t. &{} -Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta , \\ &{} - z_i \le x_i \le z_i, \ \forall i=1,\ldots ,n, \\ &{} \xi \ge 0,\ \zeta \ge 0, \ z \ge 0. \end{array} \end{aligned}$$

(40)

Elastic Net regularization for SVM (Wang et al. (2006))

Elastic Net regularization was introduced by Zou and Hastie (Zou and Hastie 2005) in the context of regression. Later, in Wang et al. (2006), the authors proposed to use Elastic net regularization for feature selection in SVM. The problem can be described as follows (Wang et al. 2006)

$$\begin{aligned} \begin{array}{ll} \min _{x,\gamma ,\xi ,\zeta } &{} \frac{1}{m}e^{T}\xi +\frac{1}{k} e^{T}\zeta +\lambda _1 \left\| x\right\| _{1} + \frac{\lambda _2}{2} \left\| x\right\| _{2}^2\\ s.t. &{} -Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta ,\ \xi \ge 0,\ \zeta \ge 0. \end{array} \end{aligned}$$

(41)

with $\lambda _1, \lambda _2 > 0$. Similarly to SVM using $\ell _1$, (41) is equivalent to the following convex quadratic problem:

$$\begin{aligned} \begin{array}{ll} \min _{x,\gamma ,\xi ,\zeta ,t } &{} \frac{1}{m}e^{T}\xi +\frac{1}{k}e^{T}\zeta +\lambda _1 e^{T}z + \frac{\lambda _2}{2} \left\| x\right\| _{2}^2\\ s.t. &{} -Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta , \\ &{} - z_i \le x_i \le z_i, \ \forall i=1,\ldots ,n, \\ &{} \xi \ge 0,\ \zeta \ge 0, \ z \ge 0. \end{array} \end{aligned}$$

(42)

Piecewise concave exponential approximation (Le Thi et al. (2008))

For $y\in \mathbb {R}$, let $\eta _{1}$ be the function defined by

$$\begin{aligned} \eta _{1}(t)= {\left\{ \begin{array}{ll} \begin{array}{ll} 1-\varepsilon ^{-\alpha t} &{} \quad \text { if }t\ge 0 \\ 1-\varepsilon ^{\alpha t} &{} \quad \text { if }t\le 0 \end{array} \end{array}\right. } \end{aligned}$$

(43)

with $\alpha >0$. Hence, for all $x\in \mathbb {R}^{n}$, the step vector $\left| x\right| _{0}$ is approximated by $\left| x\right| _{0}\simeq \eta _{1}(x_{i})$ and the approximation of the zero-norm $\left\| x\right\| _{0}$ is determined as

$$\begin{aligned} \left\| x\right\| _{0}\simeq \sum \limits _{i=1}^{n}\eta _{1}(x_{i}).\ \end{aligned}$$

This approximation has been proposed for the first time in Bradley and Mangasarian (1998) for feature selection in SVM where the authors developed a SLA (Sucessive Linear Approximation) algorithm for the resulting approximate problem (called FSV algorithm). Later, in Le Thi et al. (2008) , the authors proposed another DC decomposition for which the follwing DCA scheme has been investiaged. Numerical experiments in Le Thi et al. (2008) showed that this new algorithm is better than FSV which is also an instance of DCA.

DCA-PiE-SVM:

Initialization Let $\epsilon$ be a tolerance sufficiently small, set $l=0$.

Choose $(x^{0},\gamma ^{0},\xi ^{0},\zeta ^{0})\in \mathbb {R}^{n+1m+k+n}$.

Repeat

• Compute $\bar{x}^{l}$ as follows

  $$\begin{aligned} \bar{x}_{j}= {\left\{ \begin{array}{ll} \begin{array}{ll} \alpha (1-\varepsilon ^{-\alpha x_{j}}) &{} \quad \text {if }x_{j}\ge 0 \\ -\alpha (1-\varepsilon ^{\alpha x_{j}}) &{} \quad \text {if }x_{j}<0 \end{array} \end{array}\right. } , j=1, \ldots ,n. \end{aligned}$$

  (44)

• Solve the linear program

  $$\begin{aligned} {\left\{ \begin{array}{ll} \min (1-\lambda )\Big (\frac{1}{m}e^{T}\xi +\frac{1}{k}e^{T}\zeta \Big )+\lambda \sum \limits _{i=1}^{n}t_{j}-\langle \bar{x}^{l},x\rangle \\ s.t \quad (x,\gamma ,\xi ,\gamma )\in K \\ \qquad -\alpha w_{j}\le t_{j},\alpha w_{j}\le t_{j},j=1..n \end{array}\right. } \end{aligned}$$

  (45)

  to obtain $(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1})$

• Increase $l$ by 1

Until

$$\begin{aligned} \left\| (x^{l},\gamma ^{l},\xi ^{l},\zeta )-(x^{l-1},\gamma ^{l-1},\xi ^{l-1},\zeta ^{l-1})\right\| \le \left\| \epsilon (x^{l},\gamma ^{l},\xi ^{l},\zeta )\right\| . \end{aligned}$$

Remember that $K$ is a polytope defined by

$$\begin{aligned} K{:=}\left\{ (x,\gamma ,\xi ,\zeta )\in \mathbb {R}^{n}\times \mathbb {R}\times \mathbb {R}_{+}^{m}\times \mathbb {R}_{+}^{k}:Ax+e\gamma +e\le \xi ,\ Bx-e\gamma +e\le \zeta \right\} . \end{aligned}$$

(46)

For more detail about DCA-PiE-SVM and its convergence properties, the reader is referred to Le Thi et al. (2008).

SCAD approximation (Le Thi et al. (2009))

The SCAD (Smoothly Clipped Absolute Deviation) penalty function has been proposed for the first time by J. Fan and R. Li (Fan and Li 2001) in the context of regression and variable selection. The SCAD penalty function is expressed as follow, for $t\in \mathbb {R}:$

$$\begin{aligned} \omega (|t|)= {\left\{ \begin{array}{ll} \begin{array}{ll} \beta |t| &{} \text { if }\quad |t|\le \beta , \\ -\frac{\left| t\right| ^{2}-2\alpha \beta |t|+\beta ^{2}}{2(\alpha -1)} &{} \text { if }\quad \beta <|t|\le \alpha \beta , \\ \frac{(\alpha +1)\beta ^{2}}{2} &{} \text { if }\quad |t|>\alpha \beta , \end{array} \end{array}\right. } \end{aligned}$$

(47)

where $\alpha >2$ and $\beta >0$ are two tuning parameters.

In Zhang et al. (2006), using the SCAD approximation, a local quadratic approximation has been proposed for features selection in SVM. This algorithm can be regarded as a reweighted $l_{2}$ procedure which is in fact a version of DCA. Later, in Le Thi et al. (2009), using a suitable DC decompostion of SCAD function the authors developed an efficient DCA based algorithm that requires one linear program at each iteration. The algorithm can be described as follow.

DCA-SCAD-SVM:

Initialization Let $\tau$ be a tolerance sufficiently small, set $l=0$.

Choose $(x^{0},\gamma ^{0},\xi ^{0},\zeta ^{0})\in \mathbb {R}^{n+1m+k+n}$.

Repeat

• Compute $\bar{x}^{l}$ as follows

  $$\begin{aligned} \bar{x}_{j}= {\left\{ \begin{array}{ll} \begin{array}{ll} 0 &{} \quad \text {if }\quad -\beta \le x_{j}\le \beta \\ (\alpha -1)^{-1}(x_{j}-\beta ) &{} \quad \text {if }\quad \beta <x_{j}\le \alpha \beta \\ (\alpha -1)^{-1}(x_{j}+\beta ) &{} \quad \text {if }\quad -\alpha \beta <x_{j}\le -\beta \\ \beta &{} \quad \text {if }\quad x_{j}>\alpha \beta \\ -\beta &{} \quad \text {if }\quad x_{j}<-\alpha \beta \end{array} \end{array}\right. } ,j=1,\ldots n, \end{aligned}$$

  (48)

• Solve the linear program

  $$\begin{aligned} {\left\{ \begin{array}{ll} \min (1-\lambda )\Big (\frac{1}{m}e^{T}\xi +\frac{1}{k}e^{T}\zeta \Big )+\lambda \sum \limits _{i=1}^{n}t_{j}-\langle \bar{x}^{l},x\rangle \\ s.t \quad (x,\gamma ,\xi ,\gamma )\in K \\ \qquad \text { }-\alpha w_{j}\le t_{j},\alpha w_{j}\le t_{j},j=1..n \end{array}\right. } \end{aligned}$$

  (49)

  to obtain $(x^{l+1},\gamma ^{l+1},\xi ^{l+1},\zeta ^{l+1})$

• Increase $l$ by 1

Until

$$\begin{aligned} \left\| (x^{l},\gamma ^{l},\xi ^{l},\zeta )-(x^{l-1},\gamma ^{l-1},\xi ^{l-1},\zeta ^{l-1})\right\| \le \left\| \epsilon (x^{l},\gamma ^{l},\xi ^{l},\zeta )\right\| . \end{aligned}$$

The reader is referred to Le Thi et al. (2009) for more details.