Abstract
In this paper, we investigate the semantics and logic of choice-driven counterfactuals, that is, of counterfactuals whose evaluation relies on auxiliary premises about how agents are expected to act, i.e., about their default choice behavior. To do this, we merge one of the most prominent logics of agency in the philosophical literature, namely stit logic (Belnap et al. 2001; Horty 2001), with the well-known logic of counterfactuals due to Stalnaker (1968) and Lewis (1973). A key component of our semantics for counterfactuals is to distinguish between deviant and non-deviant actions at a moment, where an action available to an agent at a moment is deviant when its performance does not agree with the agent’s default choice behavior at that moment. After developing and axiomatizing a stit logic with action types, instants, and deviant actions, we study the philosophical implications and logical properties of two candidate semantics for choice-driven counterfactuals, one called rewind models inspired by Lewis (Nous 13(4), 455–476 1979) and the other called independence models motivated by well-known counterexamples to Lewis’s proposal Slote (Philos. Rev. 87(1), 3–27 1978). In the last part of the paper we consider how to evaluate choice-driven counterfactuals at moments arrived at by some agents performing a deviant action.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Notes
The proof that SLDn is sound with respect to the class of all SLDn frames is a matter of routine validity check and it is thus omitted.
Observe that the uniqueness of such state is guaranteed by the functionality of RY.
The existence of σ(w, ϕ) is guaranteed by the way W(w, ϕ) is built and the uniqueness of σ(w, ϕ) by the functionality of RX.
That is, M(w, ψ, ϕ) is the smallest submodel of M(w, ϕ) such that (1) S(w, ψ)S(w, ϕ) ∈ M(w, ϕ, ψ) and (2) for all \( \overrightarrow {w_{n}},\overrightarrow {v_{m}}\in M^{(w,\phi ,\psi )} \), if \( \overrightarrow {w_{n}}\in M^{(w,\phi ,\psi )}\) and either \( \overrightarrow {w_{n}}R_{\square }^{(w,\phi )} \overrightarrow {v_{m}}\) or \( \overrightarrow {w_{n}}R^{(w,\phi )}_{\textsf {X}} \overrightarrow {v_{m}}\), then \( \overrightarrow {v_{m}}\in M^{(w,\phi ,\psi )}\).
Formally, h(n) is defined inductively as follows: h(0) = m0; h(n + 1) = succh(h(n)).
The prefix of length n of \( \overrightarrow {w_{h(n+\textsf {z})}} \) is an element of h(n) by the definition of <.
References
Aumann, R. (1995). Backward induction and common knowledge of rationality. Games Econ. Behav., 8(1), 6–19.
Baltag, A., Canavotto, I., & Smets, S. (2021). Causal Agency and Responsibility: A Refinement of STIT Logic. In A. Giordani J. Malinowski (Eds.) Logic in High Definition, Trends in Logical Semantics, volume 56 of Trends in Logic (pp. 149–176). Berlin: Springer.
Battigalli, P. (1997). On rationalizability in extensive games. J. Econ. Theory, 74, 40–61.
Battigalli, P., & Siniscalchi, M. (2002). Strong belief and forward induction reasoning. J. Econ. Theory, 106(2), 356–391.
Belnap, N., Perloff, M., & Xu, M. (2001). Facing the future: Agents and choices in our indeterministic world. Oxford University Press, Oxford.
Bennett, J. (2003). A Philosophical Guide to Conditionals. Clarendon Press, Oxford.
Bicchieri, C. (1988). Strategic behavior and counterfactuals. Synthese, 76, 135–169.
Blackburn, P., de Rijke, M., & Yde, V. (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge.
Bonanno, G. (2014). A doxastic behavioral characterization of generalized backward induction. Games Econ. Behav., 88, 221–241.
Bonanno, G. (2015). Counterfactuals and the Prisoner’s Dilemma. In The Prisoner’s Dilemma, pp. 133–155. Cambridge University Press.
Broersen, J.M. (2011a). Deontic Epistemic stit Logic Distinguishing Modes of Mens Rea. J. Appl. Log., 9(2), 137–152.
Broersen, J.M. (2011b). Making a Start with the stit Logic Analysis of Intentional Action. J. Philos. Log., 40(4), 499–530.
Broersen, J.M. (2013). Probabilistic stit Logic and its Decomposition. Int. J. Approx. Reason., 54, 467–477.
Broersen, J.M. (2014). On the Reconciliation of Logics of Agency and Logics of Event Types. In R. Trypuz (Ed.) Krister Segerberg on Logic of Actions, volume 1 of Outstanding Contributions to Logic (pp. 41–59). Netherlands: Springer.
Broersen, J.M., & Herzig, A. (2015). Using STIT Theory to Talk About Strategies. In J. Benthem, S. Ghosh, & S. Verbrugge (Eds.) Models of Strategic Reasoning. Logics, Games, and Communities (pp. 137–173). Berlin: Springer.
Broersen, J.M., Herzig, A., & Troquard, N. (2006). From coalition logic to STIT. Electron. Notes Theor. Comput. Sci., 157(4), 23–35.
Broersen, J.M., & Ramírez Abarca, A.I. (2018). Knowledge and Subjective Oughts in STIT Logic. In J.M. Broersen, C. Condoravdi, S. Nair, & G. Pigozzi (Eds.) Deontic Logic and Normative Systems, 14th International Conference (DEON 2018) (pp. 51–69). Milton Keynes: College Publications.
Canavotto, I. (2020). Where Resposibility Takes You. Logics of Agency, Counterfactuals and Norms. PhD thesis, Institute for logic, Language and Computation. University of Amsterdam.
Ciuni, R., & Horty, J.F. (2014). Stit Logics, Games, Knowledge, and Freedom. In A. Baltag, S. Smets, & J. van Benthem (Eds.) on Logic and Information Dynamics, volume 5 of Outstanding Contributions to Logic (pp. 631–656). Cham: Springer.
Ciuni, R., & Mastop, R. (2009). Attributing Distributed Responsibility in Stit Logic. In X. He, J.F. Horty, & E. Pacuit (Eds.) Logic, Rationality, and Interaction (pp. 66–75). Berlin: Springer.
Dietrich, F., & List, C. (2016). Reason-based Choice and Context-dependence: An explanatory framework. Econ. Philos., 2(32), 175–229.
Harel, D., Kozen, D., & Jerzy, T. (2000). Dynamic Logic. The MIT Press, Cambridge.
Herzig, A., & Troquard, N. (2006). Knowing how to play: Uniform choices in logics of agency. In: Proceedings of the 5th International Joint Conference on Autonomous Agents and Multi-agent Systems (AAMAS-06), pp. 209–216. The Association for Computing Machinery Press, New York.
Herzig, A., & Lorini, E. (2010). A dynamic logic of agency I: STIT, capabilities and Powers. J. Log. Lang. Inf., 19(1), 89–121.
Horty, J. F. (2001). Agency and Deontic Logic. Oxford University Press, Oxford.
Horty, J.F. (2012). Reasons as Defaults. Oxford University Press, Oxford.
Horty, J.F., & Pacuit, E. (2017). Action types in stit semantics. Rev. Symbol. Log., 10(4), 617–637.
Kalai, G., Rubinstein, A., & Spiegler, R. (2002). Rationalizing choice functions by mutltiple rationales. Econometrica, 70(6), 2481–2488.
Kooi, B., & Tamminga, A. (2008). Moral conflicts between groups of agents. J. Philos. Log., 37(1), 1–21.
Lewis, D. (1973). Counterfactuals. Harvard University Press, Cambridge.
Lewis, D. (1979). Counterfactual dependence and time’s arrow. Nous, 13(4), 455–476.
Lorini, E., & Longin, D. (2014). Eunate mayor. A logical analysis of responsibility attribution: Emotions, individuals and collectives. J. Log. Comput., 24 (6), 1313–1339.
Lorini, E., & Sartor, G. (2016). A STIT logic for reasoning about social influence. Studia Log., 104(4), 773–812.
Müller, T. (2005). On the Formal Structure of Continuous Action. In R. Schmidt, I. Pratt-Hartmann, M. Reynolds, & H. Wansing (Eds.) Advances in Modal Logic, (Vol. 5 pp. 191–209). London: King’s College Publications.
Pauly, M. (2002). A modal logic for coalitional power in games. J. Log. Comput., 12(1), 149–166.
Pearl, J. (2000). Causality. Models, Reasoning, and Inference. Cambridge University Press, Cambridge.
Perea, A. (2014). Belief in the opponents’ future rationality. Games Econ. Behav., 83, 231–254.
Placek, T., & Müller, T. (2007). Counterfactuals and historical possibility. Synthese, 154(2), 173–197.
Selten, R., & Leopold, U. (1982). Subjunctive Conditionals in Decision and Game Theory. In Philosophy of Economics, pp. 191–200. Springer.
Sen, A. (1997). Maximization and the act of choice. Econometrica, 65(4), 745–779.
Shin, H.S. (1992). Counterfactuals and a Theory of Equilibrium in Games. In C. Bicchieri M.L.D. Chiara (Eds.) Knowledge, Belief, and Strategic Interaction (pp. 397–413). Cambridge: Cambridge University Press.
Shoham, Y. (1989). Time for Action: On the Relation between Time, Knowledge and Action. In: Proceedings of the 11th International Joint Conference on Artificial Intelligence (IJCAI’89), vol. 2, pp. 954–959. Morgan Kaufmann Publishers, San Francisco.
Skyrms, B. (1998). Bayesian Subjunctive Conditionals for Games and Decisions. In Game Theory, Experience, Rationality, pp. 161–172.
Slote, M.A. (1978). Time in counterfactuals. Philos. Rev., 87(1), 3–27.
Stalnaker, R. (1996). Knowledge: Belief and counterfactual reasoning in games. Econ. Philos., 12, 133–163.
Stalnaker, R.C. (1968). A Theory of Conditionals. In R. Nicholas (Ed.) Studies in Logical Theory (pp. 98–112). Oxford: Basil Blackwell.
Stalnaker, R.C. (1998). Belief revision in games: Forward and backward induction. Math. Soc. Sci., 36(1), 31–56.
Tamminga, S. (2013). Deontic logic for strategic games. Erkenntnis, 78(1), 183–200.
Thomason, R.H., & Gupta, A. (1981). A Theory of Conditionals in the Context of Branching Time. In W.L. Harper, R.C. Stalnaker, & G. Pearce (Eds.) IFS: Conditionals, Belief, Decision, Chance and Time (pp. 299–322). Netherlands: Springer.
Troquard, N., & Vieu, L. (2006). Towards a Logic of Agency and Actions with Duration. In: European Conference on Artificial Intelligence 2006 (ECAI’06), volume 141 of Frontiers in Artificial Intelligence and Applications, pp. 775–776. IOS Press, Amsterdam.
Turrini, P. (2012). Agreements as Norms. In T. Ågotnes, J. Broersen, & D. Elgesem (Eds.) Deontic Logic in Computer Science, 11th International Conference (DEON 2011) (pp. 31–45). Berlin: Springer.
Xu, M. (1997). Causation in branching time (I): Transitions, events and causes. Synthese, 112(2), 137–192.
Xu, M. (2010). Combinations of Stit and Actions. J. Log. Lang. Inf., 19(4), 485–503.
Zambrano, E. (ed.) (2004). Counterfactual Reasoning and Common Knowledge of Rationality in Normal Form Games. Top. Theor. Econ. 4(8).
Acknowledgements
We would like to thank the participants of the audience of the following seminars and workshop at which this paper was presented: Logic Seminar (University of Maryland), LIRa Seminar (University of Amsterdam, 2020), Tsinghua Online Logic Seminar (Tsinghua University, 2020), LACN-Workshop (University of Amsterdam, 2020), Ghent-Brussels Seminar (University of Ghent and University of Brussels, 2021). We would also like to thank Paolo Santorio and two anonymous referees for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: A Completeness of SLDn
In this appendix we prove that the axiom system SLDn is complete with respect to the class of all SLDn frames.Footnote 1 The proof consists of two parts. First, we show that SLDn is sound and complete with respect to a class of Kripke models (called pseudo-models). By elaborating on a technique presented by [24], we then prove that every pseudo-model in which a formula \(\varphi \in {\mathscr{L}}_{\textsf {SLD}} \) is satisfiable can be turned into an SLDn model in which φ is satisfiable.
1.1 A.1 Pseudo-Models
Pseudo-models consist of a non-empty set W of possible states representing moment-history pairs partitioned into equivalence classes by an equivalence relation \( R_{\square } \). Intuitively, every equivalence class of \( R_{\square } \) represents a moment. Besides \( R_{\square } \), pseudo-models feature the following elements: two accessibility relations, denoted RX and RY, modeling, respectively, what happens next and what happened a moment ago; a function fdo assigning to every possible state the profile that is performed at that state; finally, a function fdev assigning to every state a set of deviant individual actions.
Remark 3
We adopt the following standard notation. For any set S, element s ∈ S, and relation \( R \subseteq S \times S\), \( R(s)= \{s^{\prime }\in S | sRs^{\prime }\} \). For any number \( n\in \mathbb {N} \), \( R^{n}\subseteq S\times S \) is defined recursively by setting: wR0v iff w = v; wRn+ 1v iff there is u ∈ S s.t. wRnu and uRv.
Definition 13 (Pseudo-model)
A pseudo-model is a tuple \(\langle {W,R_{\square }}, R_{\mathsf {X}},R_{\textsf {Y}},f_{do},\) fdev, ν〉, where \( W\neq \varnothing \), \( R_{\square }\) is an equivalence relation on W, RX and RY are binary relations on W, \( f_{do}:W\rightarrow Ag\text {-}Acts\) is the action function, \( f_{dev}: W\rightarrow 2^{Acts} \) is the deviant-choice function, and \( \nu :\text {Prop}\rightarrow 2^{W} \) is a valuation function. For any w ∈ W and i ∈Ag, let:
-
\(Acts^{w}_{i}=\bigcup \{f_{do}(w^{\prime })(i)\in Acts_{i} | w^{\prime }\in R_{\square }(w)\}\) be the actions available to agent i at \( R_{\square }(w)\);
-
\( Acts^{w}=\bigcup _{i\in Ag} Acts^{w}_{i} \) be the individual actions executable at \( R_{\square }(w) \).
Define \( R_{Ag} \subseteq W\times W\) by setting: for all \( w,w^{\prime }\in W \), \( wR_{Ag}w^{\prime }\text { iff } wR_{\square } w^{\prime }\text {and}\) \( f_{do}(w)= f_{do}(w^{\prime }) \). The elements of a pseudo-model are assumed to satisfy the following conditions:
-
1.
Properties of RX and RY: for all w, w1, w2 ∈ W,
-
1.1.
Seriality of RX: there is \( w^{\prime }\in W \) such that \( wR_{\mathsf {X}}w^{\prime } \).
-
1.2.
RX-functionality: if wRXw1 and wRXw2, then w1 = w2.
-
1.3.
RY-functionality: if wRYw1 and wRYw2, then w1 = w2.
-
1.4.
Converse: w1RYw2 iff w2RXw1.
-
1.1.
-
2.
Independence of Agents: for all w ∈ W and α ∈ Ag-Acts, if α(j) ∈ Actsw for all j ∈ Ag, then there is \( w^{\prime }\in R_{\square }(w) \) such that \( f_{do}(w^{\prime })= \alpha \).
-
3.
No Choice between Undivided Histories: for all w1, w2, w3 ∈ W, if w1RXw2 and \( w_{2}R_{\square }w_{3} \), then there is v ∈ W such that w1RAgv and vRXw3.
-
4.
Properties of fdev: for all \( w,w^{\prime }\in W \) and i ∈ Ag,
-
4.1.
Moment-invariance: if \( wR_{\square } w^{\prime }\), then \( f_{dev}(w)=f_{dev}(w^{\prime }) \).
-
4.2.
Executability of Deviant Actions: \( f_{dev}(w)\subseteq Acts^{w} \).
-
4.3.
Availability of Non-deviant Actions: \( Acts^{w}_{i} \setminus f_{dev}(w) \neq \varnothing \).
-
4.4.
(In)determinism of Choice Rules: if \( Acts^{w}_{i} \cap f_{dev}(w)\neq \varnothing \), then \(| Acts^{w}_{i} \setminus f_{dev}(w) | =1\).
-
4.1.
Definition 14 (Truth for \( {\mathscr{L}}_{\textsf {SLD}_n} \) in a pseudo-model)
Given a pseudo-model M, truth of a formula \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n} \) at a state w in M, denoted M, w⊧ϕ, is defined recursively. Truth of atomic propositions and the Boolean connectives is defined as usual. The remaining clauses are as follows: where \(\blacksquare \in \{\square , \mathsf {X},\mathsf {Y}\} \),
Theorem 2
The axiom system SLDn, defined by the axioms and rules in Table 2, is sound and complete with respect to the class of all pseudo-models.
The proof of Theorem 2 is entirely standard: soundness is proved via a routine validity check and completeness is proved via the construction of a canonical model for SLDn (see [8, Chapter 4.2]). We only provide the definition of the canonical model for SLDn and leave the rest to the reader. Let \( \mathcal {W} \) be the set of all maximal consistent sets of SLDn. Where \( w \in \mathcal {W}\) and \( \blacksquare \in \{\square , \mathsf {X},\mathsf {Y}\} \), define \( w/\blacksquare = \{ \varphi \in {\mathscr{L}}_{\textsf {SLD}_n} | \blacksquare \varphi \in w\} \).
Definition 15
The canonical SLDn model is a tuple \( \left \langle {W^{c},R_{\square }^{c},R_{\mathsf {X}}^{c},R_{\textsf {Y}}^{c},f_{do}^{c},f_{dev}^{c},\nu ^{c}}\right \rangle \), where
-
\( W^{c} = \mathcal {W}\) and \( \nu ^{c}:Prop\rightarrow 2^{W^{c}} \) is s.t., for all w ∈ Wc, w ∈ νc(p) iff p ∈ w;
-
where \( \blacksquare \in \{\square , \mathsf {X},\mathsf {Y}\} \), \( R^{c}_{\blacksquare }\subseteq W^{c}\times W^{c} \) is s.t., for all \( w,w^{\prime }\in W^{c} \), \( w R^{c}_{\blacksquare } w^{\prime }\) iff \( w/\blacksquare \subseteq w^{\prime } \);
-
\( f_{do}^{c}:W^{c}\rightarrow Ag\text {-}Acts \) is s.t., for all w ∈ Wc, \( f_{do}^{c}(w)=\alpha \) iff do(α) ∈ w;
-
\( f_{dev}^{c}:W^{c}\rightarrow 2^{Acts} \) is s.t., for all w ∈ Wc and ai ∈ Acts, \(a_{i}\in f_{dev}^{c}(w) \) iff dev(ai) ∈ w.
A.2 From Pseudo-Models to SLDn Models
Call a pointed pseudo-model any pair M, w such that M is a pseudo-model and w a state in M. By Theorem 2, for any SLDn-consistent formula ϕ, there is a pointed pseudo-model M, w such that M, w⊧φ. We want to show that M can be transformed into an SLDn model in which φ is satisfiable. To build stit models from Kripke models similar to our pseudo-models, Herzig and Lorini [24] use a construction consisting of two preliminary steps: (1) the relevant Kripke model is unraveledFootnote 2 in order to ensure that the relation RX generates a treelike ordering of the equivalence classes of \( R_{\square } \) (recall that these represent moments); (2) from a certain point on along the relation RX in the unraveled model, every equivalence class of \( R_{\square } \) is forced to be a singleton. Step (2) guarantees that there is a one-to-one correspondence between states in the unraveled model and indices in the stit model built from it. The presence of the operator Y in the language of SLDn requires us to refine the unraveling procedure in step (1). We present the said refinement in details (Steps 1 and 2 below) and only sketch the rest of the proof (Steps 3 to 4 below), which proceeds (except for a few minor modifications) as in [18, Appendix A.1.2].
Step 1: Extended language and complexity measures
Our first task is to define an unraveling procedure u that takes a pointed pseudo-model M, w and a formula \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n} \) and returns a pointed pseudo-model uϕ(M, w) satisfying:
-
(P1) M, w⊧ϕ iff uϕ(M, w)⊧ϕ.
The idea is roughly as follows: we first identify the earliest state \( w^{\prime } \) needed to determine whether ϕ is true at w; then, we unravel RX around the \( R_{\square } \)-equivalence class of \( w^{\prime } \). To make this work, we need to extend our language and introduce three complexity measures of the formulas in the extended set \( {\mathscr{L}}_{\textsf {ALD}}^{\prime } \): (i) the Y-depth of ϕ is needed to identify \( w^{\prime } \) and the state corresponding to w in the unraveled model; (ii) the size of ϕ and (iii) the c-size of ϕ are needed to define a well-founded strict partial order \( <_{c}^{S} \) on \( {\mathscr{L}}_{\textsf {ALD}}^{\prime } \). The proof that our unraveling procedure satisfies P1 will be on \( <_{c}^{S} \)-induction on ϕ (cf. Proposition 6).
Definition 16 (Extended language)
Let Prop and Acts be as before. The set \( {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \) is generated by the following grammar:
where p ∈ Prop and ai ∈ Acts.
The evaluation rule for \( \boxplus \phi \) in the class of pseudo-models is as follows:
Accordingly, \( \boxplus \phi \leftrightarrow \mathsf {X}\mathsf {Y}\phi \) and \( \boxplus \phi \leftrightarrow \phi \) are valid on all pseudo-models.
Definition 17 (Y-depth of \(\phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \))
The Y-depth d(ϕ) of \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime }\) is defined as:
Definition 18 (Size of \(\phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \))
The size S(ϕ) of \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime }\) is defined as:
Definition 19 (c-size of \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \))
The c-size c(ϕ) of \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime }\) is defined as:
Definition 20
For any \( \phi ,\psi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \), we set: \( \phi <_c^S \psi \) iff either c(ϕ) < c(ψ) or (c(ϕ) = c(ψ) and S(ϕ) < S(ψ)).
Lemma 1
\( <_c^S \) is a well-founded strict partial order between the formulas of \( {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \).
Proof
Straightforward from Def. 20. □
Lemma 2
For any \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \) and \( n\in \mathbb {N} \) such that n ≥ d(ϕ), there is \( \phi ^{\prime }\in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \) s.t. (1) \( \phi \leftrightarrow \phi ^{\prime } \) is valid on any pseudo-model, (2) \( d(\phi ^{\prime }) = n \), and (3) \( c(\phi ^{\prime })=c(\phi ) \).
Proof
Immediate from the fact that \( \phi \leftrightarrow \boxplus \phi \) is valid on any pseudo-model, that \( d(\boxplus \phi )= d(\phi )+1 \), and that \(c(\boxplus \phi )=c(\phi ) \). □
Step 2: Unraveling procedure
We adopt the following notation: where M, w is a pointed pseudo-model and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \),
-
1.
d(w, ϕ) is the greatest number n satisfying: n ≤ d(ϕ) and there is a v ∈ W such that \( wR_{\textsf {Y}}^{n} v\) (equiv. \( vR_{\mathsf {X}}^{n} w \));
-
2.
where n = d(w, ϕ), s(w, ϕ) ∈ W is the state v satisfying: \( wR_{\textsf {Y}}^{n} v\) (equiv. \( vR_{\mathsf {X}}^{n} w \)).Footnote 3
Definition 21 (d(w, ϕ)-unraveling)
Let M, w be a pointed pseudo-model and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \). The d(w, ϕ)-unraveling of M, w is the tuple
where:
-
W(w, ϕ) is the set of all sequences \( \overrightarrow {w_{n}}= w_{1}w_{2} {\dots } w_{n} \) s.t. \( w_{1} R_{\square } s_{(w,\phi )} \) and wiRXwi+ 1, where 1 ≤ i < n;
-
\( R_{\square }^{(w,\phi )}\subseteq W^{(w,\phi )}\times W^{(w,\phi )} \) is s.t. \( \overrightarrow {w_{n}} R_{\square }^{(w,\phi )}\overrightarrow {v_{m}} \) iff n = m, \( w_{i} R_{\square } v_{i} \) for i ≤ n, and fdo(wi) = fdo(vi) for i < n;
-
\( R_{\mathsf {X}}^{(w,\phi )}\subseteq W^{(w,\phi )}\times W^{(w,\phi )} \) is s.t. \( \overrightarrow {w_{n}}R_{\mathsf {X}}^{(w,\phi )} \overrightarrow {v_{m}} \) iff \( \overrightarrow {v_{m}} = \overrightarrow {w_{n}}v_{m} \) and wnRXvm;
-
\( R_{\textsf {Y}}^{(w,\phi )}\subseteq W^{(w,\phi )}\times W^{(w,\phi )} \) is s.t. \( \overrightarrow {w_{n}}R_{\textsf {Y}}^{(w,\phi )} \overrightarrow {v_{m}} \) iff \( \overrightarrow {w_{n}} = \overrightarrow {v_{m}}w_{n} \) and wnRYvm;
-
\( f_{do}^{(w,\phi )}: W^{(w,\phi )}\rightarrow Ag\text {-}Acts \) is s.t. \( f_{do}^{(w,\phi )}(\overrightarrow {w_{n}})= f_{do}({w_{n}}) \)
-
\( f_{dev}^{(w,\phi )}: W^{(w,\phi )}\rightarrow 2^{Acts} \) is s.t. \( f_{dev}^{(w,\phi )}(\overrightarrow {w_{n}})= f_{dev}({w_{n}}) \)
-
\( \nu ^{(w,\phi )}:Prop\rightarrow 2^{W^{(w,\phi )}} \) is s.t. \(\overrightarrow {w_{n}} \in \nu ^{(w,\phi )}(p) \) iff wn ∈ ν(p).
Let σ(w, ϕ) be the sequence \( w_{1}w_{2} {\dots } w_{n} \) s.t. w1 = s(w, ϕ), wn = w, and n = d(w, ϕ) + 1.Footnote 4
Remark 4
The construction of M(w, ϕ) and σ(w, ϕ) ultimately depends on w and d(ϕ). Hence, if d(ϕ) = d(ψ), then M(w, ϕ) = M(w, ψ) and σ(w, ϕ) = σ(w, ψ).
We will use the following lemma repeatedly later on.
Lemma 3
Let M, w be a pointed pseudo-model and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \). For all \( \overrightarrow {w_{n}} \) in M(w, ϕ) and v in M, if \( w_{n} R_{\square } v \), then there is \( \overrightarrow {v_{n}}\) in M(w, ϕ) such that vn = v and \( \overrightarrow {w_{n}} R_{\square }^{(w,\phi )} \overrightarrow {v_{n}} \).
Proof
The proof proceeds by an easy induction on n and relies on the fact that M satisfies condition 3 from Def. 13 (i.e., no choice between undivided histories). □
Proposition 5
For any pointed pseudo-model M, w and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \), M(w, ϕ) is a pseudo-model.
Proof
The proof follows immediately from Def. 21 and from the fact that M is a pseudo-model. To illustrate, we check that M(w, ϕ) satisfies condition 2 from Def. 13 (i.e., independence of agents): Let \( \overrightarrow {w_{n}}\in W^{({w},{\phi })} \) and α ∈Ag-Acts be s.t., for all j ∈Ag, there is \(\overrightarrow {v_{n_{j}}}\in R^{({w},{\phi })}_{\square } (\overrightarrow {w_{n}}) \) s.t. \( f^{({w},{\phi })}_{do} (\overrightarrow {v_{n_{j}}})(j) = \alpha (j) \). Then, by the def. of \( R^{({w},{\phi })}_{\square } \) and \( f^{({w},{\phi })}_{do} \), for all j ∈Ag, there is \( v_{n_{j}} \) s.t. \( v_{n_{j}}\in R_{\square }(w_{n}) \) and \( f_{do}(v_{n_{j}})(j) = \alpha (j)\). Since M satisfies condition 2 from Def. 13, it follows that there is \( u\in R_{\square }(w_{n}) \) s.t. fdo(u) = α. By Lem. 3 and the def. of \( f^{({w},{\phi })}_{do} \), we conclude that there is \( \overrightarrow {u_{n}} \in W^{({w},{\phi })}\) s.t. un = u, \( \overrightarrow {u_{n}} R^{({w},{\phi })}_{\square }\overrightarrow {w_{n}} \), and \( f^{({w},{\phi })}_{do} (\overrightarrow {u_{n}})= f_{do}(u)=\alpha \). □
The next three lemmas will be key to prove Proposition 6 below.
Lemma 4
Let M, w be a pointed pseudo-model. For any v ∈ W and \( \phi ,\psi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \), if \( wR_{\square } v\) and d(ϕ) = d(ψ), then (1) M(w, ϕ) = M(v, ψ) and (2) \(\sigma _{(w,\phi )} R_{\square }^{(w,\phi )}\sigma _{(v,\psi )}\).
Proof
(1) It is not difficult to see that, by condition 3 from Def. 13 (i.e., no choice between undivided histories), if \( wR_{\square } v\) and d(ϕ) = d(ψ), then d(w, ϕ) = d(v, ψ) and \( s_{(w,\phi )} R_{\square } s_{(v,\psi )}\). In tandem with Def. 21, the latter fact entails that M(w, ϕ) = M(v, ψ). (2) Since the last element of σ(w, ϕ) is w and \( wR_{\square } v \), it follows from Lem. 3 that there is \( \overrightarrow {v_{n}}\in W^{({w},{\phi })}\) s.t. vn = v and \( \sigma ({w},{\phi }) R^{({w},{\phi })}_{\square } \overrightarrow {v_{n}} \) (so n = d(w, ϕ) + 1 = d(v, ψ) + 1). By the def. of σ(v, ψ) and the functionality of RX, this entails that \( \overrightarrow {v_{n}} = \sigma ({v},{\psi }) \). Hence, \(\sigma ({w},{\phi }) R^{({w},{\phi })}_{\square }\sigma ({v},{\psi })\). □
Lemma 5
Let M, w be a pointed pseudo-model. For any v ∈ W and \( \phi ,\psi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \), if wRXv and d(ψ) = d(ϕ) + 1, then (1) M(w, ϕ) = M(v, ψ) and (2) \(\sigma ({w},{\phi }) R^{({w},{\phi })}_{\textsf {X}}\sigma ({v},{\psi })\).
Proof
(1) It is not difficult to see that, by the def. of d(w, ϕ) and s(w, ϕ) and the functionality of RX and RY, if wRXv and d(ψ) = d(ϕ) + 1, then d(v, ψ) = d(w, ϕ) + 1 and S(w, ϕ) = S(v, ψ). Given Def. 21, the latter fact entails that M(w, ϕ) = M(v, ψ). (2) Immediate since σ(w, ϕ) and σ(v, ψ) have the same initial state, RX is functional, and wRXv. □
Lemma 6
Let M, w be a pointed pseudo-model. For any \( \phi ,\psi \in {\mathscr{L}}_{\textup {\textsf {SLD}}_n}^{\prime } \), if d(ψ) = d(ϕ) + 1, then M(w, ψ), σ(w, ψ)⊧ϕ iff M(w, ϕ), σ(w, ϕ)⊧ϕ.
Proof
If d(w, ψ) = d(w, ϕ), then M(w, ψ) = M(w, ϕ) and σ(w, ψ) = σ(w, ϕ) by Def. 21, whence the result. If d(w, ψ)≠d(w, ϕ), then d(w, ψ) = d(w, ϕ) + 1 by the def. of d(w, ϕ). Let n = d(w, ϕ), so that d(w, ψ) = n + 1. By the def. of s(w, ϕ) and s(w, ψ), \( s_{(w,\phi )} R_{\mathsf {X}}^{n} w \) and \( s_{(w,\psi )} R_{\mathsf {X}}^{n+1} w \), and so s(w, ψ)RXs(w, ϕ) by the functionality of RX. Consider now M(w, ψ). It is easy to check that the two-element sequence s(w, ψ)s(w, ϕ) is s.t. (1) s(w, ψ)s(w, ϕ) ∈ W(w, ψ) and (2) \( S_{({w},{\psi })}S_{({w},{\phi })} (R^{(w,\phi )}_{\textsf {X}})^{n} \sigma ({w},{\psi }) \). Let
be the submodel of M(w, ψ) generated by s(w, ψ)s(w, ϕ) via \( R_{\square }^{(w,\psi )} \) and \( R_{\mathsf {X}}^{(w,\psi )} \).Footnote 5 Obviously, σ(w, ψ) ∈ W(w, ψ, ϕ). In addition, since M(w, ψ, ϕ) is obtained by “cutting” M(w, ψ) in the past taking into account the Y-depth of ϕ (recall that n = d(w, ϕ)), we have that:
-
1.
M(w, ψ), σ(w, ψ)⊧ϕ iff M(w, ψ, ϕ), σ(w, ψ)⊧ϕ.
Now, define a mapping \( f: W^{(w,\psi ,\phi )} \rightarrow W^{(w,\phi )} \) by setting: for every \( \overrightarrow {w_{m}}\in W^{(w,\psi ,\phi )} \), \( f(\overrightarrow {w_{m}})= w_{2}w_{3} {\dots } w_{m} \). That is, \( f(\overrightarrow {w_{m}}) \) is the sequence obtained by eliminating the first element of \( \overrightarrow {w_{m}} \). We now prove the following facts:
-
2.
for all \( \overrightarrow {w_{m}}\in W^{(w,\psi ,\phi )} \), \( f(\overrightarrow {w_{m}}) \in W^{(w,\phi )} \);
-
3.
f(σ(w, ψ)) = σ(w, ϕ);
-
4.
the function f is a bounded morphism from M(w, ψ, ϕ) to M(w, ϕ).
□
Proof of 2.
Let \( \overrightarrow {w_{m}}= w_{1}w_{2} {\dots } w_{m}\in W^{(w,\psi ,\phi )} \), so \( f(\overrightarrow {w_{m}})= w_{2}{\dots } w_{m} \). By the def. of W(w, ψ, ϕ), for all i s.t. 2 ≤ i < m, wiRXwi+ 1. In addition, since M(wψ, ϕ) is generated by S(w, ψ)S(w, ϕ) via S(w, ψ) and S(w, ψ), w1w2S(w, ψ)S(w, ψ)S(w, ϕ). Hence, \( w_{2} R_{\square }S_{({w},{\phi })}\). □
Proof of 3.
Straightforward from the def. of σ(w, ϕ) and σ(w, ψ), since s(w, ψ)RXs(w, ϕ). □
Proof of 4.
Let \(\blacksquare \in \{\square ,\mathsf {X},\mathsf {Y} \}\). We need to prove that, for all \( \overrightarrow {w_{n}},\overrightarrow {v_{m}}\in W^{(w,\psi ,\phi )} \), \( \overrightarrow {u_{k}}\in W^{(w,\phi )}\), ai ∈ Acts, and p ∈ Prop,
-
4.1
if \( \overrightarrow {w_{n}} R_{\blacksquare }^{(w,\psi ,\phi )} \overrightarrow {v_{m}} \), then \( f(\overrightarrow {w_{n}}) R_{\blacksquare }^{(w,\phi )} f(\overrightarrow {v_{m}}) \);
-
4.2
if \( f(\overrightarrow {w_{n}}) R_{\blacksquare }^{(w,\phi )} \overrightarrow {u_{k}} \), then there is \( \overrightarrow {v_{m}}\in W^{(w,\psi ,\phi )} \) s.t. \( f(\overrightarrow {v_{m}} ) = \overrightarrow {u_{k}} \) and \( \overrightarrow {w_{n}} R_{\blacksquare }^{(w,\psi ,\phi )} \overrightarrow {v_{m}} \);
-
4.3
\( f_{do}^{(w,\psi ,\phi )}(\overrightarrow {w_{n}}) = f_{do}^{(w,\phi )}(f(\overrightarrow {w_{n}})) \) and \( f_{dev}^{(w,\psi ,\phi )}(\overrightarrow {w_{n}}) = f_{dev}^{(w,\phi )}(f(\overrightarrow {w_{n}})) \);
-
4.5
\(\overrightarrow {w_{n}}\in \nu ^{(w,\psi ,\phi )}(p) \) iff \( f(\overrightarrow {w_{n}})\in \nu ^{(w,\phi )}(p) \).
The only relatively tricky part is 4.2 when \( \blacksquare = \square \). The proof is as follows: Let \( \overrightarrow {w_{n}}= w_{1}w_{2} {\dots } w_{n} \in W^{(w,\psi ,\phi )}\) and \( \overrightarrow {u_{k}}= u_{2}u_{3} {\dots } u_{k} \in W^{(w,\phi )} \) be s.t. \( f(\overrightarrow {w_{n}} )R_{\square }^{(w,\phi )} \overrightarrow {u_{k}} \). By the def. of W(w, ψ, ϕ), w1RXw2. In addition, by the def. of \( R^{({w},{\phi })}_{\square } \), \( w_{2}R_{\square } u_{2}\). Hence, by condition 3 from Def. 13, there is v ∈ W s.t. w1RAgv and vRXu2. It is not difficult to check that the sequence \( v \overrightarrow {u_{k}}\) is s.t.: (1) \(v \overrightarrow {u_{k}}\in M^{(w,\phi ,\psi )} \), (2) \( \overrightarrow {w_{n}} R_{\square }^{(w,\psi ,\phi )} v\overrightarrow {u_{k}} \), and (3) \( f(v\overrightarrow {u_{k}})= u_{k} \).
By standard results in modal logic [8, Prop. 2.14], fact 4 implies that
for all \( \overrightarrow {w_{n}}\in W^{(w,\psi ,\phi )} \) and \( \chi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \). Hence, M(w, ψ, ϕ), σ(w, ψ)⊧ϕ iff M(w, ϕ), σ(w, ϕ)⊧ϕ by fact 3, and so M(w, ψ), σ(w, ψ)⊧ϕ iff M(w, ϕ), σ(w, ϕ)⊧ϕ by fact 1. □
We are now ready to prove the central proposition of this part.
Proposition 6
For any pointed pseudo-model M, w and \( \phi \in {\mathscr{L}}_{\textup {\textsf {SLD}}_n}^{\prime } \), M, w⊧ϕ iff M(w, ϕ), σ(w, ϕ)⊧ϕ.
Proof
The proof is by \( <_c^S \)-induction on ϕ. The cases in which ϕ := p, ϕ := do(ai), and ϕ := dev(ai) follow immediately from Def. 21 and the fact that w is the last element of σw, p. For the inductive cases, we assume the following inductive hypothesis (IH): if M, v is a pointed pseudo-model and \( \psi \in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime }\) is s.t. \(\psi <_c^S \phi \), then M, v⊧ψ iff M(v, ψ), σ(v, ψ)⊧ψ. We omit the proof for the case in which ϕ := ¬ψ, which follows immediately from Remark 4. The other cases are as follows:
-
1.
ϕ := ψ ∧ χ.
Suppose, without loss of generality, that d(ψ) ≤ d(χ). Then, by Lem. 2, there is \( \psi ^{\prime }\in {\mathscr{L}}_{\textsf {SLD}_n}^{\prime } \) s.t. (1) \( \psi \leftrightarrow \psi ^{\prime } \) is valid in the class of pseudo-models, (2) \( d(\psi ^{\prime })= d(\chi ) \), and (3) \( c(\psi ^{\prime }) = c(\psi ) < c(\psi ) + c(\chi ) + 1 = c(\psi \wedge \chi ) \). It follows from (3) that (A) \(\psi ^{\prime } <_{c}^{S} (\psi \wedge \chi ) \) and \(\chi <_{c}^{S} (\psi \wedge \chi ) \) and from (2) that (B) \( d(\psi \wedge \chi )=max\{d(\psi ),d(\chi )\} = d(\chi )=d(\psi ^{\prime }) \). Given these facts, we reason as follows:
M, w⊧ψ ∧ χ
iff
M, w⊧ψ and M, w⊧χ
by def. of truth
iff
\(M,w\models \psi ^{\prime } \) and M, w⊧χ
by (1)
iff
\(M^{(w,\psi ^{\prime })},\sigma _{(w,\psi ^{\prime })}\models \psi ^{\prime } \) and M(w, χ), σ(w, χ)⊧χ
by IH, given (A)
iff
\(M^{(w,\psi \wedge \chi )},\sigma _{(w,\psi \wedge \chi )}\models \psi ^{\prime } \) and M(w, ψ∧χ), σ(w, ψ∧χ)⊧χ
by Remark 4
iff
M(w, ψ∧χ), σ(w, ψ∧χ)⊧ψ and M(w, ψ∧χ), σ(w, ψ∧χ)⊧χ
by (1), given
Prop. 5
iff
M(w, ψ∧χ), σ(w, ψ∧χ)⊧ψ ∧ χ
by def. of truth
-
2.
\( \phi := \square \psi \).Since \( d(\psi ) = d(\square \psi ) \), we can use Lemma 4:
\( M,w\models \square \psi \)
iff
for all v s.t. \( wR_{\square }v \), M, v⊧ψ
by def. of truth
iff
for all v s.t. \( wR_{\square }v \), M(v, ψ), σ(v, ψ)⊧ψ
by IH
iff
for all v s.t. \( \sigma _{(w,\square \psi )}R_{\square }^{(w,\square \psi )}\sigma _{(v,\psi )}\), \( M^{(w,\square \psi )},\sigma _{(v,\psi )}\models \psi \)
by Lem. 4 and the
def. of \( R_{\square }^{(w,\square \psi )} \)
iff
for all \( \overrightarrow {v_{n}}\) s.t. \(\sigma _{(w,\square \psi )}R_{\square }^{(w,\square \psi )} \overrightarrow {v_{n}}\), \( M^{(w,\square \psi )},\overrightarrow {v_{n}}\models \psi \)
with n = d(v, ψ) + 1
iff
\( M^{(w,\square \psi )},\sigma _{(w,\square \psi )}\models \square \psi \)
by def. of truth
-
3.
ϕ := Xψ.
For this case, we exploit the following facts: (A) \( \psi \leftrightarrow \boxplus \psi \) is valid in the class of pseudo-models, (B) \( \boxplus \psi <_c^S \mathsf {X}\psi \), since \( c(\boxplus \psi )=c(\psi ) = c(\mathsf {X}\psi )\) and \( S(\boxplus \psi )= S(\psi ) +1 < S(\psi ) +2= S(\mathsf {X}\psi ) \).
M, w⊧Xψ
iff
for all v s.t. wRXv, M, v⊧ψ
by def. of truth
iff
for all v s.t. wRXv, \( M,v\models \boxplus \psi \)
by (A)
iff
for all v s.t. wRXv, \( M^{(v,\boxplus \psi )},\sigma _{(v,\boxplus \psi )}\models \boxplus \psi \)
by IH, given (B)
iff
for all v s.t. \( \sigma _{(w,\mathsf {X}\psi )} R_{\mathsf {X}}^{(w,\mathsf {X}\psi )} \sigma _{(v,\boxplus \psi )}\),
by Lem. 5 and the
\( M^{(w,\mathsf {X}\psi )},\sigma _{(v,\boxplus \psi )}\models \boxplus \psi \)
def. of \( R_{\mathsf {X}}^{(w,\mathsf {X}\psi )} \)
iff
for all \( \overrightarrow {v_{n}}\) s.t. \( \sigma _{(w,\mathsf {X}\psi )} R_{\mathsf {X}}^{(w,\mathsf {X}\psi )}\overrightarrow {v_{n}}\),
with \( n=d(v,\boxplus \psi )+1 \)
\( M^{(w,\mathsf {X}\psi )},\overrightarrow {v_{n}}\models \boxplus \psi \)
iff
for all \( \overrightarrow {v_{n}}\) s.t. \( \sigma _{(w,\mathsf {X}\psi )} R_{\mathsf {X}}^{(w,\mathsf {X}\psi )}\overrightarrow {v_{n}} \), \( M^{(w,\mathsf {X}\psi )},\overrightarrow {v_{n}}\models \psi \)
by (A), given Prop. 5
iff
M(w, Xψ), σ(w, Xψ)⊧Xψ
by def. of truth
The remaining cases are proved in a similar way. In particular, the case in which ϕ := Yψ follows from Lemma 5 and the fact that RY is the converse RX, while the case in which \( \phi :=\boxplus \psi \) follows from Lemma 6 and the fact that \(\boxplus \psi \leftrightarrow \psi \) is valid on any pseudo-model. □
Step 3: Dividing histories
We now want to show that a pseudo-model like M(w, ϕ) (where \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n} \)) can be turned into an SLDn model. The idea is simple: we take equivalence classes determined by \( R^{({w},{\phi })}_{\square }\) as moments and we show that \( R^{({w},{\phi })}_{\textsf {X}}\) induces a treelike ordering on moments. Before doing this, we take an extra step to ensure that the states in W(w, ϕ) and the moment-history pairs in the resulting SLDn model will be in a one-to-one correspondence.
Definition 22 (X-depth of \(\phi \in {\mathscr{L}}_{\textsf {SLD}_n} \))
The X-depth x(ϕ) of \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}\) is defined as:
Definition 23
Let M, w be a pointed pseudo-model and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n} \). Then, M(w, ϕ, x) is the tuple obtained from M(w, ϕ) by replacing \( R_{\square }^{(w,\phi )} \) with the relation \( R_{\square }^{(w,\phi ,x)} \) defined by setting, for all \( \overrightarrow {w_{n}},\overrightarrow {v_{m}}\in W^{(w,\phi )} \),
So, in M(w, ϕ, x), all sequences of length n > d(w, ϕ) + x(ϕ) + 1 belong to a singleton equivalence class of \(R_{\square }^{(w,\phi ,x)} \). It is immediate to check that M(w, ϕ, x) is still a pseudo-model. In addition, the next proposition follows straightforwardly from Proposition 5 and from the fact that \( R_{\square }^{(w,\phi )} \)-equivalent states are separated in M(w, ϕ, x) by taking into account the modal X-depth of φ.
Proposition 7
For any pointed pseudo-model M, w and \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n} \), M, w⊧ϕ iff M(w, ϕ, x), σ(w, ϕ)⊧ϕ.
Step 4: From pseudo-models to SLDn models
Let \( \phi \in {\mathscr{L}}_{\textsf {SLD}_n}\) be an SLDn-consistent formula and M, w a pointed pseudo-model s.t. M, w⊧ϕ. Then, M(w, ϕ, x), σ(w, ϕ)⊧ϕ by Prop. 7. Define \(\mathcal {T}= \langle Mom,m_{0},<\rangle \) so that:
-
Mom is the quotient set of W(w, ϕ) by \( R_{\square }^{(w,\phi ,x)} \);
-
m0 = [s(w, ϕ)] is the equivalence class in Mom of the one-element sequence s(w, ϕ).
-
\( < \subseteq \textit {Mom}\times \textit {Mom}\) is s.t., for all \( [\overrightarrow {w_{n}} ], [\overrightarrow {v_{m}}] \in \textit {Mom}\), \( [\overrightarrow {w_{n}} ] < [\overrightarrow {v_{m}}] \) iff all prefixes of length n of sequences in \( [\overrightarrow {v_{m}}] \) are in \( [\overrightarrow {w_{n}}] \) (i.e., iff n < m and, for all \( \overrightarrow {u_{m}}\in [\overrightarrow {v_{m}}] \), \( \overrightarrow {u_{n}}\in [\overrightarrow {w_{n}}] \)).
It is not difficult to check that \( \mathcal {T}\) is a DBT structure. In addition, there is a one-to-one correspondence between possible states in the pseudo-model M(w, ϕ, x) and indices in \( \mathcal {T}\). To see this, where \( n\in \mathbb {N} \) and \( h\in \textit {Hist}^{\mathcal {T}} \), let h(n) be the n-th moment on h.Footnote 6 Any index \( [\overrightarrow {w_{n}}]/h \) can then be re-written as h(n)/h. Finally, let z = d(w, ϕ) + x(ϕ) + 1. Observe that Definition 23 and the functionality of \(R_{\mathsf {X}}^{(w,\phi )}\) ensure that, for all n > z, h(n) is a singleton (we write \( \overrightarrow {w_{h(n)}} \) for its only element). Define a mapping \( \omega : \textit {Ind}^{\mathcal {T}} \rightarrow W^{(w,\phi )}\) by setting: for all \( h(n)/h\in \textit {Ind}^{\mathcal {T}} \),
Intuitively, the function ω finds, for every index h(n)/h, the “witness” of h in h(n). It does so by picking a singleton moment on h that occurs later than h(n) and by selecting the prefix of length n of its unique element.Footnote 7 It is an easy exercise to prove that ω is a bijection. We write ω− 1 for its inverse.
Now, where \( \mathcal {T} \) is defined as dabove, define \( {\mathscr{M}}= \left \langle {\mathcal {T},\mathbf {act},\mathbf {dev},\pi }\right \rangle \) so that:
-
\( \mathbf {act} : \textit {Ind}^{\mathcal {T}} \rightarrow Ag\text {-}Acts\) is s.t. \( \mathbf {act}(h(n)/h)= f_{do}^{(w,\phi )}(\omega (h(n)/h)) \);
-
\( \mathbf {dev}:\textit {Mom}\rightarrow 2^{Acts} \) is s.t. \( \mathbf {dev}([\overrightarrow {w_{n}}]) = f_{dev}^{(w,\phi )}(\overrightarrow {w_{n}})\);
-
\( \pi : Prop\rightarrow 2^{\textit {Ind}^{\mathcal {T}}} \) is s.t. h(n)/h ∈ π(p) iff ω(h(n)/h) ∈ ν(w, ϕ)(p).
Proposition 8
\( {\mathscr{M}} \) is a SLDn model.
Proof
We noticed above that \( \mathcal {T} \) is a DBT structure. It is immediate to see that the function dev is well defined because \( f_{dev}^{(w,\phi )}\) satisfies condition 4.1 from Def. 13. In addition, dev also satisfies conditions 3, 4, and 5 from Def. 4 because \(f^{({w},{\phi })}_{dev} \) satisfies the corresponding conditions 4.2, 4.3, and 4.4 from Def. 13. For the remaining conditions the proof can be easily adapted from the proof of Proposition A.1.23 in [18, p. 211]. □
Proposition 9
For all formulas \( \psi \in {\mathscr{L}}_{\textsf {SLD}_n} \) and indices h(n)/h in \( {\mathscr{M}} \),
Proof
The proof is by induction on the complexity of ψ. The cases for propositional variables, Boolean connectives, and formulas like do(ai) and dev(ai) follow straightforwardly from the def. of \( {\mathscr{M}} \). The proof for the cases in which \( \psi := \square \chi \) and ψ := Xχ can be easily adapted from the proof of Proposition A.1.24 in [18, pp. 211-212]. Finally, the case in which ψ := Yχ is analogous to the case in which ψ := Xχ. □
Proposition 9 and the fact that M(w, ϕ, x), σ(w, ϕ)⊧ϕ entail that \( {\mathscr{M}}, \omega ^{-1}(\sigma _{(w,\phi )})\models \phi \). Since ϕ is an arbitrary SLDn-consistent formula and \( {\mathscr{M}} \) is an SLDn model, we can then conclude that SLDn is complete w.r.t. the class of all SLDn models.
B Proofs of Propositions 3 and 4
Proof of Proposition 3
We only present the proof for the left-to-right direction of DisX and for Cen1, as the remaining cases are similar. Let \( {\mathscr{M}} = \left \langle {\left \langle {\textit {Mom},m_{0},<}\right \rangle ,\mathbf {act},\mathbf {dev},\preceq ,\pi }\right \rangle \) be either a rewind model or an independence model and m/h an index in \( {\mathscr{M}} \). Recall that, for any h ∈ Hm, succh(m) is the successor of m on history h and that tm is the instant to which m belongs. Definition 2 ensures that, for any h ∈ Hm and \( h^{\prime }\in H_{m^{\prime }} \), \( \mathsf {t}_{m} = \mathsf {t}_{m^{\prime }} \) iff \( \mathsf {t}_{succ_h (m)} = \mathsf {t}_{succ_{h^{\prime }} (m^{\prime })} \). Below, we will repeatedly use this fact without explicit mention.
(DisX, L-R) If  , then
, then  . There are two cases. Case 1: There is no \( h^{\prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \). Then, there is no \( h^{\prime } \) s.t. \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \mathsf {X}\varphi \), otherwise \({\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \), against the hypothesis. Hence,
. There are two cases. Case 1: There is no \( h^{\prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \). Then, there is no \( h^{\prime } \) s.t. \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \mathsf {X}\varphi \), otherwise \({\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \), against the hypothesis. Hence,  by Def. 8 (i). Case 2: There is \( h^{\prime }\in \textit {Hist} \) s.t. \({\mathscr{M}}, \mathsf {t}_{succ_h (m)}/h^{\prime }\models \varphi \wedge \psi \) and, for all \( h^{\prime \prime }\in \textit {Hist} \), if \({\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime \prime }\models \varphi \wedge \neg \psi \), then \( h^{\prime \prime }\not \preceq _{h} h^{\prime }\). If \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \wedge \psi \), then \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \mathsf {X}\varphi \wedge \mathsf {X}\psi \). Take any h∗∈Hist s.t. (∗) \( {\mathscr{M}}, \mathsf {t}_{m}/h^{*}\models \mathsf {X}\varphi \wedge \neg \mathsf {X}\psi \). We want to show that \( h^{*}\not \preceq _{h} h^{\prime }\). By the def. of truth, (∗) implies that \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{*}\models \varphi \wedge \neg \psi \), and so \( h^{*}\not \preceq _{h} h^{\prime }\) by our hypothesis. Hence,
by Def. 8 (i). Case 2: There is \( h^{\prime }\in \textit {Hist} \) s.t. \({\mathscr{M}}, \mathsf {t}_{succ_h (m)}/h^{\prime }\models \varphi \wedge \psi \) and, for all \( h^{\prime \prime }\in \textit {Hist} \), if \({\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime \prime }\models \varphi \wedge \neg \psi \), then \( h^{\prime \prime }\not \preceq _{h} h^{\prime }\). If \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{\prime }\models \varphi \wedge \psi \), then \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \mathsf {X}\varphi \wedge \mathsf {X}\psi \). Take any h∗∈Hist s.t. (∗) \( {\mathscr{M}}, \mathsf {t}_{m}/h^{*}\models \mathsf {X}\varphi \wedge \neg \mathsf {X}\psi \). We want to show that \( h^{*}\not \preceq _{h} h^{\prime }\). By the def. of truth, (∗) implies that \( {\mathscr{M}}, \mathsf {t}_{succ_{h}({m})}/h^{*}\models \varphi \wedge \neg \psi \), and so \( h^{*}\not \preceq _{h} h^{\prime }\) by our hypothesis. Hence,  by Definition 8 (ii).
by Definition 8 (ii).
(Cen1) Assume that \( {\mathscr{M}},m/h\models \lozenge \varphi \wedge \lozenge \psi \). Then, (∗) there is \( h^{\prime }\!\in \! H_{m} \) s.t. \( {\mathscr{M}}{\kern -.3pt},{\kern -.3pt}m{\kern -.3pt}/{\kern -.3pt}h^{\prime }\!\models \! \varphi {\kern -.3pt}\wedge {\kern -.3pt} \lozenge \psi \). Take any \( h^{\prime \prime }\!\in \! H_{m} \). We want to show that  . Given (∗), the vacuous case is excluded. So, consider any history h∗ s.t. (2) \({\mathscr{M}}, \mathsf {t}_{m}/h^{*}\models \varphi \wedge \neg \lozenge \psi \). We want to show that \( h^{*}\not \preceq _{h^{\prime \prime }} h^{\prime }\). Since \( {\mathscr{M}},m/h^{\prime \prime }\models \lozenge \psi \) and \( {\mathscr{M}},\mathsf {t}_{m}/h^{*}\not \models \lozenge \psi \), h∗∉Hm, i.e., h∗ branches off from \( h^{\prime \prime }\) earlier than m. Since \( h^{\prime }\in H_{m} \), this means that \( past\_ov(h^{\prime \prime },h^{\prime }) \supset past\_ov(h^{\prime \prime },h^{*})\), and so (3) \( h^{*} \not \preceq _{h^{\prime \prime }} h^{\prime } \) by Def. 9. Since h∗ is an arbitrary history satisfying (2), (1) and (3) suffice to conclude that
. Given (∗), the vacuous case is excluded. So, consider any history h∗ s.t. (2) \({\mathscr{M}}, \mathsf {t}_{m}/h^{*}\models \varphi \wedge \neg \lozenge \psi \). We want to show that \( h^{*}\not \preceq _{h^{\prime \prime }} h^{\prime }\). Since \( {\mathscr{M}},m/h^{\prime \prime }\models \lozenge \psi \) and \( {\mathscr{M}},\mathsf {t}_{m}/h^{*}\not \models \lozenge \psi \), h∗∉Hm, i.e., h∗ branches off from \( h^{\prime \prime }\) earlier than m. Since \( h^{\prime }\in H_{m} \), this means that \( past\_ov(h^{\prime \prime },h^{\prime }) \supset past\_ov(h^{\prime \prime },h^{*})\), and so (3) \( h^{*} \not \preceq _{h^{\prime \prime }} h^{\prime } \) by Def. 9. Since h∗ is an arbitrary history satisfying (2), (1) and (3) suffice to conclude that  . Hence,
. Hence,  , as \( h^{\prime \prime }\) is an arbitrary history in Hm.
, as \( h^{\prime \prime }\) is an arbitrary history in Hm.
Proof of Proposition 4: Part 1
To see that \( \mathsf {Exp_{\square }} \) is valid on any rewind model, let \( {\mathscr{M}} = \left \langle {\left \langle {\textit {Mom},m_{0},<}\right \rangle ,\mathbf {act},\mathbf {dev},\preceq ^{R}}\right \rangle \) be a rewind model and m/h any index in \( {\mathscr{M}} \). Assume that  . We have to show that
. We have to show that  . Since
. Since  by hypothesis, there are two cases. Case 1: There is no \( h^{\prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}},\mathsf {t}_{m}/h^{\prime }\models \phi \). Then, for any \( h^{\prime \prime }\in H_{m} \),
by hypothesis, there are two cases. Case 1: There is no \( h^{\prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}},\mathsf {t}_{m}/h^{\prime }\models \phi \). Then, for any \( h^{\prime \prime }\in H_{m} \),  by Def. 8 (i). Hence,
by Def. 8 (i). Hence,  by Def. 7. Case 2: There is \( h^{\prime }\in \textit {Hist} \) s.t. (1) \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \varphi \wedge \square \psi \) and (2) for all \(h^{\prime \prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime \prime }\models \varphi \wedge \neg \square \psi \), \( h^{\prime \prime }{\not \preceq ^{R}_{h}} h^{\prime } \). Take any h∗∈ Hm. We want to show that
by Def. 7. Case 2: There is \( h^{\prime }\in \textit {Hist} \) s.t. (1) \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \varphi \wedge \square \psi \) and (2) for all \(h^{\prime \prime }\in \textit {Hist} \) s.t. \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime \prime }\models \varphi \wedge \neg \square \psi \), \( h^{\prime \prime }{\not \preceq ^{R}_{h}} h^{\prime } \). Take any h∗∈ Hm. We want to show that  . By (1), we know that (3) \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \varphi \wedge \psi \). So, consider any \(h^{\prime \prime \prime }\in \textit {Hist} \) s.t. (4) \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime \prime \prime }\models \varphi \wedge \neg \psi \). We want to prove that \( h^{\prime \prime \prime }\not \preceq ^{R}_{h^{*}} h^{\prime } \), i.e., that \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \) and \( h^{\prime \prime \prime }\not \prec ^{R}_{h^{*}} h^{\prime } \). In order to prove that \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \) we need to prove the following:
. By (1), we know that (3) \({\mathscr{M}}, \mathsf {t}_{m}/h^{\prime }\models \varphi \wedge \psi \). So, consider any \(h^{\prime \prime \prime }\in \textit {Hist} \) s.t. (4) \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime \prime \prime }\models \varphi \wedge \neg \psi \). We want to prove that \( h^{\prime \prime \prime }\not \preceq ^{R}_{h^{*}} h^{\prime } \), i.e., that \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \) and \( h^{\prime \prime \prime }\not \prec ^{R}_{h^{*}} h^{\prime } \). In order to prove that \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \) we need to prove the following:
Observe that:
-
(a) \( {\mathscr{M}}, \mathsf {t}_{m}/h^{\prime \prime \prime }\models \varphi \wedge \neg \square \psi \) by (4), and so \( h^{\prime \prime \prime }{\not \preceq ^{R}_{h}} h^{\prime } \) by (2). By the definition of \( {\preceq _{h}^{R}} \), it follows that \( h'{\prec ^{R}_{h}} h^{\prime \prime \prime } \), i.e., that
$$ \begin{array}{lll} past\_ov(h,h^{\prime}) \supset past\_ov(h,h^{\prime\prime\prime}),& or&\\ past\_ov(h,h^{\prime}) = past\_ov(h,h^{\prime\prime\prime})& \text{and} \ n\_sep(h,h^{\prime}) < n\_sep(h,h^{\prime\prime\prime}) ,& or\\ past\_ov(h,h^{\prime}) = past\_ov(h,h^{\prime\prime\prime})&\text{and}\ n\_sep(h,h^{\prime}) = n\_sep(h,h^{\prime\prime\prime}) & \text{and} \ \\ n\_dev(h^{\prime\prime\prime}) < n\_dev(h^{\prime}). \end{array} $$ -
(b) Since h, h∗∈ Hm, for all \( m^{\prime }\leq m \), the initial segment of h up to \( m^{\prime } \) and the initial segment of h∗ up to \( m^{\prime } \) are equal.
-
(c) \( past\_ov(h,h^{\prime }) =past\_ov(h^{*},h^{\prime }) \). In fact, \( {\mathscr{M}},m/h\models \square \neg \phi \) by hypothesis, while \( {\mathscr{M}},\mathsf {t}_{m}/h^{\prime }\not \models \square \neg \phi \) by (1). Hence, \( h^{\prime } \) must branch off from h at some moment \( m^{\prime }< m \). Since, by (b), the initial segment of h up to \( m^{\prime } \) is the same as the initial segment of h∗ up to \( m^{\prime } \), \( h^{\prime } \) must also branch off from h∗ at \( m^{\prime } \). Thus, \( h\cap h^{\prime } = h^{*}\cap h^{\prime }\).
-
(d) \( past\_ov(h,h^{\prime \prime \prime }) =past\_ov(h^{*},h^{\prime \prime \prime }) \): analogous to (c).
-
(e) \( num\_sep(h,h^{\prime }) =num\_sep(h^{*},h^{\prime }) \). In fact, by (b), h and h∗ are undivided at all moments \( m^{\prime \prime }< m \). By the condition of no choice between undivided histories, this means that, for all such \( m^{\prime \prime } \), \( \mathbf {act}(m^{\prime \prime }/h)= \mathbf {act}(m^{\prime \prime }/h^{*}) \). Now, as we have seen in item (c), there is a moment \( m^{\prime }< m \) s.t. \( h^{\prime } \) branches off from both h and h∗ at \( m^{\prime }\). Since \( \mathbf {act}(m^{\prime }/h)= \mathbf {act}(m^{\prime }/h^{*}) \), it follows that, for all i ∈Ag, \( \mathbf {act}(m^{\prime }/h)(i)\neq \mathbf {act}(m^{\prime }/h^{\prime })(i) \) iff \( \mathbf {act}(m^{\prime }/h^{*})(i)\neq \mathbf {act}(m^{\prime }/h^{\prime })(i) \). Hence, \( |\{i\in \textit {Ag} | \mathbf {act}(m^{\prime }/h)(i)\neq \mathbf {act}(m^{\prime }/h^{\prime })(i)\} | = |\{i\in \textit {Ag} | \mathbf {act}(m^{\prime }/h^{*})(i)\neq \mathbf {act}(m^{\prime }/h^{\prime })(i)\} |\).
-
(f) \( num\_sep(h,h^{\prime \prime \prime }) =num\_sep(h^{*},h^{\prime \prime \prime }) \): analogous to (e).
From items (c) to (f) it follows that \( h'{\prec ^{R}_{h}} h^{\prime \prime \prime } \) iff \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \); from this and item (a) it follows that \( h^{\prime }\prec ^{R}_{h^{*}} h^{\prime \prime \prime } \). The proof that \( h^{\prime \prime \prime }\not \prec ^{R}_{h^{*}} h^{\prime } \) proceeds in a similar way.
Proof of Proposition 4: Part 2
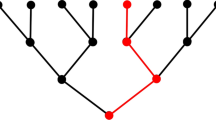
To see that \( \mathsf {Exp_{\square }} \) is invalid in some independence model, consider Fig. 7. Assume that: (1) for any agents i ∈Ag ∖{1} and moment \( m^{\prime }\), \( Acts^{m^{\prime }}_{i} =\{vc_{i} \}\), (2) for any moment \( m^{\prime }\) not depicted in the figure \(Acts^{m^{\prime }}_{1} =\{vc_{1} \}\), and (3) for any moment \( m^{\prime }\), \( \mathbf {dev}(m^{\prime }) =\varnothing \). It is not difficult to check that the defined structure is an SLDn frame. As shown in the figure, let p be true at t2/h5, t2/h6, t2/h11, t2/h12 and q be true at t2/h5, t2/h6, t2/h7, and t2/h8. Then, \( \mathsf {t}_{2}/h_{1} \models \square \neg p \) and  . In fact, (1) the most similar history to h1 where p is true at time t2 is h5, as all unconstrained agents (i.e., all agents) do the same types of action on h1 and h5 at all times, and (2) \( \square q \) is true at t2/h5. On the other hand,
. In fact, (1) the most similar history to h1 where p is true at time t2 is h5, as all unconstrained agents (i.e., all agents) do the same types of action on h1 and h5 at all times, and (2) \( \square q \) is true at t2/h5. On the other hand,  . Consider, in fact, history h3: The most similar history to h3 where p is true at time t2 is h11, as all unconstrained agents do the same types of action on h3 and h11 at all times. Since q is false at t2/h11,
. Consider, in fact, history h3: The most similar history to h3 where p is true at time t2 is h11, as all unconstrained agents do the same types of action on h3 and h11 at all times. Since q is false at t2/h11,  . Therefore,
. Therefore,  .
.
Remark 5
The model depicted in Fig. 7 satisfies the conditions of uniformity of menus and of identity of overlapping menus from Section 3.2. Hence, \( \mathsf {Exp}_{\square } \) remains invalid in the class of independence models satisfying these conditions.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canavotto, I., Pacuit, E. Choice-Driven Counterfactuals. J Philos Logic 51, 297–345 (2022). https://doi.org/10.1007/s10992-021-09629-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-021-09629-1