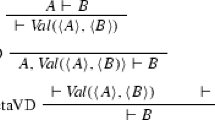Abstract
We present a revenge argument for non-reflexive theories of semantic notions – theories which restrict the rule of assumption, or (equivalently) initial sequents of the form φ ⊩ φ. Our strategy follows the general template articulated in Murzi and Rossi [21]: we proceed via the definition of a notion of paradoxicality for non-reflexive theories which in turn breeds paradoxes that standard non-reflexive theories are unable to block.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Beall, J. (2009). Spandrels of truth. Oxford: Oxford University Press.
Beall, J., & Murzi, J. (2013). Two flavors of Curry’s Paradox. The Journal of Philosophy, CX(3), 143–65.
Beall, J., & Ripley, D. (2014). Non-classical theories of truth. In M. Glanzberg (Ed.) The Oxford Handbook of Truth. Oxford: Oxford University Press.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2012). Tolerant, classical, strict. Journal of Philosophical Logic, 41(2), 347–85.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2013). Reaching transparent truth. Mind, 122, 841–866.
Curry, H. (1942). The inconsistency of certain formal logics. Journal of Symbolic Logic, 7, 115–7.
Field, H. (2008). Saving truth from paradox. Oxford: Oxford University Press.
Field, H. (2017). Disarming a paradox of validity. Notre Dame Journal of Formal Logic, 58(1), 1–19.
Fjellstad, A. (2017). Non-classical elegance for sequent calculus enthusiasts. Studia Logica, 105(1), 93–119.
French, R. (2016). Structural reflexivity and the paradoxes of self-reference. Ergo, an Open Access Journal of Philosophy, 3.
Halbach, V., & Horsten, L. (2006). Axiomatizing Kripke’s theory of truth. Journal of Symbolic Logic, 71, 677–712.
Heck, Jr. R. G. (2007). Self-reference and the languages of arithmetic. Philosophia Mathematica, 15, 1–29.
Horsten, L. (2009). Levity. Mind, 118(471), 555–581.
Horsten, L. (2012). The Tarskian Turn. Deflationism and axiomatic truth. Cambridge: MIT Press.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43, 439–469.
McGee, V. (1991). Truth, vagueness and paradox. Indianapolis: Hackett Publishing Company.
McGee, V. (1992). Maximal consistent sets of instances of Tarski’s schema (T). Journal of Philosophical Logic, 21(3), 235–241.
Meadows, T. (2014). Fixed points for consequence relations. Logique et Analyse, 333–357.
Moschovakis, Y. (1974). Elementary induction on abstract structures. North-Holland.
Murzi, J., & Rossi, L. (2021). Generalised revenge. Australasian Journal of Philosophy, 98(1), 153–177.
Murzi, J., & Rossi, L. (2018). Naïve validity, Synthese. Online first: https://doi.org/10.1007/s11229-017-1541-6.
Nicolai, C., & Rossi, L. (2018). Principles for object-linguistic validity: from logical to irreflexive. Journal of Philosophical Logic, 47, 549–577.
Priest, G. (2006). Doubt Truth to be a Liar. Oxford: Oxford University Press.
Restall, G. (2000). An introduction to substructural logics. New York: Routledge.
Ripley, D. (2012). Conservatively extending classical logic with transparent truth. Review of Symbolic Logic, 354–78.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–64.
Ripley, D. (2013). Revising up. Philosophers’ Imprint, 13(5).
Ripley, D. (2015). Comparing substructural theories of truth. Ergo, 2(13), 299–328.
Rosenblatt, L. (2020). Maximal non-trivial sets of instances of your least favorite logical principle. The Journal of Philosophy, 117(1), 30–54.
Schroeder-Heister, P. (1984). A natural extension of natural deduction. Journal of Symbolic Logic, 49, 1284–1299.
Soames, S. (1999). Understanding truth. Oxford: Oxford University Press.
Tennant, N. (2012). Cut for core logic. Review of Symbolic Logic, 5(3), 450–479.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4, 498–535.
Zardini, E. (2013). It is not the case that [p and ‘it is not the case that p’ is true] nor is it the case that [p and ‘p’ is not true]. Thought, 1(4), 309–19.
Zardini, E. (2013). Näive logical properties and structural properties. The Journal of Philosophy, 110(11), 633–44.
Zardini, E. (2014). Naïve truth and naïve logical properties. Review of Symbolic Logic, 7(2), 351–384.
Zardini, E. (2015). Getting one for two, or the contractors’ bad deal. Towards a unified solution to the semantic paradoxes. In T. Achourioti, K. Fujimoto, H. Galinon, & J. Martinez-Fernandez (Eds.) Unifying the Philosophy of Truth (pp. 461–93). Springer.
Acknowledgements
We wish to thank an anonymous reviewer for helpful comments on a previous draft as well as the FWF (project number 29716-G24) for generous financial support.
Funding
Open access funding provided by Paris Lodron University of Salzburg.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Murzi, J., Rossi, L. Non-reflexivity and Revenge. J Philos Logic 51, 201–218 (2022). https://doi.org/10.1007/s10992-021-09625-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-021-09625-5