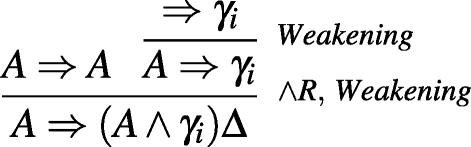Abstract
I explore, from a proof-theoretic perspective, the hierarchy of classical and paraconsistent logics introduced by Barrio, Pailos and Szmuc in (Journal o f Philosophical Logic, 49, 93-120, 2021). First, I provide sequent rules and axioms for all the logics in the hierarchy, for all inferential levels, and establish soundness and completeness results. Second, I show how to extend those systems with a corresponding hierarchy of validity predicates, each one of which is meant to capture “validity” at a different inferential level. Then, I point out two potential philosophical implications of these results. (i) Since the logics in the hierarchy differ from one another on the rules, I argue that each such logic maintains its own distinct identity (contrary to arguments like the one given by Dicher and Paoli in 2019). (ii) Each validity predicate need not capture “validity” at more than one metainferential level. Hence, there are reasons to deny the thesis (put forward in Barrio, E., Rosenblatt, L. & Tajer, D. (Synthese, 2016)) that the validity predicate introduced in by Beall and Murzi in (Journal o f Philosophy, 110(3), 143–165, 2013) has to express facts not only about what follows from what, but also about the metarules, etc.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Notes
Recall that R ∨ is a double-line rule in the calculus given in Section 2.
Admissibility is defined for metainferences in the same way that it is defined for inferences: an admissible rule is one whose addition to the existing rules of the system doesn’t change the system’s set of theorems, or, in this case, the set of derivable metainferences. Thus, to prove that a rule is admissible, we need to show that if certain instances of the premise metainferences hold, the relevant instance of the conclusion metainference holds as well.
Nonetheless, here is a sketch of a proof that push is admissible: Assume that the (meta)sequent
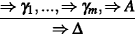 holds. So there is a proof tree whose leaves are ⇒ γ1,...,⇒ γm,⇒ A and whose root is ⇒Δ. We show by induction on the proof height how to construct a proof tree of
holds. So there is a proof tree whose leaves are ⇒ γ1,...,⇒ γm,⇒ A and whose root is ⇒Δ. We show by induction on the proof height how to construct a proof tree of 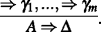 For a height of 1, if the sequent ⇒ A isn’t active in the proof, then there is a proof tree of
For a height of 1, if the sequent ⇒ A isn’t active in the proof, then there is a proof tree of 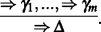 Using \(Wea{k_{1}^{b}}\), we can weaken with A on the left of the bottom sequent and get the result. If ⇒ A is active in the proof, then there are three options: Δ is derived either by Ref1 or by ∨ R or by ∧ R. In the first case A ∈Δ and so A ⇒Δ is an identity axiom (and from there the proof is trivial). In the second case, there is some B such that A ∨ B ∈Δ. So
Using \(Wea{k_{1}^{b}}\), we can weaken with A on the left of the bottom sequent and get the result. If ⇒ A is active in the proof, then there are three options: Δ is derived either by Ref1 or by ∨ R or by ∧ R. In the first case A ∈Δ and so A ⇒Δ is an identity axiom (and from there the proof is trivial). In the second case, there is some B such that A ∨ B ∈Δ. So 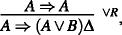 and from there with the Weak1 rules the proof is trivial.
and from there with the Weak1 rules the proof is trivial.In the third case, there are two options: (i) there is some 1 ≤ i ≤ m such that γi ∧ A ∈Δ, and (ii) A is of the form B ∧ C and B (or C) ∈Δ. In the case of (i) we reason:
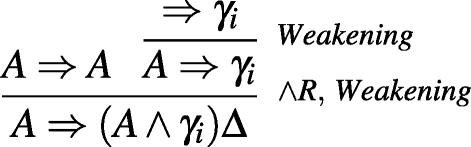
And once again, enough applications of the Weak1 rules will get the job done. As for (ii), B ∧ C ⇒ B(C)Δ is clearly derivable, and then we weaken m times with ⇒ γ1,...,⇒ γm respectively. The inductive step is analogous for, given Cut-elimination, we can assume that the proof involves only sequents with an empty left-hand side.
References
Avron, A. (1991). Simple consequence relations. Information and Computation, 92, 105–139.
Barrio, E., Rosenblatt, L., & Tajer, D. (2015). The logics of strict-tolerant logic. Journal of Philosophical Logic, 44(5), 551–571.
Barrio, E., Rosenblatt, L., & Tajer, D. (2016). Capturing naive validity in the Cut-free approach. Synthese. https://doi.org/10.1007/s11229-016-1199-5.
Barrio, E., Pailos, F., & Szmuc, D. (2020). A hierarchy of classical and paraconsistent logics. Journal of Philosophical Logic, 49, 93–120. https://doi.org/10.1007/s10992-019-09513-z.
Beall, J. (2011). Multiple-conclusion LP and default classicality. Review of Symbolic Logic, 4(2), 326–336. https://doi.org/10.1017/S1755020311000074.
Beall, J., & Murzi, J. (2013). Two flavors of Curry paradox. Journal of Philosophy, 110(3), 143–165.
Blok, W., & Jónsson, B. (2006). Equivalence of consequence operations. Studia Logica, 83(1), 91–110.
Cobreros, P., Égré, P., Ripley, D., & van Rooij, R. (2013). Reaching transparent truth. Mind, 122(488), 841–866.
Dicher, B., & Paoli, F. (2019). ST, LP, and tolerant metainferences. In Başkent, C., & Ferguson, T.M. (Eds.) Graham Priest on Dialetheism and Para consistency. Dordrecht: Springer, pp.383–407.
Hlobil, U. (2018). The Cut-free approach and the admissibility-Curry. Thought: a Journal of Philosophy, 7: 40–48. https://doi.org/10.1002/tht3.267.
Hlobil, U. (2019). Faithfulness for Naive Validity. Synthese, 196, 4759–4774.
Lewis, D. (1974). Tensions. In Munitz, M.K. & Unger, P.K. (Eds.), SemanticsandPhilosophy. New York: New York University Press, pp. 49–61.
Pailos, F. (2020). A fully classical truth theory characterized by substructural means. Review of Symbolic Logic, 13(2), 249–268.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Priest, G. (2008). An Introduction to Non-Classical Logic, second edition. Cambridge, MA: Cambridge University Press.
Ripley, D. (2012). Conservatively extending classical logic with transparent truth. Review of Symbolic Logic, 5(2), 354–378.
Ripley, D. (2013). Paradoxes and Failures of Cut. Australasian Journal of Philosophy, 91(1), 139–164.
Scambler, C. (2020). Classical logic and the strict tolerant hierarchy. Journal of Philosophical Logic, 49, 351–370.
Wansing, H., & Priest, G. (2015). External Curries. Journal of Philosophical Logic, 44(4), 453–471.
Woods, J. (2018). Intertranslatability, theoretical equivalence, and perversion. Thought: a Journal of Philosophy, 7, 58–68.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper was supported by a Minerva fellowship at Freie Universität Berlin. The paper benefited from fruitful discussions with Robert Brandom, Ulf Hlobil, Dan Kaplan, Shuhei Shimamura, Carl Posy, Ran Lanzet, Gil Sagi, Aviv Keren, David Kashtan, Balthasar Grabmayr, Michael Goldboim, Jonathan Fiat, and Filippos Papagiannopoulos. I would also like to thank two anonymous referees for this journal, for helpful comments and suggestions.
Appendix
Appendix
Lemma 2.8.
For all n ≥ 1, and for all \({\Gamma }\subseteq SEQ^{n-1}({\mathscr{L}}),\ A\in SEQ^{n-1}({\mathscr{L}})\):
⊧CLΓ ⇒nA iff ⊧CLlower(Γ ⇒nA).
Proof
By Theorem 2.6 ⊧CLΓ ⇒nA iff \(\models _{L_{n+1}}{\Gamma }\Rightarrow _{n}A\). By Theorem 2.7 the latter is the case iff \(\models _{L_{n}}lower({\Gamma }\Rightarrow _{n}A)\), and once again by Theorem 2.6 (since lower(Γ ⇒nA) is a metainference of level n − 1), that’s the case iff ⊧CLlower(Γ ⇒nA). □
Proposition 3.3.
Here are some useful facts about these axioms:
-
(i)
\(Wea{k_{n}^{b}}\) for n ≥ 1 is redundant: given the well-known Weakening rule (for inferences), it follows by induction for all n, via \(Tra{n_{n}^{c}}\).
-
(ii)
For each instance of such axioms/rules r of level n (except for \(Wea{k_{n}^{b}}\) which is redundant, given (i)), lower(r), higher(r) instantiate that same axiom/rule at levels n − 1,n + 1, respectively.
-
(iii)
Given Cut, metan-Cut (for n ≥ 1) is derivable via \(Tra{n_{n}^{c}}\).
Proof
(i) By induction. Assuming \(Wea{k_{n}^{b}}\) is derivable, we can derive \(Weak_{n+1}^{b}\) from \(Wea{k_{n}^{b}}\) and \(Tran_{n+1}^{c}\) in the following way:

Part (ii) is easy to prove, and so it is left for the reader as an exercise.
Part (iii) is proven by induction on n. The base case, Cut, is given. Assume that the claim holds for n, and let \({\Gamma }=\{\gamma _{1},...,\gamma _{m}\}\subseteq SEQ^{n}({\mathscr{L}}),A\in SEQ^{n}({\mathscr{L}})\). Then metan+ 1 − Cut is derivable from metan − Cut (guaranteed by the inductive hypothesis) and \(Tran_{n+1}^{c}\):

□
Proposition 3.5.
For all \(n\in \mathbb {N}\cup \{0\}\), and for every metainference Γ ⇒nA: \(\vdash _{CL^{\infty }}{\Gamma }\Rightarrow _{n}A\) iff \(\vdash _{CL^{\infty }}lower({\Gamma }\Rightarrow _{n}A)\).
Proof
By induction. I shall prove the claim for n = 0, 1, 2, and then turn to the inductive step.
The n = 0 case is the deduction theorem, which is known to hold in CL, so \(\vdash _{CL^{\infty }}{\Gamma }\Rightarrow {\Delta }\) iff \(\vdash _{CL^{\infty }}(\wedge {\Gamma })\supset (\vee {\Delta })\), which is \(\vdash _{CL^{\infty }}lower({\Gamma }\Rightarrow {\Delta })\).
The n = 1 case follows from the deduction theorem along with the fact that CL coincides with its external logic. Let  be some metainference of level 1. By the deduction theorem, for all 1 ≤ i ≤ m: \(\vdash _{CL^{\infty }}{\Gamma }_{i}\Rightarrow {\Delta }_{i}\) iff \(\vdash _{CL^{\infty }}lower({\Gamma }_{i}\Rightarrow {\Delta }_{i})\), and \(\vdash _{CL^{\infty }}{\Sigma }\Rightarrow {\Pi }\) iff \(\vdash _{CL^{\infty }}lower({\Sigma }\Rightarrow {\Pi })\). Now, by m + 1 applications of the transitivity rules, we can replace each of these sequents with its equivalent one, and get that
be some metainference of level 1. By the deduction theorem, for all 1 ≤ i ≤ m: \(\vdash _{CL^{\infty }}{\Gamma }_{i}\Rightarrow {\Delta }_{i}\) iff \(\vdash _{CL^{\infty }}lower({\Gamma }_{i}\Rightarrow {\Delta }_{i})\), and \(\vdash _{CL^{\infty }}{\Sigma }\Rightarrow {\Pi }\) iff \(\vdash _{CL^{\infty }}lower({\Sigma }\Rightarrow {\Pi })\). Now, by m + 1 applications of the transitivity rules, we can replace each of these sequents with its equivalent one, and get that  Since CL coincides with its external logic, the latter holds iff
Since CL coincides with its external logic, the latter holds iff
which is 
We also need to prove the n = 2 case. It is enough to show that for each instance r of a rule/axiom of level 2, lower(r) is derivable in \(CL^{\infty }\), and that for each instance q of a rule/axiom of level 1, higher(q) is derivable in \(CL^{\infty }\). If so, then:
-
1.
For each proof tree of metainferences of level 2 whose leaves are r1,...,rn and whose root is b there is a proof tree of metainferences of level 1 (a “regular” proof tree) whose leaves are lower(r1),...,lower(rn) and whose root is lower(b).
-
2.
For each proof tree of metainferences of level 1 whose leaves are l1,...lm and whose root is q, there is a proof tree of level 2 whose leaves are higher(l1),...,higher(lm) and whose root is higher(q).
Let us begin with the first claim. Consider an instance r of some rules/axiom of level 2. It is necessarily one of the structural rules, and so by Proposition 3.3 lower(r) also instantiates that same axiom/rule at level 1.
Consider then the axioms and rules of level 1, namely, the regular sequent rules and axioms of CL. We have to show that for each instance of some such axiom/rule q, higher(q) is derivable in \(CL^{\infty }\). I shall discuss two cases, and leave the rest as an exercise.
 can be derived in the following way:Footnote 1
can be derived in the following way:Footnote 1

(ii) The proof of the higher(R¬) case is more complex. I shall discuss the top-to-bottom direction, but the proof of the other direction is analogous. What we need to prove is that for all Γ,Δ,A:

What we really need to show is that the metarule push:  is admissible in \(CL^{\infty }\).Footnote 2 If so, then whatever is derivable with push will be derivable without it. And so, for all Γ,Δ,A:
is admissible in \(CL^{\infty }\).Footnote 2 If so, then whatever is derivable with push will be derivable without it. And so, for all Γ,Δ,A:

But actually, push is admissible simply because CL coincides with its external logic.Footnote 3 That completes the proof of the n = 2 case.
Now, suppose that the claim holds for some n ≥ 2. We want to show that it holds for n + 1. Since all the rules and axioms of levels n,n + 1 are structural, this is an immediate result of Proposition 3.3: for each instance r of some axiom/rule of level n, higher(r) instantiates that same axiom/rule at level n + 1, and for each instance q of some axiom/rule of level n + 1, lower(q) instantiates that same axiom/rule at level n. This completes the entire proof. □
Theorem 3.11.
For all m ≥ 2, for all \(n\in \mathbb {N}\cup \{0\}\), and for every metainference Γ ⇒nA: \(\vdash _{L_{m}^{\infty }}{\Gamma }\Rightarrow _{n}A\) iff \(\vdash _{L_{m-1}^{\infty }}lower({\Gamma }\Rightarrow _{n}A)\).
Proof
By nested induction.
Base case: m = 2, n = 0. The relevant rules governing inference (metainference of level 0) are those of CL0. But it is known that ⊩CLΓ ⇒Δ iff ⊩STlower(Γ ⇒Δ). I shall also discuss the n = 1 case. Consider a proof tree of a metainference (of the first level) Γ ⇒1A. Now, by Proposition 3.3: \({L_{2}^{1}}=CL^{0}\cup Weak_{1}\cup Ref_{1}\cup Aux_{1}\cup Sub_{1}\) and so for each instance of axiom/rule \(r\in {L_{2}^{1}}\): \(\vdash _{ST^{0}}lower(r)\). Hence, \(\vdash _{ST^{0}}lower({\Gamma }\Rightarrow _{1}A)\). We also need to show that for each instance of axiom/rule q ∈ ST0, higher(q) is derivable in \({L_{2}^{1}}\). Once again, the proof is similar to that of Proposition 3.5: it relies on the fact that all the operational rules of ST0, which are also the operational rules of \({L_{2}^{1}}\), are double-line rules. Therefore, it is easy to prove that their higher versions are derivable, using instances of Sub1. For example, both directions of higher(R∨) are derivable as follows:

Hence, \(\vdash _{{L_{2}^{1}}}{\Gamma }\Rightarrow _{1}A\) iff \(\vdash _{ST^{0}}lower({\Gamma }\Rightarrow _{1}A)\).
For n > 1, however, observe that \({L_{2}^{n}}\) and STn− 1 have only structural rules at these levels, and so the proof is trivial, given Proposition 3.3.
Inductive step: Assume that the claim holds for some m; then we have to show that it holds for m + 1, for all n. For 0 ≤ n ≤ m − 1, the relevant rules are those of CLm− 1, and we know from Proposition 3.5 that \(\vdash _{CL^{m-1}}{\Gamma }\Rightarrow _{n}A\) iff \(\vdash _{CL^{m-2}}lower({\Gamma }\Rightarrow _{n}A)\). For n = m, note that \(L_{m+1}^{m}\) and \(L_{m}^{m-1}\) have the same rules (modulo degrees) which are all structural (at level m of \(L_{m+1}^{m}\) and at level m − 1 of \(L_{m}^{m-1}\) ), and so, once again, the claim holds, by Proposition 3.3. The same method of proof also applies to all n > m. This completes the proof. □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Golan, R. Metainferences from a Proof-Theoretic Perspective, and a Hierarchy of Validity Predicates. J Philos Logic 51, 1295–1325 (2022). https://doi.org/10.1007/s10992-021-09616-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-021-09616-6




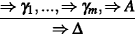 holds. So there is a proof tree whose leaves are ⇒ γ1,...,⇒ γm,⇒ A and whose root is ⇒Δ. We show by induction on the proof height how to construct a proof tree of
holds. So there is a proof tree whose leaves are ⇒ γ1,...,⇒ γm,⇒ A and whose root is ⇒Δ. We show by induction on the proof height how to construct a proof tree of 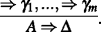 For a height of 1, if the sequent ⇒ A isn’t active in the proof, then there is a proof tree of
For a height of 1, if the sequent ⇒ A isn’t active in the proof, then there is a proof tree of 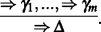 Using
Using 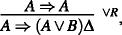 and from there with the Weak1 rules the proof is trivial.
and from there with the Weak1 rules the proof is trivial.