Abstract
I develop and defend a truthmaker semantics for the relevant logic R. The approach begins with a simple philosophical idea and develops it in various directions, so as to build a technically adequate relevant semantics. The central philosophical idea is that truths are true in virtue of specific states. Developing the idea formally results in a semantics on which truthmakers are relevant to what they make true. A very natural notion of conditionality is added, giving us relevant implication. I then investigate ways to add conjunction, disjunction, and negation; and I discuss how to justify contraposition and excluded middle within a truthmaker semantics.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Anderson, A., & Belnap, N. (1962). Tautological entailments. Philosophical Studies, 13(1), 9–24.
Anderson, A., & Belnap, N. (1963). First degree entailments. Mathematische Annalen, 149(4), 302–319.
Armstrong, D. (1997). A world of states of affairs. Cambridge: Cambridge University Press.
Berto, F., & Restall, G. (2018). Negation on the australian plan. Journal of Philosophical Logic.
Church, A. (1951). The weak positive implication calculus. Journal of Symbolic Logic, 16, 238.
Dunn, J. (1966). The algebra of intentional logics. PhD thesis, University of Pittsburgh.
Dunn, J., & Restall, G. (2002). Relevance logic. In Gabbay, D., & Guenthner, F. (Eds.) Handbook of philosophical logic. 2nd edn., (Vol. 6 pp. 1–136). Dordrecht: Kluwer Academic.
Fine, K. (1974). Models for entailment. Journal of Philosophical Logic, 3(4), 347–372.
Fine, K. (1976). Completeness for the semilattice semantics with disjunction and conjunction (abstract). Journal of Symbolic Logic, 41(2), 560–560.
Fine, K. (2014). Truth-maker semantics for intuitionistic logic. Journal of Philosophical Logic, 43(2–3), 549–577.
Fine, K. (2017). A theory of truth-conditional content I: conjunction, disjunction and negation. Journal of Philosophical Logic, 46(6), 625–674.
Fine, K. (2017). A theory of truth-conditional content II: subject-matter, common content, remainder and ground. Journal of Philosophical Logic, 46(6), 675–702.
Fine, K. (2017). Truthmaker semantics. In Hale, B., Wright, C., Miller, A. (Eds.) A companion to the philosophy of language (pp. 556–577): Blackwell.
Fine, K., & Jago, M. (2019). Logic for exact entailment. Review of Symbolic Logic, 12(3), 536–56.
Forrest, P. (2002). Nonclassical mereology and its application to sets. Notre Dame Journal of Formal Logic, 43(2), 79–94.
Mares, E. (2004). Relevant logic: a philosophical interpretation. Cambridge: Cambridge University Press.
Mares, E. (2009). Relevance and conjunction. Journal of Logic and Computation. https://doi.org/10.1093/logcom/exp068.
Mares, E.D. (1996). Relevant logic and the theory of information. Synthese, 109(3), 345–360.
Moh, S.-K. (1950). The deduction theorems and two new logical systems. Methodos, 2, 56–75.
Orlov, I.E. (1928). The calculus of compatibility of propositions. Matematicheskii Sbornik, 35, 263–286.
Prior, A.N. (1949). Determinables, determinates and determinants. Mind, 58 (229), 1–20.
Restall, G. (1995). Information flow and relevant logics. In Seligman, J., & Westerståhl, D. (Eds.) Logic, language and computation: the 1994 Moraga proceedings (pp. 463–477): CSLI Press.
Restall, G. (1999). Negation in relevant logics: how I stopped worrying and learned to love the routley star. In Gabbay, D., & Wansing, H. (Eds.) What is negation? Vol. 13 of applied logic series (pp. 53–76): Kluwer.
Restall, G. (2004). Relevant and substructural logics. Handbook of the history of logic: logic and the modalities in the twentieth century (pp. 289–398). North-Holland.
Rodriguez-Pereyra, G. (2006). Truthmaking, entailment, and the conjunction thesis. Mind, 115(460), 957–982.
Routley, R. (1984). The american plan completed: alternative classical-style semantics, without stars, for relevant and paraconsistent logics. Studia Logica, 43(1), 131–158.
Routley, R., & Meyer, R. (1972). The semantics of entailment II. Journal of Philosophical Logic, 1, 53–73.
Routley, R., & Meyer, R. (1972). The semantics of entailment III. Journal of philosophical logic, 1, 192–208.
Routley, R., & Meyer, R. (1973). The semantics of entailment I. In Leblanc, H. (Ed.) Truth, syntax, and semantics (pp. 194–243). North-Holland.
Urquhart, A. (1972). Semantics for relevant logics. Journal of Symbolic Logic, 37(1), 159–169.
Urquhart, A. (1972). The semantics of entailment. PhD thesis: University of Pittsburgh.
van Fraassen, B. (1969). Facts and tautological entailments. Journal of Philosophy, 66(15), 477–487.
Wilson, J. (2017). Determinables and determinates. In Zalta, E (Ed.) The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/determinate-determinables/.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: The Logic R
\(\textbf {R}^{\rightarrow }\) is the implicational fragment of R, axiomatised by:
- (Identity):
-
\(A \rightarrow A\)
- (Prefixing):
-
\((A \rightarrow B) \rightarrow ((C \rightarrow A) \rightarrow (C \rightarrow B))\)
- (Contraction):
-
\((A \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow B)\)
- (Permutation):
-
\((A \rightarrow (B \rightarrow C)) \rightarrow (B \rightarrow (A \rightarrow C))\)
with modus ponens, \(A, A \rightarrow B / B\) as the only rule. For ∧ and ∨, we add:
- (∧-introduction):
-
\(((A \rightarrow B) \wedge (A \rightarrow C)) \rightarrow (A \rightarrow B \wedge C) \)
- (∧-elimination):
-
\(A \wedge B \rightarrow A\) \(A \wedge B \rightarrow B\)
- (∨-introduction):
-
\(A \rightarrow A \vee B\) \(B \rightarrow A \vee B\)
- (∨-elimination):
-
\(((A \rightarrow C) \wedge (B \rightarrow C)) \rightarrow (A \vee B \rightarrow C)\)
- (Distribution):
-
\((A \wedge (B\vee C)) \rightarrow ((A \wedge B)\vee (A \wedge C))\)
plus adjunction, A,B/A ∧ B, as a rule. This gives the positive fragment, R+. For negation, we add:
- (Contraposition):
-
\((A \rightarrow B) \rightarrow (\neg B \rightarrow \neg A)\)
- (Reductio):
-
\((A \rightarrow \neg A) \rightarrow \neg A\)
- (Double negation):
-
\(\neg \neg A \rightarrow A\)
The resulting logic is R. A ∘ B can be defined in R as \(\neg (A \rightarrow \neg B)\). In R+, we may treat it is a primitive and add an axiom: \(A \circ B \rightarrow C \leftrightarrow (A \rightarrow (B \rightarrow C))\).
Appendix B: Semantics
We now define formal models, based on the philosophical principles for which I argued through Sections 3–7. To keep proofs brief, I will treat ∘ and ∨ as defined connectives, with A ∨ B =df¬(¬A ∧¬B) and \(A \circ B =_{\text {df}} \neg (A \rightarrow \neg B)\).
Definition 1 (Models)
Models are tuples  , where S and \(P \subseteq S\) are sets of states; \(\sqsubseteq \) and ≼ are partial orders on S; M is an operation on P; and V+ and V− are functions from S to sets of primitive sentence letters. Models must satisfy the following conditions (where ‘s ≼Pu’ abbreviates ‘s ∈ P and s ≼ u’):
, where S and \(P \subseteq S\) are sets of states; \(\sqsubseteq \) and ≼ are partial orders on S; M is an operation on P; and V+ and V− are functions from S to sets of primitive sentence letters. Models must satisfy the following conditions (where ‘s ≼Pu’ abbreviates ‘s ∈ P and s ≼ u’):
- (C1):
-
\(\sqsubseteq \) is a partial order with a minimal element
 such that any pair s,u ∈ S has a \(\sqsubseteq \)-least upper bound, s ⊔ u ∈ S.
such that any pair s,u ∈ S has a \(\sqsubseteq \)-least upper bound, s ⊔ u ∈ S. - (C2):
-
≼ is a partial order which distributes over ⊔: if s ≼ u then ∀t : s ⊔ t ≼ u ⊔ t.
- (C3):
-
If s ≼Pt ⊔ u, then there is a \(t^{\prime } \preceq _{P} t\) such that \(s \preceq _{P} t^{\prime } \sqcup u\).
- (C4):
-
If s ≼Pt ⊔ u and u ∈ P then uM ≼ t ⊔ sM.
- (C5):
-
p ∈ V+s iff ∀u ≼Ps: p ∈ V+u; and p ∈ V−s iff ∀u ≼Ps: p ∈ V+u.
- (C6):
-
For all s ∈ P: sMM = s; p ∈ V+s iff p∉V−sM; and p ∈ V−s iff p∉V+sM.
Definition 2 (Truthmaking and falsitymaking relations)

These models synthesise ideas from [8] and [26], and many of the subsequent proofs borrow from theirs. (Given the interrelation of these moving parts, we cannot assume that their results hold without proof.) The formal treatment of ≼ using (C2)–(C5) derives from Fine, whereas the formal treatment of negation and mates is due to Routley. Fine analyses negation via ≼, whereas here it is analysed directly in terms of falsitymaking. The philosophical interpretation here differs both from Fine’s and Routley’s. Neither author mentions truthmakers in those works and [8] understands ≼ in terms of extension of a theory, rather than determinacy of states.
Lemma 1 (Disjunction)
Disjunction has the following (derived) clauses:

Proof
\(s \Vdash A \vee B\) iff \(s \Vdash \neg (\neg A \wedge \neg B)\) iff  iff ∀u ≼Ps:
iff ∀u ≼Ps:  or
or  iff ∀u ≼Ps: \(u \Vdash A\) or \(u \Vdash B\).
iff ∀u ≼Ps: \(u \Vdash A\) or \(u \Vdash B\).  iff
iff  iff \(s \Vdash \neg A \wedge \neg B\) iff \(s \Vdash \neg A\) & HCode \(s \Vdash \neg A\) iff
iff \(s \Vdash \neg A \wedge \neg B\) iff \(s \Vdash \neg A\) & HCode \(s \Vdash \neg A\) iff  . □
. □
Lemma 2 (Heredity)
-
(a)
\(s \Vdash A\) iff for all \(u \preceq _{P} s: u \Vdash A\)
-
(b)
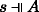 iff for all
iff for all 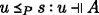
Proof
By double induction on A. The base cases follow immediately from (C5), so suppose both (a) and (b) hold for all B less complex than A and consider these cases.
-
A := ¬B. For (a): \(s \Vdash \neg B\) iff
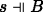 iff
iff 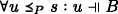 (by IH) iff \(\forall u \preceq _{P} s: u \Vdash \neg B\). For (b):
(by IH) iff \(\forall u \preceq _{P} s: u \Vdash \neg B\). For (b):  iff \(s \Vdash B\) iff \(\forall u \preceq _{P} s: u \Vdash B\) (by IH) iff
iff \(s \Vdash B\) iff \(\forall u \preceq _{P} s: u \Vdash B\) (by IH) iff  .
. -
A := B ∧ C. For (a): \(s \Vdash B \wedge C\) iff \(s \Vdash B\) and \(s \Vdash C\) iff ∀u ≼Ps: \(u \Vdash B\) and \(u \Vdash C\) (by IH) iff \(\forall u \preceq _{P} s: u \Vdash B \wedge C\). For (b):
 iff
iff  or
or  iff ∀u ≼Ps∀t ≼Pu:
iff ∀u ≼Ps∀t ≼Pu:  or
or 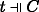 (if by transitivity of ≼; only if by IH) iff
(if by transitivity of ≼; only if by IH) iff  .
. -
\(A := B \rightarrow C\). For (a) left-to-right: assume \(s \Vdash B \rightarrow C\), \(t \Vdash B\), and u ≼Ps. Then \(s \sqcup t \Vdash C\) and u ⊔ t ≼ s ⊔ t (by C2). Now assume v ≼Pu ⊔ t. Then v ≼Ps ⊔ t (by transitivity of ≼), so \(v \Vdash C\) (by IH only if). Since v was arbitrary, we infer ∀v ≼ u ⊔ t : C, hence \(u \sqcup t \Vdash C\) (by IH if), and so \(u \Vdash B \rightarrow C\).
Right-to-left is by contraposition. Assume
 . So for some \(t \Vdash B\),
. So for some \(t \Vdash B\),  . By hypothesis, there is some v ≼Ps ⊔ t such that
. By hypothesis, there is some v ≼Ps ⊔ t such that 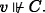 . By (C3), there is some u ≼Ps such that v ≼ u ⊔ t. By hypothesis,
. By (C3), there is some u ≼Ps such that v ≼ u ⊔ t. By hypothesis, 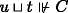 and so
and so 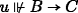 .
.For (b), left-to-right: assume
 , u ≼Ps, and v ≼Pu. Then v ≼Ps, hence
, u ≼Ps, and v ≼Pu. Then v ≼Ps, hence  for any v ≼Pu, hence
for any v ≼Pu, hence 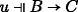 for any u ≼Ps. Right-to-left: assume
for any u ≼Ps. Right-to-left: assume  . Then since u ≼Pu, by definition
. Then since u ≼Pu, by definition 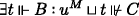 for any u ≼Ps and so
for any u ≼Ps and so  .
.
□
Corollary 1
-
(a) If \(s \Vdash A\) and s ≼ u then \(u \Vdash A\); and if
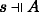 and s ≼ u then
and s ≼ u then  .
. -
(b) If s ∈ P, then the
 , and
, and 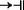 clauses simplify to:
clauses simplify to:

-
(c) \(s \Vdash A\) implies \(s \Vdash A \vee B\)
Proof
For (a), assume \(s \Vdash A\), u ≼ s, and t ≼Pu. By transitivity of ≼, t ≼Ps. So by lemma 2, \(t \Vdash A\) for any t ≼Pu, and hence \(u \Vdash A\). The  case is similar. For (b), the left-to-right directions follow by the reflexivity of ≼ (given s ∈ P) and the right-to-left directions follow directly from lemma 2. For (c), \(s \Vdash A\) iff ∀u ≼PA (2) only if ∀u ≼PA ∨ B (b) iff \(s \Vdash A \vee B\) (2). □
case is similar. For (b), the left-to-right directions follow by the reflexivity of ≼ (given s ∈ P) and the right-to-left directions follow directly from lemma 2. For (c), \(s \Vdash A\) iff ∀u ≼PA (2) only if ∀u ≼PA ∨ B (b) iff \(s \Vdash A \vee B\) (2). □
Lemma 3 (Crossover)
For all prime states s:
-
(a) \(s \Vdash A\)
-
(b) iff
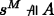
Proof
By double induction on A. Assume s is prime throughout. The base cases follow immediately from (C5), so suppose both (a) and (b) hold for all B less complex than A and consider these cases.
-
A := ¬B. For (a): \(s \Vdash \neg B\) iff
 iff
iff  (by IH) iff
(by IH) iff  . (b) is similar.
. (b) is similar. -
A := B ∧ C. For (a): \(s \Vdash B \wedge C\) iff \(s \Vdash B\) and \(s \Vdash C\) iff
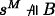 and
and 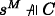 (by IH) iff
(by IH) iff  (1(b)). For (b):
(1(b)). For (b):  iff
iff  or
or 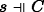 iff
iff  or
or  (by IH) iff
(by IH) iff  .
. -
\(A := B \rightarrow C\). For (a): \(s \Vdash B \rightarrow C\) iff \(\forall u \Vdash B: s \sqcup u \Vdash C\) iff \(\neg \exists u \Vdash B:\)
 (given sMM = u) iff
(given sMM = u) iff  (1b, given s ∈ P). For (b):
(1b, given s ∈ P). For (b): 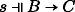 iff
iff  (1b) iff
(1b) iff  .
.
□
Corollary 2 (Star)
For any s ∈ P: \(s \Vdash \neg A\) iff  and
and  iff
iff  .
.
Corollary 3 (Negation)
-
(a) \(s \Vdash \neg A\)
-
(b) iff
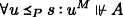
Corollary 4 (Equivalent Models)
Let \(\Vvdash \) be the relation defined recursively by the \(\Vdash \)-clauses for p, A ∧ B, and \(A \rightarrow B\), and 3(a) for ¬A. Then for any model M: \(s \Vvdash A\) iff \(s \Vdash A\).
Proof
2 is immediate from definition 1 and crossover (3). 3 follows from 2 and heredity (2). 4 follows from 3. □
2 shows that, for prime states at least, matehood can do the work of the Routley star. 3 shows that we can effectively do away with the falsitymaking relation altogether and work only with truthmaking (as reflected in 4). This fact will simplify the completeness proof.
We can now derive the expected clauses for intensional conjunction from its definition \(A \circ B =_{\text {df}} \neg (A \rightarrow \neg B)\):
Lemma 4 (Intensional conjunction)
Intensional conjunction has the following (derived) clauses:

Proof 6
For the truthmaking clause, left-to-right: suppose \(s \Vdash \neg (A \rightarrow \neg B)\) and let s+ ≼Ps. Then by definition,  for some \(t \Vdash A\). By lemma 2,
for some \(t \Vdash A\). By lemma 2,  for some u ≼Ps+M ⊔ t, hence by 2, \(u^{M} \Vdash B\) and by (C4), s+ ≼Pt ⊔ uM. This holds for all s+ ≼Ps and so s ≼ t ⊔ uM, \(t \Vdash A\), and \(u \Vdash B\). Right-to-left: suppose \(t \Vdash A\), \(u \Vdash B\), and s ≼ t ⊔ u and assume s+ ≼Ps. By (C3), s+ ≼ t ⊔ u+ for some u+ ≼Pu and so, by (C4), u+M ≼Ps+M ⊔ t. By 2, \(u^{+} \Vdash B\), so by 2,
for some u ≼Ps+M ⊔ t, hence by 2, \(u^{M} \Vdash B\) and by (C4), s+ ≼Pt ⊔ uM. This holds for all s+ ≼Ps and so s ≼ t ⊔ uM, \(t \Vdash A\), and \(u \Vdash B\). Right-to-left: suppose \(t \Vdash A\), \(u \Vdash B\), and s ≼ t ⊔ u and assume s+ ≼Ps. By (C3), s+ ≼ t ⊔ u+ for some u+ ≼Pu and so, by (C4), u+M ≼Ps+M ⊔ t. By 2, \(u^{+} \Vdash B\), so by 2,  and so by 2,
and so by 2,  . Since s+ is prime, by definition
. Since s+ is prime, by definition  and so \(s \Vdash \neg (A \rightarrow \neg B)\).
and so \(s \Vdash \neg (A \rightarrow \neg B)\).
For the falsitymaking clause:  iff \(s \Vdash A \rightarrow \neg B\) iff \(\forall u \Vdash A: s \sqcup u \Vdash \neg B\) iff
iff \(s \Vdash A \rightarrow \neg B\) iff \(\forall u \Vdash A: s \sqcup u \Vdash \neg B\) iff  . □
. □
As expected, a truthmaker for both conjuncts truthmakes their intensional conjunction, and any determinate of a falsemaker for the intensional conjunction is a falsemaker for at least one of its disjuncts:
Corollary 5
(i) If \(s \Vdash A\) and \(s \Vdash B\) then \(s \Vdash A \circ B\); and (ii) if  then, for any u ≼Ps, either
then, for any u ≼Ps, either  .
.
Proof 7
For (i): since s ≼ s ⊔ s, \(s \Vdash A\) & HCode \(s \Vdash B\) implies \(s \Vdash A \circ B\). For (ii): suppose  and u ≼Ps but
and u ≼Ps but  (to show
(to show  ). Then by 2, \(u \Vdash A \circ B\), by 3, \(u^{M} \Vdash A\), and so by 4,
). Then by 2, \(u \Vdash A \circ B\), by 3, \(u^{M} \Vdash A\), and so by 4,  . Since uM ≼PuM ⊔ uM, (C4) implies uMM ≼PuMM ⊔ uM, hence u ≼Pu ⊔ uM and, by 2,
. Since uM ≼PuM ⊔ uM, (C4) implies uMM ≼PuMM ⊔ uM, hence u ≼Pu ⊔ uM and, by 2,  . □
. □
As is usual in models for relevant logics, we define validity in terms of truth(making) at a designated state  in all models. Since our models feature both truthmaking and falsitymaking relations, we might define entailment in terms of preservation of truthmakers (from premises to conclusion), or in terms of falsitymaker preservation (from conclusion to premises), or both. As it happens, it doesn’t matter which definition we adopt.
in all models. Since our models feature both truthmaking and falsitymaking relations, we might define entailment in terms of preservation of truthmakers (from premises to conclusion), or in terms of falsitymaker preservation (from conclusion to premises), or both. As it happens, it doesn’t matter which definition we adopt.
Definition 3 (Validity)
A is true on M, \(M \Vdash A\), iff  in M. A is valid, ⊧A, iff true on all models. A set Γ is true on M when all its members are.
in M. A is valid, ⊧A, iff true on all models. A set Γ is true on M when all its members are.
Definition 4 (Entailment)
Γ entails A on M, Γ⊧MA, iff for all states s in M, \(s \Vdash A\) if \(s \Vdash {\Gamma }\). Γ 2-entails A on M, \({\Gamma } {\models _{M}^{2}} A\), iff for all states s in M: (i) \(s \Vdash {\Gamma }\) only if \(s \Vdash A\) and (ii)  only if
only if  . Entailment (and 2-entailment) simpliciter is entailment (2-entailment) on all models.
. Entailment (and 2-entailment) simpliciter is entailment (2-entailment) on all models.
Lemma 5 (Entailment)
-
(a)
\(M \models A \rightarrow B\) iff A⊧MB
-
(b)
\(A {\models ^{2}_{M}} B\) iff A⊧MB
Proof
For (a): \(M \models A \rightarrow B\) iff in M,  iff for all \(s \Vdash A\) in M:
iff for all \(s \Vdash A\) in M:  iff for all s in M: \(s \Vdash A\) only if \(s \Vdash B\) (since
iff for all s in M: \(s \Vdash A\) only if \(s \Vdash B\) (since  ) iff A⊧MB. For (b), left-to-right is trivial. For right-to-left, assume A⊧MB. Then
) iff A⊧MB. For (b), left-to-right is trivial. For right-to-left, assume A⊧MB. Then  iff ∀u ≼Ps:
iff ∀u ≼Ps:  (lemma 2) iff
(lemma 2) iff  (lemma 3) iff
(lemma 3) iff  (since A⊧MB) iff
(since A⊧MB) iff  (3) iff
(3) iff  (2), and so \(A {\models ^{2}_{M}} B\). □
(2), and so \(A {\models ^{2}_{M}} B\). □
Note the following corollary, which holds even in the absence of (C1):
Corollary 6 (Rule Contraposition)
\(\models A \rightarrow B\) iff \(\models \neg B \rightarrow \neg A\).
Proof
For any model M: \(\models _{M} A \rightarrow B\) iff A⊧MB iff \(A {\models ^{2}_{M}}\) iff ∀s: ( only if
only if  ) iff ∀s: (\(s \Vdash \neg B\) only if \(s \Vdash \neg A\)) iff ¬B⊧M¬A iff \(\models _{M} \neg B \rightarrow \neg A\). □
) iff ∀s: (\(s \Vdash \neg B\) only if \(s \Vdash \neg A\)) iff ¬B⊧M¬A iff \(\models _{M} \neg B \rightarrow \neg A\). □
Appendix C: Soundness and Completeness
Theorem 1 (Soundness)
If A ∈R then ⊧A
Proof
We need to show that each axiom of R is valid and that both modus ponens and adjunction preserve validity. For modus ponens, if  then \(s \Vdash A\) implies
then \(s \Vdash A\) implies  , hence if
, hence if  then
then  . For adjunction, if
. For adjunction, if  and
and  then
then  .
.
For the axioms: each is of the form \(A \rightarrow B\). So, given lemma 5, we need show only that, for any state s in any model, if \(s \Vdash A\) then \(s \Vdash B\). Identity, ∧-elimination, and double negation are trivial, and ∨-introduction is immediate from corollary 1(c). The remaining cases are as follows:
- Prefixing::
-
Suppose \(s \Vdash A \rightarrow B\) and assume \(t \Vdash C \rightarrow A\) and \(u \Vdash C\). We show \((s \sqcup t) \sqcup u \Vdash B\). By definition, we have \(t \sqcup u \Vdash A\) and so \((t \sqcup u) \sqcup s \Vdash B\). Since (t ⊔ u) ⊔ s = s ⊔ (t ⊔ u), the result follows.
- Contraction::
-
Suppose \(s \Vdash A \rightarrow (A \rightarrow B)\) and assume \(u \Vdash A\), to show \(s \sqcup u \Vdash B\). Then \((s \sqcup u) \sqcup u \Vdash B\) and, since (s ⊔ u) ⊔ u = s ⊔ (u ⊔ u) = s ⊔ u, the result follows.
- Permutation::
-
Suppose \(s \Vdash A \rightarrow (B \rightarrow C)\) and assume \(t \Vdash B\) and \(y \Vdash A\), to show \((s \sqcup t) \sqcup u \Vdash C\). Then \(s \sqcup u \Vdash B \rightarrow C\), so \((s \sqcup u) \sqcup t \Vdash C\). Since (s ⊔ u) ⊔ t = (s ⊔ t) ⊔ u, the result follows.
- ∧-introduction::
-
Suppose \(s \Vdash (A \rightarrow B) \wedge (A \rightarrow C)\) and assume \(u \Vdash A\), to show \(s \sqcup u \Vdash B \wedge C\). Then \(s \Vdash (A \rightarrow B)\) and \(s \Vdash (A \rightarrow C)\), hence \(s \sqcup u \Vdash B\) and \(s \sqcup u \Vdash C\), and so \(s \sqcup u \Vdash B \wedge C\).
- ∨-elimination::
-
Assume \(s \Vdash (A \rightarrow C) \wedge (B \rightarrow C)\) and \(u \Vdash A \vee B\). Then \(s \Vdash A \rightarrow C\), \(s \Vdash B \rightarrow C\). Now consider any t ≼Ps ⊔ u. By (C1), there is some v ≼Pu such that t ≼Ps ⊔ v. So \(v \Vdash A \vee B\), hence \(v \Vdash A\) or \(v \Vdash B\) and, either way, \(s \sqcup v \Vdash C\). Then by lemma 2, \(t \Vdash C\), for all t ≼Ps ⊔ u, and hence \(s \sqcup u \Vdash C\).
- Distribution::
-
Assume \(s \Vdash A \wedge (B\vee C)\), so that \(s \Vdash A\) and \(s \Vdash B \vee C\). Assume u ∈ P and u ≼ s. Then \(u \Vdash B\) or \(u \Vdash C\); and, given lemma 2, \(u \Vdash A\). So either \(u \Vdash A \wedge B\) or \(u \Vdash A \wedge C\), and so \(s \Vdash (A \wedge B) \wedge (A \wedge C)\).
- Contraposition::
-
Assume \(s \Vdash A \rightarrow \neg B\) but
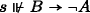 . Then \(\exists u \Vdash B:\)
. Then \(\exists u \Vdash B:\) . Then ∃t ≼Ps ⊔ u st
. Then ∃t ≼Ps ⊔ u st  , so \(t^{M} \Vdash A\). So \(s \sqcup t^{M} \Vdash \neg B\). By (C1), there is a v ≼Pu such that t ≼Ps ⊔ v, so by (C1), vM ≼Ps ⊔ tM, so \(v^{M} \Vdash \neg B\), so
, so \(t^{M} \Vdash A\). So \(s \sqcup t^{M} \Vdash \neg B\). By (C1), there is a v ≼Pu such that t ≼Ps ⊔ v, so by (C1), vM ≼Ps ⊔ tM, so \(v^{M} \Vdash \neg B\), so 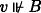 , so
, so 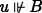 . Contradiction.
. Contradiction. - Reductio::
-
Assume \(s \Vdash A \rightarrow \neg A\) but
 . Then \(s^{M} \Vdash A\), so \(s \sqcup s^{M} \Vdash \neg A\). We also have sM ≼ sM ⊔ sM (reflexivity and idempotence of ⊔), hence s ≼ s ⊔ sM (by C1 and sMM = s), and so (by 2) \(s \Vdash \neg A\): contradiction.
. Then \(s^{M} \Vdash A\), so \(s \sqcup s^{M} \Vdash \neg A\). We also have sM ≼ sM ⊔ sM (reflexivity and idempotence of ⊔), hence s ≼ s ⊔ sM (by C1 and sMM = s), and so (by 2) \(s \Vdash \neg A\): contradiction.
□
Definition 5 (Deduction and Theories)
Γ ⊩RA just in case there is a finite sequence of sentences A1,…,An where A = An and each Ai≤n is either in Γ, or the conjunction of some previous Aj,Ak (i.e. j,k < i), or for some Ak<i, we have \(A_{k} \rightarrow A_{i} \in \textbf {R}\). A theoryT is any set of sentences closed under deduction: if A ∈ T and Γ ⊩RA then A ∈ T. A theory is prime iff either A ∈ T or B ∈ T whenever A ∨ B ∈ T. TR and PR are the sets of all theories and all prime theories, respectively.
This definition of deduction is not the classical one, for we must ensure that theorems are not automatically derivable from any premises. We do not have \(B \vdash _{\textbf {R}} A \rightarrow A\), for example, even though \(A \rightarrow A\) is valid.
Lemma 6 (Prime theories)
Assume that Γ is closed under disjunction and T is a theory which does not intersect Γ. Then there is a prime theory \(T^{+} \supseteq T\) which does not intersect Γ.
Proof
A standard syntactic result for theories in R; see, e.g., Fine [8]. □
Definition 6 (Canonical model)
The canonical model \({\mathcal{M}}^{R}\) is a tuple
where TR, PR, and R are as above and:
-
\(S \sqcup _{\textbf {R}} U = \{ B \mid \exists A \in U : A \rightarrow B \in S \}\); set \(S \sqsubseteq _{\textbf {R}} U\) iff S ⊔RU = U
-
For S ∈ PR, \(S^{M_{\textbf {R}}} = \{ A \mid \neg A \notin S \}\)
-
\(V_{\textbf {R}}^{+}S = \{ p \mid p \in S\}\)
-
\(V_{\textbf {R}}^{-}S = \{ p \mid \neg p \in S\}\)
The canonical model deviates from our philosophical characterisation in that (i) MR here is none other than the standard canonical model Routley star and (ii) we model determination using the converse of set inclusion. Nevertheless, the approach meets the the formal requirements on a model and greatly simplifies the completeness proof.
Lemma 7 (Theory heredity)
A ∈ S iff, for all prime \(U \supseteq S\), A ∈ S.
Proof
Left-to-right is trivial. For right-to-left, assume A∉S, and let  . Then Γ is disjunction-closed (since
. Then Γ is disjunction-closed (since  ) and Γ ∩ S = ∅. So by lemma 6, there is a prime \(U \supseteq S\) such that Γ ∩ U = ∅, hence A∉U. Contraposing, if A ∈ U for all \(U \supseteq S\) then A ∈ S. □
) and Γ ∩ S = ∅. So by lemma 6, there is a prime \(U \supseteq S\) such that Γ ∩ U = ∅, hence A∉U. Contraposing, if A ∈ U for all \(U \supseteq S\) then A ∈ S. □
Lemma 8
\({\mathcal{M}}^{\textbf {R}}\)is a model.
Proof
We need to demonstrate that each of (C1)–(C6) hold of \({\mathcal{M}}^{\textbf {R}}\):
- (C1):
-
We must show that (i) \(\sqsubseteq _{\textbf {R}}\) is a partial order on TR; (ii) R is its minimal element; and (iii) S ⊔RU ∈ TR for every S,U ∈R.
(i): A standard proof (e.g. Dunn and Restall [7]) shows that the permutation, prefixing, and contraction axioms guarantee that ⊔R is commutative, associative, and idempotent. It is then a standard result of order theory that defining \(S \sqsubseteq _{\textbf {R}} U\) iff S ⊔RU = U results in a partial order.
(ii): If A ∈ S then, since \(A \rightarrow A \in \textbf {R}\), we have A ∈R ⊔RS. If A ∈R ⊔RS then \(B \rightarrow A \in \textbf {R}\) for some B ∈ S. Then B ⊩RA (definition 5) and so, since S is a theory (definition 5), A ∈ S. So R ⊔RS = S and hence \(\textbf {R} \sqsubseteq _{\textbf {R}} S\) for every state S.
(iii): This requires that each S ⊔RU is a theory (by definition 5’s lights), which is a standard syntactic result (e.g. Fine [8]).
- (C2):
-
Clearly \(\supseteq \) is a partial order; we show it distributes over ⊔R. Suppose \(S \supseteq U\) and A ∈ U ⊔ T. Then for some B ∈ U, \(B \rightarrow A \in T\) and B ∈ S, hence A ∈ S ⊔ T. So \(S \sqcup T \supseteq U \sqcup T\).
- (C3):
-
Suppose \(S \supseteq T \sqcup U\) and S is prime, and let \({\Gamma } = \{ A \mid \exists B \notin S : A \rightarrow B \in U \}\). To show Γ is closed under disjunction, suppose A1,A2 ∈Γ. Then there are B1,B2∉S such that \(A_{1} \rightarrow B_{1}, A_{2} \rightarrow B_{2} \in U\). Since \(A_{1} \rightarrow B_{1}, A_{2} \rightarrow B_{2} \vdash _{\textbf {R}} A_{1} \vee A_{2} \rightarrow B_{1} \vee B_{2}\) and U is ⊩R-closed, we have \(A_{1} \vee A_{2} \rightarrow B_{1} \vee B_{2} \in U\). Since S is prime, B1 ∨ B2∉S, hence A1 ∨ A2 ∈Γ. Moreover, Γ does not intersect T. For if there were any A ∈Γ∩ T then, by definition, there would be some B∉S such that \(A \rightarrow B \in U\), hence B ∈ S: contradiction. So, by lemma 6, there is a prime theory \(T^{+} \supseteq T\) which also does not intersect Γ. Now suppose B ∈ T+ ⊔ U. Then there is an A ∈ T+ such that \(A \rightarrow B \in U\), hence B ∈ S (else Γ and T+ would intersect) and so \(T^{+} \sqcup U \subseteq S\).
- (C4):
-
Suppose S,U ∈ P, \(S \supseteq T \sqcup U\) and A ∈ T ⊔ SM. Then for some B ∈ SM, \(B \rightarrow A \in T\) and hence, given contraposition, \(\neg A \rightarrow \neg B \in T\). B ∈ SM implies ¬B∉S, hence ¬B∉T ⊔ U. Then ¬A∉U (else we get ¬B ∈ S), hence A ∈ UM, and so \(U^{M} \supseteq T \sqcup S^{M}\).
- (C5):
-
Trivial, given lemma 7.
- (C6):
-
We show that, for all s ∈ P: (i) SMM = S; (ii) p ∈ V+s iff p∉V−sM; and (iii) p ∈ V−s iff p∉V+sM. We use the fact that
 and so, since S is a theory, ¬¬A ∈ S iff A ∈ S. For (i): \(A \in S^{M_{\textbf {R}}M_{\textbf {R}}}\) iff \(\neg A \notin S^{M_{\textbf {R}}}\) iff ¬¬A ∈ S iff A ∈ S. For (ii): \(p \in V_{\textbf {R}}^{+}S\) iff p ∈ S iff ¬¬p ∈ S iff \(\neg p \notin S^{M_{\textbf {R}}}\) iff \(p \in V_{\textbf {R}}^{-}S^{M_{\textbf {R}}}\). For (iii): \(p \in V_{\textbf {R}}^{-}S\) iff ¬p ∈ S iff \(p \notin S^{M_{\textbf {R}}}\) iff \(p \notin V_{\textbf {R}}^{+}S^{M_{\textbf {R}}}\).
and so, since S is a theory, ¬¬A ∈ S iff A ∈ S. For (i): \(A \in S^{M_{\textbf {R}}M_{\textbf {R}}}\) iff \(\neg A \notin S^{M_{\textbf {R}}}\) iff ¬¬A ∈ S iff A ∈ S. For (ii): \(p \in V_{\textbf {R}}^{+}S\) iff p ∈ S iff ¬¬p ∈ S iff \(\neg p \notin S^{M_{\textbf {R}}}\) iff \(p \in V_{\textbf {R}}^{-}S^{M_{\textbf {R}}}\). For (iii): \(p \in V_{\textbf {R}}^{-}S\) iff ¬p ∈ S iff \(p \notin S^{M_{\textbf {R}}}\) iff \(p \notin V_{\textbf {R}}^{+}S^{M_{\textbf {R}}}\).
□
Lemma 9 (Truth)
For any state S in \({\mathcal{M}}^{\textbf {R}}\): \(S \Vdash A\) iff A ∈ S.
Proof
By induction on A. The base case is given by the definition of \(V_{\textbf {R}}^{+}\); so assume the result holds for all B less complex than A and consider these cases:
-
A := ¬B. \(S \Vdash \neg B\) iff \(U \Vdash \neg B\) for all prime \(U \supseteq S\) (lemma 2) iff
 for all prime \(U \supseteq S\) (corollary 2) iff B∉UM for all prime \(U \supseteq S\) (by hypothesis) iff ¬B ∈ U for all prime \(U \supseteq S\) (definition of MR) iff ¬B ∈ S (lemma 6).
for all prime \(U \supseteq S\) (corollary 2) iff B∉UM for all prime \(U \supseteq S\) (by hypothesis) iff ¬B ∈ U for all prime \(U \supseteq S\) (definition of MR) iff ¬B ∈ S (lemma 6). -
A := B ∧ C. \(S \Vdash B \wedge C\) iff \(S \Vdash B\) and \(S \Vdash C\) iff B ∈ S and C ∈ S (by hypothesis) iff B ∧ C ∈ S (since B,C ⊩RB ∧ C).
-
\(A := B \rightarrow C\). \(S \Vdash B \rightarrow C\) iff \(\forall U \Vdash B: S \sqcup _{\textbf {R}} U \Vdash C\) iff ∀U ∋ B : C ∈ S ⊔RU (by hypothesis) iff \(B \rightarrow C \in S\) (by definition of ⊔R).
□
Theorem 2 (Completeness)
If ⊧A then A ∈R.
Proof
By contraposition. Assume A∉R. Then by lemma 9,  in \({\mathcal{M}}^{\textbf {R}}\). and, by lemma 8,
in \({\mathcal{M}}^{\textbf {R}}\). and, by lemma 8,  . □
. □
Definition 7 (Closed models)
A model is closed when, for any of its states s,u: \(s \sqcup u \Vdash A\) if \(s \Vdash A\) and \(u \Vdash A\). A is valid on the class of closed models, ⊧CA, when  in every closed model.
in every closed model.
Theorem 3
RM is sound and complete on the class of closed models: A ∈RM iff ⊧CA.
Proof
For soundness: suppose \(s, u \Vdash A\) in a closed model \({\mathcal{M}}\). By closure, \(s \sqcup u \Vdash A\), hence \(s \Vdash A \rightarrow A\) and so  . For completeness, we show that the canonical model formed from RM in place of R is closed. Suppose S and U are RM-theories, each containing A. Since \(A \rightarrow (A \rightarrow A)\) is a theorem, \(A \rightarrow A \in S\). By construction, \(S \sqcup _{\textbf {RM}} U = \{B \mid \exists A \in U: A \rightarrow B \in S \}\) and so A ∈ S ⊔RMU. □
. For completeness, we show that the canonical model formed from RM in place of R is closed. Suppose S and U are RM-theories, each containing A. Since \(A \rightarrow (A \rightarrow A)\) is a theorem, \(A \rightarrow A \in S\). By construction, \(S \sqcup _{\textbf {RM}} U = \{B \mid \exists A \in U: A \rightarrow B \in S \}\) and so A ∈ S ⊔RMU. □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jago, M. Truthmaker Semantics for Relevant Logic. J Philos Logic 49, 681–702 (2020). https://doi.org/10.1007/s10992-019-09533-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-019-09533-9




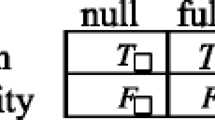
 such that any pair s,u ∈ S has a
such that any pair s,u ∈ S has a  iff for all
iff for all 
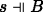 iff
iff 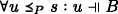 (by IH) iff
(by IH) iff  iff
iff  .
. iff
iff  or
or  iff ∀u ≼Ps∀t ≼Pu:
iff ∀u ≼Ps∀t ≼Pu:  or
or 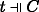 (if by transitivity of ≼; only if by IH) iff
(if by transitivity of ≼; only if by IH) iff  .
. . So for some
. So for some  . By hypothesis, there is some v ≼Ps ⊔ t such that
. By hypothesis, there is some v ≼Ps ⊔ t such that 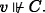 . By (C3), there is some u ≼Ps such that v ≼ u ⊔ t. By hypothesis,
. By (C3), there is some u ≼Ps such that v ≼ u ⊔ t. By hypothesis, 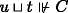 and so
and so 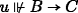 .
. , u ≼Ps, and v ≼Pu. Then v ≼Ps, hence
, u ≼Ps, and v ≼Pu. Then v ≼Ps, hence  for any v ≼Pu, hence
for any v ≼Pu, hence 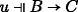 for any u ≼Ps. Right-to-left: assume
for any u ≼Ps. Right-to-left: assume  . Then since u ≼Pu, by definition
. Then since u ≼Pu, by definition 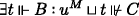 for any u ≼Ps and so
for any u ≼Ps and so  .
.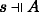 and s ≼ u then
and s ≼ u then  .
. , and
, and 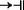 clauses simplify to:
clauses simplify to:

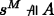
 iff
iff  (by IH) iff
(by IH) iff  . (b) is similar.
. (b) is similar.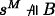 and
and 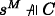 (by IH) iff
(by IH) iff  (1(b)). For (b):
(1(b)). For (b):  iff
iff  or
or 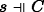 iff
iff  or
or  (by IH) iff
(by IH) iff  .
. (given sMM = u) iff
(given sMM = u) iff  (1b, given s ∈ P). For (b):
(1b, given s ∈ P). For (b): 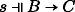 iff
iff  (1b) iff
(1b) iff  .
.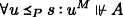
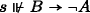 . Then
. Then  . Then ∃t ≼Ps ⊔ u st
. Then ∃t ≼Ps ⊔ u st  , so
, so 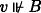 , so
, so 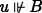 . Contradiction.
. Contradiction. . Then
. Then  and so, since S is a theory, ¬¬A ∈ S iff A ∈ S. For (i):
and so, since S is a theory, ¬¬A ∈ S iff A ∈ S. For (i):  for all prime
for all prime