Abstract
This is part one of a two-part paper, in which we develop an axiomatic theory of the relation of partial ground. The main novelty of the paper is the of use of a binary ground predicate rather than an operator to formalize ground. This allows us to connect theories of partial ground with axiomatic theories of truth. In this part of the paper, we develop an axiomatization of the relation of partial ground over the truths of arithmetic and show that the theory is a proof-theoretically conservative extension of the theory PT of positive truth. We construct models for the theory and draw some conclusions for the semantics of conceptualist ground.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Partial ground is the relation of one truth holding either wholly or partially in virtue of another [13, 15].Footnote 1 To illustrate the concept, consider a couple of paradigmatic examples:
-
(1)
The truth of the disjunction that 5 + 7 = 12 or 1 = 2 holds wholly in virtue of the truth of its only true disjunct that 5 + 7 = 12.
-
(2)
The truth of the conjunction that 5 + 7 = 12 and 2 × 2 = 4 holds partially in virtue of the truth of its first conjunct that 5 + 7 = 12 and partially in virtue of the truth of its other conjunct that 2 × 2 = 4.
Partial ground in this sense is a strict partial order on the truths: it is irreflexive—no truth partially grounds itself—and it is transitive—partial grounds are inherited through partial grounding.Footnote 2 Thus, partial ground gives rise to a hierarchy of grounds, in which the partial grounds of a truth rank “strictly below” the truth itself. The aim of this paper is to axiomatize this hierarchy over the truths of arithmetic.Footnote 3
The main novelty of the paper is that we will use a ground predicate rather than an operator to formalize partial ground. This approach to formalizing partial ground has several philosophical benefits, which we will outline in more detail in the following section. So far, however, most authors have eschewed the approach for reasons we’ll discuss in detail in the following section as well. Ultimately, we argue, the benefits of the approach outweigh it’s perceived drawbacks. Most importantly, the predicate approach will allow us to connect theories of partial ground with axiomatic theories of truth. In particular, once we’ve formulated the usually accepted principles of partial ground using a ground predicate, we can bring out the truth-theoretic commitments of theories of partial ground, in the sense that we can show that the resulting theory of partial ground is a conservative extension of the well-known theory PT of positive truth [16, p. 116–22].
2 The Predicate Treatment of Partial Ground
In this paper, we will formalize partial ground using the relational predicate ◃ of sentences—our ground predicate. We’ll add this predicate to the language of PA, where we may obtain a unique name ⌜φ⌝ for every sentence φ using the technique of Gödel-numbering. Here and in the following, we shall take the relata of partial ground to be (true) sentences, the idea being that partial ground is a relation on the truths (for further discussion of this assumption, see p. 6 below). Thus, we can formalize example (1) from above by:
where \(\overline {n}\) is the numeral for the natural number n. In contrast, most authors formalize partial ground using the operator ≺ of sentences—the (partial) ground operator.Footnote 4 In the case of our example, these authors would add the ground operator to the language of PA, and then formalize example (1) by:
The syntactic difference between the two approaches is that the ground predicate takes terms denoting sentences as arguments, while the ground operator takes sentences themselves as arguments.
The predicational theory of partial ground that we will develop in this paper subsumes the standard operational theory of partial ground, in the sense that for all sentences φ and ψ, if φ≺ψ is derivable in the latter theory, then ⌜φ⌝ ◃ ⌜ψ⌝ is derivable in our theory. The converse direction, however, does not hold in general: there are sentences φ and ψ such that ⌜φ⌝ ◃ ⌜ψ⌝ is derivable in our theory, while φ≺ψ is not derivable in the standard theory of partial ground.Footnote 5 Thus, on the predicate approach we are able to obtain a strictly stronger theory of partial ground.
But there are other reasons to prefer the predicate approach over the operator approach:
2.1 Quantification over Truths
The predicate approach has greater expressive strength than the operator approach. In particular, using the ground predicate, we can formalize ground-theoretic principles involving quantification over truths in a natural way. Take the two principles stating that partial ground is an irreflexive and transitive relation on the truths as an example. On the predicate approach, we can directly formalize these principles as:
where the intended range of the quantifiers is the set of all truths.Footnote 6 On the operator approach, in contrast, we can (prima facie) only formalize these principles by affirming the instances of the following schemata for all sentences φ, ψ, and θ:
Thus, on the operator approach, we can achieve quantification over truths only by moving to quantification over sentences in the meta-language, while on the predicate approach, we can directly express quantification over truths in the object language.Footnote 7
Moreover, the strategy of moving to quantification in the meta-language fails once we consider principles involving existential quantifiers. Think for example of the intuitively plausible principle that a sentence is true iff its truth is either fundamental or grounded in some other truth. On the predicate approach, we can straightforwardly formalize this principle as:
where T r is a unary truth predicate that applies to all and only the true sentences and F u n d is a unary predicate that applies to all and only the sentences whose truth is fundamental. Moreover, we could plausibly define this predicate F u n d by postulating that:
Then, in a predicational theory of ground with this definition, we’ll be able to derive the claim that a sentence is true iff its truth is either fundamental or grounded in some other truth. On the operator approach, in contrast, we could not even formalize the principle in the first place: there simply is no way to express the nested universal and existential quantification over truths on that approach.
Finally, using quantification over truths, we can define useful ground-theoretic concepts directly in our object language. Take the concept of weak partial ground as an example [13, p. 51–53]. This is the relation of one truth being a “stand-in” for another in the context of partial ground. Following [13, p. 52], we can define weak partial ground in terms of our ordinary, strict notion of partial ground by saying that the truth of φ weakly partially grounds the truth of ψ just in case the truth of φ strictly partially grounds any truth that the truth of ψ grounds. It then follows, for example, that any truth weakly partially grounds itself, since clearly it strictly partially grounds any truth that it itself strictly partially grounds. Or, for another example, if the truth of φ strictly partially grounds the truth of ψ, then the truth of φ also weakly partially grounds the truth of ψ. This follows immediately from the transitivity of (ordinary strict) partial ground.Footnote 8 But conversely, it may very well happen that the truth of φ weakly partially grounds the truth of some ψ without strictly grounding it. Just think of the case where ψ is identical to φ: we’ve just seen that the truth of φ weakly grounds itself, but by the irreflexivity of strict partial ground (see p. 2) φ does not strictly partially ground itself.Footnote 9
On the predicate approach, we can define a binary predicate ⊴ for this relation by postulating:
On the operator approach, in contrast, we can’t define weak partial ground in this way—there we need to introduce a primitive operator ≼ for the relation together with the semantic postulate that for all sentences φ and ψ:
Thus, on the operator approach, we need to introduce additional syntax and additional semantics to deal with weak partial ground, while on the predicate approach we can use standard first-order definitions in the object language.
2.2 Truth and Partial Ground
A major benefit of the predicate approach is that it allows us to study the connections between partial ground and truth in a natural setting. It should be clear that partial ground is conceptually related to truth—partial ground is a relation on the truths after all. In axiomatic theories of truth, the concept is standardly formalized by means of a unary predicate of sentences [16]. By formalizing partial ground analogously using a relational predicate, we create a ground-theoretic framework in which we can fruitfully study the connections between truth and partial ground. For example, we will show in this paper that if we formulate the usually accepted principles for partial ground using a ground predicate, the resulting theory turns out to be a conservative extension of the well-known theory of positive truth [16, p. 116–22]. In other words, the predicate approach allows us to make the truth-theoretic commitments of theories of ground explicit. In the second part of this paper, we shall investigate the connections between partial ground and truth further. There we shall show, for example, that we can formulate a typed solution to Fine’s puzzle of ground [14] in our axiomatic framework.
2.3 Semantics of Partial Ground
Finally, the ground predicate allows us to use classic model-theoretic methods to study the semantics of partial ground. In the literature on ground, we usually distinguish between conceptualist and factualist notions of ground [5, p. 256–59], [7, p. 14f]. On a conceptualist notion, ground is a relation on fine-grained, conceptually individuated truths. For example, on a conceptualist notion, we would typically say that if φ is a true sentence, then the truth of φ ∨ φ holds in virtue of the truth of φ, but not the other way around. On a factualist conception, in contrast, ground is a relation on coarse-grained, worldly individuated facts. On this conception, we would typically deny that if φ is a true sentence, the fact that φ ∨ φ holds in virtue of the fact that φ, since the two facts are the same—albeit expressed differently. The notion of partial ground that we are interested in here is a conceptualist notion of ground.
It is currently an open problem to provide a formal semantics for a conceptualist notion of ground.Footnote 10 On the operator approach, it is difficult to define such a semantics, since we have to start “from scratch,” as it were: we have to find the right kind of structure to interpret conceptualist ground and provide primitive semantic clauses for the ground operator. On the predicate approach, in contrast, if we can develop a consistent first-order axiomatization of conceptualist ground, we can infer the existence of a (first-order) model by the completeness theorem for first-order logic. Once we know that such a model exists, we can study it using methods of classic model theory. This should then help us determine the right kind of structure and the correct semantic clauses to interpret conceptualist ground operators, as well.
In the rest of the paper, we will develop an axiomatization of partial ground over the truths of arithmetic, which fulfills the promises from the previous list of benefits. But before we begin, we shall briefly address an argument that is sometimes brought forward against the predicate approach: Correia [5, p. 254] and Fine [13, p. 46–47] argue that we should prefer the operator approach for reasons of ontological neutrality. They argue that since on the predicate approach we have terms denoting the relata of ground, by Quine’s criterion of ontological commitment, the approach commits us to the existence of the relata of ground. Moreover, they argue that since on the predicate approach we are committed to the existence of the relata of ground, we need a background theory for them. On the operator approach, in contrast, they argue we don’t have any of that: we only need to have the (true) sentences that the ground operator acts upon. This argument is particularly forceful on a factualist conception of partial ground, where we take the relata of ground to be facts. As Correia then puts it: “it should be possible to make claims of grounding and fail to believe in facts” [5, p. 254].
In this paper, however, we work on a conceptualist notion of partial ground, where we take the relata of ground to be truths.Footnote 11 Moreover, these truths are truths of sentences. Correspondingly, we formalize partial ground using a relational predicate of (true) sentences. Thus, by Quine’s criterion of ontological commitment, we are only committed to the existence of (true) sentences. Our background theory is correspondingly simply a standard theory of syntax. These ontological commitments are metaphysically innocuous: ontologically speaking, sentences are relatively harmless entities. Moreover, on the operator approach, we need to assume the existence of sentences to formulate our theory in the first place. Thus, even though the operator approach is, strictly speaking, ontologically more parsimonious, the ontological commitments of our version of the predicate approach are fairly harmless.
3 Technical Preliminaries
To develop our axiomatization of partial ground over the truths of arithmetic, we need a background theory of arithmetic, which tells us what we need to know about arithmetic, and a background theory of syntax, which allows us to talk about the (true) sentences of arithmetic. It is well-known that PA can double as a theory of arithmetic and as a theory of syntax. This can be achieved using the technique of Gödel-numbering. In this section, we will recount the basics of this technique and fix notation.Footnote 12
Let \(\mathcal {L}\) be the language of PA. We assume that \(\mathcal {L}\) has the standard arithmetic vocabulary: an individual constant 0 intended to denote the natural number zero, a unary function symbol S intended to express the successor function on the natural numbers, and binary function symbols + and × intended to denote addition and multiplication on the natural numbers respectively. For every natural number n, we standardly define the numeral \(\overline {n}\) as the n-fold application of S to the constant 0. The numeral \(\overline {n}\) is, of course, intended to denote the number n. Note that ‘\(\overline {n}\)’ is merely a meta-linguistic abbreviation of the official object-linguistic term ‘ S…S n’. The language of truth \(\mathcal {L}_{Tr}\) is the result of extending \(\mathcal {L}\) with the unary truth predicate T r, the language of predicational ground \(\mathcal {L}_{Tr}^{\lhd }\) is the result of extending \(\mathcal {L}_{Tr}\) with the binary ground predicate \(\lhd \), and the language of (simple) operational ground \(\mathcal {L}_{\prec }\) is the result of extending \(\mathcal {L}\) with the applications of the binary ground operator ≺ over \(\mathcal {L}\): \(\mathcal {L}_{\prec }:=\mathcal {L}\cup \{\varphi \prec \psi ~|~\varphi ,\psi \in \mathcal {L}\}\).Footnote 13 In the following, we will mainly work in within \(\mathcal {L}_{Tr}^{\lhd }\).
We use the technique of Gödel-numbering to obtain names for every expression. In particular, we use a coding function # to injectively map every expression σ to a natural number #σ—the Gödel number of the expression. If σ is an expression, then we also write \(\ulcorner \sigma \urcorner \) for the numeral intended to denote #σ. This will be our name for σ. For the most part, we simply assume that we have some coding function for the language \(\mathcal {L}\), but later we will discuss theories that require coding functions for \(\mathcal {L}_{Tr}\) and even \(\mathcal {L}_{Tr}^{\lhd }\).
The theory PA of PA consists of the standard axioms for zero, the successor function, addition, and multiplication, plus all the instances of the induction scheme
over formulas φ(x) in the language \(\mathcal {L}\). We denote derivability in PA by ⊢ P A (and analogously for other systems discussed in the paper). However, if what we mean is clear from the context, we omit the subscript.
It is well-known that PA can represent any recursive function, in the sense that if f is a recursive function then there is a formula φ(x, y) such that for all natural numbers n, m:
Many syntactic functions on the codes of expressions are recursive and thus representable. For example, the function that maps the code #φ of a formula φ to the code #¬φ of its negation is recursive. It is convenient to assume that \(\mathcal {L}\) has function symbols for a finite number of those functions. Notation-wise, if f is a recursive function, then we use \(\underset {\cdot }{f}\) as our function symbol for it. In particular, we assume that we have function symbols \(\underset {\cdot }{\neg }\), \(\underset {\cdot }{\lor }\), \(\underset {\cdot }{\land }\), \(\underset {\cdot }{\exists }\), \(\underset {\cdot }{\forall }\), and \(\underset {\cdot }{=}\) for the corresponding syntactic operations on the codes of expressions. If we work in the context of a coding for \(\mathcal {L}_{Tr}\), we additionally assume a function symbol \(\underset {\cdot }{Tr}\) for the function that maps the code #t of a term t to the code #T r(t) of the atomic formula \(Tr(t)\in \mathcal {L}_{Tr}\). And if we work in the context of a coding for \(\mathcal {L}_{Tr}^{\lhd }\), we assume a function symbol \(\underset {\cdot }{\lhd }\) for the function that maps the codes #s and #t of two terms to the code \(\#(s\lhd t)\) of the atomic formula \(s\lhd t\). We can then conservatively extend our axioms with the defining equations for those functions such that for all formulas φ and ψ, for all variables v, and for all terms t:
When we work in the context of coding functions for \(\mathcal {L}_{Tr}\) and \(\mathcal {L}_{Tr}^{\lhd }\), we furthermore get of all terms s and t that:
Note that, in particular, we get that \(\vdash _{PA} \underset {\cdot }{Tr}(\ulcorner \ulcorner \varphi \urcorner \urcorner )=\ulcorner Tr(\ulcorner \varphi \urcorner )\urcorner \), for every sentence φ. The ternary substitution function sub such that for all formulas φ, terms t, and variables v s u b(#φ, #t, #v) = #φ(t/v) provided that t is free for v in φ, is recursive and thus representable. Officially, we represent this function by the function symbol \(\underset {\cdot }{sub}\) and add its defining equations to our axioms, but unofficially we often simply write \(\ulcorner \varphi \urcorner (\ulcorner t\urcorner , \ulcorner v\urcorner )\) instead of \(\underset {\cdot }{sub}(\ulcorner \varphi \urcorner ,\ulcorner t\urcorner , \ulcorner v\urcorner )\) and if there is only one free variable in φ, we often simply write \(\ulcorner \varphi \urcorner (\ulcorner t\urcorner )\). The function that maps a natural number n to the code \(\#\overline {n}\) of its numeral \(\overline {n}\) is also recursive and we will use the function symbol \(\dot {\phantom {n}}\) for this in our language. Note that, in particular, we get for all sentences φ that \(\vdash _{PA} \dot {\ulcorner \varphi \urcorner }=\ulcorner \ulcorner \varphi \urcorner \urcorner \). We write \(\ulcorner \varphi (\dot {x})\urcorner \) as an abbreviation for \(\underset {\cdot }{sub}(\ulcorner \varphi \urcorner ,\dot {x})\). This allows us to quantify over free variables in the context of names. The valuation function val that applied to (the code of) a closed term yields its denotation is also recursive and thus representable. Officially, however, we cannot have a function symbol representing the valuation function, since otherwise we run the risk of inconsistency [16, p. 32]. We will nevertheless write s° = t to say that the denotation of s is t, as if ° was a function symbol representing the valuation function. Officially, this is merely an abbreviation for the corresponding complex defining formula.
PA can also (strongly) represent every recursive set, in the sense that if S is a recursive set then there is a formula φ(x) such that for all natural numbers n:
In the following, we’ll write S e n t to abbreviate the formula that allows us to represent the recursive set of codes sentences in \(\mathcal {L}\), S e n t T r for the formula that allows us to represent the codes of sentences in \(\mathcal {L}_{Tr}\), and \(Sent_{Tr}^{\lhd }\) for the formula that allows us to represent the codes of sentences in \(\mathcal {L}_{Tr}^{\lhd }\). Similarly, V a r and C l T e r m are abbreviations for the formulas that allow us to represent the sets of (codes of) variables and closed terms. As an abbreviation for ∀x(V a r(x) → φ(x)) we write ∀v φ(v) and as an abbreviation for ∀x(C l T e r m(x) → φ(x)) we write ∀t φ(t). We also sometimes use the notation \(\forall t Tr(\ulcorner \varphi (\underset {\cdot }{t})\urcorner )\) for \(\forall x(ClTerm(x)\to Tr(\underset {\cdot }{sub}(\ulcorner \varphi \urcorner ,x)))\). This allows us to quantify over terms in the context of names.
We assume that PA has the defining axioms for all of these function symbols and predicates as axioms. Furthermore, the theory PAT extends PA with the missing instances of the induction scheme over \(\mathcal {L}_{Tr}\) and the theory PAG extends PAT with all the missing instances of the induction scheme over \(\mathcal {L}_{Tr}^{\lhd }\).
Finally, we will exclusively work in the context of the standard model of PA. This model of \(\mathcal {L}\) has the set ℕ of the natural numbers as its domain and in it 0 actually denotes the number zero, S actually denotes the successor function, and + and × actually denote addition and multiplication. In other words, we don’t allow for non-standard interpretations of the arithmetic vocabulary. We denote this model by N. A model for \(\mathcal {L}_{Tr}\), then, has the form (N, S), where N is the standard model and \(S\subseteq \mathbb {N}\) interprets the truth predicate T r. A model for \(\mathcal {L}_{Tr}^{\lhd }\) has the form (N, S, R), where (N, S) is a model of \(\mathcal {L}_{Tr}\) and \(R\subseteq \mathbb {N}^{2}\) interprets our ground predicate \(\lhd \). Thus, on our notion of a model, the interpretation of the arithmetic vocabulary is fixed, but we are allowed to freely interpret the truth predicate and the ground predicate.Footnote 14 Note that we don’t have a notion of a model of \(\mathcal {L}_{\prec }\), since finding appropriate models for this language is an open problem.
4 Axiomatic Theories of Partial Ground
4.1 Axioms for Partial Ground
We begin from the standardly accepted principles for partial ground formulated on the operator approach. The most comprehensive conceptualist system for ground on the operator approach is the pure and impure logic of ground developed by Fine [13, p. 54–71]. However, Fine’s system deals with various notions of ground and takes the full notion of ground as fundamental [13, p. 50]—it contains a system for partial ground only as a subsystem. Moreover, Fine’s system is formulated in a sequent-style, which makes it difficult to deal with for our present purpose. For these reasons, we will take the system of Schnieder [28] as our starting point. Schnieder’s system is not primarily intended as a system for partial ground: it is intended as a system for the non-causal uses of the binary explanatory connective ‘because’ from natural language [28, Fn 8, p. 446–47]. However, there are uses of ‘because’ that coincide with the present sense of partial ground: when we say that one truth holds either wholly or partially because of another truth, we can interpret this as saying that the one truth holds either wholly or partially in virtue of the other truth. The interpretation of ‘because’ is often given in the literature on ground and is sometimes even used as a paradigmatic natural language example for ground [13, p. 37–38].Footnote 15 Since Schnieder’s system is supposed to account for all non-causal uses of ‘because’, it should also cover this non-causal use of because—in other words: we can interpret Schnieder’s system as a system for partial ground.Footnote 16
Schnieder formulates his system over pure first-order logic as his base-theory, but the system can easily be adapted to the present framework. If we take Schnieder’s system and formulate it in the language \(\mathcal {L}_{\prec }\) over PA as its base-theory, we arrive at the following system:
Definition 1
The operational theory of (partial) ground OG consists of the axioms of PA, all the instances of the axiom scheme:
for sentences \(\varphi \in \mathcal {L}\), plus the following rules of inference for partial ground for all formulas \(\varphi ,\psi ,\theta \in \mathcal {L}\):
Note well that the theory OG is formulated in the language \(\mathcal {L}_{\prec }\), which explicitly doesn’t allow for iterations of ≺. This is in line with the standard restriction in the literature to un-iterated or simple instances of ground. Iterated ground raises specific technical and philosophical issues, which fall outside the scope of this article.Footnote 17
Schnieder [28, p. 452–53] shows the proof-theoretic conservativity of the propositional fragment of his system over pure propositional logic. This proof is easily extended to show the conservativity of his quantified system, which we used as our starting point, over pure first-order logic.Footnote 18 However, since we take PA as our background theory, we give a slightly different proof of the analogous result for the present context:
Proposition 1 (Schnieder)
The system OG is a proof-theoretically conservative extension of PA.
Proof
The complexity function c, which maps the code #φ of a formula φ to the code #|φ| of its logical complexity |φ|, is recursive and thus representable in PA. Let \(\underset {\cdot }{c}\) represent this function. Furthermore, let \(\underset {\cdot }{<}\) represent the recursive strictly-less-than relation < on the natural numbers. We define the translation function \({\tau }:\mathcal {L}_{\prec }\to \mathcal {L}\) recursively by saying that:
-
(i)
τ(φ) = φ, for φ an atomic formula;
-
(ii)
τ(¬φ)=¬τ(φ);
-
(iii)
τ(φ∘ψ) = τ(φ)∘τ(ψ), for ∘=∧,∨;
-
(iv)
τ(Q x φ) = Q x(τ(φ)), for Q = ∀,∃; and
-
(v)
\({\tau }(\varphi \prec \psi )=(\varphi \land \psi \land \underset {\cdot }{c}(\ulcorner \varphi \urcorner )~\underset {\cdot }{<}~\underset {\cdot }{c}(\ulcorner \psi \urcorner ))\).
Note that in clause (v), we need not translate φ and ψ, since they are, by assumption, already in \(\mathcal {L}\).
It is now easily seen by induction on the complexity of formulas that (a) for all \(\varphi \in \mathcal {L}\), τ(φ) = φ. In words: τ is constant on the arithmetic formulas. Next, we show that (b) τ preserves theoremhood over the two systems OG and PA, in the sense that for all \(\varphi \in \mathcal {L}_{\prec }\), if ⊢ O G φ, then ⊢ P A τ(φ). We show (b) by an induction on the length of derivations. Of course, we only need to consider the rules of OG that are not rules of PA. If φ = ¬(φ′≺φ′) is an instance of the axiom scheme of OG, for \(\varphi ^{\prime }\in \mathcal {L}\), then we get that \(\tau (\varphi )=_{\text {(v),(a)}}\neg (\varphi ^{\prime }\land \varphi ^{\prime }\land \underset {\cdot }{c}(\varphi ^{\prime })\underset {\cdot }{<}\underset {\cdot }{c}(\varphi ^{\prime }))\). But \(\vdash _{PA} \neg (\varphi ^{\prime }\land \varphi ^{\prime }\land \underset {\cdot }{c}(\varphi ^{\prime })\underset {\cdot }{<}\underset {\cdot }{c}(\varphi ^{\prime }))\), since \(\vdash _{PA}\forall x \neg (x\underset {\cdot }{<}x)\) and thus in particular \(\vdash _{PA}\neg (\underset {\cdot }{c}(\varphi ^{\prime })\underset {\cdot }{<}\underset {\cdot }{c}(\varphi ^{\prime }))\). So assume the induction hypothesis. For the induction step, we need to go through all the inference rules of OG case by case. Here we only discuss one case to illustrate the idea. Consider the case where the last step has been an application of the rule:
where \(\varphi \in \mathcal {L}\). First note that since \(\varphi \in \mathcal {L}\), we get that τ(φ) = φ by (a) and furthermore that (∗)⊢ P A φ by the induction hypothesis. Now consider, \({\tau }(\varphi \prec \neg \neg \varphi )=_{(v),(a)}\varphi \land \neg \neg \varphi \land \underset {\cdot }{c}(\ulcorner \varphi \urcorner ) ~\underset {\cdot }{<}~\underset {\cdot }{c}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner \varphi \urcorner )\). By (∗) we know that ⊢ P A φ and thus ⊢ P A ¬¬φ by elementary logic. And we know that \(\vdash _{PA}\underset {\cdot }{c}(\ulcorner \varphi \urcorner )~\underset {\cdot }{<}~\underset {\cdot }{c} (\underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner \varphi \urcorner )\), since \(\vdash _{PA} \forall x(Sent(x)\to \underset {\cdot }{c}(x)\underset {\cdot }{<}\underset {\cdot }{c}(\underset {\cdot }{\neg } \underset {\cdot }{\neg }x))\). The other cases are equally straightforward. Putting the two claims (a) and (b) together, the proposition follows. □
Note that the translation function used in the proof is not particularly faithful: we can derive a lot of intuitively false claims under the translation. For example, it is intuitively false that 0 = 0 ≺ ¬∃x(S x = 0), since the (logical) truth of 0 = 0 has nothing to do with the truth of (the axiom) ¬∃x(S x = 0). Nevertheless, we will get that ⊢ P A τ(0 = 0 ≺ ¬∃ x(S x = 0)) with τ defined as in the proof, since τ(0 = 0 ≺ ¬ ∃x(S x = 0)) is equal to
which is provable in PA. But this is not a counterexample to the claim in the proof, since the operational theory of ground does not prove 0 = 0 ≺ ¬∃x(S x = 0) to begin with, and all that is required for our proof is that the translation preserves theoremhood. The result, then, immediately gives us the proof-theoretic consistency of the predicational theory of partial ground:
Corollary 1 (Schnieder)
The system OG is proof-theoretically consistent.
Note that the proof-theoretic consistency of the operational theory of ground does not entail that there are models for the theory, since we have not even defined the notion of a model for its language, much less have we shown that proof-theoretic consistency in this language implies the existence of models.
We obtain our axiomatization of partial ground over the truths of arithmetic by translating the axioms and rules of the operational theory into quantified axioms, which we formulate using the ground predicate. For this purpose, we assume that we have a Gödel-numbering for \(\mathcal {L}\). Let us begin with the axiom scheme ¬(φ≺φ), for sentences \(\varphi \in \mathcal {L}\), which expresses the irreflexivity of partial ground. We straight-forwardly translate this to the quantified axiom \(\forall x\neg (x\lhd x)\). To translate the first rule:
which captures the transitivity of partial ground, we first transform the rule into the conditional (φ ≺ ψ) ∧ (ψ ≺ θ) → (φ≺θ), and then translate this conditional into the quantified axiom \(\forall x\forall y\forall z(x\lhd y\land y\lhd z\to x\lhd z)\). To translate the remaining rules, we need to use a “trick” in order to quantify over formulas that are affirmed outside the context of the ground operator. Take the rules:
which express that partial ground is a relation on the truths. Again, we first translate the rules into the conditionals (φ ≺ ψ) → φ and (φ ≺ ψ) → ψ. Then, in order to quantify over the formulas affirmed in the consequent, we use the truth predicate T r. With some simplification, we get the following transformation:
Note that we use the truth predicate T r here simply as a quantificational device: it allows us to generalize over the truths involved in partial ground outside the context of partial ground.
By applying the same strategy to the rule involving double negation, we get the following transformation:
But now we face a problem: The operational theory of ground can not only prove that if φ is a true sentence, then the truth of ¬¬φ is grounded in the truth of φ, but also that if ¬¬φ is a true sentence, then the truth of ¬¬φ is grounded in the truth of φ. Formally, we get both ⊢ O G φ → (φ ≺ ¬¬φ) and ⊢ O G ¬¬ φ → (φ ≺ ¬¬φ). But the corresponding quantified claim \(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg } x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) is not derivable from our axioms so far. In response to this, we might be tempted to simply add the T-scheme:
for all sentences \(\varphi \in \mathcal {L}\), to our theory. This would allow us to derive \(Tr(\ulcorner \neg \neg \varphi \urcorner )\to \ulcorner \varphi \urcorner \lhd \ulcorner \neg \neg \varphi \urcorner \) for every formula φ. But this is not enough. We wish to derive the full quantified claim \(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg } x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) in our theory and merely using the T-scheme this is impossible. Therefore, we will add the quantified claim as an axiom to our system.
Thus, corresponding to every rule of the operational theory of ground, we have two axioms: an upward directed axiom, like \(\forall x(Tr(x)\to x\lhd \underset {\cdot }{\neg } \underset {\cdot }{\neg }x)\), and a downward directed axiom, like \(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg } x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). In the cases of the other rules, we can moreover make some simplifications. To illustrate, consider the case of the rules involving conjunction. We get the following transformations:
Upward:
$$\left.\begin{array}{c} \frac{\varphi \ \psi}{\varphi\prec\varphi\land\psi}\\ \frac{\varphi \ \psi}{\psi\prec\varphi\land\psi} \end{array} \qquad \right\} \qquad \leadsto \qquad \forall x\forall y (Tr(x)\land Tr(y)\to x\lhd x\underset{\cdot}{\land}y~\land~y\lhd x\underset{\cdot}{\land}y) $$Downward:
$$\varphi\land \psi\to (\varphi\prec\varphi\land\psi)\land(\psi\prec\varphi\land\psi) \leadsto \forall x\forall y (Tr(x\underset{\cdot}{\land}y)\to x\lhd x\underset{\cdot}{\land}y~\land~y\lhd x\underset{\cdot}{\land}y) $$
Intuitively, the upward directed axioms say what truths a given truth grounds, while the downward directed axioms say what truths ground a given truth. And intuitively, both kinds of principles are required: we want to say both what grounds a truth and in what it is grounded.Footnote 19
Finally, we need to add some axioms to get our hierarchy “off the ground,” as it were. So far, we have no axiom that allows us to introduce the truth predicate. Thus, we are not able to prove the antecedent of any of our quantified axioms. To fix this, we propose to add some basic truth axioms that apply the truth predicate to the atomic formulas of PA—they allow us to introduce the truth predicate in the case of true equations. For this purpose, we use the standard idea from axiomatic theories of truth:Footnote 20
In words, an equation is true iff the terms flanking the equality symbol have the same denotation. These axioms get our axiomatization “off the ground,” in the sense that we can prove the truth of true equations and then use the other axioms to track partial ground through the complexity of the truths. Finally, since we wish to talk about the truths of arithmetic, we want to ensure that the truth predicate only applies to sentences of \(\mathcal {L}\). We achieve this by postulating that:
Note that from this axiom together with the axiom \(\forall x\forall y(x\lhd y\to Tr(x)\land Tr(y))\) it follows that also the ground predicate only applies to sentences of \(\mathcal {L}\):
In other words, out theory is a simply typed theory of partial ground.
We arrive at the following axiomatization:
Definition 2
The predicational theory of (partial) ground PG consists of the axioms of PAG plus the following axioms:
$$\begin{array}{@{}rcl@{}} & &\!\!\!\!\!\!\!\! \text{Basic Ground Axioms:} {\kern6.5pc}\text{Basic Truth Axioms:}\\ & &\!\!\!\!\!\!\!\! \mathrm{G}_{1}\ \forall x\neg(x\lhd x) {\kern9pc}\mathrm{T}_{1}\ \forall s\forall t(Tr(s\underset{\cdot}{=}t)\leftrightarrow s^{\circ}=t^{\circ}) \\ & &\!\!\!\!\!\!\!\! \mathrm{G}_{2}\ \forall x\forall y\forall z(x\lhd y\land y\lhd z\to x\lhd z) {\kern1.7pc}\mathrm{T}_{2}\ \forall s\forall t(Tr(s\underset{\cdot}{\neq}t)\leftrightarrow s^{\circ}\neq t^{\circ})\\ & &\!\!\!\!\!\!\!\! \mathrm{G}_{3}\ \forall x\forall y(x\lhd y\to Tr(x)\land Tr(y)) {\kern2.2pc} \mathrm{T}_{3}\ \forall x(Tr(x)\to Sent(x)) \end{array} $$Upward Directed Axioms:
U1 \(\forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\)
U2 \(\forall x\forall y ((Tr(x)\to x\lhd x\underset {\cdot }{\lor }y) \land (Tr(y)\to y\lhd x\underset {\cdot }{\lor }y))\)
U3 \(\forall x\forall y (Tr(x)\land Tr(y)\to (x\lhd x\underset {\cdot }{\land } y)\land (y\lhd x\underset {\cdot }{\land } y))\)
U4 \(\forall x\forall y (Tr(\underset {\cdot }{\neg } x)\land Tr(\underset {\cdot }{\neg } y)\to (\underset {\cdot }{\neg } x\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y))\land (\underset {\cdot }{\neg } y\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y)))\)
U5 \(\forall x\forall y ((Tr(\underset {\cdot }{\neg }x)\to \underset {\cdot }{\neg }x\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\land }y)) \land (Tr(\underset {\cdot }{\neg }y)\to \underset {\cdot }{\neg }y\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\land }y)))\)
U6 \(\forall x \forall t\forall v(Tr(x(t/v))\to x(t/v)\lhd \underset {\cdot }{\exists } v x)\)
U7 \(\forall x\forall v (\forall tTr(\underset {\cdot }{\neg } x(t/v))\to \forall t(\underset {\cdot }{\neg }x(t/v)\lhd \underset {\cdot }{\neg }\underset {\cdot }{\exists }v x))\)
U8 \(\forall x \forall v(\forall t(Tr(x(t/v))\to \forall t(x(t/v)\lhd \underset {\cdot }{\forall }v x))\)
U9 \(\forall x \forall t\forall v(Tr(\underset {\cdot }{\neg }x(t/v))\to \underset {\cdot }{\neg }x(t/v)\lhd \underset {\cdot }{\neg }\underset {\cdot }{\forall } v x))\)
Downward Directed Axioms:
D1 \(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\)
D2 \(\forall x\forall y (Tr(x\underset {\cdot }{\lor }y)\to (Tr(x)\to x\lhd x\underset {\cdot }{\lor }y )\land (Tr(y)\to y\lhd x\underset {\cdot }{\lor }y))\)
D3 \(\forall x\forall y (Tr(x\underset {\cdot }{\land }y)\to (x\lhd x\underset {\cdot }{\land } y)\land (y\lhd x\underset {\cdot }{\land } y))\)
D4 \(\forall x\forall y (Tr(\underset {\cdot }{\neg } (x\underset {\cdot }{\land } y))\to (Tr(\underset {\cdot }{\neg }x)\to \underset {\cdot }{\neg } x\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y))\land (Tr(\underset {\cdot }{\neg }y)\to \underset {\cdot }{\neg } y\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y)))\)
D5 \(\forall x\forall y (Tr(\underset {\cdot }{\neg } (x\underset {\cdot }{\lor } y))\to (\underset {\cdot }{\neg } x\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y))\land (\underset {\cdot }{\neg } y\lhd \underset {\cdot }{\neg }(x\underset {\cdot }{\lor } y)))\)
D6 \(\forall x (Tr(\underset {\cdot }{\exists } v x(v))\to \exists t(x(t/v)\lhd \underset {\cdot }{\exists } v x))\)
D7 \(\forall x \forall v(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\exists }v x)\to \forall t(\underset {\cdot }{\neg }x(t/v)\lhd \underset {\cdot }{\neg }\underset {\cdot }{\exists }v x))\)
D8 \(\forall x \forall v(Tr(\underset {\cdot }{\forall }v x\to \forall t(x(t/v)\lhd \underset {\cdot }{\forall }v x))\)
D9 \(\forall x \forall v(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\forall } v x)\to \exists t(\underset {\cdot }{\neg }x(t/v)\lhd \underset {\cdot }{\neg }\underset {\cdot }{\forall } v x))\)
4.2 Conservativity and Truth-theoretic Commitments
We will now determine the truth-theoretic commitments and the proof-theoretic strength of our predicational theory of ground.
As we have claimed in Section 2.2, the predicational theory of ground proves the well-known theory of positive truth [16, p.116–22]:
Definition 3 (‘Positive Truth’)
The theory PT of positive truth is formulated in \(\mathcal {L}_{Tr}\) and consists of the axioms of PAT and the three base truth axioms T1, T2, and T3, plus the following axioms:
-
P1 \(\forall x(Tr(x)\leftrightarrow Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\)
-
P2 \(\forall x\forall y (Tr(x\underset {\cdot }{\land }y)\leftrightarrow Tr(x)\land Tr(y))\)
-
P3 \(\forall x\forall y (Tr(\underset {\cdot }{\neg }(x\underset {\cdot }{\land }y))\leftrightarrow Tr(\underset {\cdot }{\neg }x\lor T\underset {\cdot }{\neg }y))\)
-
P4 \(\forall x\forall y (Tr(x\underset {\cdot }{\lor }y)\leftrightarrow Tr(x)\lor Tr(y))\)
-
P5 \(\forall x\forall y (Tr(\underset {\cdot }{\neg }(x\underset {\cdot }{\lor }y))\leftrightarrow Tr(\underset {\cdot }{\neg }x)\land Tr(\underset {\cdot }{\neg }y))\)
-
P6 \(\forall x \forall v(Tr(\underset {\cdot }{\forall }vx) \leftrightarrow \forall t Tr(x(t/v)))\)
-
P7 \(\forall x \forall v(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\forall }vx) \leftrightarrow \exists t Tr(\underset {\cdot }{\neg } x(t/v)))\)
-
P8 \(\forall x \forall v(Tr(\underset {\cdot }{\exists }vx) \leftrightarrow \exists t Tr(x(t/v)))\)
-
P9 \(\forall x \forall v(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\exists }vx) \leftrightarrow \forall t Tr(\underset {\cdot }{\neg }x(t/v)))\)
Proposition 2
PG ⊢ PT.
Proof
It suffices to derive P1−9. The derivation proceeds in every case by putting the upward directed and the downward directed axioms of PG together while using the axiom G3. Here we only sketch the derivation of axiom P 1:
-
1.
\(\forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) (U 1)
-
2.
\(\forall x\forall y(x\lhd y\to Tr(x)\land Tr(y))\) (G3)
-
3.
\(\forall x(Tr(x)\to Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\) (1., 2., →-Elim, and ∧-Elim)
-
4.
\(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) (D 1)
-
5.
\(\forall x(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\to Tr(x))\) (2., 4., →-Elim, and ∧-Elim)
-
6.
\(\forall x(Tr(x)\leftrightarrow Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\) (3., 5., ↔-Intro)
The other axioms can be derived analogously. □
This result connects the debate about axiomatic theories of truth with the debate about partial ground. In particular, the result shows that once we move to a shared framework for theories of truth and theories of ground, we only need to accept a theory of partial ground to get a proper theory of truth. Admittedly, this theory has to be formulated using the truth predicate, but this use is intuitively justified, since we have used the truth predicate simply as a quantificational device in formalizing the principles for partial ground.Footnote 21
Proposition 2 has several interesting consequences. First, it entails as a simple corollary that our predicational theory of ground proves all the instances of the T-scheme:
Corollary 2
PG proves the uniform T-scheme for all sentences \(\varphi \in \mathcal {L}\) :
Proof>
It is well-known that PT proves all the instances of the uniform T-scheme over \(\mathcal {L}\). The proof of this proceeds by a simple induction on the positive complexity of formulas. Our claim follows by Proposition 2. □
Second, we can use Proposition 2 and its Corollary 2 to show interesting facts about our predicational theory of ground, such as the fact that ground is hyperintensional according to our theory. Remember that a context is hyperintensional iff in the context the substitution of logical equivalents need not preserve truth-value (Cresswell [8]). Now, the set of (codes of) logical truths of \(\mathcal {L}_{Tr}^{\lhd }\) is recursively enumerable, and thus weakly representable in the PA, i.e. there is a formula φ(x) such that:
Let’s abbreviate this formula φ(x) by V a l(x). In particular, we’ll get for all formulas \(\varphi \in \mathcal {L}_{Tr}^{\lhd }\):
With this preliminaries in place, we can show the following result:
Lemma 1
PG proves that partial ground is hyperintensional in the following sense:
-
(i)
\(\vdash _{PG} \neg \forall x\forall y(\mathsf {Val}(x\underset {\cdot }{\leftrightarrow }y) \to \forall z(z\lhd x\leftrightarrow z\lhd y))\)
-
(ii)
\(\vdash _{PG} \neg \forall x\forall y(\mathsf {Val}(x\underset {\cdot }{\leftrightarrow }y) \to \forall z(x\lhd z\leftrightarrow y\lhd z))\)
Proof
Note, for example, that \(\vdash _{PG}\ \mathsf {Val}(\ulcorner {0}={0}\urcorner \underset {\cdot }{\leftrightarrow } \underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner {0}={0}\urcorner )\) and \(\vdash _{PG}\ulcorner {0}={0}\urcorner \lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner {0}={0}\urcorner \), but \(\vdash _{PG}\neg (\ulcorner {0}={0}\urcorner \lhd \ulcorner {0}={0}\urcorner )\) establishing (i) and \(\vdash _{PG}\neg (\underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner {0}={0}\urcorner \lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }\ulcorner {0}={0}\urcorner )\) establishing (ii). □
Note that the proof of Lemma 1 makes use of facts that we get from Proposition 2 and Corollary 2 in several places. Without using these facts, the lemma would be difficult to prove.
Moreover, we can show a kind of adequacy result for our axiomatization with respect to the operational theory of ground:
Proposition 3
For all sentences \(\varphi ,\psi \in \mathcal {L}\) , if ⊢ OG φ≺ψ, then \(\vdash _{PG} \ulcorner \varphi \urcorner \lhd \ulcorner \psi \urcorner \).
Proof 5
By an induction on the length of derivations in OG. The only interesting step is when the last inference in a derivation was an application of an inference rule for the partial ground operator. Consider the step where the last inference was of the form:
This means that ⊢ O G φ. Since \(\varphi \in \mathcal {L}\), we get by Proposition 1 that ⊢ P A φ and thus ⊢ P G φ. Then by applying the T-scheme we get \(\vdash _{PG} Tr(\ulcorner \varphi \urcorner )\) and from this, using the axiom U1, \(\vdash _{PG} \ulcorner \varphi \urcorner \lhd \ulcorner \neg \neg \varphi \urcorner \). The cases for the other rules are analogous. Note that we only need the induction hypothesis in the case of the rule:
which is the only rule that has formulas with the ground operator in its antecedent. We get the result immediately by applying the induction hypothesis to the antecedents and using the axioms G2, which captures the transitivity of partial ground. □
The other direction of Proposition 3, however, does not hold. This follows from the fact that the theory of positive truth and thus the predicational theory of ground is not conservative over PA. For example, positive truth proves the consistency of PA, in the sense that \(\vdash _{PT}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\).Footnote 22 Thus, by Proposition 2, \(\vdash _{PG}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\). But by Gödel’s second incompleteness theorem, we know that \((Incomp)\not \vdash _{PA}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\). Now, since \(\vdash _{PG}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\), we know using the T-scheme that \(\vdash _{PG}Tr(\ulcorner \neg Bew_{PA}(\ulcorner 0=1\urcorner ) \urcorner )\). Using the axiom U5, we can infer from this that:
But we cannot have that:
since then we would get the following derivation in the operational theory of ground:
by means of the OG rule
applied to the supposed derivation of \(\neg Bew_{PA}(\ulcorner 0=1\urcorner )\prec \neg (Bew_{PA}(\ulcorner 0=1\urcorner ) \land Bew_{PA}(\ulcorner 0=1\urcorner ))\). This would then mean that \(\vdash _{OG}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\) and thus by Proposition 1, since \(\neg Bew_{PA}(\ulcorner 0=1\urcorner )\in \mathcal {L}\), that \(\vdash _{PA}\neg Bew_{PA}(\ulcorner 0=1\urcorner )\)—which is in contradiction to (I n c o m p). Moreover, intuitively speaking, the sentence \(\neg Bew_{PA}(\ulcorner 0=1\urcorner )\) is true—we know, for example by Gentzen’s consistency proof, that PA is indeed consistent. But then the formal application of U5 to \(\neg Bew_{PA}(\ulcorner 0=1\urcorner )\) is intuitively justified: the truth of \(\neg (Bew_{PA}(\ulcorner 0=1\urcorner )\land Bew_{PA}(\ulcorner 0=1\urcorner ))\) holds indeed in virtue of the truth of \(\neg Bew_{PA}(\ulcorner 0=1\urcorner )\). So, our predicational theory of ground proves an intuitively true claim about partial ground that the operational theory does not.
Thus, we know that the predicational theory of ground is stronger than the operational theory of ground. But how strong is it exactly? Here is the answer:
Theorem 1
PG is a proof-theoretically conservative extension of PT.
Proof
The proof is similar to the proof of Proposition 1. Let \(\underset {\cdot }{c}\) represent the complexity function and \(\underset {\cdot }{<}\) represent the strictly-less-than relation on the natural numbers again. We define the translation function \({\tau }:\mathcal {L}_{Tr}^{\lhd }\to \mathcal {L}_{Tr}\) recursively by saying that:
-
(i)
\({\tau }(\varphi )=\left \{\begin {array}{ll} \varphi , & \text {~if~}\varphi \in \mathcal {L}_{Tr}\text {~atomic,}\\ Tr(s)\land Tr(t)\land \underset {\cdot }{c}(s)~\underset {\cdot }{<}~\underset {\cdot }{c}(t), & \text {~if~}\varphi =s\lhd t; \end {array}\right .\)
-
(ii)
τ(¬φ)=¬τ(φ);
-
(iii)
τ(φ∘ψ) = τ(φ)∘τ(ψ), for ∘=∧,∨; and
-
(iv)
τ(Q x φ) = Q x(τ(φ)), for Q = ∀, ∃.Footnote 23
It is again easy to see that (a) τ(φ) = φ, if \(\varphi \in \mathcal {L}_{Tr}\). Next we check that (b) the translation preserves theoremhood from PG to PT, in the sense that for all \(\varphi \in \mathcal {L}_{Tr}^{\lhd }\), if ⊢ P G φ, then ⊢ P T τ(φ). We prove this result by an induction on the length of derivations. All the arithmetic axioms and rules of PG and PT are the same and all the instances of the induction scheme over \(\mathcal {L}_{Tr}^{\lhd }\) become instances of the induction scheme over \(\mathcal {L}_{Tr}\) under τ. Thus, it suffices to show that the images of the ground-theoretic axioms are derivable in PT. Here we just show the claim for two cases:
-
In the case of the axiom G1, we get \({\tau }(\forall x\neg (x\lhd x))=\forall x\neg (Tr(x)\land Tr(x)\land \underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(x))\). We know that \(\vdash _{PA}\forall x(Sent(x)\to \neg (\underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(x)))\). Since ⊢ P T ∀x(T r(x) → S e n t(x)), the claim follows by simple logic.
-
In the case of the axiom U1, we get that \({\tau }(\forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x))=\forall x(Tr(x)\to Tr(x)\land Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\land \underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\). Now, let x be a fresh variable and assume that T r(x) for a →-Intro in PT followed by a generalization. We need to derive \(Tr(x)\land Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\land \underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). The first conjunct of the consequent is simply the assumption T r(x). By the axiom P1, \(\forall x(Tr(x)\leftrightarrow Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\), we can derive \(Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) from the first conjunct and thus we get the second conjunct. Finally, for the last conjunct of the consequent is derivable, note that ⊢ P T ∀x(T r(x) → S e n t(x)) and thus ⊢ P T T r(x) → S e n t(x), as well as \(\vdash _{PT}\forall x(Sent(x)\to (\underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\). Thus, we get the third conjunct \(\underset {\cdot }{c}(x)~\underset {\cdot }{<}~\underset {\cdot }{c}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\) by simple logic. The claim follows.
The other axioms can be derived in a similar way under τ. The theorem follows by putting (a) and (b) together. □
The theorem has two important immediate consequences:
Corollary 3
The theory PG is proof-theoretically consistent.
Corollary 4
The theory PG has the same arithmetic theorems as the theory ACA of arithmetical comprehension.Footnote 24
Proof
This follows from the facts that PG is a conservative extension of PT and that PT has the same arithmetical theorems as ACA.Footnote 25 □
Thus, Propositions 2 and Theorem 1 allow us to determine the proof-theoretic strength of our predicational theory of ground. Moreover, philosophically speaking, together the theorems shows that our predicational theory of ground and the theory of positive truth say the same things about truth. Since PG is a conservative extension of PT, the two theories prove exactly the same theorems in the language \(\mathcal {L}_{Tr}\). Moreover, looking at the axioms of both theories, we can see that they paint the same truth-theoretic picture, as it were. Looking at the axioms of both theories, we see that they only contain positive occurrences of the truth predicate, where T r occurs exclusively in the scope of an even number (in fact, zero) negations. In other words, according to both theories, the truths are built up successively from other, less complex truths—and never from falsehoods.Footnote 26 What the predicational theory of ground adds to this picture is that it stratifies the truths into a hierarchy according to their complexity: the result is the hierarchy of grounds. In this specific sense, the predicational framework allows us to make the truth-theoretic commitments of the theory of partial ground explicit.
4.3 Models for Partial Ground
In the last section, we have proved the consistency of the predicational theory of ground from the fact that it is a conservative extension of the consistent theory of positive truth. By the completeness theorem for first-order logic, we can infer from this that there is a first-order model of the predicational theory. But the way we proved this result does not give us any idea of what such a model looks like. In this subsection, we will construct a model for our theory “from scratch.”
Consider the set S that contains all and only the codes of formulas that are true in the standard model of arithmetic:
Then (N, S) is a model of the theory of positive truth—the standard model of PT.Footnote 27 To construct our model, we will use grounding-trees over the standard model of PT. Grounding-trees were first introduced by Correia [6].Footnote 28 Here we give a slightly different definition of grounding-trees, which is adapted to the present purpose:
Definition 4
Let (N, S) be the standard model of PT. We define the grounding-trees over (N, S) recursively by saying that for all formulas \(\varphi ,\psi \in \mathcal {L}\):
-
(i)
if #φ ∈ S, then #φ is a grounding-tree over (N, S) with #φ as its root;
-
(ii)
if
 is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ as its root, then  is a grounding-tree over (N, S) with #¬¬φ as its root;
is a grounding-tree over (N, S) with #¬¬φ as its root; -
(iii)
if
 is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ as its root, then  is a grounding-tree over (N, S) with #(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #(φ∨ψ) as its root; -
(iv)
if
 is a grounding-tree \(\mathcal {T}\) over (N, S) with #ψ as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #ψ as its root, then 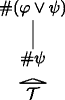 is a grounding-tree over (N, S) with #(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #(φ∨ψ) as its root; -
(v)
if
 are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}\) over (N, S) with #φ, #ψ as their roots respectively, then
are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}\) over (N, S) with #φ, #ψ as their roots respectively, then  is a grounding-tree over (N, S) with #(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #(φ∧ψ) as its root; -
(vi)
if
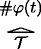 is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ(t) as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #φ(t) as its root, then  is a grounding-tree over (N, S) with #∃x
φ(x) as its root;
is a grounding-tree over (N, S) with #∃x
φ(x) as its root; -
(vii)
if
 , … are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}, \ldots \) over (N, S) with #φ(t
1), #φ(t
2),… as their roots respectively, where t
1, t
2,… are all and only the terms of \(\mathcal {L}_{PA}\), then
, … are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}, \ldots \) over (N, S) with #φ(t
1), #φ(t
2),… as their roots respectively, where t
1, t
2,… are all and only the terms of \(\mathcal {L}_{PA}\), then  is a grounding-tree over (N, S) with #∀x
φ(x) as its root;
is a grounding-tree over (N, S) with #∀x
φ(x) as its root; -
(viii)
if
 is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬φ as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬φ as its root, then 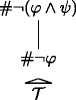 is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root; -
(ix)
if
 is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬ψ as its root, then
is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬ψ as its root, then 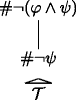 is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root; -
(x)
if
 are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}\) over (N, S) with #¬φ, #¬ψ as their roots respectively, then
are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}\) over (N, S) with #¬φ, #¬ψ as their roots respectively, then  is a grounding-tree over (N, S) with #¬(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∨ψ) as its root; -
(xi)
if
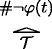 is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬φ(t) as its root,
is a grounding-tree \(\mathcal {T}\) over (N, S) with #¬φ(t) as its root,  then is a grounding-tree over (N, S) with #¬∀x
φ(x) as its root;
then is a grounding-tree over (N, S) with #¬∀x
φ(x) as its root; -
(xii)
if
 , … are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}, \ldots \) over (N, S) with #¬φ(t
1), #¬φ(t
2),… as their roots respectively, where t
1, t
2,… are all and only the terms of \(\mathcal {L}_{PA}\), then
, … are grounding-trees \(\mathcal {T}_{1},\mathcal {T}_{2}, \ldots \) over (N, S) with #¬φ(t
1), #¬φ(t
2),… as their roots respectively, where t
1, t
2,… are all and only the terms of \(\mathcal {L}_{PA}\), then  is a grounding-tree over (N, S) with #∀x
φ(x) as its root;
is a grounding-tree over (N, S) with #∀x
φ(x) as its root; -
(xiii)
nothing else is a grounding-tree over (N, S).
Mathematically speaking, the grounding-trees over (N, S) are rooted graphs, where the vertices are codes of formulas, one vertex is distinguished as the root, and the edges are constructed according to the above definition. Note that by clauses (vii) and (xii), there are infinitely wide grounding-trees over (N, S). Nevertheless, all grounding-trees over (N, S) have a finite height, where this concept is defined recursively on the construction of the grounding-trees over (N, S):
Definition 5
We define the height \(h(\mathcal {T})\) of a grounding-tree \(\mathcal {T}\) over (N, S) by saying that:
-
(i)
all grounding-trees over (N, S) of the form #φ ∈ S have height one;
-
(ii)
if \(\mathcal {T}\) is a grounding-tree over (N, S) that is constructed from grounding-trees \(\mathcal {T}_{1}, \mathcal {T}_{2}, \ldots \) over (N, S) according to clauses (ii–xii) of Definition 4, then the height of \(\mathcal {T}\) is one plus the least upper bound of the heights of \(\mathcal {T}_{1}, \mathcal {T}_{2}, \ldots \):
$$h(\mathcal{T})=lub\{h(\mathcal{T}_{1}), h(\mathcal{T}_{2}), \ldots\}+1, $$where lub is the operation of taking least upper bounds.
We call a grounding-tree over (N, S)degenerate iff it is of height one.
The argument that grounding-trees have finite height now is a simple induction on the construction of the grounding-trees, where we note that in clauses (vii) and (xii) the height of the grounding-trees \(\mathcal {T}_{1}, \mathcal {T}_{2}, \ldots \) is bounded by the (finite) logical complexity of φ. Thus, we can use induction on the height of the grounding-trees as a proof-method for claims about grounding-trees: if all degenerate grounding-trees have a property and we can show for all grounding-trees \(\mathcal {T}\) that if all grounding-trees of lower height have the property, then \(\mathcal {T}\) has the property, then all grounding-trees have the property.
For example, we can use this method to establish that the grounding-trees over (N, S) are really trees on the truths in (N, S):
Lemma 2
Let (N, S) be the standard model of PT and let \(\mathcal {T}\) be a grounding-tree over (N, S). Then for all formulas \(\varphi \in \mathcal {L}\), if #φ is a vertex in \(\mathcal {T}\), then #φ ∈ S.
Proof
The claim trivially holds for all degenerate grounding-trees over (N, S) by clause (i) of Definition 4. So assume the induction hypothesis. For the induction step, we go through all the ways in which \(\mathcal {T}\) could have been constructed according to Definition 4 and check that the claim holds. Here we only show this for clause (ii). Assume that \(\mathcal {T}\) is of the form  , where
, where  is a grounding-tree \(\mathcal {T}^{\prime }\) over (N, S) with #φ as its root. Then, since \(\mathcal {T}^{\prime }\) is a grounding-tree over (N, S) with strictly lower height than \(\mathcal {T}\), we know by the induction hypothesis that #φ ∈ S and thus \(\mathbf {N}\vDash \varphi \). But then, by classical logic, also \(\mathbf {N}\vDash \neg \neg \varphi \) and thus #¬¬φ ∈ S. The claim follows. The cases for the other clauses are analogous. □
is a grounding-tree \(\mathcal {T}^{\prime }\) over (N, S) with #φ as its root. Then, since \(\mathcal {T}^{\prime }\) is a grounding-tree over (N, S) with strictly lower height than \(\mathcal {T}\), we know by the induction hypothesis that #φ ∈ S and thus \(\mathbf {N}\vDash \varphi \). But then, by classical logic, also \(\mathbf {N}\vDash \neg \neg \varphi \) and thus #¬¬φ ∈ S. The claim follows. The cases for the other clauses are analogous. □
Next, we wish to show that the grounding-trees over (N, S) don’t contain any cycles or “loops.” This follows from the following useful lemma. Let us define the notion of an occurrence of the code #φ of a formula \(\varphi \in \mathcal {L}\) to be below an occurrence of the code #ψ of formula \(\psi \in \mathcal {L}\) in a grounding-tree \(\mathcal {T}\) over (N, S) recursively by saying that: no occurrence of any formula in a degenerate grounding-tree over (N, S) is below an occurrence of any formula in the tree, and if \(\mathcal {T}\) is a grounding-tree over (N, S) that was constructed from grounding-trees \(\mathcal {T}_{1}, \mathcal {T}_{2},\ldots \) over (N, S) according to the rules (ii–xii) of Definition 4, then all occurrences of all formulas in \(\mathcal {T}_{1}, \mathcal {T}_{2},\ldots \) occur below the root of \(\mathcal {T}\) in \(\mathcal {T}\). Then we can show:
Lemma 3
Let (N, S) be the standard model of PT. If \(\mathcal {T}\) is a grounding-tree over (N, S) with #φ as its root, for some formula φ, then, all formulas ψ whose code #ψ occurs below #φ in \(\mathcal {T}\) have a lower complexity than φ.
Proof
The claim trivially holds for degenerate grounding-trees, since no code occurs below any code in degenerate grounding-trees. So assume the induction hypothesis. For the induction step, we note that in all the ways in which a grounding-tree can be constructed from other grounding-trees, the formula whose code is at the root of the new grounding-tree is the only new formula and always has higher complexity than the roots of the grounding-trees that it is constructed from. The claim follows than by a simple application of the induction hypothesis. □
Using this lemma, we obtain:
Lemma 4
Let (N, S) be the standard model of PT and \(\mathcal {T}\) is a grounding-tree over (N, S). Then between any two nodes #φ and #ψ in \(\mathcal {T}\), for formulas \(\varphi ,\psi \in \mathcal {L}\), there is exactly one path, i.e. there are no cycles.
Proof
Degenerate grounding-trees clearly contain no cycles. So assume the induction hypothesis. For the induction step, consider some arbitrary grounding-tree \(\mathcal {T}\) with root #φ, for some formula φ. By the induction hypothesis, we know that all the trees that \(\mathcal {T}\) is constructed from don’t contain any loops. Now assume that in the last step of the construction of \(\mathcal {T}\) a loop is introduced. This would mean that #φ has to occur somewhere in the grounding-trees that \(\mathcal {T}\) was constructed from. This would mean that #φ occurs below #φ in \(\mathcal {T}\). But then by Lemma 3, we would get that |φ|<|φ|, which is impossible. The claim follows. □
Remember that a rooted tree in the mathematical sense is a rooted graph that does not contain any cycles. Thus, the grounding-trees over (N, S) are simply rooted trees over S. In a rooted tree, all edges have a natural direction, either towards or away from the root. Given Lemma 3, we can say that all the edges in a grounding-tree \(\mathcal {T}\) over (N, S) naturally point toward its root. Finally, we wish to show that the set of grounding-trees over (N, S) is transitive in the following sense:
Lemma 5
Let (N, S) be the standard model of PT. If there is a grounding-tree \(\mathcal {T}_{1}\) over (N, S) with #ψ as its root and #φ 1, #φ 2,… as its leaves and there is a grounding-tree \(\mathcal {T}_{2}\) over (N, S) with #ψ, #ψ 1, #ψ 2,… as its leaves and #θ as its root, then there is a grounding-tree \(\mathcal {T}_{3}\) over (N, S) with #φ 1, #φ 2,…, #ψ 1, #ψ 2, … as its leaves and #θ as its root.
Proof
The proof proceeds by induction on the height of \(\mathcal {T}_{2}\). If \(\mathcal {T}_{2}\) is a degenerate grounding-tree over (N, S), then \(\mathcal {T}_{1}\) is already the grounding-tree we are looking for. So, assume the induction hypothesis and let \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\) be grounding-trees as described in the statement of the proposition. Now, we go through the different ways that \(\mathcal {T}_{2}\) could have been constructed from other grounding-trees. Assume, for example, that \(\mathcal {T}_{2}\) is constructed using clause (ii) of Definition 4. Then \(\mathcal {T}_{2}\) is of the form:  and its root is #θ = #¬¬θ′. Since
and its root is #θ = #¬¬θ′. Since  is then a grounding-tree with a strictly lower height than \(\mathcal {T}_{2}\), by the induction hypothesis we get a grounding-tree \(\mathcal {T}_{3}^{\prime }\) with root #θ′ and #φ
1, #φ
2,…, #ψ
1, #ψ
2,… as its leaves. Then by a simple application of (ii) of Definition 4, we get the existence of the desired grounding-tree \(\mathcal {T}_{3}\) with root #θ = #¬¬θ′ and leaves #φ
1, #φ
2,…, #ψ
1, #ψ
2,…. The cases for the other clauses are analogous. □
is then a grounding-tree with a strictly lower height than \(\mathcal {T}_{2}\), by the induction hypothesis we get a grounding-tree \(\mathcal {T}_{3}^{\prime }\) with root #θ′ and #φ
1, #φ
2,…, #ψ
1, #ψ
2,… as its leaves. Then by a simple application of (ii) of Definition 4, we get the existence of the desired grounding-tree \(\mathcal {T}_{3}\) with root #θ = #¬¬θ′ and leaves #φ
1, #φ
2,…, #ψ
1, #ψ
2,…. The cases for the other clauses are analogous. □
The proof essentially shows that matching grounding-trees can be “glued together,” as it were.
Putting all of the above together, we can say that the non-degenerate grounding-trees over (N, S) intuitively correspond to grounding-facts in (N, S): the codes at the leaves correspond to the truths that ground and the code at the root corresponds to the truth being grounded. More formally, Lemmas 4 and 5 together allow us to define a strict partial order on the elements of S (i.e. the truths according to (N, S)): we say that a number n ∈ S is “strictly below” a number m ∈ S iff there is a non-degenerate grounding-tree connecting the two:
Definition 6
Let (N, S) be the standard model of PT. We define the relation \(\mathbf {R}\subseteq \mathbb {N}^{2}\) by saying that for all \(n,m\in \mathbb {N}\), R(m, n) iff there is a non-degenerate grounding-tree over (N, S) with n as a leaf and m as its root.
To be perfectly explicit, let’s look at how R interprets the predicate \(\lhd \) in the model (N, S, R). Consider an atomic formula of the form \(s\lhd t\) and a valuation σ in (N, S, R). Using standard first-order semantics, we get: \((\mathbf {N},\mathbf {S},\mathbf {R})\vDash _{\sigma } s\lhd t\) iff R(⟦s⟧ σ , ⟦t⟧ σ ), where ⟦t⟧ σ is the value of the term t under the assignment σ.Footnote 29 In words, a formula \(s\lhd t\) is true in (N, S, R) under an assignment σ just in case there is a non-degenerate grounding-tree over (N, S) with the value of t under σ as its root and the value of s under σ as one of its leaves.
The relation R of Definition 6, then, indeed interprets the ground predicate correctly (in the way just described):
Theorem 2
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash PG\).
Proof 12
We need to show that all the axioms of PG are satisfied in (N, S, R). Since the basic truth axioms T1, T2, and T3 are also axioms of PT, we know already that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \text {T}_{1,2,3}\) as (N, S) is the standard model of PT. For the basic ground axioms G1, G2, and G3 we get the following arguments:
-
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\neg (x\lhd x)\)
This follows from Lemma 4: Assume that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \exists x(x\lhd x)\). Thus for some variable assignment σ over (N, S, R) and some x-variant σ′ of σ,Footnote 30 we have \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} x\lhd x\) meaning R(σ′(x), σ′(x)). By Definition 6 this means that there is a non-degenerate grounding tree over (N, S) with σ′(x) as its root and σ′(x) as a leaf. But this tree would contain a loop, i.e. a path from σ′(x) to σ′(x), in contradiction to Lemma 4. Thus \((\mathbf {N}, \mathbf {S}, \mathbf {R})\not \vDash \exists x(x\lhd x)\) and thus by classical logic \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\neg (x\lhd x)\).
-
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\forall y\forall z(x\lhd y\land y\lhd z\to x\lhd z)\)
This follows from Lemma 5: Let σ be a variable assignment over (N, S, R) and σ′ an x, y, z-variant σ such that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} x\lhd y\) and \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} y\lhd z\). This means that R(σ′(x), σ′(y)) and R(σ′(y), σ′(z)). By Definition 6 this means that are non-degenerate grounding-trees \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\) over (N, S) such that \(\mathcal {T}_{1}\) has σ′(x) as a leaf and σ′(y) as its root and \(\mathcal {T}_{2}\) has σ′(y) as a leaf and σ′(z) as its root. By Lemma 5, there is a grounding-tree \(\mathcal {T}_{3}\) over (N, S) with σ′(x) as a leaf and σ′(z) as its root. Thus, R(σ′(x), σ′(z)) and thus \(\vDash _{\sigma ^{\prime }} x\lhd z\). Since σ was arbitrary, we get that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\forall y\forall z(x\lhd y\land y\lhd z\to x\lhd z)\).
-
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\forall y(x\lhd y\to Tr(x)\land Tr(y))\)
This follows from Lemma 2: Let σ be a variable assignment over (N, S, R) and σ′ an x, y-variant of σ such that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} x\lhd y\). This means that R(σ′(x), σ′(y)) and thus by Definition 6 that there is a non-degenerate grounding-tree over (N, S) with σ′(x) as a leaf and σ′(y) as its root. By Lemma 2 if follows that σ′(x), σ′(y) ∈ S. Since S interprets T r, we get that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} Tr(x)\land Tr(y)\). Since σ was arbitrary, we get \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x\forall y(x\lhd y\to Tr(x)\land Tr(y))\).
For the upward and downward directed axioms, we only consider the cases U1 and D1, as the other cases are analogous:
-
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\)
Let σ be a variable assignment over (N, S, R) and σ′ some x-variant of σ. Assume that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} Tr(x)\). This means that σ′(x) ∈ S. Since \(\mathbf {S}=\{\#\varphi ~|~\varphi \in \mathcal {L},\mathbf {N}\vDash \varphi \}\), we know that σ′(x) = #φ, for some formula \(\varphi \in \mathcal {L}\). Now, by clause (i) of Definition 4, #φ is a degenerate grounding-tree over (N, S). But then, by clause (ii) of Definition 4,
 is a non-degenerate grounding-tree over (N, S). Moreover, the root of this tree is #¬¬φ and its only leaf is #φ. Now consider \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). Since we know that σ′(x) = #φ and \(\underset {\cdot }{\neg }\) expresses the negation function on the codes of formulas, we know that \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)=\#\neg \neg \varphi \). Thus, \(\mathbf {R}({\sigma ^{\prime }}(x), {\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\) meaning \(\vDash _{\sigma ^{\prime }} x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x\). And since σ was arbitrary, we get \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\).
is a non-degenerate grounding-tree over (N, S). Moreover, the root of this tree is #¬¬φ and its only leaf is #φ. Now consider \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). Since we know that σ′(x) = #φ and \(\underset {\cdot }{\neg }\) expresses the negation function on the codes of formulas, we know that \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)=\#\neg \neg \varphi \). Thus, \(\mathbf {R}({\sigma ^{\prime }}(x), {\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x))\) meaning \(\vDash _{\sigma ^{\prime }} x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x\). And since σ was arbitrary, we get \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x (Tr(x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). -
\((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x (Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\)
Let σ be a variable assignment over (N, S, R) and σ′ some x-variant of σ. Assume that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\). This means that \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\in \mathbf {S}\). Again, since \(\mathbf {S}=\{\#\varphi ~|~\varphi \in \mathcal {L},\mathbf {N}\vDash \varphi \}\) and since \(\underset {\cdot }{\neg }\) represents the negation function on the codes of formulas, we know that \({\sigma ^{\prime }}(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)=\#\neg \neg \varphi \), for some formula \(\varphi \in \mathcal {L}\) such that \(\mathbf {N}\vDash \neg \neg \varphi \). From the latter it follows by classical logic that \(\mathbf {N}\vDash \varphi \). Moreover, we know that σ′(x) = #φ and thus that #σ′(x) ∈ S. But then we get that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash _{\sigma ^{\prime }} Tr(x)\) and by the argument for the axiom U1 that \(\vDash _{\sigma ^{\prime }} x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x\). Hence, we get \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \forall x (Tr(\underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\to x\lhd \underset {\cdot }{\neg }\underset {\cdot }{\neg }x)\), since σ was arbitrary.
□
4.4 Grounding-Trees and Conceptualist Ground
We have shown how to extend the standard model of the theory of positive truth to a standard model of our predicational theory of ground. Note, however, that our construction will not necessarily work if we start from non-standard models of the theory of positive truth. At many points in our construction, we have made use of the fact that we’re working in the standard model of the theory of positive truth. Most importantly, in our construction we have relied on the fact that the extension of the truth predicate coincides with the codes of formulas that are true in the standard model of PA. But in a non-standard model of the theory of positive truth this need not be the case. There we might have non-standard elements in the extension of the truth predicate, such as objects that according to the model are sentences with infinite complexity.Footnote 31 As a result, in such non-standard models, our construction will break down. Perhaps there is another construction that will allow us to extend non-standard models of the theory of positive truth to (non-standard) models of our predicational theory of ground. But here we leave this question open, as the point of the construction was to show what the standard model looks like.
By looking at the standard model of our predicational theory of truth, we can draw some lessons for the conceptualist semantics of ground. The model we have constructed is a model for a conceptualist notion of partial ground—it provides a semantics for our conceptualist ground predicate. Moreover, since we work in a standard first-order setting, we have a general notion of a model for predicational theories of ground. Developing a general conceptualist semantics for ground operators, in contrast, is still very much an open problem. But we can use the model that we have constructed to approach this problem. To begin with, we can interpret the operational theory of ground OG (Definition 1) over the model (N, S, R). We simply say for all formulas \(\varphi ,\psi \in \mathcal {L}\):
It then follows from Proposition 3 that this interpretation is sound with respect to OG, in the sense that for all \(\varphi ,\psi \in \mathcal {L}\), if ⊢ O G φ≺ψ, then \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \varphi \prec \psi \).Footnote 32 For assume that ⊢ O G φ≺ψ. By Proposition 3, it follows that \(\vdash _{PG}\ulcorner \varphi \urcorner \lhd \ulcorner \psi \urcorner \). Then, by Theorem 2, we get that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \ulcorner \varphi \urcorner \lhd \ulcorner \psi \urcorner \) and thus by the above definition that \((\mathbf {N}, \mathbf {S}, \mathbf {R})\vDash \varphi \prec \psi \). But this interpretation does not yet tell us what models for the language \(\mathcal {L}_{\prec }\), in which the theory OG is formulated, should look like in general. But it gives us a hint about what kind of structure we can use to interpret the language. Remember that a forest in the mathematical sense is a disjoint union of trees. Now consider:
where ⊎ denotes the operation of taking disjoint unions. Then, mathematically speaking, T is a forest. As we have said before, the (non-degenerate) grounding-trees over (N, S) intuitively correspond to individual grounding facts. The forest T, then, corresponds intuitively to the whole hierarchy of grounds. Moreover, we can equivalently rephrase our definition of R that interprets our ground predicate \(\lhd \) (Definition 6) by saying that for all \(m,n\in \mathbb {N}\):
With this definition in place, we can interpret OG over the structure (N, T). We simply equivalently restate the definition of \((\mathbf {N},\mathbf {T})\vDash \varphi \prec \psi \) by saying that for all \(\varphi ,\psi \in \mathcal {L}:\)
Now, take a look at the structure (N, T). On the above interpretation, the component N interprets the arithmetic vocabulary and in particular the names for sentences. The forest T, on the other hand, interprets the ground operator ≺. By abstracting from this, we arrive at a notion of an arbitrary model for \(\mathcal {L}_{\prec }\): The idea is that a model for \(\mathcal {L}_{\prec }\) is a pair (T, F(T)), where T is a suitable set of fine-grained truths and F(T) is a suitable forest over the elements of T. Of course, developing this idea in detail still requires a lot of work. But we wish to suggest that an intuitively plausible, graph-theoretic semantics for the ground operator can be obtained in this way. Incidentally, in forthcoming work, Litland [19] and deRosset [9] have already shown promising results in this direction—the results of this section give further support to this approach.
5 Conclusion
In this part of the paper, we’ve developed the predicational theory of partial ground PG. We’ve shown that the theory is a conservative extension of the theory of positive truth PT and thus consistent, and we’ve constructed a concrete model for PG in terms of grounding-trees. In Section 2, we’ve already pointed at some useful applications of the theory. In the second part of this paper will look more closely at applications to do with truth and partial ground. Let’s close with an important observation about one important generalization of our results.
Note that, at least in its present state, the approach of this paper only works for the relation of partial ground: as soon as we approach full ground using our ground predicate, we face problems. Full ground, remember, is the relation of one truth holding wholly in virtue of a possible plurality of others. Philosophically speaking, it is natural to suppose that the relation of full ground is more fundamental than the relation of partial ground. As Fine [13](@var1@p. 50@var1@) argues, we can define partial ground in terms of full ground: We simply say that one truth partially grounds another iff the former truth possibly together with some others fully grounds the latter truth. But conversely, Fine argues, it is not possible to define full ground in terms of partial ground. His argument runs as follows: Let φ and ψ be two true sentences. Then, intuitively, the truth of φ∨ψ holds both fully in virtue of the truth of φ and fully in virtue of the truth of ψ. Thus, both the truth of φ and the truth of ψ are full grounds of the truth of φ∨ψ. Consequently, the two truths are also partial grounds of the truth of φ∨ψ. Now consider the truth of φ∧ψ. Intuitively, the truth of φ∧ψ holds partially in virtue of the truths of φ and ψ, but not wholly in virtue of either truth. Thus, the truths of φ and ψ are partial grounds, but not full grounds of the truth of φ∧ψ. We have the following scenario: the truths of φ∨ψ and φ∧ψ have the exact same partial grounds, but different full grounds. Thus, it is unclear how we should define the full grounds of a truth solely based on its partial grounds.
If we take full ground to be more fundamental than partial ground, it is natural to think that we should develop an axiomatic theory of full ground that proves our theory of partial ground as a sub-theory. Full ground is what Correia [5, p. 255] calls a many-to-one relation: it is the relation of one truth holding in virtue of a possible plurality of others. Now, how should we reflect this fact syntactically? A first approach would be to stick to a binary ground predicate and represent the possible pluralities of truths as sets of sentences. But this approach only carries so far. Using the technique of Gödel numbering, we can only represent finite sets of sentence, but not arbitrary sets of sentences.Footnote 33 But in many cases, the plurality of full grounds is intuitively infinite. Think for example of the truth of ∀x(S(x) ≠ 0). Intuitively, the truth holds wholly in virtue of all the truths of \(S({0})\neq {0}, S(\overline {1})\neq {0}, \ldots \) taken together. For this reason, it seems that we need to adopt multigrade predicates in the style of [23], which take arbitrary sequents of terms as arguments. If we let \(\blacktriangleleft \) be such a multigrade predicate for the relation of strict full ground, we can formalize the first example as:
while we can at the same time write:
to say that the truth of S(0) ≠ 0 fully grounds the truth of S(0) ≠ 0∨0 = 0. Multigrade predicates, however, mean a significant deviation from standard logic to infinitary logic. It would be a non-trivial fact that the results of this paper still apply in this context and working out the details is beyond the scope of the present paper.Footnote 34 We leave this for future research.
Notes
For (opinionated) introductions to the concept(s) of ground, see [7, 13]. For an overview of the recent literature, see [2, 4, 24, 29]. Most research focuses on the notion of full ground: the relation of one thing holding wholly in virtue of a possibly plurality of other truths [13, p. 37]. For reasons that we will discuss more comprehensively in Section 5, we will focus on the notion of partial ground in this paper. For more on the distinction between full and partial ground, see [13, p. 50].
This is, in any case, the standard view of partial ground. Some authors have challenged this view: Jenkins [17] challenges the claim that partial ground is irreflexive and Schaffer [27] challenges the claim that partial ground is transitive. See Litland [21] and Raven [25] for a defense of the standard view against these challenges.
The main reason for taking arithmetic as the starting point here is that the standard theory of arithmetic, Peano arithmetic PA, can double in well-known ways as a theory of arithmetic and a theory of syntax (see Section 3). Thus, by taking PA as our starting point, we can effectively kill two birds with one stone: PA can function as the theory that tells us which sentences are true and function as a theory of syntax that allows us to talk about these sentences. Regardless of this technical convenience, nothing philosophically “deep” hinges on this particular theory choice. Note, however, that we’re explicitly not including truths about partial ground in the hierarchy. There are specific technical and philosophical issues that arise in the context of such truths, which shall be discussed in the second part of the paper. See also our discussion of the issue on p. 11 of this article.
We will show this rigorously in Section 4.2.
In the literature on ground, we distinguish between factive and non-factive conceptions of ground (cf. [13, p. 48–50]). On a factive conception, ground can only obtain between factive things, such as truths or facts. On a non-factive conception, the relation of ground can also hold between non-factive things, such as falsehoods or non-obtaining states of affairs. The notion of partial ground that we are working with in this paper is a factive notion of ground. Later we shall enforce this by means of axioms stipulating that the relation of partial ground can only hold between truths.
A remark is in order: We could, of course, achieve similar results on the operator approach using quantification into sentence position or propositional quantification. But propositional quantification means a significant deviation from classical logic, while on the present approach we can comfortably stay within the purview of classical (first-order) logic. This highlights another benefit of the predicate approach: it allows us to study partial ground using entirely standard methods, well-known from first-order logic and model-theory.
To see this, suppose that the truth of φ strictly partially grounds the truth of ψ and that the truth of ψ strictly partially grounds the truth of some arbitrary θ. It follows immediately by the transitivity of strict partial ground that the truth of φ strictly partially grounds the truth of θ, establishing that the truth of φ weakly partially grounds the truth of ψ.
For a (critical) discussion of the concept of weak ground, see [11].
There are semantics for factualist notions of ground in the literature. The most commonly discussed semantics for the ground operator is given by Fine [13, p. 71–74] and Fine [15, p. 7–10] in terms of truthmakers. A related algebraic semantics is given by Correia [5, p. 274–76]. But as Fine [13, Fn 22, p. 74] himself notes, these semantics are not sound for a conceptualist notion of ground.
For the distinction between truths and facts, see [12]. Note that according to Fine truths are not (true) sentences, rather they are derived entities that get their identity criteria from (true) sentences: truths according to Fine are a kind of linguistically individuated facts. In this paper, we don’t presuppose a specific metaphysical understanding of truths: they can be anything from true sentences to metaphysically robust fact-like entities in their own right.
We assume that the reader is already familiar with the basics of first-order logic and has at least a rough understanding of how Gödel-numbering works. For the details, we refer the reader to [3].
Note that we’re explicitly excluding iterations of the operator ≺ here. See also our discussion on p. 11 below.
The notation and background theory we use in this paper is adapted from the standard notation and background theory used in axiomatic theories of truth. For the reader not familiar with these conventions, we recommend [16, p. 29–38].
For a detailed discussion of the relation between ‘because’ and ‘in virtue of’, see [2, Section 4].
In fact, we can show that the fragment of Fine’s system that deals with partial ground coincides with Schnieder’s system interpreted as a system for partial ground.
Schnieder does not carry out the details himself. The proof is left to the interested reader.
A nice feature of our theory is that it proves all the instances of the T-scheme via the upward and downward directed axioms. We will show this in Section 4.2. The point is that the upward and downward directed axioms are intuitively motivated and on top of that they give us back the T-scheme.
Here s ≠ t, for terms s and t, is an abbreviation of ¬(s = t). Correspondingly, the notation \(s\underset {\cdot }{\neq }t\) is an abbreviation for the complex function term \(\underset {\cdot }{\neg }(s\underset {\cdot }{=}t)\), for terms s and t.
It is well-known that the theory of positive truth has the same theorems as the theory of compositional truth: Definition: The theory CT of compositional truth has the axioms of PAT, the two basic truth axioms T 1 and T 3 plus the following axioms:
-
C1 \(\forall x(Tr(\underset {\cdot }{\neg }x)\leftrightarrow \neg Tr(x))\)
-
C2 \(\forall x\forall y(Tr(x\underset {\cdot }{\lor }y)\leftrightarrow Tr(x)\lor Tr(y))\)
-
C3 \(\forall x\forall y(Tr(x\underset {\cdot }{\land }y)\leftrightarrow Tr(x)\land Tr(y))\)
-
C4 \(\forall v\forall x(Tr(\underset {\cdot }{\exists }vx)\leftrightarrow \exists t Tr(x(t/v)))\)
-
C5 \(\forall v\forall x(Tr(\underset {\cdot }{\forall }vx)\leftrightarrow \forall t Tr(x(t/v)))\)
For a proof of the equivalence of PT and CT, see [16, p. 120]. Note that the result depends on the fact that we start from the theory PAT in defining both PT and CT. The theories defined by the same axioms over PA as their base theory are not equivalent (see [16, p. 120]). In the following, we will often use well-known results about CT and apply them immediately to PT.
-
The unary predicate B e w P A strongly represents the set of codes of sentences provable in PA. Here we simply take it to be an abbreviation of the (long) defining formula for B e w.
Note that the translation of \(s\lhd t\) is in the same spirit as the translation of φ≺ψ in the proof of Proposition 1: while there we had \(\tau (\varphi \prec \psi )=\varphi \land \psi \land \underset {\cdot }{c}(\ulcorner \varphi \urcorner )~\underset {\cdot }{<}~\underset {\cdot }{c}(\ulcorner \psi \urcorner )\), we now have \(\tau (s\lhd t)=Tr(s)\land Tr(t)\land \underset {\cdot }{c}(s)~\underset {\cdot }{<}~\underset {\cdot }{c}(t)\). In the case of φ≺ψ we didn’t need to translate φ and ψ, since they were already assumed to be in \(\mathcal {L}\). Similarly, here we know that if \(\vdash _{PG}s\lhd t\), then by G3 and T3 we get that ⊢ P G T(s)∧T(t) and ⊢ P G S e n t(s)∧S e n t(t). In words, if \(s\lhd t\) is provable in PG, then it’s provable in PG that s and t are names of true sentences of \(\mathcal {L}\). It is effectively this limitation of PG to partial ground between truths of the language of arithmetic that enables us to prove the conservativity result.
For a definition of ACA, see [16, p. 107–8].
We can prove this result via the equivalence of PT and CT (see Fn 21 and the usual proof that CT has the same arithmetic theorems as ACA. For the details of this proof, see [16, p. 101–16 respectively]).
For this point it matters that we are talking about PT and not the equivalent theory CT. Since CT has the axiom \(\forall x(Tr(\underset {\cdot }{\neg }x)\leftrightarrow \neg Tr(x))\), where T r occurs negatively in the scope of a single negation, the theory paints a different truth-theoretic picture. According to CT, the truths are build up from less complex truths and falsehoods. The point here is that the truth-theoretic picture painted by a theory is highly sensitive to the concrete axiomatization of the theory: even though CT and PT are equivalent, they paint a different picture.
For a proof, see [16, p. 116–22].
The value of a term under an assignment is defined in the usual recursive way. In the following, we only need that the value ⟦x⟧ σ of a variable x under an assignment σ simply is σ(x).
Remember that a variable assignment σ′ is an \(\vec {x}\) variant of another variable assignment σ iff \({\sigma ^{\prime }}(\vec {x})=\sigma (\vec {x})\).
For more on non-standard models of theories of syntax and truth, see [16, p. 83–89].
Of course, the interpretation is not complete, in the sense that there are sentences \(\varphi ,\psi \in \mathcal {L}\) such that \(\vDash \varphi \prec \psi \) and ⊯ O G φ≺ψ. This follows from the argument given above in Section 4.2 for the failure of the converse direction of Proposition 3.
This follows immediately from Cantor’s theorem, which entails that the set \(\wp (\mathcal {L})\) of all sets of sentences of \(\mathcal {L}\) has a strictly bigger cardinality than \(\mathcal {L}\) itself. Note that the language \(\mathcal {L}\) of PA is countable, i.e. it has the same cardinality of as the natural numbers. Now assume that there is a coding function that injectively maps every set of sentence \({\Gamma }\subseteq \mathcal {L}\) to a unique code \(\#{\Gamma }\in \mathbb {N}\). This would mean that the cardinality of \(\wp (\mathcal {L})\) is less than or equal to the cardinality of \(\mathbb {N}\). But this would mean that the cardinality of \(\wp (\mathcal {L})\) is less than or equal to the cardinality of \(\mathcal {L}\), which is impossible. Thus there is no such coding function.
Another infinitary issue that pops up in the context of full ground is that Fine [13] argues that we need an infinitary totality (multigrade-)predicate T that applies to a sequence of terms t 1, t 2,… iff the denotations of t 1, t 2,… make up the domain of discourse. This predicate, so Fine, is needed to properly account for the full grounds of the truths of quantified statements. Once we’ve moved to a multigrade setting, accommodating such a predicate will be relatively straight-forward, but the step to multigrade predicates is, as we’ve just pointed out, non-trivial.
References
Bennett, K. (2011). By our bootstraps. Philosophical Perspectives, 25(1), 27–41.
Bliss, R., & Trogdon, K. (2014). Metaphysical grounding. In Zalta, E. N. (Ed.) The stanford encyclopedia of philosophy. Winter 2014.
Boolos, G., & et al. (2007). Computability and logic. Cambridge: Cambridge University Press.
Clark, M., & Liggins, D. (2012). Recent work on grounding. Analysis, 72(4), 812–23.
Correia, F. (2010). Grounding and truth-functions. Logique et Analyse, 53 (211), 251–279.
Correia, F. (2013). Logical grounds. Review of Symbolic Logic, 7(1), 31–59.
Correia, F., & Schnieder, B. (2012). Grounding. an opiniated introduction. In Correia, F., & Schnieder, B. (Eds.) Metaphysical grounding: understanding the structure of reality (pp. 1–36). Cambridge University Press.
Cresswell, M.J. (1975). Hyperintensional logic. Studia Logica, 34(1), 25–38.
deRosset, L. (2015). Better Semantics for the Pure Logic of Ground. forthcoming in Analytic Philosophy.
deRosset, L. (2013). Grounding explanations. Philosophers’ Imprint, 13(7), 1–26.
Derosset, L. (2014). On weak ground. Review of Symbolic Logic, 7(4), 713–744.
Fine, K. (1982). First-order modal theories III — facts. Synthese, 53(1), 43–122.
Fine, K. (2012). Guide to ground. In Correia, F., & Schnieder, B. (Eds.) Metaphysical grounding: understanding the structure of reality (pp. 37–80). Cambridge University Press.
Fine, K. (2010). Some puzzles of ground. Notre Dame Journal of Formal Logic, 51(1), 97–118.
Fine, K. (2012). The pure logic of ground. Review of Symbolic Logic, 5(1), 1–25.
Halbach, V. (2011). Axiomatic theories of truth, Cambridge University Press, Cambridge.
Jenkins, C.S. (2011). Is metaphysical dependence irreflexive? The Monist, 94(2), 267–276.
Krämer, S. (2013). A simpler puzzle of ground. Thought: A Journal of Philosophy, 2(2), 85–89.
Litland, J.E. (2015). Grounding, Explanation, and the Limit of Internality. forthcoming in Philosophical Review.
Litland, J.E. (forthcoming). Grounding grounding. Oxford studies in metaphysics.
Litland, J. (2013). On some counterexamples to the transitivity of grounding. Essays in Philosophy, 14(1), 19–32.
Litland, J.E. (2012). Topics in philosophical logic. Doctoral dissertation, harvard university. DASH: Digital access to scholarship at harvard. http://dash.harvard.edu/handle/1/9527318 (accessed May 13, 2015).
Oliver, A., & Smiley, T. (2004). Multigrade predicates. Mind, 113(452), 609–681.
Raven, M.J. (2015). Ground. Philosophy Compass, 10(5), 322–333.
Raven, M.J. (2013). Is ground a strict partial order? American Philosophical Quarterly, 50(2), 191–199.
Rosen, G. (2010). Metaphysical dependence: grounding and reduction. In Hale, B., & Hoffmann, A. (Eds.) Modality: metaphysics, logic, and epistemology (pp. 109–136). Oxford University Press.
Schaffer, J. (2012). Grounding, transitivity, and contrastivity. In Correia, F., & Schnieder, B. (Eds.) Metaphysical grounding: understanding the structure of reality (pp. 122–138). Cambridge University Press.
Schnieder, B. (2011). A logic for ‘because’. The Review of Symbolic Logic, 4(3), 445–465.
Trogdon, K. (2013). An introduction to grounding. In Holtje, M., Schnieder, B., & Steinberg, A. (Eds.) Varieties of dependence. Ontological dependence, grounding, supervenience, repsonse-dependence (pp. 97–122). Philosophia verlag.
Acknowledgments
I’d like to thank Hannes Leitgeb, Benjamin Schnieder, Albert Anglberger, Thomas Schindler, Lavinia Picollo, Johannes Stern, Martin Fischer, Tim Button, the participants of the workshop “Logical and Metaphysical Perspectives on Grounding” at the GAP.9 in Osnabrück, O. Foisch, and an anonymous referee for their helpful comments and suggestions. Part of this research was supported by the Alexander von Humboldt Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Korbmacher, J. Axiomatic Theories of Partial Ground I. J Philos Logic 47, 161–191 (2018). https://doi.org/10.1007/s10992-016-9423-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-016-9423-9




 is a grounding-tree
is a grounding-tree  is a grounding-tree over (N, S) with #¬¬φ as its root;
is a grounding-tree over (N, S) with #¬¬φ as its root; is a grounding-tree
is a grounding-tree  is a grounding-tree over (N, S) with #(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #(φ∨ψ) as its root; is a grounding-tree
is a grounding-tree  is a grounding-tree over (N, S) with #(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #(φ∨ψ) as its root; are grounding-trees
are grounding-trees  is a grounding-tree over (N, S) with #(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #(φ∧ψ) as its root;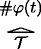 is a grounding-tree
is a grounding-tree  is a grounding-tree over (N, S) with #∃x
φ(x) as its root;
is a grounding-tree over (N, S) with #∃x
φ(x) as its root; , … are grounding-trees
, … are grounding-trees  is a grounding-tree over (N, S) with #∀x
φ(x) as its root;
is a grounding-tree over (N, S) with #∀x
φ(x) as its root; is a grounding-tree
is a grounding-tree 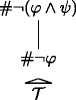 is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root; is a grounding-tree
is a grounding-tree 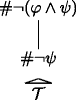 is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∧ψ) as its root; are grounding-trees
are grounding-trees  is a grounding-tree over (N, S) with #¬(φ∨ψ) as its root;
is a grounding-tree over (N, S) with #¬(φ∨ψ) as its root;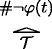 is a grounding-tree
is a grounding-tree  then is a grounding-tree over (N, S) with #¬∀x
φ(x) as its root;
then is a grounding-tree over (N, S) with #¬∀x
φ(x) as its root; , … are grounding-trees
, … are grounding-trees  is a grounding-tree over (N, S) with #∀x
φ(x) as its root;
is a grounding-tree over (N, S) with #∀x
φ(x) as its root; is a non-degenerate grounding-tree over (N, S). Moreover, the root of this tree is #¬¬φ and its only leaf is #φ. Now consider
is a non-degenerate grounding-tree over (N, S). Moreover, the root of this tree is #¬¬φ and its only leaf is #φ. Now consider