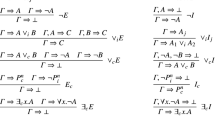A Gentzen Calculus for Nothing but the Truth

Abstract

In their paper Nothing but the Truth Andreas Pietz and Umberto Rivieccio present Exactly True Logic (ETL), an interesting variation upon the four-valued logic for first-degree entailment FDE that was given by Belnap and Dunn in the 1970s. Pietz & Rivieccio provide this logic with a Hilbert-style axiomatisation and write that finding a nice sequent calculus for the logic will presumably not be easy. But a sequent calculus can be given and in this paper we will show that a calculus for the Belnap-Dunn logic we have defined earlier can in fact be reused for the purpose of characterising ETL, provided a small alteration is made—initial assignments of signs to the sentences of a sequent to be proved must be different from those used for characterising FDE. While Pietz & Rivieccio define ETL on the language of classical propositional logic we also study its consequence relation on an extension of this language that is functionally complete for the underlying four truth values. On this extension the calculus gets a multiple-tree character—two proof trees may be needed to establish one proof.

A Signed Sequent Calculus for Exactly True Logic

In Belnap and Dunn’s well-known four-valued semantics for the logic of first-degree entailment FDE (Belnap [3, 4], Dunn [5]) the classical principles of Bivalence (every sentence is true or false) and Noncontradiction (no sentence is both true and false) are given up. This leads to four possible combinations of truth values, as sentences can now be either true and not false (T), false and not true (F), neither true nor false (N), or both true and false (B). These four combinations can be thought of as subsets of the set {1, 0} of classical truth values, so that T can be identified with {1}, F with {0}, N with $\varnothing$, and B with {1, 0}.

How can complex sentences be assigned one of these sets of truth values given the sets of truth values assigned to their parts? Dunn [5] gives the following very natural solution.

• i. ¬φ is true if and only if φ is false, ¬φ is false if and only if φ is true;

• ii. φ ∧ ψ is true if and only if φ is true and ψ is true, φ ∧ ψ is false if and only if φ is false or ψ is false;

• iii. φ∨ψ is true if and only if φ is true or ψ is true, φ∨ψ is false if and only if φ is false and ψ is false.

Suppose φ has the value T, i.e. φ is true and not false. Then Dunn’s condition i. tells us that ¬φ is false and not true, i.e. has the value F. Further reasoning along these lines leads to the following truth tables.

Definition 1

The following are truth tables for ¬, ∧, and ∨.

A more compact way to characterise the semantics of conjunction and disjunction in the Belnap-Dunn logic is to say that they correspond to meet and join in the following lattice, called L4 in [3, 4]. Negation corresponds to a top-bottom swap—leaving the other two values as they are.

Let us consider the language $\mathcal {L}_{t}$ of classical propositional logic based on {¬, ∧, ∨} and define valuations to be functions from the sentences of this language to {T, F, N, B} that respect the truth tables just given. The entailment relation of FDE can be defined as follows.

(1)

Here $\bigwedge$ denotes meet in the L4 lattice and ≤ _t denotes L4’s lattice ordering. This definition corresponds to the definition in [4]. A second definition, which proceeds by letting T and B be designated truth values, is as follows, but produces the same result.

(2)

That these two definitions indeed characterise the same notion can easily be shown on the basis of the observation that every valuation V comes with a dual V ^′ such that, for all φ, V(φ) = V ^′(φ) if V(φ)∈{T, F}, while V(φ) = N iff V ^′(φ) = B, and, vice versa, V(φ) = B iff V ^′(φ) = N. Details are left to the reader.

In a recent paper Andreas Pietz and Umberto Rivieccio ([12], henceforth P&R) remark that it is a curious feature of the Belnap-Dunn logic that B is a designated value. Prima facie, the authors remark, it seems more plausible to have only T designated. P&R then investigate the effect of defining entailment in terms of preservation of T only, while the rest of the four-valued semantics sketched above remains as is. More formally, the relation is replaced by a relation defined as follows.

(3)

The logic that is obtained in this way is called Exactly True Logic (ETL).

P&R also provide a Hilbert-style axiomatisation of ETL, which they obtain by adding a single rule (corresponding to disjunctive syllogism) to Font’s [7] Hilbert-style axiomatisation of FDE. Hence, ETL extends FDE and in particular ETL does, while FDE does not, validate ex contradictione quodlibet. However, as P&R point out, although

(4)

it is not the case that

(5)

Regarding this somewhat unusual feature, which they call anti-primeness, P&R make the following remark.

Presumably, this will not make it easy to find a nice sequent calculus for this logic. [12, p129]

As the authors further point out [12, p130], in particular sequent calculi that enjoy cut-elimination and the subformula property qualify as nice.

But in fact an analytic and cut-free sequent calculus that can characterise ETL already exists, be it that a small modification must be made in order to tailor it to this logic. In Wintein & Muskens [16] we have given a calculus whose rules (restricted to the {∧, ∨, ¬} fragment of the logic considered there) are essentially those of the $\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ calculus presented in Definition 2 below.¹ The calculus is based on four-sided sequents,² but instead of writing sequents as 4-tuples Γ₁∣Γ₂∣Γ₃∣Γ₄ of sets of sentences, we represent them in an equivalent but more convenient way as finite sets of signed sentences x : φ, where x ranges over a set of four signs and φ is a sentence of $\mathcal {L}_{t}$.

The four signs we will use are 1, $\mathsf {\overline {1}}$, 0, and $\mathsf {\overline {0}}$. While their role in the sequent calculus is purely syntactic, they also have an informal interpretation that is obtained by letting 1 correspond to {T, B}, $\mathsf {\overline {1}}$ to {F, N}, 0 to {F, B}, and $\mathsf {\overline {0}}$ to {T, N}, i.e. 1 : φ can be read as ‘ φ is true’ (or, ‘1 is an element of the value of φ’), $\mathsf {\overline {1}}:\varphi$ as ‘ φ is not true’ (‘1 is not an element of the value of φ’), 0 : φ as ‘ φ is false’, and $\mathsf {\overline {0}}:\varphi$ as ‘ φ is not false’.

Definition 2 ($\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ calculus)

All instantiations of the following rule schemes are sequent rules.

$$\begin{array}{ll} \frac{}{\Sigma,\mathsf{x}:\varphi,~ \mathsf{y}:\varphi}(R)& \qquad\frac{\Sigma,\ \mathsf{y}:\varphi} {\Sigma,\ \mathsf{x}:\lnot\varphi}(\lnot)\\ \text{if }\langle\mathsf{x},\mathsf{y}\rangle\in \{\langle\mathsf{1},\mathsf{\overline{1}}\rangle,\langle\mathsf{0},\mathsf{\overline{0}}\rangle\} &\qquad \text{if } \langle\mathsf{x},\mathsf{y}\rangle\text{ or }\langle\mathsf{y},\mathsf{x}\rangle\in \{\langle\mathsf{1},\mathsf{0}\rangle,\langle\mathsf{\overline{1}},\mathsf{\overline{0}}\rangle\} \\ \frac{\Sigma,\mathsf{x}:\varphi,~ \mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\land\psi}(\land^{1}) & \qquad\frac{\Sigma,~ \mathsf{x}:\varphi\qquad {\Sigma},~ \mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\land\psi}(\land^{2})\\ \text{if }\mathsf{x}\in\{\mathsf{1},\mathsf{\overline{0}}\} & \qquad\text{if }\mathsf{x}\in\{\mathsf{\overline{1}},\mathsf{0}\} \\ \frac{\Sigma,~ \mathsf{x}:\varphi,~ \mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\lor\psi}(\lor^{1})& \qquad\frac{\Sigma,~ \mathsf{x}:\varphi\qquad {\Sigma},~ \mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\lor\psi}(\lor^{2})\\ \text{if }\mathsf{x}\in\{\mathsf{\overline{1}},\mathsf{0}\} & \qquad\text{if } \mathsf{x}\in\{\mathsf{1},\mathsf{\overline{0}}\} \end{array} $$

A derivation, or proof attempt, for a sequent Θ is a tree of sequents, with Θ at the root, such that each sequent on the tree follows from the ones above it by one of the rules. A proof attempt is a proof tree if it is finite and all its leaves can be obtained by an application of rule (R). A sequent Θ is provable if it is at the root of (i.e. is the end sequent of) a proof tree.

It is worth noticing that there is a tight connection between the rules for connectives presented here and Dunn’s evaluation scheme mentioned above. For example rule (∧²) corresponds to the rule that φ ∧ ψ is false (not true) iff φ is false (not true) or ψ is false (not true). Other rule schemes here can be explained similarly. The following is an example of a sequent proof obtained using the $\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ calculus.

Example 1

For any φ and ψ, the sequent $\{\mathsf {1}:\varphi \land \lnot \varphi ,~\mathsf {\overline {0}}:\varphi \land \lnot \varphi ,~ \mathsf {\overline {1}}:\psi \}$ is provable:

And here is an example of a (failed) proof attempt. We will use this and the previous example for an analysis of the anti-primeness of ETL a bit further on.

Example 2

The following is a proof attempt for $\mathsf {1}: p \land \lnot p ,~\mathsf {\overline {0}}: q \land \lnot q ,~\mathsf {\overline {1}}: r$.

An easy but useful lemma shows that there is a duality between truth and non-falsity and between falsity and non-truth in this calculus.

Lemma 1

Let Θ and Θ ^′ be $\mathcal {L}_{t}$ sequents that are $\mathsf {1}\overline {\mathsf {0}}$ -isomorphisms, i.e.:

$$\begin{array}{ll} \mathsf{1} : \varphi \in {\Theta} \Leftrightarrow \mathsf{\overline{0}} : \varphi \in {\Theta}^{\prime} &\qquad \mathsf{\overline{1}} : \varphi \in {\Theta} \Leftrightarrow\mathsf{0} : \varphi \in {\Theta}^{\prime}\\ \mathsf{0} : \varphi \in {\Theta} \Leftrightarrow\mathsf{\overline{1}} : \varphi \in {\Theta}^{\prime} & \qquad \mathsf{\overline{0}} : \varphi \in {\Theta}\Leftrightarrow \mathsf{1} : \varphi \in {\Theta}^{\prime} \end{array} $$

Then Θ is provable if and only if Θ ^′ is provable.

Proof

By an inspection of the sequent rules. □

Let us turn to the connection between the calculus $\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ and the semantics of the logic. The following definition makes the informal interpretation of the four signs given above explicit by connecting sequents and the valuations refuting them.

Definition 3

Let V be a valuation and let Σ be a sequent. V refutes Σ if, for all φ,

$$\begin{array}{ll} \mathsf{1}:\varphi\in{\Sigma} \Rightarrow 1\in V(\varphi) &\qquad \mathsf{\overline{1}}:\varphi\in{\Sigma} \Rightarrow 1\notin V(\varphi)\\ \mathsf{0}:\varphi\in{\Sigma} \Rightarrow 0\in V(\varphi) &\qquad \mathsf{\overline{0}}:\varphi\in{\Sigma} \Rightarrow 0\notin V(\varphi). \end{array} $$

A signed sequent is refutable if some valuation refutes it; irrefutable if none does.

The next observation fleshes out the tight connection between the $\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ calculus and the Belnap-Dunn truth conditions a bit further.

Lemma 2

For every instantiation of a rule scheme, the bottom sequent is refuted by a valuation V iff one of the top sequents is refuted by V. In case of the (R) rule, which has no top sequents, this boils down to the statement that its bottom sequent is irrefutable.

Proof

By inspection of each of the rule schemes. □

This brings us to the completeness theorem. It already follows from the results in [10] and [16], but for the convenience of the reader we provide a short direct proof here.

Theorem 1 (Soundness, Completeness)

A sequent is provable iff it is irrefutable.

Proof

The ⇒ direction follows easily by an induction on proof depth plus the observation in Lemma 2. For the ⇐ direction, assume that Θ is not provable. We use induction on the total number n of connectives occurring in Θ. If n = 0, Θ is a set of signed propositional constants that is not a conclusion of the (R) rule. This means that Θ does not contain a pair 1 : α, $\mathsf {\overline {1}}:\alpha$, or a pair 0 : α, $\mathsf {\overline {0}}:\alpha$. The valuation V such that 1 ∈ V(α)⇔1 : α ∈ Θ and 0 ∈ V(α)⇔0 : α ∈ Θ, for all propositional constants α, refutes Θ.

If n > 0, Θ can be written as a sequent Σ, 𝜃, where 𝜃 is some signed sentence containing at least one connective and 𝜃 ∉ Σ. Inspection of the rules shows that in this case Θ follows from a sequent Θ₁ or from a pair of sequents Θ₁ and Θ₂, each containing fewer than n connectives. One of these top sequents must be unprovable and hence, by induction, refuted by some valuation V. Lemma 2 gives that Θ is refuted by the same V. We conclude that a sequent is refutable if it is unprovable. □

Remark 1

The completeness part of this proof in fact interprets the calculus as a model search procedure. For example, in order to refute

$$\mathsf{1}: p \land\lnot p ,\mathsf{\overline{0}}: q \land\lnot q ,\mathsf{\overline{1}}: r , $$

build a proof attempt as in Example 2, inspect the topmost sequent, and use it to find a V with V(p) = B, V(q) = N, and V(r) = N.

The $\mathbf {PL}_{\mathbf {4}}^{\mathbf {t}}$ calculus can be used to give proof-theoretic characterisations of more than one logic. For example, a syntactic consequence relation for FDE can be defined as follows.

(6)

Since it is easy to see that iff $\{\mathsf {1}:\gamma \mid \gamma \in {\Gamma }\} \cup \{\mathsf {\overline {1}}:\varphi \}$ is irrefutable, it follows from Theorem 1 that the syntactic and semantic entailment relations of FDE correspond.

Proposition 1

.

But other logics are characterisable as well. The calculus also provides a syntactic characterisation of ETL if initial assignments of signs to formulas are altered, as in the following definition.

(7)

At first blush it may seem that a stronger definiens is needed here, since irrefutability of $\{\mathsf {1}:\gamma \mid \gamma \in {\Gamma }\}\cup \{\mathsf {\overline {0}}:\gamma \mid \gamma \in {\Gamma }\} \cup \{\mathsf {\overline {1}}:\varphi \}$ only seems to correspond to the impossibility of all γ ∈ Γ getting the value T while the value of φ is F or N (and thus not excluding φ having the value B), but it follows from Lemma 1 and the definition in Eq. 7 that the following equivalence holds.

(8)

Completeness for ETL easily follows from Eqs. 7, 8 and Theorem 1.

Proposition 2

.

Let us analyse the anti-primeness of the logic ETL a bit further. In view of Example 1, we have that . Note that the proof in Example 1 rests on having signed sentences of the forms 1 : φ∧¬φ and $\mathsf {\overline {0}}:\varphi \land \lnot \varphi$ in a single sequent. In a proof attempt for

this feature gets lost in some branches of the attempted proof. More in particular, starting with the end sequent

$$\mathsf{1}:(p \land\lnot p )\lor(q \land\lnot q ),~\mathsf{\overline{0}}:(p \land\lnot p )\lor(q \land\lnot q ),~\mathsf{\overline{1}}: r, $$

three applications of (∨²) bring us to the following sequents that must all be proven.

$$\begin{array}{@{}rcl@{}} \mathsf{1}: p \land\lnot p ,~\mathsf{\overline{0}}: p \land\lnot p ,~\mathsf{\overline{1}}: r\\ \mathsf{1}: p \land\lnot p ,~\mathsf{\overline{0}}: q \land\lnot q ,~\mathsf{\overline{1}}: r\\ \mathsf{1}: q \land\lnot q ,~\mathsf{\overline{0}}: p \land\lnot p ,~\mathsf{\overline{1}}: r\\ \mathsf{1}: q \land\lnot q ,~\mathsf{\overline{0}}: q \land\lnot q ,~\mathsf{\overline{1}}: r \end{array} $$

The first and the last of these are provable as in Example 1, but an attempt to prove the second (or third) sequent leads to failure, as Example 2 shows, and the refuting valuation V defined by V(p) = B, V(q) = N, and V(r) = N also refutes the end sequent.

A natural first reaction to the anti-primeness of ETL might be to assume that the feature must be due to the fact that disjunction has an unusual meaning in the logic. In particular it may seem that ETL must assign a different meaning to ∨ than FDE does, as the latter is not anti-prime. We do not think that this is a correct analysis of the phenomenon, however. What is it that determines the meaning of a logical connective? Two traditional answers suggest themselves: truth conditions and inferential rules. But the truth conditions of ∨ are the same in the two logics and correspond to join in the L4 lattice, while the inferential rules are likewise the same in our analysis—they are given by the (∨¹) and (∨²) rules.

The only point where ETL and FDE differ is in their definitions of entailment³—FDE takes T and B as designated values, while ETL uses only T. It is this feature, we like to argue, that is solely responsible for the difference in behaviour.⁴

Adding Expressivity

ETL was defined in terms of a consequence relation on the language of classical propositional logic $\mathcal {L}_{t}$, but as is well known this language cannot express all truth functions on 4:={T, B, N, F}. In this section we will consider extensions of ETL to more expressive languages, one containing an extra implication and one that is functionally complete. We will also consider some extensions of FDE to the functionally complete language and compare the logics thus defined.

Adding an Appropriate Implication Connective

A first consequence of the lack of expressive power provided by {¬, ∧, ∨} is that there are no ETL tautologies and hence that no implication connective is definable in $\mathcal {L}_{t}$ that allows ETL to enjoy a deduction theorem. Restricted as it is to $\mathcal {L}_{t}$, ETL does not have what Arieli and Avron [1] call an appropriate implication connective, i.e. a connective → that corresponds to ETL entailment in the following sense.

(9)

It should be noted though, that the right-to-left direction of Eq. 9—expressing a resolution theorem—is satisfied for the connective $\rightsquigarrow$, where $\varphi \rightsquigarrow \psi := \neg \varphi \vee \psi$. Indeed, this follows immediately from the observation that α, , i.e. that modus ponens is valid in ETL.⁵

The fact that $\mathcal {L}_{t}$ does not allow for an appropriate implication connective provides a motivation⁶ to consider an extension of $\mathcal {L}_{t}$. Let $\mathcal {L}^{\supset }_{t}$ be the result of extending $\mathcal {L}_{t}$ with the connective ⊃, whose semantics is given by the following truth table.

Definition 4

The following is the truth table for ⊃.

Thus, φ⊃ψ takes the value of ψ whenever φ is T, and takes value T otherwise. An $\mathcal {L}_{t}^{\supset }$ valuation is a function from the sentences of $\mathcal {L}_{t}^{\supset }$ to 4 that respects the truth tables given in Definitions 6 and 4. Let us write V ^⊃ for the set of all $\mathcal {L}_{t}^{\supset }$ valuations. By quantifying over V ^⊃, the ETL consequence relation for $\mathcal {L}_{t}$ can be extended to one for $\mathcal {L}_{\supset }$.

(10)

That the connective ⊃ indeed is an appropriate implication connective for and satisfies modus ponens is attested by the following proposition.

Proposition 3

The following relations hold.

Proof

By inspection. □

Let us also give a syntactic characterisation of this entailment relation. It can be done by first adding rules for ⊃ to the signed sequent calculus.

Definition 5 ($\mathbf {PL}_{\mathbf {4}}^{\supset }$ calculus)

All instantiations of the rule schemes given in Definition 2 are $\mathbf {PL}_{\mathbf {4}}^{\supset }$ sequent rules. In addition, all instantiations of the following two rule schemes are $\mathbf {PL}_{\mathbf {4}}^{\supset }$ sequent rules.

$$\begin{array}{ll} \frac{\Sigma,~\mathsf{1}:\varphi,~\mathsf{\overline{0}}:\varphi,~\mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\supset\psi}(\supset^{1}) &\qquad\frac{\Sigma,~\mathsf{0}:\varphi\qquad {\Sigma},~\mathsf{\overline{1}}:\varphi\qquad {\Sigma},\ \mathsf{x}:\psi}{\Sigma,~\mathsf{x}:\varphi\supset\psi}(\supset^{2})\\ \text{if }\mathsf{x}\in\{\mathsf{\overline{1}}, \mathsf{0}\} &\qquad \text{if }\mathsf{x}\in\{\mathsf{1},\mathsf{\overline{0}}\} \end{array} $$

The definitions of derivation, proof tree, and provability of a signed sequent given in Definition 2 are extended in the obvious way.

Inspection of these rule schemes shows that Lemma 2 can in fact be extended to them and that the completeness theorem (Theorem 1) therefore also extends to the present more expressive setting. Moreover, it is easy to verify that Lemma 1 continues to hold, so that the entailment relation for the richer logic can be defined as follows.

(11)

And again Theorem 1 leads to completeness.

Proposition 4

.

A Functionally Complete Extension

Adding ⊃ to ETL turned out to be plain sailing. What about other connectives? ETL also lacks a strong negation connective and a connective expressing that two sentences are logically equivalent, so one may consider adding those and other operators as well. We will add all possible operators in one fell swoop and define a functionally complete extension $\mathcal {L}_{ti}$ (the t is for ‘truth’, the i for ‘information’) of $\mathcal {L}_{t}$, studying ETL entailment on it. This mirrors a move in the literature, where FDE consequence has been studied on functionally complete extensions of $\mathcal {L}_{t}$ (see e.g. Muskens [9, 10], Arieli and Avron [2], Ruet [15], Pynko [13], or Omori and Sano [11]).

The language $\mathcal {L}_{ti}$ we consider is defined by the following BNF.

$$\varphi ::= p\mid\lnot\varphi\mid-\varphi\mid \varphi\land\varphi\mid\varphi\otimes\varphi \mid \varphi \vee \varphi \mid \varphi \oplus \varphi $$

The truth tables of the connectives −, ⊗ and ⊕ introduced here are given by the following definition.

Definition 6

The following are truth tables for the $\mathcal {L}_{ti}$ connectives −, ⊗ and ⊕.

An $\mathcal {L}_{ti}$ valuation is a function from the sentences of $\mathcal {L}_{ti}$ to 4 that respects the above truth tables and those of ¬,∧ and ∨ as given by Definition 1. From this point on V will range over $\mathcal {L}_{ti}$ valuations.

That {∧, ∨, ¬, ⊗, ⊕, −} is indeed functionally complete with respect to all truth functions over 4 is shown in Muskens [9].⁷ One example of a connective that can be defined in $\mathcal {L}_{ti}$ is ⊃, whose truth table was given by definition 4.

$$\varphi \supset \psi := \lnot(\varphi\land-\varphi)\lor\psi $$

Clearly there are several sets of connectives that are functionally complete for 4, but the ones considered here form a natural collection from an algebraic point of view. While ∧ and ∨ correspond to meet and join in the (logical) lattice L4, ⊗ and ⊕ correspond to meet and join in the following ‘approximation of information’ lattice A4. The lattice A4 also plays a fundamental role in Belnap-Dunn logic (cf. [3, 4]).

Furthermore, while ¬ corresponds to a top-bottom swap in L4, − corresponds to a top-bottom swap in A4. Thus, ⊗, ⊕ and − are dual to ∧, ∨ and ¬ in a sense that is aptly explained by referring to the lattices L4, associated with the “truth order on 4” and A4, associated with the “information order on 4”.

Let us have a look at extensions of the FDE relation of entailment before we study ETL entailment on the extended language. The algebraic structure F O U R ⁻ := 〈4, ∧, ∨, ¬, ⊗, ⊕, −〉⁸ is an example of what Fitting [6] calls a bilattice with conflation (where − is a conflation operator) and the pair 〈F O U R ⁻,{T, B}〉 is an example of what Arieli and Avron [1] call an ultralogical bilattice. Arieli and Avron observe that the consequence relation for $\mathcal {L}_{ti}$ that is based on the class of all ultralogical bilattices is equivalent to the following consequence relation that is only based on the ultralogical bilattice 〈F O U R ⁻, {T, B}〉.⁹

(12)

In view of Eq. 2 above this notion of entailment, based on preservation of truth, is clearly an extension of . But it should be pointed out that the equivalence between the right hand sides of Eqs. 1 and 2 no longer holds after our move to $\mathcal {L}_{ti}$. The entailment relation that is defined as follows (with ≤ _t still the ordering in the L4 lattice) is also an extension of the FDE entailment relation, but it is distinct from the one defined in Eq. 12.

(13)

That the two relations are no longer coextensional in the new setting is because the elements of 4 have become definable. Let p be some arbitrary propositional constant and define t as ¬p∨−p and b as −(¬p⊗−p). It is easily seen that, for each V, V(t) = T and V(b) = B. So we have that , while is clearly not the case.

There is an obvious dual to the entailment relation given in Eq. 12 that is based on the preservation of non-falsity.

(14)

This relation is distinct from each of the relations defined in Eqs. 12 and 13, as the reader can easily verify. But the following holds.

(15)

Proof

Note that a ≤ _t b iff a ∈ {T, B} ⇒ b ∈ {T, B} and a ∈ {T, N} ⇒ b ∈ {T, N} both hold. □

The expressibility of B and N in $\mathcal {L}_{ti}$ depends on the presence of ⊗ or ⊕ and it are these connectives that make and come apart. The two relations are coextensional on the {¬, ∧, ∨, −} fragment of $\mathcal {L}_{ti}$.

Proposition 5

Let φ be a sentence of $\mathcal {L}_{ti}$ that only contains the connectives ∧, ∨, ¬ and − and let Γ be a set of such sentences. Then .

Proof

For any valuation V, let V ^′ be the unique valuation such that, for all propositional constants p, V ^′(p) = V(−p) (V ^′ is the valuation we have earlier called the dual of V). By inspection of the truth tables it is easily seen that, for any φ in the {¬,∧,∨,−} fragment of the language, V ^′(φ) = V(−φ). This means that if V is a counterexample to , V ^′ is a counterexample to and vice versa. □

So which of the three entailment relations for extended FDE considered above is the ‘right’ one? Our vote goes to for reasons of symmetry and because it is based on the L4 lattice that is so central to the logic. A definition based on L4 is also the one explicitly endorsed by Belnap [3, 4] for standard FDE.¹⁰ (See also [10, 16]).

Let us consider ETL again. Only one option presents itself when extending its entailment relation to the functionally complete language—the one in line with the definitions in Eqs. 3 and 10.

(16)

Comparing this relation with the previous ones, we see that it includes but not the other two.

Proposition 6

The following relations hold.

Proof

The first claim follows from an inspection of the definitions. The second from the observation that but not . The third from the fact that but not , where n is defined as −b. □

Readers familiar with Arieli and Avron [1] will be interested to verify that the pair 〈F O U R ⁻,{T}〉, which induces , is not an ultralogical bilattice (the reason being that the constraint a∨b ∈ {T} ⇔ a ∈ {T} or b ∈ {T} is violated). This means that Arieli and Avron’s sequent calculus for ‘ultralogical bilattice logic’ does not characterise .

All consequence relations discussed until now can be captured syntactically by the P L ₄ calculus below, which is (a notational variant of) the propositional part of the calculus considered in [16]. Sequents are redefined in the obvious way—as sets of pairs x : φ, where x is a sign and φ now is an $\mathcal {L}_{ti}$ sentence.

Definition 7 (P L ₄ calculus)

All instantiations of the rule schemes (R), (¬), (∧¹), (∧²), (∨¹) and (∨²) of Definition 2 are P L ₄ sequent rules. In addition, all instantiations of the following five rule schemes are P L ₄ sequent rules.

$$\begin{array}{ll} \frac{\Sigma,~ \mathsf{y}:\varphi} {\Sigma,~\mathsf{x}:-\varphi}(-) &\qquad \\ \text{if }\langle\mathsf{x},\mathsf{y}\rangle\text{ or }\langle\mathsf{y},\mathsf{x}\rangle\in \{\langle\mathsf{1},\mathsf{\overline{0}}\rangle,\langle\mathsf{\overline{1}},\mathsf{0}\rangle\}&\qquad \\ \frac{\Sigma,~\mathsf{x}:\varphi,~ \mathsf{x}:\psi}{\Sigma,~ \mathsf{x}:\varphi\otimes\psi}(\otimes^{1}) & \qquad\frac{\Sigma,~\mathsf{x}:\varphi\qquad {\Sigma},~ \mathsf{x}:\psi}{\Sigma,~\mathsf{x}:\varphi\otimes\psi}(\otimes^{2})\\ \text{if }\mathsf{x}\in\{\mathsf{1},\mathsf{0}\} & \qquad\text{if }\mathsf{x}\in\{\mathsf{\overline{1}},\mathsf{\overline{0}}\}\\ \frac{\Sigma,~\mathsf{x}:\varphi,~ \mathsf{x}:\psi}{\Sigma,~\mathsf{x}:\varphi\oplus\psi}(\oplus^{1}) & \qquad\frac{\Sigma,~\mathsf{x}:\varphi\qquad {\Sigma},~ \mathsf{x}:\psi}{\Sigma,~\mathsf{x}:\varphi\oplus\psi}(\oplus^{2})\\ \text{if }\mathsf{x}\in\{\mathsf{\overline{1}},\mathsf{\overline{0}}\} & \qquad\text{if }\mathsf{x}\in\{\mathsf{1},\mathsf{0}\} \end{array} $$

The definitions of derivation, proof tree, and provability of a signed sequent given in Definition 2 are extended in the obvious way again.

The good news at this point is that Theorem 1 generalises to the present setting. If Definition 3 is generalised in the obvious way, inspection of the additional rule schemes presented above will tell that Lemma 2 still goes through, so that the proof of Theorem 1 can remain unchanged.

Let us define the following syntactic relations.

These relations indeed characterise the entailment relations they were meant to.

Proposition 7

, ,

Proof

From Theorem 1, the equivalence in Eq. 15, and the relevant definitions. □

Note that showing that will now in general require two proof trees, one for preservation of truth, the other for preservation of non-falsity. For ETL it will also be the case that two proof trees are required, as Lemma 1 cannot be extended to a language containing ⊗ or ⊕. The following definition gives the right notion.

And again we have:

Proposition 8

Proof

Using Theorem 1. □

Conclusion

We have given a characterisation of Pietz and Rivieccio’s [12] Exactly True Logic by means of (a notational variant of a fragment of) the analytic and cut-free signed sequent calculus presented in [16]. This calculus was originally devised in order to characterise a generalisation of the logic of first-degree entailment in a functionally complete language. That it can also be used for ETL rests on the fact that there is some leeway in mapping unsigned sequents to the signed sequents that need to be proved. One signed calculus can therefore model more than one logic.

The anti-primeness of ETL, the fact that, as Pietz and Rivieccio observe, Eq. 5 does not hold while Eq. 4 does, will only be a stumbling-block for characterising the logic if it is insisted upon that the calculus for doing that is a traditionally two-sided (or two-signed) one. Our proofs for ETL are based upon a four-signed calculus in which premises are marked with two distinct signs. In this set-up all mystery about why and have proofs while Eq. 5 leads to a failed proof attempt and hence to refutability has disappeared.

We have also extended ETL to a functionally complete language and have compared it with FDE in this setting. Proving ETL consequence in the presence of the ‘consensus’ operator ⊗, or its ‘gullibility’ dual ⊕, in general requires the development of two proof trees in our system, as does proving FDE entailment in this context.