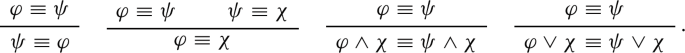Abstract
When do two sentences say the same thing, that is, express the same content? We defend two-component (2C) semantics: the view that propositional contents comprise (at least) two irreducibly distinct constituents: (1) truth-conditions and (2) subject-matter. We contrast 2C with one-component (1C) semantics, focusing on the view that subject-matter is reducible to truth-conditions. We identify exponents of this view and argue in favor of 2C. An appendix proposes a general formal template for propositional 2C semantics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
‘Jane is a lawyer’ says something about Jane’s profession, that is true just in case she is a lawyer. So one way to model the content of a meaningful declarative sentence \(\varphi \) is as a pair \( \langle \texttt{T}_\varphi , \texttt{S}_\varphi \rangle \): \(\texttt{T}_\varphi \) denotes the Truth conditions of \(\varphi \), determining the circumstances under which \(\varphi \) is true (and under which \(\varphi \) is false, if the latter are to be specified independently); \(\texttt{S}_\varphi \) denotes the Subject-matter of \(\varphi \), determining the topics that \(\varphi \) is about.Footnote 1 A growing literature incorporates topicality or subject matters into semantic/logical theory (see Epstein, 1990, Ch. 3; Burgess, 2009, Ch. 5; Yablo, 2014, Ch. 2; Berto, 2022, Ch. 2). Consensus is yet to emerge on how best to characterize these: Lewis (1988a), Yalcin (2011), Hawke (2018), and Plebani and Spolaore (2021) understand a subject-matter as a set of distinctions, determining a question; Yablo (2014) and Fine (2016a) as a collection or aggregate of possible truthmakers or falsemakers; Perry (1989) as a set of possible objects; Levesque and Lakemeyer (2000, Ch. 11) as a set of atomic sentences.
But is it essentially redundant to represent propositional contents in this twofold way? Do truth-conditions determine subject-matter? Does subject-matter determine truth-conditions? Or are these aspects of meaning irreducible to each other? To make the issue more precise, consider:
-
1C: Either,
-
\(\texttt{T}\Rightarrow \texttt{S}\): for all \(\varphi \) and \(\psi \), \(\texttt{T}_\varphi = \texttt{T}_\psi \) only if \(\texttt{S}_\varphi = \texttt{S}_\psi \),
-
or,
-
\(\texttt{S}\Rightarrow \texttt{T}\): for all \(\varphi \) and \(\psi \), \(\texttt{S}_\varphi = \texttt{S}_\psi \) only if \(\texttt{T}_\varphi = \texttt{T}_\psi \).
-
That is, either (\(\texttt{T}\Rightarrow \texttt{S}\)) there is a function f such that \( \texttt{S}_\varphi = f(\texttt{T}_\varphi )\) for every interpreted \(\varphi \), or (\(\texttt{S}\Rightarrow \texttt{T}\)) there is an f such that \( \texttt{T}_\varphi = f(\texttt{S}_\varphi )\) for every interpreted \(\varphi \). We use ‘2C’ for the denial of 1C. We call a compositional semantics—a recursive procedure for assigning contents to sentences—a one-component semantics if it entails 1C. A two-component semantics entails 2C.
We can dispatch \(\texttt{S}\Rightarrow \texttt{T}\) quickly. As Yablo (2014, Sect. 2.8) remarks, the following seems a simple counter-example:
-
(1)
Jane is a lawyer.
-
(2)
Jane is not a lawyer.
(1) and (2) seem to be about exactly the same thing(s): Jane and her profession. They differ in truth-conditions but not subject-matter.
\(\texttt{T}\Rightarrow \texttt{S}\), instead, has momentum. A prominent tradition in formal semantics, following Lewis (1970) and Montague (1974), focuses solely on truth-conditions; when motivated explicitly, appeal is typically made to the view that truth-conditions exhaust propositional content (Wittgenstein, 1974; Cresswell, 1985; Heim & Kratzer, 1997).Footnote 2 Even rival traditions (e.g., dynamic semantics) typically identify propositional content with the set of truth-supporting circumstances at which the proposition is true (Stalnaker, 1984). Lewis (1988a) and Partee (1989) argue explicitly that the subject-matter of a claim is fixed by the set of possible worlds (i.e., complete and comprehensive possible truth-supporting circumstances) at which it is true; Perry (1989) takes issue with this, but his remedy is to incorporate partial states into the space of truth-supporting circumstances. Thus, content is still identified with the circumstances at which it is true.
More recently, 2C theories are ascendant. Yablo (2014, p. 2) aims for a view that “makes subject-matter an independent factor in meaning, constrained but not determined by truth-conditions”. Hawke (2016, 2018), Plebani and Spolaore (2021) and Hoek (2022) offer 2C modifications of Lewis (1988a). The triplet Ferguson (2023a, b, c) develops an abstract 2C account proposed by two of us—PH and FB—in Berto (2022) and applies it to a variety of topics in modal and epistemic logic. Hawke et al. (2020) apply it to the logic of ordinary knowledge ascription (tackling the problem of logical omniscience). Özgün and Schoonen (2022) apply it to the logic of imagination episodes. Berto and Hornischer (2023) use it to provide an account of cognitive synonymy.
What, if anything, recommends 2C theories over \(\texttt{T} \Rightarrow \texttt{S}\) style 1C theories? We argue against \(\texttt{T} \Rightarrow \texttt{S}\) using minimal resources, then unify the case against 1C. Along the way, we separate the wheat from the chaff: we explicate two prominent (though typically implicit) arguments against \(\texttt{T} \Rightarrow \texttt{S}\), each of which, we argue, the \(\texttt{T} \Rightarrow \texttt{S}\) theorist has the resources to challenge. Our preferred argument against \(\texttt{T} \Rightarrow \texttt{S}\) appeals only to features rooted in pre-theoretic intuition and widely deployed by prior theorists: we take truth-conditions to be intimately related to logical properties, we take a conjunction to include the subject-matter of its conjuncts, and we take the subject-matter of a valid conclusion to sometimes outstrip that of its premises. To unify the case against 1C, we subsume both our case against \(\texttt{T} \Rightarrow \texttt{S}\) and the Yablovian case against \(\texttt{S} \Rightarrow \texttt{T}\) under a broader argument. We call it the argument from transparency.
We stay as neutral as possible on the nature of truth-conditions, topicality, and content. We leave it open whether truth-conditions should be formulated in terms of complete or partial states; whether a refined 1C theorist or 2C theorist ought to embrace further components to content (Fregean senses, presuppositional content), or two-dimensionalism à la Chalmers (2011); whether content has an underlying, unified structure which generates both truth-conditions and subject-matter.
Thus, 1C should not be confused with the stronger view that content is identical to truth-conditions, let alone the specific interpretation of these as given by a set of metaphysically possible worlds (Stalnaker, 1984). 2C should not be confused with the neo-Russellian view that a propositional content has structure that largely reflects the syntax of declaratives that can express it (Soames, 1987). Neo-Russellianism per se is consistent with 1C, if the subject-matter of \(\varphi \) is identified with the Russellian proposition \(\varphi \) expresses, with truth-conditions treated as derivative. It is also consistent with 2C, if a Russellian proposition generates both subject-matter and truth-conditions, but shouldn’t be identified with either.
We proceed as follows. Section 2 fixes our assumptions about truth-conditions and subject-matter. Section 3 presents a first argument against \(\texttt{T} \Rightarrow \texttt{S}\) that invites a pointed response: the argument from topic-divergent necessities. Section 4 presents a second argument against \(\texttt{T} \Rightarrow \texttt{S}\) that invites a pointed response: the argument from Yablo’s thesis. Section 5.1 presents our preferred criticism of \(\texttt{T} \Rightarrow \texttt{S}\); Sect. 5.2 criticizes on its basis specific \(\texttt{T} \Rightarrow \texttt{S}\) approaches found in the literature. Section 6 draws on the apparent topic-transparency of the connectives to broaden our case, targeting 1C in general.
We add an Appendix with an abstract template for formal 2C semantics, capable of incorporating topic-transparency for the standard connectives, while allowing fine-grained truth-conditions and neutrality on the structure of subject-matter.
2 Preliminaries
We take true, about, topic, subject-matter, follows from and cognate concepts as core to semantics, basic competence with which is reflected in ordinary meta-linguistic judgments. We thus take semantic theorizing as geared towards understanding such notions and responsive to pre-theoretic judgments on them.
2.1 Truth-conditions
We assume that there is an intimate relationship between truth-conditions and pre-theoretic judgments on logical consequence: identical truth-conditions implicate identical logical properties, and vice versa. (‘To discover truths is the task of all sciences; it falls to logic to discern the laws of truth’, Frege (1984, p. 351)). Though not completely uncontroversial (e.g., questioned in the tradition of dynamic semantics, as a helpful referee reminds us), the idea that logical consequence is tightly tied to truth preservation enjoys widespread support.
To make this precise, let \(\lfloor \varphi \rfloor \) denote \(\varphi \)’s truth set: the set of all logically possible circumstances at which \(\varphi \) is true. What we mean by this is that the function \(\lfloor \; \rfloor \) assigns to every declarative a set of truth-supporting circumstances where \(\varphi \) logically entails \(\psi \) iff \(\lfloor \varphi \rfloor \subseteq \lfloor \psi \rfloor \), \(\varphi \) and \(\psi \) are logically equivalent iff \(\lfloor \varphi \rfloor = \lfloor \psi \rfloor \), and \(\varphi \) and \(\psi \) are logically contrary iff \(\lfloor \varphi \rfloor \cap \lfloor \psi \rfloor = \emptyset \) (van Fraassen, 1968). Given this, our opening assumption is essentially that \(\varphi \)’s truth-conditions are individuated by its truth set: \(\texttt{T}_\varphi = \texttt{T}_\psi \) iff \(\lfloor \varphi \rfloor = \lfloor \psi \rfloor \). (We often take \(\varphi \)’s falsity set to be a function of its truth set, for simplicity. But we’ll discuss views that spell out truth and falsity conditions separately. Then \(\varphi \)’s truth-and-falsity-conditions can be taken as a pair.)
Then patterns of logical entailment, equivalence, or contrariety will constrain truth-conditional semantics (as per standard semantics textbooks, e.g., Chierchia and McConnell-Ginet (1990)). For example, the entailment from ‘Jim is unmarried and male’ to ‘Jim is male’ corresponds to a truth-conditional law:
-
(3)
At every logically possible circumstance, if ‘Jim is unmarried and male’ is true then ‘Jim is male’ is true, too.
It’s controversial how fine-grained the space of logically possible circumstances needs to be for \(\lfloor \; \rfloor \) to do its job. (Complete worlds? Partial situations? Inclusion of some metaphysically impossible circumstances?) It’s also controversial whether a comprehensive theory of content also needs truth-supporting circumstances that misrepresent truth-conditions—logically impossible circumstances (see, e.g., Priest (2005)) where logic is different. We maintain neutrality on both counts.
Because we take \(\lfloor \varphi \rfloor \) to individuate the truth-conditions for \(\varphi \), it conveniently simplifies our discussion to assume that \(\lfloor \varphi \rfloor = \texttt{T}_\varphi \): \(\varphi \)’s truth-conditions just are given by its truth set. (Or, by its truth set \(\lfloor \varphi \rfloor \) and falsity set \(\lfloor \lnot \varphi \rfloor \) in pair.)
We use \(\lnot \) and \(\wedge \) for the propositional connectives, typically expressed by ‘not’ and ‘and’. We assume they exhibit basic truth-conditional properties that uncontroversially correspond to mundane patterns of valid reasoning. For example, \(\varphi \wedge \psi \) is true only if both \(\varphi \) and \(\psi \) are true (at any logically possible circumstance) reflects the validity of Simplification in ordinary discourse. This is not to deny that ‘not’ and ‘and’ sometimes serve further functions in natural language, of course (e.g., dynamic conjunction, Humberstone, 2011, Sects. 5.11–5.12; meta-linguistic negation, Horn, 1989, Ch. 6; intensional conjunction, Humberstone, 2011, Sect. 5.16).
2.2 Subject-matter
We use t for an arbitrary topic and boldface to denote individual topics, e.g., Jane’s profession, mathematics. For our argument to have broad applicability, we maintain neutrality on the nature of topics. Some (Lewis, 1988a; Roberts, 2012; Plebani & Spolaore, 2021) link topics to questions: ‘Our topic is the number of stars’ comes with the nearby question, ‘How many stars are there?’ On the other hand, any kind of worldly object or event may serve as a conversational topic: ‘Our topic today is Barack Obama’; ‘In this module we’ll talk about the French revolution’. The two strands may pull in opposite directions (Hawke, 2018; Berto, 2022, Ch. 2). So we simply denote the topic associated with object a as \({\textbf{a}}\), leaving it open whether \({\textbf{a}}\) just is a, or the set of possible ways things can be with respect to a, or the states involving a as a constituent, or something else yet.
Next, there is an intuitive distinction between a sentence being wholly about a topic or only partially about a topic (Lewis, 1988b): \(\varphi \) is partly about t just in case part of what \(\varphi \) says is about t (‘Jane practices karate and Jim practices judo’ is only partly about Jane). \(\varphi \) is wholly about t just in case no part of what \(\varphi \) says isn’t about t (‘Jane practices karate and judo’ is wholly about Jane). We’ll use ‘about’ inclusively, allowing partial aboutness.
Let \(\lceil \varphi \rceil \) denote \(\varphi \)’s topic set: all that \(\varphi \) is about. We take it that \(\varphi \)’s subject-matter is individuated by \(\lceil \varphi \rceil \): \(\texttt{S}_\varphi = \texttt{S}_\psi \) iff \(\lceil \varphi \rceil = \lceil \psi \rceil \). It conveniently simplifies our discussion to assume that \(\lceil \varphi \rceil = \texttt{S}_\varphi \): \(\varphi \)’s subject-matter just is its topic set.Footnote 3
Overall, \(\lfloor \varphi \rfloor \) and \(\lceil \varphi \rceil \) denote two integral aspects of \([\varphi ]\), the content of \(\varphi \). Let’s now focus on their relation.
3 From topic-divergent necessities
Here’s a first argument against \(\texttt{T} \Rightarrow \texttt{S}\).
3.1 The argument
The orthodox view on truth-conditions (or, the closest we have to one) takes the truth-conditions for \(\varphi \) to be individuated by the set of metaphysically (as we say, post-Kripke) possible worlds at which \(\varphi \) is true. But combining orthodoxy with pre-theoretic judgment delivers prima facie counterexamples to \(\texttt{T}\Rightarrow \texttt{S}\):
-
(4)
\(1+1=2\).
-
(5)
\(\pi \) is irrational.
Plausibly, these are true at the same possible worlds, i.e., all of them. So, following orthodoxy, they have the same truth-conditions. But only one is about \(\pi \).
3.2 The reply
But a \(\texttt{T}\Rightarrow \texttt{S}\) theorist can claim that (4) and (5) help us to see that orthodoxy is mistaken. \(\varphi \) entails \(\psi \) iff every circumstance that verifies \(\varphi \), verifies \(\psi \). Now if the circumstances in question are constrained to the metaphysically possible worlds, (4) entails (5). But the first claim intuitively doesn’t support the second: no mathematician would take the truth of ‘\(1+1 = 2\)’ as a conclusive reason to accept ‘\(\pi \) is irrational’. We just need a refined notion of circumstance, with refined accounts of truth-conditions and entailment in tow. This is a motivation, e.g., for relevance logicians (Anderson & Belnap, 1975; Anderson et al., 1992; Beall & Restall, 2006) and situation theorists (Barwise & Perry, 1983) for supplementing the possible worlds in their model theory with partial/impossible situations. But now it is no longer obvious that such refined truth-conditions don’t determine subject-matter. Unlike (5), (4) plausibly isn’t verified by a partial situation featuring \(\pi \) but not 2.
The argument against \(\texttt{T}\Rightarrow \texttt{S}\) isn’t rescued simply by replacing (4) and (5) with presumed logical truths (say, ‘John is infected, or not’ versus ‘Jack is infected, or not’). For analogous reasoning may be deployed: to avoid the counter-intuitive prediction that ‘Obama is a lawyer’ deductively supports ‘John is infected, or not’, one had better posit partial/impossible circumstances at which the former is true but not the latter. But now it is far from clear that ‘John is infected, or not’ and ‘Jack is infected, or not’ have identical truth-conditions (or genuinely count as logical truths); only the former is true relative to a situation featuring John but not Jack.
Die-hard defenders of classical logic may be unmoved, but this is cold comfort for those less sanguine about the debates on relevance logic and logical consequence, or hoping to defeat 1C with easy counterexamples. The effectiveness of our first argument against \(\texttt{T}\Rightarrow \texttt{S}\) is mired in core disputes in philosophy of logic.
3.3 Perry, Lewis, and Fine as \(\texttt{T} \Rightarrow \texttt{S}\)
One good thing the above argument does is that it highlights resources available to \(\texttt{T} \Rightarrow \texttt{S}\) theorists. In particular, refining the space of truth-supporting circumstances may get a better fix on subject-matter. Perry (1989) argues for treating propositions as sets of partial situations, precisely to address what he calls the subject-matter problem: if propositions are merely sets of possible worlds, then if any claim is about t then every claim is about t. His argument: assume that \(\varphi \) is about t. Then, intuitively, \(\varphi \vee \lnot \varphi \) is also about t. Then, intuitively, \(\psi \wedge (\varphi \vee \lnot \varphi )\) is about t. But if the possible-worlds view is true, \(\psi \) is then about t (for, \([\psi ] = \lfloor \psi \rfloor = \lfloor \psi \wedge (\varphi \vee \lnot \varphi ) \rfloor = [\psi \wedge (\varphi \vee \lnot \varphi )]\) and, trivially, identical propositions have identical aboutness properties). Perry’s solution is to resist the identity \(\lfloor \psi \rfloor = \lfloor \psi \wedge (\varphi \vee \lnot \varphi ) \rfloor \), by resisting the identification of propositions with sets of possible worlds.
There are at least three influential accounts of subject-matter which take propositions as sets of partial situations, and can then explain the difference in subject-matter between (4) and (5) in terms of differing truth-conditions. These show how 1C semantics, in the \(\texttt{T} \Rightarrow \texttt{S}\) version, is well-established in the literature.
Perry’s account. According to Perry (1989), \(\varphi \) is about \({{\textbf {o}}}\) exactly when o is part of every situation in \(\varphi \)’s truth set \(\lfloor \varphi \rfloor \). That is, \(\texttt{T}_\varphi \) fixes \(\texttt{S}_\varphi \) via the function f that maps \(\lfloor \varphi \rfloor \) to a set of objects \(\lceil \varphi \rceil \): those that exist at every situation in \(\lfloor \varphi \rfloor \). This fits with any number of accounts of truth-conditions (e.g., classical logic, strong Kleene logic, weak Kleene logic, etc.). Note that if a disjunction is true exactly when one of its disjuncts is true, Perry’s account entails that ‘Ann is a lawyer or Bob is an accountant’ isn’t about Ann and isn’t about Bob; presumably neither Ann nor Bob is included in every situation where only one disjunct is true. To avoid this, one may drop the assumption about disjunctions (embracing, say, weak Kleene logic) or adopt a Perryean variant: \(\varphi \) is about object \({{\textbf {o}}}\) exactly when either o is part of every situation in \(\varphi \)’s truth set \(\lfloor \varphi \rfloor \) or o is part of every situation in \(\varphi \)’s falsity set \(\lfloor \lnot \varphi \rfloor \). Now ‘Ann is a lawyer or Bob is an accountant’ is about Ann and Bob because every situation that satisfies ‘Ann isn’t a lawyer and Bob isn’t an accountant’ includes Ann and Bob.
Lewis’ account. According to Lewis (1988a), a topic t is a partition (understood as a question) dividing logical space into ways a subject can be; \(\varphi \) is about t exactly when t refines the binary partition composed of \(\varphi \)’s truth set and its complement. That is, \(\texttt{T}_\varphi \) fixes \(\texttt{S}_\varphi \) via the function f that maps \(\lfloor \varphi \rfloor \) to the partitions refining its binary partition. As Lewis notes, if \(\lfloor \varphi \rfloor \) is merely a set of possible worlds, then f egregiously maps every necessary truth to the same subject-matter; but if \(\lfloor \varphi \rfloor \) also includes the partial or impossible situations where \(\varphi \) is true, the subject-matter of necessary truths (e.g., (4), (5)) can be differentiated. Note that Lewis (1988a) takes his account to only capture when a sentence is wholly about a topic. We return to this in Sect. 5.2.
Fine’s account. According to Fine (2016b), a topic t is a (potentially partial) situation, and \(\varphi \) is about t exactly when t overlaps with any of a certain subset of the partial situations at which \(\varphi \) is true: the exact verifiers and exact falsifiers of \(\varphi \). This is a 1C, \(\texttt{T}\Rightarrow \texttt{S}\) view, if one assumes that \(\varphi \)’s truth-conditions \(\texttt{T}_\varphi \) are individuated by its exact verifiers and exact falsifiers, fixing \(\varphi \)’s subject-matter as follows: \(\texttt{S}_\varphi = \lceil \varphi \rceil = f(\texttt{T}_\varphi )\) = the set of states that overlap the fusion of every state in the union of \(\varphi \)’s exact verifiers and falsifiers. Intuitively, an exact verifier for \(\varphi \) may be thought of as a wholly relevant truthmaker for \(\varphi \) and an exact falsifier for \(\varphi \) as a wholly relevant falsemaker for \(\varphi \). A truthmaker for \(\varphi \) is a situation s which, if part of a world, explains why \(\varphi \) is true at that world. A wholly relevant truthmaker for \(\varphi \) contains no parts that are irrelevant to this explanation. ‘Plato is wearing a red toga’ is made true by any situation where Plato and Socrates are both wearing red togas. But this isn’t exact: the goings-on with Socrates are irrelevant. In contrast, a situation in which Plato is appropriately attired—no more, no less—is an exact truthmaker for ‘Plato is wearing a red toga’. The fusion of \(\varphi \)’s exact verifiers and falsifiers, then, is a plausible representation of \(\varphi \)’s subject-matter insofar as it collects all and only states that are wholly relevant to \(\varphi \)’s truth or falsity. The situation that Plato and Socrates are both wearing red togas forces the truth of ‘Plato is wearing a red toga’, but doesn’t pinpoint the latter’s subject-matter, given the irrelevance of Socrates’ attire. These ideas find technical expression via natural recursive constraints on the exact verification relation between situations and sentences (written \(\vdash \)), and the exact falsification relation (\(\dashv \)), inspired by van Fraassen (1969) (cf. Yablo, 2014, Sect. 4.2):
-
\(s \vdash \lnot \varphi \) iff \(s \dashv \varphi \)
-
\(s \dashv \lnot \varphi \) iff \(s \vdash \varphi \)
-
\(s \vdash \varphi \wedge \psi \) iff s is the fusion of some t and u where \(t \vdash \varphi \) and \(u \vdash \psi \)
-
\(s \dashv \varphi \wedge \psi \) iff \(s \dashv \varphi \) or \(s \dashv \psi \)
-
\(s \vdash \varphi \vee \psi \) iff \(s \vdash \varphi \) or \(s \vdash \psi \)
-
\(s \dashv \varphi \vee \psi \) iff s is the fusion of some t and u where \(t \dashv \varphi \) and \(u \dashv \psi \)
Then, a \(\texttt{T}\Rightarrow \texttt{S}\) construal of Fine’s theory says this: \(\texttt{T}_\varphi \) is individuated by the pair \(\lfloor \varphi \rfloor = \{s : s \vdash \varphi \}\) and \(\lfloor \lnot \varphi \rfloor = \{s : s \dashv \varphi \}\), generating subject-matter \(\lceil \varphi \rceil \) as the set of states that overlap the fusion of the situations in \(\lfloor \varphi \rfloor \) and \(\lfloor \lnot \varphi \rfloor \).
4 From Yablo’s thesis
4.1 The argument
Here’s a second argument against \(\texttt{T}\Rightarrow \texttt{S}\). This exploits recent attempts to use subject-matter to explain both partial content and the logic of attitude ascriptions (Yablo, 2014, Ch. 1, Ch. 7; Hawke et al., 2020; Berto, 2022, Chs. 2–3).
The logic of cognitive attitude ascriptions is captured, one might think, by two facts:
-
(6)
Immanent Closure: “If S knows that P, and Q is part of P, then S knows that Q” (Yablo, 2014, p. 117)
-
(7)
Yablo’s Thesis: “Content-inclusion is implication plus subject-matter inclusion” (Yablo, 2014, p. 15)
But combining these with \(\texttt{T}\Rightarrow \texttt{S}\) egregiously implies that knowledge ascriptions are closed under mere entailment. So, \(\texttt{T}\Rightarrow \texttt{S}\) is false.
To unpack: note, first, that facts about same-saying and partial content seem mirrored in the logic of attitude ascriptions. Consider:
-
(8)
Jane is an experienced fisherman and an actuary.
-
(9)
Jane is an experienced fisherman.
-
(10)
Jane is a fisherman.
(9) plausibly expresses a proper part of (8)’s content: if (9) is true then (8) is at least partly true. (Ann claims ‘Jane is an experienced fisherman and an actuary’; Bob claims: ‘Jane is an experienced fisherman’; what Bob says has already been said by Ann—who said more: that Jane is also an actuary.) (10) expresses a proper part of the content of (9). (Carla says: ‘Jane is a fisherman’: Bob already said this, and more: she’s experienced.) Compare:
-
(11)
David knows that Jane is an experienced fisherman and an actuary.
-
(12)
David knows that Jane is an experienced fisherman.
-
(13)
David knows that Jane is a fisherman.
Mirroring the above, (11) cannot hold without (12), and (12) cannot hold without (13). Moreover, this doesn’t depend on David’s logical skills (Soames, 1987). An easy inference delivers knowledge that the number of apples in the hamper is less than a googol, if it is already known that there are exactly two apples. But one can have the latter knowledge without the former: one didn’t bother to draw the inference, or, as with a small child, is bereft of requisite mathematical knowledge. The relationships between (11)–(13) seem different: it is impossible to know that Jane is an experienced fisherman without knowing that she is a fisherman, no matter one’s logical or epistemic impairments. Jane being a fisherman is part of what one knows when one knows that Jane is an experienced fisherman. Likewise, one cannot believe that Jane is rich and powerful without believing that she is rich.Footnote 4
Let ‘\(\varphi \trianglerighteq \psi \)’ say that the content of \(\varphi \) contains that of \(\psi \) as a part: \(\varphi \) says whatever \(\psi \) says. Generalizing the above judgments delivers two principles:
-
(14)
Conjunction Elimination: \((\varphi \wedge \psi ) \trianglerighteq \varphi \) , \((\varphi \wedge \psi ) \trianglerighteq \psi \)
-
(15)
I-Closure: If \(\varphi \trianglerighteq \psi \), then knowing \(\varphi \) entails knowing \(\psi \).
Clearly, \(\trianglerighteq \) isn’t just entailment: if it were, (15) would egregiously imply that ordinary thinkers are logically omniscient. Now notice that (8) includes (9)’s subject-matter, and (9) includes (10)’s subject-matter. Generalizing in the obvious way delivers one elaboration of Yablo’s thesis: in particular, we take ‘is’ in the thesis as a biconditional and ‘implication’ as logical entailment, and assume that the subject-matter of \(\varphi \) includes that of \(\psi \) exactly when \(\varphi \) is about everything that \(\psi \) is about:
-
(16)
Strong Yablo: \(\varphi \trianglerighteq \psi \) iff (1) \(\varphi \) logically entails \(\psi \) and (2) \(\psi \) is about topic t only if \(\varphi \) is about t.
This amounts to identifying content-inclusion with Parry-implication (Parry, 1968; Fine, 1986; Parry, 1989; Ferguson, 2015).Footnote 5 The left-to-right direction of (16) addresses logical omniscience: one can know \(\varphi \) but not its consequence \(\psi \) when \(\psi \) expands the subject-matter of \(\varphi \). The converse direction also offers attractive explanatory power: on the plausible assumption that a conjunction merely merges the subject-matter of its conjuncts, (16) entails principle (14), explaining our reaction to, e.g., (8) and (9). With (15), it explains our reaction to (11)–(13).
Now here’s the second argument against \(\texttt{T}\Rightarrow \texttt{S}\): logical omniscience comes roaring back if one combines \(\texttt{T}\Rightarrow \texttt{S}\) with (14), (15), and (16). Consider \(\varphi \) and \(\psi \), where the former entails the latter. By (14), \(\varphi \wedge \psi \trianglerighteq \psi \). So, by the left-to-right direction of (16), \(\psi \) is about topic t only if \(\varphi \wedge \psi \) is about t. As \(\varphi \) and \(\varphi \wedge \psi \) have identical truth-conditions, it follows by \(\texttt{T}\Rightarrow \texttt{S}\) that \(\psi \) is about topic t only if \(\varphi \) is about t. Thus, by the right-to-left direction of (16), \(\varphi \trianglerighteq \psi \). But then (15) delivers: knowing \(\varphi \) entails knowing \(\psi \).
4.2 The reply
But again the \(\texttt{T}\Rightarrow \texttt{S}\) theorist can resist the argument: there are apparent counter-examples to the right-to-left direction of Strong Yablo. ‘Jane is an actuary’ plausibly Parry-implies ‘Jane is or is not an actuary’: p entails \(p \vee \lnot p\). Plausibly, p and \(p \vee \lnot p\) have the same subject-matter. But ‘Jane is or is not an actuary’ is not, one might think, part of the content of ‘Jane is an actuary’. If it were, ‘Jane is an actuary’ would be partly true whenever ‘Jane is or is not an actuary’ is true. But the latter is true if Jane is not an actuary, and then ‘Jane is an actuary’ isn’t even partly true.
4.3 Fine again
One might think that a better account of content-inclusion (and perhaps an alternative elaboration of Yablo’s thesis) is readily available to the \(\texttt{T}\Rightarrow \texttt{S}\) theorist. Suppose one embraces Fine’s recursive truthmaker semantics, with the \(\texttt{T}\Rightarrow \texttt{S}\) construal of Sect. 3.3. Then, following Fine (2017) (cf. Yablo, 2014, Sect. 3), one can say that \(\varphi \) has \(\psi \) as a part just in case any state that makes \(\psi \) true makes \(\varphi \) partially true. To elaborate: \(\varphi \trianglerighteq \psi \) iff (i) every state that exactly verifies \(\varphi \) includes some state that exactly verifies \(\psi \) and (ii) every state that exactly verifies \(\psi \) is part of some state that exactly verifies \(\varphi \). (On the \(\texttt{T}\Rightarrow \texttt{S}\) construal: \(\varphi \trianglerighteq \psi \) iff (i) if \(s \in \lfloor \varphi \rfloor \) then part of s is in \(\lfloor \psi \rfloor \) and (ii) if \(s \in \lfloor \psi \rfloor \) then s is part of a state in \(\lfloor \varphi \rfloor \).) Thus, if \(\varphi \) is true and \(\varphi \) includes \(\psi \), then \(\psi \) must also be true; if \(\psi \) is true and \(\varphi \) includes \(\psi \), then the actual world contains at least part of a truthmaker for \(\varphi \). On this account, p does not include \(p \vee \lnot p\): a possible world where \(p \vee \lnot p\) is true merely because \(\lnot p\) is true need not contain part of a truthmaker for p.
5 From topic-divergent logical equivalents
We finally present our own preferred argument against \(\texttt{T}\Rightarrow \texttt{S}\). We then use its rather minimal assumptions to specify objectionable features of the \(\texttt{T}\Rightarrow \texttt{S}\) exemplars outlined in Sect. 3.3.
5.1 The argument
The argument’s key assumptions are (17)–(21) below. Let c be any logically possible circumstance, i.e., any truth-supporting circumstance that respects the actual laws of logic. Then, for any interpreted \(\varphi \) and \(\psi \):
-
(17)
\(\varphi \wedge \psi \) is true at c iff \(\varphi \) and \(\psi \) are true at c.
-
(18)
\(\varphi \wedge \psi \) is false at c iff either \(\varphi \) is false at c or \(\psi \) is false at c.
-
(19)
If \(\varphi \) and \(\psi \) agree in their truth value assignment—true, false (or neither, or both, to accommodate various non-classical views)—at every logically possible circumstance, then \(\varphi \) and \(\psi \) have identical truth-conditions.
-
(20)
Inflation: There exists interpreted declaratives \(\alpha \) and \(\beta \) such that (i) \(\beta \) is about something that \(\alpha \) isn’t about, (ii) \(\alpha \) entails \(\beta \), and (iii) \(\beta \) anti-entails \(\alpha \) (i.e., at every logically possible circumstance, if \(\beta \) is false then \(\alpha \) is false).
(If the falsity set of a sentence is always a well–behaved function of its truth set, then (iii) is superfluous for the argument.)
-
(21)
Conjunct Containment: \(\lceil \varphi \rceil \subseteq \lceil \varphi \wedge \psi \rceil \) and \(\lceil \psi \rceil \subseteq \lceil \varphi \wedge \psi \rceil \), i.e., if \(\varphi \) or \(\psi \) is about t then so is \(\varphi \wedge \psi \).
Now (17) and (18) are paradigmatic truth-conditional facts, reflecting exceptionally mundane valid reasoning: Simplification, Adjunction, their contrapositives. Their denial is equally disturbing to classical logicians and relevance logicians (Belnap, 1977), at best changing the subject to something other than the actual truth-conditions for the standard conjunction.
To appreciate (19), recall the characterization of truth-conditions in Sect. 2.1. Perhaps there are logically impossible circumstances: worlds at which logic is different, or where the actual truth-conditional laws fail. Perhaps these are essential to semantics, with quantification over deviant circumstances crucial in assigning truth values to counter-possible conditionals or reports of anarchic attitudes like imagination (Nolan, 1997; Priest, 2005). But as such circumstances misrepresent truth-conditions, their existence is irrelevant to the truth of (19).
(20) has abundant common sense support. Take ‘No gerbil drinks whiskey’ for \(\alpha \) and ‘No gerbil drinks whiskey with British royalty’ for \(\beta \) (only the latter talks about British royalty); or ‘Obama isn’t a dentist’ for \(\alpha \) and ‘Obama isn’t both a dentist and a bachelor’ for \(\beta \) (only the latter talks about Obama’s marital status); or ‘Only humans philosophize’ for \(\alpha \) and ‘Non-human androids do not philosophize’ for \(\beta \) (only the latter talks about androids).
Combined with relatively innocuous assumptions, denying (20) issues in absurdity. Suppose \(\varphi \) entails \(\psi \) and \(\psi \) anti-entails \(\varphi \) (say, \(\varphi \) is ‘Ann is a lawyer and Bob is a lawyer’ and \(\psi \) is ‘Ann is a lawyer’). It presumably follows that \('\lnot \psi ~entails~\lnot \varphi '\) and that \('\lnot \varphi ~anti-entails~\lnot \psi '\). Denying (20), we conclude: \(\lceil \psi \rceil \subseteq \lceil \varphi \rceil \) and \(\lceil \lnot \varphi \rceil \subseteq \lceil \lnot \psi \rceil \). Now assume that negation preserves subject-matter (cf. Yablo’s case against \(\texttt{S}\Rightarrow \texttt{T}\), per). We conclude \(\lceil \varphi \rceil \subseteq \lceil \psi \rceil \); so, \(\lceil \varphi \rceil = \lceil \psi \rceil \). But this is absurd: it seems obvious that ‘Ann is a lawyer and Bob is a lawyer’ is about Bob, while ‘Ann is a lawyer’ is not.
(21) also finds support in common sense. ‘Ann is a lawyer’ is about Ann; ‘Ann is a lawyer and Bob is an accountant’ is also about Ann (among other things, such as Bob). This seems generalizable: to say \(\varphi \wedge \psi \) is to say, at least, no less than to merely say \(\varphi \).
But given (17)–(21), \(\texttt{T}\Rightarrow \texttt{S}\) is false. Per (20), let \(\alpha \) and \(\beta \) be interpreted sentences such that there is a topic t that \(\beta \) is about but \(\alpha \) is not about, \(\alpha \) entails \(\beta \), and \(\beta \) anti-entails \(\alpha \). By (19), \(\alpha \) and \(\alpha \wedge \beta \) have identical truth-conditions. For if \(\alpha \) is true at logically possible circumstance c, then \(\alpha \) and \(\beta \) are true at c (as \(\alpha \) entails \(\beta \)) and so \(\alpha \wedge \beta \) is true at c, by (17). If \(\alpha \wedge \beta \) is true at c, then \(\alpha \) is true, also by (17). On the other hand, if \(\alpha \) is false at c, \(\alpha \wedge \beta \) is false, by (18). If \(\alpha \wedge \beta \) is false at c, then \(\alpha \) is false or \(\beta \) is false, by (18), and either way, \(\alpha \) is false (as \(\beta \) anti-entails \(\alpha \)). Thus, if \(\texttt{T}\Rightarrow \texttt{S}\) holds, \(\lceil \alpha \rceil = \lceil \alpha \wedge \beta \rceil \). But (21) entails that \(t \in \lceil \beta \rceil \subseteq \lceil \alpha \wedge \beta \rceil \). As \(t \notin \lceil \alpha \rceil \), it follows that \(\lceil \alpha \rceil \ne \lceil \alpha \wedge \beta \rceil \). By modus tollens, \(\texttt{T}\Rightarrow \texttt{S}\) is false.
5.2 Critiquing \(\texttt{T}\Rightarrow \texttt{S}\) theories
Our argument in Sect. 5.1 pinpoints criticisms of the \(\texttt{T} \Rightarrow \texttt{S}\) style 1C theories from Sect. 3.3: equipping situation theory with Perry’s account of subject-matter violates assumption (20) (or, on a variation of the account, (21)), equipping it with Lewis’ account violates (21), and equipping it with Fine’s account violates (17).
Perry. Recall: Perry (1989) models subject-matter \(\lceil \varphi \rceil \) as the set of objects that exist at every situation in truth set \(\lfloor \varphi \rfloor \). It follows that if \(\alpha \) entails \(\beta \), \(\beta \) anti-entails \(\alpha \), and \(\beta \) is about t, then \(\alpha \) is about t: if object o exists at every situation where \(\beta \) is true and the only situations where \(\alpha \) is true are \(\beta \)-situations, then o must exist at every situation where \(\alpha \) is true.
Section 3.3 also considered a Perryean variant: \(o \in \lceil \varphi \rceil \) exactly when either o exists at every situation in truth set \(\lfloor \varphi \rfloor \) or at every situation in falsity set \(\lfloor \lnot \varphi \rfloor \). This variant satisfies (20): as Bob is included in any situation where ‘neither Ann nor Bob is a lawyer’ is true, ‘Either Ann or Bob is a lawyer’ is about Bob on our Perryean variant, unlike ‘Ann is a lawyer’. But it violates (21); we leave this to a footnote.Footnote 6
Lewis. Recall: Lewis (1988a) models topics as partitions of logical space, and subject-matter \(\lceil \varphi \rceil \) as the set of refinements of the binary partition that divides the space of all logically possibly circumstances into \(\lfloor \varphi \rfloor \) and its complement. Hence, \(\varphi \) is about topic (i.e., partition) t when \(t \in \lceil \varphi \rceil \). Trivially, \(\varphi \) is about its associated binary partition. But in general there is no reason why the binary partition of \(\lceil q \rceil \) and its complement should refine the binary partition of \(\lceil p \wedge q \rceil \) and its complement: the set of situations where Bob is an accountant is coarser than the set of situations where Ann is a lawyer and Bob is an accountant. Hence, on the Lewisian picture, q can be about t despite \(p \wedge q\) not being about t.
Lewis (1988a) seems aware of the issue; he dodges it by insisting that the above account of ‘aboutness’ only covers when \(\varphi \) is wholly about a topic. We do not expect Conjunct Containment (i.e., (21)) to hold when restricted to ‘wholly about’: that \(\psi \) is wholly about t does not, in general, imply that \(\varphi \wedge \psi \) is wholly about t. One part of \(\varphi \wedge \psi \)—namely, \(\varphi \)—may not be about t. Lewis (1988b) suggests that we recover partial aboutness from his account as follows: \(\varphi \) is partially about t exactly when \(\varphi \) has a part that is wholly about t. But this lands the Lewisian with another problem: they owe us an independent account of content-parthood. Lewis (1988b, Sect. VIII) suggests that \(\psi \) is part of \(\varphi \) exactly when \(\varphi \) entails \(\psi \). But this is problematic: p entails \(p \vee \lnot p\) but the truth of \(p \vee \lnot p\) (e.g., in virtue of \(\lnot p\) being true) does not guarantee that p is partially true (cf. Sect. 4.2).
Fine. Recall: Fine (2016b) provides the tools for a state-based approach to \(\texttt{T}\Rightarrow \texttt{S}\). One takes \(\texttt{T}_\varphi \) to be composed of two sets of states: a set of ‘exact verifiers’ and a set of ‘exact falsifiers’ (or only one set, if the former determines the latter). These fix subject-matter: \(\texttt{S}_\varphi = \lceil \varphi \rceil = f(\texttt{T}_\varphi )\) \(=\) the states that overlap the fusion of every state in the union of those sets. To extend this to a version of \(\texttt{T}\Rightarrow \texttt{S}\), we can then stipulate that \(\varphi \)’s truth set \(\lfloor \varphi \rfloor \) is identical to the set of its exact verifiers and \(\varphi \)’s falsity set \(\lfloor \lnot \varphi \rfloor \) is identical to the set of its exact falsifiers. But this is to interpret \(s \vdash \varphi \) (‘s is an exact truthmaker for \(\varphi \)’) as ‘\(\varphi \) is true at s’.
However, assuming (17), the preceding is no satisfactory account of truth-conditions. As it is consistent for \(s \vdash p \wedge q\) to hold without \(s \vdash p \) (the part of s that exactly verifies q might fail to exactly verify p), the proposed account of truth-conditions egregiously allows for \(p \wedge q\) to be true at s without p being true. Let \(|\varphi |\) denote the set of circumstances that exactly verify \(\varphi \). Hence, \(| \varphi |\) shouldn’t be identified with the truth set \(\lfloor \varphi \rfloor \), for we require \(\lfloor p \wedge q \rfloor \subseteq \lfloor p \rfloor \), but \(| p \wedge q | \subseteq | p |\) doesn’t hold (cf. Fine & Jago, 2019).
A better account of ‘being true’ is available to the Finean (cf. van Fraassen, 1969, pp. 483–484; Fine, 2017, pp. 668–669): \(\varphi \) is true at s iff part of s is an exact truthmaker for \(\varphi \) (i.e., s includes some t such that \(t \vdash \varphi \)). Taking entailment as truth-preservation and the logically possible circumstances as the set of all states, it is straightforwardly verified that the ensuing account of truth-conditions and subject-matter satisfies assumptions (17)–(21). Hence, setting \(\lfloor \varphi \rfloor \) to be the set of states at which \(\varphi \) is true (as defined here), we can rehearse the argument of Sect. 5.1 to show that the present account of truth-conditions and subject-matter entails 2C.
So in the end, Fine’s semantics is better interpreted along 2C lines! There are serious objections to (as above) taking its verification conditions as mere truth-conditions, while the most natural means for generating truth-conditions from them delivers a 2C framework.
6 Against 1C from transparency
If the following are true (call their conjunction Transparency), the case against 1C can be systematized, building on the argument from Sect. 5.
-
(22)
Negation Transparency: \(\lceil \lnot \varphi \rceil = \lceil \varphi \rceil \)
-
(23)
Conjunctive Transparency: \(\lceil \varphi \wedge \psi \rceil = \lceil \varphi \rceil \cup \lceil \psi \rceil \)
(With \(\varphi \vee \psi \) standing for \(\lnot (\lnot \varphi \wedge \lnot \psi )\), we have: \(\lceil \varphi \vee \psi \rceil = \lceil \varphi \rceil \cup \lceil \psi \rceil \).) These say that the truth-functional logical vocabulary is transparent with respect to subject-matter: it adds none of its own.Footnote 7
6.1 The argument
Recall how Yablo (2014, Sect. 2.8) notes that \(\texttt{S}\Rightarrow \texttt{T}\) conflicts with Transparency. If there is an f such that \(\texttt{T}_\varphi = f(\texttt{S}_\varphi )\) for all \(\varphi \), then Transparency egregiously mandates that p and \(\lnot p\) are always true in the same logically possible circumstances.
But as our argument in Sect. 5.1 shows, \(\texttt{T}\Rightarrow \texttt{S}\) also conflicts with Transparency (in conjunction with uncontentious truth-conditional facts), as Transparency implies Conjunct Containment. Indeed, given further light assumptions about truth-conditions, Transparency also implies Inflation. Consider a variant of our argument that replaces Inflation with:
-
(24)
\(\lnot \varphi \) is true at c iff \(\varphi \) is false at c.
-
(25)
\(\lnot \varphi \) is false at c iff \(\varphi \) is true at c.
Let p and q be interpreted sentences such that there is a topic t that q is about but p is not about. One easily verifies that (17), (18), (19), (24), and (25) together entail that \(\lnot p\) and \(\lnot p \wedge \lnot (p \wedge q)\) have identical truth-conditions. So, \(\texttt{T}\Rightarrow \texttt{S}\) implies that \(\lnot p\) and \(\lnot p \wedge \lnot (p \wedge q)\) have identical subject-matter. But Transparency implies \(\lnot p \wedge \lnot (p \wedge q)\) is about something that \(\lnot p\) isn’t about (for \(\lceil \lnot p \rceil = \lceil p \rceil \) and \(\lceil \lnot p \wedge \lnot (p \wedge q) \rceil = \lceil p \rceil \cup \lceil q \rceil \)). So, Transparency implies Inflation and contradicts \(\texttt{T}\Rightarrow \texttt{S}\).
This used the benign assumption that declaratives can have different subject-matter. Thus, the argument can be re-framed as a generalization of Perry’s subject-matter problem (Sect. 3.3), targeting even his own \(\texttt{T}\Rightarrow \texttt{S}\) theory: given both Transparency and uncontroversial truth-conditional facts, \(\texttt{T}\Rightarrow \texttt{S}\) implies, absurdly, that every declarative must have the same subject-matter.
Given Transparency, we may thus label our summarized case against 1C as the argument from transparency: Transparency is true; if Transparency is true then \(\texttt{S}\Rightarrow \texttt{T}\) and \(\texttt{T}\Rightarrow \texttt{S}\) are false; thus, 1C is false.
6.2 For transparency
Is Transparency true? While not dispositive, there are good reasons to accept Transparency.Footnote 8 First, Transparency has significant pre-theoretic appeal, evidenced by the many theorists who, with little ado, acknowledge or impose its constraints, e.g., Epstein (1990, Ch. 3), Levesque and Lakemeyer (2000, Sect. 11.1), Yablo (2014, Sect. 2.8), Hawke (2016, Sect. 6.1), Beall (2016, Sect. 4.2), Hawke (2018, Sect. 3.1), Fine (2020, Sect. 2), Plebani and Spolaore (2021, Sect. VI), and Hoek (2022, Sect. IV).
Second, abductive considerations support it. If the discussion topic is what you read this morning, then ‘I read the newspaper’, ‘I read a novella’, ‘I didn’t read the newspaper’, ‘I read the newspaper and a novella’, ‘I read the newspaper or a novella (I can’t remember which)’, and ‘I read neither the newspaper nor a novella’ are all fully on-topic. In contrast,‘I read the newspaper and I ate eggs for breakfast’ is clearly partly off-topic, in light of ‘I ate eggs for breakfast’ clearly being entirely off-topic. The examples can be multiplied indefinitely. Transparency best explains the copious data, by positing appropriate relationships between the subject-matter of the foregoing sentences: if negation preserves subject matter, and conjunction and disjunction merely combine subject matter, then being on-topic or off-topic is (at least partly) preserved by applying the connectives (assuming, of course, that being on- or off-topic is, predominantly, a function of subject matter).
Third, alleged counter-examples to Transparency tend to wither under scrutiny. Consider four instructive candidates.
Candidate 1. A challenge to Conjunctive Transparency:
Take ‘The people of Greece want to call their country Macedonia’ and ‘The people of Macedonia want to call their country Macedonia’. Neither is about conflict on its own, but their conjunction may well be. The conjunctive combination may alter the class of topics concerned. (Demolombe & Jones, 1995, p. 55)
Reply. We grant that (26) below is typically relevant when the discourse topic is conflict, despite neither conjunct being obviously relevant if uttered in isolation.
-
(26)
The people of Greece want to call their country Macedonia and the people of Macedonia want to call their country Macedonia.
But conjunction is accidental to this. Uttering the sentences in succession has identical conversational effect:
-
(27)
The people of Greece want to call their country Macedonia. The people of Macedonia want to call their country Macedonia.
A better explanation will leave Transparency alone and appeal to pragmatics. Taken literally, ‘The people of Greece want to call their country Macedonia’ isn’t about conflict, but is about (something like) what the people of Greece want to call their country—mutatis mutandis for ‘The people of Macedonia want to call their country Macedonia’. Per Transparency, (26) merely combines the subject matter of these sentences. Nevertheless, they are together indirectly relevant in a conversation about conflict: against the common ground, they have an obvious joint implication that clearly is about conflict: ‘The desires of the people of Greece and of Macedonia are in conflict’. That this is so does not entail that the conjunction is itself about conflict (cf. (20)).
Candidate 2. Claims can be about (perhaps non-actual) states of affairs. ‘Jane is not in Barcelona’ is about Jane not being in Barcelona, while ‘Jane is in Barcelona’ is not about Jane not being in Barcelona. (Compare the view that \(\varphi \)’s subject-matter is individuated by the structured Russellian proposition it expresses.) To bolster this, observe that if Ann lies by saying ‘Jane is in Barcelona’, it is misleading to report ‘Ann lied about Jane not being in Barcelona’ rather than ‘Ann lied about Jane being in Barcelona’ (cf. Holton, 2019). Hence, ‘Jane is in Barcelona’ and ‘Jane is not in Barcelona’ have different subject-matter, contra Transparency.
Reply. It isn’t clear that saying that Jane is not in Barcelona is yet to say anything about Jane not being in Barcelona (as when one says ‘Jane not being in Barcelona is unusual’). But grant that ‘Jane is in Barcelona’ is about Jane being in Barcelona and ‘Jane is not in Barcelona’ is about Jane not being in Barcelona. Grant that it can sometimes be misleading to report ‘Ann lied about Jane not being in Barcelona’ when Ann lies by saying ‘Jane is in Barcelona’. We should not jump to the conclusion that ‘Jane is in Barcelona’ isn’t also about Jane not being in Barcelona. As Holton (2019) notes, subtle pragmatic effects are in play: it is also easy to concoct contexts where one aptly reports ‘Ann lied about Jane not being in Barcelona’ when Ann lies by saying ‘Jane is in Barcelona’. For example, the following sounds natural if the interlocutors know that Jane fled to Madrid and that Ann was questioned by Barcelona’s authorities about Jane’s whereabouts:
-
(28)
Did Ann lie about Jane not being in Barcelona?
-
(29)
Yes, she said that Jane is in Barcelona.
Whatever is going on here, it seems implausible that what distinguishes these different contexts is that ‘Jane is in Barcelona’ varies in subject-matter: its content seems fixed.
Candidate 3. Someone asks ‘Who won the 2018 Nobel prize in literature?’ without a clue as to the answer. ‘Patti Smith did’ is an obviously relevant and wholly on-topic (whether true or not) initial response. ‘Patti Smith did not’ is obviously irrelevant and wholly off-topic, failing to meaningfully answer the pertinent question under discussion. So, ‘Patti Smith did’ and ‘Patti Smith did not’ must speak to different topics.
Reply. Suppose Ann replies to the query: ‘Patti Smith won’. Bob retorts: ‘No, Patti Smith did not’. Surely Bob can’t be accused of saying something off-topic. Indeed, a pragmatic effect can explain the initial infelicity of ‘Patti Smith didn’t win’ in context: plausibly, as an initial reply it is markedly unhelpful insofar as it is uninformative—given a large pool of potential winners, it contributes little to resolving the query, even if wholly on-topic and true. In contrast, using it to dispute an earlier reply can be markedly helpful.
Candidate 4. Consider:
-
(30)
‘Obama is a lawyer and a politician’ is about whether Obama is both a lawyer and a politician.
-
(31)
‘Obama is a lawyer and a politician’ is not about whether Obama is a lawyer or a politician.
-
(32)
‘Obama is a lawyer or a politician’ is about whether Obama is a lawyer or a politician.
-
(33)
‘Obama is a lawyer or a politician’ is not about whether Obama is both a lawyer and a politician.
It follows that the sentence in (30) and (31) is about a topic that the sentence in (32) and (33) is not about, and vice versa.
Reply. Denying (30) or (32) is hopeless, but both (31) and (33) are plausibly denied on reflection. Given that a policy is justified if it is either just or economical, Ann asks: ‘Is a basic income grant just or economical?’ Bob responds, informatively: ‘In my view, a basic income grant is just and economical’. It would be odd for Ann to complain ‘OK, but why are you talking about that?’ The oddness isn’t explained merely by the fact that Bob’s response obviously implies the unequivocally on-topic ‘A basic income grant is just’. Compare Carla’s response: ‘A basic income grant is just and e is transcendental’. Ann rightly complains: ‘OK, but why are you talking about e?’ In contrast, ‘A basic income grant is just and economical’ seems wholly on-topic: unlike Carla’s response, there is no obvious conversational advantage in cutting some content. A simple explanation: \(\varphi \wedge \psi \) is (wholly) about whether \(\varphi \vee \psi \) (among other things), so is on-topic when talking about the latter.
Similarly: Bob says ‘Let’s discuss whether quarantining Jack is cruel and ineffective’. Ann responds, informatively: ‘Quarantining Jack is cruel or ineffective, depending on the quarantine’s duration’. Bob might rightly complain that this response doesn’t completely resolve the question under discussion (i.e., isn’t ideally informative), but it would be odd for Bob to complain ‘Sure, but don’t change the subject!’ (Compare Carla’s objectionably irrelevant but very informative response: ‘Jack is a dentist’.) Explanation: \(\varphi \vee \psi \) is about whether \(\varphi \wedge \psi \) (among other things), so is on-topic in a conversation about the latter.
7 Conclusion
We have cast doubt on the efficacy of arguments against \(\texttt{T}\Rightarrow \texttt{S}\) from topic-divergent necessities and Yablo’s thesis. But the argument from topic-divergent logical equivalents is, we think, hard to resist. More generally: Transparency is a key theoretical posit in the present debate. Arguments based in Transparency can be deployed against both \(\texttt{T}\Rightarrow \texttt{S}\) and \(\texttt{S}\Rightarrow \texttt{T}\), presenting a unified case against 1C.
One may still wonder: what should a formal 2C semantics look like? In Appendix A, we provide a template for studying 2C formal systems, with some applications.
Notes
Throughout, \(\varphi \) and \(\psi \) stand for interpreted declarative sentences, while p and q stand for logically atomic declaratives. Interpretation may be understood as relative to linguistic convention and discourse context.
“A proposition is the expression of its truth-conditions” (Wittgenstein, 1974, Sect. 4.431). “A meaning for a sentence is something that determines the conditions under which the sentence is true or false” (Lewis, 1970, Sect. III). “The version of semantics I propose to defend is possible-worlds semantics...The meaning of a sentence in possible-worlds semantics is just the set of worlds in which that sentence is true” (Cresswell, 1985, pp. 3–4). “To know the meaning of a sentence is to know its truth-conditions” (Heim and Kratzer, 1997, p. 1).
Some theorists will accept that \(\lceil \varphi \rceil \) individuates \(\texttt{S}_\varphi \) but deny that \(\lceil \varphi \rceil = \texttt{S}_\varphi \). Consider a prominent stance in the literature (see Hawke (2018) for discussion): ‘topic’ and ‘subject-matter’ are essentially synonyms; the space of topics has mereological structure (in particular, topics can overlap); \(\texttt{S}_\varphi \) is best understood as a topic where \(\varphi \) is about topic t iff t overlaps with \(\texttt{S}_\varphi \). Here, \(\texttt{S}_\varphi \) determines topic set \(\lceil \varphi \rceil \), but is not identical to it (indeed, \(\texttt{S}_\varphi \) is a member of \(\lceil \varphi \rceil \)).
“The view of conjunction as a sort of mental glueing operation which one can fail to perform [or to undo] is an error. It is not as if believing (A & B) is something over and above believing A and believing B ...” (Routley & Routley, 1975, p. 211). “Knowledge of a conjunction is already knowledge of its conjuncts.... There is no obstacle here to the idea that knowing a conjunction constitutes knowing its conjuncts, just as, in mathematics, we may count a proof of a conjunction as a proof of its conjuncts, so that if \(p \wedge q\) is proved then p is proved, not just provable.” (Williamson, 2000, pp. 282–283). Also see (Humberstone, 1985, p. 407).
We require p and q where: (i) every \(\lnot q\)-situation includes o, (ii) not every \(p \wedge q\)-situation (and so not every p situation) includes o, and (iii) not every \(\lnot p \vee \lnot q\)-situation includes o. If (i) holds, q is about \({{\textbf {o}}}\), on our Perryean account. If (ii) and (iii) hold, \(p\wedge q\) isn’t about o, on our Perryean account. The following example does the job: take ‘Ann is fussy about fashion’ for p and ‘Ann either doesn’t like Bob’s outfit or doesn’t like Carla’s outfit’ for q (so \(\lnot q\) is ‘Ann likes Bob’s outfit and likes Carla’s outfit’). Then (i) is satisfied. Situations where Ann likes Bob’s outfit, or doesn’t like Bob’s outfit, include Bob. So situations where Ann both likes Bob’s outfit and likes Carla’s outfit include Bob. (ii) is satisfied. Not every situation where Ann is fussy about fashion and either dislikes Bob’s outfit or Carla’s outfit is a situation that includes Bob. Some such situations include only Ann and Carla: Ann is fussy about fashion and dislikes Carla’s outfit. (iii) is satisfied. Not every situation where either Ann isn’t fussy about fashion or likes both Bob’s outfit and Carla’s outfit is one that includes Bob. Some such situations include only Ann. Altogether, on our modified Perryean account, ‘Ann doesn’t like Bob’s outfit or doesn’t like Carla’s outfit’ is about Bob, but ‘Ann is fussy about fashion and either doesn’t like Bob’s outfit or doesn’t like Carla’s outfit’ isn’t about Bob.
On negation, remember Wittgenstein (1974, Sect. 5.44): “And if there was an object called ‘\(\sim \)’, then ‘\(\sim \sim p\)’ would have to say something other than ‘p’. For the one proposition would then treat of \(\sim \), the other would not.”
If further constraints are allowed, truth sets may well be recoverable from verification conditions. Suppose we take a certain subset of states to be the possible states, for an appropriate construal of ‘possible’. The truth set \(\lfloor \varphi \rfloor \) can then presumably be identified as the possible states that contain an exact verifier for \(\varphi \). But this just reiterates our point: if every interpreted sentence has exact falsifiers, \(\lfloor \varphi \rfloor \) can be recovered from \(\varphi \)’s verification conditions only with constraints—here, a demarcation of possible states—that encode basic truth-conditional facts. This is to superimpose the machinery of the proposal in Sect. A.2 on truthmaker semantics.
\(\textsf {AC}\) consists of: the axioms stating double negation elimination; idempotence, commutativity, and associativity for \(\wedge \) and \(\vee \); DeMorgan laws; distributivity; and the rules
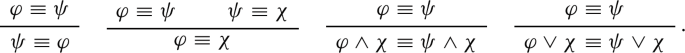
Consider \(\varphi = p \wedge q\) and a state s where p is both true and false and q is just false, then, following FDE, \(\varphi \) isn’t true at s but \(\varphi \vee (p \wedge \lnot p)\) is true at s.
In fact, in Hornischer (2020), it is established that \(\varphi \equiv \psi \) is derivable in \(\textsf {AC} + (41) \)iff \(\varphi \) and \(\psi \) are equivalent in FDE and have the same atoms. So characterizes content equivalence in the 2C semantics using possibly incomplete and inconsistent states (with constraints mimicking FDE) rather than only classical states.
References
Anderson, A., & Belnap, N. (1975). Entailment: The logic of relevance and necessity I. Princeton University Press.
Anderson, A., Belnap, N., & Dunn, J. (1992). Entailment: The logic of relevance and necessity II. Princeton University Press.
Barwise, J., & Perry, J. (1983). Situations and attitudes. CSLI Publications.
Beall, J., & Restall, G. (2006). Logical pluralism. Oxford University Press.
Beall, J. C. (2016). Off-topic: A new interpretation of weak Kleene logic. Australasian Journal of Logic, 13(6), 136–142.
Belnap, N. (1977). A useful four-valued logic. In J. Dunn & G. Epstein (Eds.), Modern uses of multiple-valued logic (pp. 8–37). D. Reidel Publishing Co.
Berto, F. (2022). Topics of thought: The logic of knowledge, belief, imagination. Oxford University Press.
Berto, F., & Hornischer, L. (2023). Cognitive synonymy: A dead parrot? Philosophical Studies, 180, 2727–2752.
Burgess, J. P. (2009). Philosophical logic. Princeton University Press.
Chalmers, D. (2011). Propositions and attitude ascriptions. Nous, 45, 595–639.
Chierchia, G., & McConnell-Ginet, S. (1990). Meaning and grammar: An introduction to semantics. MIT Press.
Cresswell, M. (1985). Structured meanings: The semantics of propositional attitudes. MIT Press.
Demolombe, R., & Jones, A. J. I. (1995). Reasoning about topics: Towards a formal theory. In Proceedings of the fall symposium on formalizing context, MIT. AAAI Press.
Epstein, R. L. (1990). The Semantic foundations of logic Propositional logics (Vol. 1). Kluwer Academic Publishers.
Ferguson, T. (2015). Logics of nonsense and Parry systems. Journal of Philosophical Logic, 44, 65–80.
Ferguson, T. (2023a). Subject-matter and intensional operators I: Conditional-agnostic analytic implication. Philosophical Studies, 180, 1849–1879.
Ferguson, T. (2023b). Subject-matter and intensional operators II: Applications to the theory of topic-sensitive intentional modals. Journal of Philosophical Logic, 52, 1673–1701.
Ferguson, T. (2023c). Subject-matter and intensional operators III: State-sensitive subject matter and topic-sufficiency. Review of Symbolic Logic, Online First. https://doi.org/10.1017/S1755020323000230
Fine, K. (1986). Analytic implication. Notre Dame Journal of Formal Logic, 27, 169–79.
Fine, K. (2016a). Angellic content. Journal of Philosophical Logic, 45(2), 199–226.
Fine, K. (2016b). Constructing the impossible. In Walters & Hawthorne (Eds.), Conditionals, probability, and paradox: Themes from the philosohy of Dorothy Edgington. Oxford University Press.
Fine, K. (2017). A theory of truthmaker content I: Conjunction, disjunction and negation. Journal of Philosophical Logic, 46(6), 625–674.
Fine, K. (2020). Yablo on subject-matter. Philosophical Studies, 177(1), 129–171.
Fine, K., & Jago, M. (2019). Logic for exact entailment. The Review of Symbolic Logic, 12(3), 536–556.
Frege, G. (1984). Der Gedanke: Eine Logische Untersuchung, translated as ‘Thoughts’. In B. McGuiness (Ed.), Collected papers on mathematics, logic, and philosophy (pp. 351–72). Blackwell.
Goodman, J. (2019). Agglomerative algebras. Journal of Philosophical Logic, 48(4), 631–648.
Hawke, P. (2016). Questions, topics and restricted closure. Philosophical Studies, 73(10), 2759–2784.
Hawke, P. (2018). Theories of aboutness. Australasian Journal of Philosophy, 96(4), 697–723.
Hawke, P., Özgün, A., & Berto, F. (2020). The fundamental problem of logical omniscience. Journal of Philosophical Logic, 49(4), 727–766.
Heim, I., & Kratzer, A. (1997). Semantics in generative grammar. Wiley-Blackwell.
Hoek, D. (2022). Questions in action. Journal of Philosophy, 119(3), 113–143.
Holton, R. (2019). Lying about. Journal of Philosophy, 116, 99–105.
Horn, L. (1989). A natural history of negation. University of Chicago Press.
Hornischer, L. (2020). Logics of synonymy. Journal of Philosophical Logic, 49, 767–805.
Humberstone, L. (1985). The formalities of collective omniscience. Philosophical Studies, 48, 401–423.
Humberstone, L. (2011). The connectives. MIT Press.
Levesque, H., & Lakemeyer, G. (2000). The logic of knowledge bases. MIT Press.
Lewis, D. (1970). General semantics. Synthese, 22(1/2), 18–67.
Lewis, D. (1988a). Relevant implication. Theoria, 54(3), 161–174.
Lewis, D. (1988b). Statements partly about observation. Philosophical Papers, 17, 1–31.
Montague, R. (1974). Formal philosophy: Selected papers of Richard Montague. Yale University Press.
Nolan, D. (1997). Impossible worlds: A modest approach. Notre Dame Journal of Formal Logic, 38, 535–572.
Özgün, A., & Schoonen, T. (2022). The logical development of pretense imagination. Erkenntnis. https://doi.org/10.1007/s10670-021-00476-9
Parry, W. T. (1968). The logic of C.I. Lewis. In I. Schlipp (Ed.), The philosophy of C.I. Lewis (pp. 115–154). Cambridge University Press.
Parry, W. T. (1989). Analytic implication: Its history, justification and varieties. In J. Norman & R. Sylvan (Eds.), Directions in relevant logic (pp. 101–118). Kluwer Academic Publishers.
Partee, B. H. (1989). Speaker’s reply. In Allen, S., (Ed.), Possible worlds in humanities, arts and sciences. Proceedings of nobel symposium (Vol. 65, pp. 152–161). Walter de Gruyter.
Perry, J. (1989). Possible worlds and subject matter. In The problem of the essential indexical and other essays, 1st edition (pp. 145–160). CSLI Publications.
Plebani, M., & Spolaore, G. (2021). Subject matter: A modest proposal. The Philosophical Quarterly, 71(3), 605–622.
Priest, G. (2001). An introduction to non-classical logic (2nd ed., Vol. 2008). Cambridge University Press.
Priest, G. (2005). Towards non-being: The logic and metaphysics of intentionality. Oxford University Press.
Roberts, C. (2012). Information structure: Towards an integrated formal theory of pragmatics. Semantics and Pragmatics, 5, 1–69.
Routley, R., & Routley, V. (1975). The role of inconsistent and incomplete theories in the logic of belief. Communication and Cognition, 8, 185–235.
Soames, S. (1987). Direct reference, propositional attitudes, and semantic content. Philosophical Topics, 15, 47–87.
Stalnaker, R. (1984). Inquiry. MIT Press.
van Fraassen, B. (1968). Presupposition, implication, and self-reference. Journal of Philosophy, 65, 136–157.
van Fraassen, B. (1969). Facts and tautological entailments. Journal of Philosophy, 66(15), 477–487.
Williamson, T. (2000). Knowledge and its limits. Oxford University Press.
Wittgenstein, L. (1974). Tractatus logico-philosophicus. Routledge.
Yablo, S. (2014). Aboutness. Princeton University Press.
Yalcin, S. (2011). Nonfactualism about epistemic modality. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 295–332). Oxford University Press.
Acknowledgements
Variations on the ideas included in this paper were presented at the Exploring Hyperintensional Semantics workshop (November 2018) at Utrecht University; during the Chair Mercier Lectures at the Université Catholique de Louvain; at the 9th Summer School in Philosophy at the University of Hamburg; to the MUMBLE Research Group, Department of Philosophy, University of Turin; to the Metaphysics and Logic Group at Arché in St Andrews; and to the Lingnan Faculty Research Seminar (October 2021) at Lingnan University, Hong Kong. We are grateful to the various audiences, as well as to two anonymous referees for this journal, for helpful comments and objections. This research is published within the project ‘The Logic of Conceivability’, funded by the European Research Council (ERC CoG), Grant No. 681404. Moreover, this publication is part of the project ‘Foundations of Analogical Thinking’ (Project No. 322-20-017) of the research program ’PhDs in the Humanities’, which is (partly) financed by the Dutch Research Council (NWO). Moreover, this publication is part of the project ‘The Semantics of Knowledge and Ignorance’ (ECS Project No. 23603221), funded by the Early Career Scheme of the University Grants Council (UGC) of Hong Kong.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Formal 2C systems
Appendix A: Formal 2C systems
We sketch a template for a 2C propositional semantics that can be made concrete by filling in specific choices depending on one’s needs.
1.1 A.1 Truthmaker semantics as 2C semantics?
One might think that we have hit upon the perfect candidate for a 2C semantics in Sects. 3.3 and 5.2: one can simply use Fine’s truthmaker semantics as a plausible common basis from which to generate, without further machinery, both the truth-conditions and subject-matter for any \(\varphi \). However, the bare Finean faces a dilemma: assure plausible truth-conditions, or assure Transparency.
First horn. Suppose a Finean semanticist admits at least two interpreted sentences p and q with no exact falsifiers and disjoint exact verifiers (i.e., no exact verifier for p has a common part with one for q, and vice versa). ‘2 is even’ and ‘Every bachelor is male’ may be good candidates. It follows that p and q have distinct Finean subject-matter. By the account of \(\vdash \) and \(\dashv \) in Sect. 3.3, p and \(p \vee \lnot q\) have identical Finean subject-matter: since \(\lnot q\) has no exact verifiers, the exact verifiers for \(p \vee \lnot q\) are exactly those for p; since p has no exact falisifiers, \(p \vee \lnot q\) has no exact falsifiers, as no state is a fusion of an exact falsifier for p and an exact falsifier for \(\lnot q\). Similarly, q and \(p \wedge \lnot q\) have identical Finean subject-matter: there are no exact verifiers for \(p \wedge \lnot q\) and the exact falsifiers for \(p \wedge \lnot q\) are the exact verifiers for q. Thus, by Finean lights, \(p \vee \lnot q\) and \(p \wedge \lnot q\) have distinct subject-matter, and Transparency is refuted. But there are independent reasons to accept Transparency (Sect. 6) and, anyway, it is implausible that, say, ‘Every bachelor is male’ has the same subject-matter as ‘2 is even and not every bachelor is male’.
Second horn. The Finean can instead insist that every interpreted sentence has exact falsifiers. But this muddies our aforementioned trick (Sect. 5.2) for generating truth-conditions from exact verifiers (\(\varphi \) is true at s iff part of s is an exact truthmaker for \(\varphi \)). Let p and q be interpreted sentences that are obvious (pre-theoretic) logical contraries (e.g., ‘Lincoln is an unmarried male’, ‘Lincoln is married’). The Finean in question allows a state s that contains an exact falsifier for \(\lnot (p \wedge q)\) and so an exact verifier for \(p \wedge q\). As \(p \wedge q\) is contradictory, s is logically impossible. But then so much for the claim that truth-conditions can be directly generated from exact verification conditions, without further constraint: the truth set \(\lfloor p \wedge q \rfloor \) cannot, on the present view, be identified with the set of states containing an exact verifier for \(p \wedge q\), as the latter contains s, a logically impossible state (i.e., a state that misrepresents truth-conditional laws).Footnote 9
1.2 A.2. A template
Instead, we build a template for a simple formal 2C semantics that, by design, can incorporate both truth-conditional facts and Transparency.
We work with the propositional language built from atomic sentences \(p_0 , p_1, \ldots \) with the Boolean connectives \(\lnot , \wedge , \vee \). We write \({\mathcal {L}}\) for the set of sentences. We now use \(\varphi , \psi , \chi \) as variables for sentences in \({\mathcal {L}}\) and \(p,q,r,\ldots \) as variables for atomic sentences. As discussed in Sect. 2, a semantics should assign meaning to the sentences of \({\mathcal {L}}\), which we then can use to reason about statements of the form \(\varphi \equiv \psi \), saying that the content of \(\varphi \) is equivalent to that of \(\psi \), to the extent that \(\varphi \) and \(\psi \) have identical truth conditions and subject matter. Concretely, we want to say when such statements are true in a model of the semantics, or when they are valid (true in all relevant models).
A model (or abstract model) M is a tuple (S, T, I, J) where
-
S is a set whose elements are called states.
-
T is a set whose elements are called topics.
-
\(I : {\mathcal {L}} \rightarrow {\mathcal {P}}(S)\) is a function, called truth assignment, which maps each sentence \(\varphi \) to a set of states \(I(\varphi ) \subseteq S\). Here \(s \in I(\varphi )\) means that \(\varphi \) is true at state s.
-
\(J : {\mathcal {L}} \rightarrow {\mathcal {P}}(T)\) is a function, called topic assignment, which maps each sentence \(\varphi \) to a set of topics \(J(\varphi ) \subseteq T\). Here \(t \in J(\varphi )\) means that \(\varphi \) is about topic t.
Given M, we write \(\lfloor \varphi \rfloor _M\) for \(I(\varphi )\) and \(\lceil \varphi \rceil _M\) for \(J(\varphi )\); we omit the subscript ‘M’ if clear from context. We say that \(\varphi \equiv \psi \) is true in M (short \(\varphi \equiv _M \psi \)) if \(\lfloor \varphi \rfloor = \lfloor \psi \rfloor \) and \(\lceil \psi \rceil = \lceil \varphi \rceil \).
This system resembles (though is not identical to) the conceptivist system studied by Fine (1986) (drawing on Parry (1968)), the topic logic discussed by Burgess (2009, Ch. 5) (drawing on Epstein (1990)), the issue-based theory defended by Hawke (2018), and the system for TSIM-operators studied by Berto (2022). For a related algebraic approach, see Goodman (2019).
We have defined our language and models in a deliberately abstract way. This leaves two paths for adding structure and specifying more refined theories. On the one hand, one could elaborate the language (e.g., to include first-order linguistic devices) or the models (e.g., to enhance the space of topics with a specific structure, such as the partition structure of Lewis (1988a), deployed by Plebani and Spolaore (2021), among others). On the other hand, one could constrain the class of models. We briefly illustrate the second technique.
1.3 Instances of the template
The states in our abstract models can act like open impossible worlds: truth can be assigned to sentences without constraint. For example, there are abstract models where \(s \in \lfloor p \rfloor \cap \lfloor \lnot p \rfloor \), or where \(s \notin \lfloor p \rfloor \cup \lfloor \lnot p \rfloor \). To avoid this, one can impose constraints familiar from the preceding discussion.
-
(34)
For all sentences \(\varphi \) and \(\psi \), \(\lfloor \varphi \wedge \psi \rfloor = \lfloor \varphi \rfloor \cap \lfloor \psi \rfloor \). (Cf. (17) and (18).)
-
(35)
For all sentences \(\varphi \) and \(\psi \), \(\lceil \varphi \wedge \psi \rceil = \lceil \varphi \rceil \cup \lceil \psi \rceil \). (Cf. (23).)
-
(36)
For all sentences \(\varphi \), \(\lfloor \lnot \varphi \rfloor = S \setminus \lfloor \varphi \rfloor \).
-
(37)
For all sentences \(\varphi \), \(\lceil \lnot \varphi \rceil = \lceil \varphi \rceil \). (Cf. (22).)
-
(38)
For all sentences \(\varphi \) and \(\psi \), \(\lfloor \varphi \vee \psi \rfloor = \lfloor \varphi \rfloor \cup \lfloor \psi \rfloor \).
-
(39)
For all sentences \(\varphi \) and \(\psi \), \(\lceil \varphi \vee \psi \rceil = \lceil \varphi \rceil \cup \lceil \psi \rceil \).
Let’s call models satisfying the constraints (34) –(39) classical 2C models.
Here is an example of a classical 2C model. In fact, it plays an important role, analogous to canonical models in modal logic. So we call it the canonical classical 2C model \(M_c := ( W_c , T_c , I_c, J_c)\). It is defined as follows. Let \(\textsf {At} = \{p_0 , p_1, \ldots \}\) be the set of atomic sentences. Let \(W_c\) be the set of functions from \(\textsf {At}\) to \(\{0,1\}\). So the states are (Ersatz-) possible worlds. Let \(T_c := \textsf {At}\). So the possible topics of sentences are identified with the atomic sentences. Define \(I_c\) recursively as follows for states \(s \in W_c\) (i.e., functions from \(\textsf {At}\) to \(\{0,1\}\)).
-
\(s \in I_c (p)\) iff \(s(p) = 1\)
-
\(I_c (\lnot \varphi ) = W \setminus I_c (\varphi ) \)
-
\(I_c (\varphi \wedge \psi ) = I_c(\varphi ) \cap I_c(\psi )\)
-
\(I_c (\varphi \vee \psi ) = I_c(\varphi ) \cup I_c(\psi )\).
Finally, define \(J_c(\varphi )\) to be the set of atomic sentences occurring in \(\varphi \).
The canonical classical 2C model helps to characterize content-equivalence.
Proposition 1
For any two sentences \(\varphi \) and \(\psi \), the following are equivalent.
-
(1)
\(\varphi \) and \(\psi \) have the same content in all classical 2C models; i.e., for all classical 2C models M, \(\varphi \equiv _M \psi \).
-
(2)
\(\varphi \) and \(\psi \) have the same content in the canonical 2C model; i.e., \(\varphi \equiv _{M_c} \psi \).
-
(3)
\(\varphi \) and \(\psi \) are classically equivalent and have the same atomic sentences.
Proof
(1) \(\Rightarrow \)(2) is trivial. For (2)\(\Rightarrow \)(3), note that \(\lfloor \varphi \rfloor = \lfloor \psi \rfloor \) in the canonical model means that \(\varphi \) and \(\psi \) have the same truth-value under any classical valuation s, so they are classically equivalent. And \(\lceil \varphi \rceil = \lceil \psi \rceil \) in the canonical model means that \(\varphi \) and \(\psi \) have the same atoms. For (3)\(\Rightarrow \)(1), fix any 2C model. First, since \(\varphi \) and \(\psi \) are classically equivalent and states act like classical valuations (given the constraints), \(\lfloor \varphi \rfloor = \lfloor \psi \rfloor \). Second, if \(\varphi \) and \(\psi \) have the same atoms, say, \(p_1, \ldots , p_n\), then, by transparency, \(\lceil \varphi \rceil = \lceil p_1 \rceil \cup \ldots \cup \lceil p_n \rceil = \lceil \psi \rceil \). \(\square \)
In previous work, one of us—LH—(Hornischer, 2020) has shown that the above notion of content-equivalence is exactly axiomatized by the following calculus: take the calculus \(\textsf {AC}\) of Fine (2016a) and add (using our notation) the axiom \(\varphi \equiv \varphi \vee (p \wedge \lnot p)\) for all atomic p occurring in \(\varphi \).Footnote 10 Then \(\varphi \equiv \psi \) is derivable in this calculus if and only if \(\varphi \) and \(\psi \) are synonymous according to our above classical 2C semantics.
One need not concentrate on the classical setting. One could replace (36) with a weaker constraint, making room for incomplete states, at which a sentence \(\varphi \) is neither true nor false:
-
(40)
For all sentences \(\varphi \), \(\lfloor \varphi \rfloor \cap \lfloor \lnot \varphi \rfloor = \emptyset \).
If the rest of the constraints (34)–(39) are imposed, the resulting logic mimics strong Kleene logic (e.g., Priest, 2001, Ch. 7). Alternatively, one could drop even (40), allowing inconsistent states where a sentence \(\varphi \) can be both true and false, like in the logic FDE (e.g., Priest, 2001, Ch. 8). The characteristic axiom from above (i.e., \(\varphi \equiv \varphi \vee (p \wedge \lnot p)\) with p an atom of \(\varphi \)) is not valid for this class of models.Footnote 11 However, the following content-equivalence is preserved.Footnote 12
-
(41)
\(\varphi \vee ( \varphi \wedge \psi ) \equiv \varphi \vee ( \varphi \wedge \lnot \psi )\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hawke, P., Hornischer, L. & Berto, F. Truth, topicality, and transparency: one-component versus two-component semantics. Linguist and Philos 47, 481–503 (2024). https://doi.org/10.1007/s10988-023-09408-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10988-023-09408-y