Abstract
Extant attempts to incorporate intensionality into the grammar either systematically over-generate, or systematically under-generate. In this paper, building on Keshet (Linguist and Philos 33(4):251–283, 2011), we aim to reconcile a scopal account of de re with the possibility of de re readings out of scope islands. By adapting compositional techniques for dealing with exceptionally scoping indefinites (Charlow, in On the semantics of exceptional scope, PhD thesis, Rutgers University, 2014; The scope of alternatives: indefiniteness and islands. Linguist and Philos 43(4):427–472, 2020), we develop an intensional grammar in which exceptional de re is achieved via cyclic scope. World-sensitive expressions are converted into scope-takers via a constrained inventory of type-flexible operators. Type flexibility explains the possibility of apparently island-violating de re by predicting the possibility of cyclic scope-taking. We argue that the resulting theory—which we dub the flexible scope theory—is sufficiently expressive to address the under-generation issues of current accounts, while still capturing constraints on de re in an explanatory fashion.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In an intensional context, nominal predicates may be interpreted de re or de dicto. Under the de re interpretation, (1) can be true even if George’s beliefs don’t pertain to Red Sox players, but rather to a group of people who, unbeknownst to him, happen to be Red Sox players. On the de dicto interpretation, George’s desires pertain to Red Sox players, and (1) need not entail that any Red Sox players actually exist. Theoretically, the standard way of cashing this out is to assume that predicates in general are world sensitive.

There are two broad camps for incorporating world-sensitivity into a compositional semantics—the Scope Theory of Intensionality (sti) and the Binding Theory of Intensionality (bti). The bti is extremely expressive, but must be supplemented with a binding theory for world variables. The sti is much more restrictive, but seemingly under-generates—addressing these under-generation issues will be a central focus of this paper.
The state of the art scope theory is Keshet’s (2008, 2011) split intensionality. Split intensionality succeeds in addressing some of the worst under-generation issues, but others remains. Concretely, Keshet’s (2010) account of exceptional de reFootnote 1 runs into some apparently insurmountable obstacles.
In this paper, I’ll aim to improve on split intensionality by presenting a new take of the sti, which I’ll call the flexible scope theory, whereby expressions can receive exceptional de re interpretations via cyclic scope-taking, facilitated by a minimal inventory of type-shifters. The flexible scope theory will preserve a central insight of Keshet’s split intensionality theory—namely, that de re involves scoping at an edge position. The resulting theory will bear a non-accidental family resemblance to Charlow’s (2014, 2020) theory of exceptionally scoping indefinites.
2 The scope theory and its discontents
2.1 The binding theory vs. the scope theory
According to the Binding Theory of Intensionality (bti), there are expressions in the object language (world pronouns) denoting variables ranging over possible worlds; according to, e.g., von Fintel and Heim ’s (2011) implementation, the Logical Form (lf) for a simple Determiner Phrase (dp) such as the lawyers involves the predicate lawyers taking a covert world pronoun as its first argument, as illustrated below.

World pronouns are assumed to be bona fide pronouns, and therefore may be bound or free. According to the bti, a de re interpretation arises when a covert world pronoun is bound by a non-local binder. The lf for (2) according to the bti, where lawyers is interpreted de re, is schematized in (3).


The bti completely divorces world-sensitivity from scope, and is therefore extremely expressive. Concretely, as shown by Percus (2000) and others, the bti, if not restricted, can generate a range of unattested de re interpretations. We discuss the constraints on de re at length in Sect. 5. On such a theory, there is a need for a binding theory for world variables. It is far from obvious that such a theory can be made to follow from independently motivated restrictions on pronominal binding.Footnote 2
According to the Scope Theory of Intensionality (sti)Footnote 3, on the other hand—at least, on its simplest form—world-sensitivity tracks scope. There is no need for world pronouns on such a theory. In order to account for the for the de re interpretation of lawyers in (2), the sti says that the dp scopes above the intensional verb want, as schematized in (4)Footnote 4

An appealing feature of the sti is that it is much more constrained than the bti—concretely, it predicts that constraints on de re interpretations should track constraints on scope. Unfortunately, it immediately runs into some problems. For example, dps embedded inside of constituents known to be scope islands can nevertheless receive de re readings. Consider for example (5)—it can be true in a context in which Roger falsely believes a group of linguists to be philosophers, and furthermore, believes that they are all drunk.

However, embedded finite clauses are generally considered to be islands for scope-taking operations (May 1977), as illustrated by the absence of a wide scope reading of the universal in (6):Footnote 5

Furthermore, even if scope-taking could exceptionally violate a scope island in order to achieve a de re interpretation, as pointed out by Keshet , this makes bad predictions for the scopal interaction between the Quantificational Phrase (qp) and the embedding operator. Keshet (2011, p. 254) illustrates this with example (7). As he observes, everyone in this room must be interpreted de re, otherwise the conditional antecedent would be contradictory. (7) can’t mean however: everyone in this room x is s.t. if x were outside, it would be empty; the conditional antecedent is a universal statement about everyone (actually) outside. Therefore the quantificational force of everyone must scope below the conditional operator.

In order to address this and similar issues while maintaining a constrained theory of de re, Keshet (2008, 2011) develops a more nuanced take on the sti: split intensionality. The idea, briefly, is that there is a privileged position at the clause edge in which dps can be interpreted de re relative to an embedding verb, without scoping out of a scope island. In the next section, we survey split intensionality, pointing out its advantages over the bti, before discussing some apparently insurmountable problems for the theory.
2.2 Split intensionality
The state of the art in the sti is Keshet’s (2008, 2011) split intensionality. Split intensionality is designed to address under-generation issues of the sti. As alluded to above, one of the primary issues for the sti is the fact that de re readings are not constrained by scope islands. Keshet ’s solution involves positing a distinguished position at the clause edge, beneath the embedding predicate, but above an operator dubbed up (after Montague 1970), written \(\wedge \). Keshet assigns (5) the lf below. To quote (Keshet 2011, p. 264): “[...] this creates an intensional twilight zone, where dps may be evaluated de re relative to an operator, but still scope beneath this operator in terms of quantificational force.” This is illustrated for the de re reading of the linguist in (5), in Fig. 1.
The technicalities of split intensionality won’t be so important for our purposes, but concretely: Keshet assumes a compositional regime in which the interpretation function is parameterized to an evaluation world, which may be extensionalized in order to resolve a type mismatch (Heim and Kratzer ’s 1998intensional function application, see also von Fintel and Heim 2011). The purpose of the \(\wedge \) is to trigger a syncategorematic rule intensional abstraction, defined below:

The result of doing intensional abstraction below the landing site of the dp, is that the dp ends up evaluated relative to the global evaluation world, whereas the predicate is evaluated relative to the \(\lambda w'\) introduced by \(\wedge \). This is illustrated in Fig. 2.Footnote 6
As the reader will surely have noticed, something additional needs to be said for examples involving quantificational dps, which are of type \(\mathtt {(e\rightarrow t)\rightarrow t)}\)—if a quantifier qrs above an up-operator, there will be a type mismatch, since the scope site is of type \(\mathtt {e\rightarrow s \rightarrow t}\). Keshet ’s solution is to posit a syncategorematic rule especially for quantificational dps, based on Büring ’s (2005) argument saturation. We provide a simplified version of Keshet ’s proposal below:

Composing a qp with an intensional scope site “passes up” the world argument of the scope site, as illustrated below for the example Roger thinks that every linguist is drunk, with every linguist interpreted de re.
It should be clear that scoping a quantifier over an up-operator allows the restrictor to be interpreted de re with respect to the embedding predicate, while the quantificational part of the qp’s meaning takes narrow scope with respect to the embedding predicate.
2.3 Problems for Split Intensionality
2.3.1 Doubly-embedded scope islands
One immediate prediction made by split intensionality is that configurations involving doubly-embedded scope islands only allow an XP in the inner-most scope island to be interpreted de re relative to the minimally c-commanding embedding predicate. This is illustrated schematically in Fig. 4—if both \(\omega \) and \(\omega '\) embed scope islands, then split intensionality only allows XP to be interpreted de re relative to \(w'\). This is because XP can only scope as high as the edge of the minimally containing scope island.
Keshet suggests, counter-intuitively, that this prediction is a good one. The argument is based on judgments involving the antecedent of counterfactual conditionals. As a baseline, Keshet observes that a counterfactual with a tautological antecedent sounds odd, illustrated via the contrast below.

The key observation here is: if the dp three professors were interpreted de re relative to some higher operator, then the antecedent has a chance of no longer being tautological. If the entire counterfactual statement in (10b) were embedded under an attitude verb, the dp three professors could be interpreted de re relative to the higher operator only by violating the islandhood of the condition antecedent. Split intensionality therefore predicts that (10b) should not be rescuable via embedding under a higher attitude verb. This indeed appears to be the case, as illustrated by (11):

A de re interpretation of three professors relative to thinks would require an lf such as the one in Fig. 5, which should be ruled out by syntactic constraints on scope-taking.
One problem with Keshet ’s argument is that indefinites, which are independently known to take exceptional scope, seem to give rise to parallel judgments. To elaborate, consider (12). This has a salient reading which can be paraphrased as: there’s a relative of John’s x, s.t. if x were John’s friend, John would be in x’s will. This reading (apparently) involves a relative of John’s taking exceptionally wide scope out of the conditional antecedent.

Just as before, a tautological antecedent gives rise to oddness:

Now, observe that if we embed the entire conditional statement in (13) under an attitude verb the result is still odd, as illustrated by (14). By way of contrast, (15) has a perfectly sensible reading (that doesn’t involve Mary doubting a tautology), just in case a relative of John’s is interpreted de re.


Since it’s independently possible for a relative of John’s to take exceptional scope out of the counterfactual antecedent, and furthermore scope feeds de re according to split intensionality, it’s prima facie mysterious on this theory why (14) doesn’t have a sensible reading—it suggests that whatever the explanation for the oddness of (14) is, it shouldn’t be based on scope, and therefore weakens this particular argument in favor of split intensionality.
Moreover, it is possible to come up with sentences which are parallel to example (14) which nevertheless have a sensible reading. (16) provides a baseline—the counterfactual statement sounds odd, since the antecedent is tautological. Furthermore, (17) has a sensible reading, just in case three syntacticians is interpreted de re.


The relevant test case is (18). To my ear, this has a sensible reading just in case three syntacticians is interpreted de re. I don’t have a full understanding of why Keshet ’s original examples sound so odd, but I would speculate that the oddness has its source in a repetition of the NP restrictor.

Looking now beyond the specific cases discussed by Keshet , its clear in the general case that de re readings out of doubly-embedded scope islands are possible (see Grano 2019 for different arguments for the same conclusion). (19), for example, doesn’t necessarily entail that Mary’s beliefs involve anyone being in this room—it can be true in a scenario in which there’s a group of people X who are actually in this room; Mary believes that X are actually outside.

2.3.2 Bäuerle’s puzzle
Another problem for split intensionality, and for scope theories more generally, is Bäuerle’s puzzle (Bäuerle 1983). Bäuerle’s puzzle involves a scope paradox that emerges on classical scope theories of intensionality. Keshet (2010, p. 692) illustrates the puzzle with the following example, after Bäuerle .

The crucial observation is that (20) has a reading with the following properties:
-
every Red Sox player is interpreted de re.
-
five star hotel downtown is interpreted de dicto.
-
some five star hotel downtown takes scope over every Red Sox player.
(20) could be true under this reading in the following situation: George has mistaken the Red Sox players for the Yankees, and he thinks that this group of people are all staying in the same five star hotel downtown. To see the scope paradox, consider that on a split intensionality theory, to be interpreted de re, and dp must scope above an up-operator at the clause edge. The lf for the target reading must therefore fulfill the requirements listed below, which give rise to a contradiction by transitivity:
-
\(\forall > \wedge \)
-
\(\wedge > \exists \)
-
\(\exists > \forall \)
Keshet ’s response is tied to the observation that some five star hotel downtown is an expression that can take exceptional scope. Keshet adopts a theory of exceptionally scoping indefinites according to which they are interpreted as choice-functional variables, existentially bound from their scope site. Under the target reading, therefore, (20) has the lf below.Footnote 7

Because Keshet ’s response is wedded to a particular analysis of exceptionally scoping indefinites, it’s not going to be sufficiently general.Footnote 8 This is because Bäuerle’s puzzle generalizes to non-exceptionally-scoping qps. Consider (22)—this has a reading on which exactly three Red Sox players is interpreted de re, every hotel room is interpreted de dicto, but every takes scope over exactly three. To illustrate, (22) can be true in a scenario where: George has mistaken a group of people staying in a hotel for Yankees—they are actually Red Sox players. He believes that people from this group are staying three-to-a-room, and they trashed their hotel rooms.

Since every hotel room isn’t an exceptional scope taker, the same strategy isn’t available for having it take wide quantificational scope over exactly three Red Sox players, while being interpreted low for the purposes of de re/de dicto. It seems that, in general, a problem with Keshet ’s approach, and scope theories in general, is tying quantificational and intensional scope too tightly together.Footnote 9
3 Scope theory redux
3.1 Bootstrapping an intensional fragment
In this section, we’ll start from minimal means and bootstrap a different way of achieving world-sensitivity that (I’ll argue) slices the pie in just the right way. Rather than assuming that the interpretation function  is relativized to a world parameter, I’ll simply assume that we want our semantics to deliver world-sensitive values. In (24) we characterize the space of intensional values by defining a type constructor \(\textsf {S}\). \(\textsf {S}\) is a function from types to types—it takes a type \(\textsf {a}\) and gives back an intensional type, i.e., a functional type \(\textsf {s} \rightarrow \textsf {a}\), where \(\textsf {s}\) is taken to be the type of a world.
is relativized to a world parameter, I’ll simply assume that we want our semantics to deliver world-sensitive values. In (24) we characterize the space of intensional values by defining a type constructor \(\textsf {S}\). \(\textsf {S}\) is a function from types to types—it takes a type \(\textsf {a}\) and gives back an intensional type, i.e., a functional type \(\textsf {s} \rightarrow \textsf {a}\), where \(\textsf {s}\) is taken to be the type of a world.

One straightforward way of achieving an intensional fragment is to assume that predicates are world-sensitive. The denotation we assume for simple predicates is illustrated in (25) with swim.

Since definite descriptions give rise to de re/de dicto ambiguities, they must exhibit world-sensitivity, and therefore be parameterized to a world argument, just like predicates. If we assume a Fregean analysis of definite descriptions, then there is only one way of implementing this—we must treat definite descriptions as individual concepts (i.e., world-sensitive individuals).Footnote 10 I’ll therefore assume that definite descriptions are of type \(\textsf {S}\,\textsf {e}\), as illustrated below:

Thinking through the simple mechanical puzzle of how to compose the meanings in (25) and (26) will be a necessary first step on the road to achieving exceptional de re. First of all, observe that attempting to compose the predicate with the dp results in a type mismatch, assuming that Function Application (fa) is the only composition rule we have available.

What we want is a composition principle which extracts the type \(\textsf {e}\) part of the argument, the type \(\textsf {e} \rightarrow \textsf {t}\) part of the predicate, and does fa, while tracking world-sensitivity: we’ll dub this operation World-sensitive Function Application (wfa). We cash out wfa via the infix operator \(\circledast \) in (28), to accomplish just this.Footnote 11

Definite descriptions may now compose in-situ via wfa.
This begs the question of how arguments without an outer layer of world-sensitivity, such as proper names, compose with predicates. If we assume that proper names are expressions of type \(\textsf {e}\), the most straightforward way of integrating them into our putative compositional regime is to first furnish them with a trivial outer layer of world-sensitivity, at which point composition can proceed via wfa. In order to accomplish this, we’ll define a type-shifting operation which will ultimately play a similar role to Keshet ’s up operator, therefore we’ll also call it up (written \(\wedge \)). Our up-shifter simply takes an a and turns it into a trivially intensional a adding a vacuous \(\lambda w\).Footnote 12 Note that we’ve defined the up-shifter in a maximally polymorphic way—it simply takes something of any type and and returns its intensional value.

With our up-shifter in hand, composition of a sentence with a proper name may proceed smoothly via wfa.
At this point, we have a theory which automatically derives de dicto readings for definite descriptions in embedded clauses. In Fig. 8, we consider such a case. We assume a standard theory of attitude verbs such as doubt, according to which they compose with propositional arguments of type \(\textsf {S}\,\textsf {t}\). Note that just like proper names, the argument of an attitude verb must be up-shifted before composition may proceed via wfa.
Just as under split intensionality, insertion of the up-shifter at the edge of the intensional environment creates an “intensional twilight zone”, driven here by the needs of composition. Intuitively, we might expect to be able to derive a de re interpretation by qr-ing the definite over the up-shifter at the edge of the embedded clause, just as in Keshet ’s theory. We can assume that qr leaves behind a trace, interpreted as a variable of type \(\textsf {e}\), which composes via wfa once up-shifted. What we observe is that the definite can’t compose at its scope-site via wfa, as illustrated in Fig. 10. We need a way of taking a world-sensitive individual, and turning it into an intensional scope-taker.
Concretely, we need to somehow extract just the type \(\textsf {e}\) part of the definite description at the scope site, and feed it into the scope, while ensuring that the world argument of the dp is interpreted relative to the same world as the scope. Below, we define an operator bind (\(\star \)) in order to accomplish just this. Note that, just like the up-shifter, bind is defined in a maximally polymorphic way: it takes an intensional a, and a function from an a to an intensional b, and returns an intensional b.

Applying bind to a description such as the linguist gives back the result in (31). Note that the type signature of the scope in Fig. 10 (\(\textsf {e} \rightarrow \textsf {S}\,(\textsf {S}\,\textsf {t)}\)) is an instantiation of the polymorphic type \(\textsf {e} \rightarrow \textsf {S}\,\textsf {b}\).

Scoping the linguist over an up-shifter resolves the type variable \(\textsf {b}\) as \(\textsf {S}\,\textsf {t}\). The result is a doubly world-sensitive proposition, where the world-sensitivity of the description is interpreted relative to the outer layer of world-sensitivity—this may compose in-situ with an attitude verb via wfa. This is illustrated in Fig. 10.
We’ve achieved a limited account of exceptional de re, in line with Keshet ’s split intensionality. At first blush, it seems as if this intensional grammar will have exactly the same shortcomings as Keshet ’s theory: namely it will fail to account for exceptional de re in its full generality. It turns out, however, that the intensional grammar we’ve sketched is significantly more powerful. We’ll illustrate this in the next section, by looking at doubly-embedded scope islands.
3.2 Generalizing exceptional de re
Now that we’ve motivated up and bind, we have everything we need to derive exceptional de re in its full generality, without ever violating a scope island. What will be crucial will be the polymorphism of our type-shifters. The general account will hinge on the observation that a doubly world-sensitive proposition may itself be bind-shifted and scoped over an up-shifter. In order to illustrate how this derives exceptional de re in its full generality, consider example (32).

Let’s go through the computation where the philosopher is interpreted de re step-by-step. First, we bind-shift the dp, and scope it above the up-shifter inserted at the edge of the embedded clause. This is illustrated in Fig. 11.
The embedded clause itself now denotes a doubly world-sensitive proposition. Since bind is polymorphic, there is nothing preventing us from bind-shifting the embedded clause, and qr-ing it over the up-shifter at the edge of its containing clause; it leaves behind a trace of a propositional type. In order to compose the propositional trace with the embedding predicate, it is first up-shifted, then composition proceeds via wfa. This is illustrated in Fig. 12.
Zooming out, the resulting lf involves cyclic scope, as schematized in Fig. 13. This is reminiscent of the account of exceptionally scoping indefinites proposed by Charlow (2020), which is itself a distant cousin of Dayal ’s (1996) account of Baker’s ambiguity. Syntactically, as noted by Charlow (2020), there are some precedents for movement operations of this kind in the overt syntax, such as snow-balling pied-piping in Finnish (see Huhmarniemi 2012).Footnote 13
3.3 Multiple embeddings and intermediate readings
It’s possible to construct examples in which a dp is interpreted de re relative to some lower operator, but de dicto relative to some higher operator (see Keshet and Schwarz 2019 and Grano 2019 for discussion). For example, (33) can be true in a scenario in which there’s a linguist who both Sam and Tom falsely believe to be a biologist. Mary falsely believes them to be a philosopher, and furthermore, Mary thinks that Tom hopes Sam invites this person. We can account for this reading if the philosopher can be interpreted de re relative to hope, but de dicto, relative to think.

On the flexible scope theory, we can cash this out in much the same way as Keshet (2011), by scoping the philosopher to the edge of the most deeply embedded clause, over an up-shifter, ensuring that philosopher is evaluated relative to an outer-layer of world-sensitivity. The embedded clause composes with hope via wfa—this is schematized in (34). A more detailed derivation is suppressed, but should be straightforward to reconstruct.

Similarly, it’s easy to construct a scenario in which Mary, Tom, and Sam all have false beliefs about the profession of the referent of the dp, but the speaker knows that the referent is a philosopher. On this reading, the dp receives a total de re interpretation. Since the procedure for deriving de re interpretations is recursive, this can be easily achieved on the flexible scope theory by scoping the philosopher to the edge of the embedded clause, followed by scoping the embedded clause itself. Again, the derivation is schematized in (35):

3.4 Exceptional scope and the monad laws
Readers familiar with functional programming and/or category theory may recognize the type constructor \(\textsf {S}\), alongside the operations \(\star \) and \(\wedge \), as a monad, a mathematical construct commonly used for modeling “effectful” computation (see, e.g., Wadler 1995). Concretely, the tuple \((\textsf {S}, \wedge , \star )\) is an instantiation of the Reader monad.Footnote 14\(^,\)Footnote 15 To qualify as monad, the operations \(\wedge \) and \(\star \) must obey three laws: Left Identity, Right Identity, and Associativity.

\(\textsf {S}\) is an instantiation of an existing, well understood monad — the Reader monad. Any monad additionally entails a corresponding enrichment of fa, which can be defined in terms of \(\star \) and \(\wedge \) as in (37)—this is just wfa. Our definition of wfa was therefore not arbitrary, but follows from the definitions of \(\star \) and \(\wedge \) (we’ll frequently take advantage of this equivalence in the following sections).Footnote 16

A consideration of the laws can help us understand why exactly a monad is necessary for accounting for exceptional scope. Consider again a schematic lf for the exceptional de re reading of the philosopher in the following example involving two layers of embedding:


By associativity, this is guaranteed to be equivalent to the following:

By left identity, this is guaranteed to be equivalent to the following, i.e., an lf involving island-violating qr:

In general, given a type constructor \(\textsf {M}\), if there are operations \(\eta _{\textsf {a} \rightarrow \textsf {M}\,\textsf {a}}\) and \(\gg \!\!=_{\textsf {m}\,\textsf {a} \rightarrow (\textsf {a} \rightarrow \textsf {M}\,\textsf {b}) \rightarrow \textsf {M}\,\textsf {b}}\), which obey the monad laws, the natural language correlate is that expressions of type \(\textsf {M}\,\textsf {a}\) should exhibit exceptional scope behavior. In the current setting, \(\textsf {m} = \textsf {S}\), \(\eta = \wedge \), and \(\gg \!\!== \star \). Intensionality, as modelled by \(\textsf {S}\), therefore slots neatly into a broader category of phenomenon which exhibit exceptional scope.
An exemplar is Charlow’s (2014, 2020) account of the exceptional scope of indefinites, and indeed this work very much inspired the strategy for accounting for exceptional de re pursued here. Charlow models the indeterminacy associated with indefinites. Exceptional scope is accounted for via the logic of cyclic-scope taking, which by the monad laws, as we’ve just seen, is equivalent to bona fide scoping out.
One way of seeing why a monad is necessary for accounting for exceptional scope is to consider other ways in which we might lift expressions of type \(\textsf {S}\,\textsf {a}\) into scope-takers. Consider, e.g., the following operation, for. This operation takes an intensional value, and returns a scope taker that expects a \(\textsf {b}\) and returns an \(\textsf {S}\,\textsf {b}\).

If we apply \(\mathtt {for}\) to a dp, and scope it to the edge of an up-shifted proposition (type \(\textsf {S}\,\textsf {t}\)), there is no way of getting back something of type \(\textsf {S}\,(\textsf {S}\,\textsf {t})\); rather, what we get is a doubly world-sensitive proposition of type \(\textsf {S}\,(\textsf {S}\,(\textsf {S}\,\textsf {t}))\). Intuitively, this is because, \(\texttt {for}\) doesn’t provide a way of unifying the \(\lambda w\) associated with the dp, with the \(\lambda w\) introduced by the up-shifter. Scoping out the embedded clause via \(\mathtt {for}\) would simply result in something of too high a type—we assume here that declarative sentences must ultimately denote a value of type \(\textsf {S}\,\textsf {t}\).
The operation \(\mathtt {for}\) is map with the arguments flipped—map is an operation that maps a function of type \((\textsf {a} \rightarrow \textsf {b})\) into something of type \(\textsf {S}\,\textsf {a}\). The type constructor \(\textsf {S}\) and \(\mathtt {map}\) constitute a functor, a strictly weaker notion than a monad—in fact, a monad entails a functor.Footnote 17
What makes the difference here is that monadic bind, i.e., \(\star \), builds in a way of collapsing two layers of intensionality into one. It is this property that allows for an account of exceptional scope in terms of cyclic scope over an up-shifter.
3.5 Evidence for scope: the nested DP constraint
So far, to get to the core of the account of exceptional de re proposed here, we’ve focused exclusively on de re interpretations of definite descriptions, putting quantificational dps to one side. Based on what we’ve seen so far, it may seem as if dps may be receive de re interpretations arbitrarily, relative to any structurally higher intensional operator. Is there really any independent reason to believe that the de re interpretation of a definite dp is tied to its scope-taking ability, given the lack of any obvious restrictions on de re readings? In this section, we’ll see initial evidence that de re readings are in fact subject to a systematic structural restriction—one that patterns with independently motivated restrictions on scope-taking.
Romoli and Sudo (2009) discuss possible readings of examples involving a dp nested inside of another dp, such as (44). Given that the nested dp is embedded in complement of an attitude verb, by the logic of the de re/de dicto ambiguity, there are four possible readings of the sentence. The first two readings are the most salient—the entire nested dp can be interpreted (i) totally de re or (ii) totally de dicto. Of particular interest is the availability of mixed readings: (iii) president is interpreted de re, and wife de dicto, and (iv) president is interpreted de dicto, and wife de re. Romoli and Sudo argue that only (iii) is available; (iv) is systematically unavailable. As we’ll see, this falls out automatically if de re is fed by scope-taking, even given the expressive power of the system outlined here.

Romoli and Sudo ask us to consider the following context: “Mary is watching television and sees Barack Obama, the actual president, and his sister besides him. Also, she doesn’t know who he is and she thinks that the woman besides him must be is his wife.” (p. 430). As they observe, (44) is judged to be true in this scenario. On the flexible scope theory, we can easily generate this by scoping the president out of its container (cf. Heim and Kratzer 1998), to the edge of the embedded clause.
It is, however, often assumed that dp is a scope island, primarily in order to account for Larson’s generalization.Footnote 18 The flexible scope theory is sufficiently expressive to account for the attested mixed reading without scoping the contained dp out of its container. Briefly, the logic is as follows: we scope the president to the edge of the containing dp, over an up-shifter, and then cyclic scope proceeds as usual.
First, the contained dp scopes to the edge of the container, over an up-shifter, deriving a doubly world-sensitive individual as the value of the nested dp—president is interpreted relative to the outer later of world-sensitivity, and wife is interpreted relative to the inner layer.
Next, the nested dp is bind-shifted, and scopes out over an up-shifter at the edge of the embedded clause, leaving behind an intensional trace, which composes in-situ via wfa. The result, as usual, is a doubly world-sensitive proposition, of type \(\textsf {S}\,(\textsf {S}\,\textsf {t})\): president is interpreted relative to the outer layer of world-sensitivity, and wife is interpreted relative to the inner layer of world-sensitivity, as illustrated in Fig. 16. This corresponds to Romoli and Sudo ’s attested mixed reading.
Moving on, now let’s consider the mixed reading that is argued by Romoli and Sudo to be unattested. Romoli and Sudo ask us to consider the following context: “Mary sees Bono Vox on TV with his wife Alison Hewson. Mary wrongly believes that he is the president, and furthermore, that the nice woman next to him is his sister. Thus, the wife-relation is actually true, but the characterization of Bono Vox as the president is not.” (p. 430). As Romoli and Sudo observe, our sentence (repeated in (45)) is intuitively false in such a context.

As Romoli and Sudo point out, this is a rather mysterious restriction on a theory such as the bti. This restriction however naturally falls out from the flexible scope theory (and indeed, any scopal approach to de re). This is because, for president to be interpreted de dicto and wife de re, the president should scope within the embedded clause, below the up-shifter at the clause edge, whereas the containing dp should scope above the up-shifter, as schematized in the following (illicit) lf:

This lf must be disallowed, on independent grounds, since it involves an unbound trace.Footnote 19 Scope theories therefore make a good prediction for restrictions on de re readings—here we’ve shown that it’s possible for a scope theory to avoid the over-generation worries associated with the classical sti and its successors, while still retaining an explanation for the nested dp constraint. Scope theories have other explanatory virtues too, which we’ll come back to once we completed our exposition of the flexible scope theory in the next section.
4 Intensional scope and quantificational scope
So far, our fragment has one glaring omission—we’ve said nothing yet about quantificational dps such as every boy. Relatedly, we’ve said nothing regarding how definite descriptions come to denote individual concepts in the first place. This section will address both of these issues, and it will turn out that all of the machinery that we need is in fact already in place. In the next subsection, we’ll begin with a discussion of how definite descriptions come to denote individual concepts.
4.1 DP-internal composition
On the flexible scope theory, definite dps are interpreted as individual concepts—how do we account of this compositionally? Let’s begin by assuming that definite determiners receive a classical Fregean interpretation.Footnote 20 There is, of course, no semantic reason to make determiners themselves world-sensitive.

There’s a straightforward way of composing a determiner with a predicate within the confines of our existing compositional regime—namely, we simply up-shift the determiner, and compose it with the predicate via wfa. This is exactly parallel to the procedure of composing a proper name with a predicate, only the function-argument relation is reversed.Footnote 21

We can use the monad laws to simplify the result: an individual concept.

The exact same strategy is also be applicable to quantificational determiners. We first up-shift the determiner, and compose it with the restrictor via wfa.


Again, we can use left identity to simplify the result—a world-sensitive quantifier.

In the next section, we’ll tackle the problem of how world-sensitive quantifiers enter into composition
4.2 Composing quantifiers
As discussed in the previous section, determiners are up-shifted and compose with their restrictor via wfa—for the definite determiner, the result is an individual concept, and for a quantificational determiner, the result is a world-sensitive quantifier. We know how to compose an individual concept with a verbal predicate, namely via wfa; world-sensitive quantifiers in subject position may compose in much the same way, only the function-argument relationship is reversed.

Unsurprisingly, quantifiers in object position must scope out via qr in order to resolve a type-mismatch. At this point, there’s a compositional wrinkle that needs to be addressed—so far, we’ve been assuming that qr to an intensional scope-site creates a derived predicate of type \(\textsf {e} \rightarrow \textsf {S}\,\textsf {t}\), which is what we expect if we naively apply Heim and Kratzer ’s Predicate Abstraction (pa). This is exactly what we want for bind-shifted definites, but a world-sensitive quantifier can’t compose with such a scope. In order to compose the world-sensitive quantifier at its scope site, we assume that movement can also create a world-sensitive derived predicate of type \(\textsf {S}\,(\textsf {e} \rightarrow \textsf {t})\); we indicate this abstraction schema via \({\bar{\lambda }}\).Footnote 22 Assuming that this option is available, the world-sensitive quantifier may compose with its scope simply via wfa. This is illustrated in Fig. 17.
At this point, note that our intensional grammar predicts the availability of an interesting possibility: A world-sensitive quantifier may itself be bind-shifted, and scoped above an up-shifter, in which case it must leave behind an extensional higher-order trace of type \((\textsf {e} \rightarrow \textsf {t}) \rightarrow \textsf {t}\). The higher-order trace may itself compose just like a world-sensitive quantifier, once up-shifted. This is illustrated in Fig. 18.
The result is something familiar: a doubly world-sensitive proposition. The restrictor boy is interpreted relative to the outer layer of world-sensitivity, and the quantificational meaning component semantically reconstructs. The possibility of leaving behind a higher-order trace will be crucially implicated in our account of Fodor ’s third reading, discussed in the next section, and ultimately, Bäuerle’s puzzle. The intuition will be that the final landing site of a qp marks its intensional scope, whereas the higher-order trace marks its quantificational scope.

The use of higher-order traces here bears a resemblance to semantic theories of reconstruction (see, e.g., Cresti 1995 and von Fintel and Heim 2011). It’s worth mentioning that the extent to which overt movement allows for semantic reconstruction is a somewhat vexed issue (see, e.g., Fox 1995; Romero 1998, and Poole 2017 for critical discussion), but nothing in the flexible scope theory crucially hinges on the qr-based approach to scope; indeed there are many theories of scope-taking which don’t require explicit reference to variables and assignments (see Appendix). In the more general case, it would require further stipulation to rule out lfs involving higher-order abstraction.Footnote 23
4.3 Fodor’s third reading
Fodor (1970) famously discussed sentences such as (57) (this particular example is taken from von Fintel and Heim 2011, p. 100). She observed that it has at least three readings, which she labels specific de re, non-specific de dicto, and non-specific de re.

On the specific de re reading, (57) says that there’s a hat that is actually just like mine, and Mary happens to want to buy it. In our terms, this reading involves both wide intensional and quantificational scope. There are a number of routes to this reading in the flexible scope theory, but perhaps the simplest would be to bind-shift a hat just like mine and scope it over want, leaving behind an extensional trace.

On the non-specific de dicto reading, (57) says that Mary’s desire consists of the following: buying a hat that is just like mine; any such hat will do. In our terms, this reading involves both narrow intensional and quantificational scope. Just as before, the intensional and quantificational meaning components scope together. We derive it by simply scoping a hat just like mine locally below want.

The non-specific de re reading is of particular interest, as it is here that quantificational scope and intensional scope diverge. Concretely, on this reading (57) says something like the following: Mary has a desire to buy any hat that satisfies a particular condition, e.g., one that suits her. Unbeknownst to Mary, my hat happens to suit her. She may not be aware of it, but her desires encompass my hat. In our terms, this reading involves narrow quantificational scope but wide intensional scope. How do we achieve this in our system? We simply take advantage of the possibility of leaving behind a higher-order trace, as discussed in the previous section. The quantificational part of a hat just like mine semantically reconstructs below want (see von Fintel and Heim 2011, chapter 8 for discussion of this strategy); intensional effects can thereby outscope quantificational effects. The derivation of the third reading is illustrated in the lf in Fig. 19.
There is, of course, logically a fourth potential reading we may consider—a specific de dicto reading. If we consider our original example, repeated below as (61), this would amount to a context in which there is a particular hat that Mary wants to buy, and she wants to buy it under the description “a hat just like mine”. There is a broad consensus in the literature that Fodor ’s fourth reading is in fact unavailable (see von Fintel and Heim 2011, chapter 8; Keshet and Schwarz 2019, a.o. for discussion),Footnote 24

Even with the expressive power of the flexible scope theory, it’s not possible for quantificational effects to outscope intensional effects.Footnote 25 Why is this? A fundamental design feature of the flexible scope theory is that logical operators, such as determiners, receive their classical (extensional) meanings, and only manage to interact with world sensitive things via type-lifting. In order to achieve quantificational effects out-scoping intensional ones, we’d need to posit a determiner that quantifies over individual concepts. In order to account for the absence of Fodor ’s fourth reading, we speculate that there simply aren’t any natural language determiners that do this as part of their inherent meaning—natural language determiners are Generalized Quantifiers (gqs) over individuals, and must be up-shifted in order to interface with an intensional grammar via wfa.
4.4 An account of Bäuerle’s puzzle
Now that we’ve convinced ourselves that our fragment can handle quantificational dps, we’re finally at a point where we can present the resolution to Bäuerle’s puzzle. Since quantificational and intensional scope are divorced in a systematic way, the resolution turns out to be surprisingly straightforward. Consider again the problematic sentence, repeated in (62):

Recall, the reading we’re interested in is the one on which: (i) every Red Sox player is interpreted de re, and takes narrow quantificational scope below some; (ii) some five star hotel downtown is interpreted de dicto, and takes wide quantificational scope within the embedded clause, over every. Consequently, we want the intensional effects of every Red Sox player to outscope its quantificational effects, and we want the quantificational effects of some five star hotel downtown to outscope the quantificational effects of every Red Sox player. We can achieve this by scoping just every Red Sox player over an up-shifter, and semantically reconstructing its quantificational effects via a higher-type trace.
The derivation is shown in Fig. 20: some five star hotel scopes to a position below the up operator, whereas every Red Sox player scopes to a position above the up-shifter, leaving behind a higher-type trace below some five star hotel. The quantificational effects of the universal semantically reconstruct below the existential, but the up-shifter demarcates intensional scope—the restrictor of the universal is interpreted relative to the outer layer of world sensitivity, whereas the restrictor of the existential is interpreted relative to the inner layer.
4.5 Negative Polarity Items
Additional evidence for a theory which allows intensional effects and quantificational effects to scope together, or for intensional effects to outscope quantificational effects, but not vice versa, comes from the interaction between Negative Polarity Item (npi) and de re readings. In a sentence such as (65), no unicorn (the npi licensor) can be interpreted de dicto, while the npi any Soviet republic is interpreted de re, i.e., (65) is true in a scenario in which John thinks the following: No unicorn lives in Russia, Poland, Slovenia, etc., but doesn’t know anything about the history of these countries.Footnote 26

The structure of this example is reminiscent of Bäuerle’s puzzle: in a classical scope theory, the fact that the npi is licensed suggests that the licensor scopes over the npi, but the fact that the npi is interpreted de re and the licensor is interpreted de dicto suggests the opposite. This tension can be easily resolved within the flexible scope theory by allowing the intensional effects of any former Soviet republic to outscope its quantificational effects. The idea would be that any former Soviet republic scopes above an up-shifter, above the licensor, but the quantificational part semantically reconstructs.Footnote 27 This is illustrated in the lf below:
One potential issue raised by this analysis is that it suggests that semantic reconstruction feeds npi licensing. This is not straightforward, since A-movement bleeds npi licensing, despite the fact that A-moved qps can semantically reconstruct. This is illustrated by the examples below—(66c) acts as a control, and shows that an NPI is licensed by high negation in the complement of seem; (66a) shows that an A-moved qp can indeed semantically reconstruct; finally the target (66b) shows that A-movement bleeds npi licensing.

This paradigm is however a problem for any theory of npi licensing, especially given that scope can clearly feed npi licensing, even when the licensor doesn’t surface c-command the npi, as in (67). As others have concluded (see Ladusaw 1979; Barker and Shan 2014, ch. 8 for recent discussion) it seems that there must be a component in the theory of npi licensing which makes reference to linear order.

4.6 Scope freezing
A well-known constraint on quantificational scope in English is scope freezing in a family of configurations including the Double Object Construction (doc) (Larson 1990).

In light of the classical scope theory, and our discussion of scope islands, the obvious question to ask here is the following—do restrictions on scope track restrictions on de re? If they do, we expect the absence of a mixed reading where the indirect object is interpreted de dicto and the direct object is interpreted de re. As demonstrated by the acceptability of the example in (69), the direct object in fact can be interpreted de re, even if the indirect object is interpreted de dicto.

This is unexpected on a classical scope theory, but provides additional support for the flexible scope theory, in which quantificational and intensional scope are systematically divorced. In order to achieve the mixed reading of (69), we can scope every japanese novel over an up-shifter, allowing the quantificational part to semantically reconstruct. A student of his, on the other hand, scopes below the up-shifter. This is demonstrated by the lf below:Footnote 28
5 More constraints on de re
5.1 Main predicates, adverbs, and modifiers
We’ve already discussed the nested dp constraint (Romoli and Sudo 2009), and explained how scope theories in general provide an explanation for this observation. There are a number of other important constraints which have been proposed in the literature. In this section, we give a cursory overview of the constraints on de re which have been proposed, and offer some speculation about they may be accounted for within the flexible scope theory.
Percus (2000) points out that main predicates and adverbs cannot receive de re interpretations.Footnote 29

To briefly illustrate, the main predicate constraint rules out a putative reading of (71) where is Canadian is interpreted de re. If is Canadian could be interpreted de re, then (71) would be true in a context, e.g., in which there are a group of individuals who, unbeknownst to Mary, are actually Canadians; Mary thinks that John is a member of this group.

The adverb constraint rules out a putative reading of (72) where healthily is interpreted de re. If this were possible, then the sentence would be true in a context, e.g., in which Mary has the wrong idea about healthy eating habits—e.g., she thinks that broccoli is unhealthy. She furthermore thinks that John eats broccoli.Footnote 30

Keshet (2008) further observes that within a dp, intersective modifiers must be interpreted relative to the same evaluation world as the head noun, as illustrated by the infelicity of (73); if married could be interpreted de re while bachelor is interpreted de dicto (or vice versa), then the sentence should have a sensible reading, contrary to fact.

Keshet posits a constraint to block this:

In light of the above generalizations (as shown extensively by Percus 2000), the bti over-generates, and a distinct binding theory for world pronouns is called for, in order to block unattested de re interpretations. The flexible scope theory fares little better on the face of it.Footnote 31 Nothing in the semantics we’ve laid out prevents any expression of type \(\textsf {S}\,\textsf {a}\), which includes e.g., verbal predicates, from being bind-shifted, scoping out, leaving behind an extensional trace. If possible, this would allow us to easily derive unattested de re interpretations. The kind of derivation that must be ruled out is illustrated schematically in (75), which would allow us to derive a de re interpretation of the main predicate Canadian.

There is however a reasonably natural way of understanding constraints on de re within the flexible scope theory, once we acknowledge the possibility of syntactic restrictions on the kinds of expressions which may take scope. In order to derive the full range of attested de re interpretations, there are only two kinds of expressions which must be able to take scope: dps and scope islands, which are typically (finite) Complementizer Phrases (cps). dps and cps form a natural class syntactically — it has been argued that they are both phases in the sense of Chomsky (2000, 2001). One of the criteria that Chomsky suggests individuates phases from other constituents is that only phases may undergo movement. Extending this restriction to scope-taking, i.e., qr, makes some headway in accounting for the constraints on de re interpretations uncovered by Percus and others. For example, the lf in (75) is ruled out, since it would necessitate qr of a non-phase.Footnote 32
In previous incarnations of this paper, I explored a different way of deriving restrictions on de re interpretations, by making certain stipulations regarding the semantic type of predicates. Namely, rather than starting from the assumption that predicates have an outer layer of world-sensitivity, as in Sect. 3.1, we could instead assume from the beginning that predicates return propositions. This is illustrated in (76) for canadian—I write this alternative denotation as \(\textsf {canadian'}\).

Starting with this stipulation introduces an asymmetry between semantic predicates and arguments—arguments of type \(\textsf {S}\,\textsf {a}\) may be bind-shifted and scoped, whereas predicates are incompatible with bind. As the reader can verify independently, this alternative starting point leaves the non-quantificational fragment completely intact, and in fact results in an apparent simplification: there is no longer any need for wfa. The quantificational part of the fragment is however significantly complicated—an additional operator, not derivable just from the monadic operations bind and up is necessitated in order to incorporate quantifiers.Footnote 33
5.2 The problem of total de re
If embedded clauses may scope out, leaving behind extensional (type \(\textsf {t}\)) traces, then an unattested total de re reading may be derived for an example such as (79).Footnote 34 The problematic lf is shown in Fig. 23—the sentence is predicted to be true in case either (a) every linguist is actually drunk, and Roger believes a tautology, or (2) it’s not the case that every linguist is actually drunk, and Roger believes a contradiction.

The problem arises because we can’t distinguish between bona fide intensional values and up-shifted truth-values in the type calculus. As far as the attitude verb is concerned, its selectional requirements can be satisfied simply by vacuously lifting a truth-value. Note however it’s not clear why a speaker/hearer would ever retrieve a totally de re reading even if it were a possibility, given that it’s independently odd to claim that an individual believes a tautology/contradiction.
6 Comparison to related work
Demirok (2019) independently developed a theory of exceptional de re closely related to the one outlined in this paper, according to which de re readings are achieved by moving dps over an operator id, and shifting the island into an existential quantifier, via a covert type-shifter \(\exists \). The key-ingredients of the account are spelled-out below. Crucially, id is rigidly typed, whereas \(\exists \) is just a polymorphic existential determiner. Furthermore, Demirok assumes a compositional regime in which the interpretation function is parameterized to an evaluation world, which may be extensionalized in order to resolve a type mismatch (von Fintel and Heim ’s 2011intensional function application).

To illustrate how Demirok ’s theory derives de re out of scope islands, let’s consider a concrete example:

Focusing on the embedded clause, Demirok assumes the lf in Fig. 24—id composes with a null operator, which moves to the clause edge to create a abstraction over propositions. The universal quantifier moves to a position above id, leaving behind a higher-type (extensional) trace. The \(\exists \)-theory therefore generates a (singleton) set of propositions as the meaning of the embedded clause. Subsequently, the covert existential \(\exists \) takes this set as its restrictor, giving rise to an existential quantifier over propositions. The resulting existential quantifier scopes out, leaving behind a propositional trace, as illustrated in Fig. 25; consequently, the world argument of everyone in this room is interpreted relative to the global evaluation world and the rest of the material in the scope island semantically reconstructs.
Since \(\exists x \in \{x\}[k\,x]\) is equivalent to \(k\,x\), this amounts to the attested reading of the sentence, where in this room is interpreted relative to the utterance evaluation world. Thereby, the \(\exists \)-theory achieves the same results as the flexible scope theory.
Both the flexible scope theory and the \(\exists \)-theory derive exceptional de re via cyclic scope, but using distinct compositional mechanisms. The flexible scope theory however highlights the fact that world-sensitivity belongs to a broader class of “effects” which exhibit exceptional scope behavior.Footnote 35 On the \(\exists \)-theory, the account of exceptional de re is completely parasitic on machinery tailored to account for pied-piping in wh-questions. I leave a more detailed assessment of the relative advantages/disadvantages of the two approches to future work.
7 Conclusion and open issues
This paper primarily focused on constraints on de re. This overlooks one of the most important recent discoveries in the literature on de re/de dicto ambiguities: the existence of so-called bound de re readings (Charlow and Sharvit 2014). As shown in detail by Charlow and Sharvit (2014) a simple intensional fragment based on possible worlds, like the one developed here, isn’t expressive enough to account for bound de re. Something more is required—Charlow and Sharvit (2014) use concept generators (Percus and Sauerland 2003), but see, e.g., Cable (2018) for a semantics based on a counterpart ontology (see also Sauerland 2014). Despite the fact that we have assumed a possible world semantics with transworld individuals in this paper, the primary focus has been on the combinatorics of an intensional grammar. I am optimistic that the general strategy outlined here for “upgrading” a fragment could be used to deliver a fragment with sufficient expressive power for accounting for bound de re, perhaps along the same lines as Cable (2018).
To loop back round to where we began, we’ve bootstrapped a novel theory of intensionality—the flexible scope theory of intensionality—which preserves and generalizes the core insight of Keshet ’s split intensionality: that de re requires scope to an edge position. The resulting grammar was shown to be sufficiently flexible to account of exceptional de re, without sacrificing the virtues of a scope-based theory of intensionality more generally, such as an explanatory account of Romoli and Sudo ’s nested dp constraint, as well as the ban on de re readings of semantic predicates.
Intensional scope and quantificational scope are systematically divorced—we showed in detail that, once we’re equipped with both bind and wfa, we can account for a range of interactions between intensional and quantificational scope otherwise problematic for classical scope theories. In general, bind and wfa give rise to a system in which either (a) intensional and quantificational effects scope together, or (b) intensional effects outscope quantificational effects, but not vice versa.
Zooming out, the flexible scope theory constitutes a case study in how to go about upgrading a grammar in a modular fashion, using machinery inspired by the literature on functional programming and category. As such, the flexible scope theory of intensionality slots into a growing body of work arguing that monads have a crucial role to play in our understanding of natural lanuage semantics (see, e.g., Shan 2002, 2005; Giorgolo and Asudeh 2012; Charlow 2014; Asudeh and Giorgolo 2020, a.o.).
Editorial Policies for:
Springer journals and proceedings: https://www.springer.com/gp/editorial-policies
Nature Portfolio journals: https://www.nature.com/nature-research/editorial-policies
Scientific Reports: https://www.nature.com/srep/journal-policies/editorial-policies
BMC journals: https://www.biomedcentral.com/getpublished/editorial-policies
Notes
The term “exceptional de re”, following Demirok (2019), will be used to describe configurations in which an expression in a scope island is interpreted de re relative to an expression outside of the scope island.
But see Schlenker (2006) for some arguments in favor of world and time pronouns.
Following much of the existing literature in linguistic semantics, I’ll be using Quantifier Raising (qr) (May 1977; Heim and Kratzer 1998), i.e., literal syntactic movement, as the mechanism of choice for scope-taking in this paper. Nothing in the following discussion hinges seriously on quantifier raising, as opposed to an in-situ mechanisms for scope-taking.
A recent paper by Barker (2021) casts doubt on the accuracy of this empirical generalization, but all that is necessary for the argument to go through here is that we can find some environments in which de re readings are possible whereas exceptional quantificational scope is not.
The notational conventions adopted in this paper are as follows: Expressions of the object language are set in serif, meta-language in sans serif and types in a fixed width font. \(\lambda \)s are often suppressed in functions with multiple arguments. White-space is simply interpreted as function-argument application, which associates to the left, i.e. \(f\,x\,y\) is bracketed as \((f\,x)\,y\). Arrow notation is used for function types, which associates to the right, i.e., \(\textsf {a} \rightarrow \textsf {b} \rightarrow \textsf {c}\) is bracketed as \(\textsf {a} \rightarrow (\textsf {b} \rightarrow \textsf {c})\).
In fact, what we present here is Grano ’s adjustment of Keshet ’s analysis to bring it in line with split intensionality. Nothing in the argumentation crucially hinges on this.
See also Charlow (2020, §6.4–6.5) for a summary of issues afflicting choice-functional theories of exceptionally scoping indefinites.
See also Grano (2019) for arguments that Keshet ’s solution is unsuccessful even for exceptional scope-takers—in a nutshell, it predicts that exceptional scope-takers can only be interpreted de re relative to the minimal scope island containing the NP restrictor. This is clearly a bad prediction—exceptional scope takers can be interpreted de re even out of doubly-embedded scope islands. The following can be true if Roger has mistaken a linguist for a philosoper, and hopes that they are drunk; he reports this hope to Josie, who has made the same mistake, and she believes him.
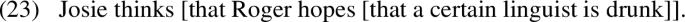
For now, we’ll defer the discussion of dp-internal compositionality, although this will become important later when we return to Bäuerle’s puzzle.
Note that the definition of \(\circledast \) is overloaded, i.e., we’re using the same symbol for two distinct operations (hence two type signatures). This is because \(\circledast \) is itself defined in terms of overloaded function application \(\textsf {A}\), defined in (27) (we borrow this technique from Charlow 2014).

This is just a way of formalizing the idea, following, e.g., Heim and Kratzer (1998), that composition proceeds via function application in a way that is insensitive to the relative linear order of function and argument.
We’ll often indicate application of a unary type-shifter as a superscript, i.e., \(a^{\wedge }:= {\wedge }\,a\).
Sometimes also called the Environment monad.
Without \(\star \), the tuple \((\textsf {S},\wedge ,\circledast )\) constitutes an applicative functor; concretely the Reader applicative. Since \(\circledast \) can be defined in terms of the monadic operations bind and up, any monad entails an applicative functor, a strictly speaking weaker notion (see McBride and Paterson 2008 for discussion). If we were to construct an intensional grammar based on the Reader applicative, we’d only have the resources to compose world-sensitivity in-situ—this is exactly because the Reader applicative lacks the resources to collapse two layers of intensionality into one.
We can define for/map in terms of our existing monadic operations, in the following way:
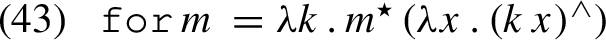
On a qr-based theory of scope-taking, this must be blocked in the syntax. In some alternative theories of scope-taking, such as Barker and Shan ’s (2014) continuation semantics, this question doesn’t even arise, and the unattested reading simply can’t be derived. See the Appendix for details. There is of course substantial evidence that the syntax should be able to generate configurations such as (46)—typically, this configuration is described as involving remnant movement (thanks to Stanislao Zompi for bringing this matter to my attention). Arguably, predicate fronting in English involves remnant movement:
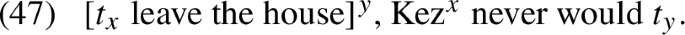
Regardless, traces cannot be interpreted as free variables. The status of remnant movement at lf is a broader question than can be addressed here, but in order to avoid an unbound trace, the remnant (i.e., the containing dp) would have to fully semantically reconstruct. See, e.g., Sternefeld (2001) for discussion.
The same questions will of course arise if we instead assumed a Russellian (i.e., a quantificational) denotation for the definite determiner. As we will defer discussion of quantificational scope until later, it is presentationally convenient to take the Fregean denotation.
Note that we’re taking advantage of the definition of wfa in terms of bind and up established in Sect. 3.4, in order to engage in simplification via the monad laws.
Concretely, we assume the availability of the following (disjunctive) abstraction principle.

This harmlessly expands the range of derivational possibilities. For example, de re interpretations of dps in non-scope-islands may be derived simply via qr, without bind, as illustrated below.
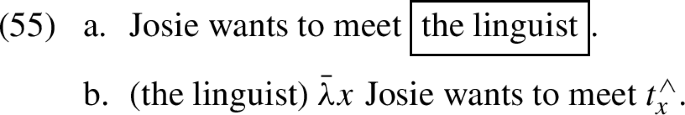
Intuitively, the reason we need to distinguish between two types of scope sites is that our intensional grammar explicitly handles both intensional scope (hence scope sites of type \(\textsf {e} \rightarrow \textsf {S}\,\textsf {b}\)), and quantificational scope lifted into an intensional setting (hence, scope sites of type \(\textsf {S}\,(\textsf {e} \rightarrow \textsf {t})\)). In the Appendix this is explicitly factored out as two distinct instantiations of the continuation applicative.
I’m grateful to an anonymous reviewer for pressing me on this point.
In the literature on functional programming, it’s common to distinguish between the bread and butter of pure computation via function-argument application, and accompanying “effects” (see, e.g., McBride and Paterson 2008). In a formal semantic setting, effects are “extra” meaning components modeled by a type constructor such as \(\textsf {S}\), that require additional machinery, such as bind, in order to thread through the computation. We don’t model quantifier scope as an effect explicitly here, but see the Appendix.
I’m grateful to Yasu Sudo (p.c.) for bringing these facts to my attention. The judgment reported here (checked with \(\sim \)10 native English speakers) is completely at odds with the discussion of npi licensing and de re in Keshet (2011, p. 261). Keshet reports the following constrast:

For (63b) to receive a sensible reading, any class that I failed must be interpreted de re. Since (63b) sounds odd, Keshet concludes that de re is blocked, since it would involve scoping over the licensor. I’m not sure why (63b) sounds as odd as it does, but simplifying the example results in a significant improvement:
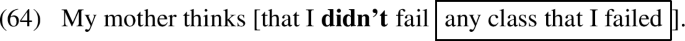
And furthermore, that as long as the quantificational part of the npi is interpreted within the scope of the licensor at lf, then the npi is licensed.
If the conclusions here are correct, they have an interesting consequence for the analysis of scope freezing. qr-ing the indirect object over the direct object can’t be ruled out per se (cf. Bruening 2001), but rather whatever constraint gives rise to scope freezing must be stated specifically in relation to quantificational scope.
Sudo (2014) discusses a systematic class of apparent exceptions to Percus ’s main predicate generalization. Sudo argues that these apparent exceptions have a different source, and that Percus ’s generalization remains in place.
Percus (2000) focuses on quantificational adverbs, which introduce additional compositional complications.
This is true of scope theories of intensionality more generally.
I’m grateful to an anonymous reviewer for suggesting the possibility that only phases may take scope.
Concretely, the additional operator needed is cotraverse \((\textsf {c})\)—it takes a higher-order function f and returns a higher-order function which takes a function with an intensional return value, and returns an intensional value. It can be defined in terms of bind and up as follows, but it necessitates pushing the world-sensitivity of m outwards by flipping its arguments:
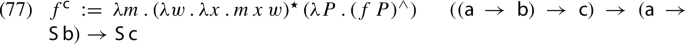
In this alternative setting, determiners compose with their restrictor and scope via \(\textsf {c}\).

I’m grateful to Julian Grove (p.c.) for pointing this out.
The notational conventions adopted in this appendix for applicative functors are inspired by Kobele (2018).
Charlow (2014) presents this as a continuation monad although in fact only ever uses the operations of a continuation applicative. Unlike other applicative functions, the continuation applicative has an interesting property—it entails the existence of a continuation monad, because \(m^{\mu }\) can be defined as \(m\,\circ \,(\uparrow )\). There is in fact no difference in expressive power between the continuation applicative and monad.
Arguably a simpler way of proceeding would be to bind-shift predicates and use the ordinary continuation applicative for composition. This would however over-generate and allow us to derive de re readings of predicates.
References
Asudeh, A., & Giorgolo, G. (2020). Enriched meanings: Natural language semantics with category theory. Oxford: Oxford University Press.
Barker, C. (2002). Continuations and the nature of quantification. Natural Language Semantics, 10(3), 211–242. https://doi.org/10.1023/A:1022183511876.
Barker, C. (2021). Rethinking scope islands. Linguistic Inquiry. https://doi.org/10.1162/ling_a_00419.
Barker, C., & Shan, C.-C. (2014). Continuations and natural language. Oxford: Oxford University Press.
Bäuerle, R. (1983). Pragmatisch-semantische Aspekte der NP-Interpretation. In M. Faust, R. Harweg, W. Lehfeldt, & G. Wienold (Eds.), Allgemeine Sprachwissenschaft, Sprachtypologie und Textlinguistik (pp. 121–131). Tübingen: Gunter Narr.
Bruening, B. (2001). QR obeys superiority - Frozen scope and ACD. Linguistic Inquiry, 32(2), 233–273. https://doi.org/10.1162/00243890152001762.
Büring, D. (2005). Binding theory. Cambridge: Cambridge University Press.
Cable, S. (2018). A choice functional semantics for de re attitudes. Unpublished manuscript, University of Massachusetts Amherst.
Charlow, S. (2010). Can DP be a scope island? In T. Icard, & R. Muskens (Eds.), Interfaces: Explorations in logic, language and computation (pp. 1–12). Berlin: Springer. https://doi.org/10.1007/978-3-642-14729-6_1.
Charlow, S. (2014). On the semantics of exceptional scope. PhD thesis, Rutgers University.
Charlow, S. (2020). The scope of alternatives: indefiniteness and islands. Linguistics and Philosophy, 43(4), 427–472. https://doi.org/10.1007/s10988-019-09278-3.
Charlow, S., & Sharvit, Y. (2014). Bound ‘de re’ pronouns and the LFs of attitude reports. Semantics and Pragmatics, 7(3), 1–43. https://doi.org/10.3765/sp.7.3.
Chomsky, N. (2000). Minimalist inquiries. In R. Martin, D. Michaels, & J. Uriagereka (Eds.), Step by step: Essays on minimalist syntax in honor of Howard Lasnik (pp. 89–155). Cambridge, MA: MIT Press.
Chomsky, N. (2001). Derivation by phase. In M. J. Kenstowicz (Ed.), Ken Hale: A life in language (pp. 1–52). Cambridge, MA: MIT Press.
Cohn-Gordon, R. (2016). Monad transformers for natural language - Combining monads to model effect interaction. Unpublished manuscript, Stanford University.
Cresti, D. (1995). Extraction and reconstruction. Natural Language Semantics, 3(1), 79–122. https://doi.org/10.1007/BF01252885.
Dayal, V. (1996). Locality in WH quantification. Dordrecht: Springer.
Demirok, Ö. (2019). Scope theory revisited - Lessons from pied-piping in wh-questions. PhD thesis, Massachussetts Institute of Technology.
Fodor, J.D. (1970). The linguistic description of opaque contents. PhD thesis, Massachussetts Institute of Technology.
Fox, D. (1995). Economy and scope. Natural Language Semantics, 3(3), 283–341. https://doi.org/10.1007/BF01248820.
Giorgolo, G., & Asudeh, A. (2012). Monads for conventional implicatures. In A. Aguilar Guevara, A. Chernilovskaya, & R. Nouwen (Eds.), Proceedings of Sinn und Bedeutung 16 (Vol. 1, pp. 265–276). https://ojs.ub.uni-konstanz.de/sub/index.php/sub/article/view/425.
Grano, T. (2019). Choice functions in intensional contexts - Rehabilitating Bäuerle’s challenge to the scope theory of intensionality. In R. Stockwell, M. O’Leary, Z. Xu, & Z. Zhou (Eds.), Proceedings of the\(36^{th}\)West Coast Conference on Formal Linguistics (pp. 159–164). Somerville, MA: Cascadilla Proceedings Project.
Heim, I., & Kratzer, A. (1998). Semantics in generative grammar. Malden, MA: Blackwell.
Huhmarniemi, S. (2012). Finnish A’-movement: Edges and islands. PhD thesis, University of Helsinki.
Keshet, E. (2008). Good intensions - Paving two roads to a theory of the de re / de dicto distinction. PhD thesis, Massachussetts Institute of Technology.
Keshet, E. (2010). Possible worlds and wide scope indefinites: A reply to Bäuerle 1983. Linguistic Inquiry, 41(4), 692–701.
Keshet, E. (2011). Split intensionality: A new scope theory of de re and de dicto. Linguistics and Philosophy, 33(4), 251–283. https://doi.org/10.1007/s10988-011-9081-x.
Keshet, E., & Schwarz, F. (2019). De re/de dicto. In J. Gundel, & B. Abbott (Eds.), The Oxford handbook of reference (pp. 167–202). Oxford: Oxford University Press.
Kobele, G. M. (2018). The cooper storage idiom. Journal of Logic, Language and Information, 27(2), 95–131. https://doi.org/10.1007/s10849-017-9263-1.
Ladusaw, W.A. (1979). Polarity sensitivity as inherent scope relations. PhD thesis, University of Texas at Austin.
Larson, R. K. (1990). Double objects revisited - Reply to Jackendoff. Linguistic Inquiry, 21(4), 589–632.
May, R. (1977). The grammar of quantification. PhD thesis, Massachussetts Institute of Technology.
McBride, C., & Paterson, R. (2008). Applicative programming with effects. Journal of Functional Programming, 18(1). https://doi.org/10.1017/S0956796807006326.
Montague, R. (1970). English as a formal language. In B. Visentini (Ed.), Linguaggi nella societa e nella tecnica (pp. 188–221). Edizioni di Communita.
Percus, O. (2000). Constraints on some other variables in syntax. Natural Language Semantics, 8(3), 173–229. https://doi.org/10.1023/A:1011298526791.
Percus, O., & Sauerland, U. (2003). On the LFs of attitude reports. In M. Weisgerber (Ed.), Proceedings of Sinn und Bedeutung 7 (pp. 228–242). https://doi.org/10.18148/sub/2003.v7i0.805.
Poole, E. (2017). Movement and the semantic type of traces. PhD thesis, University of Massachusetts Amherst.
Romero, M. (1998). Focus and reconstruction effects in wh-phrases. PhD thesis, University of Massachusetts Amherst.
Romoli, J., & Sudo, Y. (2009). De re/de dicto ambiguity and presupposition projection. In A. Riester, & T. Solstad (Eds.), Proceedings of Sinn und Bedeutung 21 (Vol. 2, pp. 1017–1034). https://ojs.ub.uni-konstanz.de/sub/index.php/sub/article/view/181.
Sauerland, U. (2005). DP is not a scope island. Linguistic Inquiry, 36(2), 303–314. https://doi.org/10.1162/0024389053710657.
Sauerland, U. (2014). Counterparts block some ‘de re’ readings. In L. Crnič, & U. Sauerland (Eds.), The art and craft of semantics: A festschrift for Irene Heim (Vol. 2, pp. 65–85). Cambridge, MA: MITWPL.
Schlenker, P. (2006). Ontological symmetry in language - A brief manifesto. Mind & Language, 21(4), 504–539. https://doi.org/10.1111/j.1468-0017.2006.00288.x.
Shan, C.-c. (2002). A continuation semantics for interrogatives that accounts for Baker’s ambiguity. In B. Jackson (Ed.), SALT XII (pp. 246–265). Ithaca, NY: Cornell University.
Shan, C.-c. (2005). Linguistic side effects. PhD thesis, Harvard University.
Sternefeld, W. (2001). Semantic vs. syntactic reconstruction. In C. Rohrer, A. Rossdeutscher, & H. Kamp (Eds.), Linguistic form and its computation (pp. 145–182). Stanford, CA: CSLI Publications.
Sudo, Y. (2014). On de re predicates. In R.E. Santana-LaBarge (Ed.), Proceedings of the\(\mathit{31}^{{st}}\)West Coast Conference on Formal Linguistics (pp. 447–456). Somerville, MA: Cascadilla Proceedings Project.
Szabó, Z.G. (2010). Specific, yet opaque. In M. Aloni, H. Bastiaanse, T. de Jager, & K. Schulz (Eds.), Logic, language and meaning (pp. 32–41). Berlin: Springer.
von Fintel, K., & Heim, I. (2011). Intensional semantics. Unpublished textbook, MIT.
Wadler, P. (1995). Monads for functional programming. In J. Jeuring, & E. Meijer (Eds.), Advanced functional programming (pp. 24–52). Berlin, Heidelberg: Springer. https://doi.org/10.1007/3-540-59451-5_2.
Acknowledgements
I’m grateful to Stefan Kaufmann, and two anonymous reviewers for Linguistics and Philosophy. I owe a particular debt to the first reviewer, whose consistently insightful suggestions greatly influenced the final published version of this paper. I’d also like to thank Matthew Gotham and Julian Grove for detailed feedback on early drafts, as well as Keny Chatain, Ömer Demirok, Kai von Fintel, Patrick Niedzielski, Roger Schwarzchild, and Yasu Sudo. Finally, I’d like to express my appreciation to audiences at the MIT LF reading group on March 1, 2020, and wccfl 38 held at UBC on March 7, 2020, where earlier versions of this work were presented. I take sole responsibility for any remaining errors.
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: An in-situ fragment using the continuation applicative
Appendix: An in-situ fragment using the continuation applicative
The intensional grammar outlined here, as its central component, a general mechanism for scope-taking, to model both intensional and quantificational scope—in the paper, this was cashed out in terms of qr (May 1977). The central features of the grammar are also compatible with a continuation-based approach to scope-taking (Barker 2002; Barker and Shan 2014), which will allow us to model quantificational scope explicitly using a type-shifting regime parallel to the one that we developed to model intensionality.
Although Barker and Shan don’t present continuations explicitly in this fashion, underlying their approach is the continuation applicative functor. Formally, the continuation applicative is the tuple \((\frac{\textsf {r}}{.},.^{\uparrow \kappa },.^{\downarrow \kappa })\), where \(\frac{\textsf {r}}{.}\) is the type constructor for scopal types, lift (\(.^{\uparrow \kappa }\)) is a generalization of Montague lift, and Scopal Function Application (sfa) (\(.^{\downarrow \kappa }\)) is an enriched form of fa for scopal values.Footnote 36

Barker and Shan introduce a notational convention for reasoning about scope, using the continuation applicative: tower notation. The operations of the continuation applicative can be rewritten in tower notation, as in (83). For perspicuity, we’ll use tower notation to reason about continuized meanings for the remainder of this appendix.

Derivations involving scope-takers, such as every linguist proceed via sfa by lifting non-scope-takers. This is illustrated in (84b) for the sentence “Josie likes every linguist” in a purely extensional setting. Notice the parallel with the applicative fragment sketched at the beginning of Sect. 3.1.

We can rewrite the result in (84b) as an ordinary lambda term, as in (85a). In order to retrieve something of a propositional type (here: \(\textsf {t}\)), we need to apply (85a) to the identity function. Barker and Shan call this operation lower (86).


We presented our intensional grammar explicitly in terms of a Reader monad, which, as we discussed, entails an applicative functor, which we’ll call the intensionality applicative, consisting of \((\textsf {S},.^{\uparrow \sigma },.^{\downarrow \sigma })\) (where \(.^{\uparrow \sigma }\) is up and \(.^{\downarrow \sigma }\) is wfa).

An important property of applicative functors is that they compose (McBride and Paterson 2008)—this means that, since \(\frac{\textsf {r}}{\textsf {.}}\) and \(\textsf {S}\) are both applicative functors \(\textsf {S} \circ \frac{\textsf {r}}{\textsf {.}}\) is guaranteed to be an applicative functor. We’ll use \(\textsf {S} \circ \frac{\textsf {r}}{\textsf {.}}\) to reason about quantificational scope lifted into an intensional fragment, i.e. scope-takers with an outer-layer of world-sensitivity.

Charlow (2014) pioneered a technique in linguistic semantics whereby something of type \(\textsf {F}\,\textsf {a}\) can be lifted into an inhabitant of a continuation applicative via the monadic bind operation associated with \(\textsf {F}\). We implicitly took advantage of this in the main body of the paper in the basic theory of de re readings for definite descriptions. We can use tower notation to represent the result of applying bind to a definite description, which resulted in something of type \(\textsf {(e} \rightarrow \textsf {S}\,\textsf {r}) \rightarrow \textsf {S}\,\textsf {r}\),Footnote 37

Since applicative functors compose, \(\frac{\textsf {r}}{\textsf {.}} \circ \textsf {S}\) is also an applicative functor. We can use this applicative to model intensional scope-takers, as opposed to scope-takers with an outer-layer of world-sensitivity.

We now have everything we need to achieve the same results as our qr-based fragment for definites. Bind-shifted definites are inhabitants of a continuation applicative, and may be lifted into an inhabitant of \(\frac{\textsf {S}\,\textsf {r}}{.} \circ \textsf {S}\) by lifting \(.^{\uparrow \sigma }\) and applying it to the definite via \(.^{\downarrow \kappa }\), as in (91)—this parallels up-shifting the extensional trace left behind by a bind-shifted definite in the qr-based fragment.Footnote 38

The final value is almost what we want, but we need to get rid of the scopal tier. As the final step in the derivation, we lower the result of Fig. 26, resulting in a doubly world-sensitive proposition, where the definite is interpreted relative to the outer layer of world-sensitivity.

We can lift a quantificational determiner into the intensionality applicative via \(.^{\uparrow \sigma }\), and compose it with a predicate via \(.^{\downarrow \sigma }\). The result is a scope-taker with an outer layer of world-sensitivity, i.e., something of type \(\textsf {S} \circ \frac{\textsf {t}}{\textsf {e}}\). This is illustrated in (93).

N.b., that an inhabitant of the intensionality applicative, such as a verbal predicate, can be lifted into an inhabitant of \(\textsf {S} \circ \frac{\textsf {t}}{\textsf {.}}\) by lifting \(.^{\uparrow \kappa }\) into the intensionality applicative via \(.^{\uparrow \sigma }\), and applying it to the predicate via \(.^{\downarrow \sigma }\). Composition then proceeds via the operations of the \(\textsf {S}\,\left( \frac{\textsf {t}}{\textsf {.}}\right) \) applicative.

Cases involving wide intensional scope and narrow quantificational scope (i.e., the third reading), can be accounted for by bind shifting a world-sensitive quantifier.

Rewriting (95) in tower-notation brings out the parallel with higher-order traces. We have a multi-tiered scope-taker with intensional scope sitting on top tier, above quantificational scope.

The extensional part of the meaning Q can be lifted into an intensional scope-taker via \(.^{\uparrow \sigma }\), and composition can proceed just as it does for world-sensitive quantifiers.


Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

























 ”
”
 ”
”


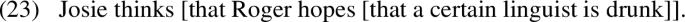

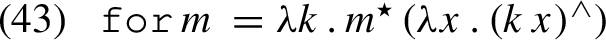
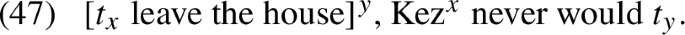

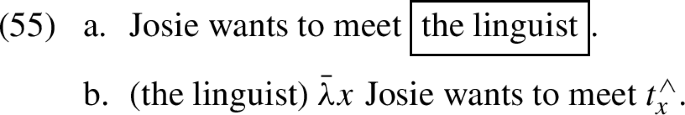


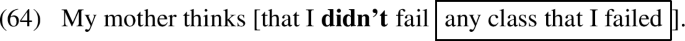
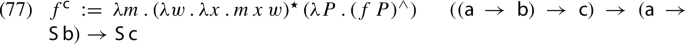


 ”
”