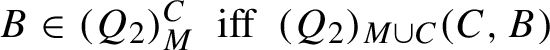Abstract
This paper gives a uniform account of the meaning of generalizations with explicit exceptions that employ the prepositions “but”, “except”, and “except for”. Our theory is that exceptives depend on generalizations, which can but need not be universal, whose generality they limit, and some of whose exceptions they comment on. Every generalization intrinsically partitions its domain of applicability into regular cases, which are as it says to expect, and exceptions, which are not. A generalization’s exceptions are instances that falsify it if sufficiently prevalent. These two facts underpin the meaning of exceptives as combining a generality claim with an exception claim, giving correct truth conditions for the several ways the three exceptive prepositions are used, and significantly improving on existing semantic accounts in the literature. We support this by analyzing a wide range of examples. The analysis applies whether or not the phrase following the exceptive preposition is a DP, and whether or not the generalization is expressed with a quantifier. We further argue that these exceptive prepositions are synonymous, contrary to the widely held view that a difference in meaning explains their different syntactic distributions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Exceptive expressions like the English prepositions “but”, “except”, and “except for”, and counterparts in other languages, attracted renewed attention in the mid-1980s (Keenan and Stavi , 1986; Hoeksema , 1987). A broad consensus on their syntactic distribution and meaning emerged by the mid-1990s (von Fintel 1993, 1994; Moltmann 1995) and remains widely influential today (Hoeksema 1996; Moltmann 1996; Gajewski 2008; Hirsch 2016). It has gradually become clear, however, that this account—which we will label ‘the received view’—is inconsistent with substantive empirical evidence. This paper explains why, and proposes a new analysis of exceptives that improves theoretically and also empirically on earlier proposals.
1.1 The received view
Three tenets are central to the received view.
-
(I)
Exceptives co-occur only with positive and negative universal generalizations.
-
(II)
Exceptives mark out counterexamples that would falsify the generalization were they not excluded from its domain.
-
(III)
The meaning of exceptives explains their syntactic distribution.
This contemporary view’s first two facets reaffirm medieval ideas about exceptives. William of Ockham’s 14th century logic espoused (I).
An exceptive proposition is never properly formed unless its non-exceptive counterpart is a universal proposition. Hence, “A man except Socrates is running” is not properly formed.Footnote 1
(II) is prefigured in Peter of Spain’s 13th century writings.
An exceptive word [e.g. præter] indicates a relationship of a part actually existing in a whole to its whole.Footnote 2
The third facet is a twentieth century addition. The most thoroughly worked out 1990s accounts of exceptives’ meaning are those of (von Fintel 1993, 1994; Moltmann 1995). Both aimed to show that exceptives occur only with universal generalizations—indeed, to explain why this must be so. Von Fintel held that the phrase following “but” must be definite and accordingly could be treated as denoting a set, here written C. He proposed that a statement of the general form (1)


Von Fintel argued that the only quantifiers Q for which the requisite smallest set X exists are the positive universal quantifiers every and all and the negative universal quantifier no. Relying on an additional assumption that adding an exceptive to a grammatical sentence shouldn’t ipso facto yield a necessarily false sentence—which would be the case if Q weren’t a universal quantifierFootnote 4—he claimed that fact (I) is explained by what exceptives mean, so (III) and (I) hold. And he showed that when Q is universal, what exceptives mean entails that when a statement of the form (1) is true, C = \(A- B\) for positive universal quantifiers, and \(A\cap B\) for negative universals. From his semantics for statements of form (1), it follows that “Q As are B” is false when C is non-empty; so (II) holds too.
Moltmann (1995) was (as far as we know) the first to recognize that non-definite DPs can follow exceptives like “but”, and she presented a more complex analysis of what exceptives mean, one that allows for such DPs. Her analysis also predicts that exceptives can only co-occur with positive or negative universal quantifiers, i.e. (I), as well as that an exceptive excludes all counterexamples from the quantifier’s domain. We defer a detailed discussion of Moltmann’s account to the Appendix.
1.2 Empirical considerations
A substantial range of evidence has been adduced that shows (I) is not correct, beginning especially with García-Álvarez (2003). Exceptives actually co-occur fully grammatically with non-universal generalizations, and García-Álvarez pointed out how readily “except” is licensed by “most,” “many,” and “few.”

Even “but”, the English exceptive with the most restrictive privileges of occurrence, co-occurs happily with non-universal statements.

The ready availability of data like these shows that (I) is not true. Therefore no analysis of exceptives which predicts (I) is correct either.
Once one acknowledges the co-occurrence of exceptives with non-universal generalizations, it is evident that (II) fails as well. Sentence (5) in no way entails the falsity of “Few people expected the 1946 film ‘It’s a Wonderful Life’ to become a classic piece of Americana” (more about this sentence in Sect. 4.1). Similarly, the first sentence in

can be true while at the same time, “We are available most days” is true—indeed, that would normally be the case. Furthermore, the consistency of the second sentence in (8) with the first shows that exceptions (days when we are not available) can exist outside the subset referenced by the exception DP, so that, referring to the schema (1), \(A-B \not \subseteq C\). While any exception is a counterexample to a universal generalization, some quantity of exceptions is consistent with the truth of any non-universal generalization.Footnote 10
We note in passing that these sentences are genuine exceptive sentences. Suppose a skeptic objected that non-universal sentences containing an exceptive phrase really just mean what they mean without the exceptive phrase but with an additional comment that the added phrase describes some exceptions. We can see that this objection is mistaken by considering examples like (9).

If the objection were correct, sentence (9) would be a contradiction, since a person can’t consistently both support and oppose gay marriage. This sentence is, in reality, not merely consistent but actually true. Also sentence (10)

doesn’t entail that few people are adults, despite the fact that all adults know either more than a dozen or else a dozen or fewer color names. So non-universal generalizations with exceptives actually are what they appear to be.
So much for (I) and (II). Claim (III) is also mistaken. While it may very well be the case that the meaning of exceptives partially explains which quantifiers they co-occur with, including non-universal ones, the fundamental problem with (III) is something else. It is widely recognized that the exceptive expressions “but”, “except”, and “except for” differ pairwise in their syntactic distribution. What seems not so widely recognized is that they do not differ in meaning. This conclusion follows from two empirically verifiable premises: (A) Sentences in which one of these exceptive prepositions is grammatically interchangeable with another mean the same. Replacing one exceptive preposition by the other does not change the meaning.Footnote 11 (B) Each of these exceptive prepositions means the same in all sentences where it occurs grammatically—regardless of whether it can be grammatically replaced there by a different exceptive. Readers can verify these premises by examining sentences containing exceptives, including the many examples presented in this article. Sections 4 and 5’s empirical discussions provide much pertinent evidence.Footnote 12
We close this empirical assessment by observing that claim (I) fails in the inverse direction too. There are universal generalizers that the exceptive “but” cannot grammatically co-occur with, for instance universally interpreted possessive determiners and bare plurals.

The received view of exceptives’ meaning and distribution is quite elegant. Unfortunately, it doesn’t fit the empirical facts. There are non-universal generalizations with exceptives, and contextual features apart from meaning are essential to accounting for each exceptive’s detailed syntactic distribution—apparently including lexical and morphosyntactic features.
Of course, there still can be, indeed there are, semantic reasons why no exceptive expression can occur in certain contexts, for instance why all of them are unacceptable in (12).

The reason is explained in Sect. 2.2.
1.3 Recent analyses of what exceptives mean
It is a robust intuition that exceptives are about exceptions; and being an exception is not a property of a thing but a relation between it and a generalization. Accordingly, Peters and Westerståhl (2006) and García-Álvarez (2009) proposed that exceptives are licensed by generalizations—in general, not just universal generalizations. Both proposals presuppose an intuitive notion of what generalizations are, as well as that they come in two flavors—positive and negative.
Peters and Westerståhl (2006) agreed with von Fintel and most other writers that an exceptive phrase narrows a generalization that licenses it by restricting the generalization’s domain, resulting in a more restricted generalization they called the Generality Claim, i.e. von Fintel’s Domain Subtraction: \(Q(A- C,B)\). They further proposed that exceptives introduce an Exception Claim about some of the licensing generalization’s exceptions, ones that are described by the exception DP. Their proposal for the exception claim extended to non-universal quantifiers an idea of Moltmann’s. In addition to inheriting the complexity of her analysis, the proposal gives some exception DPs incorrect or ambiguous truth conditions.
García-Álvarez (2009) proposed that all generalizations make defeasible universal statements and suggested formalizing this concept in non-monotonic logic. His leading idea is that every instantiation of a true non-universal generalization is presumed to be true unless ‘defeated’ by a countervailing fact, and what exceptive phrases do is state countervailing facts. He proposes that an exceptive’s non-monotonic licensing generalization is precisely the unrestricted generality claim of the exceptive sentence; so domain subtraction is not needed. It is not clear to us how this would function for universal generalizations, whose instantiations are not defeasible in his sense. While the idea to apply non-monotonic logic to the analysis of exceptives is interesting, we shall not pursue it here, but stick to the usual format of classical truth-conditional semantics.
We propose here an analysis that keeps a Generality Claim (see also Sects. 3.1 and 6.3), and has a much simpler version of the Exception Claim, which nevertheless remedies the problems of earlier accounts. As is clear from the examples already discussed, in the most general case we should replace the simple schema (1) with the following:

For example, consider (14).

The Generality Claim is that if you remove the exceptions—Deirdre’s Bostonian friends—no other Bostonians were at the party: \(Q_1(A-C,B)\). Now note that (14) doesn’t necessarily say that all of Deirdre’s Bostonian friends were at the party; it is perfectly consistent that some of them weren’t. We will see (Sects. 4.2–4.4) that this ambiguity is real, and it shows up for bare plural exception DPs as well: in some cases a universal-like reading is intended, in others an existential one. Peters and Westerståhl (2006) took this to require distinguishing a strong and a weak reading of exceptives. Here we show that the ambiguity resides in the identity of the quantifier \(Q_2\), so the same analysis works in all cases, and avoids overgeneration. The Exception Claim, then, becomes simply that \(Q_2\) As that are Cs are exceptions.
1.4 Plan
The next section takes steps toward clarifying the concept of generalization by formulating three intuitively necessary conditions on them. Section 3 spells out our formal proposal for what exceptives mean—how they modify the meaning of generalizations that license them. In Sect. 4 we look at a wide variety of exceptive phrases, showing how our semantic analysis applies to them and comparing it with what they intuitively mean, paying due attention to pragmatic as well as semantic considerations. Section 5 briefly discusses generalizations expressed by means other than a lexical quantifier. Section 6 concludes and lists a number of further issues raised by our analysis. The Appendix solves a technical problem related to exception DPs which are Boolean combinations of proper names, and compares our account to the one in Moltmann (1995).
2 Generalizations
This section states some basic facts about generalizations, and introduces terminology that will be used in the sequel.
2.1 Basic terminology
Every generalization is about members of a set, the generalization’s domain. A generalization says members of its domain are alike in a specified respect—thereby bifurcating members into what we call regular cases (which are as the generalization specifies) and exceptions (which are not). A key component of any generalization is its generalizer, which determines the extent to which regular cases must exceed exceptions in order for the generalization to be true. Besides generalizations that brook no exceptions, i.e. are false if even one member of the domain is not as the generalization specifies—the universal generalizations—there are also generalizations that can be true even when some members of their domain are exceptions.
One may distinguish generalizations from their verbal expressions. Generalizations in language employ a property expression to specify how regular cases differ from exceptions. All regular cases of a positive (negative) generalization have (lack) the property; correspondingly, all exceptions of a positive (negative) generalization lack (have) the property.
For our purposes here, generalizers can thus be identified with certain binary relations between sets, i.e. with certain binary (type \(\langle 1,1\rangle \) generalized) quantifiers.Footnote 13 Generalizers are often expressed in English by determiners, and various other kinds of expressions are also used. Regardless of the syntactic construction used, the interpretation is a binary relation between sets.
We usually use the letter A for the domain and B for the extension of the property, and, in view of the schema (13), we use \(Q_1\) for the generalizer and \(Q_2\) for the quantifier associated with the exception phrase. Since only members of its domain are relevant to whether or not a generalization is true, the equivalence
-
(Conserv) \(Q_1(A,B) \Leftrightarrow Q_1(A,A\cap B)\)
always holds. That is, \(Q_1\) is a conservative quantifier.Footnote 14
In the examples given so far, A was the extension of a noun following a determiner, but this is not always the case; consider (15).

Here \(Q_1\) is most and the domain A is the set of England’s (cricket) players.Footnote 16
\(Q_1(A,B)\) means the relation \(Q_1\) holds between A and B. When this expresses a generalization, \(Q_1(A,B)\) holds iff the balance of regular cases to exceptions is as required by \(Q_1\). When \(Q_1\) is positive, regular cases, i.e. those in the set \(A\cap B\), have to overbalance exceptions, i.e. elements of \(A- B\), for \(Q_1(A,B)\) to hold. When \(Q_1\) is negative, \(A- B\) must overbalance \(A\cap B\). We sometimes write \(Q_1(A,B)\) for the generalization itself; thus, the generalization is true when \(Q_1(A,B)\) holds.
2.2 Properties of generalizations
In a generalization \(Q_1(A,B)\), exchanging \(A'\) for A results in a similar generalization \(Q_1(A',B)\) over the domain \(A'\). If \(Q_1\) and B do not change, the relationship required between \(A\cap B\) and \(A- B\) for the first generalization to be true must also hold between \(A'\cap B\) and \(A'- B\) for the second to be true. Thus one can sensibly speak of changing a generalization into a similar one by changing what is in the domain, for instance inserting new members or removing old ones.
Similarly, for a verbally expressed generalization \(Q_1(A,B)\), it is meaningful to speak of what its truth value would be in circumstances other than the actual ones. The generalization involves a property P, whose actual extension is B, and talk about the generalization’s truth value in other circumstances translates into discussion of whether \(Q_1(A,B')\) would hold, where \(B'\) is P’s extension in those circumstances.
We avail ourselves of these convenient ways of speaking when formulating the properties of generalizations below. First, for every generalization, positive or negative, regular cases support its truth and exceptions count against it. This basic fact allows us to see that (RM) must hold.

For example, (16a) self-evidently entails (16b), and (17a) entails (17b).


Regular cases of (16a) are humans bipeds; regular cases of (17a) are elephants that are not albino. Exceptions to (16a) are humans with other than two feet, and exceptions to (17a) are albino elephants. The property of generalization (16b) extends the property of (16a) by adding some of the exceptions of (16a): humans with one foot (or more than two). Likewise, the property of (17b) shrinks the property of (17a) by turning some exceptions—albino elephants with more than one tusk—into regular cases.
This translates into familiar properties of generalizers. We can reformulate (RM) as follows:

We also have two left monotonicity properties.

This too corresponds to properties familiar in the literature on quantifiers. Peters and Westerståhl (2006) call \(Q_1\) left SE monotone (left SW monotone) if \(Q_1(A,B)\), \(A\subseteq A'\), and \(A- B = A' -B\) (\(A\cap B = A'\cap B\)) entails \(Q_1(A',B)\).Footnote 17 (LM)(a) matches these properties in the positive and negative case, respectively. Similarly, (LM)(b) matches the following properties in the positive and negative case: \(Q_1\) is left NE monotone (left NW monotone) if \(Q_1(A,B)\), \(A'\subseteq A\), and \(A\cap B = A'\cap B\) (\(A-B = A'-B\)) entails \(Q_1(A',B)\).
Now \(Q_1\) is called smooth if it is left NE and SE monotone, and co-smooth if it combines the NW and SW properties. Thus, (LM) entails (LM\('\)):

Perhaps surprisingly, (LM\('\)) implies (RM\('\)): using only the conservativity property, one verifies the following fact.Footnote 18

Our final property of generalizations concerns the number of regular cases. Roughly, as the size of the domain increases, so does the required number of regular cases. This seems obvious, since the truth of a generalization is conditioned on the balance of regular cases versus exceptions. There are various ways to translate this into a precise requirement on generalizers; (RU) below is a minimal condition. To state it, say that a domain A for \(Q_1\) is informative if there is a set B such that \(Q_1(A,B)\), and a set \(B'\) such that \(\lnot Q_1(A,B')\).

To apply (RU), we can make use of the fact (RM) that generalizers are right monotone. It follows immediately that the quantifier at least k (\(k\ge 1\)) is not a generalizer. If it were, the regular cases for \(\textit{at least k}\,(A,B)\) would be \(A\cap B\), since at least k is mon\(\uparrow \). But then (RU) fails already with \(m = k+1\). This explains why the sentences in (12) (repeated here) are bad.

On the other hand, the mon\(\downarrow \) at most k (\(k\ge 0\)), a special case of which is no, satisfies (RU): for any m, take A such that \(|A| = k+m\).Footnote 20 Also, most, defined as \(\textit{most}\,(A,B) \Leftrightarrow |A\cap B|>|A-B|\), satisfies (RU): it suffices, given m, to take A such that \(|A|\!\ge 2m\).
To get a little more from (RU), assume that \(Q_1\) satifies not only Conserv and Ext (see footnote 14) but also isomorphism invariance (Isom), which then means that only the cardinalities \(|A\cap B|\) and \(|A-B|\) matter for the truth value of \(Q_1(A,B)\). We can now derive from (RU) the commonly stated claim (e.g. von Fintel 1993, pp. 128–129) that no left increasing (\(\uparrow \) mon, or persistent) quantifier licenses exceptives:

We note that (RU) excludes symmetric interpretations of “many”, where \(\textit{many}\,(A,B)\) simply says that the size of \(A\cap B\) exceeds some contextually given number. Our tentative conclusion is that symmetric “many” is not a generalizer, but other interpretations of “many” (as in natural readings of (4) and (16)) can be.
Finally, let us repeat that the conditions on generalizations and generalizers presented in this subsection are claimed to be necessary, not sufficient. We are not aware of any precise characterization of the concept of generalization. An obvious issue are proportional quantifiers like at least two-thirds of the, which satisfy (LM\('\)) (hence (RM\('\))) and (RU). These expressions do not license exceptives:

Is this because at least two-thirds of the is not a generalizer, or because not all generalizers license exceptives? We shall not pursue this issue. Our modest aim here has been to outline a notion of generalization clear enough for a basic tenet of exceptives to make good sense, namely, that exceptives must be licensed by generalizations.
2.3 Generalizations with cardinality constraints
Linguistic expressions of generalizations sometimes add cardinality restrictions on the domain which, at least at first sight, may seem not to fit the analysis given so far. Consider (21).

The domain is the set of America’s states, but (21) adds the claim that these number fifty altogether. The thing to note here is that although it would in principle be possible to analyze this sentence with the quantifier all fifty\( \,(A,B) \Leftrightarrow A\subseteq B \; \& \; |A|=50\), that quantifier is not a generalizer in our sense: it cannot be \(Q_1\) in the schema (13), as (22) shows.

The generality claim here is that if you remove Southern states, all the remaining states permit voting by mail—it is not also that the remaining states number 50. The generalizer in (22) is simply \(Q_1 = all \); the cardinality claim is an extra conjunct of the truth conditions. Cardinality constraints on a generalization’s domain do not arise from its generalizer and do not prevent it from satisfying universals (RM), (LM), and (RU).
Concerning these universals, we note a final issue, to do with the generalizers almost all and almost no, which also license exceptives.

“Almost all As are B” says that \(A\!-\!B\) is small. Does it also say that \(A\!-\!B\) is non-empty? In (23a) there is some sort of implication that the borders are open to some non-citizens, but is this a semantic entailment or a pragmatic implicature? If the former, (RM) is too strong. Almost all is then not strictly mon\(\uparrow \), since \({ almost~all}\,(A,B)\) and \(B\subseteq B'\) doesn’t imply \({ almost~all}\,(A,B')\) if \(A-B'\) is required to be non-empty; analogously for almost no. If the implication is pragmatic, (RM) is fine.
It is not hard to formulate slightly weaker, but more complicated, versions of (RM) and (LM) that cover the case when the entailments are semantic.Footnote 23 The weak versions of mon\(\uparrow \) and mon\(\downarrow \) would still correlate with positive and negative generalizers, respectively. Since that correlation is what matters in this paper, we shall not discuss further fine-tuning of the monotonicity properties of generalizers here.
3 The meaning of exceptive expressions
Picking up from Sect. 1.3, we can now state uniform truth conditions for generalizations with exceptions as in the schema (13), repeated here,

where A, B, C are sets, \(Q_1\) and \(Q_2\) are (Conserv and Ext) type \(\langle 1,1\rangle \) quantifiers, \(Q_1\) being the generalizer.
3.1 The operator Exc
As explained, the meaning of generalizations with exceptions is spelled out in terms of a Generality Claim and an Exception Claim. Examples (24) and (25) are typical cases.


Thus, in (24), \(Q_1\) is the quantifier all, a positive generalizer, \(Q_2\) is a few, A is the set of beachgoers, B the set of fully clothed people, and C the set of swimmers. Similarly for (25), where \(Q_1\) is no, a negative generalizer. The generality claims in (24) and (25) restrict the domains, beachgoers and students, respectively, to non-swimmer beachgoers and non-senior students. The exception claims say that specified members of the excluded subdomains are exceptions.
We introduce a bit of notation in order to clarify how the semantics covers both (24) and (25). For any type \(\langle 1,1\rangle \) quantifier \(Q_1\), we define the set operation \( pol (Q_1)\) (over subsets of the discourse universe) as follows:

In particular, when \(Q_1\) is a generalizer, \( pol (Q_1)\) is simply the identity function on sets for negative \(Q_1\), and the complement function for positive \(Q_1\).
Using \( pol \) we define the operation Exc that formalizes the meaning of the exceptive prepositions “but”, “except”, and “except for”. These prepositions together with their exception DP modify the meaning of every generalizer \(Q_1\) in the same way, yielding a combination of a restricted generalization and an exception claim. More precisely, Exc combines with the exception DP’s semantic components \(Q_2\) and C to yield the following semantic operator \( Exc (Q_2,C)\) on generalizers \(Q_1\).
Definition 1
(Exc)
-
\( Exc (Q_2,C)(Q_1) = ( GC , EC )\)
where GC and EC are the binary relations between sets defined by
-
\( GC (A,B) \,\Leftrightarrow \, Q_1(A-C,B)\)Footnote 26
-
\( EC (A,B) \,\Leftrightarrow \, Q_2(A\cap C, pol (Q_1)(B))\)
Thus, with a domain A and extension B of the host generalization’s property, \( GC (A,B)\) expresses the generalization’s Generality Claim, and \( EC (A,B)\) its Exception Claim. For (24a), pol(all)(were fully clothed) = \(\overline{ were\ fully\ clothed }\), i.e. the set of things that were not fully clothed. And for (25a), pol(no)(were failed by the teacher) = \( were\ failed\ by\ the\ teacher \). So GC and EC, with the appropriate set arguments, are precisely the claims stated in (24b) and (24c), and in (25b) and (25c).
Exc assembles the truth conditions of sentences of the form (13) from the ingredients \(Q_1\), \(Q_2\), C, A, and B. With a view to both connected and free uses of exceptive prepositions, it is natural that the first stage of assembly takes in just the exception phrase’s meaning (involving \(Q_2\) and C) and yields a second assembly operation which in turn takes in the meanings of a host generalizer (\(Q_1\)), its domain, and its scope, and outputs the sentence’s generality claim and exception claim (see also (32) below).
The reason we take \( Exc (Q_2,C)(Q_1)\) to output the pair of a generality claim and an exception claim, rather than the conjunction of those claims, is that it is argued that the two claims do not have the same status. An illustration of their possible difference is the ‘pedantry’ of answering question (27) with (29), as contrasted with the naturalness of answering (28) in the same factual circumstances, reflecting the possible secondary status of the exception claim.



Hoeksema (1987) and others have argued that the exception claim is not an asserted proposition but rather something like a presupposition or possibly an implicature. Note, however, that for the ‘hard’ exceptive prepositions “but”, “except”, “except for”, it really seems inconsistent to deny the exception claim: witness the contrast between (30) and the ‘soft’ exceptives in (31).


The issue is complex and we do not attempt to settle it here. We acknowledge its existence by formally distinguishing between an exceptive sentence’s generality claim and its exception claim, but in this paper’s empirical assessment of the theoretical predictions of our analysis we follow the common practice of treating the two claims as if they were conjoined.
The main innovation in Definition 1 is our version of the Exception Claim. Besides being remarkably simple compared to other proposals we are aware of (most of which rely on second-order quantification over sets to state truth conditions, while Exc does not), it is empirically sound for universal as well as non-universal generalizations. To substantiate this, we go through a wide variety of examples in the next two sections, many of them not discussed before, and check that our analysis accords with intuition. Before we get to that, two more comments about our analysis will be made.
3.2 Compositionality
Our aim is to give a uniform analysis of the meaning of sentences expressing generalizations with exceptions, not to make a specific proposal regarding syntactic rules or the structure of such sentences. We can, however, illustrate roughly how our analysis could apply to connected exceptives with a structure along the general lines of (32).

Here the interpretations of the expressions under the various nodes are written beneath the category labels. In particular, DPs are interpreted as type \(\langle 1\rangle \) quantifiers, \((Q_2)^C\) is the type \(\langle 1\rangle \) quantifier obtained by ‘freezing’ the restriction argument of \(Q_2\) to C,Footnote 27 and similarly for \((Q_1)^A\) and \(( Exc (Q_2,C)(Q_1))^A\).
We see that already for sentences of this simple form, the analysis with Exc will yield second-level compositionality in the sense of Pagin and Westerståhl (2010), not quite ordinary (first-level) compositionality. That is, the meaning of a complex expression is determined not by the meanings of its immediate constituents (and the mode of composition), but by the meanings of the immediate constituents of those immediate constituents. The reason is that the application of Exc at the PP requires access to both \(Q_2\) and C, but the interpretations of the daughters of that PP are Exc and \((Q_2)^C\), respectively, and there is in general no way to uniquely decompose a type \(\langle 1\rangle \) quantifier \((Q_2)^C\) into \(Q_2\) and C, which occur two levels down. Similarly, at the higher DP node one needs access to both \(Q_1\) and A, but one level below one has only \((Q_1)^A\). In fact, there are some indications that second-level compositionality is all we can expect for certain linguistic constructions, precisely because DP interpretations are not always uniquely decomposable.Footnote 28
These remarks concern sentences of the form (32). As we will see, particularly in Sect. 5, there are much more complex sentences with exceptives for which our semantic analysis is still correct, but the problem of deriving this meaning in a (first- or second-level) compositional way seems much harder.
Finally, as is often pointed out, the analysis in Moltmann (1995) is (first-level) compositional. However, we show in Appendix B that this is entirely due to the fact that her account does not apply to non-universal generalizations with exceptions. The problem is not just that some assumption about the set C is not satisfied (see the next subsection), but rather that applying Moltmann’s analysis to non-universal cases yields truth conditions that are not even close to the correct ones. Of course, this is not an oversight on her part; on the contrary, her analysis explicitly builds in that the generalizer must be universal. So it is unsurprising that it yields nonsensical results when applied to generalizers like most, for example. Our point here is that for an account that uniformly covers universal as well as non-universal generalizations with exceptions, there is no known first-level compositional solution.
3.3 Inclusion condition and exception conservativity
Our account does not assume that the set C from the exception DP is a subset of the domain A. The so-called Inclusion Condition, that \(C\subseteq A\), has been built into earlier analyses of exceptives, but Peters and Westerståhl (2006, Ch. 8) pointed out that it is empirically incorrect. Consider (33).

There is obviously no assumption here that all foreigners in the discourse universe are students. This observation is related to a general fact about generalizations with exceptions: only the members of \(A \cap C\) ‘matter’ for the truth of sentences of the form (13). This property was called Exception Conservativity in Peters and Westerståhl (2006).
(Econserv) A sentence of the form (13) remains true (false) when C is replaced by \(A\cap C\).
The reader can check that it holds for all sentences with exceptives in this article. It is immediate that Definition 1 ensures Econserv; more precisely, each of (EC) and (GC) remains true (false) when C is replaced by \(A\cap C\).
Once you think of it, exception conservativity is as obvious as ordinary conservativity. Both properties seem to have the status of semantic universals. But neither the analysis in von Fintel (1993) nor the one in Moltmann (1995) satisfies exception conservativity in general. Indeed, the inclusion condition, which both these analyses enforce, requires an exceptive sentence to entail that \(C\subseteq A\)—i.e. \(C- A = \emptyset \)—and thus is inconsistent with Econserv, which proscribes any entailment by an exceptive sentence about \(C-A\). Sentence (34) is another stark illustration of how the inclusion condition conflicts directly with intuition.

4 A survey of exception DPs
This section surveys, mostly with actually occurring examples, a variety of DPs that combine with “but” or “except” in generalizations with exceptions. As Moltmann observed, not all of these DPs are definite. In fact, although the literature almost exclusively discusses definite exception DPs, non-definite ones are very common, and especially with these the corresponding set C may also contain regular cases even with universal generalizations. The contrast in this respect between “except two Cs” and “except the two Cs” is illustrated in Sect. 4.5 below. It also appears with DPs that have both a definite and a non-definite reading, or (to put it slightly differently) a universal and an existential reading, see Sects. 4.2–4.4.
For most kinds of exception DP, we consider both universal and non-universal exceptives, and check whether the intuitive meaning agrees with the meaning given by Definition 1. We treat the truth conditions of sentences of the form (13) as the conjunction of the generality claim and the exception claim. Separating the positive and the negative cases for convenience of discussion, these truth conditions are as follows.Footnote 29

There are also generalizations where the exception DP is not explicitly quantified, i.e. when there is no explicit quantifier \(Q_2\). Sections 4.1, 4.2, 4.6 and Appendix A discuss how \(Q_2\) and C can then be recovered so that \((E^+)\) or \((E^-)\) applies in these cases too.
Some of the example types are familiar from the literature, but many are not. As far as we can see, our survey is fairly exhaustive, covering the main kinds of English exception DPs.
4.1 Proper names
The meaning of universal sentences of the form (13) where the exception DP is a proper name, first discussed in Keenan and Stavi (1986), seems completely uncontroversial in the literature.Footnote 30


Footnote 32 With s as Sanders and b as George W. Bush, the truth conditions of (35) and (36) can be concisely expressed as \(A-B = \{s\}\) and \(A\cap B = \{b\}\), respectively. For example, (36) says that Bush is a Republican, that he lost New Hampshire and won the Presidency, and that no other Republican has done that.
To apply our interpretation scheme, we need to find the relevant set C. In these cases, it is obvious (and taken for granted by everyone writing about exceptives) that \(C = \{s\}\) in (35), and \(C = \{b\}\) in (36). Furthermore, it is natural to take \(Q_2\) to be the quantifier \({ all\,}_\text {ei}\), ‘all with existential import’, defined by

In Appendix A we give a general recipe for finding C and \(Q_2\) when the exception DP is a proper name (or a Boolean combination of proper names). For now, we just note that plugging the choices above into (\(E^{+}\)) and (\(E^{-}\)), respectively, yields exactly the desired conditions, as the reader can verify.
(37) and (5) (repeated here as (38)) express non-universal generalizations with proper names as exception DPs.

Here the truth conditions are different. Consider (38). With c as Frank Capra and \(C = \{c\}\), the generality claim according to (\(E^{-}\)) is that the number of people, not counting Frank Capra, who expected “It’s a Wonderful Life” to become a classic is small. But then it can certainly be the case that even if one includes Frank Capra, the total number of people with this expectation is still small. Then, the generalization also holds without removing the exceptions. Although this cannot happen for universal generalizers, it can for (38).
Exceptive sentences like these completely undermine the view that exceptives serve to save the truth of a host generalization that would be false were exceptions not removed from its domain. Sentence (38) is not merely consistent with (39); it essentially entails it.

Similar remarks apply to (37): adding one more exception could scarcely undermine a true “most” statement. The function of exceptives in sentences like these is not merely to remove exceptions from the domain of their host generalization but especially to draw attention to particular exceptions.
The exception claim of (38), using (\(E^{-}\)) with \(Q_2\) as above, is simply that \(\emptyset \ne A\cap \{c\}\subseteq B\). That is, Frank Capra (belongs to the set of people and) is an exception: he did expect “It’s a Wonderful Life” to become a classic. As far as we can see, this, conjoined with the generality claim, is precisely what a speaker uttering (38) is committed to. In particular, (38) does not say that Frank Capra is the only exception; on the contrary, it invites the pragmatic conclusion that a small number of other people had the same expectation.
(\(E^{+}\)) and (\(E^{-}\)) also correctly interpret non-universal sentences containing exceptive “but”, such as (6) and (7) (repeated here as (40) and (42)).


Each of these sentences says China is an exception. As the analysis predicts, (40) says a weakened economy does not explain a decline in [Hong Kong’s] imports from China though it does explain why imports from most other countries declined; (41) says China would have a chance of getting to the New World before Europeans claimed everything there though most other Asian countries wouldn’t; and (42) says China can offer Egypt financial assistance and investment though few other countries can.
Just like “except”, “but” can be licensed by “most”, “many”, and “few”. The meaning is the same for both, in universal as well as non-universal generalizations.
4.2 Bare plurals
Bare plural DPs are well known to be understood sometimes with a universal-like interpretation that is truth-conditionally tantamount to generic quantification over a set of individuals, and interpreted other times as existential-like quantification over these individuals.

A variety of mechanisms have been proposed for constructing these interpretations and constraining them according to context (Carlson 1977; Chierchia 1998; Krifka 2003; Cohen 2007).
Notably, both interpretations of bare plural exception DPs are found in the Exception Claim of generalizations with exceptions, where they amount to different choices of the quantifier \(Q_2\). For convenience in discussing these interpretations of sentences of the form (13), we represent the generic bare plural reading with \(Q_2 = { all\,}_\text {ei}\), and the existential reading with \(Q_2 = { some}\).
Consider some examples.

Here the second sentence makes clear that all school-going toddlers are exceptions. With A as ‘student’, B as ‘begins school on September 4th’, C as ‘toddler’, and \(Q_2\) as \({ all\,}_\text {ei}\), condition \((E^{+})\) delivers

The exception claim is that some students are toddlers and all such students don’t begin school on September 4th. Clearly these are exactly the right truth conditions for the first sentence of (44). Now consider (45).

It is plausible to understand the author as meaning not that all European physicians are exceptions, i.e. had entered the Ottoman Court, only that some had. This is precisely what \((E^{-})\) gives with the existential reading of “physicians”, that is, with \(Q_2\) as \({ some}\) and C as the set of physicians.
We find the same phenomenon with non-universal generalizations.


The context of (46) favors interpreting it as meaning no foreigners are allowed to read Reference News, whereas (47) does not plausibly claim that all Russian tourists visit Manzhouli, only that some do.
Let us take a closer look at the first conjunct of (47). Here A is ‘foreign (non-Chinese) tourist in China’, B is ‘visiting Manzhouli’, C is ‘Russian’, and with the existential reading of the bare plural, \((E^-)\) says that \({ relatively\, few}\,(A-C, B)\), i.e. \(|(A-C) \cap B|\) is relatively small, and that \(A \cap C \cap B \ne \emptyset \). This seems correct, as far as it goes. Pragmatics adds further implications. The author’s decision to include the adverb “relatively” suggests he thinks the statement needs this qualification in order to be true, even though the qualifier does not semantically require the unqualified version to be false. Similarly, the decision to exclude Russian tourists suggests, though it does not require, that without this exclusion the generalization would not be true. Together the author’s choices suggest he thinks Russian visitors are more numerous than the few non-Russian foreigners whom he apparently believes visit Manzhouli; that is: few non-Russian foreigners and barely more Russian ones visit Manzhouli. Such pragmatic considerations are quite generally involved in the connection between what speakers mean to communicate and the literal meaning of what they say. All of this agrees with taking \((E^-)\) to represent the semantic truth conditions.
For another example, \((E^{+})\) interprets the first sentence of (8), repeated here,

with its exception DP understood existentially, as meaning that we are not available some Sundays though we are available most other days, which is fully consistent with (8).
It is worth noting that which reading the exception DP has in these examples is apparently not determined by what is predicated of it. Universal-like and existential-like readings are both available for pragmatic influences to disambiguate, or not.
Bare plural exception DPs are hardly mentioned in the literature. Neither Hoeksema, nor von Fintel, nor Moltmann discusses them. This is a pity since they are quite common and, as we have seen, afford excellent examples of what sentences with exceptives mean, and do not mean.
4.3 Plural definite descriptions
Singular definites, or definite descriptions, in exception DPs behave essentially like proper names. Definite plural DPs are a bit different because they have an existential-like interpretation in addition to their universal-like one.

Sentence (49a) reasonably claims only that some windows are open, whereas (49b) says that all of them are closed.
Various proposals exist for producing these readings of definite plurals (Löbner 1985; Schwarzschild 1994, 1996). The choice of a definite plural DP’s interpretation is more widely agreed to be pragmatically determined than is the case with bare plurals (e.g. Brisson 1998). Because a definite plural exception DP’s reading affects the exception claim, we regard \(Q_2\) in the latter’s truth conditions as (i) \({ some}\) in the existential-like case and (ii) \({ the}\,_\text {pl}\) in the universal-like case, where the quantifier \({ the\,}_\text {pl}\) and related quantifiers \({ the}\, n\) are defined as follows.Footnote 39

Consider sentences (51)–(53).



A universal interpretation of the definite plural is plausible in all of these, and (\(E^{+}\)) and (\(E^{-}\)) give the correct results. For example, the condition for (52) (after some regimentation), according to (\(E^{-}\)), is that the number of natural harbors on the coastline remaining when you set aside the estuaries in the northwest is small (maybe even zero), and that more than one estuary in the northwest has a natural harbor, and that all of these harbors lie on the coastline. This seems to be just a very round-about way of saying what (52) says.
Nadathur and Lassiter (2018) report experimental results that may reflect a universal/existential ambiguity in interpretation of definite plural exceptive phrases similar to that of bare plurals and of possessives. They asked English speakers to judge whether sentences like

are true descriptions of collections of colored marbles, presenting collections in which various proportions of blue marbles had a dot and all other colored marbles either had (with “every”) or didn’t have a dot (with “no”). All presentations of a sentence and marbles satisfied the generality claim; so true/false responses reflect just the subject’s judgment of the exceptive claim. When all blue marbles were exceptions, the sentence was uniformly judged true; and when no blue marbles were exceptions, it was judged false for all but a small minority of presentations.
Interestingly, when some but not all blue marbles had a dot (i.e. both regular cases and exceptions exist), a significant number of subjects judged the sentence true and many others judged it false. In this condition, subjects were more likely to judge a sentence with “every” false and one with “no” true, more or less independent of what proportion (strictly between 0 and 1) of blue marbles had a dot. This statistically significant finding suggests that in contexts like this experiment, where no communicative purpose is involved, readers are somewhat more likely than chance to give definite plural exception DPs a universal-like interpretation when the host generalizer is positive and an existential-like interpretation when it is negative.
Malamud (2012) demonstrated how powerful a pragmatic force a speaker’s manifest communicative purpose is in disambiguating the definite plural’s reading. It will not be surprising if experiments using contexts designed to favor one of these interpretations over the other show that pragmatic considerations like this readily overpower the moderate bias engendered by a positive or negative host generalization. Much interesting empirical work remains to be done on how definite plural exception DPs are disambiguated between universal-like and existential-like readings.
4.4 Possessive DPs
Possessive DPs also have existential as well as universal readings, and when they occur as exception DPs, the ambiguity again transfers to the exceptive DP containing them. To illustrate, consider (55).

Sentence (55a) most likely says all of Harry’s exam results are excellent. But (55b) doesn’t say that her neighbors bring back Mary’s dogs when all of them run away; rather they do this already when even one runs away.
Possessive sentences involve a possessor relation R, which often has to be supplied by context. (For example, are Mary’s dogs in (55b) the ones she owns, or the ones she is looking after for her brother?) We can treat phrases like “Mary’s” as complex determiners, with two possible interpretations:Footnote 43

Now consider the sentences in (57).

A plausible reading of (57a) is that all of Deirdre’s friends are exceptions (allowed to enter the building). But as we noted in Sect. 1.3, (57b) (= sentence (14)) clearly has a reading on which some but not all of her Bostonian friends were at the party. Applying \((E^-)\) with \(C = \{a\!: a \text { is a friend of Deirdre}\}\) and \(Q_2\) as \({ Deirdre's}_1\) and \({ Deirdre's}_2\), respectively, straightforwardly gives these interpretations.
4.5 Numerical exception DPs
A numerical DP is one formed with a numerical Det, which we take to be Dets interpreted by quantifiers \(Q_2\) such that \(Q_2(C,D)\) states a property, often a numerical estimate, of \(|C\cap D|\).Footnote 44 Examples are “two”, “at most three”, “more than five”, “a few”, “between two and four”, etc. Consider (58).

Let A interpret “restaurant”, C “children free”, and let B be the set of things we tried. According to \((E^{+})\), (58) says that

This seems exactly right. Similarly if we replace “every” by “no” and use \((E^{-})\). We also get correct results when “two” is replaced by “at most two”, or “a few”, or “at least two” (although use of the latter in sentences like (58) seems slightly deviant).
It is instructive to compare (58) to (60).

By our analysis in Sect. 4.3, (60) should mean the following (on the universal interpretation of syntactically definite plurals).

This is slightly stronger: (61) implies (59) (since  implies \(|A\cap C\cap \overline{B}|=2\)), but not vice versa. (59) leaves open that we also tried a children free restaurant; but that is ruled out by (61), which says that there are exactly two children free restaurants, and we didn’t try either of them, though we tried all the other restaurants. Again, this seems to be in perfect accord with the intuitive meanings of (58) and (60).
implies \(|A\cap C\cap \overline{B}|=2\)), but not vice versa. (59) leaves open that we also tried a children free restaurant; but that is ruled out by (61), which says that there are exactly two children free restaurants, and we didn’t try either of them, though we tried all the other restaurants. Again, this seems to be in perfect accord with the intuitive meanings of (58) and (60).
More exotic properties of numbers sometimes appear with exceptives:

Again, \((E^+)\) yields the intended meaning (at least when “all but an odd number of main trunks” is read as “all trunks except an odd number of main trunks”).
4.6 Boolean combinations of names
For the operator Exc to provide a general semantic analysis of exceptive sentences, we need a systematic way to interpret exception phrases with no explicit Det or implicit quantifier as a quantifier of the form \((Q_2)^C\). That is, we need a systematic way to find \(Q_2\) and C. In Sect. 4.2 we saw how that can be done for bare plurals. In this section we suggest such an analysis for exception DPs that are proper names and Boolean combinations thereof. We take such names, used as DPs, to be interpreted by Montagovian individuals: given an individual a, define the type \(\langle 1\rangle \) quantifier \(I_a\) by

In Sect. 4.1, our account in effect relied on the fact that \(I_a\) can be decomposed as follows:

This gives correct truth conditions, and it seems obvious that in this case \(C = \{a\}\), but we didn’t explain why it is obvious, nor did we motivate the choice \(Q_2 = { all\,}_\text {ei}\). Furthermore, Boolean combinations of proper names occur frequently, and their meaning is usually straightforward, as in (2), repeated here as (63):

Here the exception DP in (13) is interpreted by \(I_{23} \wedge I_{239}\), where

Obviously, C in (13) should be \(\{23,239\}\), but what about \(Q_2\)? \(I_{a} \wedge I_{b}\) can be decomposed as \(I_{a} \wedge I_{b} = ({ all\,}_\text {ei})^{\{a,b\}}\), and plugging this into \((E^+)\) gives

But this is incorrect for (63), since (with A as the set of natural numbers and B as the set of those expressible as the sum of at most eight cubes) it does not entail that both 23 and 239 are numbers, i.e. that \(\{23,239\}\subseteq A\). However, with the alternative decomposition,

which is also correct, we obtain

which is equivalent to the obviously correct truth conditions for (2):

Similarly, consider (65).

With the obvious choice of A, B, c, h, the correct truth conditions of (65) are

That is, Christina and Henry are both professors, at least one of them was present at the meeting, but no other professor was present.Footnote 47 This is exactly what we get from \((E^{-})\) with the following decomposition.

This decomposition allows either or both to be exceptions, and eliminates the problem discussed in Peters and Westerståhl (2006) of how to obtain the fact that (65) entails that both Christina and Henry are professors, even if only one of them was present at the meeting. But how do we find the correct decompositions? Still more problematically, how do we find them for a sentence like (67)?

Sentence (67) too seems to have a perfectly clear meaning: Christina, Henry, and Sue are all professors, Christina was present, and at least one of Henry or Sue was also present, but no other professors were present.Footnote 48
It turns out that there is in fact a principled way of finding decompositions which, when plugged into Exc, yield correct truth conditions for all sentences like these. Very roughly, C is the smallest subset of the named individuals on which the truth of the Exception Claim depends, and \(Q_2\) is a particular kind of relativization of Q to C. The technical details are given as the two-step Recipe in Appendix A.
4.7 Other exceptions
One can generalize over very different kinds of entities than the ordinary individuals or objects that make up the domain for most of the examples we have considered so far. And the exception expression that follows an exceptive preposition isn’t always a DP. The following examples from Huddleston and Pullum (2006) illustrate this.Footnote 49

Likewise, Moltmann (1995) gives the following examples.

A syntactic feature of these examples that intrigued the authors of Huddleston and Pullum (2006) is that not one of them has a DP following “except”! Significantly, though, in every single case the exception phrase denotes a member of the domain of applicability over which the generalization licensing “except” ranges. In fact, Von Fintel (1994) mentions a similar example.

These generalizations’ domains span a wide spectrum: from locations and times, through feelings, topics of discussion, things to do, advice, statements, information, and questions, to requests and choices. Eleven of the generalizations are positive or negative universal ones. Only (68i) and (70) are non-universal, and negative.
All thirteen examples have the semantic equivalent of a definite singular term as the complement of “but” or “except”—that is, an expression which denotes an individual location or whatever the example excludes. (68i), for instance, has a particular (syntactically subordinate) question after “except”. The meaning is as in \((E^-)\), with A as the set of questions, \(Q_2 = { all}_{\,\text {ei}}\), \(C = \{\text {`What had they been doing?'}\}\), \(Q_1\) = few, and B = ‘things the speaker asked’. Sentence (68i) is accurately paraphrased ‘few questions were asked by me except the question of what they had been doing’.
In fact, every example in the list is interpreted by applying the operator Exc to an appropriate choice of \(Q_2\), C, \(Q_1\), A, and B. It is straightforward to choose the sets and quantifiers that make the corresponding paraphrase correct. The exceptive phrase connects with, and its occurrence is licensed by, an explicitly quantified DP in all these examples except (68a). In this example, “except” is associated with the locative interrogative “where”, and the negative universal generalization that licenses “except” means ‘I don’t know anywhere to look except in the garden’ or, equivalently, ‘There is nowhere except in the garden that I know to look’. Thus A is the set of locations, \(Q_2 = { all}_{\,\text {ei}}\), C = {the garden’s interior}, \(Q_1\) = no, and B = ‘places I know to look’.
5 Other generalizer expressions
We noted in Sect. 1.2 that universal generalizations expressed by definite or bare plural DPs don’t license the exceptive preposition “but” (examples (11a), (11b)). They do, however, license “except” and “except for”, as García-Álvarez (2009) pointed out.Footnote 50

These exceptives are also licensed by certain generalization-expressing definite singular DPs.

García-Álvarez (2009) made the point that these examples show exceptives are not licensed solely by lexical quantifiers; and in Sect. 4.7 we saw an exceptive licensed by a locative interrogative pronoun in (68a). The bare singular noun “plenty” also licenses exceptives.

Another interesting feature of some of these generalizations is that their domain is not simply the extension of the licensing DP’s noun, as is the case for most examples in the exceptives literature.Footnote 52 Sentence (72a) says people other than Kitty Carlisle on the celebrity panel were fooled by the imposters; she was the only panelist who wasn’t. According to (72b), staking is mandatory for plants belonging to non-dwarf varieties of the garden dahlia. Interpreting the noun in sentences like these as denoting a group or kind of individuals is essential for understanding the sentence as expressing a generalization. The noun “plenty” in (73) does not denote the generalization’s domain but instead expresses its generalizer, whose meaning is similar to “many” or “much”. The domain is denoted by the noun’s (partly elided) complement phrase—the members are things/stuff to like in a contextually available truck’s cab.Footnote 53
Nevertheless, the prepositions “except” and “except for” mean exactly the same in these sentences as elsewhere, namely what exceptive “but” also means where it can occur (see Sect. 1.2). When this meaning, Exc, combines with the exception DP’s meaning, the result operates on the generalizer, domain, and property of the licensing generalization exactly as we saw in Sects. 3 and 4, and outputs the appropriate Generality Claim and Exception Claim. The semantic behavior of exceptives in sentences (71)–(73) offers no surprises. These examples’ novel aspect lies instead at the syntax-semantics interface, where locating the generalizer and domain is less straightforward than in familiar examples of generalizations.
There are more challenging cases still. Does (74) contain a generalizer? If so, what is it and what is its domain?

From (75) we see that (74) can be understood as a generalization.

This fully grammatical exceptive sentence means, roughly:

This fact shows (74) does have a reading as a positive universal generalization whose domain is areas of medical practice. The problem is to uncover what in this sentence’s syntactic structure along with its lexical items constitutes the structural and semantic basis for the generalization that licenses the exceptive phrase in (75) and for compositional assembly of the meaning (76).
Sentences like those in (71), (72), (73), and (75) are further evidence of how uniform the meaning of exceptives is across their wide range of occurrences. These examples also add insight into how widely exceptive-licensing generalizations range beyond the received view that only universals are licensers.
6 Conclusion and further issues
The main contribution of this paper is the discovery that the meaning of sentences expressing generalizations with the ‘hard’ exceptives “but”, “except”, and “except for” can be given as the combination of the two claims—a Generality Claim and an Exception Claim—succinctly formalized with the operator Exc in Sect. 3.1. In agreement with earlier literature on exceptives, exception phrases on our analysis introduce a set C, but—contrary to much of that literature—the role of C is not to mark the boundary between a generalization’s regular cases and its exceptions. That boundary is drawn by the generalization itself and does not depend on the exception phrase. Instead, the role of C is (a) to determine which elements of the generalization’s domain are withheld from the Generality Claim, and (b) to combine with a quantifier \(Q_2\), also given by the exception phrase, to state the Exception Claim: that \(Q_2\,C\)’s are exceptions. This is compatible for many \(Q_2\) with not all domain members in C being exceptions, as well as, for less-than-universal generalizations, with the existence of exceptions outside C.
Many further issues remain to explore. We end by mentioning a few of these.
6.1 Compositionality
We saw in Sect. 3.2 that with a straightforward syntax for simple sentences with connected exceptives, our analysis will yield second-level compositionality at most. For free exceptives finding a compositional account seems even harder. Whether (first-level) compositionality is achievable for a semantically adequate analysis of exceptives is an open question. The analysis in Moltmann (1995) is compositional, but covers only a restricted class of generalizations with exceptions; Appendix B spells this out in detail.
6.2 Logic
Given a semantics for exceptives, one would also like to study their logic. This could be done in various logical frameworks, such as first-order logic with generalized quantifiers, syllogistic or ‘natural’ logic, or non-monotonic logic. Natural questions of complete axiomatizability, decidability, and expressive power arise in these settings. To the best of our knowledge, these issues are completely unexplored for logics designed to deal with exceptives.
Intuitions about inference might also help justify, or perhaps problematize, the semantic analysis. For an instance of the latter, consider

This example was suggested to us by Eric Johannesson, who pointed out that the inference is not valid under our semantics. Should it be valid? More generally, when is the following schema valid?

It turns out that this question is related to the formulation of the Generality Claim. So far we have used the standard version, in which all members of C are removed from A in the restriction argument of \(Q_1\), but we also mentioned the alternative possibility of removing only the exceptions in C (footnotes 24 and 26). This makes no difference for universal generalizers, but it can matter for non-universal ones.
6.3 The Generality Claim
To repeat, the standard Generality Claim is this:

If only the exceptions in C are removed, we have instead:

Fact 2 describes the logical relations between the two versions. The monotonicity properties below were defined in Sect. 2.2. A type \(\langle 1,1\rangle \) quantifier \(Q_1\) is called intersective (co-intersective) if \(A\cap B = A'\cap B'\) (\(A- B = A'- B'\)) implies \(Q_1(A,B) \Leftrightarrow Q_1(A',B')\).
Fact 2

Thus, for all generalizers—since (LM) holds for them—(GC) entails (GC\('\)), by (a). And by (b), (GC) and (GC\('\)) are equivalent for universal generalizers, since no is intersective and all is co-intersective (this equivalence can of course easily be verified directly). Less obviously, with an intersective reading of “few”, (GC) and (GC\('\)) are equivalent. But one can show that for most, and for proportional many and few, (GC) is strictly stronger than (GC\('\)).
It follows that which generality claim is correct affects only example sentences whose generalizer is one of those three quantifiers. The difference, as we pointed out earlier, has no impact on empirical arguments in this article. Where the choice between (GC) and (GC\('\)) affects truth conditions, for instance of example (8)—“We are available most days but Sundays”—the difference lies in whether Sundays that we are available count toward truth of the generality claim. If not, then (GC) is correct; otherwise the weaker (GC\('\)) captures what Exc means.Footnote 56 We have found reliable intuitions about this matter elusive.
Interestingly, however, one checks that \(Q_1(A,B)\) implies \(Q_1(A- (C\cap pol (Q_1)(B)), B)\) exactly when \(Q_1\) is either right mon\(\uparrow \) and left NE monotone or else right mon\(\downarrow \) and left NW monotone. Thus interpreting exceptives with (GC\('\)) counts (78) as valid for all generalizers, including the one in (77), by (RM) and (LM)(b), whereas interpreting them with (GC) makes (78) valid only for generalizers that are left monotone decreasing.
This shows that intuitions about inferences such as (77) might help settle this open empirical question. To make a justified choice between (GC) and (GC\('\)) one needs to examine more actual examples, as well as inferences involving exceptives with “most”, “many”, and proportional “few”, such as (78).
6.4 Negative polarity items
The DP “no critic except Clark” isn’t monotone (let alone monotone decreasing), but (79) is fine, and so is (80).


Gajewski (2008) argues data like these show what we call the exception claim is hidden from the NPI licensing process. But when an NPI occurs in the scope of a quantifier that has a co-occurring exceptive, the quantifier itself is always the licenser of the NPI. An NPI-licensing quantifier is always negative; the exception claim for a positive generalizer doesn’t license NPIs (cf. “almost every”, which doesn’t license NPIs). We conclude that sentences like (79) and (80) are in accordance with our analysis of exceptives, and with basic semantic ideas about NPI-licensing. What remains to be described is, of course, how syntax allows this licensing to happen and interfaces with compositional semantic interpretation of the resulting sentences.
6.5 Exception DPs without nouns?
It is quite common to find what looks like an exceptive with a numerical exception DP that is missing its noun.

It might seem that this is simply a case of eliding the noun (“student” and “states”), and so the usual analysis should apply with \(C=A\). But it doesn’t. The standard Generality Claim would then be \(Q_1(\emptyset ,B)\), which is trivially true for (81) and trivially false for (82). Clearly, these trivial claims have nothing to do with what those sentences mean.
What (81) means, apparently, is that the number of students who didn’t pick the flower & peace sign strip was exactly two. That is, it means all _ except two(students , \( \textit{picked the flower \& peace sign strip})\). So a second guess would be to use the quantifiers expressed by all _ except n in the analysis of these sentences.Footnote 59 But it is not clear just what “most” says in (82) about what proportion of states collect a state tax, nor how to capture this part of the meaning.
We conclude that, perhaps surprisingly, (81) and (82) are not of the exceptive form considered in this article with an elided exception noun. This is further supported by the fact that the noun denoting A is apparently repeated after \(Q_2\):

This again is synonymous with “Clear all except two fields”, but that meaning is not obtained with the operation Exc. We leave this issue for further work.
Notes
Summa Logicæ Part II:18; translated by Alfred J. Freddoso and Henry Schuurman.
Syncategoreumata Tract. IV,7; translated by Joke Spruyt.
Or very nearly so; see Peters and Westerståhl (2006, pp. 308–309), for discussion of which quantifiers actually satisfy von Fintel’s two conditions.
(3) and (5) quoted in García-Álvarez (2003).
Proceedings of the American Society of Foresters (1915, 10:1, p. 5).
Such violations of (II) appear only with non-universal generalizations, whose very existence contravenes (I). In the case of non-definite exception DPs, which Moltmann could analyze but von Fintel couldn’t, the set C such a DP references can include regular cases, not only exceptions, even with universal generalizations. So (II) fails in this manner also, as example (14) and Sect. 4.2 show.
Von Fintel (1994) noticed an instance of this generalization but, being committed to his view of what “but” means, he resorted to pragmatics to account for the evident synonymy of a sentence containing “but” and a paired sentence with “except for”: “The perceived equivalence of universal statements modified by but-phrases or free exceptives then merely conceals the different way these readings come about.” (p. 168)
García-Álvarez (2009) also argued that:
[C]onnected and free uses of an EP are not correlated with an underlying lexical ambiguity in the exception marker and differ just with respect to the source of the generalization that the EP serves to qualify. (p. 118)
Since we treat quantifiers as relations, we use standard types like \(\langle 1,1\rangle \) (rather than, say, \(\langle \langle e,t\rangle ,\langle \langle e,t\rangle ,t\rangle \rangle \)) to indicate the number and arity of their arguments. Accordingly, we write Q(A, B) rather than \(Q(A)(B)=1\).
It is also clear that \(Q_1\) satisfies Extension (Ext): the universe outside A and B doesn’t matter for the truth value of \(Q_1(A,B)\) either. Recall that a (global) generalized quantifier Q is, on every universe M, a (local) relation \(Q_M\) between subsets of M. Ext for \(Q_1\) says that if \(A,B\subseteq M\subseteq M'\), then \((Q_1)_M(A,B) \Leftrightarrow (Q_1)_{M'}(A,B)\). This justifies dropping the subscript \(_M\), as we normally do here. Conserv and Ext are of course characteristic of many quantifiers that are not generalizers, for example, of all others that interpret determiners.
“England’s players” is a DP in (15), as it is in “England’s players are well paid”. And “most of England’s” is not a complex determiner.
The compass directions South-East etc. come from the representation of these properties in the so-called number triangle; see Peters and Westerståhl (2006, Ch. 5).
See Peters and Westerståhl (2006, Ch. 5.6) for a proof.
A stronger version would be to let a function f, for every domain A (or for every domain size |A|), yield the minimal number of regular cases required for \(Q_1(A,B)\) to be true, and require that f be monotone (\(A\subseteq A' \Rightarrow f(A)\le f(A')\)) and unbounded. This would eliminate the need for Isom in (19) below, but (RU) suffices for our purposes here.
|A| is the cardinality of A. If \(\textit{at most k}\,(A,B)\), then \(|A\cap B| \le k\), so \(|A\cap B| + |A-B| \le k + |A-B|\). That is, \(|A| \le k + |A-B|\), so \(k+m \le k + |A-B|\), which, since k is finite, entails that \(m\le |A-B|\) = the number of regular cases.
Suppose \(Q_1\) has these properties and also satisfies (RU), and that the regular cases for \(Q_1(A,B)\) are in \(A\cap B\) (if they are in \(A-B\), replace \(\cap \) by − below). Since \(Q_1\) is non-trivial there are A, B such that \(Q_1(A,B)\). By Conserv, we may assume \(B\subseteq A\). Let \(m > |A|\). By (RU), there is an informative domain \(A'\) such that for all \(B'\), \(Q_1(A',B') \Rightarrow |A'\cap B'|\ge m\). Since \(A'\) is informative, it follows that \(|A'| > |A|\). But then we can embed (A, B) in the domain \(A'\), i.e. there are \(B_0 \subseteq A_0 \subseteq A'\) s.t. \(|B_0|=|B|\) and \(|A_0-B_0|=|A-B|\). By Conserv, Ext, and Isom, \(Q_1(A_0,B_0)\). Since \(Q_1\) is \(\uparrow \) mon, \(Q_1(A',B_0)\). So we should have \(|A'\cap B_0|\ge m\), but this is impossible since \(|A'\cap B_0| = |A\cap B| < m\).
Since (LM) entails (RM), both universals would need to be amended. In mathematical contexts, however, where phrases like “almost all’, “almost everywhere’, “almost sure’, etc. are given precise meanings (say, “Almost all A are B” meaning that the set \(A-B\) has measure 0), there is no such entailment (the empty set has measure 0) and (RM) holds.
Alternatively, the Generality Claim could be: All fully clothed or non-swimmer beachgoers were fully clothed. This would remove only exceptions from the Generality Claim’s domain, where (24b) can remove some regular cases too. The difference can matter for non-universal generalizers like “most” and proportional “many” and “few”—even if it is immaterial for universal generalizers (as we will show in Sect. 6.3). Which option is the correct choice of Generality Claim is not important to this article’s use of evidence about non-universal generalizers, but the issue should be settled with other empirical evidence. Although we do not attempt to do that here, Sect. 6.2 points out a variety of intuitive judgment that might be less delicate than how many regular cases a generalization with exceptive that is true allows C to contain.
Recall the notion of an informative domain for \(Q_1\) defined in Sect. 2.2. Say that \(Q_1\) itself is informative if it has at least one informative domain. Obviously, generalizers should be informative. The point of stating this very weak non-triviality requirement is that the following holds.
(i) A quantifier which is both mon\(\uparrow \) and mon\(\downarrow \) cannot be informative.
This fact guarantees that the three cases in definition (26) are mutually exclusive. For suppose \(Q_1\) is mon\(\uparrow \), mon\(\downarrow \), and informative. Then there are sets \(A,B,B'\) such that \(Q_1(A,B)\) and \(\lnot Q_1(A,B')\). Since \(Q_1\) is mon\(\downarrow \) we get \(Q_1(A,\emptyset )\), and since it is mon\(\uparrow \) we get \(Q_1(A,B')\), a contradiction.
The alternative to \( GC \), mentioned in footnote 24, that removes only exceptions in C from the domain A, is: \( GC' (A,B) \,\Leftrightarrow \, Q_1(A-(C\cap pol (Q_1)(B)), B)\)
Type \(\langle 1\rangle \) corresponds to \(\langle \langle e,t\rangle ,t\rangle \) in the functional version, so our interpretation of DPs is entirely standard. The formal definition of \((Q_2)^C\) is as follows (see Peters and Westerståhl 2006, Ch. 4.5.5, for discussion): for each M and each \(B\subseteq M\),
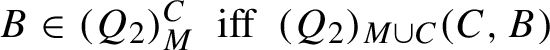
See Appendix A for more about decomposition of type \(\langle 1\rangle \) quantifiers, and Peters and Westerståhl (2013) for an indication that second-level compositionality might be a rather common phenomenon in natural languages.
A rough estimate says that 90% of the examples discussed in the literature on exceptives have a proper name as the exception DP. What is uncontroversial is their truth conditions, not the proper way to arrive at these conditions. For example, Keenan and Stavi treated phrases like “every _ except Jim” as determiners, but this is not generally agreed on.
G. A. Russell, ‘Physicians at the Ottoman Court’, Medical History 34 (1990), p. 243.
https://www.nytimes.com/1991/09/24/world/the-real-news-in-china-comes-out-in-restricted-periodicals.html. Interestingly, the use of “virtually”makes the generalization (slightly) less-than-universal.
When “the n” is analyzed as a quantifier. In an exception DP, “the n” needn’t be a generalizer; it’s \(Q_2\) in the scheme (13). In order to serve as \(Q_1\), “the n” would have to be a generalizer with a cardinality constraint added as discussed in Sect. 2.3.
For a detailed study of the semantics of possessives, which in particular explains how the two interpretations of “Mary’s”, as well as the interpretation of sentence (15), fit into a general interpretation scheme for possessive DPs, see Peters and Westerståhl (2013).
Keenan and Stavi (1986) calls these cardinal Dets.
Moltmann (1995, Section 6.2) reports a different intuition about (65), namely, that the sentence is false if both Christina and Henry were present at the department meeting. We do not share this intuition, at least not as a general semantic constraint on exception DPs that are disjunctions of proper names. One might think we could get that reading by using exclusive disjunction instead. But this approach will not work when we have three or more disjuncts, as in “No professor except Christina or Henry or Sue was present at the department meeting”. With exclusive disjunction, this sentence would be false when two of them were present, but true when all three were. Speculating about intuitions pertaining to a few examples out of context is not very helpful. This is an empirical question and needs to be settled with careful analysis of reliable data.
It is easy to imagine a situation where the speaker knows all this, without knowing which of Henry and Sue was present, or if both were.
Chapter 7, Section 5.1(g), p. 642. We thank Geoffrey Pullum for bringing them to our attention.
Examples (71) and (72) are in his Chapter 1.
Australian Transport News 27 March 2018.
Apart from possessive DP licensers, as discussed in footnote 16.
Also, jokingly speaking of the fictional dinosaur Barney as an exception in (71b) requires reconcilation with the intended meaning that the zoological order Anura persisted after the clade Dinosauria became extinct. The generalization is not about dinosaur lifespans, which were much longer than frog lifespans.
For (a), suppose \(Q_1\) is positive and left SE monotone. (GC) is \(Q_1(A-C,B)\) and (GC\('\)) is \(Q_1(A-(C-B),B)\). But \(A-C \subseteq A-(C-B)\), and \((A-C)-B = (A- (C-B)) - B\), so by left SE monotonicity, \(Q_1(A-C,B)\) entails \(Q_1(A-(C-B),B)\). The case when \(Q_1\) is negative and left SW monotone is similar. For (b), let \(Q_1\) be negative and intersective. (GC) is \(Q_1(A-C,B)\) and (GC\('\)) is \(Q_1(A-(C\cap B),B)\). But \((A-C)\cap B = (A- (C\cap B)) \cap B\), so it follows by intersectivity that (GC) holds iff (GC\('\)) holds. The positive case is similar.
(GC) says that there are (far) more non-Sundays when we are available than non-Sundays when we are unavailable, whereas (GC\('\)) says that there are (far) more days we are available than non-Sundays we are unavailable. (The domain A is the set of all days during one year.)
Where \(\textit{all} \_ except \, n(A,B) \Leftrightarrow |A - B|=n\).
This is the particular relativization of Q promised at the end of Sect. 4.6. (84) says that \((Q_2)_M(A,B)\) iff \( A=C\; \& \;(Q^\text {rel})_M(A,B)\), where \(Q^\text {rel}\) is the usual relativization of Q.
Taking (84) to define \((Q_2)_M\) for every M. The proof uses that \(Q_M\) lives on \(W_{Q_M}\), and that decomposable quantifiers are Ext.
Apart from notation, (87) differs from Moltmann’s definition in three ways: (i) Moltmann formulates (c1) and (c2) not only for M but for all ‘appropriate extensions’ \(M'\) of M; (ii) ‘\(\exists U\in W(Q_M)\)’ below is replaced by ‘\(\exists U \,Q_M(U)\)’; (iii) her definition actually makes the whole exceptive DP denote a set of individuals, rather than a set of sets of individuals.


For example, consider (c1). Let \(X=A\) and take any \(a\in C\). Our ‘reasonable assumption’ in this case is that there is \(Y\subseteq C\) such that \(a\in Y\) and \(Q_2(C,Y)\). By (c1), we have \(Y\subseteq A\), so \(a\in A\). This shows that \(C\subseteq A\).
As to the assumption that \(W_{Q_M} = C\), see Peters and Westerståhl (2006, Ch. 3.4.1) for an argument that this in fact holds in practically all interesting cases.
As far as we can see, Moltmann doesn’t explicitly claim that her analysis of quantified exception DPs also applies, or can be adapted, to non-quantified DPs such as Boolean combinations of proper names. Decomposition is not mentioned, but she does ask the reader to verify that (her version of) (87) applied to “Every boy except John or Bill got an A” gives the result that, in fact, we would obtain using our recipe (Moltmann 1995, p. 254). (As we saw in footnote 47, she is unhappy with that result, but that is a separate issue.)
References
Barwise, J., & Cooper, R. (1981). Generalized quantifiers in natural language. Linguistics and Philosophy, 4, 159–219.
Brisson, C. (1998). Distributivity, maximality, and floating quantifiers. PhD thesis. Rutgers University.
Carlson, G. N. (1977). A unified analysis of the English bare plural. Linguistics and Philosophy, 1, 413–457.
Chierchia, G. (1998). References to kinds across language. Natural Language Semantics, 6, 339–405.
Cohen, A. (2007). Between kinds and properties: Bare plurals across languages. Proceedings of SALT, 17, 53–70. https://doi.org/10.3765/salt.v17i0.2970.
Gajewski, J. (2008). NPI any and connected exceptive phrases. Natural Language Semantics, 16, 69–110.
García-Álvarez, I. (2003). Quantifiers in exceptive NPs. In G. Garding, & M. Tsujimura (Eds.), Proceedings of the XXII West Coast Conference in Formal Linguistics (pp. 207–216). Somerville, MA: Cascadilla Press.
García-Álvarez, I. (2009). Generality and exception. A study in the semantics of exceptives. PhD thesis. Stanford University.
Hirsch, A. (2016). An unexceptional semantics for expressions of exception. University of Pennsylvania Working Papers in Linguistics, 22(1), Article 16. https://repository.upenn.edu/pwpl/vol22/iss1/16.
Hoeksema, J. (1987). The logic of exceptions. In A. Miller, & J. Powers (Eds.), Proceedings of the 4th Eastern States Conference on Linguistics (pp. 100–113). Ohio: Ohio State University.
Hoeksema, J. (1996). The semantics of exception phrases. In J. van der Does & J. van Eijck (Eds.), Quantifiers, logic, and language (pp. 145–177). Stanford: CSLI Publications.
Huddleston, R., & Pullum, G. (Eds.). (2006). The Cambridge grammar of the English language. Cambridge: Cambridge University Press.
Keenan, E., & Stavi, J. (1986). A semantic characterization of natural language determiners. Linguistics and Philosophy, 9, 253–326.
Krifka, M. (2003). Bare NPs: Kind-referring, indefinites, both, or neither? Proceedings of SALT, 13, 180–203. https://doi.org/10.3765/salt.v13i0.2880.
Löbner, S. (1985). Definites. Journal of Semantics, 4, 279–326.
Malamud, S. A. (2012). The meaning of plural definites: A decision-theoretic approach. Semantics and Pragmatics, 5, 1–58.
Moltmann, F. (1995). Exception sentences and polyadic quantification. Linguistics and Philosophy, 18, 223–280.
Moltmann, F. (1996). Resumptive quantifiers in exception phrases. In H. de Swart, M. Kanazawa, & C. Pinón (Eds.), Quantifiers, deduction, and context (pp. 139–170). Stanford: CSLI Publications.
Nadathur, P., & Lassiter, D. (2018). An experimental look at the negative implications of exceptives. In S. Hucklebridge, & M. Nelson (Eds.), Proceedings of NELS 48 (Vol. 2, pp. 201–210). Amherst: GSLA, Department of Linguistics, University of Massachusetts.
Pagin, P., & Westerståhl, D. (2010). Compositionality I: Definitions and variants. Philosophy Compass, 5(3), 250–264.
Peters, S., & Westerståhl, D. (2006). Quantifiers in language and logic. Oxford: Oxford University Press.
Peters, S., & Westerståhl, D. (2013). The semantics of possessives. Language, 89(4), 713–759.
Schwarzschild, R. (1994). Plurals, presuppositions and the sources of distributivity. Natural Language Semantics, 2(3), 201–248.
Schwarzschild, R. (1996). Pluralities. New York: Kluwer Academic Publishers.
von Fintel, K. (1993). Exceptive constructions. Natural Language Semantics, 1, 123–148.
Von Fintel, K. (1994). Restrictions on quantifier domains. PhD thesis. University of Massachusetts at Amherst.
Westerståhl, D. (2008). Decomposing generalized quantifiers. Review of Symbolic Logic, 1(3), 355–371.
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Thanks for helpful suggestions and comments to Johan van Benthem, Cleo Condoravdi, Paul Dekker, Dun Deng, Ivan García-Álvarez, Eric Johannessen, Lauri Karttunen, Ed Keenan, Shalom Lappin, Dan Lassiter, Mingming Liu, Prerna Nadathur, Peter Pagin, Geoff Pullum, audiences at the University of Gothenburg, Stanford University, Stockholm University, Tsinghua University, Universidad del Pais Vasco/Euskal Herriko Univertsitatea, and Waseda University, and three anonymous referees. We dedicate this paper to Ed Keenan, who has been a longtime friend and source of inspiration. He was the first (together with Jonathan Stavi) to raise the issue of exception sentences in the context of generalized quantifiers. The second author was supported by a grant from the Swedish Research Council.
Appendix
Appendix
1.1 A. A recipe for decomposition
Recall (footnote 14) that a global quantifier Q maps each non-empty set M to a local quantifier \(Q_M\) on M, which, in the cases discussed here, is a unary or binary relation between subsets of M. Following Westerståhl (2008) we say that a global type \(\langle 1\rangle \) quantifier Q is decomposable if there is a Conserv and Ext type \(\langle 1,1\rangle \) quantifier \(Q_2\) and a set C such that \(Q = (Q_2)^C\). As we saw in Sect. 4.6, decomposition is not unique. We shall describe a method of finding both C and \(Q_2\) which gives the correct result when Q interprets an exception DP which is a Boolean combination of proper names. For simplicity, we assume in this Appendix that we are working in a finite domain M.
A local type \(\langle 1\rangle \) quantifier \(Q_M\) lives on a set C if for all \(B\subseteq M\), \(Q_M(B) \Leftrightarrow Q_M(C\cap B)\) (Barwise and Cooper 1981). One easily shows that the class of sets that \(Q_M\) lives on is a filter: closed under finite intersections and supersets. It follows (since M is finite) that there is a smallest live-on set; call it \(W_{Q_M}\).
It is not hard to verify that any Boolean combination of \(I_{a_1},\ldots ,I_{a_n}\) lives on \(\{a_1,\ldots ,a_n\}\). But it can also live on a smaller set. For example, \(I_a \vee \lnot I_a\) lives on \(\emptyset \); indeed, any trivial quantifier lives on \(\emptyset \). Also, \((I_a \vee \lnot I_a) \wedge I_b\) lives on \(\{b\}\). To describe the situation, we introduce the following characterization of \(W_{Q_M}\). Say that \(Q_M\) depends on \(a\in M\) if there is \(B\subseteq M\) such that it is not the case that \(Q_M(B) \Leftrightarrow Q_M(B\cup \{a\})\).
Fact 3
\(W_{Q_M} = \{a\in M\!: Q_M \text { depends on } a\}\)
Proof
Let \(D = \{a\in M\!: Q_M \text { depends on } a\}\). To show that \(Q_M\) lives on D, take \(B\subseteq M\), with \(B = \{a_1,\ldots , a_n,b_1,\ldots ,b_m\}\), where the \(a_i\) are in D and the \(b_j\) not. Then:
Next, suppose that \(Q_M\) lives on C; we show that \(D \subseteq C\). Suppose not, and take \(a\in D - C\). There is \(B_0\) such that

Since \(a\not \in C\), we have \((B_0\cup \{a\})\cap C = B_0\cap C\). But this contradicts (i) and the fact that for all B, \(Q_M(B) \Leftrightarrow Q_M (B\cap C)\). \(\square \)
Now let Q be a decomposable type \(\langle 1\rangle \) quantifier. We need to find a decomposition \((Q_2)^C\) that works when Q is a Boolean combination of Montagovian individuals. Recall from Sect. 4.6 that making the right choice of \(Q_2\), among several available ones, is crucial for getting correct truth conditions for exceptives. We saw that for \(Q = I_{a_1} \wedge \ldots \wedge I_{a_n}\) and \(Q = I_{a_1} \vee \ldots \vee I_{a_n}\), choices that work are \(Q_2 =\) (all of) the n and \(Q_2 =\) some of the n, respectively. But what about other combinations?
- Recipe:
-
Step 1 (finding C): Let C be \(W_{Q_M}\).
Step 2 (finding \(Q_2\)): Let \(Q_2\) be the type \(\langle 1,1\rangle \) quantifier defined by:

The construction in (84) is from Westerståhl (2008), where it is shown that \(Q_2\) is Conserv and Ext, and \(Q = (Q_2)^C\).Footnote 62
For example, if \(Q = I_{a_1} \wedge \ldots \wedge I_{a_n}\), then \(C =W_{Q_M} = \{a_1,\ldots ,a_n\}\) and

So \(Q_2\) is distinct from the n, and from \({ all\,}_\text {ei}\), but

Only the first two of these decompositions give the right result for exception DPs that are conjunctions of proper names by requiring \(\{a_1,\ldots ,a_n\} \subseteq A\) if they denote \(a_1,\ldots ,a_n\).
The recipe works for all Boolean combinations of proper names. Consider again sentence (67).

Here \(Q = I_c \wedge (I_h \vee I_s)\), and Q depends on each of Christina, Henry, and Sue, so we take \(C = W_{Q_M} = \{c,h,s\}\). Applying (84) we obtain

Plugging this into \((E^{-})\) gives

which is exactly what we want.
Summing up, the recipe, when the interpretation Q of the exception DP is a Boolean combination of \(I_{a_1},\ldots ,I_{a_n}\), say \(Q = bc(I_{a_1},\ldots ,I_{a_n})\), is to choose \(C=W_{Q_M}\), which is a subset of \(\{a_1,\ldots ,a_n\}\), and then define \(Q_2\) as in (84). Plugging this into \((E^{-})\) we obtain

and similarly for \((E^{+})\). Note that we only get \(a_i \in A\) for those \(a_i\) that \(bc(I_{a_1},\ldots ,I_{a_n})\) depends on; in practice, this doesn’t seem to be a limitation.
The recipe also works for non-universal generalizations. Consider the following variant of (5).

Applying the recipe, we obtain from \((E^-)\) (with A as ‘people’ and B as the set of those expecting the film to become a classic)

That is, the number of people, besides Frank Capra and James Stewart, who expected the film to become a classic is small, but both Capra and Stewart had this expectation. That seems to be what (86) means.
1.2 B. Moltmann’s analysis
As we said, Friederike Moltmann was the first to attempt a general analysis of sentences fitting the schema (13) for any kind of exception DP. She was also the first to use the live-on property from Barwise and Cooper (1981) in the analysis of exceptives. To compare our truth conditions \((E^+)\) and \((E^-)\) with those of Moltmann (1995) we need a few definitions.
First, following Moltmann, let

For example, if \(Q_M\) is the principal filter generated by C, \(W(Q_M) = \{C\}\), and if \(Q_M = ({ three}^C)_M\), \(W(Q_M) = \{X\subseteq C\!: |X| = 3\}\).
Next, consider these two conditions:

We need to assume that (c1) and (c2) are mutually exclusive. Then Moltmann’s analysis can be reconstructed as follows, in the terminology used here.Footnote 63
Let \(\varphi \) be a sentence of the form (13).

(c1) corresponds to positive generalizations, and (c2) to negative ones. Moltmann further imposes a ‘homogeneity condition’, which essentially amounts to saying that when \(\varphi \) is a meaningful sentence of the form (13), either (c1) or (c2) holds. This is to insure that only universal generalizations with exceptions are meaningful, but we have seen ample evidence to the contrary. What we can do is compare (87) to our \((E^+)\) and \((E^-)\) when \(Q_1\) is in fact universal.
A first concern is exception conservativity. Indeed, when \(Q=(Q_2)^C\), Econserv holds almost trivially according to (87), because of the following fact.

As we have seen from several examples, there is no need to assume that C is a subset of A, even if the only part of C that ‘matters’ to the truth or falsity of (13) is \(C\cap A\). So (c1) and (c2) are too strong in this respect. We can still check what happens when in fact \(C\subseteq A\).
Fact 4
If \(W_{Q_M} = C\subseteq A\subseteq M\), \(Q_1\) = every, and \(Q = (Q_2)^C\), the right-hand side of (87) is equivalent to \((E^+)\). Similarly for \(Q_1\) = no and \((E^-)\).Footnote 65
Proof
Let \(Q_1\) = every; the case \(Q_1\) = no is similar. Suppose \(C\subseteq A\) and \(Q = (Q_2)^C\), where \(W_{Q_M} = C\), and assume \(Q_2\) is Conserv and Ext. Then:

The right-hand side of (87) is

and \((E^+)\) reduces in the present case, using Conserv, to

We show that (molt) and (pw) are equivalent. Suppose that (pw) holds, and let \(U = C-B\). Thus, \(U\subseteq C\) and \(Q_2(C,U)\). Let \(X = B\cup (C-B)\). Then \(B = X-U\). It remains to check that \(A\subseteq X\). Take \(a\in A\). If \(a\in B\), then \(a\in X\). If \(a\not \in B\), then \(a\in C\), by the first conjunct in (pw). So \(a\in C-B \subseteq X\).
Conversely, suppose U, X are as in (molt). Then \(A-C \subseteq X-U = B\), so the first conjunct in (pw) holds. We claim:

For, by assumption, \(U\subseteq C\). If \(a\in U\) and \(a\in B\), then \(a\in X-U\); contradiction. Thus, \(U\subseteq C-B\). Suppose now \(a\in C-B\). If \(a\not \in U\), we have \(a\in X-U\), since \(C\subseteq A\subseteq X\). But \(X-U=B\), so \(a\in B\); contradiction. This proves (a), and thereby \(Q_2(C,C-B)\). \(\square \)
Given that Moltmann’s truth conditions as expressed in (87) are rather more complex than \((E^+)\) and \((E^-)\) and rely on additional theoretical notions, this perhaps not immediately obvious fact shows that there is no clash between the two—in the special case where the assumptions hold.Footnote 66 On the other hand, \((E^+)\) and \((E^-)\) don’t assume \(C\subseteq A\), and the conditions in (87) fail completely for non-universal generalizers. To give an example just for illustration, consider

where \(C\subseteq A\), \(|(A-C)\cap B|=5\), \(|(A-C)- B|=10\), \(|C\cap B|=4\), and \(|C-B|=2\). Obviously, no one would say that (89) is true in these circumstances: there are twice as many non-Bs in \(A-C\) as there are Bs. In other words, the generality claim \( most (A-C,B)\) fails badly. But the relevant condition in (87) is

which is true with \(U=C-B\) and \(X = B\cup U\) (then \(|A\cap X| = 11\) and \(|A- X| = 10\)).
What about compositionality? Moltmann says her semantics is compositional, and faults von Fintel’s for not being so, and she is quite right: switching to a functional view of DP meanings, her interpretation can be written

where, given the scheme (13), \(Q=(Q_2)^C\) and \(Q'=(Q_1)^A\). This is not only compositional but allows function application to be the only semantic composition rule.
However, as we have seen, this interpretation scheme only gives the correct result when \(Q'\) is \( every ^A\) or \( no ^A\) (and, in addition, \(C\subseteq A\)). For other generalizers, like most, it is not even close to giving resonable truth conditions. Which is not surprising, since Moltmann’s homogeneity condition in effect stipulates that generalizers must be universal. We conclude that the problem of finding a compositional account of the meaning of all generalizations with exceptions is very much open.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peters, S., Westerståhl, D. The semantics of exceptives. Linguist and Philos 46, 197–235 (2023). https://doi.org/10.1007/s10988-022-09349-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10988-022-09349-y