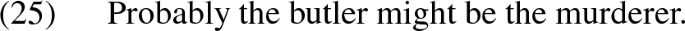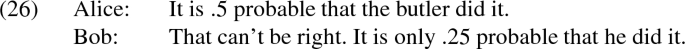Abstract
The view that if-clauses function semantically as restrictors is widely regarded as the only candidate for a fully general account of conditionals. The standard implementation of this view assumes that, where no operator to be restricted is in sight, if-clauses restrict covert epistemic modals. Stipulating such modals, however, lacks independent motivation and leads to wrong empirical predictions. In this paper I provide a theory of conditionals on which if-clauses are uniformly interpreted as restrictors, but no covert modals are postulated. Epistemic if-clauses, like those in bare conditionals, restrict an information state parameter which is used to interpret an expressive layer of the language. I show that this theory yields an attractive account of bare and overtly modalized conditionals and solves various empirical problems for the standard view, while dispensing with its less plausible assumption.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The restrictor view of conditionals is usually understood as the view that the role of if-clauses is to restrict operators, typically quantifiers of different categories. To appreciate the motivation for the view, consider the following sentences.

Roughly, (1-a) means that some occasions on which Alice takes the bus are occasions on which she arrives late; (1-b) means that some epistemic possibilities where Alice took the bus are possibilities on which she arrived late. Thus, in (1-a), the if-clause restricts the range of ‘sometimes’ to occasions where Alice takes the bus, while in (1-b), it restricts the range of ‘might’ to epistemic possibilities where she took the bus.
The restrictor view is a general idea, rather than a specific theory: many different theories can result from it by filling in the details of how if-clauses restrict operators, and of the semantics of the operators they restrict. In particular, most of the major traditional theories of conditionals can be retrieved by making specific assumptions on the kind of operators that if-clauses restrict (see Kratzer, 1981; Rothschild, 2021).
Among scholars interested in compositional semantics, the restrictor view has gained near-universal acceptance. The reason is that it seems to be the only candidate for a fully general theory of the semantics of conditionals. It accounts in a straightforward way for the semantics of sentences like those in (1), involving modals and adverbs of quantification, whereas no other theory seems able to achieve that.
There is, however, a wrinkle in this beautiful picture. Surprisingly, this wrinkle concerns the simplest kind of conditionals, so-called bare conditionals, exemplified by (2):

To uphold the restrictor view as a general story on conditionals, one needs to maintain that the if-clause in (2) is a restrictor. But (2) contains ostensibly no operator which the if-clause could serve to restrict. This seems to lead inevitably to the conclusion that (2) contains a covert operator which the if-clause restricts. On the standard story (Kratzer, 1986, 2012), this covert operator is assumed to be an epistemic necessity modal.
It thus seems that the viability of the restrictor view as a general account of conditionals rests on the plausibility of the assumption that (2) contains a covert modal. Unfortunately, no independent evidence seems to confirm this assumption (see Schulz, 2010, for discussion). On the contrary, as we will see, there are several reasons to think that (2) does not contain a modal—especially not an epistemic necessity modal. This is worrying: if the only candidate for a general account of conditionals turns out not to work for bare conditionals, we are left with no candidate at all.
In this paper, I argue that it is in fact possible to develop a version of the restrictor view which handles (2) without invoking covert modals.
The first step towards this solution is to construe the restrictor view a bit differently than usually done: if-clauses are not, as the view is often put, restrictor arguments of operators. They are restrictor operators: operators which function by restricting a semantic parameter, which may in turn serve as domain for another operator. This is not a novel idea: a prominent existing implementation of the restrictor view (Kratzer, 1981; von Fintel, 1994) in fact treats if-clauses in this way. In the literature, however, this conceptual difference has gone largely unnoticed. But the difference is crucial for our purposes: if if-clauses restrict semantic parameters, and not operators, then a sentence containing an if-clause need not contain an operator which the if-clause restricts. This at least allows for the possibility that (2) contains no covert operators.
However, we still need a story about just what semantic parameter the if-clause in (2) would be restricting. This is where new ideas are needed.
I propose that conditionals like (2) belong to an expressive layer of natural language, containing items which do not contribute to the proposition expressed, but instead modulate the attitude recommended by the speaker towards certain propositions. The compositional semantics for this layer makes reference to an information state parameter, just like standard compositional semantics makes reference to a possible world parameter. The role of the if-clause in (2) is to restrict this parameter.
Here is a suggestive way to put the idea: when (2) is asserted, the role of the if-clause in (2) is to restrict the information state of the adressee, leading to a hypothetical state which contains the information that Alice took the bus. The main clause then functions as a recommendation to accept that Alice arrived late relative to this hypothetical state. In this way, the if-clause allows (2) to function as a recommendation to conditionally accept the consequent under the supposition of the antecedent.Footnote 1
This sketch is not quite accurate: the actual proposal is more abstract, as it needs to account not just for what happens when (2) is asserted, but also when (2) is merely assessed, or occurs embedded. Nevertheless, the proposed semantics for (2) together with the proposed account of assertion leads roughly to the above diagnosis of the role played by the if-clause when (2) is asserted.
Technically, the theory builds on the semantic architecture described in Ciardelli (2021). This paper provides further motivation for that proposal, and pursues a tighter integration with the restrictor view, extending the empirical scope of the theory to if-clauses which restrict non-epistemic modals. This is crucial, among other things, to account for ambiguities of conditionals involving such modals, pointed out by Geurts (2004).
In addition to dispensing with the need to stipulate covert modals, the proposal solves several problems that the covert modal account faces. At the same time, it retains a uniform account of if-clauses as restrictor operators—that is, operators which restrict semantic parameters. To be sure, if-clauses are not treated as restricting always the same semantic parameter. But notice that the if-clauses in (1-a) and (1-b) also restrict different parameters (a set of occurrences/situations in one case, a set of worlds in the other), so this degree of freedom is needed anyway.
If something like what I am suggesting here is right, then solving the puzzle of bare conditionals teaches us something not just about the compositional semantics of conditionals, but also about the semantic architecture of natural language and the semantics-pragmatics interface, providing further motivation for an expressivist account of epistemic vocabulary.
The paper is organized as follows. Section 2 describes two standard versions of the restrictor view. Section 3 shows that both versions require us to postulate the presence of covert operators in the logical form of bare conditionals. Section 4 discusses four problems for this assumption. Section 5 describes the positive proposal. Section 6 spells out its predictions, showing how the problems are solved. Section 7 discusses extra evidence for the account, deals with some potential worries, and extends the empirical coverage of the account. Section 8 concludes.
2 Background on the restrictor view
The view that if-clauses function semantically as restrictors is compatible with different views of how this contribution comes about compositionally. In the literature, two main views are discussed. I will quickly introduce both views, and then present a precise implementation of one of them.
Syntactic implementation. The most common version of the restrictor view, which goes back to Lewis (1975), analyzes if-clauses as being, syntactically, restrictor arguments of other operators. Thus, consider (3):

The idea is that the main operator in (3) is ‘must’, which we denote as \(\Box \). This is analyzed as a binary operator, just like the determiner ‘every’. The first of the two arguments is called the restrictor argument. The word if does not make any semantic contribution, but simply marks a clause as occupying the restrictor argument of an operator. Thus, letting \(\textsf {A}\) and \(\textsf {B}\) stand for ‘Alice leaves’ and ‘Bob stays’, the logical form of (3) is \(\Box (\textsf {A},\textsf {B})\).
While this implementation of the restrictor view is extremely common, it is mostly rejected by those authors who have engaged with the question of how if-clauses restrict modals (von Fintel, 1994; Schulz, 2010; Kratzer, 2012; Mandelkern, 2018). One problem with it is that, being designed with sentences of the form ‘if \(\textsf {A}\), operator \(\textsf {B}\)’ in mind, it does not scale up easily to more complex sentences (cf. Gillies, 2010). For instance, consider:

On a natural interpretation of (4), the first if-clause simultaneously restricts both modals in the consequent, while the second if-clause co-restricts the second modal (i.e., Charlie is under an obligation to stay in case both Alice and Bob leave). It is not easy to see what syntactic assumptions the above story would have to make to predict this result.Footnote 2
Semantic implementation. A more sophisticated implementation of the restrictor view (Kratzer, 1981, 2012; von Fintel, 1994) takes if-clauses to fulfil their restrictor role via a semantic route: if-clauses operate by restricting a contextual parameter, which is then used in the interpretation of operators contained in the main clause. Thus, a construction ‘if \(\textsf {A}\), \(\textsf {B}\)’ can be analyzed as corresponding to a structure \(\textsf {A}\Rightarrow \textsf {B}\), whose semantics has the form \([\![\textsf {A}\Rightarrow \textsf {B}]\!]^{w,f,\dots ,}=[\![\textsf {B}]\!]^{w,f+\textsf {A},\dots }\): to assess \(\textsf {A}\Rightarrow \textsf {B}\) is to assess \(\textsf {B}\) relative to a parameter which has been “restricted” by \(\textsf {A}\).
To illustrate how this works, consider again (3), which on this view has the logical form \(\textsf {A}\Rightarrow \Box \textsf {B}\). Let \({{\mathbf {\mathsf{{A}}}}}\) and \({{\mathbf {\mathsf{{B}}}}}\) denote, respectively, the set of worlds where Alice leaves, and the set of worlds where Bob stays. According to the standard view (Kratzer, 1981), the interpretation of a modal relies on a contextual parameter called the modal base, which is a function f associating to each possibly world w a set f(w) of “accessible” worlds.Footnote 3 In the case of a deontic modal like the one in (3), f maps a world w to the set of worlds that comply with the relevant norms, as they are in w. The effect of the if-clause ‘if \(\textsf {A}\)’ is to transform the contextually given modal base f into \(f+\textsf {A}\), defined by \((f+\textsf {A})(w)=f(w)\cap {{\mathbf {\mathsf{{A}}}}}\).
In combination with the standard semantics for \(\Box \) as a universal quantifier over the accessible worlds, this yields:
That is, (3) is true if among the worlds that comply with the rules, all worlds in which Alice leaves are worlds in which Bob stays. This is the correct analysis of (3) as a statement of conditional obligation.
This version of the restrictor view requires no revisionary assumptions on the syntax of natural language: the if-clause can restrict the modal while remaining in situ. To appreciate the advantage, notice that (4) can now be analyzed as having a logical form which closely mirrors its surface form, namely, \(\textsf {A}\Rightarrow (\Diamond \textsf {B}\wedge (\textsf {B}\Rightarrow \Box \textsf {C}))\). The semantics then delivers the prediction that the initial if-clause restricts both modals:
The semantic implementation of the restrictor view will form the starting point for the positive proposal below. For this reason, in the remainder of this section I will give a fully precise implementation of the theory.
Formalization. We will work with a simple formal language extending propositional logic with the modals \(\Box \) and \(\Diamond \) and the conditional construction \(\Rightarrow \). As customary in the formal semantics literature on modals, each occurrence of a modal is indexed by a variable i, which determines the specific modal base used to interpret it, and thus the ‘flavor’ of the modal (deontic, epistemic, teleological, etc). Likewise, each occurrence of a conditional is indexed by a variable i, which determines the particular modal base that the conditional restricts.Footnote 4
Definition 2.1
The language \(\mathcal {L}_0\) is given by the following syntax, where p is taken from a given set \({\mathcal {P}}\) of atomic sentences and i from a set \({\mathcal {I}}\) of modal base variables:
As background for the semantics, I assume a model \(M=\langle W,V\rangle \) which provides a universe W of possible worlds, as well as a valuation function \(V:{\mathcal {P}}\times W\rightarrow \{0,1\}\) which assigns a truth value to each atomic sentence at each world.
As usual, sentences of the language are assigned truth values relative to a world w and an assignment function f. In our setting, the role of f is simply to determine, for each variable i, a modal base \(f_i\) which yields the set of worlds \(f_i(w)\) that the modals \(\Box _i\) and \(\Diamond _i\) range over.
The clauses for the modals are familiar from modal logic: \(\Box _i\alpha \) is true at w if \(\alpha \) is true at all worlds accessible from w via the corresponding modal base \(f_i\), and \(\Diamond _i\alpha \) is true if \(\alpha \) is true at some of these worlds. Conditionals are interpreted as restrictors of modal bases: the semantic value of \(\alpha \Rightarrow _i\beta \) is just the semantic value of \(\beta \) relative to a new assignment obtained by restricting the modal base \(f_i\) to the \(\alpha \)-worlds.
Definition 2.2
(Semantics) The truth value \([\![\alpha ]\!]^{w,f}\) of a sentence \(\alpha \in \mathcal {L}_0\) relative to a world w and an assignment f is given by the following clauses:
-
\([\![p]\!]^{w,f}=V(p,w)\)
-
\([\![\lnot \alpha ]\!]^{w,f}=1-[\![\alpha ]\!]^{w,f}\)
-
\([\![\alpha \wedge \beta ]\!]^{w,f}=\min ([\![\alpha ]\!]^{w,f},[\![\beta ]\!]^{w,f})\)
-
\([\![\Box _i\alpha ]\!]^{w,f}=1\iff \forall w'\in f_i(w):[\![\alpha ]\!]^{w',f}=1\)
-
\([\![\Diamond _i\alpha ]\!]^{w,f}=1\iff \exists w'\in f_i(w):[\![\alpha ]\!]^{w',f}=1\)
-
\([\![\alpha \Rightarrow _i\beta ]\!]^{w,f}=[\![\beta ]\!]^{w,f+_i\alpha }\), where
-
\(f+_i\alpha \) is the assignment which is like f, except that it maps the variable i to the modal base \(f_i+\alpha \)
-
\(f_i+ {\alpha }\) is the modal base given by: \((f_i+\alpha )(w)=f_i(w)\cap [\![{\alpha }]\!]^f\)
-
\([\![\alpha ]\!]^{f}=\{w\in W\mid [\![\alpha ]\!]^{w,f}=1\}\)
-
With this concrete implementation of the semantic version of the restrictor theory on the table, let us now turn to the main issue of this paper.
3 Covert modals
The bare conditionals puzzle. If if-clauses are restrictors, what are they doing in sentences like (5)—so-called bare conditionals?Footnote 5

The problem is most striking in the syntactic version of the restrictor view, which holds that if-clauses spell out the restrictor argument of some operator. If one wants to maintain this as a general theory of conditionals, one is then forced to admit that the syntax of (5) contains some covert operator that the if-clause is a restrictor of.
On the semantic version of the restrictor view, we could in principle analyze (5) as involving no covert operators, and having the logical form \(p\Rightarrow _i q\) for some i. Here, the antecedent restricts the modal base \(f_i\). But the consequent q is insensitive to this change, since it does not contain any modal. So, \(p\Rightarrow _i q\) is equivalent to q. This is wrong: the if-clause in (5) is not redundant. For this to be the case on this view, however, the consequent of (5) must contain some covert operator which is sensitive to the parameter restricted by the if-clause.
Both implementations of the restrictor view thus require us to suppose that (5) contains a covert operator. This is indeed what Kratzer (1986) famously proposed: more specifically, she proposed that the logical form of (5) contains a silent epistemic necessity modal. Thus, the proposed logical form for (5) is \(p\Rightarrow _e\Box _e q\), where e is the variable corresponding to the epistemic modal base.
Evidence for covert modals? If epistemic modals can occur covertly, we would expect this to be possible not just in bare conditionals, but in other sentences as well. Some evidence for this comes from an ambiguity pointed out by Geurts (2004). Consider (6), involving a deontic must:

This sentence has two readings which, following Geurts, we will call the O-reading and the C-reading.
-
O-reading: conditional obligation. This is the reading which is true in the following context: Alice and Bob are colleagues working in the same place. It is required that one of them be present at the meeting tonight, but they are free to decide among them who. Thus, neither Alice nor Bob is under an obligation to stay; however, both are under a conditional obligation to stay in case the other leaves.
-
C-reading: inference to an obligation. This is the reading which is true in the following context: again, Alice and Bob are colleagues. One of them is required to be present at the meeting. This time, however, the company calendar determines exactly which meetings Alice must attend, and which ones Bob must attend. We don’t know who is required to be present today, but we know that Alice and Bob are responsible employees. Thus, if one of them leaves, it follows that it is the other who must stay.
The assumption that sentences can contain covert epistemic modals provides the resources to predict this ambiguity. Indeed, suppose d and e are the variables corresponding to the deontic and epistemic modal base. Then we can maintain that the first reading arises from interpreting (6) as having the logical form \(p\Rightarrow _d\Box _d q\) (if-clause restricts the deontic modal) while the second reading arises from the logical form \(p\Rightarrow _e\Box _e\Box _d q\) (if-clause restricts the covert epistemic modal), which is available since the epistemic modal \(\Box _e\) is allowed to be silent at surface form.
Thus, the assumption that sentences can contain covert epistemic modals does some work not only in the analysis of bare conditionals, but also in the analysis of conditionals where overt modals are present. Once we dispense with covert modals—as we will below—we need to make sure that the ambiguity of (6) is still accounted for.
4 Against covert modals
The existing implementations of the restrictor theory require the presence of covert epistemic modals in the logical form of bare conditionals. But are those modals there? In this section I will review several arguments against this hypothesis (see also von Fintel, 2007; Schulz, 2010; Mandelkern, 2018).
Problem 1: independent motivation. The assumption that epistemic modals can occur covertly in English is badly in need of independent motivation. If plain sentences like ‘Alice went to London’ were ambiguous between their ordinary interpretation and an epistemic one, this would provide some independent evidence for the possibility of epistemic modals occurring covertly. The same would be true if one could see some syntactic clues of the presence of unpronounced modals. But there seems to be no such evidence. The absence of clues also raises concerns about how speakers acquiring English could figure out that there are such modals and learn their distribution. Also, if bare conditionals contained modals, it seems natural to expect that some languages would require these modals to be expressed overtly. But there is, to my knowledge, no language where English bare conditionals are obligatorily translated as involving a modal. Thus, several potential sources of evidence for the covert modal hypothesis fail to provide support for it.
Problem 2: overgeneration. Without a theory that restricts their distribution, the idea that epistemic necessity modals can occur covertly also leads to massive over-generation of readings. Consider (7):

In addition to the plain logical form \(p\wedge q\), it could in principle convey the forms \(\Box _e(p\wedge q)\), \(\Box _e p\wedge q\), \(p\wedge \Box _e q\), among others. Notice that these sentences are pairwise not logically equivalent in the standard account, and thus lead to different propositions being expressed. If this were right, (7) should be felt to be highly ambiguous. But this is clearly not the case.
Problem 3: bare conditionals under uncertainty. The next argument came up multiple times in disputes concerning conditionals.Footnote 6 Suppose a lottery urn contains 100 marbles: 90 are white, and 10 black. Suppose a marble has been drawn, at random, but its color has not been revealed. Consider:

Given the information we have, (8) can be neither accepted nor rejected with certainty; all we can say is that, given that most of the marbles are white, (8) is quite likely.
Now imagine, instead, that we are not sure whether the draw has taken place. Consider:

The situation seems to be exactly the same. Again, (9) can be neither accepted nor rejected with certainty; intuitively, we feel uncertain about it. Given that most of the marbles are white, however, (9) is quite likely.
Now suppose the if-clause in (9) restricts a covert epistemic necessity modal. Then (9) means that in all the worlds compatible with the available evidence in which a marble is drawn, it is white. This is simply false: the available evidence is compatible with worlds in which a black marble is drawn. And we know it is false. So, if that is what (9) means, we should be able to reject (9) with certainty in the given situation. But we are not.
In response, a proponent of covert modals could say that the covert epistemic modal in (9) is not a universal modal but some other kind of modal (of course, to get a predictive theory they should then say more about what this modal is). But this strategy seems unlikely to succeed, for the following reason: by definition, an epistemic modal statement depends for its truth on what the available evidence is; in our example, there is no uncertainty about what the available evidence is; therefore, there is no uncertainty about the status of epistemic modal statements; but we are uncertain about (9); thus, (9) cannot be an epistemic modal statement.Footnote 7
Moreover, a view that renders the conditional (9) a modal statement misses the exact parallel between the two cases we considered: (8) and (9) are assessed in exactly the same way in the given situation. There seems to be no reason to think that (9) is any more epistemic in its subject matter than (8) is.
Problem 4: anaphora to bare conditionals. The fourth problem has been pointed out by von Fintel (2007). Consider this dialogue:

The most salient reading of Bob’s reply here can be paraphrased as follows:

This is a restricted probability claim, i.e., a claim of high conditional probability. The problem is how Bob’s utterance in the dialogue above gets to mean this. What is the anaphoric item that referring to?
Suppose it refers to the proposition expressed by Alice. According to the standard story, this is an epistemic claim of conditional necessity. Bob’s claim should then mean that it is likely that this conditional necessity obtains, i.e., that it is likely that the available evidence renders it necessary that the butler used a knife if he did it. This is quite different from (11).
In response to this problem, Kratzer (2012) claims that the anaphora picks out the proposition expressed by the consequent of Alice’s claim, but that Bob’s utterance is understood, via a phenomenon of modal subordination (Roberts, 1989), in a context which is still restricted by the previous if-clause, producing a restricted probability claim.
An alternative solution is proposed by von Fintel and Gillies (2015). They suggest that the compositional structure of Alice’s conditional in (10) involves two sub-sentential constituents at the top-level: (i) a function from modal operators to propositions, and (ii) the modal operator must. The proposition expressed by Bob results from the anaphoric item that picking up the interpretation of the first sub-sentential constituent, which then gets applied to a probability operator to yield the right reading.
Both of these solutions, however, do not extend to similar examples. Imagine that Alice, Bob, and Charlie are discussing the crime. Alice makes the statement in (10). A few hours later, Bob says to Charlie:

Again, Bob’s claim can be paraphrased as in (11). But here, neither of the above solutions seems plausible. A Kratzer-style account would take the expression “what Alice said” to refer to the proposition that the butler did it with a knife; a von Fintel-Gillies account would take it to refer to an unsaturated constituent. But neither of these objects could plausibly be the referent of the expression “what Alice said”: not the first, since Alice did not say that the butler did it with a knife; and not the second, since that is not even the kind of object one can agree or disagree with—whereas one can certainly agree or disagree with what Alice said.Footnote 8
It seems quite clear that the natural referent for “what Alice said” is whatever is expressed by Alice’s assertion—a bare conditional. And so, we need a content for bare conditionals that, when embedded under probably, simultaneously provides both a restrictor and a scope argument for the probability operator, yielding the same result as (11). It is far from trivial to see how exactly this can happen. It seems clear, however, that in order for this to work, the logical form of a bare conditional should not contain a modal of its own; otherwise, B’s claim in (10) would contain two modals, whereas it seems to contain just one—the probability modal.Footnote 9
5 Proposal
The observations in the previous section create trouble for the hypothesis that bare conditionals contain a covert epistemic modal. That is bad news for the standard versions of the restrictor view, which necessitate this hypothesis. Is it also bad news for the view as such? That depends on whether one can develop a restrictor-based account that does without covert modals. In this section, I motivate and describe such an account.
5.1 Towards a solution: epistemic vocabulary and expressivism
In recent years, it has been argued by many that the standard theory of the semantics and pragmatics of modals is not quite right for the most common use of epistemic modals.Footnote 10 An alternative view holds that, in typical occurences, epistemic modals do not contribute to the proposition expressed, but rather somehow modulate the attitude expressed, or recommended, by the speaker towards the prejacent proposition. I will refer to these uses of epistemic modals as expressive uses.Footnote 11 Thus, e.g., in a typical situation, sentences like (13-a) and (13-b) do not express propositions; rather, by asserting (13-a) one recommends to regard the proposition that Alice is in London as possible; and by asserting (13-b) one recommends high credence in it. The function of ‘might’ and ‘probably’ is to allow the speaker to recommend such attitudes.Footnote 12

It is natural to take a similar perspective on conditionals. By asserting (14), a speaker does not recommend plain acceptance of a proposition; rather, she recommends conditional acceptance of a proposition on the supposition of another.Footnote 13 Thus, in (14), the conditional construction does not yield a conditional proposition, but rather allows the speaker to express, and recommend, the attitude of conditional acceptance.

Our working hypothesis will be that modals and if-clauses are similar. Both have expressive and factual (i.e., non-expressive) occurrences. Their factual occurrences make a truth-conditional contribution in the way described in Sect. 2; their expressive occurrences make their semantic contribution in a post truth-conditional layer of compositional semantics, where they modify the attitude expressed towards certain propositions.
What exactly does compositional semantics deliver as a semantic value for sentences involving expressive vocabulary?
A natural idea (to be refined) is that semantics delivers a relation of acceptance between sentences and information states. Thus, the semantic map that interprets sentences involving epistemic vocabulary will take the form \([\![\cdot ]\!]^{s,\dots }\) where s is an information state. The semantics will say, for instance, that ‘might p’ is accepted relative to s if according to the information in s, it is possible that p; and ‘probably p’ is accepted relative to s if according to the information in s, it is probable that p.
This relation of acceptance can then be put to work in the semantics-pragmatics interface. In particular, the assertion of a sentence can be construed as a proposal to adopt an information state that accepts it (see, e.g., Yalcin, 2007, 2011; Rothschild, 2021). In this way, acceptance conditions play a natural role in a theory that views communication as a process of coordinating information states.
Now comes the crucial observation for our purposes: this approach naturally provides something for if-clauses in bare conditionals to restrict, namely, the information state parameter. We can assign to a bare conditional like (14) a modal-free logical form \(p\Rightarrow q\), and interpret it as:
where \(s+p\) yields the restriction of the information state s to the p-worlds. This is naturally construed as the hypothetical state that results from the supposition of p in s. Thus, what the clause predicts is that a bare conditional is accepted in an information state if and only if the consequent is accepted in the hypothetical state resulting from the supposition of the antecedent. This is nothing but the celebrated Ramsey test idea (so called after a remark in Ramsey, 1929): to accept a conditional is to accept the consequent under the supposition of the antecedent.
By asserting the conditional, a speaker proposes to adopt a state that has this property. That is, she proposes to adopt a state that conditionally accepts the consequent on the supposition of the antecedent. This is the prediction we wanted for the assertion of a bare conditional.
This discussion suggests an interpretation of bare conditionals which: (i) makes intuitive predictions about acceptance and assertion; (ii) interprets the if-clause in accordance with the restrictor view, as restricting a semantic parameter; and (iii) does not require us to postulate the presence of any covert operators in the logical form of bare conditionals.
This sounds promising. In order to see whether the problems raised in Sect. 4 are solved, however, we need to say more about how the semantics actually works. In fact, combining the idea sketched here with the most popular non-propositional accounts of epistemic vocabulary, namely, dynamic semantics (Dekker, 1993; Veltman, 1996; Gillies, 2004; Willer, 2013), domain semantics (Yalcin, 2007), and the semantic of Moss (2015), would not yield a solution. Instead, I build on the Attitude Semantics developed in Ciardelli (2021), integrating it with the semantic restrictor theory described in Sect. 2.
5.2 Building the theory
Core ideas. The central idea of Attitude Semantics (AS) is that the compositional semantics of the post-propositional layer specifies what it takes to bear a certain attitude to a sentence in a given information state. In other words, the semantic interpretation map has the form \([\![\cdot ]\!]^{s,a,\dots }\), where s is an information state and a is an attitude parameter. This map takes a sentence \(\varphi \), possibly containing expressive vocabulary, to a value \([\![\varphi ]\!]^{s,a,\dots }\in \{0,1\}\). If \([\![\varphi ]\!]^{s,a,\dots }=1\) we say that s supports the attitude a to \(\varphi \). The semantics of expressive vocabulary is very simple: expressive if-clauses work by restricting the information state parameter, while expressive modals work by shifting the attitude parameter. Now let’s see how these ideas can be implemented for a simple formal language.
Formal language. Our starting point is the language \(\mathcal {L}_0\) given in Definition 2.1. We will refer to sentences in this language as factual sentences, since they express propositions and thereby represent the world as being in a certain way. Crucially, we will take this language to formalize only factual (i.e., non-expressive) occurrences of modals and conditionals. The full language extends \(\mathcal {L}_0\) with expressive conditionals (denoted \(\Rightarrow \)) and the expressive modals ‘must’ (\(\Box \)), ‘might’ (\(\Diamond \)), and ‘probably’ (\(\Delta \)). Notice that expressive occurrences of \(\Box ,\Diamond ,\) and \(\Rightarrow \) are not indexed to a modal base variable, since they do not operate with a modal base but with the information state parameter. Since expressive vocabulary interacts in subtle ways with connectives (see Hawke and Steinert-Threlkeld, 2020, for a recent overview), and since the issues we are concerned with here seem unrelated to these puzzles, we set aside Boolean compounds of sentences involving this vocabulary. Moreover, since it is unclear whether genuine expressive sentences can be supposed—and, if they can, how their supposition works exactly—we also restrict to the case of factual antecedents.
Definition 5.1
(Expressive language) The set \(\mathcal {L}_1\) is given by the following recursive definition, where \(\alpha \in \mathcal {L}_0\) is a factual sentence:
Information states and suppositions. We model an information state as a probability distribution. To avoid irrelevant complications, we suppose W to be finite, so that s can be seen as a map \(s:W\rightarrow [0,1]\) such that the sum of the values s(w) is 1. The probability \(s({\mathbf {p}})\) of a proposition \({\mathbf {p}}\subseteq W\) is the sum of the probabilities s(w) for \(w\in {\mathbf {p}}\). The live possibilities for the state s are the worlds which are assigned positive probability.
Definition 5.2
(Live possibilities) If s is an information state, then \(L_s=\{w\in W\mid s(w)>0\}\)
An information state s can be restricted in a natural way to a proposition \({\mathbf {p}}\) by restricting the set of live possibilities to the worlds \(w\in {\mathbf {p}}\). Conceptually, this can be taken to formalize the process of supposing \({\mathbf {p}}\) in s. Formally, it corresponds to the standard operation of conditionalization.
Definition 5.3
(Conditionalization) Let s be an information state and let \({\mathbf {p}}\subseteq W\) be a proposition. The conditionalization of s on \({\mathbf {p}}\) is the information state \(s+{\mathbf {p}}\) given by:
If \(s({\mathbf {p}})=0\), that is, if \({\mathbf {p}}\) is fully ruled out by s, then \(s+{\mathbf {p}}\) is undefined.Footnote 14 Notice that, if \(s+{\mathbf {p}}\) is defined, the new set of live possibilities is obtained simply by restricting the old one to \({\mathbf {p}}\), that is, \(L_{s+{\mathbf {p}}}=L_s\cap {\mathbf {p}}\).
Semantics. Sentences in the language \(\mathcal {L}_1\) are interpreted relative to three parameters: an information state s; an assignment f, as in Sect. 2; and an attitude parameter a, corresponding to a “degree of acceptance”.Footnote 15 For our purposes, the values of a are full acceptance (denoted \(\forall \), also called just acceptance below), partial acceptance (\(\pi \)) and compatibility (\(\exists \)). Intuitively, these attitudes amount to regarding a sentence as certain (\(\forall \)), probable (\(\pi \)), or possible (\(\exists \)). Other values for the attitude parameter could be considered as well, but we will not need them here.
The semantics inductively defines the value of \([\![\varphi ]\!]^{s,a,f}\), i.e., in what cases a state s supports an attitude a to sentence \(\varphi \) relative to the assignment f. For factual sentences \(\alpha \in \mathcal {L}_0\), the compositional semantics given in Sect. 2 yields truth conditions relative to worlds, and thus a proposition. The corresponding support conditions are derived as follows:
-
\([\![\alpha ]\!]^{s,\forall ,f}=1\iff \forall w\in L_s: [\![\alpha ]\!]^{w,f}=1\)
-
\([\![\alpha ]\!]^{s,\exists ,f}=1\iff \exists w\in L_s: [\![\alpha ]\!]^{w,f}=1\)
-
\([\![\alpha ]\!]^{s,\pi ,f}=1\iff s([\![\alpha ]\!]^{f})\ge t\)where t is a fixed thresholdFootnote 16
In words, \(\alpha \) is fully accepted in s if the available information implies that \(\alpha \) is true; \(\alpha \) is compatible with s if the available information does not rule out that \(\alpha \) is true; and \(\alpha \) is partially accepted in s if the available information renders it probable that \(\alpha \) is true.
Expressive modals function as shifters of the attitude parameter: \(\Box \) indicates full acceptance, \(\Diamond \) compatibility, and \(\Delta \) partial acceptance.
-
\([\![\Box \varphi ]\!]^{s,a,f}=[\![\varphi ]\!]^{s,\forall ,f}\)
-
\([\![\Diamond \varphi ]\!]^{s,a,f}=[\![\varphi ]\!]^{s,\exists ,f}\)
-
\([\![\Delta \varphi ]\!]^{s,a,f}=[\![\varphi ]\!]^{s,\pi ,f}\)
Finally, in line with the restrictor view, expressive if-clauses are restrictors, which target the information state parameter.
-
\([\![\alpha \Rightarrow \varphi ]\!]^{s,a,f}=[\![\varphi ]\!]^{s+\alpha ,a,f}\) where \(s+\alpha :=s+[\![\alpha ]\!]^f\)
Content, assertion, and entailment. In a truth-conditional semantics, the semantic map \([\![\cdot ]\!]^{w,f}\) can be put to work in an account of communication as follows. A context of use c determines a relevant assignment function \(f_c\). The content of sentence \(\alpha \) in context c is a proposition, obtained by abstracting over the world parameter:
Relative to an information state s, we can say that this content is accepted (\(L_s\subseteq [\![\alpha ]\!]^{f_c}\)), probable (\(s([\![\alpha ]\!]^{f_c})\ge t\)), or possible (\(L_s\cap [\![\alpha ]\!]^{f_c}\ne \emptyset \)). An assertion of \(\alpha \) in c can then be construed a proposal to the conversational participants to coordinate on an information state that accepts \([\![\alpha ]\!]^{f_c}\).
In a similar vein, in our setting we can define the content of a sentence \(\varphi \) in context c by abstracting over the information state and attitude parameters. In this way, what we get is a set of state-attitude pairs:
We call such an object an x-content (for expressive content). Relative to an information state s, we can talk of such a content as being accepted (in case \(\langle s,\forall \rangle \in [\![\varphi ]\!]_{\textsf {AS}}^{f_c}\)), probable (\(\langle s,\pi \rangle \in [\![\varphi ]\!]_{\textsf {AS}}^{f_c} \)), or possible (\(\langle s,\exists \rangle \in [\![\varphi ]\!]_{\textsf {AS}}^{f_c} \)). In the case of factual sentences, these relations boil down to the same as in truth-conditional semantics. E.g., acceptance of the x-content expressed by a factual sentence \(\alpha \) amounts to acceptance of the corresponding proposition:
Attitudes towards non-factual x-contents also reduce to attitudes towards propositions, but in a non-trivial way. For instance, as we will see shortly, accepting a conditional does not amount to accepting a proposition, but to conditionally accepting a proposition on the supposition of another.Footnote 17
With the new, more general construal of acceptance we can still characterize an assertion of \(\varphi \) in context c as a proposal to the conversational participants to coordinate on a state that accepts the x-content \([\![\varphi ]\!]_{\textsf {AS}}^{f_c}\) expressed by \(\varphi \) in c.
Finally, different notions of entailment can be defined in this semantics. The most salient is in terms of preservation of acceptance: an entailment is valid if the conclusion is accepted by any state that accepts the premises.Footnote 18
6 Predictions
Bare conditionals without covert modals. Consider again:

In AS, this is formalized simply as \(p\Rightarrow q\), without any epistemic modal. The semantics yields the following results about the full acceptance conditions of this sentence:
In words, \(p\Rightarrow q\) is accepted iff q is accepted under the assumption of p. Thus, we predict that acceptance of a conditional conforms to the Ramsey test view. If we further spell out what this means, we get:
Thus, \(p\Rightarrow q\) is fully accepted if and only if among the live possibilities, all the p-worlds are q-worlds. That is, one is certain of \(p\Rightarrow q\) iff one can rule out the possibility that \(p\wedge \lnot q\). This seems the correct prediction.Footnote 19
An assertion of \(p\Rightarrow q\) is a proposal to adopt a state that fully accepts the sentence. Given the full acceptance conditions, we predict that by asserting \(p\Rightarrow q\) one recommends conditional acceptance of q given p. So, now we have a precise account of how exactly the conditional construction allows a speaker to recommend the attitude of conditional acceptance. Crucially, this account involves treating the if-clause as a restrictor.
Ambiguity of conditionals involving root modals. Consider again (6), repeated below, involving a deontic must in the consequent:

We saw in Sect. 3 that this sentence is ambiguous between two readings, and that the covert modal hypothesis yields an account of the ambiguity. The present proposal does not postulate the existence of covert modals. However, we can still correctly predict that (16) is ambiguous. The two readings arise from two different ways of analyzing the if-clause in (16).
If we interpret the if-clause as a restrictor of the deontic modal base, we get to the logical form \(p\Rightarrow _d\Box _d q\). This is a factual sentence: it expresses the proposition that Bob is under a conditional obligation to stay in case Alice leaves. This captures the O-reading of (16).
If we interpret the if-clause as an expressive restrictor, we get the logical form \(p\Rightarrow \Box _d q\). This is not a factual sentence, so it does not express a proposition. By asserting this sentence, one expresses conditional acceptance of the proposition that Bob must stay, under the supposition that Alice leaves. This captures the C-reading.
Thus, both readings of (16) can be predicted. However, the ambiguity does not stem from the possible presence of a covert epistemic modal, but rather from the fact that, just like modals, so also if-clauses are ambiguous between expressive and factual interpretations.
Bare conditionals under uncertainty. Consider again the bare conditional (17) in the lottery scenario above.

If we spell out the semantics of this sentence, we get:
-
\([\![d\Rightarrow w]\!]^{s,\forall , f}=1\iff L_s\cap [\![d]\!]^f\subseteq [\![w]\!]^f\)
-
\([\![d\Rightarrow w]\!]^{s,\exists , f}=1\iff L_s\cap [\![d]\!]^f\cap [\![w]\!]^f\ne \emptyset \)
-
\([\![d\Rightarrow w]\!]^{s,\pi , f}=1\iff (s+[\![d]\!]^f)[\![w]\!]^f\ge t\)
Thus, the status of \(d\Rightarrow w\) in a state s depends on the set \(L_s\cap [\![d]\!]^f\) of live possibilities in s where a marble is drawn. If the marble is white in all these possibilities, the sentence is fully accepted in s, i.e., it is regarded as certain; if it is white in some of these possibilities, the sentence is compatible with s, i.e., it is regarded as possible; and if the probability that it is white restricted to this set of possibilities is high, then the sentence is partially accepted in s, i.e., it is regarded as probable.
Now, in the scenario described above, each marble corresponds to a live possibility. This means that the marble is white in some but not all of the possibilities in \(L_s\cap \,[\![d]\!]^f\). Therefore, it is predicted that \(d\Rightarrow w\) should be regarded as possible but not certain. We thus correctly predict uncertainty about (17).
Moreover, in the scenario it is rational to assign the same probability to each marble. This means that the conditional probability of white given that the draw has taken place is .9. Assuming this is above the threshold t for high probability, \(d\Rightarrow w\) is predicted to be regarded as probable.
Thus, unlike the covert epistemic modal account, we can do justice to the intuition that in the given scenario, (17) is not certain, but it is possible and in fact quite likely. What is crucial for this is the fact that, like factual sentences, bare conditionals are not modalized claims: they do not contain any operator that grammatically fixes the attitude parameter, but instead they can be assessed from the perspective of different attitudes.Footnote 20
Anaphora to conditionals. Finally, consider again:

The observation is that Bob’s assertion is a claim of high conditional probability, equivalent to the following:

The challenge was how to derive this compositionally. On the view that Alice’s claim involves a covert epistemic modal, it was unclear how to do that: if ‘that’ refers to the content of A’s claim, then B’s claim should be a second-order epistemic statement, quite different from (19).
In AS, the problem has a straightforward solution. By asserting the conditional \(p\Rightarrow q\), Alice expresses the following x-content:Footnote 21
The anaphors ‘that’ or ‘what Alice said’ used by Bob simply pick up this content. Our semantics of \(\Delta \) as an attitude shifter amounts to interpreting it as the following function from x-contents to x-contents:
When we apply this function to the content \([\![p\Rightarrow q]\!]_{\textsf {AS}}\) which is picked up by the anaphor, we get that the following content is expressed by Bob:
Thus, we predict that what Bob expresses in the above dialogue is exactly the same thing that he could have expressed by asserting (19). Moreover, recall that by making an assertion, a speaker proposes to adopt a state that accepts the corresponding content. Now, the acceptance conditions for Bob’s claim are as follows:
That is, an information state s accepts Bob’s statement iff it assigns high conditional probability to q given p. Thus, we predict that what Bob expresses by his assertion is the view that the conditional probability of q given p is high. This is the prediction we wanted.
To illustrate the generality of the solution, consider the following variant of the puzzle:

Again, we can construe the anaphor as picking out the content expressed by Alice, namely, \([\![p\Rightarrow q]\!]_{\textsf {AS}}\). Our semantics above amounts to treating \(\Diamond \) as denoting the function \(\lambda C.\{\langle s,a\rangle \mid \langle s,\exists \rangle \in C\}\). When we apply this function to the content of the anaphor we get the same content that would be expressed by the sentence \(\Diamond (p\Rightarrow q)\). This sentence is acceptable in a state in case q is true in some of the live p-possibilities. Thus, we predict that, by his assertion, Bob expresses that he regards it at possible, given that the butler did it, that he used a knife. Again, this seems right.
Thus, we can now assign bare conditionals with contents that are suitable referents for the anaphoras in the previous dialogues. Two things were crucial to achieve this result: first, the relevant contents are not propositions; if they were, then Bob’s claim in (18) would ascribe high probability to a proposition, whereas intuitively, it is an ascription of high conditional probability.Footnote 22 The second crucial feature of the account is that the content of a bare conditional does not build in any epistemic quantification. In this way, when this content is given as input to an operator like ‘might’ or ‘probably’, what we get is not a second-order epistemic claim, but a claim of conditional possibility or probability.
Summary of predictions. Combining attitude semantics with the semantic restrictor theory described in Sect. 2 we obtain a theory which does not require the ad hoc postulation of covert epistemic modals. This obviates the theoretical problems described above (Problem 1) and allows us to avoid the overgeneration issue (Problem 2). It correctly predicts that bare conditionals are assessed like factual sentences in situations of uncertainty (Problem 3). And it gives us a modal-free content for bare conditionals which allows us to interpret anaphoras to conditionals (Problem 4). At the same time, we inherit the advantages of the restrictor view: we still have a general account of if-clauses as restrictors, and we can still account for the ambiguity of conditionals involving root modals.
7 Further issues
7.1 More evidence: conditional questions
So far, we focused on declarative sentences. But if-clauses occur in other kinds of sentences as well, as witnessed by the following interrogative:Footnote 23

Since the restrictor view aspires to be a fully general account of if-clauses, we should be able to provide an analysis of (21) based on the assumption that the if-clause is a restrictor. But since there is no obvious operator to restrict, the challenge we faced for bare conditionals also arises here.
Suppose one resorts again to a covert epistemic necessity modal. Then (21) asks which individual x is such that the evidence implies that if there is an accomplice, it is x. This is not the right result. To see why, suppose we are sure the evidence is compatible with different people being the accomplice. Then we are certain that there is no individual x such that the evidence implies that if there is an accomplice, it is x. So, we should perceive (21) as being just as defective as (22):

But this is not the case. In the described situation, (21) seems a perfectly meaningful question to entertain.
This speaks against (21) being epistemically modalized: intuitively, (21) is not a question about the evidence, but a question about the facts. When asking (21), what one is asking is who the accomplice actually is. However, one is asking this under the supposition that there is an accomplice. In other words, by asking (21), one first sets up a hypothetical context by restricting to words where Axton has an accomplice. Then one asks, relative to this context, who this accomplice is.
Assuming this analysis is on the right track, the question is how to derive it compositionally, on the assumption that if-clauses are restrictors.
On the view that if-clauses restrict operators, it is not clear how to do that. What operator would the if-clause in (21) be restricting?
By contrast, the view that if-clauses can restrict an information state parameter delivers the above prediction in a natural way. Let us see how. Suppose, following recent work on inquisitive semantics (Ciardelli et al. 2018), that the semantics of interrogatives is given by specifying resolution conditions relative to an information state. That is, interrogatives \(\textsf {Q}\) are interpreted by a map of the form \([\![\textsf {Q}]\!]^{s,\dots }\), which takes the value 1 when Q is resolved by the information available in s. For instance, the question ‘who is the accomplice?’ is resolved in a state s just in case all the live possibilities \(w\in L_s\) agree on who the accomplice is (i.e., the same individual is the accomplice in all the live possibilities).
Now consider (21): syntactically, it involves an if-clause modifying an interrogative main clause. That is, (21) is naturally analyzed as a conditional \(\textsf {A}\Rightarrow \textsf {Q}\) with an interrogative consequent. We can analyze the if-clause as a restrictor of the information state parameter, obtaining:
This says that to resolve a conditional interrogative is to resolve the consequent under the assumption of the antecedent. This seems correct. E.g., this predicts that (21) is resolved in a state s if all the live possibilities in s in which Axton has an accomplice agree on who this accomplice is.
Now suppose that, in typical situations, by asking a question one requests information that resolves the question. Then we predict that by asking a conditional question, one requests information that resolves the consequent under the assumption of the antecedent. I.e., one formulates the request for information specified by the consequent (in our example, identify the accomplice), but only in restriction to the antecedent worlds (those in which there is an accomplice). This vindicates the intuition described above about the effect of asking of a conditional question.
Thus, looking at conditional questions provides an independent source of evidence for the view that if-clauses need not always restrict operators, but may instead restrict an information state parameter of the semantics.
7.2 Truth ascriptions
In the proposal we just described, non-factual sentences do not express propositions, but a more general sort of contents, that we called x-contents. As we described above, x-contents are things towards which one can have an attitude. However, they are not evaluable in terms of truth at a world—at least, not when they do not correspond to a proposition.
However, in natural language we do ascribe truth to claims involving expressive conditionals and modals. Consider, for instance:

Here, the anaphor ‘that’ presumably refers to the content that Alice expressed by her modal claim. But this content is not a proposition, so it cannot be true or false. Is Bob just making a bad category mistake?
Before sketching a response to the objection, notice that the worry is not specific to our view. Rather, it arises for anyone who holds that the function of certain declarative sentences is not to describe the world. For instance, it is famously a matter of debate whether the function of evaluative claims and moral claims is to describe facts about the world, or rather to manifest certain attitudes. Yet the following dialogue is unremarkable.

I think it is fair to doubt whether ‘true’ as used in such responses means the same as ‘true’ in a more substantive philosophical sense. In the latter use, truth is a kind of correspondence between language and the world: a sentence is true if it describes things as being in a way they actually are.
By contrast, it seems plausible that what Bob is doing in (23) and (24) is merely to express his agreement with Alice’s claim—to manifest a certain alignment of attitudes—which is of course possible regardless of whether Alice’s claim is capable of being true in the substantive sense.
This view goes well with a deflationist account of truth ascriptions. According to that view, to claim of something that is true amounts to claiming that very thing. Thus, in (23), Bob’s claim is equivalent to the claim that the butler might have done it, and in (24), it is equivalent to the claim that the tiramisù was delicious. Here is one possible way to implement the idea compositionally: in Sect. 6 we interpreted ‘probable’ as a function from x-contents to x-contents; we can treat ‘true’ as a function of the same kind: the identity function.
This vindicates the deflationist idea that ‘A is true’ is equivalent to A. In the case of the dialogue in (23), Alice claims that \(\Diamond b\), and thereby expresses the x-content \([\![\Diamond b]\!]_{\textsf {AS}}=\{\langle s,a\rangle \mid [\![\Diamond b]\!]^{s,a}=1\}\). In Bob’s utterance, the anaphor ‘that’ refers to that x-content. Applying the truth predicate returns the same x-content, \([\![\Diamond b]\!]_{\textsf {AS}}\). So we predict that by his utterance, Bob is merely endorsing Alice’s modal claim, and not describing it as true in the more substantive sense.
Of course, this story is not the only option available to us. My aim in presenting it is merely to illustrate the point that truth ascriptions like the one in (23) are not necessarily a problem for the present account.Footnote 24
7.3 A uniform treatment of modals
In this paper, we have strived to retain a unified account of conditionals, interpreting if-clauses uniformly as restrictors. To be sure, such clauses do not all restrict the same thing. But it seems uncontroversial that that would be too much uniformity to ask, since it is clear from the canonical examples in (1) that if-clauses can restrict different sorts of objects (e.g., a set of occasions in (1-a) and a modal base in (1-b)). What is crucial is that a general scheme underlies all these cases: a clause of the form ‘if \(\alpha \)’ always targets some kind of parameter and restricts it to the objects that satisfy \(\alpha \).
One could, however, complain with some justice that in the process, we have given up a uniform treatment of modals: in the proposed account, expressive modals shift a semantic parameter, while factual modals quantify over accessible worlds. These are two quite different treatments. But it seems implausible to maintain that must and may are simply ambiguous, especially in light of the stability of this ambiguity cross-linguistically.
Fortunately, however, we can in fact isolate a common core to the semantics of must and may across their occurrences. This is given by their semantics as shifters of the attitude parameter. Indeed, a factual occurrence of a modal can be decomposed in two parts: one part is just the bare operator \(\Box \) or \(\Diamond \), interpreted as a shifter of the attitude parameter; the other part is an operator \(@_i\), whose role is to relativize the modal claim to a modal base. More precisely, \(@_i\) operates by shifting the point of evaluation from a world w to the information state \(f_i(w)\).Footnote 25
-
\([\![@_i\varphi ]\!]^{w,f}=[\![\varphi ]\!]^{f_i(w),\_,f}\)
In this clause, the symbol ‘\(\_\)’ stands for a null value. In order for \([\![\varphi ]\!]^{f_i(w),\_,f}\) to be well-defined, a value for the attitude parameter must be supplied by some modal inside \(\varphi \). If that does not happen, we can stipulate that the result is undefined. We can then derive the semantics that we assigned above to the factual modals \(\Box _i,\Diamond _i\) from the interaction of the operator \(@_i\) and the semantics of \(\Box ,\Diamond \) as attitude shifters:
Thus, we may assume that modals like ‘must’ and ‘may’ make a uniform semantic contribution, but that some of their occurrences are “anchored” by a modal base operator, giving rise to factual readings, while others are “free”, giving rise to expressive readings.Footnote 26
7.4 Extension to attitude ascriptions
A puzzle analogous to our Problem 4 above arises for attitude ascriptions. In this section, I show that our solution extends naturally to that case. To see the problem, consider first the following statement.

This statement ascribes a conditional belief: it describes Charlie as believing, conditionally on the supposition that the butler did it, that he did it with a knife. It is a strength of the restrictor theory that this can be predicted, by treating the if-clause as a restrictor of the attitude verb.
However, the problem with anaphora discussed above also strikes here. Consider:

Intuitively, what Bob is saying here could be rephrased as in (25). But in the standard version of the restrictor view, it is not clear how this reading might come about. If ‘so’ picks out the content of the bare conditional, which in that view is a certain modal proposition, then (26-b) is predicted to ascribe to Charlie a categorical belief in a modal proposition, rather than a conditional belief in a non-modal proposition.
Our solution extends naturally to this variant of the puzzle. Suppose we treat the belief operator \(\textsf {Bel}\) as similar to \(@_i\) above: the role of \(\textsf {Bel}\) is to shift the point of interpretation from a world w to an information state (the doxastic state \(s_x^w\) of the relevant agent at w) and an attitude (say, probabilistic acceptance, \(\pi \), but this won’t matter for our purposes):Footnote 27
In words, x believes \(\varphi \) in case x’s doxastic state probabilistically accepts \(\varphi \). One way to obtain this result compositionally is to analyze the belief operator \(\textsf {Bel}\) as a function from x-contents C and agents x to propositions:
Now we are in a position to deal with the little dialogue above. Alice asserts \(b\Rightarrow k\), and thereby expresses the x-content \([\![b\Rightarrow k]\!]_{\textsf {AS}}\). The anaphor ‘so’ in Bob’s utterance picks out this content. Bob’s claim is then associated with the following proposition:
So, Bob’s sentence is true in case Charlie has a certain conditional belief: namely, in case his doxastic state updated with the supposition that the butler did it results in a hypothetical state that assigns high probability to the proposition that he did it with a knife. This is the result we wanted.
Again, notice that two things were crucial to achieve this result: first, the content of the bare conditional \(b\Rightarrow k\) is not a proposition, so that to ascribe belief in this content is not to ascribe belief in a proposition (instead, it is to ascribe belief in a proposition given another); and second, this content does not involve any modal, so that the resulting belief ascription does not involve any layer of modality beyond the one provided by the attitude verb itself.
It is worth noting that this strategy extends beyond belief ascriptions. For instance, one could give a similar account of ascriptions involving want, provided one extends the repertoire of attitudes in the semantics to include non-cognitive attitudes like desire.
8 Conclusion
Let me close by summarizing the main conclusions we have reached.
First, the debate between the operator view and the restrictor view has often been viewed as a debate as to where to locate the source of the epistemic quantification associated with bare conditionals: operator theories took the source of quantification to be the conditional, while restrictor theories took the source to be a covert modal. However, I have argued that both positions share a false presupposition: there is no epistemic quantification associated with bare conditionals, just like there is none associated with factual sentences like ‘it’s raining’. There is a universal quantification associated with the assertion of such sentences. But this comes from the speech-act of assertion, with its connection to acceptance, rather than from a grammatical item in the logical form of the sentence.
Second, I think the restrictor view is right: if-clauses are restrictors. But not, as often supposed, restrictor arguments. Rather, they are restrictor operators—operators which restrict semantic parameters. Sometimes these parameters provide the domain for a quantifier, for instance a modal, generating the effect of a restricted quantified claim. Other times, however, the relevant parameters feed directly into the pragmatics, leading to conditional assertions, conditional acceptance, conditional probability judgments, and so on. Recognizing this leads to an implementation of the restrictor view that shares the generality of the standard theory, but improves on its empirical predictions, and simultaneously dispenses with its most dubious assumption—the existence of covert epistemic modals.
Notes
What is described here is in the spirit of the suppositionalist view of conditionals, which has been articulated most explicitly by Edgington (1986, 1995, 2014) (see also Bennett, 2003). However, Edgington does not say much about the compositional semantics of conditionals. The present work can be seen as a way to show that a suppositional account of bare conditionals can be derived from the assumption that, semantically, if-clauses can serve to restrict an information state parameter that plays a key role in the syntax/semantics interface.
The Kratzerian framework actually uses two semantic parameters to interpret a modal. In addition to the modal base f, one also has an ordering source g, which determines a pre-order of the accessible worlds. To simplify the discussion, I set aside this parameter, since its presence is immaterial to our concerns. Restoring ordering sources in the proposal is straightforward.
This indexing is necessary since a sentence might contain modals of different flavors, in which case, the if-clause may in principle be construed as targeting either. To avoid overgeneration, it is natural to assume that the indexing of if-clauses is subject to pragmatic constraints: in particular, logical forms yielding vacuous restrictions—restrictions which are immaterial to the semantics of the sentence—will be pragmatically ruled out as deviant (for the idea of a pragmatic ban against structural redundancy see, e.g., Katzir and Singh, 2014).
Notice that I do not classify conditionals containing will and would as bare conditionals. There is broad consensus in the semantic literature that will and would are modals. As such, they may be restricted by if-clauses. See Cariani and Santorio (2018) for an account.
Versions which are specifically directed at the epistemic necessity view of bare conditionals are given in Edgington (2008), Mandelkern (2018), Ciardelli (2021). Versions directed at necessity-based accounts of counterfactuals have been given by DeRose (1994), Edgington (2008), Moss (2013), Schulz (2014). In the domain of future discourse, an analogous point has been made by Belnap et al. (2001) and Cariani and Santorio (2018).
Kratzer (2012) maintains that the epistemic modal in bare conditionals is universal but can pick different salient bodies of evidence. But what would the salient body of evidence be, in our story, that produces the intuitions reported above? Kratzer allows the salient body of evidence to be the whole actual world—in which case the conditional is interpreted as the material conditional. But this is not what is going on here. To see this, imagine that the proportions of white and black marbles were reversed. Then we would judge (9) to be unlikely. But the material conditional may well be very likely, provided the antecedent is very unlikely. So, the interpretation of (9) which gives rise to the above intuitions is not the material one.
See also Khoo (forthcoming) for a similar argument to the same conclusion.
In some approaches, including the one to be developed below, a sequence of two epistemic modals collapses, in the sense that one of the two modals comes out as redundant. That might seem to provide a way out of the problem we just pointed out; but it does not, since the sequence is predicted to collapse to the innermost modal. Thus, in our example, it is the probability modal that would be obliterated, not the necessity modal.
I believe that there are also non-expressive uses of epistemic modals. These are readings in which the epistemic modal is used to make a claim about a clearly discernible, contextually salient body of information—for instance, the evidence available to a detective or the content of a database. These uses behave differently from expressive uses: the puzzling phenomena which have been argued to speak against the standard account (faultless disagreements, epistemic contradictions, embedding failures) do not arise for them. A story about how both kinds of readings can stem from a unified semantics for these modals is given in Sect. 7.3.
Different theories of the semantics of epistemic modals are compatible in this view, including those by Veltman (1996), Swanson (2006, 2016), Yalcin (2007), Rothschild (2012), Willer (2013), Moss (2015), Hawke and Steinert-Threlkeld (2020). It is important to point out that these theories (unlike speech-act views like the one of Schnieder (2010)) do not deny that epistemic modals make a proper compositional semantic contribution. Similarly, in the proposal below, sentences involving epistemic vocabulary have a compositional semantic value. This value is simply not a proposition.
For views along these lines, see Gillies (2004) and Yalcin (2007). An analogous view focusing on conditional probability was taken, in the footsteps of Adams (1975), by Edgington (1995) and Bennett (2003). We will not rehearse the arguments for this sort of view here. Rather, we will see that a view along these lines allows for a solution to the problems above, which in turn can be seen as a merit of the approach.
If one wants to allow for the possibility of supposing propositions which are assigned probability 0, one can model information states as binary Popper functions \(s(\cdot |\cdot )\) (Popper, 1959), and define \(s+{\mathbf {p}}\) by letting \((s+{\mathbf {p}})(\mathbf{r }|\mathbf{q })=s(\mathbf{r }|{\mathbf {p}}\cap \mathbf{q })\). If we then define the abbreviation \(s({\mathbf {p}}):=s({\mathbf {p}}|W)\), the semantics below can be stated unchanged.
Though this informal characterization is appropriate in the present context, it may ultimately be too restrictive. One might want, e.g., to extend the semantics to allow for values of the parameter a which correspond to non-cognitive attitudes; this would allow us to give a semantics for, say, want, along the lines of the semantics for believe sketched in Sect. 7.4.
Alternatively, it would be unproblematic to let this threshold be contextually supplied.
Note that factual sentences are associated both with a proposition, \([\![\alpha ]\!]\), and with an x-content, \([\![\alpha ]\!]_{\textsf {AS}}\) (dropping the superscripts \(f_c\) for ease of readability). These two objects are inter-derivable: the way to derive \([\![\alpha ]\!]_{\textsf {AS}}\) from \([\![\alpha ]\!]\) is given by the semantic clause for atomic sentences specified above. In the other direction, we can set \([\![\alpha ]\!]=\max \{\mathbf{p }\subseteq W\mid \langle s,\forall \rangle \in [\![\alpha ]\!]_{\textsf {AS}}\text { for some state }s\text { with }L_s=\mathbf{p }\}\). More generally, a proposition induces an x-content, and can for most purposes be identified with that content. However, there are many x-contents, such as the ones expressed by \(\Diamond p\) and \(p\Rightarrow q\), that are not induced by any proposition. In this sense, we can think of the notion of x-content as a generalization of the notion of proposition suitable to capture also the contents of non-factual sentences.
See Bledin (2014) for a defence of this construal of logical consequence. This is not the only notion of consequence that can be defined in the framework: with a slightly more general repertoire of attitudes (as in Ciardelli, 2021), we can also define a probabilistic notion of consequence, in the style of Adams (1975).
At least when the antecedent is compatible with the available information. If this is not the case, the clause for the conditional is undefined. Interpreting undefinedness as presupposition failure, this is in line with the common assumption that indicative conditionals presuppose the epistemic possibility of their antecedent (see, e.g., von Fintel, 1998; Gillies, 2009, 2010). However, we might want to avoid making such conditionals undefined (see Ciardelli, 2020, for some arguments). We can do so by using Popper functions as suggested in Footnote 5.3. In terms of the logic, this is basically the choice between a strict and a variably strict account of conditionals. This means that both choices are compatible with the present proposal.
In Ciardelli (2021) it is also shown that, if we construe subjective probability as a measure of how supported a sentence is by the available evidence, then a variant of the present semantics predicts that the probability of \(p\Rightarrow q\) is the conditional probability of q given p, in accordance with Adams’ Thesis. Thus, we could in fact predict that, in the given example, adopting the obvious probability distribution leads to assigning a probability of .9 to (17).
I omit reference to the assignment, since it plays no role for this particular case. Of course, in general it is important to keep track of contextual parameters when dealing with anaphora.
Of course, one could try to find a proposition which has high probability just in case the conditional probability of q given p is high; but we know from the vast literature on triviality results (see Khoo and Santorio, 2018, for an overview) that there are very serious obstacles to this enterprise.
There are also conditional imperatives, such as ‘If the screen freezes, restart the machine’. I do not discuss them here, since it is not obvious whether they pose a special challenge. According to Kaufmann (2011), the semantics of an imperative involves a modal operator. If she is right, this operator can be restricted by the if-clause, and the imperative thereby conveys a conditional obligation.
Thanks to the editor for pushing me to say more on this point.
Strictly speaking, \(f_i(w)\) is just a set of worlds, whereas above we took an information state to be a probability distribution. However, the quantitative component of a state is needed only for the interpretation of the modal ‘probably’. If we are just dealing with the modals ‘must’ and ‘may’, the above semantics is well-defined when s is modeled as a set of worlds.
Note that, given our treatment of modals as attitude shifters, a sequence of modals collapses to the innermost modal unless there is an intervening @ operator that anchors the inner modal to a modal base. I take this to be a good prediction. Consider a sentence like (i):
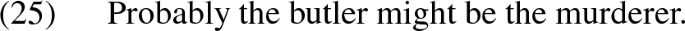
This is hard to interpret. The only reading of (i) seems to be one where the inner might is not an expression of compatibility on the part of the speaker, but a statement of fact that some body of information, not entirely available to the speaker, fails to rule out the butler.
Our view explains this observation: assuming a pragmatic ban against redundancy, the logical form \(\Delta \Diamond b\) is ruled out as deviant, since the operator \(\Delta \) in it is redundant. However, provided a salient epistemic modal base \(f_i\) is around, the LF \(\Delta @_i \Diamond b\) is available. This predicts that the only reading of (i) is one where might is not used expressively, but factually.
The editor points out the following discourse as an interesting puzzle:
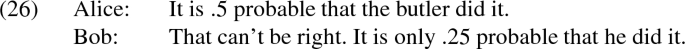
Say Alice’s claim is formalized as \(\Delta _{.5} b\). Bob says that this can’t be right. Given our account, his claim is equivalent to \(\lnot \Diamond \Delta _{.5} b\), which contains an iteration of expressive modals. If such iterations collapse, don’t we get a problem here?
I will sketch two possible responses, without choosing between them. The first: Bob’s response would indeed be deviant due to redundancy if it targeted an expressive modal claim. Therefore, by charity when we hear Bob respond in this way, we conclude that he intends his anaphora to pick out a factual claim—which is possible since the LF of Alice’s claim could be \(@_i \Delta _{.5} b\): what Bob is targeting is not an expression of middling credence, but a claim that the evidence justifies this degree of credence. And indeed, it seems that as we change Alice’s claim to make an expressive interpretation more prominent, Bob’s reply sounds more awkward.

Alternatively, one could concede that Bob’s response in (ii) targets the content expressed by \(\Delta _{.5} b\), and is indeed equivalent to \(\lnot \Diamond \Delta _{.5} b\). According to the semantics, this collapses to \(\lnot \Delta _{.5} b\), so the prediction is that Bob’s reply is equivalent to “it is not .5 probable that the butler did it” (for the treatment of negation, see Ciardelli, 2021). This does not seem unreasonable. But then, why isn’t Bob’s reply perceived as deviant due to redundancy? A natural explanation appeals to the fact that epistemic modals also function as evidential markers, signaling indirect evidence (von Fintel and Gillies, 2010). The reason Bob chooses to say that can’t be right and not that isn’t right could be to emphasize the evidential status of his rejection. If so, the modal can would be making a contribution after all, albeit in a semantic component that, admittedly, is not reflected in our simple account (see von Fintel and Gillies, 2010, for a proposal).
References
Adams, E. (1975). The logic of conditionals: An application of probability to deductive logic. Dordrecht: Springer.
Beddor, B., & Goldstein, S. (2018). Believing epistemic contradictions. The Review of Symbolic Logic, 11(1), 87–114.
Belnap, N., Perloff, M., & Xu, M. (2001). Facing the future: Agents and choices in our indeterminist world. Oxford: Oxford University Press.
Bennett, J. F. (2003). A philosophical guide to conditionals. Oxford: Oxford University Press.
Bledin, J. (2014). Logic informed. Mind, 123(490), 277–316.
Cariani, F., & Santorio, P. (2018). Will done better: Selection semantics, future credence, and indeterminacy. Mind, 127(505), 129–165.
Ciardelli, I. (2020). Indicative conditionals and graded information. Journal of Philosophical Logic, 49(3), 509–549.
Ciardelli, I. (2021). Restriction without quantification: Embedding and probability for indicative conditionals. To appear in Ergo: An Open Access Journal of Philosophy.
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2018). Inquisitive semantics. Oxford: Oxford University Press.
Dekker, P. (1993). Transsentential meditations. Ups and downs in Dynamic Semantics. Ph.D. thesis, ILLC, University of Amsterdam.
DeRose, K. (1994). Lewis on ‘might’ and ‘would’ counterfactual conditionals. Canadian Journal of Philosophy, 24(3), 413–418.
Edgington, D. (1986). Do conditionals have truth conditions? Crítica: Revista Hispanoamericana de Filosofía, 18(52), 3–39
Edgington, D. (1995). On conditionals. Mind, 104, 235–329.
Edgington, D. (2008). Counterfactuals. Proceedings of the Aristotelian Society, 108(1part1), 1–21. https://doi.org/10.1111/j.1467-9264.2008.00233.x.
Edgington, D. (2014). Indicative conditionals. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (Winter 2014 edition). https://plato.stanford.edu/archives/win2014/entries/conditionals/.
Egan, A., Hawthorne, J., & Weatherson, B. (2005). Epistemic modals in context. In G. Preyer & G. Peter (Eds). Contextualism in philosophy (pp. 131–170). Oxford: Oxford University Press.
Geurts, B. (2004). On an ambiguity in quantified conditionals. Manuscript, University of Nijmegen. Available at http://ncs.ruhosting.nl/bart/papers/conditionals.pdf.
Gillies, A. (2004). Epistemic conditionals and conditional epistemics. Noûs, 38(4), 585–616.
Gillies, A. (2009). On truth-conditions for if (but not quite only if). Philosophical Review, 118(3), 325–349.
Gillies, A. S. (2010). Iffiness. Semantics & Pragmatics, 4(1), 1–41.
Hawke, P., & Steinert-Threlkeld, S. (2020). Semantic expressivism for epistemic modals. Linguistics and Philosophy, 44, 475–511.
Hawthorne, J., Rothschild, D., & Spectre, L. (2016). Belief is weak. Philosophical Studies, 173(5), 1393–1404.
Katzir, R., & Singh, R. (2014). Hurford disjunctions: Embedded exhaustification and structural economy. Proceedings of Sinn und Bedeutung, 18, 201–216. https://ojs.ub.uni-konstanz.de/sub/index.php/sub/article/view/313.
Kaufmann, M. (2011). Interpreting imperatives. New York: Springer.
Khoo, J. (2018). Disjunctive antecedent conditionals. Synthese. https://doi.org/10.1007/s11229-018-1877-6.
Khoo, J. (Forthcoming). The meaning of if. Oxford: Oxford University Press.
Khoo, J. & Santorio, P. (2018). Probability of conditionals in modal semantics. Lecture Notes for a course at NASSLLI 2018, available at https://justindkhoo.files.wordpress.com/2020/06/ks-nasslli2018.pdf
Kratzer, A. (1981). The notional category of modality. In H. Eikmeyer & H. Rieser (Eds.), Words, worlds, and contexts: New approaches in word semantics (pp. 38–74). Berlin: Walter de Gruyter.
Kratzer, A. (1986). Conditionals. Chicago Linguistic Society, 22(2), 1–15.
Kratzer, A. (2012). Modals and conditionals: New and revised perspectives. Oxford: Oxford University Press.
Lewis, D. (1975). Adverbs of quantification. In E. Keenan (Ed.), Semantics of natural language (pp. 3–15). Cambridge: Cambridge University Press.
MacFarlane, J. (2011). Epistemic modals are assessment-sensitive. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 144–178). Oxford: Oxford University Press.
Mandelkern, M. (2018). Talking about worlds. Philosophical Perspectives, 32(1), 298–325.
Moss, S. (2013). Subjunctive credences and semantic humility. Philosophy and Phenomenological Research, 87(2), 251–278.
Moss, S. (2015). On the semantics and pragmatics of epistemic vocabulary. Semantics & Pragmatics, 8(5), 1–81.
Popper, K. (1959). The logic of scientific discovery. New York: Basic Books.
Ramsey, F. P. (1929). General propositions and causality. In H. Mellor (Ed.), F. P. Ramsey, Philosophical papers (pp. 145–163). Cambridge: Cambridge University Press, 1990.
Reich, I. (2009). What asymmetric coordination in German tells us about the syntax and semantics of conditionals. Natural Language Semantics, 17(3), 219–244.
Roberts, C. (1989). Modal subordination and pronominal anaphora in discourse. Linguistics and Philosophy, 12(6), 683–721.
Rothschild, D. (2012). Expressing credences. Proceedings of the Aristotelian Society, 112(1part1), 99–114. https://doi.org/10.1111/j.1467-9264.2012.00327.x.
Rothschild, D. (2021). A note on conditionals and restrictors. In J. Hawthorne & L. Walters (Eds.), Conditionals, probability, and paradox: Themes from the philosophy of Dorothy Edington. Oxford: Oxford University Press. https://doi.org/10.1093/oso/9780198712732.003.0003.
Schnieder, B. (2010). Expressivism concerning epistemic modals. The Philosophical Quarterly, 60(240), 601–615.
Schulz, K. (2010). Troubles at the semantics/syntax interface: Some thoughts about the modal approach to conditionals. Proceedings of Sinn und Bedeutung, 14, 388–404. https://ojs.ub.uni-konstanz.de/sub/index.php/sub/article/view/479.
Schulz, M. (2014). Counterfactuals and Arbitrariness. Mind, 123(492), 1021–1055.
Swanson, E. (2006). Something might might mean. Unpublished manuscript, University of Michigan.
Swanson, E. (2011). How not to theorize about the language of subjective uncertainty. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 249–269). Oxford: Oxford University Press.
Swanson, E. (2016). The application of constraint semantics to the language of subjective uncertainty. Journal of Philosophical Logic, 45(2), 121–146.
Veltman, F. (1996). Defaults in update semantics. Journal of Philosophical Logic, 25(3), 221–261.
von Fintel, K. (1994). Restrictions on quantifier domains. Ph.D. thesis, University of Massachusetts, Amherst.
von Fintel, K. (1998). The presupposition of subjunctive conditionals. The Interpretive Tract, 25, 29–44.
von Fintel, K. (2007). If: The biggest little word. Slides from a plenary address given at the Georgetown University Roundtable. Available at http://web.mit.edu/fintel/fintel-2007-if-gurt.pdf.
von Fintel, K. & Gillies, A. (2010). Must... stay... strong! Natural Language Semantics, 18(4), 351–383.
von Fintel, K. & Gillies, A. (2015). Hedging your ifs and vice versa. Manuscript, MIT, Rutgers University, available at http://web.mit.edu/fintel/fintel-gillies-2015-hedging.pdf.
Willer, M. (2013). Dynamics of epistemic modality. Philosophical Review, 122(1), 45–92.
Yalcin, S. (2007). Epistemic modals. Mind, 116(464), 983–1026.
Yalcin, S. (2011). Nonfactualism about epistemic modality. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 295–332). Oxford: Oxford University Press.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Thanks to two anonymous L&P reviewers for precious feedback, and to Lucas Champollion, Paul Egré, Matt Mandelkern, Adrian Ommundsen, Seth Yalcin, and Dietmar Zaefferer for discussions on topics related to this paper. Special thanks to Justin Khoo for detailed and insightful comments on a previous version of the paper, which led to substantial improvement.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ciardelli, I. The restrictor view, without covert modals. Linguist and Philos 45, 293–320 (2022). https://doi.org/10.1007/s10988-021-09332-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10988-021-09332-z