A graph model for probabilities of nested conditionals

Abstract

We define a model for computing probabilities of right-nested conditionals in terms of graphs representing Markov chains. This is an extension of the model for simple conditionals from Wójtowicz and Wójtowicz (Erkenntnis, 1–35. https://doi.org/10.1007/s10670-019-00144-z, 2019). The model makes it possible to give a formal yet simple description of different interpretations of right-nested conditionals and to compute their probabilities in a mathematically rigorous way. In this study we focus on the problem of the probabilities of conditionals; we do not discuss questions concerning logical and metalogical issues such as setting up an axiomatic framework, inference rules, defining semantics, proving completeness, soundness etc. Our theory is motivated by the possible-worlds approach (the direct formal inspiration is the Stalnaker Bernoulli models); however, our model is generally more flexible. In the paper we focus on right-nested conditionals, discussing them in detail. The graph model makes it possible to account in a unified way for both shallow and deep interpretations of right-nested conditionals (the former being typical of Stalnaker Bernoulli spaces, the latter of McGee’s and Kaufmann’s causal Stalnaker Bernoulli models). In particular, we discuss the status of the Import-Export Principle and PCCP. We briefly discuss some methodological constraints on admissible models and analyze our model with respect to them. The study also illustrates the general problem of finding formal explications of philosophically important notions and applying mathematical methods in analyzing philosophical issues.

1 Introduction

Conditional sentences are a hard nut to crack. Analysis fails in terms of propositional calculus with the conditional as the material implication. It is obvious that conditionals are not ordinary factual sentences—their truth value and truth conditions are a notorious problem. It is also not clear what the proper logic of conditionals should be: what are the appropriate axioms and what are the rules of inference?

Our approach in the paper is to focus on the probabilities of conditionals. We propose a kind of game (process) semantics, so conditions under which the respective game is won (lost) have to be specified. This means that we assume that it is reasonable to speak of circumstances in which the status of the conditional is settled, and in particular that the notion of truth conditions is essential in our account. The construction of the appropriate graphs (and the corresponding probability spaces) relies on this assumption.¹

Adams took the first steps towards analysis of the probability of conditionals and made an important pioneering contribution, defining the probability of a conditional A→B as P(B|A) (Adams 1965, 1970, 1975, 1998). This stipulation seems very natural for many examples. Indeed, consider the roll of a fair die and the conditional: If it is even, then it is a six. Intuitively, the probability of this conditional is 1/3, which is exactly the conditional probability P(It is a six| It is even).²

Adams’ thesis (also called ‘Stalnaker’s thesis’) that probabilities of simple conditionals can be defined as conditional probabilities is attractive as it resolves many problems and is coherent with intuitive judgement for many examples. However, the applicability of this approach is limited and the triviality results of Lewis (1976) (see Hajek 2011 for elegant generalizations) indicate that this is a fundamental problem.

Simple conditionals are only the first step in the enterprise: we want to deal with nested conditionals, conjoined conditionals, and perhaps also with other combinations. However, Adams declared that his approach does not extend to compound conditionals: “we should regard the inapplicability of probability to compounds of conditionals as a fundamental limitation of probability, on a par with the inapplicability of truth to simple conditionals” (Adams 1975, 35).³ Our approach is different: we think that it is possible to compute the probabilities of conditionals (simple and compound) by modeling them within appropriate probability spaces (the technical devices used are Markov graphs, which represent Markov chains). Therefore, our approach differs from Adams’ in two important respects: (i) we believe that it is possible to apply the notion of probability to compound conditionals; (ii) we believe that the notion of truth conditions is applicable to conditionals. They are usually much more complex than for conditional-free sentences, as we need game scenarios in our approach, which are formally sequences of possible worlds, not worlds simpliciter.⁴

The intuitive judgements of the probability of conditionals are unproblematic for a limited number of cases only, which shows that we have to be very cautious when speaking about probability. Matters become rather complicated when we take the context into account. Using the notion of probability in a purely intuitive sense might lead to misunderstandings and contradictions—contrary to Laplace’s claim, we are not good intuitive statisticians, as many empirical results show. So it is necessary to construct a formal model which will give a precise meaning to our understanding of the notion of the probability of conditionals. This will enable us to move from purely qualitative to quantitative analysis. This problem has already been discussed extensively and there are many results available—we present a short overview in Sect. 3.

The aim of this article is to present a formal model which allows the probabilities of conditionals to be computed; here we focus on right-nested (compound) conditionals, but the model can be applied to a wider class of examples. This model is an extension of the model for simple conditionals defined in Wójtowicz and Wójtowicz (2019). In a nutshell, the idea is to compute the probability of conditionals by means of Markov chains, which have a very simple, intuitive and natural illustration in the form of graphs. These graphs exhibit the “inner dynamics” of the conditional and allow to identify its (usually context-sensitive) interpretation. We associate a graph G_α (representing a Markov chain) with the conditional α in question, taking the respective interpretation into account when necessary. This graph is connected in a canonical way with a probability space S_α, in which the conditional α is represented as an event, therefore its probability can be computed in a formally sound way. In this way our intuitive assessments are given a precise formal underpinning, and our intuitions can be elucidated by formal means.

In our opinion, the graph model fulfills its role better (at least in some respects) than other models known from the literature because it is formally very simple, intuitive and more flexible.

The structure of the article is as follows:

In Sect. 2, Formal model for conditionals we give a short analysis of the requirements an adequate model has to meet—in particular, which problems we expect to be solved by the graph model.

In Sect. 3, Right-nested conditionals, we discuss the problem of the interpretation of nested conditionals and indicate that there are (at least) two context-dependent intuitive interpretations.

In Sect. 4, Some classic results, we recall some of the results, focusing on the results obtained with the use of Stalnaker Bernoulli space by van Fraassen and Kaufmann; some of McGee’s results are also presented.

In Sect. 5, The graph model for a simplified case, we present the idea of modeling conditionals in terms of graphs, taking a simple conditional A→B as an example. The section also contains a presentation of the needed notions of Markov graph (chains) theory, as this is the formalism we use in our model.

In Sect. 6, The graph model for right-nested conditionals, we present the graph-theoretic representation for both interpretations of right-nested conditionals (i.e. the shallow and the deep interpretation); we compute the corresponding probabilities and show that they agree with the results known from the various models of Kaufmann and McGee.

In Sect. 7, Multiple-(right)-nested conditionals, we show how to generalize our approach to the case of more complex nested conditionals of the form A₁→(A₂→…→(A_n→B)…). The graphs for both the shallow and the deep interpretations are obtained in a straightforward way and make the computations very easy. We also discuss the problem of a longer conditional where the conditional operator is interpreted in a non-uniform, “mixed” way, i.e. as shallow for some occurrences and as deep for others. We discuss the problem in more detail for conditionals of length four, i.e. of the form A₁→(A₂→(A₃→B)) as they are still natural, but complex enough for interesting phenomena to occur.

In Sect. 8, Formal models for conditionals revisited we show that our model solves some of the specific issues (the status of IE and PCCP), that it fulfills the methodological criteria formulated in Sect. 1 and that according to these criteria it fares better than other available models. A direct comparison with the Stalnaker Bernoulli model is also made (7.3).

Section 9 is a short Summary.

2 Formal models for conditionals

Formal models of conditionals which allow the use of the concept of probability in a mathematically correct way and without the risk of falling into paradoxes are built to clarify and sharpen the intuitions of ordinary language users. There are numerous “test sentences” for which the probability judgements are intuitively obvious (as in the If it is even, it is a six example), and the model should respect them. After all, we are talking about conditionals and not about some exotic operator which we are trying to introduce into the language. Generally speaking, we want to “translate” the results of qualitative analysis into quantitative language, hoping that the formal models will allow vague notions to be explicated, shed light on the state of the art, and inspire discussion by presenting formal results (which might happen to be technical counterparts of intuitive claims).⁵ In particular we expect them to provide a better understanding of (at least some of) the debated issues. We also think, that it is useful to keep in mind possible methodological virtues of the model and we consider generalizability and simplicity to be important in this context (2.2.1 and 2.2.2). A resume and discussion of these issues is to be found in Sect. 7. In the paper, letters A, B, C… symbolize non-conditional propositions. We will usually use italics for propositions, and letters without italics for the corresponding events.

2.1 Two important principles

Two important principles discussed in the literature devoted to probability of conditionals are: (i) the Import-Export Principle; (ii) PCCP. We remind them briefly (2.1.1 and 2.1.2), we hope this will be useful for the readers, as these principles are discussed in the technical fragments of the text.

2.1.1 The Import-Export Principle

An important problem (indirectly related to the issue of generalization) is the status of the Import-Export (IE) Principle. This is very attractive as it simplifies matters enormously: right-nested conditionals A→(B→C) are reduced to simple conditionals (A${\wedge}$B)→C. Its consequence is accepting that P(A→(B→C)) = P((A${\wedge}$B)→C).⁶

On one hand, such a rule is extremely convenient because computing the probabilities is simpler, and generalization to a wide class of conditionals like A →(B →(C→D)) is straightforward. On the other hand, there are natural examples where P(A→(B→C)) ≠ P(B→(A→C)), but this means that the Import-Export Principle is violated. A good model should identify these cases and explain under which presuppositions it is justified to accept the IE Principle. In particular it is important to discuss it in the context of the possible interpretations (deep versus shallow) of right-nested conditionals. We show that in our model IE can be proved for the deep interpretation (also for the multiple-right-nested conditionals), and that it is generally not true under the shallow interpretation.

2.1.2 PCCP

Is P(A→B) = P(B|A)? Namely, is the probability of the conditional equal to the conditional probability? (We will use the familiar acronym PCCP henceforth.) It would be nice to have PCCP as it gives a very simple way of computing probabilities. Also, we have strong intuitions linking the probability of conditionals with the conditional probability, as the classic quotation from Ramsey states.⁷ But on the other hand, we have Lewis’ and Hajek’s triviality results (Lewis 1976; Hajek 2011, 2012).⁸ So, the formal model for conditionals must identify the relationships between the probability of the conditional and the respective conditional probability in order to shed light on the status of (the appropriate version of) PCCP.⁹ We prove P(A→B) = P(B|A) for the simple conditional A→B, and identify and prove the generalizations of PCCP for the deep and the shallow interpretations of the right-nested conditional A→(B→C).

2.2 Methodological aspects

We consider generalizability and simplicity to be important features of formal models for conditionals. Generalizability (and flexibility) might be viewed to be good indicators that the model will also be applicable in cases which were not a direct motivation for its creation. The simplicity of the model makes it applicable.

2.2.1 Generalizability and flexibility

Regardless of whether we analyze simple conditionals A→B, nested conditionals A→(B→C) and (A→B)→C, conjoined conditionals (A→B)${\wedge}$(C→D), or conditional conditionals (A→B)→(C→D), the conditional operator → which occurs in them is, in principle, similar. So, if we have a definite method of building a model for probabilities of simple conditionals A→B, a natural hypothesis is that this method will also be applicable in cases in which complex formulas will stand for A and B. If there are any contexts in which the operator → is given different interpretations, our model should be able to represent this fact.

2.2.2 Formal simplicity

An attractive model needs to be “user friendly” as modeling conditionals should be as simple as possible. If we think of the problem also in practical terms—for instance, if we are interested in analyzing decision-making processes (based on evaluating the probabilities of conditionals)—it is important to have a method which is of practical as well as purely theoretical interest. In short, formal treatment of more complex cases must be feasible.

3 Right-nested conditionals

In ordinary life we often utter sentences which have the structure of a nested conditional A→(B→C). Examples are abundant:

• a. If the match is wet, then it will light if you strike it.

• b. If John had broken his leg while skiing in Davos in 2017, it would hurt if he went skiing.

• c. If John takes medication A, then if he takes medication B, he will have an allergic reaction.¹⁰

The first example is known from the literature. The last two sentences are our toy examples in this section. All these conditionals are right-nested, i.e. they have the same form A→(B→C), but the evaluation of their probabilities might depend on the interpretation.

In (a) we quite obviously mean the same match, which is wet, which is struck, and which lights or not: a unity of action, place and time (like in an ancient tragedy). Borrowing terminology from Kaufmann (2015), we call this interpretation deep. However, in (b) we obviously do not mean the claim that the leg would have hurt if John had continued skiing with his leg broken in Davos in 2017. The sentence does not apply to this particular unfortunate skiing holiday. This is obvious in light of the common knowledge concerning broken legs and there is no need even to mention it. What we mean is rather that this accident would have some consequences for John’s later life: speaking informally, John’s life would be “redirected” to a route where the probability of pain while skiing is greater. We mean subsequent skiing holidays, not 2017 in Davos. So, the context imposes a different interpretation of this sentence in a natural way: following Kaufmann (2015) we call it shallow.

For the last sentence (c), the interpretation is not so obvious. (We will use the natural abbreviation MED for (c).) To fix attention, we think in terms of days, i.e. we perform the appropriate observations (Which medications are taken? What is the reaction?) within the span of a single day. When interpreting MED, we analyze either whether

• i. taking B at the same moment (i.e. the same day) as taking A will cause the allergic reaction, or whether

• ii. taking B any time after taking A will cause the allergic reaction.

These different interpretations should have their counterparts in two different sets of truth conditions. Imagine two agents, Alice and Bob, who observe consecutive days in John’s life (i.e. whether he took A, whether he took B, and whether an allergic reaction occurs). Alice thinks that MED will turn out to be true, but Bob claims the opposite, so they make a bet. We can say that they are going to play the MED game.

Assume that they have been watching John since Monday.

Monday: John does not take A but takes B and has an allergic reaction. Alice and Bob agree that the bet has not been decided as the antecedent A has not occurred. Indeed, John’s allergic reaction is irrelevant with respect to the relationship expressed in MED. The game continues.

Tuesday: John takes A but does not take B. Alice and Bob agree that the bet has not been decided: the internal antecedent has not occurred (and it does not matter whether he has had an allergic reaction). So, the game continues.

Wednesday: John does not take A but takes B and has an allergic reaction. This is exactly the situation in which Alice’s and Bob’s opinions differ:

Bob: Unfortunately, you win! Indeed, John took A (remember that was yesterday), and here is the winning combination, i.e. “medication B + an allergic reaction”!

Alice counters: I’m afraid not! The bet was about John having an allergic reaction provided he took both the medications A and B on the same day—not just some allergic reaction of an unknown etiology that incidentally occurred after John took only medication B on that day. This is obvious from the context and means that the bet is undecided: we have to wait until John takes A and B on the same day, and we will see what happens then.

Who is right? This is a matter of interpretation based on some (tacit) presuppositions.¹¹ Alice accepts the deep interpretation (i), whereas Bob accepts the shallow interpretation (ii). We think that—at least in the case of some medications—both the interpretations might be legitimate depending on the context, in particular on the medical (biochemical) findings and also on the features of the individual (John).

Anyway, if we are going to make a bet on MED, we must first define the terms (in particular, when the game is won and lost), i.e. we have to agree on an interpretation of the conditional. The crucial difference is what happens after John has taken medication A but not medication B, therefore the bet has not yet been settled. Alice and Bob give different answers:

Alice (deep interpretation): the game is restarted. We have to observe John’s behavior anew, and wait until a day when John takes both medications A and B (and the history of his taking A on previous days has no influence on the probabilities of taking the medications and the reaction). If the allergic reaction occurs, I win; if it does not, I lose.

Bob (shallow interpretation): the game proceeds on different terms as we now treat the condition of taking medication A as fulfilled “forever”. If John’s taking B is followed by an allergic reaction, you will win (regardless of whether John has taken A that day). If it is not, you will lose.¹²

We will turn to the problem of computing the probabilities of MED later, when the necessary technical tools have been introduced. However, it is intuitively clear that depending on the interpretation, the probabilities might differ vastly.¹³ It might well be that two rational agents assign different probabilities to the same conditional, even if they agree on the probabilities of the factual (“atomic”) sentences. This can be a result of interpreting them in a different way (e.g. deep versus shallow) or relying on some assumptions concerning the context. We claim that the presented model explains this phenomenon by (formally) identifying these interpretations.¹⁴

4 Some classic results

Adams defines the probability of a conditional A→B by setting P(A→B) := P(B|A). This simplifies matters, but this stipulation rests on quite controversial assumptions. For instance it is (by definition) necessary to accept PCCP as a general principle (but this thesis is disputed, and arguments against it cannot be neglected). This approach cannot be easily extended to compound conditionals. But this means, that P might behave not like a genuine probability function, as it might happen, that P(α) and P(β) are defined, but P(α→β) is not.¹⁵

The possible worlds semantics has become standard in treating modalities, so it is not surprising that there have been attempts to account for the problem of conditionals (both their truth conditions and probabilities) in these terms (the classic papers are, for instance, Stalnaker 1968, 1970; Stalnaker and Thomason 1970). The general idea is familiar: if [α] is the set of worlds corresponding to the proposition α (i.e. in which α is true), then the probability of the proposition α is given by P([α]) (where P is the probability distribution defined on the set of possible worlds). This is natural for propositions not containing conditionals, but it is far from obvious how to apply it to conditionals. In general, it is not clear which set of possible worlds should be assigned to A→B (i.e.—what is [A→B]). There have been numerous attempts to overcome this problem. One proposal is to interpret conditionals as random variables which are given appropriate values at different possible worlds, and the probability of the conditional A→B (or generally, its semantic value) is defined as the conditional expected value (Jeffrey 1991; Stalnaker and Jeffrey 1994). McGee (1989) provides an axiomatic framework for compound conditionals: the rules (C1)–(C8) (McGee 1989, 504) are axioms for a probability calculus for conditionals. The corresponding semantics is based on the idea of the selection function on possible worlds given in Stalnaker (1968): for every world w and proposition A, f(w, A) is the w-nearest world in which A is true. The probability of A→B is then computed by using the probability distribution of such selection functions f (and of course, we have to check what happens to proposition B in these w-nearest A-worlds).¹⁶ This leads to an interesting construction of the probability space, with important consequences (however, it is formally quite intricate). For instance, it is possible to prove that every probability distribution defined on atomic propositions extends in a unique way to right-nested conditionals of arbitrary length (Theorem 4, McGee 1989, 507).¹⁷ One of the features of McGee’s account is that the Import-Export Principle is satisfied—indeed, it is one of the postulates.¹⁸ So, MeGee’s account (implicitly) presumes the deep interpretation of the conditional (see Sect. 2 for the preliminary discussion on deep and shallow interpretation, and Sect. 5 for the formal models), as the Import-Export Principle is a typical feature of it.

An interesting proposal was made by van Fraassen (1976) and developed in a series of papers by Kaufmann (2004, 2005, 2009, 2015). It is based on the idea of a Stalnaker Bernoulli probability space which consists of infinite sequences of possible worlds (not worlds simpliciter).¹⁹

This model has the advantage of being general; in particular it also makes it possible to compute not only the probabilities of right-nested conditionals A→(B→C), but also of left-nested conditionals (A→B)→C, conjoined conditionals (A→B)${\wedge}$(C→D), and conditional conditionals (A→B)→(C→D).²⁰ However, there is also a price to pay: the Stalnaker Bernoulli space consists of all infinite sequences, which makes the computations tedious, and imposes certain limitations, especially for modeling more complex situations and contexts.²¹ But even more importantly, the way the probability space is defined imposes the shallow interpretation of right-nested conditionals, which leads to unintuitive consequences in many cases. This approach is not compatible with McGee’s approach, as the Import-Export Principle generally fails.²²

Kaufmann’s formula for the probability of the right-nested conditional computed within the Stalnaker Bernoulli space is:

${\rm{P}}_{{\rm{BS}}}^{*}$(A→(B→C)) = P(BC | A) + P(B^c | A)P(C | B), where B^c is the complement of B (i.e. it corresponds to $\neg$B) and BC is the intersection of B and C.

P is the function in the initial probability space, where the sentences A, B, C are represented (as events A, B, C) but no events correspond to the conditionals in this initial space. ${\text{P}}{^{*}_{\text{BS}}}$ is the probability distribution within the Stalnaker Bernoulli space, where conditionals are interpreted as events (and have a formally defined probability).

The advantage of this approach is that it provides an explicit formula for computing the probabilities, but its scope of applicability is limited. Consider the wet match example: If the match is wet, then it will light if you strike it, which has the form W→(S→L). Assume that the probabilities are as follows (Kaufmann 2005, 206): (a) of the match getting wet = 0.1; (b) that you strike it = 0.5; (c) that it lights given that you strike it and it is dry = 0.9; (d) that it lights given that you strike it and it is wet = 0.1. Moreover, striking the match is independent of its wetness. Kaufmann’s formula gives the result ${\rm{P}}_{{\rm{BS}}}^{*}$(W→(S→L)) = 0.46, which is counterintuitive as we would expect the probability to be 0.1. Kaufmann proposes a modification of the Stalnaker Bernoulli model which incorporates causal dependencies (Kaufmann 2005, 2009). It is based on the idea of using random variables (following Stalnaker and Jeffrey 1994) and it gives the proper result, i.e. 0.1 for the wet match example. The formula for the probability of the conditional in this model is very simple:

$$ {\text{P}}^{*}(A{{{\to}}}(B{{{\to}}}C)) = {\text{ P}}({\text{C}}\,|\,{\text{AB}}) $$

(i.e. it obeys the Import-Export Principle). So, both the interpretations (deep and shallow) can be accounted for by the known models, but for each of the interpretations a different model is needed. There is no way to account for both within one model just by “adjusting its parameters”.

5 The graph model for a simplified case

5.1 The general idea

Our model for nested conditionals will be given in terms of Markov graphs and in this section we present all needed formal tools. To introduce the idea, we first present the model for a simple conditional of the form A→B.²³ Imagine John who buys coffee every day on his way to work. He always buys Latte, Espresso or Cappuccino (denoted by L, E, C respectively). John is choosing coffee at random (but with fixed probabilities). The conditional in question is $\neg$L→E:

If John does not order a Latte, he will order an Espresso.

How are we going to compute its probability? First, we need a formal representation of John’s habits, which is given by a probability space S = (Ω, Σ, P), with Ω = {L,E,C}; P(E) = p; P(C) = q; P(L) = r. The σ-field Σ is the power set 2^Ω (it consists of 8 events). But obviously—as both common sense and the triviality results show—there is no event in the space S = (Ω, Σ, P) corresponding to the conditional $\neg$L→E.²⁴ This means that we have to define another probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ where the conditional $\neg$L→E will be given an interpretation as an event (i.e. as a measurable subset of ${\Upomega^{*}}$). To avoid misunderstanding, we will use the symbol [α] to denote the event in the constructed probability space corresponding to the proposition α. For instance, [$\neg$L→E]$^{*}$ will be the event in the space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ corresponding to the proposition If John does not order Latte, he will order an Espresso. Informally speaking, this new space ${{{{\text{S}}}}^{*}}$ will consist of sequences of events (scenarios) which decide the conditional, and the probabilities of such sequences will be defined in a straightforward manner using probabilities from the sample space S. Here we present the general idea and motivations, and a formal definition of ${{{{\text{S}}}}^{*}}$ for the general case is given in Sect. 5.4.

Of course, we have to assume that it is reasonable to speak of circumstances in which the status of the conditional is settled. The notion of truth conditions is essential in our account, in particular they will play a role in the construction of the probability space ${{{{\text{S}}}}^{*}}$. Indeed, we ascribe the probabilities to sentences in terms of fair bets: how much are we going to bet on the conditional α i.e. on winning the “α -Conditional Game”?²⁵ In order to give a formal model, we need to know exactly how the conditional α is interpreted, i.e. what the rules of the game are. In particular, we need to know when the bet is won, when it is lost, and how we should proceed if it is still undecided.

So, we can think of our toy example in terms of a “Non-Latte-Espresso Game”: every day John orders a coffee and evaluating the probability of $\neg$L→E depends on the possible scenarios. If it is an Espresso or Cappuccino, the game finishes and the bet is decided (Espresso—we win; Cappuccino—we lose). But it is of critical importance for the model to decide what to do when John orders Latte (i.e. when the antecedent is not fulfilled). A priori there are four possibilities:

• 1. We win the game.

• 2. We lose the game.

• 3. The game is cancelled (and nothing else happens).

• 4. The game is continued until we are able to settle the bet.

The first option reduces the conditional $\neg$L→E to a material implication, but this is not the right solution. The second choice is even less natural as it means we really played the “Neither-Latte-nor-Cappuccino Game”, without any conditional involved. The third choice is pessimistic: it means that we cannot model the probability of the conditional in cases when the antecedent is not fulfilled (so, in fact we abandon the construction of the model).²⁶ So, we choose the last solution which means that the bets are not settled and the game continues.²⁷ We assume that it is reasonable to think of performing a series of trials with unchanging conditions (“travelling across possible worlds”).²⁸ This idea is expressed by, for example, van Fraassen: “Imagine the possible worlds are balls in an urn, and someone selects a ball, replaces it, selects again and so forth. We say he is carrying out a series of Bernoulli trials” (van Fraassen 1976, 279). So, the truth conditions (which enable the probability of the conditional to be evaluated) are formulated in terms of sequences of possible worlds.

Of course, if we speak of restarting the game this means that the probabilities of the atomic events have not changed. These are some possible scenarios of the game:

• E (Espresso)—we WIN.

• LE (Latte, Espresso)—we WIN.

• LL….LE(Latte, Latte, …, Latte, Espresso)—we WIN.

• C (Cappuccino)—we LOSE.

• LC (Latte, Cappuccino)—we LOSE.

• LL…LC (Latte, Latte, …, Latte, Cappuccino)—we LOSE.

It is clear that scenarios of this form exhaust the class of scenarios that settle the bet. They cannot be represented in the simple probability space Ω = {L, E, C} which models John’s single choices, therefore we need a different space in which the scenarios (i.e. possible courses of the game) can be imbedded and their probabilities evaluated. The to-be-constructed probability space ${{{{\text{S}}}}^*} = \left( {{\Upomega^*\!,} \, {\Upsigma ^*\!,} \, {{{{\text{P}}}}^{*}}} \right)$ will consist of scenarios which settle the game (the bet)—i.e. of the form L…LE or L…LC (these sequences will be elementary events i.e. elements of the ${\Upomega^{*}}$). We have to ascribe appropriate probabilities to such sequences, and we make use of the fact, that in the space S = (Ω, Σ, P) probabilities of choosing Espresso, Cappuccino or Latte are given (p, q, r respectively). It is clear that the probability of ordering three Lattes in a row and a “follow-up Espresso” (i.e. LLLE) is rrrp (so we set ${\text{P}}^{*}$(LLLE) = r³p). Formal details are elaborated in Sect. 5.4.

We will use the formalism of Markov chains, which are an important tool in stochastic modeling in physics, biology, chemistry, finance analysis, social sciences etc.²⁹ However, they are not so widely used for modeling linguistic phenomena (however, see Bod et al. 2003), thus for the convenience of the reader we present the relevant notions here. Regardless of the technical details, the intuitive idea is fairly simple: we think about a system evolving in time (time being discrete) which is always in one of a range of possible internal states.³⁰ It is helpful to view the evolution of the system as a result of a series of actions occurring with fixed probabilities (like tossing a coin, choosing a coffee, drawing a ball from an urn etc.).

First, we give an illustration using a classic example of a Markov chain; the general definitions are given later.

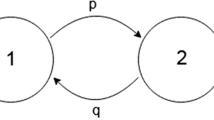
5.2 Gambler’s Ruin

Consider a coin flipping game, one of the player is the Gambler. At the beginning of the game, the Gambler has one penny, the opponent has two pennies.³¹ After each flip of the coin, the loser transfers one penny to the winner and the game restarts on the same terms. Assume that the Gambler bets on Heads; fix the probability of tossing Heads to be p, and of tossing Tails to be q (p + q = 1). Formally this means that we have defined a simple probability space S = (Ω, Σ, P) describing a single coin toss with: Ω = {H,T}; Σ = 2^Ω; P(H) = p, P(T) = q. Obviously, the coin does not remember the history of the game so the probabilities (of tossing Heads/Tails) do not change throughout the whole game. This simple feature of Markov chains (i.e. memorylessness) is crucial for our purposes.

We can represent the current state of the game as the number of the Gambler’s pennies, which means that the possible states of the system are 0, 1, 2, 3. The game starts in state 1 (one penny) and the transitions between states occur as a consequence of one of two actions: the coin coming up Heads or Tails (H,T). The game stops when it enters either state 0 (Gambler’s Ruin) or state 3 (Gambler’s victory). They are called absorbing states.

The game allows for a very natural graphical representation, with the arrows indicating the transitions between the states (p, q being the respective probabilities). For instance, the probability of getting from 1 to 2 is p; the probability of getting from 1 to 0 is q. Both states 0 and 3 are absorbing—so with probability 1 the process terminates (formally: remains) in these states.

The graphical representation of the dynamics of the game is given in Fig. 1.

Fig. 1

Gambler’s ruin

It is convenient to think of the process (for instance of the scenario of a game) in terms of travelling within the graph, from one vertex to another, until the process stops. The vertices represent the states of the system, the edges represent transitions and we can think of them as representing actions. Tossing H (Heads) means, that the Gambler wins one penny, so the state changes from n to n + 1 (1$\mapsto$2 or 2$\mapsto$3). Tossing T (Tails) means, that the Gambler has to transfer one penny to his opponent, so the state changes from n to n−1 (2$\mapsto$1 or 1$\mapsto$0). So we can naturally track the possible scenarios of the game (i.e. ending either with victory or with loss) as possible paths in the graph.

Here are some examples of winning paths: HH (tossing Heads twice) generates the path 1$\mapsto$2$\mapsto$3; HTHH generates 1$\mapsto$2$\mapsto$1$\mapsto$2 $\mapsto$3; HT…HTHH generates 1$\mapsto$2$\mapsto$…1$\mapsto$2$\mapsto$1$\mapsto$2$\mapsto$3.

Scenarios (paths) for losing the game are: T(1$\mapsto$0); HTT (1$\mapsto$2$\mapsto$1$\mapsto$0); HT…HTT (1$\mapsto$2$\mapsto$1$\mapsto$…$\mapsto$2$\mapsto$1$\mapsto$0).

It is clear what the probabilities of these scenarios are: for instance the probability of HTHH is pqpp (the tosses of the coins are independent, so we simply multiply the probabilities).

Of course these sequences do not appear in the initial probability space S = (Ω, Σ, P). This means that we start with a simple probability space S = (Ω, Σ, P) and we have to construct an appropriate “derived” probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ (depending on the rules of the game). It is helpful to view the new space as “generated” by the graph as possible travel scenarios.

We denote this probability space by ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$, the star * indicates that it is different from the simple initial probability space S. The ${\Upomega^{*}}$ consists of all sequences settling the Gambler’s Ruin game, i.e.:

$$ \Upomega^{*} \, = \, \{ \left( {{\text{HT}}} \right)^{{\text{n}}} {\text{HH}}, \, \left( {{\text{HT}}} \right)^{{\text{n}}} {\text{T}}:{\text{ n}} \ge 0\} , $$

(here (HT)ⁿ means the sequence HT repeated n times, i.e. (HT)ⁿ = HT….HT).

The probabilities of the elementary events are set according to the following rules:

$$ \begin{aligned} & {\text{P}}^{*}({{\text{HH}}}) \, = pp = p^{2} \\ & {\text{P}}^{*}({{\text{HTHH}}}) \, = pqpp = p^{3} q \\ & \ldots \\ & {\text{P}}^{*}\left({({{\text{HT}}})^{{{\rm n}}} {\text{HH}}} \right) \, = \, ({pq})^{{{\rm n}}} pp = p^{n + 2} q^{{{\rm n}}} \\ \end{aligned} $$

$$ \begin{aligned} & {\text{Similarly:}} \\ & {\text{P}}^{*}({\text{T}}) \, = q \\ & {\text{P}}^{*}({{\text{HTT}}}) = ({pq})q = pq^{2} \\ & \ldots \\ & {\text{P}}^{*}\left({({{\text{HT}}})^{{{\rm n}}} \text{T}} \right) = ( {{pq}} )^{{{\rm n}}} q = p^{n} q^{{{{\rm n}} + 1}} \\ \end{aligned} $$

Computing the probability of the Gambler’s victory within ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ amounts to computing the probability of the event in ${{{{\text{S}}}}^{*}}$ which is the counterpart (interpretation) of the sentence The Gambler wins the game. This event consists of all winning scenarios. In the paper we use [α] to denote the event corresponding to the sentence α in the appropriate probability space, so we can write:

$$ \left[ {The\;Gambler\;wins\;the\;game} \right] = \{ \left( {{\text{HT}}} \right)^{{\text{n}}} {\text{HH:}}{\text{n}} \ge 0\} $$

Therefore:

$$ P^{*}\left( {\left[ {The\; \, Gambler\; \, wins\; \, the\; \, game} \right]} \right) = {\text{P}}^{*}(\{ \left( {{\text{HT}}} \right)^{{\text{n}}} {\text{HH:}}{\text{n}} \ge 0\} ) \, = \mathop \sum \limits_{n = 0}^{\infty } \left( {pq} \right)^{n} p^{2} = \frac{{p^{2} }}{1 - pq} $$

The probability of the Gambler’s Ruin is $\frac{1 - p}{{1 - pq}}$. For p = 1/2 (a fair coin) the probability of the Gambler’s Ruin is 2/3; the probability of winning is 1/3.

The power of the Markov graph theory is revealed by the fact, that the corresponding probabilities can be computed in a direct way by examining the graph and solving a simple system of linear equations. Indeed, let P(n) denote the probability of winning the Gambler’s Ruin game, which starts in state n, for n = 1, 2. Obviously:

P(0) = 0, as The Gambler has already lost;

P(3) = 1, as The Gambler has already won.

To compute the probabilities P(1), P(2) we reason in an intuitive way. Being in the state n, we can either:

• toss Heads with probability p—then we are transferred to the state n + 1, and our chance of winning becomes P(n + 1);

• toss Tails with probability q—then we are transferred to the state n − 1, and our chance of winning becomes P(n − 1).

So, P(1) = pP(2) + qP(0) and P(2) = pP(3) + qP(1). Our system of equations is therefore:

$$ \begin{aligned} & {\text{P}}(0) = \, 0 \\ & {\text{P}} (1) = p{\text{P}}(2) \, +\, q{\text{P}}(0) \\ & {\text{P}} (2) \, = p{\text{P}}(3) \, +\, q{\text{P}}(1) \\ & P(3) \, = \, 1 \\ \end{aligned} $$

The solution (i.e. the probability of the Gambler’s victory) is (as before) $P(1) = \frac{{p^{2} }}{1 - pq}$.

An important feature of the gambling process is that the probabilities of atomic actions H and T remain fixed throughout the whole process (homogeneity), and the history of the game does not influence the effects (memorylessness). This means that the next step depends only on the present state of the process, not on the whole past. (This applies to our Non-Latte-Espresso example: we assume that the probabilities of choosing Latte, Espresso or Cappuccino are fixed—they do not depend on the type of coffee John ordered the previous time.)

In the Gambler’s ruin game, we distinguish in a natural way three states: START (i.e. 1), WIN (i.e. 3) and LOSS (i.e. 0). This will be the standard situation when constructing graphs representing conditionals because (i) our Conditional Games always have to start and (ii) we need to be able to decide whether the game was won or lost.

For completeness we now present some formal definitions concerning Markov chains.

5.3 The general definition of a Markov chain

Markov chains are random processes with discrete time (formally: sequences of random variables, indexed by natural numbers),³² which satisfy the property of memorylessness, i.e. the Markov property. A Markov chain is specified by identifying:

• 1. A set of states S = {s₁,…,s_N};

• 2. A set of transition probabilities p_ij ≥ 0, for i,j = 1,…,N—i.e. the probabilities of changing from state s_i to state s_j. The probabilities obey the equations: $\mathop \sum \nolimits_{k = 1}^{N} p_{ik}$ = 1, for i = 1,..,N (which means, that the probabilities of going from state s_i to any of the possible states sum up to one). These probabilities are fixed throughout the whole process.

Any Markov chain can be described by a N-by-N matrix, with the probabilities p_ij being the respective entries.³³ States with p_ii = 1 (which means, that the system will never get out of the state s_i) are called absorbing. In general there need not be any absorbing states (we might want to simulate a never-ending or a very long-term process), or there might be many of them. But in the article we restrict ourselves to the case where there are two absorbing states: WIN and LOSS; we also specify a state START (as in The Gambler’s Ruin game). We also assume that there is a path leading from any state to one of the absorbing states.

5.4 The probability space ${{{{\text{S}}}}^{*}} = \left( {{{\varvec\Upomega}^{*}}, {{\varvec\Upsigma} ^{*}},{{{{\text{P}}}}^{*}}} \right)$ associated with the Markov graph

We want to use Markov graphs to model processes in which the system in question might change its state after some action/event have taken place. The structure of the Markov graph in question depends on the situation we want to model, for instance on the rules of the game, the causal nexus etc. The graph exhibits the dynamics of the system, allows to track its evolution and represents the probabilities of the system to pass from one state to another.

The evolution of the system depends on the actions, which affect the state of the system. An action is represented within the graph as a transition from one state to another, i.e. as an arrow in the graph. Of course, which of the actions are ascribed to the arrows in the graph depends on the situation we want to model. A clear example is provided by the Gambler’s Ruin game.³⁴

Take S = (Ω, Σ, P) to be the initial probability space, in which the actions (tossing a coin, drawing a ball from an urn, buying coffee etc.) are represented. These actions can change the state of the system. The dynamics of the process is represented by the Markov graph G, and our aim is to construct the corresponding probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$, which represents the possible scenarios of the process (game). We are interested in modeling conditionals, so we restrict our attention to graphs which have an initial state START and two absorbing states WIN and LOSE: when the system reaches one of the absorbing states, it comes to a stop. The general idea is very intuitive:

• (i) The set of elementary events $\Upomega^{*}$ onsists of sequences of actions (scenarios) which lead the system from the initial state START to an absorbing state (i.e. WIN or LOSS).

• (ii) The probability ${\text{P}}^{*}$ of such a sequence is defined by multiplying the probabilities of the actions (which are defined in the initial space S).

Formally: let G be the Markov graph corresponding to the conditional in question, S = (Ω, Σ, P) be the sample probability space. The set of elementary events is Ω = {${\text{A}}_{1}$,…,${\text{ A}}_{{\text{m}}}$}, and the probabilities of elementary events in S are P(${\text{A}}_{{\text{i}}}$) = p_i.³⁵ The $\Upomega^{*}$ consists of finite sequences of events from Ω according to the following rule: the sequence ${\text{A}}_{{{\text{i}}_{1} }}$…${\text{A}}_{{{\text{i}}_{{\text{n}}} }}$ is an elementary event in $\Upomega^{*}$ if there is a sequence of states $s_{{i_{1} }}$…$s_{{i_{n + 1} }}$ of the Markov graph G, such that:

• (i) $s_{{i_{1} }}$ = START;

• (ii) $s_{{i_{n + 1} }}$ is an absorbing state (i.e. WIN or LOSS) (and no of the states $s_{{i_{1} }}$…$s_{{i_{n} }}$ is an absorbing state);

• (iii) For any k = 1,…, n, ${\text{A}}_{{{\text{i}}_{{\text{k}}} }}$ leads from the state $s_{{i_{k} }}$ to $s_{{i_{k + 1} }}$.

The probability ${\text{P}}^{*}$ of the elementary event (i.e. sequence) ${\text{A}}_{{{\text{i}}_{1} }}$…${\text{A}}_{{{\text{i}}_{{\text{n}}} }}$ is defined as $p_{{i_{1} }}$…$p_{{i_{n} }}$ (where $p_{{i_{k} }}$ = P(${\text{A}}_{{{\text{i}}_{{\text{k}}} }} )$).³⁶ By definition, we consider finite paths only (the process has to terminate). $\Upomega^{*}$ is therefore at most countable.

The respective σ-field $\Upsigma^{*}$ is the power set of $\Upomega^{*}$, i.e. $\Upsigma^{*}$ = 2$^{\Upomega^{*}}$.

${\text{P}}^{*}$ has been defined for elementary events and it extends in a unique way to all sets X⊆$\Upomega^{*}$ by the standard formula $\mathop {{\text{P}}^{*}\left( {\text{X}} \right) \, = \sum }\nolimits_{{\omega \in {\text{X}}}} {\text{P}}^{*} \left( \omega \right)$.

${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ is the probability space corresponding to the graph. It should be stressed, that we cannot construct the graph knowing S only—we also have to know, how the events from S affect the game.³⁷ Therefore, the “ingredients” needed to define ${{{{\text{S}}}}^{*}}$ are: (i) the initial probability space S = (Ω, Σ, P) and (ii) the Markov graph G which models the game. If we model a conditional α then the corresponding graph G_α has to represent its interpretation and the probability space ${{{{\text{S}}}}^{*}}$_α is based on G_α (and obviously the sample space S). This is clearly shown in the case of deep and shallow interpretations of the right-nested conditional (Sects. 5.1 and 5.2).

5.5 Absorption probabilities of the Markov chain

We are interested in the probability of winning (losing) the game, i.e. in the absorption probabilities of the Markov chain. The idea has been given for the Gambler’s ruin example. Now consider the general case of a Markov chain with N states s₁,…, s_N. To make the presentation consistent with the general approach in this text we assume that there are two absorbing states, say s₁ (LOSS) and s_N (WIN).

The process is described by the transition probabilities p_ij, for i,j = 1,2,…,N. As s₁ and s_N are absorbing states, it means that:

$$ \begin{array}{lll} {p_{11}} = {\rm{1}};& p{_{1i}} = 0&\quad {\rm{for}}\;{\rm{i}} \ne {\rm{1}}.\\ {p_{NN}} = {\rm{1}}; & p{_{Ni}} = 0 &\quad {\rm{for}}\;{\rm{i}} \ne {\rm{N}}. \\ \end{array} $$

Let P(i) be the probability of eventually reaching state s_N, starting from state i. By definition, P(1) = 0 and P(N) = 1 (the game is already over).

Fact: The probabilities P(i) are the unique solution of the system of equations:

$$ \begin{aligned} & {\text{P}}\left( {1} \right) = 0 \\ & {\text{P}}\left( {\text{N}} \right) = 1 \\ & {\text{P}}\left( {\text{i}} \right) = \mathop \sum \limits_{k = 1}^{N} p_{ik}\cdot {\text{P}}\left( {\text{k}} \right) ,\quad {\text{for i}} = {2}, \ldots ,{\text{N}} - {1} \\ \end{aligned} $$

So, we have in general a linear system of N equations with N variables, and the solution is straightforward.³⁸

We finish with the observation that (apart from some degenerate cases) the probability that the process will be eventually absorbed is 1. This means, that the probabilities of the finite sequences (i.e. the $\Upomega^{*}$ in the constructed probability space) sum up to 1. This means, that we do not need any infinite sequences (paths) in our construction of ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$.

5.6 The Markov graph for $\neg$ L ${{\to}}$ E

The game for the conditional If John does not order a Latte, he will order an Espresso is represented by the graph in Fig. 2.

Fig. 2

The graph for the simple conditional $\neg$L→E

Computing the probability of victory is simple. We take the corresponding probabilities of choosing Espresso, Cappuccino and Latte to be p, q, r. This means, that in our simple probability space S = (Ω, Σ, P) modeling John’s choices, P(E) = p, P(C) = q, P(L) = r. The system of equations for this Markov graph consists of one equation only:

$$ {\text{P}}_{{{\text{START}}}} = p + r \cdot {\text{P}}_{{{\text{START}}}} $$

P_START is the probability of getting from the initial point (i.e. START) to the state WIN. The result is P_START = $\frac{p}{1 - r}$ = $\frac{p}{p + q}$, which is equal to the conditional probability P(E|$\neg$L) in the initial space.³⁹

The probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ that represents the game is quite simple. $\Upomega^{*}$ consists of all the possible scenarios (settling the bet), i.e. $\Upomega^{*}$ = {LⁿE, LⁿC: n ≥ 0}. They might be viewed as paths in the graph, starting at START and ending at one of the absorbing states (either WIN or LOSS). The probabilities of the elementary events are:

$$ \begin{aligned} & {\text{P}}^{*}\left( {{\text{L}}^{{\text{n}}} {\text{E}}} \right) = r^{n} p,\quad {\text{for}}\quad {\text{ n}} \ge 0; \\ & {\text{P}}^{*}\left( {{\text{L}}^{{\text{n}}} {\text{C}}} \right) \, = r^{n} q,\quad {\text{ for }}\quad {\text{n}} \ge 0. \\ \end{aligned} $$

The σ-field $\Upsigma^{*}$ is the power set of $\Upomega^{*}$ (as $\Upomega^{*}$ is countable): $\Upsigma^{*}=2^{\Upomega^{*}}.$ The probability of any event X∈$\Upsigma^{*}$ is defined in the standard way as the sum of the series

$$ {\text{P}}^{*}\left( {\text{X}} \right) \, =\, \mathop \sum \limits_{{\omega \in {\text{X}}}} {\text{P}}^{*} (\omega ) $$

The interpretation of the conditional $\neg$L→E as an event in this space consists of the scenarios leading to a win, i.e.

$$ [\neg L {{\to}} E]^{*} \, = \, \{ {\text{L}}^{{\text{n}}}\,{\text{E}}:\,{\text{n}} \ge 0\} . $$

Its probability is:

$$ {\text{P}}^{*}([\neg L {{\to}} E]^{*}) \, = \mathop \sum \limits_{n = 0}^{\infty } pr^{n} = \frac{p}{1 - r} = \frac{p}{p + q} $$

Of course, this probability equals P_START. The probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ corresponds to the graph; indeed, this is the probability space underlying Markov graph formalism (reassuring us that the equations for the graph are legitimate).

$$ {\text{P}}^{*}([\neg L {{\to}} E]^{*}) = {\text{P}}_{{{\text{START}}}} = \frac{p}{1 - r} = \frac{p}{p + q} = {\text{ P}}({\text{E}}| \neg {\text{L}}) $$

where P is the probability function from the initial probability space S = (Ω, Σ, P).

The event [$\neg$L→E]$^{*}$ within ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ represents the conditional If John does not order a Latte, he will order an Espresso. But also the sentences John buys an Espresso (i.e. E) and John buys a Cappuccino (i.e. C) are interpreted in ${{{{\text{S}}}}^{*}}$ in an obvious way: [E]$^{*}$ = {E}; [C]$^{*}$ = {C}. This is possible as these one-element sequences describe the simplest scenarios settling the bet. Also the sentence John buys a Latte is given an interpretation in ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$, but here we have to be careful. As our aim is to represent the settled games, so we need not (and even cannot) represent in our space the claim John buys a Latte—and this is the end of the whole story (this would require the scenario “L” which is not present in ${{{{\text{S}}}}^{*}}$). But the interpretation of John buys a Latte consists of the set of sequences starting with L. Formally, [L]$^{*}$ = {LⁿE, LⁿC: n≥1}. Observe, that P$^{*}$([E]$^{*}$) = P(E); P$^{*}$([C]$^{*}$) = P(C) and P$^{*}$([L]$^{*}$) = P(L), which means that the probabilities of events from S have been preserved in ${{{{\text{S}}}}^{*}}$ (which is a natural and desirable situation).⁴⁰

The construction of the graph and probability space for simple conditionals A→B is well behaved with respect to the negation. We expect the probability of $\neg$($\neg$L→E), i.e. It is not the case that if John does not order a Latte, he will order an Espresso to be 1−P$^{*}$([$\neg$L→E]$^{*}$). In our case losing the game If John does not order a Latte, he will order an Espresso amounts to winning the game If John does not order a Latte, he will order a Cappuccino. We can use our space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma^{*}},{{{{\text{P}}}}^{*}}} \right)$ to compute its probability, as the sentence $\neg$L→C has an interpretation [$\neg$L→C]$^{*}$ = {LⁿC: n ≥ 0}. Finally, P$^{*}$([$\neg$($\neg$L→E)]$^{*}$) = P$^{*}$([$\neg$L→C]$^{*}$) = 1−P$^{*}$([$\neg$L→E]$^{*}$). This is obvious even without computing: all the scenarios which do not lead to victory lead to defeat.⁴¹ So, in general, P$^{*}$([$\neg$(A→B)]$^{*}$) = P$^{*}$([A→$\neg$B]$^{*}$) = 1−P$^{*}$([(A→B)]$^{*}$).

5.7 The general features of the Stalnaker Bernoulli model

The Stalnaker Bernoulli models and Kaufmann’s results (see Kaufmann 2004, 2005, 2009; van Fraassen 1976) were a very important source of inspiration for our model. For the sake of comparison we consider the Stalnaker Bernoulli space built for the same set of atomic actions as in our example, i.e. {L, E, C}, and the conditional $\neg$L→E. The corresponding Stalnaker Bernoulli space ${{{{\text{S}}}}^{**}} = \left( {{\Upomega^{**}}, {\Upsigma ^{**}},{{{{\text{P}}}}^{**}}} \right)$ is defined in the following way:

$\Upomega^{**}$ is the set of all infinite sequences consisting of the events L, E, C;

$\Upsigma^{**}$ is the σ-field defined over $\Upomega^{**}$;

${\text{P}}^{**}$ is a probability measure defined on $\Upsigma^{**}$.

Informally we can think of the infinite sequences as unfolding scenarios (relative to which the conditional will be settled and its probability will be computed). Any particular infinite sequence of events (which come from the initial Ω = {L, E, C}) has null probability. But the relevant events in the big space ${{{{\text{S}}}}^{**}}$ modeling the conditionals are appropriate “bunches” of sequences—and these events have non-zero probabilities. This involves constructing an appropriate σ-field. It is not the power set of $\Upomega^{**}$ (this would be too big), but the formal details of the construction need not concern us here.

In the Stalnaker Bernoulli space, the “bunches” are constructed from sequences starting with an initial finite (perhaps empty) sequence of L’s, followed by a E or C—but later an arbitrary infinite sequence follows. The probabilities of events modeling the appropriate scenarios of the games are as we expect them to be:

${\text{P}}^{**}$({LⁿEX^∞: X^∞ is an arbitrary infinite sequence from L, E, C}) = rⁿp.

${\text{P}}^{**}$({LⁿCX^∞: X^∞ is an arbitrary infinite sequence from L, E, C}) = rⁿq.

Such sets generate the appropriate σ-field. Within this space the appropriate construction can be conducted which leads to the result that:

$$ {\text{P}}^{**}([\neg L {{\to}} E]^{**}) = \frac{p}{p + q} = {\text{ P}}({\text{E}}| \neg {\text{L}}) $$

So our result is consistent with the result within the Stalnaker Bernoulli model (and also to McGee’s account). In general, in all these models it is true that ${\text{P}}^{*}$(A→B) = P(B|A), which means that the ${{\text{P}}}^{*}{{\text{CCP}}}$ principle holds. We use the star * to stress that ${\text{P}}^{*}$ is the probability distribution in the (constructed) space ${{{{\text{S}}}}^{*}}$, whereas P is the probability distribution from the initial space S. A and B are sentences not containing the conditional operator.⁴²

6 The graph model for right-nested conditionals

We illustrate the general approach by a familiar example of drawing balls from an urn, which allows the crucial feature of the model to be exhibited (in particular, the possible interpretations of the compound conditional). The advantage of this illustration is that it fits very nicely with the possible worlds account, where a proposition is identified with a set of possible worlds (the balls might be thought of as possible worlds which are truth makers). For the sake of the example, we assume that there are white, red and green balls in the urn, which means that the propositions “The ball is White”, “The ball is Green”, “The ball is Red” are identified with sets of balls. Of course, no event in this space corresponds to the conditional $\neg$W→G (If the ball is not White, it is Green) as no particular set of balls could be considered the right interpretation. Even without the triviality results, this is a very awkward idea.⁴³ In our approach, which is more of a “possible scenarios model” or a game-theoretic semantics, no problems of this kind arise.

Assume moreover that the balls have one other feature, for instance mass. So the balls are either Heavy or Light. We assume that these two “dimensions” (mass/color) are independent, so all possible sorts of balls can appear in the urn. We want to consider right-nested conditionals like:

$$ H {{\to}} \, (\neg W {{\to}} G) $$

i.e. If the ball is Heavy, then if it is not White, it is Green.⁴⁴

As we think of this conditional in terms of a game (bet), we have to make sure what the exact terms of the game are.

There are six types of balls in our urn:

HW—Heavy White balls

HG—Heavy Green balls

HR—Heavy Red balls

LW—Light White balls

LG—Light Green balls

LR—Light Red balls

Some events are of particular interest: H = HW$\cup$HG$\cup$HR; L = LW$\cup$LG$\cup$LR; W = HW$\cup$LW etc.⁴⁵

There is a probability distribution (as there is some definite number of balls of each kind), so there is an initial probability space S = (Ω, Σ, P), with Ω = {HG, HR, HW, LG, LR, LW}. In order to define the probability of the conditional H→($\neg$W→G), we need a probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ where the conditional H→($\neg$W→G) is given an interpretation as an event [H→($\neg$W→G)]$^{*}$$\in \Upsigma^{*}$. As in the Non-Latte-Espresso Game, the probability space will be associated with the respective graph defining the rules of the game (depending on the interpretation of the conditional).

But before we start The Nested Conditional Game, we have to decide when the game is (1) won, (2) lost, or (3) continued. Two cases are obvious:

• If we draw an HG, i.e. a Heavy Green ball, we WIN;

• If we draw an HR, i.e. a Heavy Red ball, we LOSE.

But what happens in the other cases? The case of Light balls is not controversial:

• If it is a Light ball (of any color, i.e. an LW or LG or LR), we restart the game. Restarting means we put the ball back into the urn and draw again, of course still paying attention to the weight and color.⁴⁶

The last case remains: a Heavy White ball. Depending on the interpretation (deep versus shallow), the game is either:

• 1. restarted on the same terms;

• 2. continued on modified terms.⁴⁷

Both the interpretations lead to different graphs, different corresponding probability spaces, and different formulas for the probabilities.

6.1 The deep interpretation

The rules of the game for the deeply interpreted conditional are simple: we draw the first ball and if we draw (HG) or (HR), the game is decided. In all other cases, the game is not decided and restarts from the beginning, which means that we still pay attention to the weight! This is because if we interpret the conditional If the ball is Heavy, then if it is not-White, it is Green as if the ball is Heavy, then this particular ball has to fulfill the condition: if it is not-White, it is Green. The graph for the game is given in Fig. 3:

Fig. 3

The graph for the deep interpretation of the conditional H→($\neg$W→G)

There is only one equation to solve:

$$ {\text{P}}_{{{\text{START}}}} = {\text{ P}}\left( {{\text{HG}}} \right) + r{\text{P}}_{{{\text{START}}}} $$

where r = P(HW) + P(LW) + P(LG) + P(LR)

The solution is straightforward: P_START = $\frac{{\text{P}}\left( {{\text{HG}}} \right)}{{\text{P}}\left({{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}$

We need to define a probability space ${\rm{S}}_{{\rm{deep}}}^{*} = \left( {\Upomega _{{\rm{deep}}}^{*},{\rm{ }}\Upsigma _{{\rm{deep}}}^{*},{\rm{ P}}_{{\rm{deep}}}^{*}} \right)$ in which the conditional H→($\neg$W→G) has a counterpart as an event. The space is connected with the graph in an obvious way by considering the paths within the graph which lead to victory: they consist of some loops (“dummy moves”) followed by a decisive move. The “dummy moves” are: HW, LW, LG, LR (nothing happens, the game is restarted). The decisive moves are HR and HG. So, any such path will have the form Xⁿ(HG), Xⁿ(HR), where X is one of HW, LW, LG, LR. A winning path is, for example, (HW)(LR)(LG)(HG), a losing path is, for example, (HW)(HW)(LG)(LG)(LR)(HR). So:

$$ \Upomega_{{{\text{deep}}}}^{*} = \{{\text{X}}^{{\text{n}}} \left( {{\text{HG}}} \right),{\text{ X}}^{{\text{n}}} \left( {{\text{HR}}} \right){: }\;{\text{n}} \ge 0\} $$

The probability of any particular path is computed by multiplying the probabilities. For instance, the probability of the path (LG)(LG)(LR)(HW)(LR)(HG) is P(LG)⋅P(LG)⋅P(LR)⋅P(HW)⋅P(LR)⋅P(HG). The set of winning scenarios consists of admissible scenarios ending with a HG (Heavy Green) ball, i.e.

$$ [H {\to} \, (\neg W {\to} G)]_{{{\text{deep}}}}^{*} \, = \, \{ {\text{X}}^{{\text{n}}} \left( {{\text{HG}}} \right){:}\,{\text{ n}} \ge 0\} $$

Its probability is easily computed within the space ${\rm{S}}_{{\rm{deep}}}^{*}$:

$$ {\text{P}}^{*}_{{{\text{deep}}}} (H {\to} \, (\neg W {\to} G)) \, = \,\mathop \sum \limits_{n = 0}^{\infty } {\text{P}}\left( {{\text{HG}}} \right)\cdot\left( {{\text{P}}\left( {\text{X}} \right)} \right)^{{\text{n}}} = \frac{{{\text{P}}\left( {{\text{HG}}} \right)}}{{1 - {\text{P}}\left( {\text{X}} \right)}} = \frac{{{\text{P}}\left( {{\text{HG}}} \right)}}{{{\text{P}}\left( {{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}} $$

Of course, this agrees with the result computed within the graph, i.e.

$$ {\text{P}}_{{{\text{START}}}} = \frac{{{\text{P}}\left( {{\text{HG}}} \right)}}{{{\text{P}}\left( {{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}} $$

To sum up: ${\text{P}}^{*}_{{{{\rm deep}}}} (H {\to} \, (\neg W {\to} G)) \, = {\text{ P}}_{{{{\rm START}}}} = \frac{{{\text{P}}\left( {{\text{HG}}} \right)}}{{{\text{P}}\left( {{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}}$

This is analogous to Alice’s probability for MED (Sect. 2). Applying this formula to the wet match probabilities from Sect. 3, we get:

$$ {\text{P}}^{*}_{{{\text{deep}}}} \left( {W {\to} \, \left( {S {\to} L} \right)} \right) \, = \, 0.{1} $$

which agrees with Kaufmann’s result obtained within the causal model, (Kaufmann 2005, 209–210).

Informally, we might say that under the deep interpretation of the conditional H→($\neg$W→G) we really need only observe Heavy balls, as only among these balls can the Nested Conditional Game be settled. In a sense, our game is reduced to the Colorful Conditional Game played with Heavy balls only.⁴⁸ Light balls might be ignored as they do not matter (which means the color distribution among Light balls does not matter).⁴⁹

For completeness, we conclude with presenting the deep interpretation in the general case A→(B→C). The corresponding Markov graph is given in Fig. 4.

Fig. 4

The graph for the deep interpretation of the conditional A→(B→C)

The probability space is defined in the following way (see the formal definition in Sect. 5.4):⁵⁰

$$ \Upomega_{{{\text{deep}}}}^{*} \, = \, \{ \left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}} \right), \, \left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}^{{\text{c}}} } \right)\!:\;{\text{n}} \ge 0\} . $$

The probabilities ${\rm{P}}_{{\rm{deep}}}^{*}$ of the elementary events are defined in the obvious way:

$$ \begin{aligned} & {\text{P}}^{*}_{{{\text{deep}}}} \left({\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}} \right)} \right) \, = \left( {{\text{P}}\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)} \right)^{{\text{n}}}{\text{P}}\left( {{\text{ABC}}} \right) \\ & {\text{P}}^{*}_{{{\text{deep}}}} \left( {\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}^{{\text{c}}} } \right)} \right) \, = \, \left( {{\text{P}}\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)} \right)^{{\text{n}}}{\text{P}}\left( {{\text{ABC}}^{{\text{c}}} } \right) \\ \end{aligned} $$

The interpretation of the conditional A→(B→C) in ${\rm{S}}_{{\rm{deep}}}^{*}$ is:

$$ \left[ {A {\to} \, \left( {B {\to} C} \right)} \right]_{{{\text{deep}}}}^{*} \, = \, \{ \left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}} \right){:}\,{\text{n}} \ge 0\} . $$

So, we have:

$$ {\text{P}}^{*}_{{{\text{deep}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, = \mathop \sum \limits_{{{\text{n}} = 0}}^{\infty } {\text{P}}\left( {{\text{ABC}}} \right)\left( {{\text{P}}\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)} \right)^{{\text{n}}} = \frac{{{\text{P}}\left( {{\text{ABC}}} \right)}}{{1 - {\text{P}}\left( {\left( {{\text{AB}}} \right)^{{\text{c}}} } \right)}} = \frac{{{\text{P}}\left( {{\text{ABC}}} \right)}}{{{\text{P}}\left( {{\text{AB}}} \right)}} = {\text{P}}({\text{C}}\left| {{\text{AB}}} \right.). $$

6.2 The shallow interpretation

Under the shallow interpretation of the conditional, after drawing the first Heavy White ball, the rules of the game change and the game continues in a different way.⁵¹ From now on we no longer pay attention to the weight, we only take colors into account. We might say informally that we lost the ability to distinguish weight, so we switched to the Purely Colorful Conditional Game ($\neg$W→G)—still played within the same urn.⁵²

So, the interpretation of the conditional

If the ball is Heavy, then if it is not White, it is Green

can be described in the following way:

If I draw a Heavy ball, then—provided we continue the game (i.e. it has not been settled in this first move)—anytime later on if the ball is not-White, it is Green (regardless of its weight).

We might describe drawing a Heavy White ball as a kind of “Activating Event” which changes the conditions of the latter phase of the game, or we might think of it in terms of an updating rule which changes the terms of the game (or “transfers” us to a different game from now on).⁵³

The stochastic graph for the shallow interpretation is given in Fig. 5:

Fig. 5

The graph for the shallow interpretation of the conditional H→($\neg$W→G)

We can write down the equations for success in this graph:

$$ \begin{aligned} & {\text{P}}_{{{\text{START}}}} = {\text{ P}}\left( {{\text{HG}}} \right) {\text{P}}_{{{\text{WIN}}}} + {\text{ P}}\left( {\text{L}} \right) {\text{P}}_{{{\text{START}}}} + {\text{P}}\left( {{\text{HW}}} \right) {\text{P}}_{{{\text{COLORS}}}} + {\text{P}}\left( {{\text{HR}}} \right) {\text{P}}_{{{\text{LOSS}}}} \\ & {\text{P}}_{{{\text{COLORS}}}} = {\text{ P}}\left( {\text{G}} \right) + {\text{P}}\left( {\text{W}} \right) {\text{P}}_{{{\text{COLORS}}}} \\ \end{aligned} $$

P_START is the probability of winning the game when we start from START. P_COLORS is the probability of winning the game when starting from the node COLORS, which is the starting point of the Purely Colorful Conditional Game. P_WIN = 1, P_LOSS = 0 (the game is already finished). The solution is:

$$ {\text{P}}_{{{\text{START}}}} = \frac{{{\text{P}}\left( {{\text{HG}}} \right) + {\text{ P}}\left( {{\text{HW}}} \right)\frac{{{\text{P}}\left( {\text{G}} \right)}}{{1 - {\text{P}}\left( {\text{W}} \right)}}}}{{{\text{P}}\left( {\text{H}} \right)}} $$

Which simplifies to:

$$ {\text{P}}_{{{\text{START}}}} = {\text{ P}}({\text{G}}|{\text{H}}) \, + {\text{P}}({\text{W}}|{\text{H}}){\text{P}}({\text{G}}|{\text{W}}^{{\text{c}}} ). $$

Just as in the deep case, we need to define a probability space ${\rm{S}}_{{\rm{ shallow }}}^{*} = \left( {\Upomega _{{\rm{ shallow }}}^{*},{\rm{ }}\Upsigma _{{\rm{ shallow }}}^{*},{\rm{ P}}_{{\rm{ shallow }}}^{*}} \right)$ in which the conditional H→($\neg$W→G) has a counterpart as an event. And again, the space is connected to the graph in an obvious way and consists of these paths within the graph which lead to victory.

For completeness, we present the general construction for a conditional A→(B→C). The Markov graph is analogous to the graph for H→($\neg$W→G) and has the form given in Fig. 6 (next page).

Fig. 6

The graph for the shallow interpretation of the conditional A→(B→C)

The space ${\rm{S}}_{{\rm{ shallow }}}^{*} = \left( {\Upomega _{{\rm{ shallow }}}^{*},{\rm{ }}\Upsigma _{{\rm{ shallow }}}^{*},{\rm{ P}}_{{\rm{ shallow }}}^{*}} \right)$ consists of paths starting in START and terminating in one of the states WIN, LOSS. It is defined according to the formal definition from Sect. 4.4. This means, that:

$$ \Upomega_{{{\text{shallow}}}}^{*} \, = \, \{ \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}} \right), \, \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}^{{\text{c}}} } \right), \, \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{AB}}^{{\text{c}}} } \right)\left( {{\text{B}}^{{\text{c}}} } \right)^{{\text{k}}} \left( {{\text{BC}}} \right), \, \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{AB}}^{{\text{c}}} } \right)\left( {{\text{B}}^{{\text{c}}} } \right)^{{\text{k}}} \left( {{\text{BC}}^{{\text{c}}}): } \right. \;{\text{n}},{\text{k}} \ge 0\} . $$

For instance, (A^c)ⁿ(ABC) is the sequence consisting of n events A^c followed by the event ABC. (A^c)ⁿ(AB^c)(B^c)^k(BC) it the sequence consisting of n events A^c followed by the event AB^c, than by k events B^c and finally by the event ABC. Such sequences are elementary events in $\Upomega_{{{\text{shallow}}}}^{*}$. Their probabilities ${{\text{P}}}_{{{\rm shallow}}}^{*}$ are obtained by multiplying the probabilities taken from the sample space S = (Ω, Σ, P). $\Upsigma_{{{\text{shallow}}}}^{*}$ is the power set of $\Upomega_{{{\text{shallow}}}}^{*}$, and ${{\text{P}}}_{{{\rm shallow}}}^{*}$ is defined by the familiar formula ${\rm{P}}^{*}$(X) = $\mathop \sum \nolimits_{{{\upomega } \in {\text{X}}}} {\text{ P}}^{*} \left( {\upomega } \right)$. The structure of $\Upomega_{{{\rm shallow}}}^{*}$ is more complex than in the deep case. For instance, there is the path (AB^c)(A^cBC) which leads to victory, and the path (AB^c)(A^cBC^c) which leads to loss (these paths do not even appear in $\Upomega_{{\rm{deep}}}^{*}$).

The interpretation of the conditional A→(B→C) in ${\text{S}}_{{{\rm shallow}}}^{*}$ is the event

$$ \left[ {A {\to} \, \left( {B {\to} C} \right)} \right]^{*} = \{ \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{ABC}}} \right), \, \left( {{\text{A}}^{{\text{c}}} } \right)^{{\text{n}}} \left( {{\text{AB}}^{{\text{c}}} } \right)\left( {{\text{B}}^{{\text{c}}} } \right)^{{\text{k}}} \left( {{\text{BC}}} \right){:}\,{\text{n}},{\text{k}} \ge 0\} . $$

and its probability can be computed either by solving the system of equations for the Markov graph, or by direct computation in the space ${\text{S}}_{{{\rm shallow}}}^{*}$ (which involves some computation with infinite series). Regardless of the method, we get the formula:

$$ {\text{P}}^{*}_{{{\text{shallow}}}} \left( {\left[ {A {\to} \, \left( {B {\to} C} \right)} \right]^{*}} \right) \, = {\text{ P}}({\text{BC}}|{\text{A}}) \, + {\text{P}}({\text{B}}^{{\text{c}}} |{\text{A}}){\text{P}}({\text{C}}|{\text{B}}) $$

This agrees with Kaufmann’s formula for the probability of a right-nested conditional under the shallow interpretation (in the Stalnaker Bernoulli model). Applying the formula to our example (A = H, B = $\neg$W; C = G), we get the already known result.

The shallow interpretation is natural in some cases, but examples where it leads to very unnatural consequences are also abundant, as the wet match example clearly shows.

Is it better to play the deep or the shallow game? It depends. In some cases, the probabilities coincide, sometimes ${\text{P}}_{{\rm{deep}}}^{*}$ is bigger, sometimes ${\text{P}}_{{{\rm shallow}}}^{*}$. The formulas are:

$$ \begin{aligned} & {\text{P}}^{*}_{{{\text{deep}}}} (H {\to} \, (\neg W {\to} G)) \, = \frac{{{\text{P}}\left( {{\text{HG}}} \right)}}{{{\text{P}}\left( {{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}} \\ & {\text{P}}^{*}_{{{\text{shallow}}}} (H {\to} \, (\neg W {\to} G)) \, = {\text{ P}}({\text{G|H}}) \, + {\text{P}}({\text{W|H}}) \cdot {\text{P}}({\text{G|W}}^{{\text{c}}} ) \\ \end{aligned} $$

Consider three cases:

• 1. If P(HW) = P(HG) = P(HR) = P(LW) = P(LG) = P(LR) = $\frac{1}{6}$, then ${\text{P}}^{*}_{{{\text{deep}}}} (H {\to} \, (\neg W {\to} G)) \, = {\text{ P}}^{*}_{{{\text{shallow}}}} (H {\to} \, (\neg W {\to} G)) \, = \frac{1}{2}.$

• 2. If P(HW) = P(HG) = P(HR) = $\frac{1}{6}$; P(LW) = 0; P(LG) = 0; P(LR) = $\frac{1}{2}$, then $\begin{aligned} & {\text{P}}^{*}_{{{\text{deep}}}} (H {\to} \, (\neg W {\to} G)) \, = \frac{1}{2}. \\ & {\text{P}}^{*}_{{{\text{shallow}}}} (H {\to} \, (\neg W {\to} G)) \, = \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{5} \, = \, \frac{2}{5}. \\ \end{aligned}$

• 3. If P(HW) = P(HR) = $\frac{1}{6}$; P(HG) = 0; P(LW) = 0; P(LG) = $\frac{2}{3};$ P(LR) = 0, then

  $$ \begin{aligned} & {\text{P}}^{*}_{{{\text{deep}}}} (H {\to} \, (\neg W {\to} G)) \, = \, 0. \\ & {\text{P}}^{*}_{{{\text{shallow}}}} (H {\to} \, (\neg W {\to} G)) \, = \, 0 \,+ \, \frac{1}{2} \cdot \frac{4}{5} = \frac{2}{5}. \\ \end{aligned} $$

6.3 Some specific issues

6.3.1 The Import-Export Principle

The Import-Export Principle states that:

$$ P(A {\to} (B {\to} C)) = P((A {\wedge} B) {\to} C) $$

Is this true? We discuss this issue separately for the deep and the shallow interpretation. To keep things simple, we focus on the previously discussed example, i.e. on the conditional H→($\neg$W→G). The Import-Export Principle in this case would have the form:

$$ P(H {\to} (\neg W {\to} G)) = P((H {\wedge} \neg W) {\to} G) $$

In both these formulas we have used a very simplified notation (and committed a slight abuse of language), as we really think about two different probability functions P(.) from different spaces. We have to be careful, but in this case it is clear what we mean.

6.3.1.1 The Import-Export Principle under the deep interpretation

What is the probability of ((H${\wedge}$$\neg$W)→G)? This is a simple conditional, the corresponding graph for which was defined in Sect. 6.1, and the corresponding probability is $\frac{{\text{P}}\left( {{\text{HG}}} \right)}{{\text{P}}\left({{\text{HG}}} \right) + {\text{P}}\left( {{\text{HR}}} \right)}$, which agrees with ${\text{P}}_{{\rm{deep}}}^{*}$(H→($\neg$W→G)). This means that the Import-Export Principle holds for the deep interpretation. This is not surprising—intuitively, it should! We only pay attention to color among the Heavy balls, so we are interested in the outcome of the game only when the ball is Heavy and is non-White. Similarly, in the MED example (under the deep interpretation), we only observe John on the days when he has taken medication A.

So, for the deep interpretation the Import-Export Principle works, which means that we can compute the probabilities very easily.⁵⁴ The graph formalism allows to prove the following equation:

${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) = ${\text{P}}^{*}$((A${\wedge}$B)→C) = P(C|AB).

So, obviously, for the deep interpretation the antecedents of the conditional can be exchanged:

${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) = ${\text{P}}_{{\rm{deep}}}^{*}$(B→(A→C)).

This is intuitive if we think of the Heavy/Green balls game: winning the If not White, then Green game played with the Heavy balls only is the same as winning the If Heavy, then Green game played with the non-White balls. This agrees with McGee’s theory—the Import-Export Principle is his axiom (C7) (McGee 1989, 504).

6.3.1.2 The Import-Export Principle under the shallow interpretation

If the Import-Export Principle was true for the shallow conditional, this would mean that:

${\text{P}}_{{{\rm shallow}}}^{*}$(A→(B→C)) = ${\text{P}}^{*}$((A${\wedge}$B)→C);

${\text{P}}_{{{\rm shallow}}}^{*}$(B→(A→C)) = ${\text{P}}^{*}$((B${\wedge}$A)→C).

Obviously, A${\wedge}$B≡B${\wedge}$A, so ${\text{P}}^{*}$((A${\wedge}$B)→C) = ${\text{P}}^{*}$((B${\wedge}$A)→C). So, the IE Principle would imply that ${\text{P}}_{{{\rm shallow}}}^{*}$(A→(B→C)) = ${\text{P}}_{{{\rm shallow}}}^{*}$(B→(A→C)). But, in general

$$ {\text{P}}^{*}_{{{\text{shallow}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, \ne {\text{ P}}^{*}_{{{\text{shallow}}}} \left( {B {\to} \, \left( {A {\to} C} \right)} \right), $$

which means that for the shallow interpretation the Import-Export Principle does not hold. This is intuitive: the first condition changes the rules of the game, so depending on what the first condition is, the probabilities can differ greatly.⁵⁵ In particular, the order of the antecedents in the conditional is very important. The following graphs represent the two sentences H→($\neg$W→G) and $\neg$W→(H→G), and they illustrate the general rule (Fig. 7):

Fig. 7

The left graph corresponds to H→($\neg$W→G)), the right graph to $\neg$W→(H→G)

6.3.2 ${{\text{P}}}^{*}{{\text{CCP}}}$

From an abstract point of view, the ${{\text{P}}}^{*}{{\text{CCP}}}$ principle expresses the idea that it is possible to compute the probability of conditionals as a function of conditional probabilities in the sample space.⁵⁶ If we accept this general principle, then finding analogues of ${{\text{P}}}^{*}{{\text{CCP}}}$ amounts to expressing the probability ${\text{P}}^{*}$(A→(B→C)) in terms of conditional probabilities from the sample space S. We think that this retains some fundamental intuitions of Ramsey expressed in the well-known quotation (footnote 7).

Taken the problem in a more abstract setting, we want to know whether ${\text{P}}^{*}$(A→(B→C)) can be expressed as a function of conditional probabilities in the sample space S.⁵⁷ In other words, we want to identify the appropriate equation:

$$ {\text{P}}^{*}\left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, = \, \Psi \, \left( { \ldots entries\;of\;the\;form\;of\;conditional\;probabilities\;within\;S \ldots } \right). $$

For the simple conditional, ${\text{P}}^{*}$(A→B) is given via a particularly simple function ${\Psi}$(….), namely ${\text{P}}^{*}$(A→B) = P(B|A). There is no obvious analogue for A→(B→C)—for instance the equation ${\text{P}}^{*}$(A→(B→C)) = P(B→C|A) does not make sense, as B→C has no interpretation in the sample space S as an event. So, for right-nested conditionals A→(B→C) the function ${\Psi}$(….) in the analogue of ${{\text{P}}}^{*}{{\text{CCP}}}$ must be more complex. It is quite obvious, that the functions ${\Psi}$(….) will be different for the deep and shallow interpretations, as ${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) and ${\text{P}}_{{{\rm shallow}}}^{*}$(A→(B→C)) differ.

6.3.2.1 ${{\text{P}}}^{*}{{\text{CCP}}}$ under the deep interpretation

Under the deep interpretation, the Import-Export Principle holds, i.e.

$$ \text{P}^{*}(A {\to} (B {\to} C)) = \text{P}^{*}((A{\wedge} B) {\to} C) $$

(A${\wedge}$B)→C is a simple conditional, and its probability is given by the formula:

$$ \text{P}^{*}((A{\wedge} B) {\to} C) = \text{P}\text{(C|AB)}. $$

This means, that ${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) = P(C|AB). The function ${\Psi}$(….) has therefore a very simple form, we really need only one conditional probability form S. It is also easy to show, that the following formula is true:

$$ {\text{P}}^{*}_{{{\text{deep}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, =\, {\text{ P}}_{{\text{A}}} \left( {{\text{C}}|{\text{B}}} \right) $$

P_A is the standard probability measure obtained from P by conditionalizing on A: P_A(X) := P(X|A).⁵⁸ This means, that under the deep interpretation, the probability of the conditional A→(B→C) equals probability of the conditional B→C relatively to a new sample probability space, obtained from S by conditionalizing on A. This is intuitive: consider our conditional H→($\neg$W→G). The probability of winning the “H→($\neg$W→G)-game” is really the probability of winning the “($\neg$W→G)-game” restricted to Heavy balls only.⁵⁹

The equation ${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) = P_A(C|B) definitely looks like ${{\text{P}}}^{*}{{\text{CCP}}}$. And it satisfies the general requirement: probability of the (nested) conditional A→(B→C) is expressed as a function of conditional probabilities from the sample space S, as the arguments of the function ${\Psi}$(….) are P(ABC) and P(AB).

6.3.2.2 ${{\text{P}}}^{*}{{\text{CCP}}}$ under the shallow interpretation

For the shallow interpretation, the formula for the probability of the right-nested conditional is:

$$ {\text{P}}^{*}_{{{\text{shallow}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, = {\text{ P}}({\text{BC}}\left| {\text{A}} \right.) \, + {\text{ P}}({\text{B}}^{{\text{c}}} \left| {\text{A}} \right.){\text{P}}({\text{C}}\left| {\text{B}} \right .) $$

As in the deep case, the probability of the conditional A→(B→C) is expressed as a combination of conditional probabilities from the initial sample space S. The function ${\Psi}$(…) is more complex than in the deep case, but still fairly simple, with only three arguments: ${\text{P}}({\text{BC}}\left| {\text{A}} \right.)$, ${\text{P}}({\text{B}}^{{\text{C}}} \left| {\text{A}} \right.)$ and ${\text{P}}({\text{C}}\left| {\text{B}} \right.)$.⁶⁰

In conclusion, we can say that the ${{\text{P}}}^{*}{{\text{CCP}}}$ principle holds for the deep interpretation in a straightforward way, the formula for equation ${\text{P}}_{{\rm{deep}}}^{*}$(A→(B→C)) being formally quite analogous to the original formula ${\text{P}}^{*}$(A→B) = P(B|A). For the shallow interpretation there is no such purely formal analogy, but the probability ${\text{P}}_{{{\rm shallow}}}^{*}$(A→(B→C)) is calculated as a function of conditional probabilities in the sample space S. We think that this retains the fundamental intuition of Ramsey (and PCCP).

7 Multiple-(right)-nested conditionals

We have considered conditionals of the form A→(B→C), but we can also think of more complex conditionals D→(A→(B→C)). Three ‘→’ connectives appear within this conditional. The distinction between the deep and shallow interpretation is not interesting for the simple conditional (either it does not make sense, or the interpretations coincide), so it cannot be reasonably applied to the last conditional. So, the ‘→’ between ‘B’ and ‘C’ is neutral in this respect, but the other two symbols (i.e. after A, and after D), can be given different interpretations. A priori there are four possible interpretations: deep-deep; deep-shallow; shallow-deep; shallow-shallow. In this section we consider only the uniform interpretations, i.e. deep-deep and shallow-shallow.

Consider the sentence:

If John takes medication D, then if he takes A, then if he takes B, then he will have an allergic reaction.

Depending on the interactions between the medications (some combinations might cause permanent changes, which would not occur if only one of the mediations was taken), different interpretations of the conditional will be justified.

Take the familiar example of Heavy/Light and White/Green/Red balls, but now we assume that still another “orthogonal” property can be defined, e.g. Big/Small.⁶¹ Now consider the conditional:

If the ball is Big, then if it is Heavy, then if it is not-White, it is Green

i.e. B→[H→($\neg$W→G)]. This conditional can be interpreted in different ways, and we can identify the interpretations in terms of graphs.

7.1 The deep–deep interpretation

If we assume the deep-deep interpretation we win by drawing a BHG (Big Heavy Green) ball. We lose by drawing a BHR (Big Heavy Red) ball. All other balls just restart the game. The graph for the deep-deep interpretation is given in Fig. 8.

Fig. 8

The graph for B→[H→($\neg$W→G)] under the deep-deep interpretation

The equation is also simple:

$$ {\text{P}}_{{{\text{START}}}} = {\text{ P}}\left( {{\text{BHG}}} \right) + r {\text{P}}_{{{\text{START}}}} $$

where r = P(S) + P(BL) + P(BHW) = 1 – (P(BHG) + P(BHR)).⁶²

So finally:

$$ {\text{P}}^{*}_{{{\text{deep}}}} (B {\to} \, [H {\to} \, (\neg W {\to} G)]) \, = \frac{{{\text{P}}\left( {{\text{BHG}}} \right)}}{{{\text{P}}\left( {{\text{BHG}}} \right) + {\text{P}}\left( {{\text{BHR}}} \right)}} $$

As expected, it is equal to the conditional probability P(G|BHW^c) in the initial probability space S = (Ω, Σ, P). Both the Import-Export Principle and the ${{\text{P}}}^{*}{{\text{CCP}}}$ principle hold under the deep-deep interpretation. The formula generalizes to conditionals of arbitrary length, like A₁→(A₂→(…→(A_n→B)…). The graph for the deep-deep-…-deep interpretation is given in Fig. 9.

Fig. 9

The graph for A₁→(A₂→(…→(A_n→B)…)

The equation for the graph is:

P_START = P(A₁…A_nB) + P((A₁….A_n)^c) P_START, which means that:

$$ {\text{P}}_{{{\text{START}}}} = \frac{{{\text{P}}\left( {{\text{A}}_{1} \ldots {\text{ A}}_{{\text{n }}} {\text{B}}} \right)}}{{{\text{P}}\left( {{\text{A}}_{1} \ldots {\text{ A}}_{{\text{n }}} } \right)}} $$

So finally:

$$ {\text{P}}^{*}_{{{\text{deep}}}} (A_{{1}} {\to} \, \left( {A_{{2}} {\to} \, \left( { \ldots {\to} \, \left( {A_{n} {\to} B} \right) \ldots } \right)} \right) )\, = \frac{{{\text{P}}\left( {{\text{A}}_{1} \ldots {\text{ A}}_{{\text{n }}} {\text{B}}} \right)}}{{{\text{P}}\left( {{\text{A}}_{1} \ldots {\text{ A}}_{{\text{n }}} } \right)}} = {\text{P}}\left( {{\text{B}}|{\text{A}}_{{1}} {\text{A}}_{{2}} \ldots {\text{A}}_{{\text{n}}} } \right) $$

Obviously, the Import-Export Principle also works:⁶³

$$ {\text{P}}^{*}\,_{\text{deep}}(A_1 {\to} (A_2 {\to} ( \ldots {\to} (A_{n} {\to} B) \, \ldots ))) = \text{P}^{*}((A_{1}{\wedge} A_{2}{\wedge} \ldots {\wedge} A_{n} ) {\to} B)$$

7.2 The shallow-shallow interpretation

The same procedure can be applied to the shallow-shallow interpretation. Consider again the conditional

If the ball is Big, then if it is Heavy, then if it is not-White, it is Green

i.e. B→[H→($\neg$W→G)]

but this time we assume that both conditionals are shallow, which means that

• i. Drawing S restarts the game.

• ii. Drawing BL redirects us to the H→($\neg$W→G) game (interpreted in the shallow way).

• iii. Drawing BHW redirects us directly to the $\neg$W→G game.

• iv. Drawing BHG leads to victory.

• v. Drawing BHR leads to loss.

The graph is more complex (Fig. 10).

Fig. 10

The graph for B→[H→($\neg$W→G)] under the shallow-shallow interpretation. The thick line (leading from MASS-COLORS to COLORS) represents the transfer from the “first-internal” game H→($\neg$W→G) to the “internal-internal” game $\neg$W→G

The respective probability can be computed by writing down the system of linear equations with three variables: P_START, P_MASS-COLORS, P_COLORS. The corresponding probability space ${{{{\text{S}}}}^{*}} = \left( {{\Upomega^{*}}, {\Upsigma ^{*}},{{{{\text{P}}}}^{*}}} \right)$ consists (intuitively speaking) of all scenarios leading from START to any of the absorbing states WIN, LOSS. It can be constructed using the general definition given in Sect. 5.4.⁶⁴

7.3 Mixed interpretations

In the last paragraph, we considered the deep-deep and shallow-shallow interpretations (also for conditionals of arbitrary length). We can produce appropriate graphs for conditionals of arbitrary length. In general, for conditionals containing n sentences, there are 2ⁿ⁻² possible interpretations, and consequently 2ⁿ⁻² corresponding graphs. For long conditionals this is of no philosophical importance as conditionals of length, for instance, 200 are not natural. But examples of conditionals of length 4 are natural, both in everyday communication, and, for instance, in juristic texts, where hypothetical situations, variants and scenarios that depend on many conditions are commonplace. So in this section we focus on conditionals of length four, i.e. of the form A₁→(A₂→(A₃→B)). The results can be easily generalized to conditionals of arbitrary length.

For the purpose of the discussion in this paragraph, take the symbol ⇒ for the deep interpretation, and ⊃ for the shallow one; → will be neutral. So, the four possible interpretations of the conditional can be written as:

• 1. A₁⇒(A₂⇒(A₃→B)), i.e. deep-deep;

• 2. A₁⇒(A₂⊃(A₃→B)), i.e. deep-shallow;

• 3. A₁⊃(A₂⇒(A₃→B)) i.e. shallow-deep;

• 4. A₁⊃(A₂⊃(A₃→B)) i.e. shallow-shallow.

If we use the If the ball is Big, then if it is Heavy, then if it is not-White, it is Green example, i.e. B→[H→($\neg$W→G)], we can explain these four interpretations by fixing the rules of the game in different ways:

• 1. B⇒[H⇒($\neg$W→G)] (deep-deep): one ball, which has to be Big, Heavy and Non-White—and we win if this particular ball is Green.

• 2. B⇒[H⊃($\neg$W→G)] (deep-shallow): if we get a Big Heavy ball, then the game (provided it has not been settled) changes into a Purely Colorful Game W→G.

• 3. B⊃[H⇒($\neg$W→G)] (shallow-deep): after a Big ball has been drawn, the game (provided it has not been settled) is continued as H⇒($\neg$W→G) (i.e. deeply interpreted).

• 4. B⊃[H⊃($\neg$W→G)] (shallow-shallow): a Big ball initiates the [H⊃($\neg$W→G)] game (interpreted in the shallow way).

(1) and (4) have been discussed in Sects. 8.1 and 8.2.

The corresponding graphs for these interpretations are obtained easily, and computing the probabilities is straightforward. Figure 11 contains two graphs: the left is for B⇒[H⊃($\neg$W→G)] i.e. deep-shallow; the right is for B⊃[H⇒($\neg$W→G)] i.e. shallow-deep.

Fig. 11

The graphs for: B⇒[H⊃($\neg$W→G)] (deep-shallow interpretation—left) and for B⊃[H⇒$\neg$W→G)] (shallow-deep interpretation—right)

The probabilities can be computed by solving the appropriate systems of equations for graphs in Fig. 11.

Remember that the Stalnaker Bernoulli spaces approach imposes the shallow interpretation. McGee’s account is concerned with the deep interpretation, so none of these accounts can deal with “mixed interpretations” of the conditionals. But mixed interpretations are not just a formal game, consider for instance the sentence:

If John had broken his leg in the mountains in 2017, then if we went hiking, it would hurt if he had a heavy rucksack.

The first conditional is shallow (we do not mean continuing his hiking with the broken leg), but the second is deep: hiking with a heavy rucksack would cause trouble (obviously not hiking on Monday and having a heavy rucksack on Tuesday). So, the structure is:

$$ B \supset [H \Rightarrow \left( {R {\to} L} \right)] $$

B—John broke his leg

H—John went hiking

R—John had a heavy rucksack

L—The leg hurts.

This situation cannot, to our knowledge, be handled in the models known from the literature.

8 Formal models for conditionals revisited

In this chapter we shortly summarize our findings concerning the status of the Import-Export Principle and PCCP (9.1), discuss some methodological issues (9.2) and compare our model with the Stalnaker Bernoulli model (9.3).

8.1 IE and PCCP

How does the model solve important questions concerning conditionals?

8.1.1 The Import-Export Principle

This has already been discussed in Sect. 5. It is known that the Import-Export Principle works for the deep interpretation, i.e.

$$ {\text{P}}^{*}_{{{\text{deep}}}} (A {\to} (B {\to} C)) = {\text{P}}^{*}_{{{\text{deep}}}} (B {\to} (A {\to} C)) = \text{P}^{*}((A{\wedge} B) {\to} C) = \text{P(C|AB)} $$

For the “multiple-deep” interpretation of the nested conditional, the Import-Export Principle also works (see Sect. 6):

$${\text{P}}^{*}_{\text{deep}}(A_1 {\to} (A_2 {\to} ( \ldots {\to}(A_n {\to} B) \ldots ))) = \text{P}^{*}((A_{1} {\wedge} A_{2}{\wedge} \ldots {\wedge} A_{n} ) {\to} B) = \text{P(B|(A}_{1} \text{A}_{2} \ldots \text{A}_{\text{n}} )).$$

For the shallow interpretation, the Import-Export Principle is not true, which also is intuitive: fulfilling the first condition changes the rules of the game, so depending on what the first condition is, the probabilities can differ greatly. So, generally:

$$ {\text{P}}^{*}_{{{\text{shallow}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) \, \ne {\text{ P}}^{*}_{{{\text{shallow}}}} \left( {B {\to} \, \left( {A {\to} C} \right)} \right) $$

The graph model corresponds to McGee’s model in the sense that it allows to account for the deep interpretation. It also allows to account for the shallow interpretation, sharing this feature with the Stalnaker Bernoulli model. However, its advantage is that it allows to account for both these interpretations at once, in particular allowing to describe mixed conditionals (Sect. 8.2).

8.1.2 PCCP

For the deep interpretation, the formula

$$ {\text{P}}^{*}_{{{\text{deep}}}} \left( {A {\to} \, \left( {B {\to} C} \right)} \right) = {\text{ P}}\left( {{\text{C}}|{\text{AB}}} \right) $$

is true, so ${{\text{P}}}^{*}{{\text{CCP}}}$ holds in this version. For the shallow interpretation, we have the following formula:

$$ {\text{P}}^{*}_{{{\text{shallow}}}} (A {\to} \, \left( {B {\to} C} \right)) = {\text{ P}}({\text{BC}}|{\text{A}}) + {\text{P}}({\text{B}}^{{\text{c}}} |{\text{A}}){\text{P}}({\text{C}}|{\text{B}}) $$

The components on the right side are all conditional probabilities from the initial, simple probability space. The equation retains the spirit of the simple version of ${{\text{P}}}^{*}{{\text{CCP}}}$: it makes it possible to compute the probability of the nested conditional as a function (a combination) of conditional probabilities from the initial space.⁶⁵

The results concerning PCCP obtained within this article correspond to the results obtained within the other known models. Its superiority consists in the fact, that it can be generalized to longer and mixed conditionals.

8.2 Methodological aspects

Our aim is to give a philosophically justified account of conditionals and we hope that graph model meets these criteria. But in the present study we focus on the methodological advantages. In Sect. 2.2 we mentioned generalizability and simplicity in this context. These notions are not entirely clear, and important issues to address in this context arise: (i) Should the account for right-nested conditionals be an extension of the rule for simple conditionals? (ii) What are the prospects of the final theory (of probabilities of conditionals) being coherent? (iii) How is simplicity to be understood?⁶⁶

In order to make an assessment, we will indicate some features of our model and compare it with the Stalnaker Bernoulli model (which was a very important source of inspiration for us). However, regardless of the advantages of the Stalnaker Bernoulli models and the importance and depth of van Fraassen’s and Kaufmann’s results, we think that modeling the conditional in terms of finite scenarios and graphs rather than sets of infinite paths is more intuitive.

8.2.1 Generalizability and flexibility

For simple conditionals A→B, the strategy is to build a (simple) graph representing the flow of the game. When both A and B occur, the game is won; for A and $\neg$B, it is lost. For $\neg$A, the bets are not settled, and the game is restarted. So, loosely speaking, the general rule is:

(RESTART) If the antecedent is not true—then restart!

Dealing with conditionals of the form A→(B→C) amounts to building a (more complex) graph as well. Just as in the simple case, if the antecedent A is false, the game is restarted. If both A and B→C occur (i.e. the conditional B→C happens to be true), the game A→(B→C) is won. If A and $\neg$(B→C) occur (i.e. the conditional B→C happens to be false), the game A→(B→C) is lost. The difference with respect to the simple case A→B is that now it might happen that A is true, whereas B→C does not have a settled status (think of Tuesday in the MED example). In this situation the bet in the game A→(B→C) is not settled and we have to decide what to do now. The decision depends on the interpretation of the conditional. Under the deep interpretation, the whole game is restarted (we might say that the fact that A has taken place is forgotten and we start our observation anew). Under the shallow interpretation, A is considered to be decided once and forever, and we restart only the game B→C. So, the general mechanism of creating the graph for A→(B→C) is similar to the simple case A→B: we also have to make a decision as to how the game is to be continued, and depending on our interpretation we fix the appropriate rules (and the graph). The RESTART rule for building graphs for A→(B→C) is therefore a natural extension of the rule for (A→B). In this sense, the theory for right-nested conditionals might be considered to be an extension of the model for simple conditionals.⁶⁷

Observe also that the graphs for the nested conditional A→(B→C) contain a subgraph for the simple conditional (B→C) so that we can “track” the simple (sub)conditional within the graph for the compound conditional. So, the model for more complex cases is a straightforward extension of the model for simpler cases.

This does not yet prove the claim that the final theory (still under construction) will be coherent. The final theory might use quite different methods to handle different cases. Such situations happen in mathematics, even if mathematicians usually struggle for an elegant, uniform theory. However, we think that the fact that it is possible

• i. to model both the deep and shallow interpretations of right-nested conditionals,

• ii. to model longer conditionals which allow mixed (deep/shallow) interpretations,

• iii. to incorporate into the model both the global and local readings of the simple conditional (see Wójtowicz and Wójtowicz 2019)

provides a good motivation to work on the general theory and gives hope that it can be constructed.

8.2.2 Formal simplicity

We can graphically represent right-nested conditionals and—thanks to the properties of Markov graphs—computing the probabilities is straightforward and simple (as only solving a system of linear equations is needed). If we also think of the problem in practical terms—for instance, if we are interested in analyzing decision-making processes (based on evaluating the probabilities of conditionals)—it is important to have a method which is also of practical in addition to theoretical interest.⁶⁸ The Stalnaker Bernoulli model is more general in the sense of the possibility of formally representing diverse conditionals in one space, but with more complicated methods this comes with the price of computing the corresponding probabilities.

However, the problem of whether the Markov graph account is conceptually simpler than the Stalnaker Bernoulli account is subtle. The notion of conceptual simplicity has a pragmatic flavor and obviously depends on the criteria. Our probability space is countable, so the probability distribution on elementary events extends to arbitrary events by a simple rule. By contrast, the Stalnaker Bernoulli space has cardinality of the continuum, so the σ-field has to be constructed with care as it cannot be taken to be the power set of Ω. The graph model is ontologically simpler in the sense that finite structures are involved and the universe of constructed objects, i.e. graphs, is countable, i.e. it is smaller than the universe of the Stalnaker Bernoulli space. However, this is not a decisive criterion as in mathematics this kind of conceptual simplicity can be misleading.⁶⁹

However, regardless of the possibility of giving a general criterion of simplicity, we think that our model has the following advantages:

• i. it provides a simple method of giving a formal explication of interpreting the conditional, and the possibility of giving a graphical representation is also very useful;⁷⁰

• ii. computing the probabilities is much simpler (solving systems of linear equations).

Colloquially speaking, we show both graphs to an agent who is in doubt about the interpretation of the conditional A→(B→C) and ask, “which game corresponds to what you have in mind?” When the decision has been met, we show the simple method of computing the probability of the conditional in question. We think that choosing between two graphs is intuitive and easy to understand for the agent. By contrast, using the Stalnaker Bernoulli model will enforce the identification of the appropriate (infinite) class of infinite sequences. Moreover, the Stalnaker Bernoulli model enforces the shallow interpretation, therefore the agent who has the deep interpretation in mind will have first to “translate” the conditional in question (eliminating the deeply interpreted conditional) and then identify the appropriate class of sequences for the translated conditional.

8.3 Comparison with Stalnaker Bernoulli spaces

Is our model or the Stalnaker Bernoulli model more general? Consider any set of non-conditional sentences {A₁,…,A_n}. Every finite sequence can be imbedded into the Stalnaker Bernoulli universe in a natural way, for instance by “gluing” it with the set of all infinite sequences formed from the sentences {A₁,…,A_n}, i.e. the cylindrical set $\mathop \prod \nolimits_{{k{\mathbb{N}}}} X_{k}$, where $X_{k}$ = {A₁,…,A_n}. The Stalnaker Bernoulli space might therefore be considered to contain all possible sequences, i.e. all possible scenarios of all possible games. Seen from this angle, the Stalnaker Bernoulli model looks more general: every set of scenarios generated by a graph is represented in the Stalnaker Bernoulli space. In the Stalnaker Bernoulli space, all right-nested conditionals can be modeled within one space, but the construction of the space imposes the shallow interpretation. The deep interpretation requires a different model, and mixed conditionals are out of reach.

Importantly, in our model there is no one single space representing all conditionals. It is exactly the other way around: all conditionals are represented by respective graphs (and corresponding probability spaces). So, in some sense the Stalnaker Bernoulli model is more universal in terms of modeling all conditionals within one space. On the other hand, the graph model is more flexible with respect to identifying and explaining interpretations. It also offers more “user-friendly” computational recipes.

9 Summary

We have given a model in which it is possible to assign a probability ${\text{P}}^{*}$ to every right-nested conditional of the form (A₁→(A₂→(…→(A_n→B)…)), depending on the interpretation of the conditional (i.e. whether the connectives are given the deep or the shallow meaning). A₁,…, A_n, B are (non-conditional) sentences which are interpreted as events in the initial probability space S = (Ω, Σ, P). This general result obviously covers the simplest but philosophically very important case of the conditional A→(B→C).

This aim has been achieved by defining appropriate graphs: for the conditional α = A→(B→C) in question, we have formally defined two graphs G_α-deep and G_α-shallow (Figs. 4 and 6) that correspond to the deep and the shallow interpretations. These graphs represent the “logico-causal” structure of the respective interpretation.

The graphs G_α-deep and G_α-shallow are associated with two different probability spaces ${\text{S}}_{{\rm{deep}}}^{*}$, ${\text{S}}_{{{\rm shallow}}}^{*}$. In both these spaces, the conditional A→(B→C) has its interpretation as an event. Of course, these events are different because they correspond to different (deep versus shallow) readings of the conditional (and moreover they live in different probability spaces). The probabilities ${\text{P}}_{{\rm{deep}}}^{*}$ and ${\text{P}}_{{{\rm shallow}}}^{*}$ of the conditional A→(B→C) computed in the respective spaces ${\text{S}}_{{\rm{deep}}}^{*}$, ${\text{S}}_{{{\rm shallow}}}^{*}$ (Sects. 6.1, 6.2) coincide with Kaufmann’s results for shallow and with McGee’s results for the deep interpretation.

A very important feature of the model is that the probability of α can be computed in a straightforward way by directly solving the appropriate system of linear equations for the graph G_α, which is usually much simpler than direct computations within the appropriate probability space. The simplification is substantial if we consider more complex conditionals.

So, taking into account the analyses above, we claim that—at least when right-nested conditionals are considered—the presented model is more versatile and universal then the models known from the literature.