Introduction

Climate change is modifying forest ecosystems’ distribution and productivity as well as their mitigation potential (McDowell et al. 2020). Yet there is a great uncertainty in the quantification of climatic risks for most forest ecosystems (Purves and Pacala 2008; Anderegg et al. 2022), and our understanding of how different adaptation options influence resilience is still very limited for most forest-types (Lindner et al. 2014; Lynch et al. 2021). Temperate dry forests are highly exposed to an increase in temperatures and aridity, with longer and more intense droughts that can jeopardize key ecosystem services (Carnicer et al. 2011; Clark et al. 2016; Senf et al. 2020; Socha et al. 2023). In particular, the Mediterranean basin is a hotspot of climate change and a region with important vulnerabilities in ecosystem services provision (Schröter et al. 2005). Regional air temperatures in this region have risen during the last decades over the worldwide average (Cramer et al. 2020), and droughts have increased in the frequency, intensity, and duration since 1920 (Vicente-Serrano et al. 2014). The impact of these climatic changes is already being noticeable in the marginal rear edge of tree species distributions that are increasingly experiencing tree growth reductions and die back processes (e.g., Gazol and Camarero 2022). Euro-Mediterranean countries have also experienced during the last century intense land use changes associated with rural depopulation (Newsham and Rowe 2023). These changes have resulted in forest expansion on abandoned agricultural land but also in forest densification in abandoned forests, such as plantations and coppices (Gómez-Aparicio et al. 2009; Domingo et al. 2020). The resulting ecosystems can provide important ecosystem services but can also exhibit emerging risks and disservices, exacerbating climate change impacts (Varela et al. 2020). High densities and intense competition can make these forests very vulnerable to wildfires and recurrent droughts, highlighting the relevance of forest structure and management as a key driver of future forest responses to climate (Vilà-Cabrera et al. 2023).

The dynamics of social-ecological systems (SES) such as Mediterranean forests conform to complex coupled dynamics among human and natural processes that have received increasing attention over the last decades (e.g. Blondel 2006; Liu et al. 2007). Of particular interest is the study of resilience that reflects the ability of a SES to absorb perturbations, preventing the system from being pushed towards an alternative state or basin of attraction (Holling 1973; Folke et al. 2004). The concept SES resilience is of high relevance for the Mediterranean region, particularly for SES at the Mediterranean-semiarid ecotone that are highly vulnerable to desertification (Martínez-Valderrama et al. 2022), i.e., a shift towards an alternative degraded state driven by changes in aridity or policies (Reyer et al. 2015).

The resilience of Mediterranean forests to drought is driven by biological factors that operate at different levels of biological organization, but also for human-driven processes that conditionate ecosystem stability following drought (i.e., via changes in stand structure and composition). The biological factors controlling drought responses—from the leave to the community—have received increasing attention over the last years: Leaf and plant-level strategies ranging from stomal and hydraulic control to plasticity allows plants to buffer water stress at different scales (e.g. Moreno-Gutiérrez et al. 2012; McDowell et al. 2022); tree level factors driving growth stability following drought have been largely investigated through tree-ring analyses following an engineering resilience perspective (sensu Nikinmaa et al. 2020) (e.g. Lloret et al. 2011; DeSoto et al. 2020; van Mantgem et al. 2020; Veuillen et al. 2023); and community-level stability following drought has been linked to differential species strategies in mixed forests (e.g. Sanchez-Martinez et al. 2023).

A growing number of studies in the Mediterranean and elsewhere also show that management—via changes on stand structure—can play an important role for forest stability following drought (e.g., Moreno-Gutiérrez et al. 2012; Giuggiola et al. 2013; Jones et al. 2019; Domingo et al. 2020; Lucas-Borja et al. 2021a). For example, tree ring studies show that a reduction in tree density improves tree growth of remnant trees, but also improves stand-level stability following drought (D’Amato et al. 2013; Magruder et al. 2013; Bottero et al. 2017). Similarly, experimental and modeling studies show that thinning improves growth responses to drought (i.e., Sohn et al. 2016a; Andrews et al. 2020). Nevertheless, the benefits of reduced thinning—particularly on resilience—are very variable among forest-types suggesting idiosyncratic dynamics (Sohn et al. 2016b; Castagneri et al. 2022). In the same direction, forest simulation studies suggest strong specific site effects driven by altitude, species composition, thinning intensity reductions and the temporal scales of analyses, making it difficult to establish general management guidelines (Elkin et al. 2015; Ameztegui et al. 2017).

Understanding the role of stand structure and management regime on forest resilience is of critical importance to develop effective mitigation and adaptation strategies in a scenario of increasing aridity. Stand and forest-level responses to drought imply non-linear feedback over time between tree growth, environmental variability, and competition. These feedback and their effects cannot be investigated alone through experimental studies or dendrochronological analysis that consider trees in isolation or under constant structural conditions (e.g., Sánchez-Salguero et al. 2017). For example, tree growth reductions driven by increasing aridity and competition can ameliorate stand-level competition intensity and thus feedback into an improvement of individual tree growth (Marqués et al. 2021). These responses can differ across size classes that exhibit differential growth responses and drought sensitivity (Lucas-Borja et al. 2021b). Furthermore, a given management regime alters the competitive scenario which can act as a stabilizing factor at the stand level or on the contrary amplify drought effects. Understanding how these processes interact and scale up to control forest resilience is non-intuitive and requires the use of models. Specifically, we need models that reach a reasonable balance between biological realism and complexity so we can understand model behavior and identify the mechanisms underlying resilience.

In this paper, we investigate the resilience of a maritime pine forest (Pinus. pinaster Ait.) in Central Spain in relation to increasing aridity and two policy-management regimes. A combination of sandy soils with low nutrient content and very low water retention capacity, as well as scarce annual average precipitation, makes the productivity of these dry-edge forests highly dependent on water availability and—on average—lower than other maritime pine forests in the species range (Madrigal-González et al. 2017a; Aguirre et al. 2022). The forest has been managed since the XIX century following a shelterwood regeneration method and a harvesting rotation period of 80–100 years. This method widely used in Spanish public forests is oriented towards the maintenance of multiple functions—e.g., wood, resin extraction, prevention of soil erosion, game, and aesthetic values (Rodríguez-García et al. 2014). Historical analyses suggest that this SES has been resilient to several last century intense climatic impacts, such as an intense drought period in 1940s but also to windstorms and peaks of firewood demand during cold periods (Madrigal-González et al. 2017a). Since the 1920´s however, average temperatures have been on the rise in the region, increasing the frequency, intensity, and duration of the drought periods (Vicente-Serrano et al. 2014; Moreno-Fernández et al. 2021b). This aridity increment is considered a major driver of observed tree growth reductions and die-off events in the region (e.g., Prieto-Recio et al. 2015), raising concerns on long term sustainability—i.e., capacity of the SES to continue providing key ecosystem functions—if aridity continues increasing.

To investigate the resilience of this forest to increasing aridity we developed an analytical size-structured model of forest dynamics parameterized and validated with historical individual tree—and stand-level data. Analytical models of forest dynamics consider the non-linearities and feedback associated with tree growth, competition and structured population dynamics and allows us to explore how productivity and other forest functions scale up from tree to the stand and the forest landscape (e.g., Kohyama 1991, 1993; Hara 1993; Strigul et al. 2008). The model explicitly describes forest structure as the result of tree growth in each cohort, and plastic phenotype adjustments in response to aridity and growing stocks (competition). We investigated forest drought resilience with respect to two forest functions; wood stock and yield, that underlie several key supporting and provisioning ecosystem services in this SES. The preservation of forest stock is linked to the maintenance of a permanent vegetation cover which enhances biodiversity, microclimate, and soil development (e.g., Madrigal-González et al. 2010). In contrast, yield maintenance is linked to timber and firewood provision, a key function for generating economic inputs and fostering a bioeconomy chain value in these depopulated rural areas (e.g., Hetemäki et al. 2017). Prioritization of either of these two functions reflect the two extremes of a continuum of attitudes from forest users and policy objectives; one focused on forest conservation values and environmental protection and another one more inclined to prioritize productivity and economic benefits over conservation. It also reflects different views on mitigation and carbon farming targets, depending on whether we want to target long term carbon residency, or alternatively prioritize carbon sequestration rate. To assess forest resilience to drought we compared forest responses to these two contrasting management regimes and a scenario of increasing aridity. Specifically, we assessed the following three different scenarios: (i) A “business as usual scenario (BAU)” in which we addressed how increasing aridity influenced forest structure and dynamics under current management, (ii) A “conservation scenario (CS)” in which the aim is to maintain a given forest stock under increasing aridity and (iii) a “productivity scenario (YS)” in which we explore the existence of management strategies that allow for a sustainable yield production under increasingly arid conditions.

Material and methods

Study area

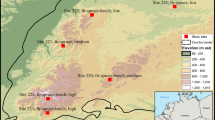
The studied ecosystem is part of a large-homogeneous pine-covered landscape across sandy flatlands in Central Spain (up to 30,000 ha of woodlands and pine forests, mostly Pinus pinaster Ait. and Pinus pinea L.) (Fig. 1). Soils are sandy and highly unconsolidated with low nutrient content and very low water retention capacity which make ecological conditions harsher particularly in terms of water availability (Gómez-Sanz and García-Viñas 2011). Climate is temperate with a warm-dry summer characteristic of the Mediterranean-type climate (Kottek et al. 2006). The long-term annual average precipitation is 430–470 mm with principal rainy events occurring in spring and autumn. The annual average temperature is 12 °C with an average minimum temperature below 0 °C in winter and average maximum temperatures above 30 °C in summer. Climate is represented by high inter-annual variability, where precipitation can vary by ≈300–600 mm from year to year. Pines contribute to the maintenance of a sparse understory through stem flow, shade, and pine debris (Madrigal-González et al. 2010) but in the absence of pines the ecosystem could move towards another state dominated by other species or even a degraded state due to the unstable sandy soils. Because of climatic seasonality and edaphic conditions, these “dry-edge” ecosystems occupy the low-end position along a productivity-aridity gradient for P. pinaster (commonly known as maritime pine) in Spain (i.e., Gandullo and Sánchez-Palomares 1994; Serrada et al. 2008; Aguirre et al. 2022).

Fig. 1
figure 1

a Location of the study area. b Regional context of dry-edge forests. c Forest Landscape (public forest nº 48) (Ortophoto source: PNOA WMS server)

Full size image

Biotic and abiotic data

We used historical sources of biotic information that are available in the historical archive of the public forest nº 48 named ‘Común Grande de las Pegueras’ (≈ 7500 ha; altitude: 841 m.a.s.l.; geographical location: 41° 19′N–4° 12′ W; central Iberian Peninsula, Segovia province, Spain). The dominant tree species is P. pinaster, which has remained a representative species during the Holocene in the area (Morales-Molino et al. 2012). Nonetheless, other pines (P. sylvestris L., P. nigra Arnold) and oaks (Quercus ilex L., Q. faginea Lam. and Q. pyrenaica Willd.) are marginally present in the forest, particularly in sites with higher soil moisture nearby seasonal streams or located in depressions. The forest landscape is managed through the permanent block system in a rotation period of 80–100 years with thinning from below oriented towards promoting multiple functions (e.g., resin, fungi, firewood, prevention of soil erosion, or aesthetic functions) (Rodríguez-García et al. 2014). The regeneration is achieved using the shelterwood systems over the last 20–30 years of the rotation period (Moreno-Fernández et al. 2021b).

We used data from historical archives to parameterize and validate the model. These archives include both stand—and tree-level data and were available in five out of the nine updates of the forest management planning: 1922–1932, 1942–1952, 1952–1962, 1962–1972 and 1992–2002. The forest landscape was spatially divided according to historical management prescriptions in different nested units that ensure a sustainable yield in space and time. The forest was subdivided in three large units (“secciones”) and ten management units (“cuarteles”) that are replicates subjected to similar spatio-temporal management prescriptions and have an extension of approximately 160 ha each one. Each cuartel includes four “tramos” units that represent different stages in the harvesting and regeneration process, and each “tramo” includes four “tranzones” and that can be assimilated to a forest stand. Each plan was recorded every 10 years starting in 1912. We used the tree-level data to parameterize tree growth functions and the forest-level observations (i.e. “cuartel” units) for model validation. Specifically we used historical forest-level observations describing changes in forest structure to fit the model to observed dynamics and to infer unknown parameters (i.e., mortality).

Stand-level data consisted on aggregated observations describing stand structure. This included the number of trees per ha and diameter class and basal area. Basal area, however, was not included in the first management plan update. The sampling method chosen for the eight first updates was “enumeration cruising”, this is, they measured all the trees with d.b.h. above a given threshold. In the case of the last available update (2002), foresters used this method only in some management units but for other units they followed a systematic sampling. This method consists on laying out a 200 × 200 m grid and a 16 m radius plot in the intersection points of the grid (modes). The total number of trees measured could exceed 500,000 trees. For example 620,471 trees (1932), 638,867 (1942) 614,021 (1945), 605,831(1962), 719,598 (1972), 737,852 (1982), 768,704 (1992) and 777,044 trees (2002).

Tree level data were part of information historically gathered to assess wood volume stocks and forest wood volume increments along different periods and were obtained according to a traditional method used in massive stock inventories at the time (see for details Madrigal-González and Zavala 2014). Tree-level data consisted of measurements of representative tree individuals (“prototype trees”). Measurements included tree age, tree diameter, tree height, volume, bark width or tree form parameter. The number of stands sampled differed depending on the total number of trees planned to be cut down to this purpose each decadal period: eight in the decade 1922–1932; eleven stands in 1942–1952; eleven stands in 1952–1962; nine stands in 1962–1972 and twenty-two stands in 1992–2002. These stands were 40–50 hectares in size on average, and they were often selected to be representative of the different sections of the forest. Mean stocks (mean wood volume) were 44.5 m3/ha (± 22.4 std dev.). Prototype tree individuals belonging to four different diameter classes were cut down and measured in these stands at five different periods: 1922–1932, 1942–1952, 1952–1962, 1962–1972 and 1992–2002. The exact number of trees sampled was not provided for all the updates. For example, in the fifth update of the management prescriptions they fell 80 trees and in the sixth update they fell 333 trees. The number of trees used in our study was: 30 trees in the period 1922–1932, 40 trees in the period 1942–1952, 40 trees in the period 1952–1962, 28 trees in the period 1962–1972, and 405 trees in the period 1992–2002. Each tree stem was then cut into smaller pieces for a more accurate assessment of stem volume by applying the cylinder equation to each different piece. Pieces were a maximum of two meters long and the last piece is therefore any size between zero and two meters.

Foresters used tree-level data to estimate forest wood stocks. For this purpose, they derived tapper coefficients that relate the stem as a sole cylinder with the stem volume computed as the sum of volumes of each piece of stem. Foresters measured both diameter at breast height (d.b.h.) and longitude of the main trunk. Diameter was measured with calipers and trunk longitude was measured with a stick which was equal to the distance between the eye and the extreme of the arm extended frontwards. This stick was held with the hand keeping the arm extended frontwards. During the procedure, the technician moved from the base of the tree out as to cover with the stick the whole tree. The distance from this point to the base of the tree equals the height of the tree. With these coefficients per class diameter, an assessment of the total wood volume stock was calculated. Every individual tree of the forest (> 500,000 trees in the whole forest) was counted and measured and wood volume was assessed by applying the above coefficients to correct for bias due to stem diameter reduction towards the top of the tree. We used the wood volume per hectare as a surrogate of competition in every forest section. This measurement integrates both tree density and tree size and thus comprises both symmetric and asymmetric competition (Madrigal-González and Zavala 2014; Marqués et al. 2018). Observed changes in wood volume stocks by size class over time (Fig. S4, see Madrigal-González et al. 2017a, b for details) allows us to test the predictions of dynamical size-structured models of forest dynamics over time.

We used different environmental variables to examine potential correlations with tree growth commonly used as surrogate of energy and water available for tree growth. The climatic variables included initially in the growth model were: Mean annual temperature, mean annual precipitation, frequency of dry years (\(I_{A}\)), the most intense drought of the decade, and mean drought balance. Soils in this forest are relatively homogeneous due to the sandy texture throughout the whole forest. i.e., a sandy fraction of more than 90% throughout the forest (Gómez Sanz and Garcia-Viñas 2011). An exception are forest fringes along riparian areas (“Cega” river) and are dominated by other species not included in the analyses. For this reason, we did not incorporate spatial soil variability in the drought variable.

We used \(I_{A}\) to parameterize the tree growth model because it had the best explanative on tree growth in relation to other climatic variables explored in the analyses. This tree growth model was developed in a previous paper using the same data set and models (Madrigal-González and Zavala 2014). The frequency of dry years (\(I_{A}\)), is a function of the Standardized Precipitation-Evapotranspiration Index (SPEI), which is considered a reliable measurement of climatic aridity (Vicente-Serrano et al. 2010). We estimated \(I_{A}\) as follows: First, we assigned a SPEI value for each year and defined \(I_{A}\) as the frequency of dry years in a decade; this is, the number of years with SPEI values below the long-term mean, which is fixed in 0. We calculated SPEI values for different time lags ranging from 1 month to several years. In our case study, we used the 120-month SPEI for August (September of the previous year to August of the year in progress) (it results from 10 years multiplied by 12 months each year; growing periods extended in this data for 10 years). Hence, for each decadal period of tree growth, we used a decadal period of climatic conditions (SPEI). We used SPEI records with 0.5 degrees spatial resolution and with monthly precipitation and temperature data stored in version 3.20 of the CRU database for the period 1901–2011 (http://climexp.knmi.nl/).

The analytical model of forests dynamics

We developed an analytical model of forest dynamics to test the hypothesis that forest landscape dynamics emerge from tree population dynamics—influenced by size, climate, and management-, and competition. The observed patterns in the last century forest landscape dynamics are defined by aggregated changes in size distribution. The objective was therefore to obtain an analytical model—defined by the minimum set of parameters—that predicts the observed pattern. Then, we used the fitted model to assess likely forest responses under increasing arid conditions and different management options. The proposed forest model follows the classical size-structured population model (Metz and Diekmann 1986; Cushing 1998). Unlike individual-based forest models which describe individual trees as discrete interacting particles (i.e., Lagrangian approach), partial-differential equations systems describe individuals aggregated by continuous size distributions and time (i.e., Eulerian approach). Both individual-based models of forest dynamics and partial differential equations converge under some conditions (e.g. Strigul et al. 2008; Magal and Zhang 2017). Specifically, partial differential equations systems are considered the mathematical limit of individual based stochastic models of forest dynamics when the number of particles is very large (e.g., Oelschläger 1989). In previous work (Zavala et al. 2007), we proposed a general analytical framework to describe stand dynamics employing a size-structured tree population which considers competition acting on either growth or mortality rates. Here, we use a simpler version that captures the basic features of the studied forest system. The size variable \(x\) represents the d.b.h. (diameter at breast height) (Kohyama 1991, 1992). The unknown function \(u\left( {x,t} \right)\) represents the population density for d.b.h. of trees in the stand per ha, that is, \(\mathop \smallint \limits_{{x_{1} }}^{{x_{2} }} u\left( {x,t} \right)dx\) is the number of trees with d.b.h. in the interval \(\left[ {x_{1} ,x_{2} } \right]\) per ha. Table 1 summarizes the main variables used to adjust the model. Both independent variables size x and time t are continuous.

Table 1 Main variables and parameters involved in the size-structured model of stand dynamics
Full size table

The model assumes a maximum d.b.h., called \(x_{M}\), reachable by trees in the absence of harvesting. We estimated maximum tree size from observations, together with the rest of the parameters involved in tree individual growth. The minimum d.b.h. for a tree to be considered a recruit is denoted by \(x_{0}\). As in any size-structured model, the changes in size distribution depend on three rates: size growth, mortality, and recruitment. In this model cohort tree growth rate, \(g\), depends on cohort size \(x\), aridity (index \(I_{A}\)) and on the density-dependent competition.

We describe growth size-dependency through a family of growth rates, proposed in Zavala et al. (2007), that, in the absence of competition effects, gives a unimodal equilibrium tree distribution for certain parameters values:

$$g_{1} \left( x \right) = ax\left( {1 - \left( {\frac{x}{{x_{M} }}} \right)^{s} } \right)exp\left( { - bx} \right),$$
(1)

where parameters \(a\) and \(s\) are positive and \(b\) is positive or zero. The case \(b = 0\) corresponds to Richards’s growth law (Richards 1959).

We used the frequency of dry years, \(I_{A}\) to parameterize the tree growth model because it had the best explanative on tree growth in relation to other climatic variables explored in the analyses. We developed this tree growth model in a previous paper using the same data set and models (Fig. S3, Madrigal-González and Zavala 2014). Hence, we will use the resulting tree growth model as a function of \(I_{A}\) to parameterize the analytical forest dynamic model (see below). To compare models, we applied the Corrected Akaike Information Criterion (AICc) (more conservative than AIC for model selection in small datasets). For parameter estimation, including error confidence intervals we used a simulated annealing to maximize the likelihood function during parameter estimation (see Table 1). The dependence of the growth rate on the aridity index \(I_{A}\) is introduced by expressing parameter \(a\) in terms of \(I_{A}\) as a linearly decreasing function; \(a = a_{1} - a_{2} \cdot I_{A}\), with \(a_{1}\),\(a_{2} > 0\).

We described resource competition through the variable wood volume (stand stock), defined as:

$$V\left( t \right) = \mathop \smallint \limits_{{x_{0} }}^{{x_{M} }} \;\;\;v\left( x \right)u\left( {x,t} \right)dx ,$$
(2)

where \(v\left( x \right)\) represents the average wood volume of a tree of size \(x\).

We obtained the final form of the growth rate \(g\) as the product of \(g_{1}\) and a negative exponential of wood volume to describe the competition:

$$g\left( {x,V} \right) = ax\left( {1 - \left( {\frac{x}{{x_{M} }}} \right)^{s} } \right)exp\left( { - bx - cV} \right) = g_{1} \left( x \right)exp\left( { - cV} \right) ,$$
(3)

where \(c\) is a positive parameter.

The mortality rate was:

$$m\left( x \right) = m_{0} \;\;{\text{if}}\;\; x\,\epsilon \left[ {x_{0} ,x_{C} } \right],\;{\text{and}}\;m\left( x \right) = m_{C} \;\;{\text{if}}\;\;x\,\epsilon \left[ {x_{C} ,x_{M} } \right]$$
(4)

where \(x_{C}\) is the d.b.h. from which trees are harvested, \(m_{0}\) integrates both natural mortality—i.e. self-thinning of trees smaller than \(x_{C}\)—and trees harvested before reaching the harvest tree size \(x_{C}\) (i.e. thinning for below). Finally, \(m_{C}\) is the harvesting rate which is the mortality rate for trees greater than tree harvest size (\(x_{C}\)) and it is taken to be 1 over the meantime to be harvested once the tree reaches the harvesting size (\(x_{C} )\). We parameterize the model using data from multiple stands differing in their structure due to time since the last management intervention. This allows us to treat as continuous the managing process of periodical cuts, which is intrinsically discrete but uniformly distributed in time across the ensemble of stands. To estimate recruitment we follow a sustainability criterion implying that at least one seedling becomes a juvenile that eventually substitutes a removed tree. Certainly, increasing aridity would eventually slow down or completely collapse regeneration driving the current forest system to a shrub or grass dominated ecosystem, but our aim is to study how forest structure drives the stability of productivity rather than identifying ecosystem tipping points and regeneration bottlenecks. On the other hand, historical records and current field studies reveal a strong regeneration resilience (se Andivia et al. 2018), so we consider our assumption reasonable.

Following this assumption, the recruitment rate that the total population is described as

$$P\left( t \right) = \mathop \smallint \limits_{{x_{0} }}^{{x_{M} }} \;\;\;u\left( {x,t} \right)dx: = P$$
(5)

Hence, we have the following recruitment rate:

$$g\left( {x_{0} ,V\left( t \right)} \right)u\left( {x_{0} ,t} \right) = r\left( t \right): = \mathop \smallint \limits_{{x_{0} }}^{{x_{M} }} \;\;\;m\left( x \right)u\left( {x,t} \right)dx .$$
(6)

The proposed model for an initial tree distribution \(u_{0} \left( x \right)\) reads as follows:

$$u_{t} \left( {x,t} \right) + \left( {g\left( {x,V\left( t \right)} \right)u\left( {x,t} \right)} \right)_{x} = - m\left( x \right)u\left( {x,t} \right)$$
(7)
$$g\left( {x_{0} ,V\left( t \right)} \right)u\left( {x_{0} ,t} \right) = \mathop \smallint \limits_{{x_{0} }}^{{x_{M} }} \;\;m\left( x \right)u\left( {x,t} \right)dx$$
(8)
$$u\left( {x,0} \right) = u_{0} \left( x \right)$$
(9)

We provide a full list of model parameters and values in Table 1. The volume associated with the trees that are cut per unit of time (10 years) per ha is the wood volume extraction rate and it is considered a surrogate of the forest yield, denoted by \(w\left( t \right)\):

$$w\left( t \right) = \mathop \smallint \limits_{{x_{C} }}^{{x_{M} }} \;\;m_{C} v\left( x \right)u\left( {x,t} \right)dx.$$
(10)

System (7)–(9 possesses a unique solution under simple hypotheses on functions \(g\left( {x,V} \right)\), \(m\left( x \right)\) and \(u_{0} \left( x \right)\) (Calsina and Saldaña 1995; Kato 2004). This solution, the temporal evolution of the tree distribution, has not an explicit expression but it is approximated as sharply as needed by the appropriate numerical scheme. The long-term behavior of the system can be described analytically by a steady-state \(\underline {u} \left( x \right)\) (see Supporting information).

The resulting partial differential equation system defined by Eqs. (7)–(9) describes the mean field size distribution of the forest landscape rather than representing a stand distribution. Forest landscape dynamics usually imply spatial processes associated with environmental heterogeneity, neighborhood competition and dispersal (e.g., Ameztegui et al. 2017). Mean field models, as opposed to spatially explicit models, consider “average” competitive interactions, uniform dispersal as well as spatially homogenous resources over the landscape (Pacala and Deutschman 1995). Yet mean field representations tend to converge with spatially explicit stochastic individual based models in open forests or forests with low patch variability (see Strigul et al. 2008). Because of aridity and shelterwood thinning, dry-edge pine forests have a rather low and homogeneous tree density across suggesting mean field approximations represent a valid first order approximation.

Model validation

The partial differential equations system describing forest dynamics has overall nine parameters, six parameters to describe the growth function and three parameters to describe mortality. The six unknown growth model parameters are \(a_{1}\) and \(a_{2}\) that describe growth dependency of aridity (\(I_{A}\)), \(b\) and c that describe the competition effects, \(s\), a shape parameter and \(x_{M}\) that defines maximum tree size. We adjusted these six growth parameters by fitting growth functions to historical observations from fallen trees (see previous section, Table 2). We describe mortality by three parameters: harvest tree size (\(x_{C}\)), harvesting rate (\(m_{C}\)), and mortality before tree harvesting (\(m_{0}\)). Parameters \(x_{C}\) and \(m_{C}\) are known and are defined according to different management scenarios. Hence, the only unknown parameter of the forest model is \(m_{0}\) which describes tree mortality rates before harvesting and that integrates both natural mortality (e.g. self-thinning) and felling of trees below the harvest size (e.g. thinning for below or preparatory thinning). Given the impossibility to estimate last century \(m_{0}\) from observations, we can proceed in different ways. One possibility is to leave it as a non-estimated free parameter and then perform sensitivity analyses. However, given that we have data of last century forest dynamics—i.e. the observed pattern that we want to predict with the model—we can conduct an inverse parameterization that allows us both to estimate \(m_{0}\) and to validate the forest model (i.e. to assess if the model predicts last century dynamics pattern). Indirect parameter estimation allows us to estimate parameters that are difficult to estimate in the field but when we have extensive observations of the predicted pattern, allowing us to estimate the value of the unknown parameter that best fit the match between observed and predicted forest dynamics (see previous examples in Purves et al. 2007; Lines et al. 2019). For the model validation and parameter estimation we also hypothetically considered that the climatic variable aridity (\(I_{A}\)) was unknown and we estimated both the “parameters “\(m_{0}\)” and “\(I_{A}\)” values that resulted in the best fit among predicted and observed forest dynamics. This double parameterization –with both an unknown and a known parameter—is conducted as a model validation process to test if the values of predicted “\(I_{A}\)” agree with observed “\(I_{A}\)” values. A good agreement among observed and predicted “\(I_{A}\)” suggests the resulting forest dynamic model has internal consistency and it is a biologically meaningful solution (not just a mathematical optimum solution).

Table 2 Model parameter estimates and 95% Confidence Intervals (95% CI_low and 95% CI_high, respectively) used in the simulations
Full size table

Parameter estimation \((m_{0}\) and \(I_{A}\)) and model validation procedure was as follows: First we deployed historical archives that include a direct accounting of forest structure for the different forest stands and management units considered in this study during the 1932–2002 period. We performed, for each decade in this period, a stand structure projection for a range of \(m_{0}\), and \(I_{A}\) values, and we chose those values yielding the best match between observed and predicted stand structure at the end of the decade. In the optimization numerical method, we used all the landscape stands (i.e., observations from three “cuarteles”) and we fitted observed changes in the diametric distributions for all the stands (i.e. landscape dynamics). We took as initial conditions the data at the beginning of each decade and then compared the solution of the PDE problem with the real data at the end of the decade. As the result depends on every choice of parameters \(m_{0}\) and \(I_{A}\), we performed an optimization procedure to obtain the best possible approximation to historical observations. Finally, we test whether obtained values (\(I_{A}\)) of the aridity for each decade fit the historical records. To perform the projection of stand structure from one specific time to another one—i.e., to find the corresponding solution of the partial differential equation problem for finite time intervals-, we followed the numerical methods introduced in Angulo and López-Marcos (2004), Angulo et al. (2013) and Abia et al. (2014). These numerical schemes have shown good behavior in the integration on both finite time integration cases and long-term integration in the quest for equilibrium states (see convergence properties in Angulo and López-Marcos 2004). Problem optimization was developed with the use of a particle swarm optimization algorithm (see Supporting information for details). As an indicator of goodness of fit we included the relative squared error for each decade in the second column (MS error, Table S1) that shows the agreement between observed and calculated densities. The mean of these values () (i.e. equivalent to mean square error) is 1.64e−2 which in percent indicates that the model is 98.36% reliable.

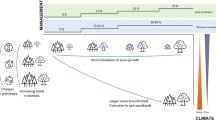
Definition of policy-management scenarios

We developed three scenarios to investigate the forest capacity to maintain a given function (e.g. production or productivity), in response to a stressor (e.g., increasing aridity). Long-term forest structure was represented by the model steady-state solution for integers values of \(I_{A}\) (see Supporting information).

  1. (a)

    The “Business as usual” (BAU) allowed us to assess likely effects of increasing aridity under the current management regime (i.e., \(x_{C} = 40\) cm and \(m_{C} = 1\) (10 years)−1). We use growth rate values reported in Table 2. The value of \(m_{0}\) (\(m_{0}\) = 0) assumes that most mortality takes place at the sapling and seedlings stages before juveniles reach the recruitment stage defined by \(x_{0}\) (e.g., Andivia et al. 2018). As we are using the stationary stand distribution, we do not specify the initial conditions in the form of stand size-structure, but rather in terms of mean forest tree density obtained from historical forest census (P = 83.16 trees per ha).

  2. (b)

    In the “Conservation oriented scenario” (CS), we examined which management is needed to preserve forest stock as the climate becomes increasingly arid. We fixed a wood volume (\(V\) = 50 m3 ha−1; i.e. current mean stand volume in the forest), and then we searched for management strategies (i.e., \(m_{C}\) and \(x_{C}\) values), that kept this stock constant.

  3. (c)

    In the “Yield oriented scenario” (YS) we fixed the yield (wood volume extraction rate; \(w = 10\) m3 (10 years)−1 ha−1) and we explored which management strategies as defined by \(m_{C}\) and \(x_{C}\), were required to keep the yield constant under rising aridity.

Finally, we also investigated whether, for a given aridity condition, there was a management strategy (\(m_{C}\) and \(x_{C}\)) that kept both forest stock and maximized yield. For this purpose, we calculated numerically, for each integer value of the aridity index from \(I_{A}\) = 1 to \(I_{A}\) = 9, the wood volume extraction rate for the different combinations of parameters \(m_{C}\) and \(x_{C}\) that keep \(V\) = 50 m3 ha−1. The result was that there were no significant differences between them. Given an aridity index, the different conservation strategies for the same stock led to approximately the same wood volume extraction rate.

Similarly, we tried to optimize the stock based on forest management strategies that keep the wood volume extraction rate constant but it gave similar results –i.e. for a fixed aridity index, the strategies that preserve the wood volume extraction rate were associated with roughly the same forest stock.

Model simulation results

Under the “Business as usual” (BAU) scenario both forest stock-standing wood volume, v (t), and yield—wood volume extraction rate, w(t), decreased linearly with increasing aridity, although yield reduction was more pronounced (Fig. 2). Maintaining current management in conjunction with a rise in aridity resulted in a progressive reduction in both the number of large trees (d.b.h. \(x\) > 40 cm) and in landscape structural diversity (i.e., a more even-sized forest distribution) (Fig. 3).

Fig. 2
figure 2

Model simulations of a wood volume (stock) (m3 ha−1) and b and wood volume extraction rate (yield) (m3 (10 years)−1 ha−1) under the Business as usual management (BAU) (\(x_{C} = 40\) cm and \(m_{C} = 1\) (10 years)−1) and an increasing aridity (index \(I_{A}\))

Full size image
Fig. 3
figure 3

Stationary stand structure with a Business as usual management (BAU) (harvesting/mortality rate (mc) = 1 cm and harvest diameter (xc) = 40 (10 years)−1), for alternative values of the aridity index. Labels vertical axis label: U (forest tree population density per ha) horizontal axis label: d.b.h. (diameter at breast height)

Full size image

In the “Conservation oriented scenario” (CS), we observed that it was possible to maintain a given level of forest stock under increasing aridity providing adequate adjustments in the management regime. As aridity increases, forest yield decreases linearly (Fig. 3a), yet there were combinations of parameters \(m_{C}\) and \(x_{C}\) values that resulted in stock maintenance. The combination of those values described a quasi-logarithmic relationship (Fig. 4). As aridity increased, this curve shifted toward the upper-left direction (Fig. 4). This is, for a given harvesting rate level, it was necessary to increase harvest tree size to maintain the stock. Similarly, maintaining both stock and harvest tree size required lowering the harvesting rate.

Fig. 4
figure 4

Relationship between increasing aridity (index \(I_{A}\)) and a wood volume extraction rate (m3·(10 years)−1 ha−1) under the Conservation Scenario (CS) (wood volume fixed in 50 m3 ha−1); and b wood volume (m3 ha−1) under the Yield Scenario (wood volume extraction rate in 10 m3·(10 years)−1 ha−1)

Full size image

In the “Yield oriented scenario” (YS), we observed that as aridity rose, forest wood stock decreased linearly (Fig. 6) but there were combinations of parameters \(m_{C}\) and \(x_{C}\) values for which yield (biomass extraction rate) stayed constant. The combination of these values followed a quasi-logarithmic relationship (Fig. 6). As aridity increased, this curve shifted towards the lower-right direction (Fig. 5, left column). This is, for a given harvesting rate, it was necessary to decrease harvest tree size. Similarly, maintaining both yield and harvest tree size required an increasing harvesting rate.

Fig. 5
figure 5

Different management regimes that preserve forest stock (50 m3 ha−1) for different values of increasing aridity (shown for values \(I_{A}\) = 1, \(I_{A}\) = 5 and \(I_{A}\) = 9) under the Conservation Scenario (CS). The plots on the left row show the possible combinations of harvesting/mortality rate and harvest diameter (\(m_{C}\) and \(x_{C}\). respectively) that keep constant the stock target. The other two rows exhibit the stand structure in two extreme combinations of \(m_{C}\) and \(x_{C}\). a, d, g Labels vertical axis label: Xc (harvest tree size) horizontal axis label mc (harvest/mortality rate), b, c, e, f, h, i vertical axis label: U (forest tree population density per ha) horizontal axis label: d.b.h. (diameter at breast height)

Full size image
Fig. 6
figure 6

Different management regimes that preserve the wood volume extraction rate (10 m3·(10 years)−1 ha−1) for different values of increasing aridity (shown for values \(I_{A}\) = 5, \(I_{A}\) = 6 and \(I_{A}\) = 7) under the Yield Scenario (YS). The plots on the left row shows the possible combinations of harvesting/mortality rate and harvest diameter (\(m_{C}\) and \(x_{C}\). respectively) that keep constant the wood volume extraction rate. The other two rows exhibit the stand structure in two extreme combinations of \(m_{C}\) and \(x_{C}\). Labels a, d, g vertical axis label: Xc (harvest tree size) horizontal axis label mc (harvest/mortality rate) b, c, e, f, h, i vertical axis label: U (forest tree population density per ha) horizontal axis label: d.b.h. (diameter at breast height)

Full size image

Under CS and YS scenarios (both including increasing aridity), our model identified a positive relationship between parameters \(x_{C}\) (harvest tree size) and \(m_{c}\) (harvest/mortality rate) indicating that maintaining the stock or the yield requires simultaneously high or low values of both parameters. This is, a sustained stock or yield that could only be attained by either harvesting small trees at a low rate or by harvesting large trees at a faster rate (Figs. 5, 6). These two possible strategies would originate alternative diametric distributions and forest structure. A low harvest size (low \(x_{C}\)) and a low harvest/mortality rate (high \(m_{c}\)) will form a flattened and positive-skewed forest diametric distribution with a mean tree size around harvest size. Alternatively, setting a high harvest tree size and increasing the harvest rate, led to a lifted and negative-skewed diametric distribution with a peak around the harvest size. Finally, we did not observe significant differences among yield values nor a set of parameters maintaining constant stock and maximizing yield.

Discussion

During more than a century, multiple-use forestry has successfully balanced ecosystem preservation and service demands from local forest users (Moreno-Fernández et al. 2021b) but resilience boundaries under increasing aridity remain uncertain. Understanding the mechanisms driving forest level stability in response to increasing aridity is critical, particularly in arid prone ecosystems where ecosystem retreat is threatening multiple ecological and socioeconomic services (Mátyás 2010).

Scaling from tree growth to forest resilience

Our results confirm that observed patterns in forest dynamics result from the interaction of tree growth and competition, with tree growth being size-dependent and constrained by climate. Growth and size dependency are well-known (Coomes and Allen 2007; Stephenson et al. 2014), with younger or smaller trees exhibiting faster growth rates which enables them to rapidly gain space to compete for resources (Uriarte et al. 2004). Competitive effects in dry-prone ecosystems result from a reduction in resource availability and involve competition for both light and below ground resources (i.e., water and nutrients) (e.g. Weiner 1984; Forrester et al. 2022). Forest stock (estimated as wood volume) can be a better proxy for neighborhood competition than diameter because allometric of height-diameter adjustments in response to limiting resources (i.e. tree elongation with small diameter increments in reaction to height growth (e.g. Zavala et al. 2011; Lines et al. 2012). The effect of stand structure on vulnerability, has been also shown from studies addressing different ecosystem levels and disparate methodological approximations, pointing out to thinning as an efficient drought adaptation measure (e.g. Moreno-Gutiérrez et al. 2012; Sohn et al. 2016b; Bottero et al. 2017; Schmitt et al. 2020).

In agreement with previous studies, competition effects are highly dependent on climatic conditions (Sánchez-Salguero et al. 2015). Climate conditions have been shown to modulate neighborhood competition (Marqués et al. 2021), and temperature and precipitation constraints on tree growth are considered of key importance in the southernmost dry limits of the tree species distribution (Herrero et al. 2013). The effects of aridity (i.e., the response to the number of dry months period), is explained by the low water retention of sandy soils in combination with high-limited stomatal responsiveness resulting in growth suppression and drops in productivity (Salazar-Tortosa et al. 2018). Climate warming in Mediterranean forests is increasing water demand and decreasing water supply due to higher soil evapotranspiration and lower or more irregular precipitation, all of which would increase competition for water (Linares et al. 2010; Jump et al. 2017).

Forest resilience to drought is frequently assessed using tree dendrochronological analysis, which offers direct estimates on climate variability effects on tree growth (e.g., D’Amato et al. 2013; Bottero et al. 2017; Sánchez-Salguero et al. 2017). The scope of tree-ring data analyses, however, is commonly limited to few trees without considering feedback from stand structure and competition. In size-structured populations, such as forests, size distribution has a key importance on population dynamics (Kohyama 1991, 1993), for example through size-specific effects linked to drought tolerance (e.g., Nolan et al. 2021; Christopoulou et al. 2022) or through competitive effects (Weiner 1984; Marqués et al. 2021). Tree growth is a dynamical size-dependent process (Coomes and Allen 2007; Gómez-Aparicio et al. 2011) which results from feedback with population structure through competition (Kohyama 1993). Growth suppression for a given individual influences phenotypic responses of other neighboring individuals, with compensatory or synergistic effects (Linares et al. 2010; D’Amato et al. 2013) that can influence drought stand-level responses e.g., productivity (Andrews et al. 2020). Forest management operates at the stand level, modifying stand structure and generating a new competitive scenario that can influence overall stand stability in response to climatic variation (e.g., Elkin et al. 2015; Ameztegui et al. 2017).

Model comparisons and caveats

Scaling feedback between tree growth, competition and climate to the landscape requires the use of computational and mathematical models. There are a wide variety of approximations depending on their purpose, mechanisms and hypotheses built in the model—and hence in their complexity (e.g., Shifley et al. 2017; Burgmann and Seidl 2022). Empirical models such as yield tables and distribution models have been successful in forestry, nevertheless as new social demands and risks emerge; from timber production to resilience, managers require new approximations to tackle these challenges (Shifley et al. 2017; del Río et al. 2017). Models of forest resilience also are very varied, ranging from analytical approaches to complex landscape simulators (Albrich et al. 2020). Individual based simulators (Elkin et al. 2015) have shown important effects of stand structure and thinning on forest responses to drought depending on thinning intensity, elevation, target species and temporal scale. Similarly, Ameztegui et al. (2017) show that thinning effects on stand productivity were relevant in the short term but the effect vanished after 30–40 years, independently of the site and climate scenario. In the high end of the model complexity gradient, processed-based simulators incorporate explicitly a high number of biological processes operating at various levels of biological organization (e.g., Battaglia and Sands 1998). For example, process-based models project tree growth from tree-ring data in response to several climatic drivers (e.g., Sánchez-Salguero et al. 2017), however they do not consider feedback with stand structure and competition which precludes scaling up tree growth responses to the forest level. Process-based models can include more detailed physiological processes such as assimilation rate, transpiration, recruitment, mortality etc., depending on the model. This level of detail can allow exploration of CO2 fertilization effects (e.g., Madrigal-González et al. 2015), demographic compensation processes via regeneration and mortality (e.g., Elkin et al. 2015; Ameztegui et al. 2017) or resource dynamics (e.g. water balance, Molina and del Campo 2012). As the number of processes and parameters in the model increases, it becomes increasingly difficult to understand model behavior in relation to specific hypotheses. This decreases the model heuristic value and makes its parameterization and application more difficult. In contrast, analytical—low complexity models (i.e., low number of parameters) facilitate both mathematical and biological model intelligibility (Bugmann and Seidl 2022). Specifically, our model identifies the role of size-structure dynamics—and often overlooked mechanism—as a key factor modulating forest-level resilience in response to drought. Further studies and in particular, application of this approximation to other ecosystems should circumvent a number of limitations. Firstly, climate change and recurrent drought events may exacerbate water shortage leading to dieback processes and collapse recruitment (Carnicer et al. 2011; Kunstler et al. 2021; Shriver et al. 2022). Although field studies suggest tree replacement through a facilitation effect (Andivia et al. 2018), aridity could impede natural or even artificial regeneration. Secondly, forest landscape dynamics, typically, imply spatial processes associated with environmental heterogeneity, neighborhood competition and dispersal. Further studies, however, should contrast this mean field approximations with spatially explicit approximations including a diffusion term or an equation describing patch dynamics (Moorcroft et al. 2001; Kohyama 2006) so a wider range of management regimes and ecosystem-types can be represented.

Policy-management scenarios

Understanding how forests will respond to increasing aridity and how to reduce their vulnerability, i.e., increasing their resilience through adaptation measures—is key to reconcile mitigation and conservation targets with sustainable management (e.g., D’Amato et al. 2011; Bradford and Bell 2016). On one hand harvesting for biomass and other products imply recurrent stock reductions offering an opportunity for implementing cost efficient adaptation measures in depopulated rural areas. This is, decreasing forest vulnerability to drought and wildfires, while fostering a bioeconomy chain value (Hetemäki et al. 2017). On the other hand, harvest intensification can jeopardize key services such as soil stability and biodiversity preservation. In particular, the combination of climate change and overexploitation could result in synergistic effects accelerating the transitions (i.e. “tipping point”) towards another ecosystem state (Reyer et al. 2015). For example, shrubs and grasses could eventually dominate the overstory (e.g. Baudena et al. 2020) or the ecosystem can move towards a degraded state if grasses and shrub species fail to colonize the system and soil is lost.

Current management (i.e., shelterwood method in conjunction with thinning) (BAU) has seemingly maintained a sustained ecosystem service provision for more than a century (Moreno-Fernández et al. 2021b). Yet our results indicate that maintaining current management under increasing aridity can compromise long-term ecosystem provision—i.e., with decreasing forest stocks and yield—and shift forest structure towards more homogeneous forests and smaller tree-dominated forests. These results suggest the need to readjust forest management regimes to new climatic conditions to ensure ecosystem provision and reduce climatic vulnerability. The two alternative management scenarios analyzed exemplify two seemingly conflicting views, one oriented towards the conservation of forest biomass (i.e., conservation scenario, CS)—including forest cover and vertical structure—and the other scenario aimed to maintain a constant biomass supply (yield-oriented scenario, YS). For any policy scenario, the management strategy (i.e., the modulation of harvest size and harvest/mortality rate) results in very long-term forest structure that will foster different forest functions and biodiversity. Nevertheless, the range of possibilities for the yield scenario is more restricted.

Maintenance of forest biomass (i.e., CS) implies a reduction of the wood extraction rates as the aridity increases, whereas the maintenance of extraction rates in conjunction to rising aridity result in a drop in standing stocks. CS also involves heterogeneous forests including large trees and seems to balance conservation, mitigation and adaptation goals. Furthermore, it can fit multiple use-forestry to diversify incomes depending on market conditions. For example, traditional forest management favored open forests (see the low tree density) to promote large-diameter trees capable of ensuring pastoralism and to produce resin (Rodríguez-García et al. 2014). Then, the maintenance of the resin exploitation as an ecosystem function under the forecasted aridity (Giorgi and Lionello 2008) would require maintaining current forest stocks and promoting relatively large trees. In fact, large trees have been shown critical for the maintenance of regeneration through intraspecific facilitation (Andivia et al. 2018). For example, the existence of large trees influences for carbon storage (Mildrexler et al. 2020; Hernández-Alonso et al. 2023), provision of shelter to the new cohorts (Andivia et al. 2018; Moreno-Fernández et al. 2018) and biodiversity (Le Roux et al. 2015). A heterogeneous forest structure may be more resilient to perturbations (Ols and Bontemps 2021) and large dominated trees seem to suffer less during pronounced droughts perhaps because they have a consolidated root space and/or can reach the water table (Madrigal-González and Zavala 2014).

On the contrary, a management oriented towards the maintenance of a supply of forest biomass as fuel (YS) may maximize forest removals to increase profitability by extracting small trees (Prinz et al. 2019) and reducing standing stocks (Dalmonech et al. 2022). The range for which the YS scenario is sustainable at increasing aridity is much more restricted (Fig. 6). In concordance with our results, many studies indicate concomitant increments of temperature and the consequent rise in aridity (Giorgi and Lionello 2008) lead to drops in growth of Mediterranean species (Martin-Benito et al. 2011; Sánchez-Salguero et al. 2017), particularly for our target species P. pinaster (Férriz et al. 2021). Recurrent growth suppression in P. pinaster dry-edge ecosystems can lead to dieback processes (Moreno-Fernández et al. 2021a; Prieto-Recio et al. 2015) and a collapse in regeneration which can ultimately lead to a tipping over a degraded state, particularly in these sand dune ecosystems. Reduction in tree growth along with simplification in forest structure can hinder ecosystem provision services but can also have indirect effects on biodiversity—for example increasing plant diversity vulnerability which maintains pollinator networks and wild herbivores (Madrigal-González et al. 2010) or limiting nesting sites of endangered species such as the imperial eagle (Aquila heliaca Savigny) (González et al. 1992).

Trade-offs between extraction rates, and wood stocks and aridity have already been reported (Palosuo et al. 2008; Moreno-Fernández et al. 2015; Morán-Ordóñez et al. 2020). All of this highlights the trade-offs between functions and their subsequent structure, e.g., promotion of carbon stocks in heterogeneous forests versus intensive biomass extraction for bioenergy in homogeneous forests. In addition, climate natural solutions may counteract climate change, and, in fact, an ongoing debate exists on forest carbon sequestration capacity as climate change impacts are on the rise (Anderegg et al. 2022). Moreover, forests will continue facing pressure for biomass and timber production (Manolis et al. 2019) and its mitigation capacity critically depends on the spatial scale; forest regeneration rate (carbon sequestration) in relation to biomass use (carbon emission). This highlights the importance of landscape level approximations in order to achieve sustainable solutions (e.g. Cumming 2011; Honkaniemi et al. 2020) and in particular, the need of developing tools for forest planning at large scales (e.g., forest, regional, landscape) that allow us to assess trade-offs and ecosystem services under different management and climatic scenarios.