Introduction

Quantifying landscape diversity has fascinated scientists for several decades (Romme 1982; Ricotta et al. 2000; Carranza et al. 2007). Landscape diversity encompasses a range of phenomena; one of the most often considered aspects is the diversity of land cover types (Carranza et al. 2007) or habitats (e.g. Romme 1982; Ricotta et al. 2000). However, various ways of quantifying landscape diversity lead inherently to different results (e.g. Nagendra 2002; Şentürk and Özkan 2017). The various approaches may also differ in that how effectively they characterize the landscapes (e.g. Khare et al. 2019).

An approach to quantifying landscape diversity is applying indices on the proportion of separate land cover types at a single spatial resolution. This approach to landscape diversity can be calculated for either small regions (alpha-diversity, e.g. Liu et al. 2014; Kratschmer et al. 2019) or a large, complete study extent (gamma-diversity, e.g. Dušek and Popelková 2017). However, if characterizing the variation of land cover types at a single spatial scale, i.e. calculating either alpha-diversity or gamma-diversity, the spatial configuration, which is a crucial component of diversity, is ignored (Supplementary Material S1; Walz 2011; Dušek and Popelková 2012). A solution is provided by the third type of diversity termed beta-diversity, which reflects the variation between spatial units (Whittaker 1960), and thus it characterizes the spatial configuration of the study area. A possible approach to capture beta-diversity is calculating alpha-diversity indices based on individual land cover types but at multiple scales (e.g. Shannon diversity index, SHDI – Reynolds et al. 2018; Gao et al. 2021; Barbaro et al. 2022; Simpson index – Schindler et al. 2013, Rao index – Díaz-Varela et al. 2016). This approach to beta-diversity has become widespread in landscape ecology thanks to studies that drew attention to the importance of scale-dependent analyses (e.g. Wu et al. 2002; Jackson and Fahrig 2015). Another opportunity is using the formulae of alpha-diversity indices but calculating them based on the proportion of land cover type combinations. Though this approach is rarely applied, e.g. Ricotta and Carranza (2013) calculated the Rao index for land cover type combinations. There are further possibilities of quantifying beta-diversity that could be adapted from the field of community ecology.

In general, the measurement of diversity is analogous in community and landscape ecology (Peters and Goslee 2001). Thus, diversity indices of community ecology can be applied in landscape ecology if substituting “species” for “land cover type” (see e.g. Romme 1982). In community ecology, the diversity indices measuring directly beta-diversity (e.g. Jaccard index, Sorensen index, Juhász-Nagy’s compositional diversity function etc.) are fundamental as they provide deeper insight into the spatial structure of communities (Bartha et al. 2011; Ricotta 2017). These diversity indices present definitely an opportunity for landscape ecology. In the current study, we show a case study for applying a diversity measurement approach from community ecology by adapting Juhász-Nagy’s functions to landscape context.

Juhász-Nagy’s information theory based framework (hereinafter: “Juhász-Nagy’s framework”) was originally developed for quantifying the diversity and structure of communities (Juhász-Nagy 1976, 1984, 1993; Juhász-Nagy and Podani 1983; Podani et al. 1993). The framework was developed to be able to (1) take gradients into account, and (2) handle multiscale data. In the first place, it contains a function termed compositional diversity (CD). CD measures the diversity of species combinations typically based on the observed patterns. The more species combination occur and the more even they are distributed the higher the CD value is reached. Furthermore, the framework coherently includes another function, termed associatum (AS) offering insight into the spatial structure (Bartha et al. 1998). AS calculates the difference between the expected (assuming independence) and the observed CD values. The value of AS is low in the case of random pattern and the more aggregated the pattern the higher the value it takes.

Both CD and AS should be calculated at multiple spatial scales and analysed as the function of the scale (Juhász-Nagy and Podani 1983; Podani et al. 1993). Their response to the changing scale has been identified as indicators of the spatial organization of plant communities (see Bartha et al. 1998). Furthermore, these functions help capture the spatial scale holding the most information by identifying the unit size corresponding to the maxima of the functions (ACD, AAS). These unit sizes are known to be characteristic of the plant community types (Bartha et al. 1995; Campetella et al. 2004), also termed characteristic areas (Podani et al. 1993). They reflect the status of the plant community regarding naturalness, succession and further community processes (Bartha et al. 1995, 2004; Virágh et al. 2008). A graphical representation termed coenostate space (Bartha et al. 1998) enables the joint examination of the maxima and the characteristic areas. Visual examination of the coenostate space also provides insights into community patterns (Campetella et al. 2004; Virágh et al. 2008). Thus, the application of the functions presents an opportunity for landscape-scale assessments.

Landscape diversity is typically assessed at actual conditions (hereinafter: “actual diversity”; e.g. Romme 1982; Burnett et al. 1998). However, the actual habitat diversity of a specific landscape may be misleading without a neutral model to compare to. For instance, a potentially less diverse landscape could be thought being in a bad state of naturalness due to its low actual diversity value, even though it is near to its potential. The potential diversity calculated from the potential landscape composition (hereinafter: “potential diversity”) can serve as a neutral model to compare actual diversity to. One notable representation of potential landscape cover is potential natural vegetation (PNV, Tüxen 1956). PNV embodies vegetation that could persist at a given site and date, under certain environmental conditions, without ongoing human management (Tüxen 1956; Somodi et al. 2021). Hence, PNV takes into account the abiotic conditions of landscapes, including those that emerged as a result of human activity (e.g. diversion of river flow by dams), but excludes active ongoing human management of the vegetation itself (e.g. livestock grazing). Although, the possibility of PNV to serve as a neutral model has been voiced (Ricotta et al. 2002; Somodi et al. 2021), only a few applications exist (Lenz and Stary 1995; Ricotta et al. 2000). Moreover, usage of the multiple potential natural vegetation (MPNV; Somodi et al. 2012) concept as a neutral model can be even more beneficial. In this framework, the full vegetation potential of the landscapes is estimated in a probabilistic context (Somodi et al. 2012; e.g. Somodi et al. 2017; Fischer et al. 2019).

In our study, we aimed at advancing the assessment of landscape diversity on three fronts:

  1. (1)

    Introducing Juhász-Nagy’s framework at the landscape scale to assess landscape compositional diversity and landscape structure in a coherent framework.

  2. (2)

    Identifying the scale holding the most information to support the choice of scale for computation-intensive analyses not allowing multiscale assessment.

  3. (3)

    Evaluating the actual landscape diversity and structure of Hungary against a neutral model represented by (M)PNV.

Materials and methods

Study sites

We examined the diversity and the structure of both the entire Hungary and nine smaller regions within the country (Fig. 1, Table 1.) delineated based on the vegetation-based landscape regions of Hungary (Molnár et al. 2008).

Fig. 1
figure 1

Study sites: Hungary and nine of its regions. Subplot a shows the position of Hungary in Europe, and b shows the topography of the county. Subplot c shows the nine regions used as study sites delineated based on the vegetation-based landscape regions of Hungary (Molnár et al. 2008). Larger regions encompass all smaller regions coloured according to the larger region’s legend

Full size image

We intentionally selected regions with contrasting topography and human-induced transformation state to facilitate generalization of our findings and detection of the interrelationships between topography, transformation and diversity. We had to consider the shape of the polygons as well. The closer the shape of the region is to a full circle, the higher sample size can be achieved, when enlarging spatial units. We applied the same methodology to all of the 9 + 1 study sites.

Table 1 Basic characteristics of the study sites
Full size table

Data

Datasets of both actual and potential vegetation are available for Hungary, in a hexagonal grid holding 714.07 m diameter cells (area: 35 ha). In both cases, we considered the same, in total 39 (semi)natural vegetation types (Bölöni et al. 2011; Supplementary Material S2). One hexagon can host multiple vegetation types in both the actual and the potential data.

Actual vegetation data were obtained from the Hungarian Actual Habitat Database (MÉTA, Molnár et al. 2007; Horváth et al. 2008) in the presence/absence form. The multiple potential natural vegetation (MPNV) predictions obtained by Somodi et al. (2017) and by updated model runs of the same framework with additional data as it has become available served as potential vegetation data. These predictions are estimations of the potential survival capability of the examined vegetation types for each hexagonal cell. They were produced by gradient boosting models trained on actual vegetation data and corresponding environmental variables. We binarised the raw probability values since Juhász-Nagy’s functions need binary input data (Juhász-Nagy and Podani 1983). A specific binarization threshold, i.e. the mean of the predicted values in the known absence locations, was used that was found to enhance direct comparability across vegetation types (Somodi et al. 2017; Konrád et al. 2022).

Application of Juhász-Nagy’s framework to landscape scale

Juhász-Nagy’s information theory-based functions (Fig. 2; Juhász-Nagy and Podani 1983; Podani et al. 1993) were applied to analyse the diversity and structure of the studied regions. Landscape compositional diversity was measured using the compositional diversity (CD) function. CD characterizes the diversity of observed land cover type combinations formed by land cover types that co-occur in the same spatial unit. It builds on a similar core equation (Eq. 1) as the Shannon diversity index (Shannon and Weaver 1949; Eq. 2), thus it also calculates entropy. The core difference is that CD is calculated based on the probability of landscape units holding a specific land cover type combination (Supplementary Material S1). Thus, CD measures the compositional variation of types between spatial units (beta-diversity), as opposed to the diversity of types (alpha-diversity and gamma-diversity) traditionally measured using Shannon diversity. In the current study, land cover types were represented by vegetation types, thus vegetation type combinations were analysed. Thus, hereinafter we present details using terminology corresponding to vegetation type data.

$${CD}_{observed}\;=\;-\;\sum p_k{\text{log}}_2p_k$$
(1)

In Eq. 1 symbol \({p}_{k}\) means the observed probability of the \(k\)th vegetation type combination, i.e. the ratio of spatial units holding the \(k\)th vegetation type combination and the number of all spatial units. Calculating CD at different spatial resolutions and plotting it against spatial scale usually shows a unimodal curve. The range of CD is \([0, N]\), where \(N\) is the number of vegetation types. The higher its value the greater the landscape diversity is. Thus, the minima are reached, when only one combination, i.e. either a single vegetation type or all vegetation types, is present in all spatial units. The maximum is reached, when all the possible, i.e. \({2}^{N}\) (\(N\) = number of vegetation types) combinations are present with equal frequencies. However, this is rather a theoretical case.

Fig. 2
figure 2

Conceptual framework of the study. a Flowchart of the applied methods. Note, Shannon diversity (not shown in the figure) was calculated at the same resolutions as Juhász-Nagy’s functions. MPNV: multiple potential natural vegetation; AV: actual vegetation; CD: compositional diversity; AS: associatum. b Calculation of Juhász-Nagy’s functions, i.e. the compositional diversity (CDobserved) and the associatum (AS) based on a sample landscape data of two vegetation types (A, B). p: probability, i.e. the ratio of spatial units holding a given vegetation type or vegetation type combination and the number of all spatial units. CDexpected: expected compositional diversity with the assumption of independence. It can be calculated similarly to CDobserved, however, inner cells are resulted by multiplying the marginals with each other

Full size image

To demonstrate and evaluate the difference between the Shannon diversity index and CD, the former was also calculated scale-dependently (Shannon and Weaver 1949; Eq. 2, Supplementary Material S1).

$$H\;=\;-\;\sum p_j{\text{log}}_2p_j$$
(2)

In Eq. 2 symbol \({p}_{j}\) means the proportion the \(j\)th vegetation type among all the vegetation types.

Juhász-Nagy offered another function within this coherent framework (Fig. 2b; Juhász-Nagy 1984) to characterize the spatial structure of species occurrence, termed associatum (AS), which is adaptable to characterize land cover patterns. AS is the difference between the expected and observed diversity of vegetation type combinations. Thus, AS measures the overall spatial dependence of vegetation types within the landscape (Eq. 3).

$${\text{AS}}\,{\text{ = }}\,{\text{CD}}_{{{\text{expected}}}} \, - \,{\text{CD}}_{{{\text{observed}}}},$$
(3)

where

$${\text{CD}}_{{{\text{expected}}}} \, = \, - \,\sum\limits_{{{\text{k}} = 1}}^{{2^{{\text{N}}} }} {{\text{p}}_{{\text{k}}} } {\text{log}}_{2} {\text{p}}_{{\text{k}}},$$
(4)

where \({p}_{k}\) is the expected probability of the \(k\)th combination of the all \({2}^{N}\) possible combinations, where \(N\) is the number of vegetation types. The expected probability of the \(k\)th combination can be calculated assuming independence and thus as the product of the probabilities (\({p}_{P}\)) of vegetation types present (P) and the “1 – probabilities” (\(1-{p}_{Q}\)) of the vegetation types absent (Q) in the \(k\)th combination (Eq. 5):

$$p_k\;=\underset{P\epsilon k}{\;\prod}p_P\ast\prod_{Q\not\in k}\left(1\;-\;p_Q\right)$$
(5)

Equations 4–5 provide a didactic approach of calculating \({CD}_{expected}\), however, this is not an effective way. For this reason Eq. 6 is used, which is equivalent to the approach of Eqs. 4–5 (Supplementary Material S3) and provides a much simpler calculation way:

$${CD}_{expected}\;=\;-\;\sum_{i=1}^N\left(p_i{\text{log}}_2p_i\;+\;\left(1\;-\;p_i\right){\text{log}}_2\left(1\;-\;p_i\right)\right)$$
(6)

In Eq. 6 symbol \({p}_{i}\) means the proportion of the spatial units, in which the \(i\)th vegetation type is present.

If AS is zero, i.e. the expected and the observed diversity are equal, a random pattern is implied, where vegetation types occur independently from one another. Typically, AS also shows a curve with one maximum if plotted against increasing spatial unit size (e.g. Podani et al. 1993).

Procedure of spatial scaling

As the main goal of the current study was the exploration of landscape diversity and structure, we aimed at maximizing the sample size in each step of spatial scaling (Podani et al. 1993). Hereinafter, we term CD and AS calculated based on potential or actual vegetation as “potential CD”, “actual CD”, “potential AS”, and “actual AS”, respectively. The same applies to the maxima of the functions and to the characteristic areas.

Initially, we calculated Juhász-Nagy’s functions (and also the Shannon diversity index) based on the binarized data of vegetation types available in all of the hexagons separately for both potential and actual vegetation (Fig. 2a). Then, these indices were calculated at a series of spatial scales at least until reaching the maximum value of the functions per study area.

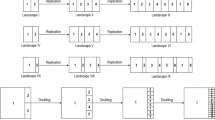
To represent coarser scales, iteratively and radially enlarged rosettes were used as spatial units (Fig. 3). At each step, the rosette gained a new row of hexagons around the spatial unit of the previous step. Preliminary results suggested that the introduction of an extra step between the 7- and 19-hexagon rosettes is needed to achieve finer resolution near the beginning of the sequence of spatial unit sizes. Therefore, a 13-hexagon rosette was additionally introduced that somewhat differed from the other rosettes in its shape, but represented medium size between the 7- and 19-hexagon rosettes. Data were assigned to rosettes in a moving window scheme (Fig. 4, Supplementary Material S4; e.g. Riitters et al. 1997; Luck and Wu 2002). The presence of a vegetation type was assigned to a rosette if at least one of the hexagons belonging to the rosette contained the vegetation type. Rosettes spanning beyond the area of the given region were excluded from analyses. Thus, the sample size, i.e. the number of rosettes, decreased in each step.

Fig. 3
figure 3

Main properties of the 35-ha-hexagon and rosettes used as spatial units for calculation of compositional diversity (CD) and associatum (AS). In the aggregation steps, representing the series of increasing sampling units, we radially enlarged rosettes yielding units consisting of 7, 19, 37 etc. hexagons. * is an exception from the calculation of the number of hexagons given at the bottom of the plot

Full size image
Fig. 4
figure 4

Scheme of spatial scaling by the moving window design. Spatial units, i.e. hexagon and rosettes of different sizes, are shown in a small study area for demonstration. This demonstrative study area is marked with a black boundary for each scaling step shown. Note, the spatial units overlap starting from the 7-cell rosette in the aggregated data. Thus, only the central hexagon of the spatial units is coloured according to the presence/absence data. Aggregation by any presence (technically i.e. aggregation by maximum) should be applied within the window (spatial unit with thick red border). Thus, aggregated data of an enlarged unit, i.e. rosette was 1 if the vegetation type was present in any of the hexagons covered by the window. The aggregated data was assigned to the rosette when data for all hexagons covered by the window is available. Otherwise, a not available (abbreviated as “NA”) value was assigned to the enlarged unit. The red, dashed arrow indicates the movement of the window between two steps

Full size image

After calculating the actual and the potential CD and AS values at different spatial scales, they were plotted as a function of the spatial scale for each region. CDmax, ASmax and the characteristic areas (ACD, AAS), i.e. the area of the rosette in hectare that produced the maxima, were identified. The coenostate space (Bartha et al. 1998) was also presented by plotting CDmax against ASmax and ACD against AAS. Paired samples sign test (Dixon and Mood 1946) was applied to the difference between potential and actual CDmax, ASmax, ACD and AAS. In order to avoid inter-dependence of samples, i.e. overlapping regions, only data of small regions (see Table 1) were used when performing statistical tests.

All analyses were done in the R statistical environment (R Core Team 2020) using the “sf” (Pebesma 2018) package. A separate package applying the framework to the landscape scale (“LandComp”) was developed to adjust the framework to typical landscape scale input data and assure smooth application. The new package made use of code parts of the package developed for community analysis (Tsakalos et al. 2022). A coordinate reference system optimized to Hungary, i.e. the Hungarian National Projection (HD72/EOV; EPSG: 23700), was used throughout the study.

Results

Both CD and Shannon diversity appeared to be scale-dependent in our analysis. Shannon diversity followed a monotonous increasing trend with actual and potential diversity nearing each other towards coarser scales (Supplementary Material S5). On the contrary, the absolute maxima of the CD were clearly discernible for the majority of the regions (Fig. 5, Supplementary Material S6, S7).

Fig. 5
figure 5

Values of Juhász-Nagy’s information theory functions along an increasing scale for Hungary. Dashed lines link the CDmax and ASmax with the respective spatial unit sizes, i.e., ACD and AAS. For plots of other regions see Supplementary Material S7

Full size image

In the case of a few regions (Bakony, Körös-Maros Interfluve, Southern Bükk), potential CD showed a decreasing trend, which points to the potential ACD being possibly smaller than the size of the hexagonal unit (i.e. <35 ha). Thus, in these three cases, it is possible that the potential CDmax values were underestimated.

A significant difference was found between potential and actual CDmax (paired samples sign test, p < 0.05). In all regions, the potential CDmax definitely exceeded the actual CDmax values. However, the difference between the potential and actual CDmax was remarkably smaller in the case of (semi)natural regions (e.g. Bakony, Őrség, Southern Bükk) compared to that of transformed ones (e.g. Baranya Hills, External Somogy, Körös-Maros Interfluve, Mezőföld & Velence hills; Fig. 6). Difference between potential and actual diversity was also reflected by Shannon diversity index, higher potential diversity was found in the case of all study sites (Supplementary Material S5).

Fig. 6
figure 6

Coenostate spaces sensu Bartha et al. (1998). In subfigure a maximal values of Juhász-Nagy’s information theory functions, i.e. compositional diversity (CD) and associatum (AS) are plotted against each other. In subfigure b the unit sizes corresponding to maxima of the functions, i.e. characteristic areas are plotted against each other. Grey lines link the potential (red) and actual (blue) landscape state of the regions. The more natural the actual landscape state of a region is, the darker its symbol colour is. Symbols reflect the topography of the region. For the position of the exact regions in the coenostate space see Supplementary Material S6 and S8. (Colour figure online)

Full size image

The difference between the actual and potential ASmax was remarkable in the vast majority of the regions (Fig. 5, Supplementary Material S6, S7). However, significant difference was not found (p > 0.05) between potential and actual ASmax. In the majority of the regions (e.g. Bakony, Baranya Hills, External Somogy, Hungarian Great Plain, North Hungarian Mountains, Őrség, Southern Bükk), the potential ASmax remarkably exceeded the actual one. However, in the minority of the regions (Hungary, Körös-Maros Interfluve, Mezőföld & Velence Hills) the opposite trend was found.

An evident trend was also found regarding the characteristic areas (Fig. 5, Supplementary Material S6, S7). A significant (p < 0.05) difference was found between potential and actual ACD and AAS, as well. In the case of all regions and both indices, the potential characteristic areas were smaller than the actual ones.

The difference between the potential and actual landscape state was reflected also by coenostate spaces (Fig. 6, Supplementary Material S8). Following Bartha et al.’s (1998) interpretation guidelines, small or moderate spatial dependence was found for a few of the smaller regions (e.g. Baranya hills, Körös-Maros Interfluve) and a more pronounced spatial dependence was revealed for e.g. Hungary (Fig. 6a). The potential and actual characteristic areas were sharply separated (Fig. 6b).

Discussion

Traditional landscape measures and Juhász-Nagy's approach

Quantification of diversity has been carried out in landscape ecology analogously to community ecology (Peters and Goslee 2001; e.g. Shannon diversity index – Reynolds et al. 2018; Barbaro et al. 2022; Simpson diversity index – Schindler et al. 2013; Şentürk and Özkan 2017; Rao index – Ricotta and Carranza 2013; Şentürk and Özkan 2017). In community ecology, Whittaker (1960) recognized different approaches of diversity, i.e. alpha, beta & gamma that characterize the communities from different aspects. Though this terminology has not become widespread in the field of landscape ecology yet, these types of diversities have been measured in landscape ecology, too. Alpha- (e.g. Liu et al. 2014; Şentürk and Özkan 2017) and gamma- (e.g. Dušek and Popelková 2017) diversity relying on the land cover types characterize the local and regional landscape variation encountered. These types of diversity are typically measured using diversity indices developed for the measurement of alpha-diversity in community ecology (e.g. Shannon diversity index, Simpson diversity index etc.).

However, beta-diversity (e.g. Ricotta and Carranza 2013; Barbaro et al. 2022) has the potential to be more sensitive to landscape configuration. Juhász-Nagy’s framework provides the possibility to identify differences in landscape diversity even in the case of identical land cover types and evenness (Supplementary Material S1). The CD offers a measure that is sensitive to the co-occurrence of types and also identifies the scale holding the most information regarding beta-diversity (Juhász-Nagy and Podani 1983; Virágh et al. 2008). Nonetheless, other beta-diversity measures used in community ecology (e.g. Bray–Curtis dissimilarity) could be also used analogously in landscape ecology. Additionally, the Boltzmann entropy also enables the quantification of compositional and configurational heterogeneity in theory (Cushman 2018). However, there are intense debates about this approach yet (Stepinski 2022; Cushman 2023), thus further investigations are needed regarding its application.

Studies using traditional landscape diversity indices consequently show increasing landscape diversity by increasing heterogeneity of abiotic conditions (e.g. Burnett et al. 1998; Jačková and Romportl 2008). Similarly, high CDmax values were found in mountainous regions with heterogeneous topography (e.g. Northern Medium Mountains, Bakony). However, the effect of human-induced landscape alteration is less clear when applying traditional landscape diversity indices. For instance, an increase in diversity is also reported as a result of fragmentation (e.g. Malaviya et al. 2010). In contrast, Cabezas et al. (2008) found a decrease in the actual landscape diversity as a consequence of human modification of the abiotic environment. Scale-dependent analysis of CD, however, has the potential to resolve these apparent contradictions as it looks beyond alpha-diversity and thus reflects the background of diversity changes more precisely. In community ecology, CD was found useful to detect degradation even at early phase (e.g. Szollát & Bartha 1991; Bartha et al. 2004; Virágh et al. 2008). A similar pattern echoed in our landscape-scale results, where actual CDmax was always lower than potential and transformed regions had lower CDmax than more natural ones. In addition, we also found that the more human-transformed the region was, the more prominent difference occurred in the values of CDmax. This finding remains hidden when Shannon diversity is used even at multiple scales.

Besides the diversity component of Juhász-Nagy’s framework, AS delivered insight into the spatial distribution of the land cover types. The landscape is characterized indirectly by AS providing information on overall associations of the land cover types from the aspect of size or juxtaposition of landscape patches. Landscape structure is typically analysed on a single-layer map, with studying the juxtaposition of types and statistical parameters of patches (e.g. Winter et al. 2006; Zungu et al. 2020). However, assessing landscape structure is a challenge if we go beyond a single-layer representation. Using the example of vegetation: we can view the landscape as a single map with vegetation classes excluding each other, which is clearly the typical case for actual landscape and was the traditional approach to PNV as well (Tüxen 1956; Küchler 1964; Neuhäuslova et al. 1998). However, the potential vegetation types do not have to be mutually exclusive. Our MPNV and also the actual vegetation is represented as a multilayer landscape assessment. The AS function provided a possibility to assess the structure of these. Generally, high potential ASmax might be partly a result of high potential FDmax (see Bartha 1992) and partly the result of an aggregated distribution of vegetation types caused by environmental gradients.

The problem of single vs. multilayer representation is particularly acute for landscape assessment building on remote sensing, which data type is inherently of a multilayer nature. However, traditional patch statistics (e.g. Fragstats, McGarigal and Marks 1995) cannot handle multilayer representation. Thus, remotely sensed data is often classified into one layer in order to be analysed using statistical parameters of patches (e.g. Ojoyi et al. 2016; Mallie et al. 2020). However, changing to a single layer necessarily leads to information loss. Lausch et al. (2015) have already warned that reducing the information into single-layer maps may be particularly disadvantageous for landscapes without clear boundaries. In contrast, Juhász-Nagy’s framework provides an opportunity to assess landscape diversity and structure without a need to simplify multilayer representation.

Our results underline the previous finding that landscape structures are typically scale-dependent (Rescia et al. 1997; Wu et al. 2002), which justifies scale-dependent assessment of diversity and complexity (Wu 2004; e.g. Ricotta and Carranza 2013; Díaz-Varela et al. 2016). Scale dependence was equally present in the CD and Shannon diversity patterns. In the case of Shannon diversity, a monotonous trend emerged along the increasing scale in earlier investigations (Dušek and Popelková 2012; Khare et al. 2019). The same was observed in the current study, which suggested that potential and actual (alpha-) diversity would be equal if a coarse enough scale was examined. Taking into account that Shannon diversity quantifies alpha-diversity at individual scales, a large enough area holding all vegetation types eventually results in the diversity of the complete study extent, i.e. gamma-diversity. Gamma-diversity of PNV and actual (semi)natural vegetation equals for technical reasons since all the examined vegetation types do occur somewhere in Hungary. Thus, the maximum of Shannon diversity does not carry information here.

In contrast to even a scale-dependent application of Shannon diversity, Juhász-Nagy’s information theory framework is able to differentiate between patterns of land cover types. This characteristic also enables the identification of differences in landscape diversity even in the presence of an identical range of land cover types and evenness (see Supplementary Material S1). The difference in the behaviour of Shannon diversity and Juhász-Nagy’s information theory functions identified in our study further underlines that methods measuring beta-diversity are not equally effective (Khare et al. 2019). Besides the pure examination of Shannon diversity along increasing scale not being informative regarding maximum diversity as opposed to the Juhász-Nagy’s framework, the former approach was also insensitive to difference of actual and potential landscape diversity. Juhász-Nagy’s framework indicated a high difference between potential and actual CDmax for highly transformed regions and a low difference for (semi)natural regions. However, the comparison of potential and actual Shannon diversity index did not show such a trend. Thus, multiscale analysis of CD values was able to characterize the landscape even more precisely than that of the Shannon diversity index. Thus, the CD has the potential to be more sensitive to landscape configuration and to how much habitats have been preserved.

Besides the values of the functions, the spatial scale corresponding to these maximum values, i.e. the characteristic areas, and especially ACD can be informative for landscapes as well. ACD reflects the size of the sampling unit holding the highest diversity of different vegetation type combinations. In our study, potential ACD values were consistently found to be smaller than actual ACD in all the studied regions. This is well explained by the more aggregated pattern in actual vegetation type distributions. In community ecology, larger ACD was observed in the case of aggregated spatial distribution of species (Podani et al. 1993), i.e. a larger area could encounter all relevant combinations. Smaller ACD often implies a more natural state (Bartha et al. 2004; Virágh et al. 2008). Measuring the characteristic area has significance for further research as well. Since it provides the unit size holding the most information on compositional diversity or structure, it can serve as a basis to select the scale in those studies, where multiscale assessment is not possible, e.g. due to computing time or field work demand.

Comparison of the actual and potential landscape conditions

Calculation of actual landscape diversity may carry information on its own (e.g. Romme 1982). However, landscape diversity values without considering the landscape potential may be misleading. For example, a landscape with low diversity cannot be evaluated reliably in lack of knowledge of the landscape’s potential. Actually, a landscape could be considered to be in a bad state of naturalness due to its low actual diversity value, even though it is near its potential. Such a case did emerge in our study as well. The actual CDmax of the Őrség region appeared to be low, lower than that of most of the other regions (Supplementary Material S6, S8). Furthermore, its actual Shannon diversity was found to be also lower than the potential (Supplementary Material S5). Thus relying on Shannon diversity only or even inspecting CDmax without a reference, one could conclude that Őrség is probably in a bad condition. On the contrary, its actual CDmax is the closest to its potential CDmax indicating that it realizes its potential habitat combinations almost in full, which is also reflected in a large part of its area being classified as national park (Kocsis 2018).

This also shows that identification of the degree of negative human effects greatly benefits from considering the potential of the landscape (Ricotta et al. 2000; Somodi et al. 2021). However, very few studies exist that compare the actual landscape diversity to the potential landscape diversity. An exception was presented by Mander and Murka (2003), who implemented such a comparison based on soil patterns representing landscape potential and land use intensity. Another notable approach is using the PNV as a neutral model (Somodi et al. 2021; e.g. Lenz and Stary 1995; Ricotta et al. 2000). Nonetheless, the interpretation of PNV can be variable, when used as a neutral model. Ricotta et al. (2000) used classical single-layer PNV and considered it as the theoretical minimum baseline and expected the actual vegetation based diversity to exceed it due to human-induced fragmentation. As opposed to that, Lenz and Stary (1995) used the maximum potential as a neutral model for their landscape diversity. Their approach is closer to ours, where the maximal potential diversity, as measured on the multilayer MPNV estimation, was used as a reference.

Deviation from maximal potential diversity in any direction bears information. Plausibly, a lower actual diversity indicates unexploited landscape potential possibly due to the eradication of vegetation stands. By contrast, actual vegetation type diversity exceeding the maximal potential vegetation type diversity would be the result of additional vegetation types sustained by human management and thus that would be outside the range of PNV. In the current study, the received higher-than-actual maximal potential diversity values in all ten regions reflected that the landscapes of Hungary have been considerably modified and vegetation types were eradicated by human use. This reflects accurately that only 32.83% of Hungary’s territory can be considered as close to natural (Table 1). The magnitude of difference between actual and potential values of Juhász-Nagy’s functions, however, characterized the magnitude of the transformation. A relevantly smaller difference was found between the actual and potential CDmax in the case of (semi)natural regions (e.g. Bakony, Southern Bükk, Őrség) compared to the transformed landscapes holding mainly arable lands (e.g. Baranya Hills, External Somogy, Körös-Maros Interfluve, Mezőföld & Velence Hills). The same pattern was not identified by Shannon diversity, however. This is likely the result of our indices being sensitive to composition and thus being more sensitive to deviation from natural patterns. Thus, the comparison of CDmax values indicated human-induced clearance of the (semi)natural vegetation with a preference towards specific vegetation types. This is also in accordance with the historical ecology finding, that vegetation removal was conducted selectively in Hungary with loess steppes being the primary target (Biró et al. 2018). With the help of CD, regions with different level of deviation from the landscape potential were possible to be identified.

Other indices derived from Juhász-Nagy’s framework further elaborate on the differences between potential and actual landscape composition and pattern. In the case of the actual vegetation, aggregated distribution and rarity of vegetation types were observable (Hungarian Actual Habitat Database; Molnár et al. 2007; Horváth et al. 2008). This was even more conspicuous in the case of human-transformed landscapes (e.g. Körös-Maros Interfluve, Mezőföld & Velence Hills). However, there are two exceptions of the regions, Baranya Hills and External-Somogy, where rarity was extreme, but the aggregated distribution of vegetation types was not characteristic. Nevertheless, in general, potential ASmax strikingly exceeded actual ASmax (except e.g. Körös-Maros Interfluve and Mezőföld & Velence Hills). As MPNV relies on environmental data, the high potential ASmax can be a result of environmental gradients within the region (e.g. soil, topographical properties, etc.). The higher the variability of environmental factors, i.e. configurational heterogeneity of a region is the higher ASmax was resulted. For example, the Őrség is a rather homogeneous region. However, Mezőföld & Velence Hills region is characterized by remarkable topographical and pedological variation.

The magnitude of the difference between potential and actual ACD is also of interest. Southern Bükk and Őrség regions are in a comparatively natural state as also implied by small differences between potential and actual CDmax and ASmax values. However, the apparent difference between potential and actual ACD also reflects the fragmentation that is present in the region. ACD has also relevance at the ecosystem level. If it is smaller, animals can find more habitat types within the same distances, which means the landscape can thus support species requiring more than one habitat type for survival, e.g. bats (Encarnação et al. 2005; Ciechanowski et al. 2017).

The fact that potential AAS was consequently smaller than actual AAS can be a result of the neutral model nature of MPNV. The multilayer framework of MPNV shows all areas, where vegetation types could persist. Thus, the potential presence of vegetation types is more homogeneous in space than the fragmented actual occurrences of vegetation types. Consequently, in the case of MPNV, the distribution of vegetation types is more homogeneous in space and thus the same level of association appears at smaller spatial unit size.

Conclusion

Juhász-Nagy’s framework proved to be insightful regarding landscape diversity and structure as well. The framework offers analysis opportunities for multilayer complex data sources (such as multilayer model outputs and remote sensing data).

The findings of the current study highlighted the importance of quantifying landscape compositional diversity based on land cover types (e.g. vegetation type, land cover, etc.) combinations instead or additional to that of alpha-diversity. Both compositional diversity and associatum highlighted aspects that support differentiation between more and less natural conditions.

Comparison with a neutral model, i.e. the potential diversity in our case, highly supported the interpretation. We have shown that without this reference false conclusions could have been drawn. The difference between the compositional diversity of actual and potential landscape conditions closely reflected the level of human transformation and naturalness. Human-modified landscapes consistently had smaller diversity of vegetation type combinations and the maxima of these combinations appeared at larger spatial units. Additionally, associatum (AS), the sister function of CD (in the model family) also reflected differences in the spatial arrangement of vegetation types in the regions. Though the aggregated distribution of patches was observable in the case of both potential and actual vegetation, fragmentation of actual vegetation was also reflected by larger actual characteristic areas of associatum. Hence, maximum values of Juhász-Nagy’s functions and corresponding spatial scales can be used as indicators in landscape studies.

Application of the approach can be extremely useful when analysing landscapes with gradients or multilevel landscape data gained by remote sensing for example. Another particular advantage of the approach is the identification of scales holding the most information. This can be a guideline for studies that cannot complete multiscale assessments.