Introduction

Forest degradation and clearing are major causes of global biodiversity loss (Pereira et al. 2010; Rands et al. 2010), as at least two-thirds of terrestrial organisms are associated with forests and particularly tropical rainforests, due to their uniquely rich biodiversity (FAO and UNEP 2020; Wilson & Peter 1988). Indeed, the fragmentation of forests into smaller patches can lead to habitat loss and increase isolation, resulting in forests near the edge having the highest risk of being influenced by edge effects (Lindenmayer & Fischer 2006). A recent study on habitat fragmentation found that nearly 50% of the world’s forests are less than 500 m away from a forest edge, and in the case of tropical forests, almost one-fifth of all the remaining forest area is now less than 100 m from the edge (Haddad et al. 2015). A key result of fragmentation is that the increase in canopy gaps in forests near the edge allows more sunlight to reach the forest floor, leading to higher air temperatures than in the closed-canopy forest, which in turn reduces soil moisture and relative humidity (Gascon et al. 2000; Gehlhausen et al. 2000). As a result, trees in this area are more susceptible to drought, crown damage from windthrow, and other disturbances, thus exhibiting higher mortality rates and seedling recruitment (Brando et al. 2019). Accordingly, Harper et al. (2005) and Campbell et al. (2018) also found that edge-influenced areas are less resilient and more vulnerable to invasive species and diseases, as well as microhabitat alterations and climatic stressors compared to interior (i.e., core) areas. In the long term, the light regime created by openings in the canopy at the edge favours light-demanding species and shifts the species composition toward an earlier successional stage (Swaine & Whitmore 1988). In addition, these changes can lead to a positive feedback loop in the ecosystem by further promoting disturbance of gap-phase dynamics, plant community turnover, animal distribution, and nutrient cycling (Broadbent et al. 2008; Haddad et al. 2015). The forest edge effect has been shown to be a complex process that varies across regions with different species composition, topography, history, and environmental conditions (Ibáñez et al. (2014)). Further research on this topic can play a central role in developing forest conservation and restoration strategies.

Traditionally, studies of edge effects have been conducted in the field using conventional forest inventory techniques (Didham & Lawton 1999; Harper & Macdonald 2002; Murcia 1995). However, these methods are labour-intensive and time-consuming when large areas are involved, as it is impossible to collect all the information on trees and canopy layers through traditional field surveys alone. In this context, remote sensing and Light Detection and Ranging (LiDAR) technology have been employed as a cost-effective and efficient alternative to overcome such limitations (Mura et al. 2016). LiDAR, as an active remote sensing technology, is capable of detecting both the horizontal and vertical distribution of forest vegetation (Lefsky et al. 2001; Weishampel et al. 1996; Wulder 1998), allowing the vertical structure of the canopy to be studied at a larger spatial extent. Indeed, LiDAR, when used in combination with other remote sensing instruments such as hyperspectral data, can effectively support large-scale forest change studies, especially in the tropics (Alivernini et al. 2016; Corona 2010; Vaglio Laurin et al. 2016) Furthermore, the highly detailed three-dimensional information on vegetation structure at multiple horizontal and vertical scales obtained using a comprehensive suite of structural metrics and indices can provide a more objective and reproducible method for studying forest edge effects (Kane et al. 2010; Vepakomma et al. 2018). Over the past ten years, LiDAR has been widely used to assess the role of vegetation structure and the impacts of edge effects on plant and wildlife diversity (Davies & Asner 2014; Melin et al. 2018; Vogeler & Cohen 2016; Zellweger et al. 2017). A study of bird diversity in the UK using LiDAR by Broughton et al. (2012) has shown a decline in Marsh Tits (Poecile palustris) population along forest edges, where structural complexity was lower than in the core area, and habitat structure was less favourable. The authors later concluded that LiDAR data could be used in combination with in-situ bird data to understand the spatial relationship between avian distribution and the vertical structure of the forest. More recently, Wasser et al. (2015), when using LiDAR to construct a riparian vegetation structure map, found that LiDAR data are highly comparable to conventional measurements and therefore, can be used to estimate forest characteristics and canopy structure accurately. Similarly, several authors have confirmed the suitability of LiDAR as a means to assess the heterogeneity of tree canopy structure with diversity indices at both forest plot and landscape-level (Ehbrecht et al. 2016; Rocchini et al. 2013; Senf et al. 2020; Torresani et al. 2020). These diversity indices, initially used in ecology to quantify species richness or abundance, can be applied in the same way to describe such attributes of strata in the vertical profile of forest canopies (Ehbrecht et al. 2016).

Here, we use airborne LiDAR data to assess the effects of disturbance and changes on forest structural complexity along tropical forest edges in the degraded forests of Sarolangun Regency and Batanghari Regency in Jambi, Indonesia—an area that has been heavily influenced and modified by humans over the last few decades. We first extracted 22 vegetation structural metrics from these secondary forests to achieve this goal and analyse canopy structure changes across several edge-to-interior transects. Second, we compared these data to the condition of an undisturbed interior forest in the same region. Third, we quantified changes in structural heterogeneity with respect to distance from an edge as α-, β- and γ- diversity and compared the two forest conditions to highlight the effects of forest edges on vegetation structure.

Method

Study area

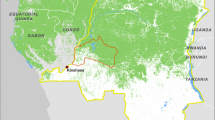
Our study area is located in Jambi Province on the island of Sumatra, Indonesia (Fig. 1). Since the arrival of the Dutch and English trading companies 400 years ago, the province’s rainforests have been increasingly modified and have experienced a massive transformation in their ecological and social landscapes due to this prolonged exploitation (Andaya 1993; Kathirithamby-Wells 1993). Furthermore, rubber (Hevea brasiliensis) and oil palm (Elaeis guineensis)—as local policies and market incentives favour them—have quickly become the two dominant cultivation systems in the whole Sumatra region and are often regarded as traditional despite having been introduced in 1906 by the Dutch (Locher-Scholten 2003). Later on, in the early 70 s of the last century, the Indonesian government started issuing logging concessions as a mean to facilitate economic growth while at the same time, initiating their resettlement program to attract more people into this cash crop business (Elmhirst 2011; Gatto et al. 2015). Consequently, as of 2014, more than 12,400 km2 of oil palm and rubber were cultivated, which correspond to about 25% of the total land cover of the province (Badan Pusat Statistik 2014). This rapid expansion has led to an even further destruction of natural habitats, resulting in a wide range of intermingling systems of small-holder low-management rubber plantations, referred to as jungle rubber (Gouyon et al. 1993). With the exception of the Harapan rainforest national reserve (Fig. 1e) and the northernmost part of the Sarolangun Regency (Fig. 1c), which can be structurally considered as primary rainforest, the majority of our study area is comprised by a fragmented mosaic of secondary rainforest intermixed with small-holder oil palm and rubber plantations.

Fig. 1
figure 1

a location of Jambi province in relation to Sumatra Island and b location of the LiDAR scans in Jambi. LiDAR derived canopy height models (CHM) are depicted for the 3 study areas: c Sarolangun Regency, d Batanghari Regency and e Harapan rainforest national reserve

Full size image

ALS data acquisition and sampling design

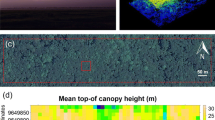
The scanning flights were carried out on a BN2T fixed-wing aircraft and operated by a local Indonesian pilot at an altitude of 15,500 ft above ground level. Due to bad weather conditions, the flying days were not consecutive but separated over 7 days between the 24th of January and the 5th of February 2020, covering 40,602 ha in three study areas (Fig. 1). LiDAR data were collected with a Riegl LMS-Q780 scanner (Riegl Laser Measurement Systems GmbH, Horn, Austria) at a near-infrared wavelength. The sensor has a scan field of view of 60° (± 30° from nadir) and a frequency rate up to 400 kHz. The raw ALS data were processed by Dimap HK Pty Limited (Kowloon, Hong Kong). The canopy height models (CHMs—raster file with cells corresponding to height of vegetation and non-ground returns) at 1 m resolution were obtained by subtracting the digital terrain model (DTM) from the digital surface model (DSM). The mean point density varied within and between study areas, ranging from 16.6 points m−2 to 40.5 points m−2. This was not considered an issue, as the difference in point density between different plots did not translate into differences in the values of extracted metrics (Camarretta et al. 2021).

To investigate the effect of forest edges on forest patches surrounded by oil palm plantations, we set up a square grid with a side length of 1 km overlaid across the Sarolangun regency and Batanghari regency study areas based on the following criteria (evaluated through visual interpretation):

  1. (1)

    Each grid cell has a minimum of 30% forested area;

  2. (2)

    Each grid cell must include other types of land use such as oil palm plantations, settlements, or cleared (fallow) lands;

  3. (3)

    The forested area in each cell must be contiguous and at least 14.28 ha (200 × 400 + (200^2 × π)/2—indicated by the yellow buffer zone) so that it is possible to set up a transect line at least 200 m away from a forest edge in all directions (see Fig. 2).

Fig. 2
figure 2

a cluster design of the sampling plots; b cluster of sampling plots in a grid cell (both sides of the transect and the furthest point are at least 200 m away from an edge, as indicated by the yellow buffer zone). c grids and transects in Sarolangun regency; and d grids and transects in Batanghari regency

Full size image

Along each transect, a cluster of five square sampling plots of size 500 m2 was created, with plots being 50 m apart from each other (Fig. 2a). For each grid cell, one transect line was placed perpendicularly to the edge such that both sides of the transect and its furthest point are at least 200 m away from any other edge (Fig. 2b). In total, there were 105 transects and 525 sampling plots between the two study areas (51 transects in Sarolangun Regency and 54 transects in Batanghari Regency—Fig. 2c and d, respectively).

In addition, sampling plots from the less degraded forest areas (located in the Northern part of the Sarolangun Regency and in the Harapan rainforest national reserve) were also chosen for the analysis (Fig. 3). These plots, resembling an interior forest condition, served as a reference for the comparison with the transects plots along the edges.

Fig. 3
figure 3

Selection of sampling plots (black dots) in: a Northern-most forest in Sarolangun (within the buffered forest interior), b Harapan rainforest national reserve

Full size image

Metric extraction and calculation

The extraction of the metrics was carried out in R Studio version 4.0.0 (R Core Team 2018). The clipping of individual point clouds from the height normalized LiDAR dataset was conducted with the function “lasclip()” in the lidr package (Roussel et al. 2020). For each sampling plot, a set of forest structural metrics was computed from all available points (Table 1). These metrics were selected as they were found to be of importance in segregating different land use types in the same region (Camarretta et al. 2021).

Table 1 List of the 22 metrics extracted from the LiDAR point clouds, and their description
Full size table

Data analysis

Statistical analysis

To identify whether forest structure differed significantly at the forest edge, we conducted Analysis of Variance (ANOVA) and Tukey’s post-hoc tests between plots from the distance groups and between fragmented and interior forest conditions. The Shapiro–Wilk test of normality and Levene’s test of homoscedasticity were applied to the data for all the metrics prior to any analysis. The Shapiro–Wilk test was performed using the “shapiro.test()” function in the stats package (R Core Team 2018) and the Levene’s test was performed using the “leveneTest()” function in the car package (Fox & Weisberg 2019). If the data fails to reject the null hypothesis in both tests, Kruskal–Wallis test was conducted, otherwise one-way ANOVA was used. Metrics that resulted in significant differences between fragmented forest and interior forest, were classified into three groups: metrics related to canopy height (first group), structural indices (second group) and metrics associated with canopy gaps (third group). Afterwards, a Principal Component Analysis (PCA) was applied on these groups to find out which metric was responsible for the most variance.

In addition to these statistical analyses, the magnitude of the edge effect was also quantified as the percent change of fragmented forest plots compared to the interior forest condition (Harper et al. 2005):

$${\text{EE}}\, = \,\frac{{e\,{-}\, i}}{ i}$$
(1)

where e is the individual value of the parameter from the near-edge plots, and i is the mean value of the parameter in the interior forest group. A negative EE represents a decrease in the near-edge plot compared to the interior forest condition, while a positive EE indicates a reverse effect.

Canopy height diversity analysis

To quantify and compare vegetation structural complexity between a fragmented rainforest condition and an interior forest condition, sampling plots extracted from the CHM were classified into multiple classes of 5 m height bins and diversity in canopy height was interpreted as the abundance of these classes. In the context of this study, α-diversity was used to describe the structural heterogeneity within a forest patch (1 sampling plot = 1 forest patch), β-diversity as the between-patch heterogeneity and γ-diversity as the overall heterogeneity. According to Hill (1973) and Jost (2007), when calculating diversity, in addition to the index of diversity, one should also take into consideration which order of diversity should be used. While the diversity of order zero only expresses the mere species richness and order two is too sensitive to dominant species, the diversity of order one has the advantage of being “fairest” as it treats all species (in this case, canopy height classes) according to their frequency without favouring one over another. Therefore, the first order of α-, β- and γ- diversity (1Dα, 1Dβ, 1Dγ) was used to quantify the diversity of canopy height classes in this study. Shannon entropy (H), a widely used index of diversity in ecology and the basis of this analysis, was defined as:

$${\text{H}}\, = \, - \,\sum\nolimits_{i\, = \,1}^{s} {p_{i} \, \times \,\ln (p_{i} )\,{\text{with}}\,0\, \le \,H \le \,\ln (N)}$$
(2)

where S is the number of different classes in a forest patch, pi is the proportional abundance of each height class, and N is the total number of pixels within a forest patch.

Within patch diversity (1Dα) was then obtained by converting the Shannon Index to its exponential value. The overall 1Dγ diversity of each distance group was calculated from the abundance matrix of height classes and the mean between-patch diversity 1Dβ as:

$$^{1} {\text{D}}_{{\upbeta }} \, = \,^{1} {\text{D}}_{{\upgamma }} /^{1} {\text{D}}_{{\upalpha }}$$
(3)

where 1Dα is the mean diversity of all plots and 1Dγ is the pooled diversity index per distance group. All diversity calculations were conducted using the vegan package in R studio (Oksanen et al. 2019). Non-metric Multi-Dimensional Scaling (NMDS) was applied to the same abundance matrix used to calculate 1Dα. In NMDS, the diversity of each plot in the canopy height class abundance matrix is ordinated in multi-dimensional space, with the number of dimensions being the number of different height classes. As a result, in the 2D Cartesian space, the sampling plots were displayed as points where the distance between them represents their relative similarities/dissimilarities.

Result

Structural comparison between close-to-edge plots and interior forests

The results of the statistical tests between plots along the transects and between these plots and interior forest plots are shown in Fig. 4. In general, there were no significant differences for any metric obtained from the plots along the transects (i.e., 0–200 m). Interestingly, metrics related to canopy height (Fig. 4a–j) and canopy structural indices (Fig. 4k–p) had a wider distribution range than those related to canopy gaps (Fig. 4q–v), while the number and size of canopy gaps tended to be low in all transect plots. Low gap frequency and smaller gap size also resulted in a reduced total area of gaps in the canopy and a high vegetation cover of 98% for most plots, regardless of distance from the edge (Fig. 4q). An increase in mean value with regards to distance from forest edge was observed in maximum canopy height, 25th, 50th and 75th height percentiles, and ENL, but these differences were not statistically significant. No similar trend was observed for the remaining metrics, as the values of the different distance groups were comparable.

Fig. 4
figure 4

Comparison of the 22 LiDAR-derived metrics between close-to-edge rainforest (in 5 distance groups) and interior forest (IF) plots. Median values are depicted by solid lines, while mean values are depicted in dashed lines. Letters represent the results of Tukey’s post-hoc pairwise comparison: Groups were assigned with a new letter if there were significant differences, otherwise, they had the same letter

Full size image

Inclusion of the sampling plots from the less disturbed areas in Sarolangun, and Harapan National Reserves (group IF) in the dataset resulted in significant differences for 16 metrics (Fig. 4). The maximum and mean canopy heights in this group were consistently (1.6 times) higher than in the original five plots along the transects. Their distribution ranges were also 1.6—2.3 times larger than in the other groups (Figs. 4a and b). For standard deviation of height, plots in the IF group were 56% higher than in the remaining groups (Fig. 4c). For kurtosis, skewness, and entropy of height points, the values of the IF group were similar to those of the transect plots (Fig. 4d–f). In the IF group, the percentage of points above 2 m increased by 7%, but the percentage of points above mean height decreased by 5%. Regarding the height percentiles, plots from the interior forest were taller than their counterparts in the close-to-edge rainforest, as the mean value for the 25th, 50th, and 75th height percentiles in the IF group were 81%, 60% and 63% higher than the other groups, respectively (Fig. 4h–j). In terms of the canopy and structural indices (Fig. 4k–p), forests in the IF had a more complex structure, with a 36 and 32% increase in the Rumple and LAI indices, respectively, and a 56% increase in ENL (Fig. 4k, l and o). The values of FHD, calculated either as Shannon Evenness or Shannon Diversity, showed a significant increase in the IF group (Figs. 4m and n).

The IF group had a significantly smaller total canopy gaps area and a smaller maximum gap size than the other groups. On average, the total canopy gaps area recorded per plot in the forest interior was 12.7 m2, and the maximum gap size was 8.67 m2, while these values increased twofold in the degraded rainforest (Fig. 4q and r). Similar results were found for the number of canopy gaps, as plots in the interior forest had a mean of 4.15 gaps per plot, compared to 5.59 in the close-to-edge plots (Fig. 4u). The mean gaps size also decreased in the IF group (Fig. 4t). In addition, the 200 m plot group showed intermediate behaviour between a degraded and an interior forest condition for these four metrics (Fig. 4q, r, t and u). Finally, no significant difference was found in either minimum gap size or vegetation cover, as close-to-edge and interior forest values were virtually identical (Fig. 4s and v).

Principal component analysis

To determine which metric explained the most variance between groups, four PCA were performed on the 15 metrics with significant differences among the groups (Fig. 5). The group of canopy height metrics consists of maximum height, mean height, standard deviation of height, percentage of points above 2 m, 25th, 50th and 75th height percentile (Fig. 5a). The group of structural indices includes Rumple index, LAI, ENL, FHD (Diversity) and FHD (Evenness) (Fig. 5b). The third group consists of mean gap size, maximum gap size, total gap extent, and number of gaps per plot (Fig. 5c). Finally, an overall PCA including all 15 metrics was also carried out (Fig. 5d).

Fig. 5
figure 5

Principal-component analysis of (a) 7 height-related metrics, (b) 5 structural index metrics, (c) 4 canopy gap metrics and (d) all 16 metrics

Full size image

Results from the PCA revealed that 96.3% of the variance in the canopy height group was explained by the first two principal components (Fig. 5a). In comparison, this number for the structural indices and canopy gap metrics were 89.9% and 92.5%, respectively (Fig. 5b, 5c). When putting all 15 metrics together, canopy height and structural indices exhibited a high correlation with each other (tested with Pearson’s correlation test—Table S1) and were strongly associated with the first PC (Fig. 5d). These metrics were also negatively correlated with canopy gaps, as seen in the PCA graph where they occupied different regions in PC space (see also Table S1). Thus, the canopy height and structural index axis (51.7%) explained more variance in edge effects than the canopy gaps axis (20.2%), confirming the results of the ANOVA test between the interior forest and the near-edge plots, where an increase in canopy height and structural diversity is associated with a decrease in canopy gaps.

Magnitude of edge effect in five distance groups

The magnitude of edge effect (EE) calculated for each plot according to Eq. (1) were converted to thresholds in 10% increments (< 0%, 0–10%, 10–20%, 20–30%, 30–40%, > 40%). For the canopy height and structural indices metrics, a positive value indicated that there was a reduction in the near-edge plots compared to the interior forest condition (Fig. 6). For the canopy gap metrics, a positive value represented an inverse effect in the distance groups (Fig. 6)..

Fig. 6
figure 6

Magnitude of edge effect in close-to-edge plots

Full size image

Overall, the edge effect was a strong driver of canopy height, as all metrics in this group showed a substantial reduction (40% of EE) in half of the sampling plots across all distances (Fig. 6). Regarding structural indices, ENL and Rumple index follow a similar trend but less intense as only one-third of the plots had a 40% EE value while the reduction in LAI and FHD were more evenly distributed in the EE ranges across all distances groups. For all four measures of canopy gaps, sampling plots from degraded rainforest areas had either a very high (> 40%) or a negative edge effect (Fig. 6). This was due to the fact that the mean values of interior forest plots were quite close to the medians in the other five groups (Fig. 4q, r, t, u). In addition, as shown in Fig. 5c, there was more variation in the five distance groups, while the plots in the IF group clustered near the origin (the standard deviation of the data set is greater than the mean—Table S2). Low mean values of the IF group and a high variation of the close-to-edge groups were also the reason for the absence of plots with moderate edge effects (10–20%, 20–30%, 30–40%). Finally, the high correlation between maximum gap size, mean gap size and total extent of gaps was confirmed in Fig. 6, as the plot count distribution of these three metrics was almost identical. In comparison, the number of gaps had a different distribution due to a lower correlation with the former three metrics (no plot having 10–20% or 30–40% EE, plots with more than 40% EE were halved compared to the other three metrics).

Canopy height diversity in two forest conditions

In general, α-diversity in the IF group was more diverse compared to all other groups (Fig. 7). Across all distance groups in the close-to-edge forest, there was no evidence of an increase in canopy height diversity with respect to distance from an edge, as the means of all groups were comparable and fluctuated around 3.2 (Table 2). On the other hand, plots from the interior forests were on average 23% more diverse than the others. The maximum and minimum α-diversity found in the IF group were also relatively greater than in the five other groups (Table 2).

Fig. 7
figure 7

Comparison of α-diversity of canopy height (1Dα) between the five distance groups in the close-to-edge forest and the interior forest plots

Full size image
Table 2 Summary statistics of α-, β- and γ- diversity in canopy height in the study area
Full size table

Similar results were observed for overall heterogeneity (γ-diversity—1Dγ); however, β-diversity did not differ significantly between close-to-edge forest plots and interior forest plots, as mean values in all groups ranged from 1.42 to 1.57 (Table 2). Interestingly, the overall γ-diversity in all groups was lower than the maximum within-patch diversity.

The relative dissimilarities of canopy height diversity between plots in close-to-edge forests and plots in the interior forest are also illustrated in Fig. 8. The NMDS was applied to the abundance matrix of 14 canopy height classes, and a stress level of 0.11 was obtained. The sampling plots in the fragmented rainforest were characterised by high similarity in height diversity, as the ellipsoids representing the five distance groups largely overlapped (Fig. 8). The plots in the IF group stood out from the other groups as their ordination extended further up to the top right corner in the 2D projected area.

Fig. 8
figure 8

NMDS ordination of the sampling plots from two areas in the projected 2D space. The outer ellipsoids (outlined ellipsoids) represent the boundary volume enclosing all points of a group in the multi-dimensional space. The smaller ellipsoids (filled ellipsoids) indicate the standard deviation of the distance of points within each group

Full size image

Discussions

Edge effects on canopy height, canopy gaps and forest structural complexity

In this study, although we found significantly different results between near-edge and interior forest conditions for 16 out of 22 metrics, there was no evidence of changes in forest structural complexity with respect to distance from an edge. The fact that forest structure at a distance of 200 m from the edge did not differ from forests near the edge suggests that the actual edge depth of our study area might even be more profound than we had assumed. Thus, our results were at odds with previous studies on forest edges, in which clear edge effects lasted for only about 100 m and then dropped off into the core zone (Laurance et al. 2002; Matlack 1994; Newmark 2001; Ordway & Asner 2020). However, it should be noted that these studies were conducted in large single-edge forests, whereas our study areas are characterised by fragmented patches of forest (including jungle rubber) and intermixed with oil palm plantations. This landscape spatial pattern is a critical point that influenced the edge effect, as the latter scaled positively with smaller, fragmented forest patches (Pütz et al. 2011; Tabarelli et al. 2008). In a previous study of forest fragmentation and carbon emissions, Laurance et al. (1998) simulated a hypothetical landscape with three different scenarios of forest patterns and found that fragmented forest landscapes were extremely vulnerable to edge effects. Even with a minimum logging rate of 5–10% of the total area, about 30–50% of the forest area was affected by edge effects, while this value was less than 10% for forests with only one large opening. This simulation, although too simplistic to represent actual ecological processes, can be used to interpret the results we found, especially in the fragmented forest landscape scenario, since much of our study area was very similar to this situation. It is possible that in our study area, edge-affected zones could connect with each other, either by natural regeneration or abandonment of oil palm plantation, resulting in bigger zones, thus extending the influence of edge effects to surrounding patches.

Evidence of interactions through multiple edges was first mentioned by Hardt & Forman (1989), who found a greater influence of edges on woody plant colonisation in concave forest boundaries. Later, Malcolm (1994) proposed his theory of additive interaction, which states that the total edge effects at any point within a forest patch are equal to the sum of the individual effects of the two adjacent edges. More recently, Porensky & Young (2013) took up this idea to develop their conceptual framework for edge interaction. They concluded that edge interaction could lead to three possible outcomes: a stronger edge effect, a weaker edge effect, or a completely different edge effect (emergent interaction). In our study, we observed a decrease in four canopy gaps metrics at 200 m from the edge compared to the other four distance groups along the transect (Fig. 4q, r, t, and u), indicating that forests at this distance started to have a more complex structure (similar to that of the interior forest group) than those at closer proximity to the edge. This result, together with the long-lasting edge effects discussed above, suggests that the forest edges in our study area may have a strengthening interaction in terms of edge depth. Furthermore, the high degree of similarity in all metrics across the five distance groups that we found has not previously been reported in any similar study on single edge effects, implying that this may be due to the interaction of multiple edges. This result is consistent with a recent study on multiple edge effects in a human-modified landscape across the Brazilian Atlantic Forest, which showed a homogeneous effect on forest structure such that stands along the gradient between edge and interior forest had similar values of basal area (Parra-Sanchez & Banks-Leite 2020).

Regarding the magnitude of edge effects in canopy height and canopy structural indices, we found a strong reduction across the interior-edge gradient in both groups (Fig. 6), as the mean value of EE was about 35–40% in the group of canopy height metrics and ENL, and approximately 25% in the other structural indices (except FHD (Evenness), where this value was only 9.61%) (Table S3). More importantly, since aboveground carbon storage is a direct function of canopy height and stand structure (Balima et al. 2021; Yuan et al. 2018), it is very likely that we would get a similar result for aboveground carbon due to edge effects. This relationship was confirmed by Shapiro et al. (2016) when they studied biomass decomposition in different fragmented landscapes in Congo. They reported significantly lower tree canopy height and biomass at distances of 100 and 300 m from an edge and concluded that the decline in these variables was strongly correlated with the degree of fragmentation in the landscape. Likewise, in a tropical rainforest adjacent to an oil palm plantation in Malaysia, Ordway & Asner (2020) observed a 14.85% decrease in maximum canopy height at forest edges, associated with a 22.53% depletion in aboveground carbon density, followed by a 4% decrease in dry leaf mass per area at distances ranging from 64 to 92 m. Compared to forests near the edge in their study, our fragmented forests were analogous (our mean maximum height = 21.97 m—Table S2, their mean maximum height = 21.76 m), but we observed a greater decline due to edge effects (mean EE = 38.28%). Biomass loss in our forests affected by edge effects was also hinted by a 24.13% decline in LAI (Table S3)—a key indicator of forest production and aboveground biomass. Thus, the results of our study seem to indicate a significant reduction in aboveground carbon storage due to edge effects.

Regarding gaps in the canopy, we found that the bimodal distribution of four metrics in Fig. 6 did not truly reflect the extent of the edge effects in our study area. As mentioned earlier, this was due to the low mean values of these metrics in the interior forests and the high variation in the fragmented forest plots. It is possible that the interior forests in our study area had a closed canopy with few gaps, or that the size of the sampling plots was too small (500 m2) for us to effectively capture this gap-related information. The low mean values in the interior forests also resulted in a heavy inflation of EE in this group (Table S4). In fact, the mean difference in the number of gaps per plot between the interior and close-to-edge forests was only 1.44 gaps (calculated from Table S2 and S4). This value in the total extent of gaps was 14.57 m2 per plot (291.4 m2 ha−1), suggesting that canopy gaps are less vulnerable to edge effects compared to canopy height and forest structural complexity. One possible explanation for this could be that when the canopy was opened, natural regeneration established rather quickly as light availability increased, and consequently, the canopy re-filled. In addition, we observed a steep increase (> 40—Fig. 6d) in the 25th height percentile on more than half of the plots in the close-to-edge forests, implying a shift in forest structure towards a higher share of understory trees. Overall, the 25th height percentile, total gap extent, and maximum gap size were the 3 metrics that differed most between the two forest conditions, as the 25th height percentile dropped by 44.95% on average in our secondary forest, while values of total gap extent and maximum gap size increased twofold compared to the interior forest (Table S2 and S4).

Diversity in canopy height

The result of diversity in canopy height between the two forest conditions in our study was consistent with the analysis of edge effects presented above (i.e., uniform structure of canopy height across the distance of fragmented rainforest and more complex structural heterogeneity in the interior forest). Interestingly, the overall γ-diversity in all groups was lower than the maximum diversity within-patch (Table 2). According to Jost (2007), γ-diversity is the uncertainty in species identification when the location of the sample (in a landscape) remains unknown, while α-diversity is the conditional uncertainty when the location is known. Since the information gained can never increase the uncertainty, the α-diversity should always be less than or equal to the γ-diversity. This conclusion is correct if we only quantify the diversity of order zero (richness of canopy height). However, first-order diversity also considered the proportional abundance of height classes. Therefore, the forest patch with the highest canopy height would have the same height richness as the whole landscape, but the proportional frequency of this “rare” height class is always higher in the forest patch (due to the smaller area), thus resulting in a higher diversity value. Furthermore, because γ-diversity was calculated using a set of discrete forest patches instead of a continuous landscape, a large amount of information was lost since these patches do not fully represent the entire study area. Regardless, the low mean value of the first order α-diversity (1Dα) and γ-diversity (1Dγ) in the fragmented area was able to show that structural complexity was significantly lower in this forest compared to an interior, less modified forest condition.

Our result was contrary to the widely held belief that a high disturbance rate can promote structural diversity at the landscape level by altering the light regime and creating more patches of forests with different successional stages (Turner 1989). This idea, initially proposed by Connell (1978) as an explanation for species diversity variation in plants and corals, states that maximum diversity is achieved when competition between dominant species and colonisers reaches equilibrium. Connell later coined the term “Intermediate Disturbance Hypothesis”, but it has received much criticism and has since become a controversial topic in biodiversity (Fox 2013). However, when applied to structural diversity in forests, this theory could provide a reasonable approach to interpreting the effects of disturbance on forest structural heterogeneity (Senf et al. 2020). While a low rate of disturbance can foster old-growth forests with high within-patch heterogeneity, an increase in disturbances will lead to a higher landscape-level diversity by promoting natural regeneration but also hinder the development of forests to late successional stages. Thus, the highest structural complexity is reached at an intermediate level of disturbance, when the trade-off between within-patch and landscape-level diversity is balanced. Senf et al. (2020) tested this hypothesis in two national parks in Germany and concluded that overall structural diversity was highest at a disturbance rate of 0.5–1.5% per year, but rapidly decreased once the disturbance rate exceeded 1.5%. The fact that both within-patch and overall γ-diversity were lower in our degraded forests than in interior forests suggests that disturbance caused by selective logging and cash-crop plantations in the highly fragmented lowlands of Jambi province has already crossed the intermediate limit at which structural complexity can increase.

Conclusion

This work represents a first attempt to quantify multiple edge effects in a highly fragmented and modified tropical landscape. In general, there was clear evidence of an edge effect, likely resulting from interactions between multiple edges, as we found a non-diminishing magnitude associated with a long-lasting distance and homogenous effect from edges in our fragmented degraded forests. On average, we observed a significant decrease of about 40% in all metrics of canopy height and about 25% in some metrics of canopy structure across all transect plots, suggesting that canopy height and canopy structure were more susceptible to edge effects compared to gaps in the canopy. The fact that forest degradation due to edge effects has been consistently found across many structural metrics has highlighted the importance of this phenomenon, particularly as previous studies have reported the possibility of forests affected by edges to develop a post-fragmentation equilibrium which reduces the level of structural complexity and drive the forests towards an earlier successional state (Laurance et al. 1998; Pütz et al. 2011). Regarding structural heterogeneity, our degraded forests exhibited lower levels of complexity at both patch and landscape scales, which points to the fact that the level of disturbance in the degraded forest has reached past the threshold within which overall structural diversity is positively correlated with disturbance. Our findings highlighted the capability of this technology to be implementable over large, forested areas. The complete lack of field surveys makes the approach followed here ideal for remote areas with limited accessibility, as well as making it fully replicable provided medium to high resolution LiDAR data is available (as it is now the case with many regional LiDAR acquisitions being undertaken by local administrations around the world). Furthermore, the set of structural metrics used here are among those most widely used in remote sensing applications, have already implemented extraction pipelines in R and are highly transferrable across different vegetation types and ecosystems.

Finally, given that rainforests are increasingly subjected to high and wide-spread levels of fragmentation, understanding edge effects and other landscape-scale processes will be critical for forest managers to analyse and monitor ecological changes in forests. In this context, our study has confirmed the potential of LiDAR technology to effectively study forest edge effects and the related changes in structural complexity. Future studies on this topic need to be conducted to determine an intermediate level of disturbance that could maximise structural diversity at the landscape scale and to develop interventions that minimise the effect of multiple edges.