Abstract
Context
Soaring birds depend on atmospheric uplifts and are sensitive to wind energy development. Predictive modelling is instrumental to forecast conflicts between human infrastructures and single species of concern. However, as multiple species often coexist in the same area, we need to overcome the limitations of single species approaches.
Objectives
We investigate whether predictive models of flight behaviour can be transferred across species boundaries.
Methods
We analysed movement data from 57 white storks, Ciconia ciconia, and 27 griffon vultures, Gyps fulvus. We quantified the accuracy of topographic features, correlates of collision risk in soaring birds, in predicting their soaring behaviour, and tested the transferability of the resulting suitability models across species.
Results
59.9% of the total area was predicted to be suitable to vultures only, and 1.2% exclusively to storks. Only 20.5% of the study area was suitable to both species to soar, suggesting the existence of species-specific requirements in the use of the landscape for soaring. Topography alone could accurately predict 75% of the soaring opportunities available to storks across Europe, but was less efficient for vultures (63%). While storks relied on uplift occurrence, vultures relied on uplift quality, needing stronger uplifts to support their higher body mass and wing loading.
Conclusions
Energy landscapes are species-specific and more knowledge is required to accurately predict the behaviour of highly specialised soaring species, such as vultures. Our models provide a base to explore the effects of landscape changes on the flight behaviour of different soaring species. Our results suggest that there is no reliable and responsible way to shortcut risk assessment in areas where multiple species might be at risk by anthropogenic structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The exceptionally high energetic demand of flight creates a selective pressure to minimise overall movement costs by exploiting the energy available in the landscape. For flying animals this energy is available in the form of horizontal or vertical air currents (Shepard et al. 2016a, b). Soaring land birds are highly adapted to exploit vertical currents (uplifts) using soaring-gliding flight to a degree that makes them entirely dependent on their availability. By gliding from one uplift to the next, using them as natural lifts, soaring birds can cover large distances with energetic costs shown to be as low as resting level (Duriez et al. 2014). The negligible energetic cost required for soaring-gliding flight is however offset by the disproportionate high cost of flapping flight (Pennycuick 1972, 1973). In fact, the large body mass of soaring birds, combined with their relative short and broad wings, results in low wing loading (body mass/wing area). Low wing loading makes them efficient flyers when atmospheric conditions are appropriate, but reduces their manoeuvrability and locomotor efficiency in the absence of uplifts, constraining their movements to areas and times where uplifts are available (Panuccio et al. 2012; Watanabe 2016; Shamoun-Baranes et al. 2017; Vansteelant et al. 2017).
Since the 1980s, the increasing demand for reduced emissions of greenhouse gases has led to an increasing competition between human infrastructures and flying animals in trying to exploit the energy available in the aerosphere; a competition that Smallwood described as: “(…) wind turbines are simply our means of grabbing energy in which wildlife has already been exploiting for millions of years.” (in: Köppel 2017). Several studies highlight the sensitivity of large soaring birds to wind farms due to several factors: features in the landscape that generate soaring opportunities are often the same that make wind power plants profitable, increasing the rate of encounter of soaring birds with wind farms (Nourani and Yamaguchi 2017); limited manoeuvrability and tendency of focusing their attention on the ground while foraging further increases their risk of collision (De Lucas et al. 2008; Smallwood and Thelander 2008; Marques et al. 2014); finally their low annual productivity and slow maturity amplifies even low rates of individual losses to irrecoverable population level effects ( Smallwood and Thelander 2008; Masden et al. 2010; Sanz-Aguilar et al. 2015; Allinson 2017).
In the last two decades an increasing number of publications are reviewing current measures that aim at mitigating collisions between birds and anthropogenic infrastructures while also highlighting the need for further research in this direction (Gove et al. 2013; Marques et al. 2014; Wang et al. 2015; May et al. 2017; Laranjeiro et al. 2018). Predictive modelling, based on previous knowledge about the species’ behaviour in specific environmental contexts, is considered instrumental when it comes to informing about the forecasted impact of a particular infrastructure on a species of concern. Predicting the occurrence of an energy-efficient flight behaviour such as soaring, based on environmental correlates, cannot be directly translated into a prediction of collision risk, but would help us to understand how a species uses the landscape, potentially at very fine spatial scale. Different modelling studies have shown that topography is one of the primary correlates of increased risk of collision for soaring birds due to the soaring opportunities it provides (De Lucas et al. 2008, Ferrer et al. 2012, Gove et al. 2013, 2016a, Shepard Watson et al. 2018b, Sage et al. 2019). Yet, topography has been only rarely considered as an environmental correlate in models predicting fatality rates (Smallwood et al. 2009 De Lucas et al. 2012a, b) or flight behaviour (Aurbach et al. 2018; Becciu et al. 2019; Katzner et al. 2012; Scacco et al. 2019). Studies investigating soaring behaviour increasingly rely on atmospheric information or weather-derived proxies of thermal and orographic uplifts (Bohrer et al. 2012; Dodge et al. 2014; Péron et al. 2017). However, such information suffer from a mismatch between the fine-scale nature of the uplift events and the limited spatio-temporal resolution of the atmospheric information available.
Scacco et al. (2019) demonstrated a high accuracy of static topographic features, compared to commonly used weather-derived uplift proxies, in predicting soaring behaviour and energy expenditure of the white stork Ciconia ciconia, an obligate soaring bird species. Such a focus has clear advantages for the targeted species. Yet, despite the similarities soaring species share in extracting energy from their environments, and their co-occurrence and high susceptibilities to wind farms, different soaring species tend to show different mortality rates through collision (Janss 2000; De Lucas et al. 2008; Marques et al. 2014; Martín et al. 2018), suggesting a potential drawback of focal species analyses.
Thus, the question as to whether predictive models could be transferred across species boundaries arises. Comparative studies focusing on the prediction of flight behaviour in specific landscapes allow us to look for common patterns and thus offer an opportunity to generalize and potentially transfer predictive models across species. In the attempt to maximise mitigation effects at a community level such generalized models of flight behaviour, if complemented with species-specific biologically meaningful variables, could be used to predict collision risk in specific areas.
In this study we use movement data from two obligate soaring species, the white stork Ciconia ciconia and the griffon vulture Gyps fulvus, in search for converging patterns in the way the two species use their energy landscape to soar. Both species are heavily dependent on soaring flight and on the occurrence of uplifts to move across the landscape. We therefore expect them to have similar environmental requirements to sustain their movement. However, the two species show some morphological differences as well as different foraging strategies: white storks generally forage in open fields and meadows and fly above lowlands; griffon vultures are scavengers, range from lowlands to mountainous landscapes, and have higher body mass and higher wing loading compared to storks (Pennycuick 1972). In four analytical steps we evaluated to what extent the similar flight behaviour of these two species results in a similar use of the landscape, notwithstanding ecological and morphological differences. (1) As a preparatory step, we used GPS locations and accelerometry data to identify soaring and flapping events for both species as proxies of low-cost and high-cost flight, respectively (Scacco et al. 2019). (2) We first considered only the soaring events, and compared the climbing rate (vertical speed) of both species during soaring, to assess whether differences in their morphology, or in the landscape they were exposed to, affected their soaring efficiency. (3) We then considered both soaring and flapping events, and modelled their occurrence using only topographic features, separately for each of the two species; these two models were consequently used to predict and map areas potentially suitable for either of the species to soar. (4) Finally, we compared suitable areas across species and tested the transferability of our models, that is, if areas suitable to one species could predict the soaring behaviour of the other species and vice-versa.
Materials and methods
Datasets
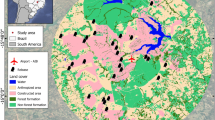
We used GPS and tri-axial accelerometry (ACC) data from two obligate soaring species. The dataset included 84 individuals from four different research projects, available on Movebank (Kranstauber et al. 2011): 57 juvenile white storks on their first migration, tagged in Germany (Flack et al. 2017, 2018), and 27 adult griffon vultures, from two Spanish populations (> 7 years old) and one French population (> 5 years old). The spatial distribution of the dataset defines the extent of the study area (Fig. 1). All animals were equipped with high-resolution, solar GSM-GPS-ACC loggers (e-obs GmbH, Munich, Germany). High-resolution GPS bursts (1 Hz) were collected every 10 or 15 min for 120, 300 or 600 s. ACC data were recorded every 10 min for 3.8 sat 10.54 Hz (40 data points per axis). For details on data collection and data availability see the supplementary material (Table S1).
Segmentation of the flight behaviour
We identified flapping (active) flight events using the ACC data. We applied k-means clustering with three clusters on DBA-z (Dynamic Body Acceleration on the z-axis) and ODBA (overall DBA) (Wilson et al. 2006), which have already been used to identify active flight in soaring birds (Nathan et al. 2012; Duriez et al. 2014; Scacco et al. 2019). We finally defined as flapping events the “most active” bursts associated to heights of more than 100 m above ground (calculated by subtracting the EEA (2013) terrain elevation value from the height above the ellipsoid). The location and height of these events were given by the GPS location closest in time (< 30 s difference). For more details see Scacco et al. (2019) and the supplementary material (S1).
Soaring flight events were characterised by the absence of flapping flight and identified using the high-resolution GPS data (1 Hz sampling positions). We calculated ground speed, vertical speed and turning angle at each GPS location and averaged them on track segments of 15 s duration (average duration of one complete soaring circle (Weinzierl et al. 2016)). Segments with average ground speed of less than 2 ms−1 were considered as non-flight segments and excluded from the analysis. We then applied the Expectation Maximization Binary Clustering (EmbC) to the average vertical speed and the absolute cumulative turning angle of the remaining flight segments (R package EmbC, Garriga et al. 2016). The EmbC segmentation algorithm clustered the 15 s flight segments along each individual’s trajectory into one of the three following behavioural categories: circular soaring (typically in thermal uplifts), linear soaring (usually in orographic uplifts along ridges) and gliding (linear flight segments where birds would loose height and cover distance without flapping their wings). By applying a smoothing function we avoided the occurrence of abrupt and unnatural behavioural changes from one segment to the next along a trajectory (see supplementary material S1.2).
The purpose of the subsequent analyses was to distinguish between the use of soaring and flapping flight, indicative of the presence and absence of atmospheric uplifts, respectively. Gliding segments were thus excluded, and segments classified as linear and circular soaring were pooled into the same general category of soaring, as both indicate the presence through use of atmospheric uplifts. The location of each segment (classified as either soaring or flapping) was defined by its centroid (mean longitude and latitude) location.
Comparison of vertical speeds
We compared the vertical speeds of the two species during soaring, while accounting for the different spatial and temporal scales of the two datasets. We modelled vertical speed using a generalized additive model (GAM) including species as categorical predictor, longitude and latitude as interacting thin plate regression splines, and hour of the day as cyclic cubic regression spline. The response variable vertical speed included negative values, therefore we first applied a translation (by adding its minimum value) and then a square-root transformation to meet the assumptions of a Gaussian distribution of the residuals. The model was fit with a Gaussian distribution and run using the R package mgcv (Woods 2003).
Soaring suitability models
We modelled the occurrence of soaring and flapping flight events based on: elevation (digital elevation model EU-DEM (EEA 2013)), terrain unevenness (ruggedness), unevenness in the slope (steepness of a terrain feature), aspect (compass direction faced by a slope) and aspect unevenness (see Hijmans (2016) and supplementary material S3). These topographic variables, all available at a spatial granularity of 100 m, were included as predictors in a random forest (RF) machine learning algorithm, after verifying the absence of multicollinearity (R package randomForest, Liaw and Wiener 2002). Data from both species were included in two separate models. RF builds many regression trees to distinguish between, and to predict, binary response variables (flapping = 0 vs soaring = 1) based on a set of predictor variables. RF is trained with a portion of the data, while the remaining observations (test data) are used to assess model performance. In our case, we built a double partitioning: (1) we randomly selected about 80% of the individuals per species (46 storks and 22 vultures), and (2) then applied a 90:10% random partitioning on these individuals and used that to build two RF models (one per species); this second step was repeated 10 times per species, where each time the algorithm was trained with a different 90% of the data and evaluated with the remaining 10%. The 20% of the individuals left out from the first partitioning did not contribute to the predictive models and were later used to cross-validate the prediction maps extrapolated from the models (Fig. S2 in supplementary material). Therefore the 90:10% partitioning allows us to measure the performance of the RF in predicting the same pool of individuals the model was built on, whereas the 80:20% partitioning represents a more realistic validation of the extrapolated maps, mimicking the situation in which an external researcher was to use these maps to predict the soaring behaviour of an independent set of individuals (Section “Cross-species prediction of soaring events”). The performance of the two RF models was evaluated in terms of: (i) area under the curve (AUC) of the receiver operating characteristic (ROC); (ii) sensitivity, proportion of soaring locations correctly classified; (iii) specificity, proportion of flapping locations correctly classified (Franklin 2009). These are threshold-dependent measurements (their values depend on our classification of the predicted probability into 0 s and 1 s), and were measured at a probability threshold where flapping and soaring were equally well classified (minimum difference between sensitivity and specificity).
Soaring suitability maps
We used the two RF models of soaring suitability (one for each species) and the topographic raster layers corresponding to the RF predictors (spatial granularity of 100 m) to extrapolate two maps of soaring suitability across the study area (Fig. 1). RF, like other machine learning algorithms, is quite unreliable when extrapolating outside the range of the predictors’ values provided for training. We thus omitted raster cells containing environmental values outside that range, and then used each of the ten runs of the RF model to predict the soaring suitability over the manipulated rasters. Each prediction layer (10 per model) was then classified into a binary map (0 or 1) using the threshold where flapping and soaring were classified with the same accuracy (Franklin 2009). We then computed the pixel average of the 10 binary layers, obtaining one final raster per species, with values ranging from 0 to 1. This final prediction map therefore informed us about the soaring suitability in each pixel but also about the model agreement. For the next steps of the analysis we included only pixels with at least 80% agreement, i.e. pixels for which at least 8 out of 10 binary layers agreed on being unsuitable or suitable for soaring (values ≤ 0.2 or ≥ 0.8). Pixels with values ≤ 0.2 were considered as unsuitable (0), pixels ≥ 0.8 as suitable (1). We then compared the soaring suitability maps obtained for the two species and we randomly sampled 100’000 locations (pixels) from areas of the map that were suitable to one or the other species (50’000 per species). We used this dataset to describe and quantify the difference between the two prediction maps in terms of topographic variables used in the models and compared their distribution.
Cross-species prediction of soaring events
For each species we used 20% of the individuals (11 storks and 5 vultures) to test whether the observed soaring events of each species could have been reliably predicted using the soaring suitability map produced from data of either species (in section “Soaring suitability maps”). We associated the location of each observed soaring or flapping event to the corresponding soaring suitability value (0 or 1) predicted by both the storks and the griffon vultures’ maps. We then ran two GLMMs (generalized linear mixed effect models) per species, using the observed soaring and flapping events as binary response variable in both models, and using soaring suitability as the only covariate: in one model the soaring suitability predicted by the storks’ map, and in the other model the soaring suitability predicted by the vultures’ map (R package lme4, Bates et al. 2014). Individual identity was included as random intercept in all models. The importance of soaring suitability as predictor was assessed comparing the AIC (Akaike Information Criterion) of each species’ model with the respective null models, from which the soaring suitability was excluded (only containing the observed soaring events as response variable and the individual identity as random intercept). Models were fitted using a Bernoulli distribution with a clog-log link function, more appropriate for unbalanced samples (in our case, considerably more soaring than flapping events) (Zuur et al. 2009). All analyses were run in R (R Core Team 2020).
Results
Segmentation of the flight behaviour
Soaring and flapping events were classified based on data collected with different instruments running on different sampling schedules (GPS and ACC, respectively). We thus compared the amount of time spent soaring relative to the total duration of the classified GPS segments, and the amount of time spent flapping relative to the total duration of the classified ACC bursts. The storks in our study spent soaring 52% of the total flight time recorded by the GPS sensor (ca. 597 h), and spent flapping 1.9% of the flight time recorded by the ACC sensor (ca. 103 h). Similarly to storks, vultures in our study were soaring for 51.8% of their flight time (based on ca. 1′764 h of GPS recordings) and flapped only for 1.6% of their flight time (based on ca. 292 h of ACC recordings).
The final dataset, excluding missing topographic information, consisted of 11′531 observations for the storks (9′797 soaring and 1′734 flapping) and 32′633 for the vultures (29′047 soaring and 3′586 flapping).
Comparison of vertical speed
We used a GAM to compare the vertical speed of the two species. The model included a total of 37′774 soaring events (9′180 from storks and 28′594 from griffon vultures). The average vertical speed in ms−1 was 0.81 ± 0.006 for the storks and 1.23 ± 0.005 for the vultures (mean ± s.e.). The model, accounting for geographic coordinates and hour of the day, predicted the vertical speed to be 0.33 ms−1 significantly higher in vultures than in storks [Vultures = 0.1 ± 0.07 (estimate ± s.e.)]. Hour of the day and geographic coordinates had also a significant effect, suggesting that climbing rate would be higher in central hours of the day and in specific regions of the study area (Table S2, Fig. S1).
Soaring suitability models
Based on 80% of the individuals (46 storks and 22 vultures), a total of 9′901 observations were available for the stork model (8′488 soaring and 1413 flapping), and 26′673 for the vulture model (24′067 soaring and 2′606 flapping). The RF model based on stork data resulted in a higher accuracy than the vulture model [AUC stork model: 0.83 ± 0.02; AUC vulture model: 0.71 ± 0.02 (mean ± s.d.); for comparison, a random model is expected to have an AUC of 0.5] (Fig. 2). The stork model also had a better ability to discriminate soaring from flapping locations, that is a higher proportion of soaring and flapping locations were correctly classified. In fact, the stork model could correctly predict, on average, 75.0% (± 2.0%) of the soaring and flapping locations, while only 63.0% (± 1.5%) were correctly predicted by the vulture model. The complete output of the two models can be found in supplementary material (Table S3). In both, the stork and vulture models, the two measures of variable importance (the decrease in accuracy and decrease in node impurity) highlighted terrain elevation, terrain ruggedness and slope unevenness as the most important variables in predicting soaring opportunities. Also the aspect (compass direction faced by a slope) proved to be an important variable, but only in the stork model (Fig. S4 in supplementary material).
ROC curves of the two soaring suitability models, in green for the stork model and in purple for the vulture model, overlaid for better comparison. The area under the curve (AUC) represents the accuracy of the models, measured on the test dataset. The gray dashed line represents a model whose accuracy is comparable to random (AUC = 0.5). Sensitivity and commission rate values were averaged across the ten runs of each model (solid dots), and the error bars show their standard deviations
Soaring suitability maps
We used the models to classify an area of about 0.95 million km2 for the storks and 0.97 million km2 for the vultures (Fig. 3A, B). Only 21% of the storks’ map was predicted to be suitable for them to soar, whereas in the case of vultures’ map, the area suitable to soar was estimated at 80%. After removing non-classified raster cells from both maps, the classified area available for comparison across species amounted to 0.86 million km2; 20.5% of this area was predicted as suitable to both species, and 18.8% unsuitable to both species to soar (Fig. 3C). 59.9% of the total area was predicted to be suitable to vultures only, whereas only 1.2% was available exclusively to storks, meaning that most of the area suitable to storks was also suitable to vultures, but not vice-versa.
Soaring suitability maps extrapolated from the stork (A) and the vulture (B) models. Both maps show in colours areas (cells) predicted to be suitable to the species to soar and in black unsuitable cells. Gray represents unclassified cells (containing missing values among the predictors). In (C) a prediction map produced by combining the suitability maps of the two species, showing in light blue cells that are suitable to both species, where the soaring opportunities overlap; in green cells that are available only to storks (not visible due to the small percentage); in purple cells suitable only to vultures; in black cells that are unsuitable to both species; in gray unclassified cells
The range of the topographic variables included in the model did not highlight any species-specific difference, suggesting that over the duration of the study, the two species were exposed to similar environments (in terms of the considered topographic parameters) (Fig. 4). The main difference between areas suitable to one or the other species concerned the distribution of aspect and terrain elevation: storks, unlike vultures, were selective for aspect, with a peak in the distribution around 200 degrees (slopes oriented S-SW) (Fig. 4D); high terrain elevations seem to be suitable for vultures to soar, but not for storks (Fig. 4A).
Cross-species prediction of soaring events
The two stork models (one using the storks’ map as co-variate, one using the vultures’ map) showed that the probability of soaring significantly increased in areas predicted as suitable by the suitability map of either species, but was stronger for the model including the prediction based on storks [Storks’ suitability map = 1.42 ± 0.12; vultures’ suitability map = 0.59 ± 0.15 (GLMM estimate ± s.e.)]. The AIC of both of the stork models was lower compared to the respective null model [AIC storks’ suitability map = 695.8; vultures’ suitability map = 859.5; null model = 870.71]. Both these results suggest that in the case of the storks, including a static soaring suitability map as covariate in the model helps to predict their soaring behaviour (Table 1A).
In contrast, both vulture models showed a weak and non-significant relationship between the soaring suitability values predicted by the two maps and the observed soaring events. The effect size was small in both cases and the AICs of both models were comparable to the null model. Consequently and in contrast to the stork models, both the static soaring suitability maps did not improve our prediction of vultures’ soaring behaviour (Table 1B).
In all models, the marginal R2, i.e. the variance explained by the fixed effects (the soaring suitability maps), was much lower than the conditional R2, the variance explained by the entire model including the random effect (individual identity). This is indicative of strong intra-specific differences in the way individuals used the landscape to soar, particularly evident in the stork models (Table 1A).
Discussion
Predicting the occurrence of soaring flight based on environmental correlates helps us understand how particular species use the landscape to fly efficiently, and can be instrumental to minimise collision risk with anthropogenic infrastructure. However, multiple species of concern often coexist in the same area, and our comparative study is a first attempt to test transferability of predictive models across species with similar flight behaviour.
Our results indicate that, despite the superficially similar soaring behaviour, white storks and griffon vultures have different environmental requirements and that soaring suitability models cannot and should not be transferred between species. The soaring suitability maps extrapolated from our models showed that only 20.5% of the classified study area was available to both species to soar. Most of the area suitable to the storks was also available to the vultures, but not vice-versa, implying that vultures had a larger area potentially available for soaring. Vultures had a higher vertical speed, soared in a variety of landscape conditions, and contrary to storks their soaring flight was not related to a specific range of aspect values. Finally, our results concerning model transferability showed that a model based on one species performed poorly in predicting the soaring events of the second species.
Both the larger area available to soar and the lower specific topographic requirements, might depict vultures as more flexible fliers. We found that the vultures’ vertical speed was higher than that of storks; due to their higher body mass and higher wing loading, vultures are known to need stronger uplifts to soar, and to depend more on the specific environmental conditions able to produce such support (Pennycuick 1973, 2008; Shamoun-Baranes et al. 2003). Therefore, the vultures’ higher climbing rate is an indication for them using disproportionately stronger uplifts (better in quality) than those used by storks. This suggests that storks are able to take advantage of weaker uplifts compared to vultures, and it seems enough for them to rely on uplift occurrence rather than on uplift quality. In contrast, vultures need stronger uplifts to support their larger mass; they therefore rely on uplift quality and should be more selective in terms of soaring conditions.
Our results therefore confirm that vultures should be using stronger uplifts, which can only be generated under specific environmental conditions, but at the same time convey vultures as flexible fliers as, based on the soaring suitability map, most of the study area was potentially available for vultures to soar.
We believe that the source of this contradiction is that our soaring suitability models are based exclusively on static topography-related covariates. A recent study showed that static topographic variables are effective in predicting the occurrence, but not so much the quality of uplifts used by storks (Scacco et al. 2019). In this follow up study, our static model based on topography confirmed its high accuracy in predicting soaring occurrence in storks, but had a lower accuracy in vultures, both in the training and test datasets. This suggests that topography alone cannot predict vultures’ soaring behaviour, probably due to limited predictive performance in uplift quality, which they heavily rely on, and for which the use of atmospheric covariates in the prediction is expected to be crucial (Aurbach et al. 2018; Becciu et al. 2019). Consequently, the contradiction which emerged from our results, featuring vultures as both flexible flyers and selective soarers, represents shortcomings of the methods used to predict the occurrence of soaring behaviour in vultures. Our soaring suitability model, without the addition of dynamic atmospheric variables, can thus not be considered a reliable representation of the soaring opportunities available to vultures.
This interpretation has implications also on modelling species occurrence at a global scale. The higher the wing loading of a species, the more its movement and it distribution will be restricted in space and time not only in relation to where, but mainly when, uplift conditions are optimal (Williams et al. 2020). The flight of such specialised species will therefore be more dependent on atmospheric conditions than on static features. This implies that more knowledge is required to accurately predict their soaring flight (Soultan and Safi 2017). The link between species’ movement capacity and biogeography (geographical distribution of species) is often overlooked, or when taken into account, it mostly relates to the obstacle posed by large ecological barriers to colonization processes (Cumming et al. 2012; Mellone 2020). In highly specialised soaring species, considering the link between biogeography and movement only in relation to colonization would underestimate the role of uplifts as essential part of the niche of these species, for which uplifts should be considered among the suite of resources they need in order to exist in a certain area. Long accepted definitions of ecological barriers such as water bodies for soaring birds, are now being revisited as more flexible than previously thought (Nourani et al. 2021), and should be adapted to accommodate the diversity in movement capacity among species.
Individual differences in flight behaviour also exist within the same species, for instance as a result of individual developmental stage (flight experience) or motivation (e.g. scavenging, hunting, migrating), which are known to affect some aspects of the birds’ flight behaviour, for example route selection (Efrat et al. 2019), flight speed, distance and duration (Sergio et al. 2014) and energy expenditure (Rotics et al. 2016). Juvenile soaring birds flying in thermal uplifts under-perform compared to adults, showing lower climbing rates in challenging wind conditions (Harel et al. 2016). In the case of the juvenile storks included in our study, by ignoring age difference we might have underestimated the strength of the uplifts adult storks would use for soaring. Such bias, if present, would however have made the storks behave more similar to the heavier vultures (because of their higher wing loading), and thus potentially increased model transferability. Storks and vultures in our study also differed in terms of motivation (foraging vs migrating) causing them to fly over different landscapes. However, we would expect such differences in motivation to manifest in a different selection of land cover types and habitat composition, variables that we did not include in our models. Our models only relied on topographic variables, and the resulting soaring suitability maps suggest that the two species experienced similar ranges of topographic parameters and therefore used similar landscapes pertaining to the variables considered (Fig. 4). In our cross-validation models, however, we found evidence for strong inter-individual differences in the use of the environment. Individual, age, or motivation specific information are rarely available or considered, and our opportunistic use of the data was in mimiking the way a conservation practitioner or an external researcher would be likely to approach the task. The final aim of our study was on testing the transferability of soaring suitability models across species boundaries and individual variation. Including intra-specific information in our soaring suitability models would, if anything, conservatively support our statements, since they further restrict model transferability.
Our predictive models of soaring opportunities represent an attempt to describe the potential energy available in the landscape to allow soaring species to move efficiently. However, the distribution of soaring opportunities is only one of the resources required by these species. Species-specific patterns of use of the landscape are also mediated by other biologically relevant factors, not targeted by this study, such as the distribution of food resources or nesting opportunities. These factors vary extensively among species and have been found to be related to vulture fatalities at wind farms (Carrete et al. 2012). Associating species-specific biologically relevant variables for all coexisting species in an area of interest, with species-specific models of flight behaviour, could inform the siting of anthropogenic infrastructures and help minimising collision risk at fine scale.
Conclusions
Static landscape features greatly influence the energy available to soaring birds in the landscape and thus their movements. For some species, static variables alone are however not sufficient and need to be associated to atmospheric information to produce more reliable predictions of flight behaviour. We suggest that using the soaring behaviour of the species to identify the occurrence of uplift events is instrumental to isolate only those uplifts that can be effectively used by that species. Thus it is possible to build an environmental model to extrapolate uplift occurrence over large areas. As tempting as it might become to apply the same predictive model to species with a similar flight behaviour, the results of this study warn against transferring model predictions across species. The extrapolated maps represent the energy available in the landscape for the species used to build the model. Energy landscapes are therefore species-specific, with the consequence that the same landscape varies in the soaring opportunities it offers to different species, and affects their movement pattern differently.
Our study advocates for a cautious and species-specific way to interpret and apply predictive modelling in conservation ecology. The use of species-specific prediction models would allow for more flexibility in the choice of the important variables to consider, including meaningful biological information that differ among species. Accounting for these differences seems crucial when predicting movement and landscape connectivity and there might be no reliable and responsible way to shortcut risk assessment in areas where multiple species are at risk of collision with anthropogenic structures.
Data availability
The storks data used for this study are deposited in the Movebank Data Repository (http://dx.doi.org/10.5441/001/1.bj96m274). The vultures data are available in Movebank upon reasonable request and with permission of the study owners (supplementary material Table S1).
References
Allinson T (2017) Introducing a new avian sensitivity mapping tool to support the siting of wind farms and power lines in the middle east and Northeast Africa. In: Köppel J (Ed) Wind energy and wildlife interactions. Presentations from the CWW2015 Conference’, Springer, 207–218
Aurbach A, Schmid B, Liechti F, Chokani N, Abhari R (2018) Complex behaviour in complex terrain-modelling bird migration in a high resolution wind field across mountainous terrain to simulate observed patterns. J Theor Biol 454:126–138
Bates D, Maechler M, Bolker B, Walker S (2014) lme4: Linear mixed-effects models using Eigen and S4, R package version 1.0–6. URL: https://cran.r-project.org/package=lme4
Becciu P, Menz MH, Aurbach A, Cabrera-Cruz SA, Wainwright CE, Scacco M, Ciach M, Pettersson LB, Maggini I, Arroyo GM, Buler JJ, Reynolds DR, Sapir N (2019) Environmental effects on flying migrants revealed by radar. Ecography 42(5):942–955
Bohrer G, Brandes D, Mandel JT, Bildstein KL, Miller TA, Lanzone M et al (2012) Estimating updraft velocity components over large spatial scales: contrasting migration strategies of golden eagles and turkey vultures. Ecol Lett 15(2):96–103
Carrete M, Sánchez-Zapata JA, Benítez JR, Lobón M, Montoya F, Donázar JA (2012) Mortality at wind-farms is positively related to large-scale distribution and aggregation in griffon vultures. Biol Cons 145(1):102–108
Cumming GS, Gaidet N, Ndlovu M (2012) Towards a unification of movement ecology and biogeography: conceptual framework and a case study on Afrotropical ducks. J Biogeogr 39(8):1401–1411
De Lucas M, Janss GFE, Whitfield DP, Ferrer M (2008) Collision fatality of raptors in wind farms does not depend on raptor abundance. J Appl Ecol 45(6):1695–1703
De Lucas M, Ferrer M, Bechard MJ, Mu ̃noz AR (2012a) Griffon vulture mortality at wind farms in southern Spain: Distribution of fatalities and active mitigation measures. Biol Conserv 147(1):184–189. https://doi.org/10.1016/j.biocon.2011.12.029
De Lucas M, Ferrer M, Janss GFE (2012b) Using wind tunnels to predict bird mortality in wind farms: the case of griffon vultures. PLoS ONE 7(11):1–7
Dodge S, Bohrer G, Bildstein K, Davidson SC, Weinzierl R, Bechard MJ et al (2014) Environmental drivers of variability in the movement ecology of turkey vultures (Cathartes aura) in North and South America. Phil Trans r Soc B 369(1643):20130195
Duriez O, Kato A, Tromp C, Dell’Omo G, Vyssotski AL, Sarrazin F, Ropert-Coudert Y (2014) How cheap is soaring flight in raptors? a preliminary investigation in freely-flying vultures. PLoS ONE 9(1):e84887
EEA (2013) European environment agency - digital elevation model over europe (EU-DEM). https://www.eea.europa.eu/data-and-maps/data/eu-dem
Efrat R, Hatzofe O, Nathan R (2019) Landscape-dependent time versus energy optimizations in pelicans migrating through a large ecological barrier. Funct Ecol 33(11):2161–2171
Ferrer M, De Lucas M, Janss GFE, Casado E, Mu ̃noz AR, Bechard MJ, Calabuig CP (2012) Weak relationship between risk assessment studies and recorded mortality in wind farms. J Appl Ecol 49:38–46
Flack A, Nagy M, Fiedler W, Couzin ID, Wikelski M (2018) From local collective behavior to global migratory patterns in white storks. Science 360(6391):911–914
Flack A, Fiedler W, Wikelski M (2017) Data from: wind estimation based on thermal soaring of birds. https://www.movebank.org/node/15294
Franklin J (2009) Mapping species distributions. Spatial inference and prediction. University Press, Cambridge
Garriga J, Palmer JR, Oltra A, Bartumeus F (2016) Expectation-maximization binary clustering for behavioural annotation. PLoS ONE 11(3):1–26
Gove B, Langston R, McCluskie A, Pullan J, Scrase I (2013) Wind farms and birds: an updated analysis of the effects of wind farms on birds, and best practice guidance on integrated planning and impact assessment. RSPB/BirdLife in the UK, in ‘Convention on the conservation of European wildlife and natural habitats - Bern Convention Bureau Meeting’
Harel R, Horvitz N, Nathan R (2016) Adult vultures outperform juveniles in challenging thermal soaring conditions. Sci Rep 6:27865. https://doi.org/10.1038/srep27865
Hijmans RJ (2016) Raster: geographic data analysis and modeling. R package version 2.5–8. https://cran.r-project.org/package=raster
Janss GF (2000) Avian mortality from power lines: a morphologic approach of a species-specific mortality. Biol Cons 95(3):353–359
Katzner TE, Brandes D, Miller T, Lanzone M, Maisonneuve C, Tremblay JA, Mulvihill R, Merovich GT Jr (2012) Topography drives migratory flight altitude of golden eagles: implications for on-shore wind energy development. J Appl Ecol 49(5):1178–1186
Köppel J (2017) From the editor - perspectives in ‘Wind energy and wildlife interactions’. In: Köppel J (ed) Wind energy and wildlife interactions. Presentations from the CWW 2015 Conference’, Springer, pp v–xiv
Kranstauber B, Cameron A, Weinzerl R, Fountain T, Tilak S, Wikelski M, Kays R (2011) The Movebank data model for animal tracking. Environ Model Softw 26(6):834–835
Laranjeiro T, May R, Verones F (2018) Impacts of onshore wind energy production on bird sand bats: recommendations for future life cycle impact assessment developments. Int J Life Cycle Assess 23(10):2007–2023
Liaw A, Wiener M (2002) Classification and regression by randomForest. R News 2(3):18–22. http://cran.r-project.org/doc/Rnews/
Marques AT, Batalha H, Rodrigues S, Costa H, Pereira MJR, Fonseca C, Mascarenhas M, Bernardino J (2014) Understanding bird collisions at wind farms: An updated review on the causes and possible mitigation strategies. Biol Conserv 179:40–52.
Martín B, Perez-Bacalu C, Onrubia A, De Lucas M, Ferrer M (2018) Impact of wind farms on soaring bird populations at a migratory bottleneck. Eur J Wildl Res 64(3):1–10
Masden EA, Fox AD, Furness RW, Bullman R, Haydon DT (2010) Cumulative impact assessments and bird/wind farm interactions: Developing a conceptual framework. Environ Impact Assess Rev 30(1):1–7.
May R, Gill A, Köppel J, Langston R, Reichenbach M, Scheidat M, Smallwood S, Voigt C, Hüppop O, Portman M (2017) Future research directions to reconcile wind turbine–wildlife interactions. In: Köppel J (ed) Future research directions to reconcile wind turbine–wildlife interactions. Springer, Berlin, pp 255–276
Mellone U (2020) Sea crossing as a major determinant for the evolution of migratory strategies in soaring birds. J Anim Ecol 89(6):1298–1301
Nathan R, Spiegel O, Fortmann-Roe S, Harel R, Wikelski M, Getz WM (2012) Using tri-axial acceleration data to identify behavioral modes of free-ranging animals: general concepts and tools illustrated for griffon vultures. J Exp Biol 215(6):986–996
Nourani E, Yamaguchi N (2017) The effects of atmospheric currents on migratory behavior of soaring birds: a review. Ornithol Sci 16(1):5–15
Nourani E, Bohrer G, Becciu P, Bierregaard RO, Duriez O, Figuerola J et al (2021) The interplay of wind and uplift facilitates over-water flight in facultative soaring birds. Proc R Soc B 288:20211603.https://doi.org/10.1098/rspb.2021.1603
Panuccio M, Agostini N, Premuda G (2012) Ecological barriers promote risk minimisation and social learning in migrating short-toed snake eagles. Ethol Ecol Evol 24(1):74–80. https://doi.org/10.1080/03949370.2011.583692
Pennycuick CJ (1972) Soaring behaviour and performance of some east african birds, observed from a motor-glider. Ibis 114(2):178–218
Pennycuick CJ (1973) The soaring flight of vultures. Sci Am 229(6):102–109
Pennycuick CJ (2008) Modelling the flying bird, Elsevier.
Péron G, Fleming CH, Duriez O, Fluhr J, Itty C, Lambertucci S et al (2017) The energy landscape predicts flight height and wind turbine collision hazard in three species of large soaring raptor. J Appl Ecol 54(6):1895–1906
R Core Team (2020),R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Rotics S, Kaatz M, Resheff YS, Turjeman SF, Zurell D, Sapir N, Eggers U, Flack A, Fiedler W, Jeltsch F, Wikelski M, Nathan R (2016) The challenges of the first migration: movement and behaviour of juvenile vs. adult white storks with insights regarding juvenile mortality. J Anim Ecol 85:938–947
Sage E, Bouten W, Hoekstra B, Camphuysen KC, Shamoun-Baranes J (2019) Orographic lift shapes flight routes of gulls in virtually flat landscapes. Sci Rep 9(1):1–10.
Sanz-Aguilar A, Sánchez-Zapata JA, Carrete M, Benítez JR, Ávila E, Arenas R, Donázar JA (2015) Action on multiple fronts, illegal poisoning and wind farm planning, is required to reverse the decline of the Egyptian vulture in southern Spain. Biol Cons 187:10–18
Scacco M, Flack A, Duriez O, Wikelski M, Safi K (2019) Static landscape features predict uplift locations for soaring birds across Europe. Royal Soc Open Sci 6(1):181440
Sergio F, Tanferna A, De Stephanis R, Jiménez LL, Blas J, Tavecchia G, Preatoni D, Hiraldo F (2014) Individual improvements and selective mortality shape lifelong migratory performance. Nature 515(7527):410–413
Shamoun-Baranes J, Leshem Y, Yom-Tov Y, Liechti O (2003) Differential use of thermal convection by soaring birds over central Israel. Condor 105:208–218.
Shamoun-Baranes J, Liechti F, Vansteelant WM (2017) Atmospheric conditions create freeways, detours and tailbacks for migrating birds. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 203(6–7):509–529
Shepard ELC, Williamson C, Windsor S (2016a) Fine-scale flight strategies of gulls in urban airflows indicate risk and reward in city living. Phil Trans R Soc B 371(1704):20150394
Shepard E, Ross A, Portugal S (2016b) Moving in a moving medium: new perspectives on flight. Phil Trans R Soc B. https://doi.org/10.1098/rstb.2015.0382
Smallwood KS, Thelander C (2008) Bird mortality in the Altamont Pass wind resource area, California. J Wildl Manag 72(1):215–223
Smallwood KS, Neher L, Bell DA (2009) Map-based repowering and reorganization of a wind resource area to minimize burrowing owl and other bird fatalities. Energies 2(4):915–943
Soultan A, Safi K (2017) The interplay of various sources of noise on reliability of species distribution models hinges on ecological specialisation. PLoS ONE 12(11):1–19
Vansteelant WM, Shamoun-Baranes J, McLaren J, van Diermen J, Bouten W (2017) Soaring across continents: decision-making of a soaring migrant under changing atmospheric conditions along an entire flyway. J Avian Biol 48(6):887–896
Wang S, Wang S, Smith P (2015) Ecological impacts of wind farms on birds: Questions, hypotheses, and research needs. Renew Sustain Energy Rev 44:599–607.
Watanabe YY (2016) Flight mode affects allometry of migration range in birds. Ecol Lett 19(8):907–914
Watson RT, Kolar PS, Ferrer M, Nygard T, Johnston N, Hunt WG, Smit-Robinson HA, Farmer CJ, Huso M, Katzner TE (2018) Raptor interactions with wind energy: case studies from around the world. J Raptor Res 52(1):1–18
Weinzierl R, Bohrer G, Kranstauber B, Fiedler W, Wikelski M, Flack A (2016) Wind estimation based on thermal soaring of birds. Ecol Evol 6(24):8706–8718
Williams HJ, Shepard E, Holton MD, Alarcón P, Wilson R, Lambertucci S (2020) Physical limits of flight performance in the heaviest soaring bird. Proc Natl Acad Sci 117(30):17884–17890
Wilson RP, White CR, Quintana F, Halsey LG, Liebsch N, Martin GR, Butler PJ (2006) Moving towards acceleration for estimates of activity-specific metabolic rate in free-living animals: the case of the cormorant. J Anim Ecol 75(5):1081–1090
Woods SN (2003) Thin-plate regression splines. J Royal Stat Soc 65(1):95–114
Zuur A, Ieno EN, Walker N, Saveliev AA, Smith GM (2009) Mixed effects models and extensions in ecology with R. Springer Science & Business Media, Berlin
Funding
Open Access funding enabled and organized by Projekt DEAL. We acknowledge funding from the Max Planck Institute of Animal Behavior. MS was supported by the German Academic Exchange Service (DAAD) and by the International Max Planck Research School for Organismal Biology. The collection of the Spanish vultures’ data was funded by the Project RNM-1925 (Junta de Andalucía) and the Comunidad de Bardenas Reales de Navarra. Environmental products courtesy of European Environmental Agency.
Author information
Authors and Affiliations
Contributions
MS KS and MW conceived and designed the study, EA JAD AF JASZ and OD provided the tracking data, MS and KS carried out the analyses, interpreted the results and wrote the first draft of the manuscript. All authors contributed suggestions and text to subsequent drafts. All authors gave final approval for publication.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scacco, M., Arrondo, E., Donázar, J.A. et al. The species-specificity of energy landscapes for soaring birds, and its consequences for transferring suitability models across species. Landsc Ecol 38, 239–252 (2023). https://doi.org/10.1007/s10980-022-01551-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-022-01551-4