Introduction

Community composition and local abundance of species, at the landscape scale, are shaped by both environmental features and biotic interactions occurring among community members. The effect of abiotic environment and biotic interactions on community assembly has been largely studied within the framework of environmental filtering (Kraft et al. 2015). This conceptual framework suggests that environmental constraints and biotic interactions contribute to select ecological traits, filtering out species with less adapted traits for a given condition, thus determining local extinctions (Kraft et al. 2015; Germain et al. 2018). These filtering effects are supposed to act on a hierarchical level, and at different spatial and temporal scales: from higher processes of regional extinction and dispersal, occurring at evolutionary timescales (Ricklefs 2004), to lower processes of environmental (e.g. landscape features) and biotic filtering (e.g. inter-specific competition or predation), that shapes species composition and abundances of local populations within a realized community, living in a given location or landscape patch (Keddy 1992; Fig. 1). This classical, well-established, heuristic approach extended toward 2000’s (e.g. Swenson et al. 2012; Whitfeld et al. 2012). However, in recent years some ecologists gave rise to a debate on the viability of the environmental filtering concept. In particular, the usefulness of observational studies in disentangling the effect of environment and within-community biotic interactions has been questioned (Kraft et al. 2015; Cadotte and Tucker 2017). This is because the ecological effects of both competition between community members and the influence of environment on species occurrence and abundance are not independent, and observational studies preclude investigation into their interplay (Kraft et al. 2015). This debate expanded the field of application of environmental filtering concept (e.g. Gearty et al. 2021), boosting research in novel approaches capable of disentangling these ecological processes (e.g. Germain et al. 2018).

Fig. 1
figure 1

Graphical representation of the study rationale and conceptual framework

Full size image

In this context, the application of Hierarchical Models—i.e. Occupancy and N-mixture models (see for instance Kéry and Royle 2015, 2020)—seems promising to better disentangle the effect of environment and biotic interactions within communities exposed to different ecological gradients or anthropogenic disturbances (Brodie et al. 2017; Montano-Centellas et al. 2021; Basile et al. 2021; Rosa et al. 2022a), because these models can be fit to a variety of ecological process (Kéry and Royle 2015, 2020) and account for imperfect detection (i.e. the difficulty of observing rare and secretive species). In fact, community Occupancy and N-mixture models have been recently developed to account for biotic interactions occurring between species and allow to disentangle the contribution of the environment from the one of biotic interactions on occurrence and local abundance of each species (see Kéry and Royle 2020 for a detailed discussion). These models can be divided in two groups: (i) models accounting for direct biotic interactions in model structure, i.e. the realized abundance or occurrence of a species has a direct effect on the realized state of another species (Waddle et al. 2010; Clare et al., 2016; Brodie et al. 2018), and (ii) models that account for symmetric interactions between species, meaning that the effect of biotic interaction is not included in model structure, but is inferred by means of residual correlation between the realized state of two species (i.e. abundance or occurrence; Pollock et al. 2014; Tobler et al. 2019). Both models, with direct and symmetric interactions, are effective to infer species interaction for both complex and reduced species pools: however, models with direct interactions are usually employed when few species are present and a clear effect of one species on another is assumed a priori (e.g. Brodie et al. 2018; Rosa et al. 2022a). Conversely, models with symmetric interaction are usually adopted when many species are analyzed or when direction of biotic interaction cannot be a priori hypothesized (but see Basile et al. 2021). Therefore, these models represent a promising and innovative framework to understand the determinants of community composition and structure, and to quantify the hierarchical processes of environmental and biotic filtering on the observed local biological communities (Kéry and Royle 2020; Ovaskainen and Abrego 2020). Specifically, significant species interactions observed after accounting for environmental filtering, can be attributable to different ecological processes, depending on the trophic level of the community members: (i) inter-specific competition for resources should result in negative interactions between species of the same trophic level, (ii) interactions occurring between species at different trophic levels, mediated by predator–prey dynamics, could both result in positive abundance interactions, when predators’ pressure is low or prey density is high, or negative abundance interactions when predators’ pressure is more pronounced (Chase et al. 2002).

The Mediterranean global biodiversity hotspot (Myers et al. 2000) is recognized as an example of human-modified dynamic landscape, constantly shaped for millennia by long-lasting and constantly evolving land use practices (Blondel and Aronson 1999). Indeed, human activities in the Mediterranean basin have determined a dynamic mosaic of different habitats and vegetation, such as scrublands, forests, and agricultural patches (Blondel 2006). Within Europe this heterogeneous landscape, where patches of different natural vegetation and agricultural land-use coexist at a small scale, is capable of maintaining high levels of both taxonomic and functional biodiversity (e.g. Burel and Baudry 1995; Potts et al. 2006; Sirami et al. 2010). For this reason, ecologists historically spent great efforts to understand the ecological processes determining biodiversity patterns within the Mediterranean region. In particular, they were intrigued by biological community assembly rules at landscape scale: considering interactive effects of historical land-use practices (e.g. Ruiz 1990; Farina 1997), patchy human perturbances such as fires (e.g. Brotons et al. 2005; Santos and Cheylan, 2013), and more recently by considering the effects of regionally diffuse dynamics, such as land-abandonment (Plieninger et al. 2014), climate change and diffusion of pathogens (e.g. Casazza et al. 2021).

Among the many biological communities exposed to anthropogenic landscape changes in the Mediterranean region, Reptiles represent one of the most endangered class of vertebrates (Cox et al. 2022). The effects of anthropogenic pressures, such as forest fires and intensive land use practices, on reptile populations and communities is therefore well studied (e.g. Ribeiro et al. 2009; Rotem et al. 2013; Guiller et al. 2022). However, a comprehensive evaluation of the effects of environmental features and biotic interactions in Mediterranean human-modified landscapes is poorly understood. In this study we aim at using observational data from a realized community at the landscape scale to evaluate if, once landscape metrics are accounted for, species interactions can still influence local abundance. Adopting community N-mixture models with symmetric interactions, we estimated differential effects of landscape and biotic interactions on the composition and local abundance of a Mediterranean reptile community, focusing on landscape metrics in an area where both natural, semi-natural and human-modified environments are present. Moreover, we also aim at inferring landscape requirements of different species within the community, to properly inform local conservation programs and landscape management plans.

Methods

Study rationale and conceptual framework

In the present study we aimed at investigating landscape-scale determinants of the local abundance of a Mediterranean reptile community, framing community assembly processes within the environmental filtering conceptual model (Keddy 1992). In our study we considered a reptile community in central Italy, which we repeatedly sampled in 52 sites, covering about 60 km2 of a Mediterranean coastal and subcoastal environment, consisting of a mosaic of natural and human-modified habitat patches. In particular, we adopted recently developed community N-mixture models, which take into account species interactions (Kéry and Royle 2020), to decouple the two hierarchies of the filtering process: environmental filtering by the landscape and biotic filtering occurring within community members (Fig. 1).

Study site

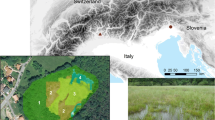
The study area (Fig. 2) is a costal and subcostal plane of about 20 × 3 km, from the sea level to 25 m a.s.l, from the Foglino forest and, southernward, up to the Fogliano Lake (Latium, Central Italy). This territory belongs to the widest area known as Pontine Plain which is the result of an extensive land reclamation of the Pontine swamps, conducted by Fascist regime between 1920 and 1936, that radically changed the landscape of the area. Different habitats and environments can be found: the Foglino forest (Fig. 2c) is a wide residual patch of the planitial and partially flooded forest dominated by deciduous oaks (last coppicing occurred in 90’s of the XX century; Lattanzi et al. 2004); other main habitat are patches of Pinus sp. plantation forests along a part of the retrodunal areas (Fig. (Fig. 2d); Mediterranean shrubs (Fig. 2e); agricultural environments, mainly for hay meadow (Fig. 2f) and open areas/pastures (Fig. 2g).

Fig. 2
figure 2

a Location of the study area in Italy; b detailed location of the study area on the Latium coastline; c–g habitats comprised within the study area, representative of the Mediterranean landscape: c Oak forests, d Pinus sp. plantation forests, e Mediterranean shrubs, f agricultural environments (hay meadow), g open areas/pastures

Full size image

In the study area, 52 linear transects (about 200 × 4 m), approximately equally divided among these different environmental typologies (9–11 transect for each typology), were placed and surveyed repeatedly over three years.

Sampling

Sampling occurred during spring and early summer over three consecutive years. We visited each of the 52 transects 4 times both in 2020 and 2021. Surveys occurred between March 3rd and July 5th (both in 2019), while we conducted 3 visits on 47 transects in 2019. Two observers (R.N. and A.R.) slowly walked each 200-m transect line and conducted standardized visual encounter surveys, recording the number of reptile individuals encountered. Surveys took place during daytime (between 8.00 and 20.00) and lasted between 10 and 20 min, according to environmental complexity of the transect. For each survey observers recorded the time of the day (HOUR) and the day of the year (DAY; i.e. the continuous count of the number of days beginning each year from January 1st).

Landscape metrics

For each sampling site we calculated four landscape metrics, supposed to influence occurrence and abundance of reptiles (Atauri and De Lucio 2001; Schindler et al. 2013). Considering that environmental features in close proximity to the transect have an influence on the transect line itself, we applied a buffer of 20 m radius along each transect line, thus obtaining a rectangular polygon with rounded edges (240 × 40 m; length x width) covering an area of almost 1 ha, which we used to estimate landscape metrics for the analysis. Starting from the Corine Land Cover 2018 layer (CLC; 100 m spatial resolution; European Environment Agency 2019a) we calculated the number of CLC categories present on each polygon, which we assumed to represent landscape diversity or land use heterogeneity across each polygon (LUH). For each polygon, we extracted the value of the net primary productivity (NPP; expressed as kgC/m2/year) from the Annual Terra Moderate Resolution Imaging Spectroradiometer (MODIS) layer (500 m spatial resolution; Running and Zhao 2021) for a given year, averaging cell values when polygon fell within two cells. From the European Environment Agency (EEA) we obtained a high-resolution layer concerning vegetation tree cover density (TCD; 10 m spatial resolution; reference year 2018; European Environment Agency 2019b), ranging from 0 to 100%, from which we calculated the median value for each polygon. From the EEA we also obtained a high-resolution layer representing the presence/absence of small woody features (SWF; 5 m spatial resolution; reference year 2015; European Environment Agency 2019c), defined as hedgerows or bushes. Combining TCD and SWF we obtained an additional layer (5 m spatial resolution), representative of the presence/absence of arboreal or shrub vegetation. From this layer we calculated the edge density for each polygon (EDGE; expressed in m/ha), which gives, for each sampling site, a measure of ecotone complexity between woody vegetation and other environmental patches (Schindler et al. 2013). All spatial analyses and layer manipulations were conducted with free software QGIS v.3.22. Edge density and polygon median values were calculated with Landscape Ecology Statistics plugin (LecoS; Jung 2016) for QGIS.

Data analysis

We analysed our repeated count data of Mediterranean reptiles using a multi-species formulation of the static binomial N-mixture model of Royle (2004) accounting for symmetric interactions between community members (Pollock et al. 2014; Tobler et al. 2019). Symmetric interactions within pair of species were estimated from the residual correlation of their realized abundances, after accounting for the environmental filtering, i.e. the effect of landscape features (Kéry and Royle 2020). These interactions may be negative or positive according to the biological process underlying relationship between species (Kéry and Royle 2020). Binomial N-mixture models estimate latent abundance state N at site i (Ni), assuming Ni ~ Poisson(λ), where λ is the expected abundance over all sites, by using repeated counts C at site i during survey j (Cij) to estimate individual detection probability p, assuming Cij|Ni ~ Binomial(Ni,p). Both parameters can be modelled as a function of environmental covariates trough a log or logit link, respectively, which conveniently allowed us to include landscape metrics as covariates. In order to model species interactions, we included site- and species- specific random effects with a Multivariate Normal (MVN) distribution (Kéry and Royle 2020). Off-diagonal elements of the variance–covariance matrix of the MVN are scaled to obtain residual abundance correlations (ρ), which measure the direction and the intensity of the interaction of each species pair considered, after the effect of environmental covariates on abundance have been accounted for (Kéry and Royle 2020). Finally, we considered temporal dynamics in our dataset by fitting a year-stratified model (Kéry and Royle 2020), i.e. by stacking the data of subsequent years and treating them as different sites, so that site i in year 2019 and site i in year 2020 appear as different rows of the dataset. This approach allows to account for trends in the data by including a temporal covariate (YEAR). Prior to building our model, we standardized covariates and checked them for collinearity, considering a cut-off for inclusion of Pearson r < 0.7 (Dormann et al. 2013). We modelled the detection process of each species as follows:

$$\log \!\rm it\left( {p_{ij} } \right) \, = \, \alpha_{0} + \, \alpha_{1} *DAY_{ij} + \, \alpha_{2} *HOUR_{ij} + d_{ij}$$

where α0 is the intercept, α1- α2 are covariate effects and δ is a random effect, assuming normal distribution, to account for possible over dispersion in the detection process (Kéry and Schaub 2011). For the abundance of each species, we modelled the filtering effect of landscape metrics on the community as follows:

$$\log \;\left( {\lambda_{i} } \right)\; = \;\beta_{0} \; + \;\beta_{1} *YEAR_{i} \; + \;\beta_{2} *LUH_{i} \; \quad+ \;\beta_{3} *EDGE_{i} \; + \;\beta_{4} *TCD_{i} + \, \beta_{5} *NPP_{i} +_{{}} \eta_{i}$$

where for a given species, β0 is the intercept, β1- β5 are covariate effects to account for temporal dynamics and landscape environmental filtering, while η is the site- and species- specific random effects with Multivariate Normal (MVN) distribution included to measure biotic interactions (Kéry and Royle 2020). We estimated model parameters using a Bayesian approach with Markov chain Monte-Carlo methods, using un-informative priors. We ran three chains, each one with 550,000 iterations, discarding the first 120,000 as a burn-in and thinning by 100. We considered that chains reached convergence when the Gelman-Rubin statistic was < 1.1 (Gelman and Rubin 1992). We considered parameters relative to environmental covariates and species interactions to have a significant effect when the 90% Credible Interval (CRI) of the posterior distribution did not cross the zero. The N-mixture model used here is derived from the static binomial N-mixture model proposed by Royle (2004), and is prone to the same criticism on parameter identifiability, assumption violation and overdispersion (e.g. Barker et al. 2018; Link et al. 2018; but see Kéry et al. 2018). Because of this, properly assessing model fit is of primary importance (Duarte et al. 2018; Costa et al. 2020, 2021). Therefore, we utilized posterior predictive checks based on χ2 statistics as a measure of the discrepancy between observed and simulated data and calculated a Bayesian p-value accordingly (Kéry and Schaub 2011). In order to obtain reliable estimates of detection, abundance and biotic interactions, we applied a threshold to count data and retained for the analysis only those species with > 3 observations for at least one study year. Analyses were conducted calling program JAGS (V4.3.1; Plummer 2003) from the R environment with package “JagsUI” (V1.5.1; Kellner 2015). The JAGS code used for the analysis is available as Supplementary Information SI.1.

Results

During three years of sampling on our transects we encountered twelve reptile species. However, some species were only occasionally encountered (turtles: Emys orbicularis; lizards: Anguis veronensis, Hemidactylus turcicus; snakes: Elaphe quatuorlineata, Zamenis lineatus, Vipera aspis), and we retained for the analysis six species. We counted a total of 2270 Reptiles (Table 1) relative to: three Lacertid lizards (Lacerta bilineata, Podarcis siculus, Podarcis muralis), one Scincid lizard (Chalcides chalcides) and two Colubrid snakes (Hierophis viridiflavus, Natrix helvetica (species descriptions are available as Supplementary Information SI.2). After evaluating goodness-of-fit of our multi-species N-mixture model with symmetric interactions, by means of posterior predictive checks, we recorded a good fit for all species included in the analysis (Supplementary Information SI.3). Convergence, assessed by means of R-hat value, was successful for all parameters monitored (maximum R-hat = 1.040). Mean individual detection probability was very low (i.e., p ~ 0.10) for almost all species (Table 1), except for the most common Lacertid lizards P. siculus and P. muralis that displayed a slightly higher detection probability (i.e., p ~ 0.20). Moreover, for the majority of species detection probability resulted to be mainly influenced by phenology (DAY), and at a lesser extent by daily activity (HOUR; Supplementary Information SI.4). Mean site abundance greatly differed among species: the most abundant species within the community being P. siculus (λ = 8.27; 90% CRI = 6.63–10.49), while for other species we estimated less than 1 individual per transect on average (λ < 1; Table 1). For what concerns the effect of landscape features on the local abundance of species, all species responded with different sensitivity and intensity to the set of landscape predictors included in the model, and complete results are resumed in Fig. 3. For instance, the abundance of both L. bilineata and C. chalcides resulted to be negatively affected by NPP, but for the latter also a negative response of TCD was observed, while EDGE had a positive effect on abundance (Fig. 3). Similarly, the most commonly observed Lacertid lizards in the study area, P. siculus and P. muralis, had different sensitivity as well as opposite responses to some landscape scale predictors of abundance. That is, P. siculus abundance was negatively affected by TCD, while P. muralis was positively affected by the same predictor and at the same time negatively affected by NPP and LUH (Fig. 3). For neither of the snake species included in the analysis we recorded a significant effect of any landscape feature on local abundance (Fig. 3). Significant temporal dynamics in the year-stratified model (i.e., YEAR predictor on abundance) were observed for three species within the studied community: P. siculus and C. chalcides showed a positive temporal dynamic during the study period, while P. muralis showed a negative dynamic (Fig. 3). Finally, after accounting for the effect of environmental predictors on abundance and measuring correlation of residual abundances, we observed mixed biotic interactions across species pairs within the community (Fig. 4). Among all species pairs, only two accounted for a significant biological interaction: L. bilineata and P. siculus showed a positive interaction (ρ = 0.58; 90% CRI = 0.25–0.81), while P. muralis and C. chalcides displayed a strong negative interaction (ρ = − 0.76; 90% CRI = − 0.92 to − 0.39).

Table 1 (a) Raw numbers of reptile counts, for the six species included in the analysis, obtained during three years of survey. (b) Estimated mean site abundance (λ) and individual detection probability (p) for the six species included in the analysis, with corresponding 90% CRI
Full size table
Fig. 3
figure 3

Plots representing posterior distributions of covariate effects for abundance predictors included in the model, for each species. Empty areas represent 100% of the posterior distribution, filled areas represent 90% CRI, bold lines within posterior distributions represent point estimates (mean) for a given parameter. When > 90% of the posterior distribution for a given predictor falls on one side of the 0 vertical line, the predictor of interest is considered to have a significant effect on the relative parameter

Full size image
Fig. 4
figure 4

Plot representing biotic interaction coefficients for all species pairs: positive abundance interactions are depicted in blue, negative abundance interactions in red, color intensity represents interaction strength. Numerical values of interaction coefficients are reported only for significant biotic interactions (90% CRI)

Full size image

Discussion

Here we used hierarchical N-mixture models, accounting for imperfect detection and symmetric species interactions, to model the effect of species interaction on residual abundance, after accounting for differential landscape requirements across a Mediterranean reptile community. We found evidence of reduced species interactions in the studied community, finding a significant correlation only for two out of the 15 species pairs tested. We a priori hypothesised that in case of inter-specific competition between community members from the same trophic level, negative abundance relationships should occur, while predator–prey interactions occurring between different trophic levels could either produce positive or negative abundance correlations (Abrams 2000). Actually, we did not observe significant interactions occurring between community members clearly belonging to two different trophic levels: that is, estimated interaction coefficients between snakes (i.e. predators) and lizards (i.e. prey) were not significant. Instead, a negative significant correlation on residual abundance occurred between the Common wall lizard (P. muralis) and the Italian three-toed skink (C. chalcides). In the study area we estimated significantly different abundances for these species, P. muralis being more abundant that C. chalcides. Moreover, opposite responses to certain landscape features were observed for these species. Both species prey mainly on invertebrates, C. chalcides having a diet more restricted to Araneae (Ciracì et al. 2022), while P. muralis, also including Araneae as a main item of its diet, possesses a wider trophic niche (Scali et al. 2016). In this context, the negative abundance interaction observed between these potentially competing species can be possibly explained by competitive exclusion (MacArthur and Levins 1964), where the more generalist, opportunistic feeder, P. muralis outperforms C. chalcides for food resources. By contrast, we observed a positive local residual abundance correlation between the Green lizard (L. bilineata) and the smaller Italian wall lizard (P. siculus), despite these species showed different responses to landscape features. While negative interactions between potentially competing species are easily explained by competitive exclusion (MacArthur and Levins 1964), positive interactions are more difficult to interpret. These kind of positive abundance correlations can be explained by mutualistic interactions or facilitation among species (e.g. Levi et al. 2013), but none of the two are known to occur among our reptile species so far. Alternatively, positive significant correlation between two potential competitors can arise from the species selecting the same habitat or resource, which has not been accounted for in the model, such as food resources or microclimatic conditions (e.g. Brodie et al. 2018). Both lizards are known to be generalist opportunistic predators, their diet being mainly composed by invertebrate prey (Angelici et al. 1997; Zuffi and Giannelli 2013), despite the larger species (L. bilineata) is known to occasionally include in its diet other lizard species, including P. siculus (Angelici et al. 1997). In this perspective, the observed positive relationship between the two species could also be partially explained as a result of a potential predator–prey interaction: that is, an interplay of both shared selection for unaccounted habitat/resources and an occasional predation of the Green lizard on the Italian wall lizard could exist. Since P. siculus is the numerically dominant species in the community and L. blineata has a markedly lower abundance, occasional predation on P. siculus should not display a strong negative effect on prey density, and in turn could contribute to release both species from inter-specific competition for invertebrate resources (Chase et al. 2002).

Linking biodiversity responses in terms of community composition and abundance to landscape features is of paramount importance for defining management plans and functional conservation programmes (e.g. Lindenmayer and Franklin 2002), however it requires a consistent response of the community to landscape structures (Watson et al. 2005). By contrast, in our study we observed differential responses of species to our set of predictors: nevertheless, some principles can still be drawn. For instance, NPP, when significant for a given species (i.e. L. bilineata, P. muralis, C. chalcides), always had a negative effect on local abundance. This result can be explained because, in the study area, patches with higher NPP are matched to intensive agricultural activities, where mechanized agriculture (e.g. hay meadows), tilling, input of nutrients from livestock manures and pesticides are present, thus determining a disturbance for the reptile community (Rotem et al. 2013; Guiller et al. 2022). The reptile community instead showed a differential effect for other landscape metrics such as TCD: abundance of P. muralis was positively influenced by tree cover, while the congener P. siculus and the skink C. chalcides were negatively affected by this feature. This finding is in line with known ecological requirements and habitat selection preferences of the studied species: in central and southern Italy P. muralis being more frequently associated with woodlands, in particular in shady, humid and structurally complex environments (Corti et al. 2010), while P. siculus and C. chalcides select ecotonal or open areas with lower density of arboreal vegetation (Corti et al. 2010). This is also confirmed by the significant effect of EDGE density on C. chalcides, indicating that local abundance of this species is positively influenced by a higher density of ecotone between woody vegetation and open areas, a landscape structure already recognized as important for herpetofauna across the Mediterranean region (e.g. Atauri and De Lucio 2001; Schindler et al. 2013). Finally, landscape/land-use heterogeneity (LUH) had a significant negative effect on P. muralis. Being this species positively associated to forest cover, this result may indicate that high levels of landscape heterogeneity, at least at the studied spatial resolution, in our context may negatively affect suitability of arboreal vegetated patches for this species requirement.

One of the major criticisms moved to the environmental filtering conceptual framework deals with the difficulty/impossibility of decoupling the effect of the environment from the one of the biotic interactions, at least unless complex experimental designs involving community manipulation are implemented (Kraft et al. 2015; Cadotte and Tucker 2017; Germain et al. 2018). That is, simple observational data are of difficult interpretation in the framework of environmental filtering, because the effect of environment and competition are confounded (Kraft et al. 2015; Germain et al. 2018). These criticisms may partly arise from the lack of an adequate analytical toolbox to treat observational data in the framework of environmental filtering: that is, observed data from a realized community are not only a product of environmental filtering and biotic filtering processes, but are also the realisation of a “detection filter” occurring during sampling, that should be considered (Roth et al. 2018). In this respect, within our reptile community Mean individual detection probability was very low (i.e., p ~ 0.10). Therefore, not properly accounting for this detection error, may result in a biased estimation of local abundances up to 80%, thus producing cascade bias for both the environmental and biotic filtering processes. Moreover, since we also observed differential temporal dynamics in the abundance of our study community, we stress that in addition to the “detection filter”, also the effect of a “temporal dynamic filter” should be accounted for, when deriving inferences from realized communities over consecutive years. As a matter of fact, the application of hierarchical N-mixture models allows to properly address these issues. To date, applications of N-mixture models with symmetric interactions to specifically partition the contribution of environmental and biotic filtering are scarce and restricted to bird communities in forest landscapes, but nevertheless encouraging (Basile et al. 2021; Montano-Centellas et al. 2021). Our results confirmed that the application of these models based on cost-effective count data, accounting for both imperfect detection and temporal dynamics, represent a viable way to disentangle the effect of the environment and biotic interactions on the filtering process of the local abundance of a Mediterranean reptile community. However, despite binomial N-mixture models accounting for species interactions provided reliable results in the study case, some limitations are present and should be considered. Indeed, only 6 out of 12 species from the realized community could have been included in the analysis, given the low number of observations recorded during the sampling. Low detection rates are particularly common for reptiles, representing a severe limitation when the goal is to obtain reliable abundance estimates or fine ecological inferences (Mc Diarmid et al. 2012), binomial N-mixture also being data demanding (Kéry and Royle 2015, 2020). For this reason, although considering that very rare species have a limited ecological relevance on the biotic interaction across the realized community, finding new tools to allow analysis of rare species is of paramount importance. In this respect, multinomial N-mixture models, relying on different sampling protocols, such as multiple observers (Costa et al 2020; Romano et al. 2021) or mark-recapture distance sampling (Rosa et al. 2022b), have proved to be a reliable and cost-effective tool to estimate abundance and other demographic parameters of amphibians and reptile populations, even when density and detection probability are low (Costa et al 2020). Therefore these model may represent a promising pathway for inferring species co-occurrence and interaction also for rare reptile species.