Introduction

Estuarine and coastal ecosystems provide a variety of important benefits over temporal and spatial scales relevant to humanity but are also some of the most heavily used and threatened natural systems globally (Lotze et al. 2006; Halpern et al. 2008; Barbier et al. 2011). However, predicting the effects of broad scale anthropogenic impacts on ecosystem functions typically measured in seafloor ecosystems at small scales is hindered by the need to address scale-up processes (Hewitt et al. 2007). Our knowledge of the functioning of marine seafloor ecosystems, in fact, mainly derives from small-scale laboratory and field studies (Gammal et al. 2019). Extrapolating the results of these experiments is critical to addressing issues most relevant to society but this is not a trivial task (Levin 1992; Dixon Hamil et al. 2016). Moreover, environmental heterogeneity is known to increase with scale, making extrapolations that do not incorporate heterogeneity prone to inaccuracy (Thrush et al. 1997b; Peterson 2000; Hewitt et al. 2007; Snelgrove et al. 2014; Lohrer et al. 2015).

Scaling is defined as the process of translating information between or across spatial and temporal scales or organizational levels (Wu 1999). Although the importance of scaling in ecology has been recognized in recent decades, how to conduct scaling across heterogeneous ecosystems remains a challenging question (Wu et al. 2006; Chave 2013). In marine environments, the high heterogeneity and the lack of high-resolution data due to the challenges related to extensively sample marine ecosystems further complicate this process (Snelgrove et al. 2014; Townsend et al. 2014). However, to successfully manage these ecosystems scientists need to find ways to map them and upscale discrete measurements despite the limited data and uncertainty. One of the simplest ways to transfer information between two scales is to assume that the broader-scale system behaves like the average value of the finer-scale system. In this case, scaling is obtained simply by multiplying the sample–scale average with the total study area. This process is often referred to as “lumping” or “direct scaling” and assumes that the relationship describing the system is linear (King 1991; Miller et al. 2004). As a consequence of the oversimplifying assumptions however, this simple upscaling procedure could produce large scaling errors (Englund and Cooper 2003).

Allometric scaling is one of the most common approaches found in scaling literature (Brown et al. 2000, 2004; West et al. 2003; Kerkhoff and Enquist 2007; Rodil et al. 2020; Fang et al. 2021). Allometry is based on the underlying concept of incomplete similarity or fractality, which implies that the fundamental features of a system exhibit an invariant, hierarchical organization that holds over a wide range of spatial scales (Barenblatt 1996; Li 2000; Brown et al. 2002). One of the main advantages of this approach is that it is characterized by relatively simple mathematical or statistical scaling functions, generally in the form of a power law (Brown et al. 2002). Nevertheless, the underlying ecological processes may be complex. Although most of the allometric equations do not directly address the problem of spatial scaling, space can be incorporated into a scaling relationship through, for example, population density or home range (Wu et al. 2006). In particular, allometry as a general method can be applied to spatial scaling when the independent variable is spatial scale instead of body mass (“spatial allometry”; Schneider 2001). While the benefit of using allometric scaling is recognized for a variety of fields, from physiology to economics, these simple power law may not be adequate to describe the upscaling of ecosystem functions (Brock 1999; Marquet et al. 2005). However, some examples exist of how allometric laws can be used to upscale, from individual to population level, the effect of sediment dwelling animals on particle and solute movement that play an important role in many sedimentary ecosystem functions (Fang et al. 2021). Nonetheless, in seafloor landscapes heterogeneity and non-linear processes can be hard to measure and incorporate in scaling process (Snelgrove et al. 2014).

Most ecological data are inherently composed of several levels of spatial structure: large-scale trends (e.g., species responses to climate conditions, migrations), multi scale patterns or patchiness (e.g., physical conditions, dispersal mechanisms, facilitation), and error (Klopatek and Gardner 2001). Structure functions attempt to describe spatial structures in the data and allow us to quantify spatial dependence and partition it amongst distance classes (Legendre and Legendre 2012). For example, previous work has demonstrated the feasibility of variograms to quantify spatial heterogeneity and explore spatial patterns and describe phenomenon as a function of space (Garrigues et al. 2006; Lausch et al. 2013). Successively, geostatistical techniques, such as kriging, that employ knowledge of the spatial covariance (as contained in the variogram) can then be used to produce a spatial model (Klopatek and Gardner 2001; Christianen et al. 2017; Zhou et al. 2017). To be able to accurately describe these spatial structures and incorporate as much heterogeneity as possible, a high amount of data is usually necessary. Such high-resolution information on the spatial arrangement of the data, provides information about patterns at different scales (Fortin and Dale 2005). While spatial analysis deals with the problems associated with spatial heterogeneity, synergistic effects arising from the interaction between species with different functionalities are also likely to confound the upscaling of ecological processes (Schenone and Thrush 2020).

Another complication posed to scaling in seafloor ecosystems involves the difficulty of extensively and intensively sampling marine environments and the consequent scarcity of data (Townsend et al. 2014). To accurately describe the relationship of a variable to changes in scale in these complex systems often requires more data than it is practical to obtain with traditional sampling (Strong and Elliott 2017). This has important consequences for marine ecosystem assessments compared to their terrestrial counterpart. Seafloor habitats in fact are often classified based on easily measured physical characteristics (e.g., depth, sediment grain size), thus overlooking much of the heterogeneity and diversity at scales relevant for the functionality of these systems (Lavorel et al. 2017). This has profound implications for management applications. Maps are critical for ecological studies and environmental management and it is common practice to estimate the delivery of ecosystem services based on coarse grained habitat maps and the use of scoring factors or average literature values for each habitat rather than using spatially explicit data (Thrush et al. 1997a, b; Hewitt et al. 2007). In our study, we addressed the issue of whether various upscaling methods commonly used in metabolic, ecophysiological and other ecological relationships are suitable to upscale species–ecosystem function relationships in heterogeneous marine landscapes, where the data available is usually limited (Table 1). We used high–resolution maps of ecosystem functions to simulate a new dataset and compare the use of different scaling approaches (direct scaling, allometric scaling, variogram/kriging). The use of simulated data to test different sampling or modelling methods is common in landscape ecology due to the impossibility to know the ‘true’ value of ecosystem functions and properties at large scale (Zurell et al. 2010). In particular, semi-virtual studies based on high-quality data are useful because they contain, and can hence depict, the ‘true’ pattern of interest (Hirzel and Guisan 2002; Albert et al. 2010). We compared approaches that account for no or low spatial heterogeneity—often used in marine systems due to data scarcity—and others that account for more heterogeneity. While high-resolution maps can be used to estimate ecosystem functions at scale, the ability to identify scaling relationships is crucial to estimate ecosystem functions and services across landscapes that cannot otherwise be extensively mapped (Thompson et al. 2017). The performance of each approach in predicting ecosystem functioning at scale was compared to estimated values calculated from the ecosystem function maps produced in Schenone et al. (2021). Current landscape ecology literature recognises the importance of accounting for heterogeneity when variables are non-normally distributed in space (Franklin 2005; Lecours et al. 2015; Gonzalez et al. 2020). However, partly due to the aforementioned challenges faced in marine habitats, current practices in seafloor ecology are clearly obsolete and lacking behind terrestrial ecology and studies that address this known but ignored issue are needed. In our study, we investigated highly heterogeneous coastal bioturbated landscapes and hypothesized that traditional scaling approaches, that fail to take into account the effect of heterogeneity and the functional interactions between different organisms, would produce a poor representation of broad-scale ecosystem functioning.

Table 1 Characteristics of the scaling methods used in this study
Full size table

Methods

Study design

For this study, we used data from a 2018 mensurative experiment that we carried out in the Whangateau Estuary (New Zealand) to quantify the relationships between multiple ecosystem functions and the density of two key species: Macomona liliana (Iredale, 1915) and Macroclymenella stewartensis (Augener, 1926). Both M. liliana (tellinid bivalve) and M. stewartensis (maldanid polychaete) are ecosystem engineers that alter the sediment and its biogeochemical properties and differentially influence various sedimentary rates and processes (Schenone et al. 2019); details of the sites and the sampling design are presented in (Schenone and Thrush 2020). Briefly, to measure fluxes, we deployed opaque benthic incubation chambers and rapid organic matter assay (ROMA, O’Meara et al. 2018) plates. Concurrently, we sampled the sediment characteristics and macrofaunal community, as well as M. liliana and M. stewartensis surface features at each station. Surface features generated by M. liliana (feeding tracks) and M. stewartensis (faecal mounds) are a reliable proxy of their density and in fact explain more variance in ecosystem functioning than their density (Schenone and Thrush 2020). Finally, we combined ecosystem functioning models that explained the relationship between field measured biogeochemical fluxes and the density of key species features, with a drone survey of the distribution of those species in the estuary to map the delivery of ecosystem functions at a 1 × 1 m resolution (Schenone et al. 2021). Maps of the distribution of each species were obtained by counting surface features in the drone images through a dedicated neural network and successively interpolating the data through kriging. These layers were then combined using the modelled relationships to produce ecosystem functions maps. In the present study, we sampled these high-resolution raster datasets as described below to build the different scaling relationships. For each scaling approach the same rasters were sampled but with different sampling strategies to better suit the approach.

Study location

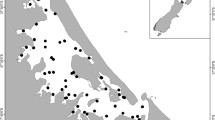
Whangateau Harbour is a sandspit-barrier estuary located on the east coast of the North Island of New Zealand. Considered to be one of the most valued estuaries within the Auckland region, it is made up of a unique mix of high-value, high-quality habitats contained within a relatively small harbour (~ 7.5 km2), with approximately 85.4% of this area being intertidal (Kelly 2009). These extensive intertidal flats are predominantly composed of medium to coarse grain sand with a relatively low percentage of mud (< 6%). Both our target species are abundant in Whangateau and dominate vast patches of the landscape as well as transitional areas where their distributions overlap. A map of the habitats of Whangateau was first developed in 2000 and successively updated in 2010 (Hartill et al. 2000; Townsend et al. 2010). These maps show that our study area is entirely covered by sandflat habitat and all of it has been characterized simply as “sand” habitat (Fig. 1).

Fig. 1
figure 1

Habitat map of the Whangateau estuary (modified from Townsend et al. 2010). The black contours highlight our study area

Full size image

Scaling

We used a semi-virtual simulation study to illustrate the consequences of the choice of the scaling method on the estimation of ecosystem services. Knowledge of the true levels of ecosystem functions at scales relevant to management and to society is impossible. Therefore, to test our hypothesis, first we estimated the total value of different ecosystem functions across the study area from the raster maps described above and presented in Schenone et al. (2021). These values were used as a surrogate of reality and used as our true values. Then, we compared the performance of different scaling approaches and assessed their results against these estimates of ecosystem functions. The results were expressed as the difference between these estimates and the scaled values for each approach. We considered the rates of three ecosystem functions: denitrification (expressed as the release of N2 from the sediment), ammonia (NH4+) efflux and organic matter degradation at the sediment surface (Co). These functions are the result of important biogeochemical sedimentary processes and underpin crucial supporting and regulating ecosystem services, such as the cycling of nutrients and organic matter (Huettel et al. 2014).

Direct scaling

To upscale and calculate the delivery of each ecosystem function across the mapped area we first sampled the ecosystem function rasters simulating ten transects with three sampling points per transect (Fig. 2). From these 30 sampling points, we calculated the mean value of each function and then multiplied it by the extent of the study (1,695,158 m2). This approach is consistent with traditional approaches that to quantify the total ecosystem services would use the available habitat characterization and assume that the whole sampling area is of one habitat class—sandflat habitat (Fig. 1)—and that the services are consistent throughout that class. Then, to produce a more accurate calculation and increase the performance of the scaling by accounting for some heterogeneity, the data was divided into 4 subunits. The subunits differed in area but were defined based on geomorphological and environmental characteristics. The subunit mean value of each function was multiplied by the area of the subunit and the total upscaled value for the study area was calculated by the sum of the four subunit values.

Fig. 2
figure 2

modified from Schenone et al. (2021); D for direct scaling, 30 locations were samples along 10 transects and successively the study area was divided in 4 subunits, showed respectively in green, red, blue and yellow; E for allometric scaling, squared polygons of increasing area and with the same centroid were used to calculated ecosystem functions at different scales; F for kriging, a grid of 50 evenly distributed locations were sampled

Conceptual design of the study. The top panels present the drone derived maps of ecosystem functions, specifically A denitrification in µmol N2 m−2 h−1, B efflux of NH4+ in µmol NH4+ m−2 h−1, C organic matter degradation at the sediment surface in g C m−2 day−1—

Full size image

Allometric scaling

We tested the presence of fractal-like relationships in the form of the power law equation:

$$Y={Y}_{0}{A}^{b}$$

where \(Y\) is the ecosystem function of interest, \({Y}_{0}\) is a scaling constant equal to the plot average value of the function, \(A\) is space in m2, and \(b\) is the scaling exponent.

We sampled the raster data from the ecosystem function maps and calculated fluxes across ten areas of different size that shared the same centroid. These areas were squares of 1 m2, 625 m2, 2500 m2, 5625 m2, 10,000 m2, 15,625 m2, 22,500 m2, 30,625 m2, 40,000 m2 and 50,625 m2 respectively. Four centroids were haphazardly chosen to develop four replicates of the scaling process. The average values from the four replicates for each surface size were plotted against the surface area to check for the presence of disjunctions that could indicate multi-fractality. The allometric model was then fitted to the data using a linear model and was evaluated graphically and by means of the r2 value. Finally, using the scaling exponent calculated from the model, we estimated the value of each function across the study area from the average 1 m2 value using the equation above.

Variogram/kriging

To understand whether the use of information about the spatial structure of ecosystem functions would help improving their upscaling and accuracy and prediction, we used a systematic sampling design and calculated functions in 50 evenly distributed points on the maps. First, we checked for the presence of global trends and anisotropy in the data. Then, for each function we calculated the empirical semivariogram. Finally, we used anisotropic kriging to interpolate and extrapolate the data to the study area and create new raster maps of each function. These kriging results were used to extract and calculate the up-scaled values of the functions across the entire study area.

The geostatistical processing was performed using ArcMap 10.7.1 software (ESRI 2019) and its Geostatistical Wizard and Geostatistical Analyst tools. All other statistical analyses were performed with R v3.6.1 (R Core Team 2013).

Results

Direct scaling underestimated the delivery of all ecosystem functions and allometry underestimated denitrification but overestimated ammonium (NH4+) efflux and organic matter degradation (Table 2). Direct scaling predicted 84.1% less denitrification than the estimated value, 84.9% less NH4+ efflux and 90.3% less organic matter degradation (Co) across the sandflat habitat. Dividing the habitat into 4 sites and calculating the sum of the predicted value for each site provided a slightly better estimate of functions but still underestimated the functional contribution of the sandflat (75.2% less denitrification, 69.7% times less NH4+ efflux and 82.5% less organic matter degradation).

Table 2 Summary of the results of the different scaling methods and comparison with the values calculated from the map of functions in Schenone et al. (2021)
Full size table

Allometric scaling performed better than direct scaling in estimating denitrification. The calculated denitrification was in fact 81.9% lower than the estimated value. However, NH4+ efflux was 2594.1% higher and Co was 14,879.9% higher. No multi-fractality was observed and all 3 functions showed very similar scaling exponents, respectively 1.18, 1.35 and 1.2.

The use of kriging provided a quantification of functions that was much closer to the estimated values. This method was able to detect and account for anisotropy in the data and the predicted functions only differed from the estimated values by 14.7, 29.4 and 3.9% for denitrification, NH4+ efflux and Co respectively.

Discussion

Using a semi-virtual dataset based on extensive, high–resolution data on the spatial distribution and delivery of ecosystem functions, we were able to compare the performance of different scaling methods in predicting denitrification, NH4+ efflux and organic matter degradation. In marine ecosystems, the difficulty of large-scale but intensive sampling and the consequent scarcity of spatially explicit data often translates into simple upscaling approaches that overlook the role of heterogeneity. Our results show that scaling performance is sensitive to the approach chosen and that methods that do not account for spatial heterogeneity lead to differences in the estimates of functions of an order of magnitude compared to those that account for it. Direct scaling showed very poor performance and underestimated all functions by more than 84%. Spatial allometry underestimated denitrification in a similar measure (81.9%) but grossly overestimated NH4+ efflux (2594.1%) and organic matter degradation (14,879.9%). The use of kriging instead led to predictions that varied less than 30% from the estimated values.

Direct scaling, one of the simplest scaling methods, merely consists in the multiplication of the plot-scale average with the total study area (King 1991; Miller et al. 2004). By doing so, it assumes that the relationships describing the system are linear and it can lead to considerable bias, because it does not account for additional variability and ignores nonlinear changes that often occurs with changes in scale (Rastetter et al. 1992; Turner and Gardner 2015). Despite the acknowledgment of its flaws, in ecosystem services assessment of seafloor ecosystems direct scaling is still often used because of our limited ability to sample and detect heterogeneity, which leads their oversimplified characterization (Lavorel et al. 2017). To improve the prediction and incorporate some measure of heterogeneity it is possible to divide the study area into a tractable number of discrete elements based on some characteristics, for example land use or different habit type (Turner and Gardner 2015). However, when we applied this concept to our study, the predictions only improved by 8–15%. Given the dependence of the performance of direct scaling on the number of sites chosen, one could expect a relationship between sampling effort and gain in performance to grow asymptotically to a level where an increase in sampling effort doesn’t produce appreciable results on the performance of the scaling.

Sampling the three functions at different scales showed the emergence of allometric relationships, with similar scaling exponents of 1.18, 1.35 and 1.2 for respectively denitrification, ammonium efflux and organic matter degradation, suggesting a common pattern in the relationship between ecosystem functioning and scale. Allometric scaling still fails to accurately predict functioning at larger scales and results in underestimated denitrification and overestimated ammonium efflux and organic matter degradation compared to our estimates. However, the fluxes measured across polygons of increasing area showed a clear allometric growth and the fitted models always had r2 > 0.9. This may indicate the presence of multi-fractality at scales bigger than those measured. For several decades allometry has focused primarily on the body size (or mass) of organisms as the fundamental variable (e.g. Taylor et al. 1982; Calder 1983; McMahon et al. 1983; Schmidt-Nielsen 1984). In biology, allometric studies have successfully scaled up metabolic and physiological relationships (e.g. Labarbera 1989; Brown et al. 2000; Schmid et al. 2000). However, the effect of scale on ecosystem functions is still poorly understood and to the authors’ best knowledge, fractal theory in marine biodiversity–ecosystem functioning research has only been applied using species body size, biomass or density (Belgrano et al. 2002; Beaugrand et al. 2010; Fang et al. 2021). The reason why the estimates of functions from allometric scaling still differ from the actual estimates can be sought in the lack of measures of heterogeneity and in the oversimplification of the scaling relationship. This approach, in fact, aims to describe the complex nature of these habitats with a rather simple mathematical function. Although this simplification represents one of the limits of the method, it is also its major appeal due to the need to find easy ways to describe complex phenomena, which would otherwise be impossible to describe when the data is scarce. Similarly to direct scaling, increasing the number of discrete sites to account for more heterogeneity would likely produce better results but increase the sampling effort.

The approach that led to the most accurate estimates of ecosystem functions was the investigation of spatial structures through variograms/kriging. Spatial statistics have a long history in the context of extrapolation (Miller et al. 2004), but they have been rarely applied to mapping seafloor ecosystem functions or the underpinning biophysical interactions rather than simple physical sediment characteristics (Wei et al. 2010; Jerosch 2013; Gaida et al. 2019). Probably one of the most commonly used methods in this context, kriging relies on autocorrelation functions to generate spatially explicit predictions (Webster and Oliver 2001). The raster dataset sampled to perform our analysis had a modelling component, which could lead to concern for circularity in our analysis. However, kriging was used to produce raster layers of the distribution of species biogenic features, which were then combined following empirically derived relationships between surface features and ecosystem functions to produce the ecosystem function maps (Schenone et al. 2021). Therefore, the semivariograms and kriging functions used to upscale ecosystem functioning in this study are very different from those used to produce the species distribution layers in the original dataset [see Fig. S1 in Supplementary Information, and the Supplementary Information provided in Schenone et al. (2021)]. Moreover, while for some functions kriging clearly outperforms the other scaling approaches, for other functions the difference is not as marked, supporting the absence of circularity. Although it produced results that quite accurately reproduced the estimated values, this process requires a larger amount of data compared to the other methods. A good estimation of the parameters of the variogram, in fact, is crucial for the subsequent kriging steps (Fortin 1999). Therefore, estimating functions at the landscape scale would typically require that at least ~ 50 sites are sampled (Fortin and Dale 2005). This number could be a realistic compromise between sampling effort and good model performance from a statistical perspective but still represents massive practical problems for many seafloor ecosystem function variables. A larger sample size—often not possible in marine ecosystems—would result in better predictions, while a smaller sample would decrease the performance. Choosing the correct sample size is therefore a trade-off between practicality and accuracy. However, when prior knowledge on the study area is available or can be easily obtained (through remote sensing for example), it can be used to tailor the sampling design.

Our findings support the importance and urgency for marine ecosystem management and spatial planning to move towards practices that recognize and account for the role of ecological variability (Zajac 1999; Zeppilli et al. 2016). Accurate estimates of ecosystem services are in fact critical for their sustainable management and for humans to perceive their value (MEA 2005; Granek et al. 2010). Soft sediment habitats are often considered to be homogeneous but are in fact are highly complex ecosystems and contain strong physical gradients that affect the distribution of species and functional performance (Hewitt et al. 2005). This results in the patchy spatial distributions of communities and ecosystem functions across multiple spatial scales (Yang et al. 2015; Thrush et al. 2017). Such patchiness is often not as apparent as in other ecosystems where above ground structures define patches (e.g. terrestrial and marine forests; Turner et al. 2001; Clark et al. 2004). Moreover, ecosystem functioning is driven by the biological activity of species and by their interactions (Wohlgemuth et al. 2017; Schenone et al. 2019). As supported by our results, if we fail to sample the spatial heterogeneity of these systems and to include its role and that of the underlying biodiversity in the scaling process, we risk miscalculating the results of important ecological processes that support critical ecosystem services (Kolasa and Pickett 1991).

Scaling and mapping ecosystem functions can allow the quantification of the ecosystem services they underpin. The choice of the scaling method therefore can deeply influence the assessment of their ecological, cultural or economic value. For example, the value of Nitrogen removal via denitrification in U.S. dollars has been estimated between $13 and $98.70/kg N (Piehler and Smyth 2011; Watanabe and Ortega 2011). Using the more conservative value of $13/kg N, the estimate of the annual cost to replace the removal of N through denitrification in our study site would be of $US 1,701,367 using kriging to up-scale and $US 235,731 using direct scaling. Rightly or wrongly, the monetising ecosystem services is often used to communicate to stakeholders and decision makers the value of the seafloor ecosystems that deliver them. Our analysis shows substantive value for resource managers in gathering good ecological data, addressing scale, and understanding ecological complexity. Although these are just approximate calculations that do not take into account changes in rates due for example to seasonal changes, they provide a useful indication that the inappropriate use of scaling can lead to differences of more than $US 1,000,000 per year in the estimate of ecosystem services. Coastal ecosystems are dynamic, and change is often driven by multiple stressors and cumulative anthropogenic effects. Therefore, the way we estimate functioning and service delivery needs to be sensitive to such changes. Maps are ultimately created with the purpose of assessing the spatial distribution of ecosystem services for management, but a map of a sandflat based on purely sedimentological features will not change even if we kill all of the resident macrofauna. A habitat characterisation that recognises the important scales of ecological variability is essential for effective management.

The data used in this study was obtained from maps of ecosystem functions with a 1 × 1 m resolution and therefore relies on their accuracy (Schenone et al. 2021). The maps were created combining high resolution remote sensing data on the distribution of key species and ecosystem functioning models that relate functions to the abundance of those species and measures of uncertainty were provided. Our findings highlight the importance of overcoming the challenge of integrating ecological variability in habitat description to improve estimated of ecosystem service. The use of empirical and theoretical models that link ecosystem functioning to biological attributes that can be measured remotely over large areas will in fact improve our understanding of heterogeneous landscape and overcome the problems associated with extensive sampling. However, our analysis highlights that in situations where functionally important landscape features cannot be extensively mapped and linked to easily quantifiable features, the ability to properly identify and use scaling relationships is crucial.