Abstract
Context
Existing demographic models of California condors have not simultaneously considered individual condor movement paths, the distribution and juxtaposition of release sites, habitat components, or the spatial distribution of threats.
Objectives
Our objectives were to develop a dynamic spatially explicit and individual-based model (IBM) of California condor demography and to evaluate its ability to replicate empirical data on demography and distribution from California (1995–2019).
Methods
We built a female-only spatially explicit California condor IBM in HexSim, using a daily timestep that allowed us to simulate the foraging behavior of condors, changes in food distribution and availability, and the ephemeral threat of lead in decaying food resources.
Results
Simulated population size was highly correlated with annual population census data once the population became established with > 50 females (r2 = 0.99). Mean simulated fecundity and mortality estimates were not significantly different from empirical trends (p > 0.05), although empirical data had higher interannual variability. The geographic distribution of modeled condors was similar to the empirical distribution with an overall accuracy of 79%, a commission error of 27%, and an omission error of 9%. Simulated movement density corresponded moderately well to the density of observed GPS locations (weighted kappa = 0.44).
Conclusions
We developed a spatially explicit California condor IBM that is well-calibrated to empirical data from California. Given its mechanistic underpinnings and flexibility to incorporate a variety of spatial and demographic inputs, we expect our model to be useful for assessing the relative risks and benefits of future condor reintroduction and management scenarios.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Population simulation models have proven useful in threatened and endangered species conservation as a tool to develop defensible predictions of future conditions, challenge long-held assumptions, and explore the consequences of management strategies through structured thought experiments (Schumaker and Brookes 2018, DeMaso and Sands 2019). To date, population simulation models for the critically endangered California condor (Gymnogyps californianus; hereafter CACO) have been aspatial (e.g., Meretsky et al. 2000; Finkelstein et al. 2012), or have accounted for space only as averaged across broad geographic zones (e.g., Green et al. 2008; Bakker et al. 2017). By design, these models do not incorporate mechanisms linking individual search behavior to environmental conditions. The advantages accrued from explicitly accounting for space and individual movement decisions in population simulations include the ability to: (1) identify patterns of population change that emerge when demography and behavior are mechanistically linked to landscape features; (2) evaluate heterogeneous risk across the landscape (e.g., Mateo-Tomás et al. 2016); (3) incorporate information on animal movement and activity-specific habitat requirements that allow for the evaluation of exposure to potential hazards; and (4) model the geographic spread and connectivity of populations over time (Grimm and Railsback 2005). Further, for species like the CACO that rely on conservation breeding and reintroductions or supplementation, spatially explicit individual-based models (IBMs) make it possible to evaluate hypothetical future reintroduction scenarios by releasing simulated individuals at specified intervals anywhere within the modeling domain (e.g., Carroll et al. 2003; Andersen et al. 2021).
Previous population models for the CACO have, for the most part, been designed to perform extrapolations from existing demographic data (e.g., Mertz 1971; Verner 1978; Meretsky et al. 2000), or to develop statistical relationships between predictor variables and observed demographic rates (e.g., Finkelstein et al. 2012; Bakker et al. 2017; Poessel et al. 2018a). Such non-mechanistic models describe individual components of a system rather than the underlying causal mechanisms (Peck 2004). In contrast, IBMs encode causal theories describing how system components interact to produce observed outcomes (Heinrichs and Marcot 2019; van der Vaart et al. 2016), which help to illuminate gaps in our knowledge of a species’ ecology, and can foster innovative science that improves our understanding of the system (Nathan et al. 2008).
In investigations involving species translocations, mechanistic models of population dynamics have inherent advantages over phenomenological approaches. This is because modeling translocations frequently requires forecasting population dynamics in parts of a species range for which there are little if any empirical data available to drive correlative inference. Population models that are both spatially explicit and mechanistic have been developed to evaluate conservation translocations for a number of species, including the European beaver (Castor fiber) (South et al. 2000), gray wolf (Canis lupus) (Carroll et al. 2003), tule elk (Cervus elaphus nannodes) (Huber et al. 2014), bull trout (Salvelinus confluentus) (Mims et al. 2019), and greater sage-grouse (Centrocercus urophasianus) (Heinrichs et al. 2019). Given the inherent ecological and socio-economic risks associated with moving organisms for conservation purposes (IUCN/SCC 2013), modeling efforts that account for individual movement and the spatial distribution of habitats can be particularly useful for comparing the efficacy of proposed translocation strategies (Seddon et al. 2007; Dunham et al. 2016).
The development of spatially explicit IBMs realistic enough to use in reintroduction programs is often complicated by a dearth of empirical data on organisms' resource selection preferences, movement dynamics, dispersion of unobvious threats, effective survivorship, and other factors. Additionally, the risk of error propagation can be magnified in highly parameterized models of species having complex movement regimes that expose them to threats that are dynamic in space and time. Nevertheless, explicitly accounting for space and individual movement in population models is sometimes necessary for describing behaviors of complex systems with emergent properties that cannot be inferred from the sum of their parts (Oro 2013).
Our primary objective was to develop an IBM of CACO demography that accounts for the geographic distribution of release sites, spatially and temporally dynamic resources and threats, and CACO movement. We also sought to evaluate our model’s ability to predict known patterns of CACO population growth, mortality, fecundity, and distribution in California over a quarter-century, from 1995 to 2019. To achieve these objectives, we designed and constructed a model that would be useful for assessing the relative risks and benefits of future condor reintroduction and management scenarios.
Methods and model development
Study species
The CACO is a critically endangered species with a global population of < 350 free-flying individuals occurring in three disjunct populations in parts of western North America (BirdLife International 2021). It experienced one of the most severe genetic bottlenecks ever recorded for a bird species (D’Elia et al. 2016), but still retains a high degree of ancestral genomic diversity that signals the potential for future adaptation (Robinson et al. 2021). Ongoing efforts to restore the species to its former range in southern and central California, Baja California, and Arizona have been well-chronicled (Walters et al. 2010). Presently, CACOs remain reliant on releasing captive bred individuals and on human intervention for survival and population growth, primarily to offset or reduce mortality from lead poisoning (Finkelstein et al. 2012; Bakker et al. 2017; Viner et al. 2020). The main pathway for lead poisoning is through scavenging on dead animals or gut piles contaminated with spent lead ammunition (Church et al. 2006).
CACOs are one of the most intensively managed species in the world. In addition to captive breeding operations spread across multiple zoos, ongoing CACO releases are occurring in Mexico and across six US. release sites, with an additional planned release site in Redwood National Park (D’Elia and Haig 2013; D’Elia et al. 2019; NPS et al. 2021). In the wild, the locations of virtually all CACOs are tracked via some form of telemetry, and many individuals are outfitted with GPS-Global System for Mobile Communications (GSM) transmitters where location, altitude, and accuracy information are recorded at 2–30 min intervals. During nesting, nestlings are monitored and, if necessary, crews enter nests to intervene and occasionally extract chicks to nearby veterinary facilities for treatment. Field crews provide supplemental clean food at release sites, and attempt to re-trap as many CACO as possible for semi-annual health checks, vaccinations, and to take individuals into captivity for chelation therapy if they have high levels of lead in their blood (Walters et al. 2010).
The CACO presents a rare opportunity in reintroduction modeling because we have tracked the number of individuals as well as their fate for 25 years. Because CACOs are derived entirely from a captive population, we essentially have complete knowledge of changes in the population through time, since its inception. Furthermore, the distribution and density of the population is intensively tracked due to the large number of individuals outfitted with GPS transmitters. Thus, we have an exceptional dataset to parameterize and evaluate the accuracy of a spatially explicit demographic model.
Study area
Our study area included the current range of the CACO in California, USA (Fig. 1). To allow future modeling scenarios to incorporate a planned reintroduction site in Redwood National Park in northwestern California (NPS et al. 2021), our modeling domain also encompassed northern California, Oregon, and Washington, USA. Data limitations precluded expanding our modeling domain to other areas, including where CACOs currently exist in the southwestern United States and Baja California, Mexico. However, we designed our model structure to allow for an expanded modeling domain in the future.
Study Area and California condor release sites in southern and central California, 1995–2019. Release sites: (1) Pinnacles National Park, (2) Big Sur, (3) San Simeon, (4) Castle Crags (5) Lion Canyon (6) Bitter Creek National Wildlife Refuge (7) Hopper Mountain National Wildlife Refuge (see Online Resource 3 for the number of California condors released at each site each year)
In California, the current range of the CACO is limited to the mountains and foothills of southern and central part of the state, where reintroductions are ongoing at four release sites: one in southern California operated by the US. Fish and Wildlife Service, two in central California along the Pacific coast operated by Ventana Wildlife Society, and one inland central California site operated by Pinnacles National Park (Fig. 1). Our model also accounts for several release sites in southern California that were in use during our study period but that are no longer operational. The climate within the study area is highly variable, with a Mediterranean-climate along the coast, alpine-climate in the mountains of the high Sierra, and desert-climate in the Mojave Desert east of the Tehachapi Mountains. Variability in climate across these regions corresponds with significant variation in ecological communities. Due to substantial topographic relief in the study area, climate and ecological communities can change rapidly over short distances.
Simulation model
We developed our CACO life history and movement simulator in HexSim (Fig. 2; Online Resource 1; Schumaker and Brookes 2018), hereafter referred to as our CACO model. HexSim is a software application for constructing spatially explicit IBMs of plant and animal species. HexSim incorporates spatial information via input maps, which are tessellated with hexagonal cells. For our CACO model, we selected a 5-km center-to-center hexagon spacing (2165 ha per hexagon), which approximates the distance at which large vultures can perceive food resources while in flight (Spiegel et al. 2013). This cell-size resulted in a model landscape of 39,835 hexagonal cells encompassing California, Oregon, and Washington, USA. HexSim input maps, subsequently referred to as hexmaps, can be static, or can contain a sequence of maps corresponding to changes over specific simulation time periods. HexSim also facilitates map construction on-the-fly as a simulation progresses, and we made extensive use of this feature in our work to describe time-specific population distributions and dynamics. We subsequently refer to these dynamic map-based depictions of model states as generated hexmaps.
HexSim models subject one or more simulated populations to a user-defined sequence of life history events. A time step consists of one cycle through this event sequence, and thus its duration is defined implicitly by event details. Here, we used HexSim to impose a daily time step upon our simulated CACOs, but with many life history events being experienced seasonally or annually. Our choice of a time-step allowed us to model daily movement, carcass deposition and degradation, resource consumption, and cumulative exposures to threats over the annual cycle. We used an ordinal day calendar in which day 1 corresponds to January 1. Our models ran for 25 simulated years, or 9125 days, and we used 50 replicate simulations to capture the variation in model output.
Our development procedure included inviting 6 experts on condor biology and management to review an initial draft model. We selected the reviewers to represent a diversity of geographic, research, and management experiences. The reviews were solicited and conducted individually, although a few reviewers communicated with each other on their responses. Our review requests consisted of a document explaining our overall project objectives and the general structure of the model, plus questions related to specifications of condor stage classes and releases, stage class vital rates (fecundity, survivorship, life span), rates of lead exposure leading to mortality, foraging parameters, daily activity budgets, and nestling feeding dynamics (see Online Resource 2). We compiled the individual review responses and used the results to guide model corrections and enhancements. We then updated specific model elements accordingly, essentially calibrating our model with the experts' knowledge.
Simulating the environment
We simulated the environment using six static hexmaps and two hexmap time series (Table 1). These maps influenced the timing, numbers, and locations of released condors, the nesting, roosting and foraging processes, and the addition of carrion and lead to the landscape.
Carrion deposition and degradation
We simulated carrion deposition and degradation across the landscape (Fig. 3; Online Resource 2). The carrion deposition processes distinguished between three carrion classes: coastal, inland, and proffered. We quantified all classes of carrion in units of CACO meals (the amount of food consumed by one CACO in a single day) and estimated that a meal was equal to approximately 1 kg of food (more precisely, 0.907 kg or 2 lbs. of food) (Koford 1953; Wilbur 1972). All classes of carrion were added to the landscape daily. Only inland carrion contained lead, which was also distributed in integer units of meals. That is, when a carcass containing M meals was added to the landscape, some number L of those meals would be designated as containing lead, with 0 ≤ L ≤ M (see “Lead contamination of carcasses”, below). When a condor consumed a meal containing lead, it then experienced a single lead exposure event. All classes of carrion degraded at a rate of 2 meals per day, which was a simplification due to uncertainty in the actual rate of carrion degradation. Carrion degradation was intended to capture both decomposition and consumption by competing scavenger species, and lead within degraded carrion was made permanently unavailable to CACOs. This process resulted in a spatial distribution of carrion, a portion of which contained lead, that changed daily (Fig. 3).
For inland carrion, we first estimated the daily probability of adding a carcass to each hexagon, and then calculated the actual amount of carrion to add (Table 1; see Online Resource 2). We computed the probability of adding a carcass to each hexagon (P) using the formula:
where X was the inland carrion potential (Table 1) hexmap value and Y was the inland carrion rate of addition parameter. After experimenting with various rates of Y to achieve reasonable values of emergent landscape-wide distribution of carrion meals, we set Y = 0.01 for all simulations. Inland carrion potential maps were based on a time series of Normalized Difference Vegetation Index (NDVI) maps rescaled from 0 to 100, that changed every 2 weeks (see Online Resource 2). NDVI is a measure of primary productivity that is known to correlate with ungulate densities in our study area (D’Elia et al. 2015). Because of the stochastic nature of carrion deposition, we drew a uniformly distributed random number in the range 0–1 (R) to compare with P (defined above), and added carrion to those hexagons where P-R > 0. For each hexagon where P-R > 0, the size of the carcass to add was specified as a number of meals (M). Due to uncertainty of carcass size distribution across the landscape we drew M from a uniform random distribution between 0 and the maximum number of inland meals, which we set to 50 to approximate the size of an adult male California mule deer (Odocoileus hemionus californicus). Fifty meals translate to 45 kg of carrion, assuming an average male deer weighs 90 kg and half of the carcass contains unconsumable parts of the animal, such as bone and hide (Wilbur 1972).
Coastal carrion was less frequently added to the landscape, tended to be larger in size, and never contained lead. Similar to inland carrion, we first determined which (if any) hexagons would receive a new coastal carcass each day, and then specified the amount of coastal carrion to add. Our map of coastal feeding habitat was binary and static, so a fixed set of hexagons (those considered coastal feeding habitats) were eligible to receive coastal carrion (see Online Resource 2). Unlike inland carrion, all eligible hexagons had the same probability of receiving a new carcass (the coastal carrion rate of addition parameter), which we set to 0.001. This reflects an assumption that coastal carrion is, on average, deposited at 10% of the maximum rate associated with inland carrion. For those hexagons receiving coastal carrion, M was drawn from a uniformly distributed random number between 0 and the maximum number of coastal meals, which we set to 200 (i.e., 181 kg) to approximate the edible biomass of an adult male California sea lion (Zalphus californianus) weighing approximately 362 kg (Schusterman and Gentry 1971).
Proffered carrion was only added to hexagons containing an active release site (i.e., a release site where CACOs were released that year). We set the carcass size of proffered carrion to the maximum number of meals for an inland carcass. Proffered carrion never contained lead.
Due to large uncertainties in decomposition rates and the size distribution of carcasses, as well as the lack of data sufficient to establish a relationship between feeding rates and survival or reproduction, we did not directly link resource acquisition to demographic rates. As a result, any introduction of additional realism into carrion size distributions or decomposition rates would have had a minor influence on the spatial arrangement of meals, and thus on emergent foraging patterns; and, such a change could not have affected the simulated CACO vital rates (Fig. 4). Nevertheless, our incorporation of these carrion deposition and degradation mechanisms will make it possible to introduce more realistic parameter values into future versions of the model, and to eventually link carrion distribution and decomposition to CACO demographic rates.
The landscape-wide daily distribution of carrion (individual scatter plot points) emerging from a single 25-year model replicate. The carrion resource depicted here does not include proffered carcasses. The daily carrion distribution is characterized by a simple measure of spatial distribution (X-axis) and the overall quantity of available resource (Y-axis). Inset maps illustrate the spatial arrangement of the carrion resource in limiting cases that are relatively sparse (bottom right) and abundant (top right). The red square illustrates the portion of the California condor's range corresponding to the inset maps, and the color bar relates inset map color to carrion abundance at the scale of individual 2165 ha hexagons
Lead contamination of carcasses
Each newly deposited non-proffered inland carcass had a probability of being assigned lead. The fraction of meals that were contaminated was set equal to the site-specific lead potential (Table 1) hexmap value, multiplied by a fitting coefficient. This sole model-fitting coefficient, which we refer to subsequently as the lead rate of addition, affected observed CACO population sizes via lead-derived mortality. Based on results from a collection of replicated tuning simulations, we adjusted the lead rate of addition (a unitless parameter) to recover the observed population size at the end of 2019, and ultimately assigned this parameter a value of 7.9 × 10–4. When a carcass was added to the landscape, the number of meals contaminated with lead was obtained by rounding α × β × M to the nearest integer, with α representing the mapped lead potential, β being the lead rate of addition parameter, and M equaling the number of meals present in the carcass.
Simulating individuals
Our CACO model was female-only, individual-based, and spatially explicit. We assumed no difference in movement behavior by males and females, an assertion supported by Rivers et al. (2014), who found that male and female CACOs used monthly home ranges of similar size throughout the year, and that breeding adults did not differ from non-breeding adults in their average monthly home range size. Whereas there is a gradual increase in average daily travel distances as CACOs age (Hall et al. 2021), we assumed no difference in movement behavior by adults and subadults because both stage classes are known to forage across extremely large home ranges (Meretsky and Snyder 1992), and the difference in average daily travel distance was minimal compared to the resolution of our simulated environment.
Simulated CACOs were classified into five distinct chronological stage classes, and our model distinguished between wild-hatched and released birds, in order to account for wild-hatched chick dependence on parents during the first two years of life. At the time of hatching, individuals were labeled fledglings, and they subsequently moved through three immature stages: immature chick (1-year-olds), mature chick (2-year-olds), and subadult (3–5-year-olds). At age 6, when CACOs typically reach their full breeding plumage (Snyder and Snyder 2000), subadult CACOs transitioned into the adult class. Only adult CACOs were reproductive. In actuality, adult CACOs bring food back to their nests to feed fledglings and are accompanied on foraging trips by immature and mature chicks (Snyder and Snyder 2000). For computational efficiency, our wild fledglings and chicks (i.e., 1–2 year old birds; hereafter dependent CACOs) were assigned resources equivalent to those of their parents, avoiding the need to simulate congruent parent and dependent foraging paths. Dependent CACOs also experienced lead exposure events identical to those of their parents. Lead consumption during foraging increased the probability of mortality from both acute and chronic exposure (see Online Resource 2). Here, acute refers to a single exposure, while chronic refers to the multiple exposures that cumulatively increase the probability of death. Released CACOs were added to the simulations on November 1st of their second year of life, making them immature chicks of age 22 months. Survival rates for released immature CACOs were prorated to reflect their being subjected to mortality in the wild during just the last 2 months of the immature stage (see “Mortality”, below). Unlike wild-hatched fledglings that fed with their parent, released CACOs foraged independently in our model.
Releases
We simulated the entire history of CACO releases conducted yearly during 1995–2019. We did not include the earlier releases that started in 1992 because those condors were eventually all brought back into captivity due to behavioral issues (Meretsky et al. 2000). The year and location of releases, as well as the number of CACOs released at each location, were specified by the release sites hexmap time series (Table 1), which was assembled from official records (Online Resource 3). Because our model was female-only, we assumed a balanced sex-ratio and always introduced one-half of the actual number of released CACOs, rounded up to the nearest integer. Our entire population of simulated CACOs descended from released individuals. Simulated releases always involved immature chicks of age 22 months, and took place on November 1 (ordinal day 305). Upon release, CACOs selected a nearby roosting site based on the roosting potential map (Table 1), and used that roost as a launching point for foraging flights until they became an adult and acquired a nest. Due to the complexities of CACO roosting ecology, we did not attempt to simulate subadult use of overnight roosts other than the roost they selected upon release; however, we recognize that these roosting events occur and may influence exposure to threats.
Nest site acquisition
Adults selected nest sites once per year on February 24 (ordinal day 55), which is the estimated median egg-lay date for CACOs in California. The number of nest sites that could be formed per hexagon ranged from zero to three, and was dictated by the nesting potential map (Table 1). Adults searching for a nest site attempted to acquire one at, or adjacent to, their roosting or previous nest site but continued to expand their search area until they were successful (see Snyder et al. 1986). In cases where the maximum number of nests were already claimed, competition with other CACOs could cause a returning adult to relocate its nest to a nearby site. Because nesting habitat does not appear to be limiting (D’Elia et al. 2015), and because CACOs can use a variety of nesting substrates (Snyder et al. 1986), we designed our model to ensure that all adults in search of a nest successfully established a nesting site; however, not all adults reproduced. As a simplification, simulated adults always initiated daily foraging flights from their nests. In reality, non-breeding adults and subadults can use overnight roosts far from their nest sites (Snyder and Snyder 2000).
Reproduction and senesce
We adopted fecundity values from Finkelstein et al. (2012), who estimated a mean observed field-based reproductive rate of 0.210 fledglings per adult female per year. This equates to 0.105 female fledglings per adult female per year. We conservatively assumed a maximum lifespan of 60 years (see Meretsky et al. 2000), and no changes in adult fecundity with age or maturity of the release program. Reproduction (i.e., hatching) took place once per year on April 22 (ordinal day 112), which is the median hatch date for CACOs in California. Clutch sizes were restricted to zero and one.
Foraging
We simulated daily foraging throughout the year (Fig. 3). Foraging involved CACOs leaving a nesting or roosting site, searching for carrion, and subsequently returning to the locations from which they departed. Foraging CACOs could either go back to a previously visited carcass or search for a new carcass. New carcass identification was guided by maps representing the gradient of carrion density constructed daily from simulated carrion location data (Fig. 3). Based on feedback from CACO experts, our simulated adult CACOs with fledglings had a 50:50 chance each day of foregoing foraging to instead remain in the nest with their fledgling.
Simulated CACOs made use of two separate strategies for locating carrion. First, we assumed individuals that fed on a carcass the previous day would return to that site if at least ten meals remained. Although somewhat arbitrary, we chose ten meals to represent a sufficient amount of food to be energetically advantageous for a CACO to return to the site. All other CACOs used generated carrion gradient hexmaps to travel to, and explore, areas of higher carrion densities until a new carcass was located. Each hexagon in a gradient map was assigned a value equal to its distance from the nearest carcass. The model constructed these maps daily, after carcass addition and degradation, in advance of foraging movements. When the number of CACOs visiting a carcass exceeded the available meals, some condors would be unable to eat. In such cases, the carrion gradient map was updated, and these CACOs continued searching for an alternate carcass.
Our model recorded simulated foraging-related movements using a pair of generated hexmaps we referred to as movement flux and excursion endpoints. The movement flux hexmap tracked hexagons traversed by CACOs as they searched for a carcass, but for computational simplicity, the maps excluded return trips to carcasses already visited, and movements from a carcass back to nesting or roosting sites. We designed the movement flux hexmap to facilitate comparison with GPS records of CACO movement in the wild, including collecting this information for just the years in which empirical data were available (2013–2019). The excursion endpoints hexmap recorded the starting and ending points of all foraging trips. This map shows where CACOs were nesting and roosting, but also illustrates the spatial distribution of the carrion upon which they fed. Both the movement flux and the excursion endpoints hexmaps were updated each time foraging took place, representing cumulative per-hexagon visitation.
Mortality
We derived stage-specific survival rates by averaging age-specific values found in Finkelstein et al. (2012) within each stage-class. To avoid overfitting the model to the data, we did not use the time-specific survival rates from Finkelstein et al. (2012) that accounted for improvements in management early in the release program. Instead, we began with the survival rates for the last year of their analyses (2010), and then calculated the increase in those rates to infer what survival would be without mortality from lead toxicosis (as described in Finkelstein et al. 2012, based on Rideout et al. 2012), which was the only mortality factor, other than age, that we explicitly accounted for in our model. Fledging survival rates were based on the probability of surviving from fledging to the end of the calendar year, as our fecundity rate already accounted for the probability of chicks surviving to fledging. Consequently, we set annual stage-specific survival rates to 0.879 (fledglings), 0.825 (immature chicks), 0.912 (mature chicks), 0.965 (subadults), and 0.973 (adults).
Finally, we simulated mortality resulting from lead exposure using a mathematical function that related the annual and lifetime number of lead exposures to the probability of death (Online Resource 2). We used this approach rather than attempting to simulate the amount of lead in a condor’s blood because the number of chronic lead exposures appears to correlate better with mortality outcomes than singular episodes of elevated blood lead levels (Nguyen et al. 2018). Our approach also required estimating fewer parameters than simulating blood lead dynamics (e.g., see Green et al. 2008), which can be influenced by CACO nutritional status and genetic predisposition, as well as by size and surface area of lead fragments (Pattee et al. 2006); these additional parameters, each carrying high uncertainty, would have greatly and unnecessarily complicated the model. Instead, tracking lead exposures allowed us to account for the probability of acute mortality from a single exposure as well as an increased probability of death from annual and lifetime chronic lead exposure. Because the exact relationship between the number of exposures and the probability of death is unknown, we developed three different functions representing a range of scenarios from optimistic to pessimistic (Online Resource 2). From these, we selected the linear function y = 1.5385x for our simulations, which was intermediate between optimistic and pessimistic scenarios. Here, x is the number of cumulative exposures over each condor’s lifetime, and y is the incremental increase in mortality from lead exposure. At the end of each calendar year (i.e., ordinal day 365), the number of annual and cumulative exposures is recorded for each individual. Then, a probability of dying from lead is calculated as the product of the incremental probabilities of death along the cumulative lead risk curves.
Model hindcast testing and calibration
We evaluated the model's performance with a hindcasting analysis to compare model results with empirical data on CACO reintroductions and population responses. Hindcasting, also called backcasting (Becker 2010), is an analysis of model prediction accuracy made by comparing model predictions to known, historic events (e.g., Beever et al. 2010; Findlay et al. 2010; Levinsky et al. 2013). Hindcasting results can be used to calibrate a model to known outcomes (e.g., Challinor et al. 2005). In order to compare the effectiveness of our initial model and of its subsequent revision based on expert reviews and input, we conducted the hindcasting analysis before and after the invited peer reviews and associated model modifications (Online Resource 2).
Our hindcasting analysis involved comparing final model results from 50 replicate runs to aspatial and spatial empirical data on CACOs collected 1995–2019. The yearly aspatial empirical data included means, minimums, maximums, standard deviation (SD), and temporal trends of population size, numbers of fledglings, overall mortality, and lead-caused mortality, as well as number of CACO releases and number of CACO release sites. We evaluated model precision as year-specific and overall mean predicted range (maximum–minimum), coefficient of variation (CV), and standard error (SE) of the mean population size. We evaluated model accuracy as the percent of years in which the observed population size fell within minimum and maximum modeled values, and within modeled means ± 1SD. The spatial empirical data included the density of 6,120,951 GPS locations from 167 CACOs tallied within each hexagon from July 2013 through December 2019 (see Online Resource 2); we compared these data with modeled movement flux densities from the model years corresponding to 2013–2019. Densities were calculated based on land area to account for hexagons straddling the land–ocean interface along the coast. Because the frequency distributions of both datasets were highly skewed, with a few hexagons around release sites containing extremely high densities, we rescaled densities to log(x + 1). Modeled data were rounded to integers prior to the log transformation so that very rarely visited hexagons (those with an average of < 0.5 CACO movements across 50 model replicates of 9125 time-steps) were treated as unused. We calculated overall accuracy, specificity, and sensitivity to compare CACO presence between modeled and empirical CACOs (Allouche et al. 2006). We calculated Cohen’s kappa (Cohen 1960) to quantify the agreement among the modeled and empirical densities while accounting for chance, and penalizing larger disagreements more than smaller disagreements.
To evaluate the sensitivity of modeled population size to lead mortality parameters, we ran 5 replicate simulations using our optimistic lead risk curve, and 5 replicate simulations using our pessimistic lead risk curve (see Online Resource 2). We also ran 5 replicate simulations of higher (+ 10%) and lower (− 10%) values of our lead rate of addition parameter. Each of the 5 replicate sets served to capture variation of the response variables. We visually compared the resulting simulated population sizes with the simulated minimum, maximum, and mean population sizes obtained from the original model parameterization. We also calculated and compared mean differences in population size at the end of the 25-year simulations.
Results
In each of our 50 simulations, we released a total of 155 female CACOs from eight release sites, over a 25-year period (9125 daily time-steps). Due to rounding necessitated by ours being a female-only model, this ended up being slightly more than the 144 CACOs actually released (Fig. S4.1a). Trends of mean simulated population size were not significantly different from the empirical population size (Fig. S4.1b.; t = 1.794, p = 0.08), although the minimum simulated population sizes exceeded the empirical population size in years 4–12 (Fig. 5). Despite deviations in population size early in the release program, annual simulated mean population size and empirical population size were highly correlated, especially after the population became established with > 50 females (Fig. 5; r2 = 0.99).
(top) HexSim model output for 50 model runs (light gray area = range; dark gray area = ± 1 standard deviation; dashed line = mean values) compared to empirical data (solid black lines) for female population from 1995 (Year 1) to 2019 (Year 25); (bottom) Correlations between the number of females predicted by HexSim and the number of condors from empirical data (divided by 2 to represent females only) for the establishment phase (< 50 females) and growth phase (> 50 females) of the population
Trends in simulated mean fecundity (i.e., numbers and rates of female fledglings per female) were not significantly different from empirical trends (Fig. S4.2a; t = 0.967, p = 0.34; Fig. S4.2b; t = 1.449, p = 0.15, respectively), although empirical values had greater interannual variability than mean simulated values (Figs. 6, S4.2, S4.5). Whereas the simulated population successfully produced offspring as soon as there were adults present (year 6), CACOs did not, in reality, produce any successful fledglings until the 10th year of releases (Fig. 6; Online Resource 3).
HexSim model output for 50 model runs (light blue area = range; dark blue area = ± 1 standard deviation; white lines = mean values) compared to empirical data (black lines) for: a number of fledglings, b fledgling rate (number of fledglings/total population), c number of deaths, d mortality rate, e number of lead deaths, f mortality rate from lead. Red lines for lead mortality in e and f indicate estimated lead mortalities adjusted to account for deaths from unknown causes and California condors missing in the wild. All numbers represent females only. (Color figure online)
Trends in simulated mean mortality (i.e., number of CACOs mortalities and CACO mortality rate) were not significantly different from empirical trends (Fig. S4.3a, t = 0.736, p = 0. 47; Fig. S4.3b, t = 1.876, p = 0.07, respectively), although empirical values had greater interannual variability than mean simulated values (Fig. 6, S4.6). Empirical mortality rates exceeded maximum simulated mortality rates in 3 of the first 10 years of the reintroduction program (Figs. 6, S4.3b).
Simulated mean lead-caused mortalities encompassed the range of unadjusted empirical lead-caused mortalities (Figs. 6, S.4.4). However, the trend of the unadjusted empirical number of lead-caused mortalities was significantly different than its simulated analog, with empirical values showing more interannual variation than modeled mean values (Figs. 6, S4.4, t = 2.532, p = 0.01). If, however, a proportionate annual number of lead-caused mortalities from known causes were applied to mortalities of unknown causes, then the adjusted empirical lead-caused mortalities were closer to simulated values in some years but were higher than mean simulated values as the population grew larger (Fig. 6). Trends in simulated mean rates of lead-caused mortality were not significantly different from empirical rates (Fig. S4.4b, t = 0.229, p = 0.82) although the two were weakly correlated temporally (Fig. S4.7b, r2 = 0.16).
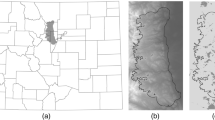
The geographic distribution of simulated CACOs was similar to the empirical distribution, with an overall accuracy of 79% (Fig. 7, Online Resource Table S2.1). Commission error (27%) was higher than omission error (9%) (Fig. 7c). The log (density) of simulated CACOs was similar to the GPS log (density), although overall accuracy (66%) was less than for the simple comparison of geographic distribution (Fig. 7, Online Resource Table S2.1). Weighted kappa for the comparison of simulated and empirical log (density) was 0.44 (i.e., classification 44% greater than chance), denoting moderate agreement (Cohen 1960).
Our model was sensitive to selection of a lead risk curve and to changes in our lead rate of addition parameter (Fig. 8). Changing the lead risk curve from linear to optimistic (lower acute and chronic mortality from lead exposure) resulted in a population that was, on average, 31% larger at the end of the simulation, while using a pessimistic lead risk curve (higher acute and chronic mortality from lead exposure) resulted in a mean population that was 53% smaller, on average, at the end of the simulation. A 10% decrease in our lead rate of addition parameter resulted in a population that was, on average, 16% larger at the end of the simulation, while a 10% increase in our lead rate of addition parameter resulted in a population that was, on average, 19% smaller at the end of the simulation.
Simulated female population from 1995 (Year 1) to 2019 (Year 25) for 50 HexSim model runs assuming a linear lead risk curve (solid black lines = minimum and maximum female population size; dashed line = mean female population size) compared to: (top) HexSim model output for 5 simulations parameterized with our pessimistic lead risk curve (red lines) and 5 simulations parameterized with our optimistic lead risk curve (blue lines); and (bottom) HexSim model output for 5 simulations parameterized with + 10% lead rate of addition (red lines) and 5 simulations parameterized with − 10% lead rate of addition (blue lines). (Color figure online)
Discussion
Our spatially explicit IBM for the CACO was well calibrated to empirical data, and should be a useful decision aid for evaluating the efficacy of future CACO reintroduction scenarios. While spatially explicit IBMs for other avian scavengers (mostly African vultures) have been constructed to assess food availability and energy budgets (Kane et al. 2014), the effect of social facilitation on foraging success (Jackson et al. 2008), the impact of food predictability on social facilitation (Deygout et al. 2010), factors influencing foraging search efficiency (Spiegel et al. 2013), and the impact of spatially explicit poisoning risk on survival rates (Monadjem et al. 2018), our IBM is unique in several respects. Importantly, our extensive use of input maps makes it easier to construct population projections for future scenarios, and allows for easy updating of the modeling environment as new information becomes available. For example, to aid reintroduction planning, our model makes it possible to specify a dynamic series of maps that control changes in the number and timing of released CACOs and proffered food. While other vulture IBMs simulate the deposition and degradation of carcasses (e.g., Monadjem et al. 2018), we added a component to track cumulative exposure rates to a toxin (lead) found in carcasses, and linked such exposures to acute and chronic mortality. We also simulated changes in the distribution of carrion across annual environmental productivity cycles, and separately modeled inland and coastal feeding habitats, thereby allowing us to simulate differences in carcass size and lead exposure among CACOs feeding on inland or marine food resources.
Hindcasting analysis revealed that our CACO model reasonably approximated empirical sizes and trends of the population, fledgling numbers and rates, total mortality and lead-caused mortality rates. We also demonstrated how the peer-review and model-revision process improved accuracy (Online Resource Table S2.1); nevertheless, emergent simulated demographic values did not always exactly match year-specific empirical values. This was expected, given the highly stochastic nature of this very small population, in both the model universe and real world. Of greater importance was the general agreement in trends, and the ability of our simulation to largely capture the real-world stochasticity within the ranges of predicted values (Table 2). These results suggest that our IBM should be useful for comparing future proposed or hypothesized reintroduction scenarios, provided that care is taken to test its sensitivity to the parameterization of key variables and input maps. This is particularly important for the lead risk map and lead exposure parameters, as our model results are sensitive to changes in the amount of lead in the environment, the relationship between acute and chronic lead exposure, and the probability of lead-caused mortality.
There were two notable differences between our simulations and empirical data. First, observed rates of total mortality early in the release program were greater than indicated by our simulations, and fell outside of the range of predicted values. This was likely associated with the increased rates of demographic stochasticity experienced by small reintroduced populations that are in the establishment phase, and because management interventions became more sophisticated and effective over time. Second, our simulations predicted an earlier onset of successful reproduction than occurred in the real world. This was likely due, at least in part, to initial problems with actual nestlings ingesting garbage and dying (Mee et al. 2007; Bakker et al. 2017). These problems were later reduced, although not fully eliminated, through management interventions (Viner et al. 2020).
The overall accuracy of our simulation in reproducing the spatial distribution of CACOs was relatively high (79%). We attempted to lower the model omission error rate (9%) at the expense of higher commission error rate (27%). We viewed omission error rates (false negatives) to be more concerning, as they led to underestimates of the CACO’s use of potentially important nesting, roosting, and feeding sites. In contrast, commission errors simply suggest where CACOs might someday be found. Our calculated commission error of 27% was likely biased high because GPS data were not available for the entire population. For example, CACOs without GPS have been observed in San Mateo and Alameda counties (ebird 2021); if those flight paths had been included in our empirical dataset, then model commission error would have been lower. Areas our model predicted would be used by CACOs, but for which there were no GPS locations, occurred mostly along the northern and southern periphery of the realized distribution (Fig. 7). The largest area where our model failed to predict CACO presence was in the southern Sierra Nevada—an area where released CACOs have recently begun exploring. However, our model did predict presence of CACOs in the portion of the southern Sierra where CACOs were recorded feeding during a study conducted from 2013 to 2015 (Hall et al. 2019). Our model did not predict CACOs crossing the Central Valley (Fig. 7), a phenomenon that is extremely rare (only one recorded instance in our empirical dataset) because condors need upward air movement to maintain soaring flight and risk being grounded over large expanses of flat terrain (Poessel et al. 2018a). The highest log (density) of empirical and modeled CACOs was around release sites and in CACO foraging habitat in the Tehachapi Mountains (Fig. 7).
Recommendations for improvement
We will improve our model as our knowledge of CACO ecology, population dynamics, and disturbance regimes grows. Model improvements will also result from the incorporation of other landscape influences on CACO demography, and from the ongoing intensive monitoring of CACOs via biotelemetry. Specifically, we anticipate potential improvements in: (1) incorporating social interactions among individuals and information sharing, and the role of tradition and learning in CACO foraging ecology; (2) disentangling our fecundity parameter into its component parts, (3) improving our carrion deposition and degradation submodel, and linking it to demographic outcomes; (4) incorporating other threats and catastrophes; (5) collecting more accurate information on the spatial distribution of carcasses and consumable lead, as well as the relationship of acute and chronic lead exposures to CACO mortality; (6) incorporating additional information to capture the impact of seasonal changes in the weather on CACO movements; and, (7) examining the impact of management interventions on CACO demography. In the meantime, our first-generation IBM for the CACO is an important step forward.
We lack a complete understanding of how CACOs make foraging or overnight roosting decisions, and expect that future opportunities to improve our model will arise as new insights emerge from the study of condor behavior, social interactions, and traditions (e.g., Bronson and Welch 2020). Our model assumed that CACO feeding behavior was driven by carcass densities within suitable feeding habitats, and that CACOs return to carcasses that have sufficient meals remaining. In reality, we know vultures use conspecific and interspecific social cues to forage more efficiently (Cortés-Avizanda et al. 2014; Kane et al. 2014) and occasionally make exploratory movements independent of feeding events. In addition, CACOs are known to frequent certain areas out of memory or tradition, particularly roost sites near foraging grounds (Snyder and Snyder 2000); yet, our model did not incorporate sociality or tradition in selecting roosting locations near foraging sites. This may partially explain why our model did not predict the distribution of CACOs extending further north in the southern Sierra Nevada foothills, where there are extensive feeding areas for CACOs, but which require flying over other high-quality feeding areas in the Tehachapi Mountains (Fig. 7, D’Elia et al. 2015; Hall et al. 2019).
Our fecundity parameter—the number of females produced per adult female per year—is an amalgam of several important demographic components that we did not model separately. Future modeling efforts could separate out the egg-laying, chick-rearing, and fledgling processes, to more clearly address mortality factors at each of these stages. Tracking the egg-laying process, and the possibility of renesting when an egg is lost, would also allow us to explore the consequences of higher rates of egg mortality in CACOs feeding on marine mammals (Burnett et al. 2013), as well as the possibility that egg-laying females may be at higher risk of lead mortality due to mobilization of medullary bone to create eggshells (Franson and Pain 2011; but see Viner et al. 2020).
Due to data limitations, our carrion submodel was imperfect and was not directly linked to CACO fecundity or mortality rates. Although our simulated carrion influenced condor movement, the daily addition of condor meals meant that food availability was more reflective of patterns of landscape productivity (Fig. 4) and was less influenced by carcass size or decomposition rate. Further, although lead decomposed with carrion, the lead rate of addition parameter was tuned to replicate the empirical population size at the end of the modeling period; therefore, our model parameterization was not sensitive to carcass size or decomposition rates. Future model iterations could more realistically replicate the carrion deposition and degradation across the annual cycle, and better estimates of these parameters would make it possible to link carrion resource acquisition to demographic outcomes.
Next-generation CACO IBMs might also address other threats and catastrophes. In particular, we see opportunities to incorporate the threat of collisions with wind turbines and powerlines (e.g., Wiens et al. 2017), the threat of wildfire, and the uptake of other toxins (e.g., DDE and mercury from consuming marine mammal carcasses; Kurle et al. 2016) that may impose additional acute or chronic impacts on fecundity or mortality (see García-Ripolles and López-López 2011). Catastrophic environmental events can have a swamping effect on small-population demography (Hart and Avilés 2014), and outside of lead poisoning, are not presently captured in our IBM. Yet, we know that catastrophes can occur, as observed in 2020 when the Dolan Fire killed approximately 10% of the CACO population near Big Sur (USFWS 2020). Explicitly accounting for such catastrophes could allow future model projections to more realistically capture environmental stochasticity (Lande 1993).
Our simulations made use of simplifying assumptions to track the deposition of lead in carrion across the landscape, and the fate of CACOs exposed to lead, because we lacked sufficient data to empirically parameterize these model components. Nevertheless, we tuned the rate of lead deposition to match the observed population size at the end of the modeled timeframe, assuming a linear relationship between mortality risk and repeated lead exposures, and a static map of lead risk. Recognizing uncertainties in the rate of lead deposition, the distribution of lead exposure risk, and the relationship between lead exposure and mortality risk, we constructed the model to allow us to easily update these parameter values and maps as new information surfaces. A significant advantage of explicitly modeling the distribution of lead across the landscape, and its impact on CACO demography, is the ability to examine the utility of future management scenarios designed to reduce or remove lead in specific areas. This is important because policy and management can alter the distribution of lead across the landscape, and the efficacy and implementation of lead reduction efforts are likely to vary across space and time. For our simulations, we assumed that the primary source of lead was from hunting, and that there were no changes in the distribution of lead deposition potential over time. Regulations have restricted the legal use of lead ammunition within the range of the CACO since 2007 (California Assembly Bill 821), and have become incrementally more restrictive from 2013 to 2019, when California phased out the use lead ammunition when taking any wildlife (California Assembly Bill 711); yet, the impact of these regulatory actions on the bioavailabity of lead has not been adequately assessed, and CACOs are still dying of lead poisoning. Although our model did a fair job of replicating the amount of lead mortality from 1995 to 2019, further analysis of the distribution of lead and its acute and chronic impacts on individual CACOs would likely improve our predictions because population outcomes in our model are sensitive to changes in lead parameters. Additionally, studying the mechanisms behind changes in movement patterns, as CACO populations grow and become less reliant on proffered food (Kelly et al. 2014; Glucs et al. 2020), could also result in a more nuanced model that explicitly tracks behavior-driven demographic changes through time.
Our IBM did not directly incorporate meteorological variables and their influence on flight behavior and decision-making (see Poessel et al. 2018a; Bonner et al. 2021). While our landscape conductance map made use of information on updraft potential, those variables were incorporated as annualized means instead of dynamic maps across the annual cycle. Given that weather and photoperiod affect monthly home range sizes (Rivers et al. 2014), and knowing that daily travel distances change throughout the year (Hall et al. 2021), incorporating dynamic meteorological data and simulating changes in the length of the photoperiod could improve our ability to predict CACO movement. If collision risks were added to the model, incorporating dynamic meteorological maps that influenced CACO movement would become even more important, given that flight altitude is also highly variable across the annual cycle (Poessel et al. 2018b).
We did not directly model management interventions (e.g., nest guarding, chelation therapy, providing veterinary care to injured or sick individuals) in our simulations. Instead, we assumed management was consistently applied throughout the duration of our simulations, as reflected in our constant fecundity and base mortality rates. Yet, we know that there were significant changes in mortality rates early in the release program (Finkelstein et al. 2012), and that there was a delay in successful breeding at the outset of the reintroduction program. As a result, our population projections overestimate female population size in the first half of the study period. Bakker et al. (2017) found that the age of the release program had a positive correlation with survival rates, largely due to improvements in management interventions over time (Bakker et al. 2017). It is possible that demographic stochasticity within an extremely small establishing population also played a role. Untangling the age of the program and population size was not possible because they are highly correlated (Bakker et al. 2017). Given that CACOs released into new areas will benefit from our modern management interventions, longitudinal mortality data from these new areas could eventually be used to parameterize future versions of the model.
Effective prediction and mitigation of the risks associated with contaminants requires an understanding of their spatio-temporal distribution (Mateo-Tomás et al. 2016). Therefore, we anticipate that management of the CACO population will benefit from our model, which explicitly links risks to both dynamic landscape spatial structures and individual behaviors. Spatially explicit IBMs are particularly well-suited for assessing alternative proposals for future CACO releases and lead reduction efforts, and for exploring the implications of environmental conditions, and of uncertainties in causal relationships. As CACO IBMs mature, we anticipate they will become even more useful for informing reintroduction decisions and the development of quantitative and spatially explicit recovery targets that are linked to demography and disturbance.
Data availability
The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
Our model is available for download at: https://www.hexsim.net/downloads.
References
Allouche O, Tsoar A, Kadmon R (2006) Assessing the accuracy of species distribution models: prevalence, kappa and the true skill statistic (TSS). J Appl Ecol 43:1223–1232
Andersen D, Yi Y, Borzée A, Kim K, Moon K-S, Kim J-J, Kim T-W, Jang Y (2021) Use of a spatially explicit individual-based model to predict population trajectories and habitat connectivity for a reintroduced ursid. Oryx 1–10 https://doi.org/10.1017/S0030605320000447
Bakker VJ, Smith DR, Copeland H, Brandt J, Wolstenholme R, Burnett J, Kirkland S, Finkelstein M (2017) Effects of lead exposure, flock behavior, and management actions on the survival of California condors (Gymnogyps californianus). EcoHealth. https://doi.org/10.1007/s10393-015-1096-2
Becker J (2010) Use of backcasting to integrate indicators with principles of sustainability. Int J Sust Dev World 17(3):189–197
Beever EA, Ray C, Mote PW, Wilkening JL (2010) Testing alternative models of climate-mediated extirpations. Ecol Appl 20(1):164–178
BirdLife International. 2021. Species factsheet: Gymnogyps californianus. Downloaded from http://www.birdlife.org. Accessed 26 May 2021.
Bonner SR, Poessel SA, Brandt JC, Astell MT, Belthoff JR, Katzner TE (2021) Drivers of flight performance of California condors (Gymnogyps californianus). J Raptor Res. https://doi.org/10.3356/JRR-20-94
Bronson IG, Welch DW (2020) A model to illustrate the potential pairing of animal biotelemetry with individual-based modeling. Anim Biotelemetry 8:36
Burnett LJ, Sorenson KJ, Brandt J, Sandhaus EA, Ciani D, Clark M, David C, Theule J, Kasielke S, Risebrough RW (2013) Eggshell thinning and depressed hatching success of California condors reintroduced to central California. Condor 115:477–491
Carroll C, Phillips MK, Schumaker NH, Smith DW (2003) Impacts of landscape change on wolf restoration success: planning a reintroduction program based on static and dynamic spatial models. Conserv Biol 17:536–548
Challinor AJ, Slingo JM, Wheeler TR, Doblas-Reyes FJ (2005) Probabilistic simulations of crop yield over western India using the DEMETER seasonal hindcast ensembles. Tellus a: Dyn Meteorol Oceanogr 57(3):498–512
Church ME, Gwiazda R, Risebrough RW, Sorenson K, Chamberlain CP, Farry S, Heinrich W, Rideout BA, Smith DR (2006) Ammunition is the principal source of lead accumulated by California condors re-introduced to the wild. Environ Sci Technol 40:6143–6150
Cohen J (1960) A coefficient of agreement of nominal scales. Educ Psychol Measur 20:37–46
Cortés-Avizanda A, Jovani R, Donázar JA, Grimm V (2014) Bird sky networks: how to avian scavengers use social information to find carrion? Ecology 95:1799–1808
D’Elia J, Brandt J, Burnett LJ, Haig SM, Hollenbeck J, Kirkland S, Marcot B, Punzalan A, West CJ, Williams-Claussen T, Wolstenholme R, Young R (2019) Applying circuit theory and landscape linkage maps to reintroduction planning for California condors. PLoS ONE 14(12):e0226491
D’Elia J, Haig SM (2013) California condors in the Pacific Northwest. OSU Press, Corvallis, OR, p 208
D’Elia J, Haig SM, Johnson M, Marcot B, Young R (2015) Activity-specific ecological niche models for planning reintroductions of California condors (Gymnogyps californianus). Biol Cons 184:90–99
D’Elia J, Haig SM, Mullins TD, Miller MP (2016) Ancient DNA reveals substantial genetic diversity in the California condor (Gymnogyps californianus) prior to a population bottleneck. Condor: Ornithol Appl 118:703–714
DeMaso SJ, Sands JP (2019) Systems analysis and simulation. In: Brennan LA, Tri AN, Marcot BG (eds) Quantitative analyses in wildlife science. The Johns Hopkins University Press, Baltimore, MD, pp 149–164
Deygout C, Gault A, Duriez O, Sarrazin F, Bessa-Gomes C (2010) Impact of food predictability on social facilitation by foraging scavengers. Behav Ecol 21:1131–1139
Dunham JB, White R, Allen CS, Marcot BG, Shively D (2016) The reintroduction landscape: finding success at the intersection of ecological, social, and institutional dimensions. In: Jachowski DS, Millspaugh JJ, Angermeier PL, Slotow R (eds) Reintroduction of fish and wildlife populations. University of California Press, Berkeley, California, pp 79–103
eBird. 2021. eBird: An online database of bird distribution and abundance [web application]. eBird, Cornell Lab of Ornithology, Ithaca, New York. http://www.ebird.org. Accessed 23 May 2021.
Findlay HS, Burrows MT, Kendall MA, Spicer JI, Widdicombe S (2010) Can ocean acidification affect population dynamics of the barnacle Semibalanus balanoides at its southern range edge? Ecology 91:2931–2940
Finkelstein ME, Doak DF, George D, Burnett J, Brandt J, Church M, Grantham J, Smith DR (2012) Lead poisoning and the deceptive recovery of the critically endangered California condor. Proc Natl Acad Sci USA 109:11449–11454
Franson JC, Pain DJ (2011) Lead in birds. In: Beyer WN, Meador JP (eds) Environmental contaminants in biota: interpreting tissue concentrations, 2nd edn. CRC Press, Boca Raton, FL, pp 563–593
García-Ripolles C, López-López P (2011) Integrating effects of supplementary feeding, poisoning, pollutant ingestion and wind farms of two vulture species in Spain using a population viability analysis. J Ornithol 152:879–888
Glucs ZE, Smith DR, Tubbs CW, Bakker VJ, Wolstenholme R, Dudus K, Burnett LJ, Clark M, Clark M, Finkelstein ME (2020) Foraging behavior, contaminant risk, and the stress response in wild California condors (Gymnogyps californianus). Environ Res 189:109905
Green RE, Hunt WG, Parish CN, Newton I (2008) Effectiveness of action to reduce exposure of free-ranging California condors in Arizona and Utah to lead from spent ammunition. PLoS ONE 3(12):e4022
Grimm V, Railsback SF (2005) Individual-based modeling and ecology. Princeton series in theoretical and computational biology, Princeton University Press, New Jersey, p 448
Hall JC, Braham MA, Nolan LA, Conley J, Brandt J, Mendenhall L, Lanzone M, McGann A, Katzner TE (2019) Characteristics of feeding sites of California condors (Gymnogyps californianus) in the human-dominated landscape of southern California. Wilson J Ornithol 131:459–471
Hall JC, Hong I, Poessel SA, Braham M, Brandt J, Burnett J, Katzner T (2021) Seasonal and age-related variation in daily travel distances of California condors. J Raptor Res 55:388–398
Hart EM, Avilés L (2014) Reconstructing local population dynamics in noisy metapopulations—the role of random catastrophes and Allee effects. PLoS ONE 9(10):e110049
Heinrichs JA, Marcot BG (2019) Applications of individual-based models. In: Brennan LA, Tri AN, Marcot BG (eds) Quantitative analyses in wildlife science. The Johns Hopkins University Press, Baltimore, MD, pp 165–179
Heinrichs JA, McKinnon DT, Aldridge CL, Moehrenschlager A (2019) Optimizing the use of endangered species in multi-population collection, captive breeding and release programs. Glob Ecol Conserv 17:558
Huber P, Greco S, Schumaker N, Hobbs J (2014) A priori assessment of reintroduction strategies for a native ungulate: using HexSim to guide release site selection. Landsc Ecol 29:689–701
IUCN/SCC (International Union for the Conservation of Nature Species Survival Commission) (2013) Guidelines for reintroductions and other conservation translocations. Version 1.0. IUCN Species Survival Commission, Switzerland, Gland, p viiii + 57
Jackson AL, Ruxton GD, Houston DC (2008) The effect of social facilitation on foraging success in vultures: a modelling study. Biol Lett 4:311–313
Kane A, Jackson AL, Ogada DL, Monadjem A, McNally L (2014) Vultures acquire information on carcass location from scavenging eagles. Proc R Soc B 281:20141072
Kelly TR, Grantham J, George D, Welch A, Brandt J, Burnett LJ, Sorenson KJ, Johnson M, Poppenga R, Moen D, Rasico J, Rivers JW, Battistone C, Johnson CK (2014) Spatiotemporal patterns and risk factors for lead exposure in endangered California condors during 15 years of reintroduction. Conserv Biol 28:1721–1730
Koford CB (1953) The California condor. Research report No. 4. National Audubon Society, New York
Kurle CM, Bakker VJ, Copeland H, Burnett J, Scherbinski JJ, Brandt J, Finkelstein ME (2016) Terrestrial scavenging of marine mammals: cross-ecosystem contaminant transfer and potential risks to endangered California condors (Gymnogyps californianus). Environ Sci Technol 50:9114–9123
Lande R (1993) Risks of population extinction from demographic and environmental stochasticity and random catastrophes. Am Nat 142:911–927
Levinsky I, Araújo MB, Nogués-Bravo D, Haywood AM, Valdes PJ, Rahbek C (2013) Climate envelope models suggest spatio-temporal co-occurrence of refugia of African birds and mammals. Glob Ecol Biogeogr 22(3):351–363
Mateo-Tomás P, Olea PP, Jiménez-Moreno M, Camarero PR, Sánchez-Barbudo IS, Martín-Doimeadios RCR, Mateo R (2016) Mapping the spatio-temporal risk of lead exposure in apex species for more effective mitigation. Proc R Soc B 283:20160662
Mee A, Rideout BA, Hamber JA, Todd JN, Austin G, Clark M, Wallace MP (2007) Junk ingestion and nestling mortality in a reintroduced population of California condors Gymnogyps californianus. Bird Conserv Int 17:119–130
Meretsky VJ, Snyder NFR (1992) Range use and movements of California condors. Condor 94:313–335
Meretsky VJ, Snyder NFR, Beissinger SR, Clendenen DA, Wiley JW (2000) Demography of the California condor: implications for reestablishment. Conserv Biol 14:957–967
Mertz DB (1971) The mathematical demography of the California condor population. Am Nat 105:437–453
Mims MC, Day CC, Burkhart JJ, Fuller MR, Hinkle J, Bearlin A, Dunham JB, DeHaan PW, Holden ZA, Landguth EE (2019) Simulating demography, genetics, and spatially explicit processes to inform reintroduction of a threatened char. Ecosphere 10(2):e02589
Monadjem A, Kane A, Botha A, Kelly C, Murn C (2018) Spatially-explicit poisoning risk affects survival rates of an obligate scavenger. Sci Rep 8:4364
Nathan R, Getz WM, Revilla E, Holyoak M, Kadmon R, Saltz D, Smouse PE (2008) A movement ecology paradigm for unifying organismal movement research. Proc Natl Acad Sci USA 105:19052–19059
Nguyen N, Saggese MD, Eng C (2018) Analysis of historical medical records of California condors (Gymnogyps californianus) admitted for lead exposure to the Los Angeles Zoo and botanical gardens between 1997 and 2012: a case series study. J Zoo Wildl Med 49:902–911
NPS (National Park Service), U.S. Fish and Wildlife Service, and Yurok Tribe (2021) Northern California condor restoration program, Final environmental assessment. Redwood National Park, Orick, CA, p 138 (Appendices)
Oro D (2013) Grand challenges in population dynamics. Front Ecol Evol 1:1–2
Pattee O, Carpenter JW, Fritts SH, Rattner BA, Wiemeyer SN, Royle JA, Smith MR (2006) Lead poisoning in captive Andean condors (Vultur gryphus). J Wildl Dis 42:772–779
Peck SL (2004) Simulation as experiment: a philosophical reassessment for biological modeling. Trends Ecol Evol 19:530–534
Poessel SA, Brandt J, Miller TA, Katzner TE (2018) Meteorological and environmental variables affect flight behaviour and decision-making of an obligate soaring bird, the California condor Gymnogyps californianus. Ibis 160(1):36–53
Poessel SA, Brandt J, Mendenhall L, Braham MA, Lanzone MJ, McGann AJ, Katzner TE (2018) Flight response to spatial and temporal correlates informs risk from wind turbines to the California condor. Condor: Ornithol Appl 120:3340–3342
Rideout BA, Stalis I, Papendick R, Pessier A, Puschner B, Finkelstein ME, Smith DR, Johnson M, Mace M, Stroud R, Brandt J, Burnett J, Parish C, Petterson J, Witte C, Stringfield C, Orr K, Zuba J, Wallace M, Grantham J (2012) Patterns of mortality in free-ranging California condors (Gymnogyps californianus). J Wildl Dis 48:95–112
Rivers JW, Johnson JM, Haig SM, Schwarz CJ, Burnett LJ, Brandt J, George D, Grantham J (2014) An analysis of monthly home range size in the critically endangered California condor Gymnogyps californianus. Bird Conserv Int 24:492–504
Robinson JA, Bowie RCK, Dudchenko O, Aiden EL, Hendrickson SL, Steiner CC, Ryder OA, Mindell DP, Wall JD (2021) Genome-wide diversity in the California condor tracks its prehistoric abundance and decline. Curr Biol 31:1–8
Schusterman RJ, Gentry RL (1971) Development of a fatted male phenomenon in California sea lions. Dev Psychobiol 4:333–338
Schumaker NH, Brookes A (2018) HexSim: a modeling environment for ecology and conservation. Landsc Ecol 33:197–211
Seddon PJ, Armstrong DP, Maloney RF (2007) Developing the science of reintroduction biology. Conserv Biol 21:303–312
Snyder NFR, Ramey RR, Sibley FC (1986) Nest-site biology of the California condor. Condor 88:228–241
Snyder NFR, Snyder HA (2000) The California condor: a saga of natural history and conservation. Academic Press, San Diego
Spiegel O, Getz WM, Nathan R (2013) Factors influencing foraging search efficiency: why do scarce lappet-faced Vultures outperform ubiquitous white-backed vultures? Am Nat 181:E102–E115
South A, Rushton S, Macdonald D (2000) Simulating the proposed reintroduction of the European beaver (Castor fiber) to Scotland. Biol Cons 93:103–116
USFWS (U.S. Fish and Wildlife Service) (2020) California condor recovery program 2020 annual population status. California condor recovery program. World Working Group on Birds of Prey and Hancock House, Ventura, California, p 5
Van der Vaart E, Johnston ASA, Sibly RM (2016) Predicting how many animals will be where: how to build, calibrate and evaluate individual-based models. Ecol Model 326:113–123
Verner J (1978) California condors: status of the recovery efforts. General technical report PSW-23/1978. U.S. forest service. Pacific Southwest Forest and Range Experiment Station, Berkeley, CA, p 30
Viner T, Kagan R, Rideout B, Stalis I, Papendick R, Pessier A, Smith ME, Burnham-Curtis M, Hamlin B (2020) Mortality among free-ranging California condors (Gymnogyps californianus) during 2010–2014 with determination of last meal and toxicant exposure. J Vet Forensic Sci 1:15–20
Walters JR, Derrickson SR, Fry DM, Haig SM, Marzluff JM, Wunderle JM Jr (2010) Status of the California condor (Gymnogyps californianus) and efforts to achieve its recovery. Auk 127:969–1001
Wiens JD, Schumaker NH, Inman RD, Esque TC, Longshore KM, Nussear KE (2017) Spatial demographic models to inform conservation planning of golden eagles in renewable energy landscapes. J Raptor Res 51:234–257
Wilbur S (1972) Food resources of the California condor. Department of Interior Administrative Report, California, Ojai, p 18
Acknowledgements
We thank Steve Kirkland, Joseph Brandt, Joe Burnett, Victoria Bakker, Myra Finkelstein, and Molly Astell for answering questions related to parameterizing our CACO model and for providing empirical data, and Rich Young for GIS support. We also thank two anonymous reviewers for helpful comments and suggestions. Marcot acknowledges support from Pacific Northwest Research Station, U.S. Forest Service. The findings and conclusions in this article are those of the authors and do not necessarily represent the views of the U.S. Fish and Wildlife Service.
Funding
The authors have no relevant financial or non-financial interests to disclose.
Author information
Authors and Affiliations
Contributions
JD, TM, NS, and BM conceived the study, and all authors contributed to the design. Analyses were performed by all authors. The first draft of the manuscript was drafted by JD, NS, SW, BM and all authors contributed to previous and final versions of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
All authors read and approved the final manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
D’Elia, J., Schumaker, N.H., Marcot, B.G. et al. Condors in space: an individual-based population model for California condor reintroduction planning. Landsc Ecol 37, 1431–1452 (2022). https://doi.org/10.1007/s10980-022-01410-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-022-01410-2