Deforestation scenarios show the importance of secondary forest for meeting Panama’s carbon goals

Abstract

Context

Tropical forest loss has a major impact on climate change. Secondary forest growth has potential to mitigate these impacts, but uncertainty regarding future land use, remote sensing limitations, and carbon model accuracy have inhibited understanding the range of potential future carbon dynamics.

Objectives

We evaluated the effects of four scenarios on carbon stocks and sequestration in a mixed-use landscape based on Recent Trends (RT), Accelerated Deforestation (AD), Grow Only (GO), and Grow Everything (GE) scenarios.

Methods

Working in central Panama, we coupled a 1-ha resolution LiDAR derived carbon map with a locally derived secondary forest carbon accumulation model. We used Dinamica EGO 4.0.5 to spatially simulate forest loss across the landscape based on recent deforestation rates. We used local studies of belowground, woody debris, and liana carbon to estimate ecosystem scale carbon fluxes.

Results

Accounting for 58.6 percent of the forest in 2020, secondary forests (< 50 years) accrue 88.9 percent of carbon in the GO scenario by 2050. RT and AD scenarios lost 36,707 and 177,035 ha of forest respectively by 2030, a carbon gain of 7.7 million Mg C (RT) and loss of 2.9 million Mg C (AD). Growing forest on all available land (GE) could achieve 56 percent of Panama’s land-based carbon sequestration goal by 2050.

Conclusions

Our estimates of potential carbon storage demonstrate the important contribution of secondary forests to land-based carbon sequestration in central Panama. Protecting these forests will contribute significantly to meeting Panama’s climate change mitigation goals and enhance water security.

Introduction

Conversion of tropical forests to other land uses is a major contributor to the rise in atmospheric carbon dioxide (CO₂; e.g., Baccini et al. 2012, Liu et al. 2015). Governments around the world are seeking creative and ambitious approaches to mitigate land-based CO₂ pollution and meet the recommendations of the Intergovernmental Panel on Climate Change to keep climate change to under 1.5 degrees Celsius (IPCC 2018). For example, the Amazon Fund, a trust instrument managed by the Brazilian National Development Bank, finances a diverse set of activities aimed at reducing deforestation in the Brazilian Amazon (Amazon Fund Activity Report(2017)http://www.amazonfund.gov.br/export/sites/default/en/.galleries/documentos/rafa/RAFA_2019_en.pdf(2017)). Similar efforts to reduce deforestation in neighboring Amazonian countries, as well as in the Congo Basin, and Indonesia are underway (FAO 2011). In 2014, the government of Panama created the “Alianza por el Millón” (Alliance for a Million), a government partnership bringing together business, non-governmental organizations, educational institutions and other organizations to reforest one million hectares (Ministerio de Ambiente 2019a). These efforts are advancing in recognition that vast areas of the world could be reforested, thereby making significant inroads to combatting climate change (Griscom et al. 2017; Bastin et al. 2019). Yet simply because an area could support forest does not mean the social and political requirements can be easily met (Holl and Brancalion 2020). For areas that are targeted for reforestation and forest restoration, initiatives will ultimately require a combination of both active reforestation, defined by tree planting on land that was previously forested (Cunningham et al. 2015), as well as passive, natural recovery where land is left fallow and natural processes of forest succession are permitted to take place (Holl and Aide 2011).

The ability of tropical secondary forest to rapidly accumulate biomass has been recognized for several decades (e.g., Flint et al. 1999; Silver et al. 2000). Recently, (Poorter et al. 2016) reported on biomass recovery for 45 sites across the Neotropics, finding that, on average, these forests accrue 120 Mg ha⁻¹ in aboveground biomass (AGB) in the first 20 years of recovery. Using the same dataset, (Chazdon et al. 2016) suggested that Latin American second-growth forests could gain as much as 8.48 Pg Carbon over 40 years. In Panama, secondary forests in moist areas on very low phosphorus soils can accrue 40% of the AGB and carbon of mature forest during the first 20 years of forest regrowth (Battermann et al. 2013). Given that these forests draw on the local species pool that is adapted to local biotic and abiotic conditions (Breugel et al. 2013, 2019) and that a major obstacle to active reforestation is lack of knowledge on survivorship and the basic growth characteristics of selected trees (Hall et al. 2011, Hall and Ashton 2016), reliance on natural forest recovery for carbon sequestration presents an attractive option for carbon sequestration initiatives.

Forest carbon-based climate change mitigation programs are occurring in a complex socio-ecological context of changing land-use patterns, which makes predicting the future landscape condition largely untenable. Scenario planning is a powerful tool for the exploration of alternative futures in land systems characterized by irreducible uncertainty, while explicitly incorporating relevant science and internally consistent assumptions about drivers, relationships, and constraints (Peterson et al. 2003; Thompson et al. 2012). Scenarios are a rigorous way of asking “What if?” and they can help decision makers better anticipate the potential consequences of alternative sets of decisions, so they can either adapt as changes occur or actively take steps to avoid undesirable futures (Chermack et al. 2001). Scenarios can be derived by researchers or planners who have a technical understanding of the system (e.g., Dale et al. 2003; Hall et al. 2012; Roriz et al. 2017). Alternatively, scenarios can be codesigned with groups of stakeholders to increase the salience of the process (McBride et al. 2017). In either case, the development of alternative pathways and the subsequent simulation and visualization of alternative scenarios is a powerful tool for decision makers tasked with planning for the short- and long-term sustainability of land systems (Mallampalli et al. 2016).

Many authors have projected changes in forest cover in view of evaluating carbon emissions and/or establishing baselines for Reduced Emissions due to Deforestation and forest Degradation (REDD +) projects (e.g., Pelletier et al. 2011; Sloan and Pelletier 2012; Stibig et al. 2014). These studies often use remote sensing-based products to estimate deforestation rates and derive empirical relationships between the location of deforestation events and spatial driver variables (Tokola 2015; Thayamkottu and Joseph 2018; Sy et al. 2019). Carbon is often assigned to classified Landsat or MODIS data from limited or localized forest inventories, such that it is difficult or impossible to disentangle local, landscape, and regional variations (Houghton et al. 2001; Tyukavina et al. 2013). Further, while obtaining deforestation rates can be challenging, quantifying forest gain has proven even more difficult, because in contrast to most deforestation events, reforestation is a gradual process and can be confounded with fields in temporary states of fallow. The challenge of accurately following reforestation signals is elevated when clear imagery is limited, as is the case in the tropics (Walker 2016). Indeed, the (Hansen et al. 2013) Global database on forest change no longer includes an assessment of forest recovery (Hansen and Potapov 2014).

Most efforts to model forest carbon dynamics rely on allometric equations derived from estimates of aboveground biomass in trees (e.g., Duncanson et al. 2019; Kellner et al. 2019) where plot-based estimates are applied to broad forest categories that do not capture the compositional or successional variation present within the landscape (Houghton et al. 2000; Graves et al. 2018). Aboveground tree carbon is readily derived but does not account for all the carbon in the forest ecosystem. Further, lack of consideration of changes in carbon stocks associated with forest loss and recovery masks the magnitude and ultimate consequences of changes resulting from policy decisions.

The objective of this study was to evaluate the effects of four deforestation scenarios, where persisting young forest grows over time, on carbon sequestration in central Panama, an area covering 23 percent of the country. Our approach is similar to that of (Sangermano et al. 2012) who used historic rates of deforestation to develop scenarios assessing win–win possibilities for carbon and biodiversity under REDD + in Bolivia. Our study improves upon recent studies evaluating forest carbon, the possible consequences of REDD + policies and conservation scenarios in Panama (Pelletier et al. 2011; Sloan et al. 2018) and beyond (e.g., Venter et al. 2009; Avitabile et al. 2016) by including widely recognized but often ignored aspects of carbon accounting. First, we go beyond studies of aboveground tree biomass by using locally derived data on both above-and below-ground tree carbon, soils, woody debris, and lianas to estimate ecosystem carbon stocks. Second, we leverage a local landscape-scale study of secondary forest dynamics to develop a locally adapted model of forest growth allowing an accurate estimate of forest carbon recovery. Tang et al. (2020) followed a similar approach in their work using remote sensing to estimate change in forest carbon in Colombia. Whereas they extracted static data from a chronosequence study, we use dynamic data to model forest growth (see below). We follow Erb et al. (2017) to calculate the hypothetical forest potential in the absence of deforestation going an additional step to also reforest all available vegetated land in our study area. Our scenarios allow us to evaluate the carbon consequences of divergent futures for central Panama and, in doing so, provide a lens through which land use decisions in other regions may be viewed to inform policy. We evaluate potential differences in direction and magnitude of ecosystem carbon dynamics by comparing them to the more commonly employed approach of relying on aboveground tree carbon or biomass in making policy decisions. Finally, we briefly discuss the implications of divergent scenarios on water provisioning ecosystem services.

Methods

Study region

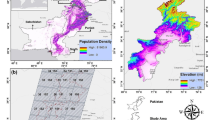
The study region encompasses the mainland area of central Panama (Fig. 1). The region includes 23 percent of the country’s land area. Just over half of the nation’s population (Instituto Nacional de Estadistica y Censo de Panama 2019) lives within the study area and it includes the Panama Canal Watershed (PCW), an area of critical economic importance where earlier projections of land cover and carbon storage have been conducted (Dale et al. 2003). The region is also highlighted for its provision and dependence on ecosystem services (Heckadon-Moreno et al. 1999; Condit et al. 2001; Ibanez et al. 2002; Hall et al. 2015). We included the area outside of the PCW owing to discussions concerning the possibility of diverting an adjacent river into the PCW in order to overcome projected water shortages (Adamowicz et al. 2019) and because of its potential role in the forest recovery in Panama described by (Wright and Samaniego 2008).

Fig. 1

Map of central Panama study area showing historical forest loss between 2016 and 2020 using (Walker 2020) PVCTS and land cover conditions at the beginning of scenario simulations. Rivers label also identifies watersheds delineated in thin black lines but where all rivers flowing into the Panama Canal Watershed (PCW) are lumped in the PCW, protected and other areas enumerated: 1 Monumento Natural Barro Colorado, 2 Zona de Protección Hidrológica Tapagra, 3 Area Silvestre Narganá, 4 Parque Nacional Charges, 5 Reserva Hidrológica Santa Isabel, 6 Parque Nacional Portobelo, 7 Paisaje Protegido Isla Galeta, 8 Parque Nacional Soberanía, 9 Parque Nacional Camino de Cruces, 10 Parque Natural Metropolitano, 11 Area de Uso Múltiple Donoso, 12 Parque Nacional Omar Torrijos, 13 Parque Nacional Santa Fé, 14 Monumento Natural Cerro Gaital, 15 Parque Nacional Altos de Campana, 16 Area de Uso Múltiple Bahía de Chame, 17 Paisaje Protegido and Bosque Protector San Lorenzo, 18–21 Area de uso diferido (con explosivos no detonados) Areas of unexploded ordinance left from US military. Note deforestation due to mining (pink color) in northwestern region of study area in 11

Data sources

Initial forest conditions

We combined two datasets to define the initial forest conditions for the scenarios. We utilized the Panama Vegetation-Cover Time-Series (PVCTS) map for 2020 to define the extent of our initial forest area (Walker 2020; Walker 2021a). The PVCTS maps depict forest-cover and forest-cover change in Panama from 1990 to 2020 at 30 m resolution. The PVCTS maps were locally calibrated and validated, shown to be highly accurate (Walker 2020), and are the best available data for this project. We assigned aboveground carbon density values to each PVCTS 2020 forest pixel using a LiDAR derived map from (Asner et al. 2013). Asner et al. (2013) developed their carbon density map for Panama using airborne LiDAR technology combined with satellite imagery from 2012. They estimated the carbon stock within 10% deviation from the plot-level, field-estimated values of carbon density, an unprecedented precision that affords the ability to measure real change in carbon stocks over time (Mascaro et al. 2011; Asner et al. 2013).

We reclassified ten of the original 24 land cover classes in the 2020 PVCTS map into a single composite Forest class consisting of High Veg, High Gallery Veg, Deciduous Plantation, Disturbed Forest, Forest Gallery, Evergreen Plantation, Wetland Forest, Water and Wetland Forest Mixed, Mature Forest, and Gallery in Mature Forest (Table SI 1). Wetland Forest and Wetland Forest Mixed together represent 0.68 percent of the study area. We acknowledge potential inaccuracies in applying a broadleaf forest growth model to wetland forest types but, given its limited extent relative to the study area and the goals of scenario projections, we feel it is acceptable. Deciduous Plantations (0.26 percent of the study area) are grown according to rules described below. Percent coverage of land use classes in the 2020 PVCTS map are found in Table SI 1. Finally, we resampled and coregistered the forest mask to 1 ha resolution using a nearest neighbor approach to match the resolution of the carbon density map produced by (Asner et al. 2013). We assigned Asner’s 2012 carbon densities values to each 1 ha forest pixel in the 2020 PVCTS forest extent. To temporally align Asner’s 2012 carbon densities with the 2020 PVCTS map, we implemented an initial 8-year spin-up whereby each forest pixel was aged + 8 years according to the carbon accumulation model described below. The combined forest extent and carbon density map was used as the initial starting conditions for our scenarios. Non-forest areas were excluded from the analysis except in the Grow Everything scenario (see below).

Deforestation rates and spatial patterns

We used (Walker 2020) PVCTS 2016–2020 deforestation maps to define the baseline rate and spatial pattern of deforestation. Because we could not simulate forest gain, we did not estimate the net change (Hansen and Potapov 2014).

Deforestation in Panama is influenced by a suite of socio-economic factors (e.g., Sloan and Pelletier 2012; Walker 2021b) that may be correlated to landscape features and human settlements. As of 2011, a large discrete deforestation event began in our study area with the clearing of forest for the Petaquilla and Cobre Panama Gold and Copper mines (Fig. 1). As these gold and copper deposits are related to belowground geology and deforestation to high-level political decisions not detectable by geographical features, we excluded this area from our analysis of the spatial allocation of deforestation. We do, however, include this in our analysis of the rate of deforestation.

To replicate the historical pattern of deforestation, we quantified the empirical relationships between the location of deforestation events and a suite of spatial driver variables and used these relationships with the Dinamica EGO cellular land-cover change model to project deforestation patterns (see model details below). Distance from Cities, Towns, Rivers, Roads, Slope, Elevation, and Conservation areas were based on spatial data from Smithsonian Tropical Research Institute (STRI). All pre-processing was performed using ESRI’s ArcGIS software and co-registered to match the spatial resolution and extent of the initial forest conditions map described above.

We evaluated the potential to stratify the study area into sub-regions to account for and regional variability in the predictive power of different spatial correlates of change within the land cover model. However, we did not identify any strata that would improve the relationships and the Weights of Evidence (see model description below) for the driver variables were linear through the full study area, suggesting that a single simulation region was best. Furthermore, constraining the rates of change to sub-regions would create artificial breaks to the patterns of sprawling development surrounding developing cities such as Panama City. Running the model with one region allowed for a natural progression of deforestation from areas that historically experienced high rates into areas of the study area that historically had little development.

Secondary growth forest data

We estimated the carbon density of young secondary forests using data from the Agua Salud Project, which is located within our central Panama study region (Stallard et al. 2010) and maintains a network of 108 secondary forest dynamics plots (SFD) distributed across a 3000 ha landscape (van Breugel et al. 2013). The Agua Salud SFD is a highly replicated chronosequence with a nested design where 2 plots per site were placed up slope and down slope to capture within site variability. The SFD is dominated by plots in forest from the first 40 years of forest recovery from pasture. Except for 2014, plots have been measured annually from 2009 to 2018 such that > 80,000 stems have been measured each year resulting in 1,100,000 measurements of 120,000 independent stems. The high plot replication within age class coupled with repeated plot measurements over time were used to develop our model estimating changes in forest biomass and carbon with time (see below). Based on extensive field visits and inventories throughout central Panama we determined that the Agua Salud SFD reasonably represents forest recovery for forests in central Panama.

Ecosystem pools: roots, soil, woody debris, and lianas

We used data from studies completed within our study area to estimate carbon stocks in tree roots, soil, woody debris, and lianas to develop ecosystem scale carbon estimates.

Sinacore et al. 2017) excavated trees up to 35 cm dbh and determined belowground biomass and carbon for roots down to 2 mm diameter (coarse roots). Average belowground allocation was found to be 27.6 percent of total tree carbon. We thus considered per ha tree AGB found by (Asner et al. 2013) to account for 72.4 percent of total tree biomass and adjusted accordingly. We did not specifically account for fine roots, some of which would have been measured in the soil carbon pool.

Neumann-Cosel et al. (2011) evaluated soil carbon in pastures, young forests and those up to 100 years old at Agua Salud. Total soil carbon for pastures was found to be 46.96 Mg C per ha for 0–20 cm depth and 58.43 Mg C per ha for 100-year-old forest and as compared with mature forest on nearby Barro Colorado Island, appear to be in the final stages of carbon accumulation (Neumann-Cosel et al. 2011). We considered the pasture carbon as a baseline with an equivalent annual increase such that our forests increase 0.11 Mg C per ha per year up to 100 years and thereafter to be in a steady state,a linear trend is supported by work completed at Agua Salud by (Püspök 2019). As (Neumann-Cosel et al. 2011) found no significant difference between carbon pools at 10–20 cm depth, for this study we consider anything below 20 cm as immobile, our ecosystem carbon only includes the mobile fraction of soil carbon or the carbon accrued above the pasture baseline.(Gora et al. (2019) measured woody debris in mature forest of Barro Colorado Island, approximately 8 km from Agua Salud. They estimated woody debris as 20.63 Mg per ha, equivalent to 9.78 Mg C per ha. In contrast our young forest recruiting from pastures has little observable woody debris (JS Hall personal observation, M. Larjavaara unpublished data). For the purposes of this study, we considered the (Gora et al. 2019) value to be achieved and in steady state by 100 years. Assuming an equivalent annual increment in woody debris carbon with forest growth, we estimated woody debris increase at a rate of 0.10 Mg C per year.

Lai et al. (2017) measured and estimated liana carbon in our Agua Salud SFD network and found a near linear increase in this pool. We used an annual increment derived from their data at 0.15 Mg C per year. This is slightly higher than the rate reported by (Heijden et al. 2015) for old secondary forest. We made the conservative assumption with respect to liana biomass accumulation, that it would be in a steady state beyond 100 years.

Modeling changes in carbon density with forest growth

Secondary forests

We used locally derived allometric equations developed by (van Breugel et al. 2011) to determine the carbon density of each plot in the SFD network. Asner et al. (2012), in turn, used these data to develop the LiDAR model that estimated carbon throughout Panama (Asner et al. 2013).

Lai et al. (2017) fit a model to changes in aboveground biomass (AGB) to the dynamic data from the Agua Salud SFD. Building on Lai et al. (2017) we used data through 2018 to fit five models and select the best model with the highest in-sample and out-of-sample accuracy (see below). We modelled aboveground biomass (AGB, Mg / ha) as a function of forest age (yr) in five candidate mixed-effect model forms:

(1) Linear: AGB = β₁ Age.

(2) Quadratic: AGB = β₁ Age + β₂ Age².

(3) Cubic: AGB = β₁ Age + β₂ Age² + β₂ Age³.

(4) Michaelis–Menten: AGB = (β₁ Age)/(1 + β₂ Age).

(5) 2-parameter asymptotic exponential: AGB = β₁ (1-e^{−β2 Age}).

In all models, the regression was forced through the origin such that a forest site has zero AGB at age zero. To account for the nested sampling design, we also included a random plot-within-site effect that accounts for variations at the site level. We included the random effect only in the linear coefficient, β₁ because we assumed that the short-term (ten-year) AGB trajectory at the plot level is near-linear within each of their shorter forest-age ranges, compared to the longer-term AGB–forest age relationship across the chronological landscape. Moreover, models with random effects beyond the linear coefficient failed to converge, yielding unreliable parameter estimations. Prior to analysis, we scaled the forest age variables by dividing it to their standard deviations. Doing so greatly assisted model convergence, especially for the more complex nonlinear Michaelis–Menten and 2-parameter asymptotic exponential models. Next, we quantified the models’ in-sample accuracy using AICc (Burnham and Anderson 2002). In addition to AICc, we also compared models with their ability to accurately predict out-of-sample new data. To do so, we used a tenfold cross validation that splits the data into ten exclusive partitions, and for each partition used 90% of the data to train the model and the remaining 10% to test model predictions. The prediction accuracy of each trained model on test data was measured as the root mean square error (RMSE) and the coefficient of determination (R²). When the best model with the lowest RMSE and/or highest R² was selected, we refit the model with the whole dataset for a more precise parameter estimation. The best model with the lowest AICc, lowest RMSE and highest R² was then used as a basis to grow forest (see below). The mixed-effect models were conducted using the nlme package (Pinheiro et al. 2018) in R v3.6.3 (R Core Team 2019).

Using a conversion factor of 0.474 (Martin and Thomas 2011) we converted aboveground biomass to carbon for the equation from the best model above. Carbon densities in the (Asner et al. 2013) data were converted to age using the best AGB-forest age regression model to allow their use in the growth model.

Plantations

Deciduous Plantations cover 0.26 percent of our study area (see above). Many of these plantations exhibit extremely poor growth (Stefanski et al. 2015) as the species planted commercially, teak (Tectona grandis), grows poorly on infertile, clay, low pH soils (Lugo et al. 1997) that dominate central Panama. For existing plantations, we assumed growth of one-half the rate of secondary forest in aboveground tree C based on observed growth and carbon accumulation in teak plantations on the dominant soils in the PCW (Hall 2013; Stefanski et al. 2015, Sinacore et al. in review), and published site index curves for the region (Keogh 1982).

Increases in ecosystem carbon

Increases in AGB and C for secondary forests and plantations were completed as described above. To estimate other ecosystem carbon pools, we applied the percent root contribution of (Sinacore et al. 2017) to the pixel level aboveground carbon data of (Asner et al. 2013) and subsequent modeled growth. As we determined soil, woody debris, and soil carbon to all increase at a uniform rate over 100 years, we then applied an annual increase of 0.36 Mg C per year (O.11 Mg C per ha soil carbon + 0.10 Mg C per ha woody debris + 0.15 Mg C per ha liana carbon = 0.36 Mg C per ha) up to year 100 after having determined forest age from the AGB-forest age relationship (see above). When converting to carbon dioxide equivalents, we divided the Mg C by the atomic mass of carbon (12.01) and then multiplied the combined atomic mass of one carbon and two oxygen (16.00 each) or 44.01.

Scenarios

The Recent Trends (RT) scenario projects a linear continuation of the observed rates and spatial allocation of deforestation during the reference period and where remaining forest continues to grow following our growth model. Rates of deforestation are based on the rate of change in the 2016–2020 deforestation maps. This equates to an annual deforestation rate of 0.43 percent. The Accelerated Deforestation (AD) scenario envisions a significant increase in the rate of deforestation. To simulate our Accelerated Deforestation (AD) scenario, growth occurs as described above. We followed the approach of (Sangermano et al. 2012) of incorporating longer term forest change data and more specifically, (Dale et al. 2003), who used the annual deforestation rate of 2.25 percent derived by Heckadon-Moreno et al. (1999) for the period of 1976–1998. To show the potential of forests in contributing to land-based carbon sequestration, we include two additional scenarios. The Grow Only (GO) scenario projects the hypothetical carbon potential of forest within our forest cover mask with no change in the spatial extent of forest in the study region and no deforestation. Our Grow Everything (GE) scenarios goes beyond the GO scenario by further permitting forest to recruit, establish, and grow on all vegetated land within the study area. Thus, the GE scenario adds an additional 530,483 ha of forest area to the other three scenarios, illustrating the ceiling for which forests could theoretically contribute to carbon sequestration up until 2050.

Simulating forest cover loss.

We use the Dinamica Environment for Geoprocessing Objects 4.0.5 (Soares-Filho et al. 2002) to simulate thirty- years (2020 to 2050) of land-cover change under RT, and AD scenarios using annual time steps. Because the Grow Only and Grow Everything scenarios include no forest-cover loss, they are not incorporated into the Dinamica model. We examined historic deforestation patterns from 2001 to 2011 in relation to a suite of spatial predictor variables (Table 1). We selected these variables based on previous experience modeling land-cover change (Thorn et al. 2016; Thompson et al. 2017), the availability of detailed GIS data for the study region, and our personal knowledge of the region.

Table 1 Driver variables used to parameterize the spatial allocation of deforestation using the Weights-of-Evidence method with the Dinamica EGO land cover change model

Dinamica EGO is a spatially explicit cellular automata model of landscape dynamics capable of multi-scale stochastic simulations that incorporate spatial feedback. Dinamica has been used to simulate land-cover change globally, including several applications in Central and South America (Gago-Silva et al. 2017; Kolb and Galicia 2017; Ramírez-Mejía et al. 2017; Roriz et al. 2017; Lima et al. 2018). Dinamica EGO uses a weights-of-evidence (WoE) method to set the transition probability for any given land-cover pixel. The WoE method employs a modified form of Bayes theorem of conditional probability (Goodacre et al. 1993; Bonham-Carter 1994) to derive weights where the effect of each spatial variable on a transition is calculated independently of a combined solution (Soares-Filho et al. 2009). Continuous variables are discretized through an iterative binning process so that individual weights can be calculated for each bin.

Dinamica EGO calculates weights (W +) for each driver variable independently then sums the W + values to create a composite transition potential map. For each driver variable, positive W + values predict the future occurrence of new deforestation patches while negative W + values predict the future absence of new deforestation patches. The Recent Trends and the Accelerated Deforestation scenarios use the same weights and resulting probability maps but differ in their rates of change. As previously noted, the Grow Only scenario contains no forest cover loss while the Grow Everything scenario expands the forest estate to its maximum potential. For a more detailed discussion of Dinamica EGO and the Weights of Evidence methods (see Thompson et al. 2020).

Within Dinamica EGO six parameters control the patterns of deforestation: the land cover transition rates, pixel level transition probabilities (W +), the ratio of “new” vs. “expansion” patches, the mean and variance of “new” and “expansion” patch sizes, and the patch shape complexity (i.e. patch aggregation). “New” deforestation patches are defined as those occurring in interior forests (i.e. at least one 1 ha pixel away from a forest edge). “Expansion” patches are defined as deforestation that occurs in forest edge pixels. Our procedure for estimating these parameters was as follows: (1) The land-cover transition rates for Recent Trends simulation are based on observed changes in the historical reference period (2016–2020). Transition rates for the AD scenario come from Heckadon-Moreno et al. (1999). All other parameters are identical for the RT and AD scenarios. (2) The ratio of new to expansion patches were set to 0.93% new and 0.07% expansion. This ratio was calculated based on the observed ratio in the historical training data. (3) The quantity and size of deforestation patches were based on a normal distribution with a mean of 1.00 ha and variance of 23.95 ha. The true mean patch size in the reference period was 1.59 ha, however the median was 1.00 ha, so to account for the heavy right skew in the patch size histogram, we set the mean patch size to 1.00 ha. (4) Patch shape complexity is controlled by an isometry parameter, which is a multiplier that increases or decreases the underlying transition probability values of neighboring cells around a seed cell. Values greater than 1 result in simpler, more aggregated shapes; values < 1 result in more complex shapes (i.e., less aggregated). We found the isometry value of 1.0 (no modification) best matched the patch shape complexity observed in the training data.

Model accuracy assessment

We assessed the performance of our land-cover change model in terms of its robustness to two key assumptions: 1) that the empirical WoE relationship derived during calibration between the spatial driver variables and disturbance events was stationary through subsequent time periods, and 2) that the patch seeding algorithm could replicate the spatial pattern of deforestation observed within the calibration period. For these assessments, we calibrated deforestation in Dinamica using the PVCTS 2011–2016 map then simulated four years of deforestation spanning 2016–2020. We used the Figure of Merit (FOM) metric to quantify the similarity between the simulated and observed PVCTS 2016–2020 maps.

The FOM is a ratio comprised of three components: Hits, Misses, and False Alarms. The numerator (Hits) represents the intersection of True Deforestation and Simulated Deforestation (i.e. change pixels in the calibration map that have been correctly simulated as change in the confirmation map). The denominator represents the union of True Deforestation and Simulated Deforestation (Misses + Hits + False Alarms), where Misses are the area of error where confirmation change is simulated as persistence, and False Alarms is the area of error where confirmation persistence is incorrectly simulated as change.

$$\begin{gathered} {\text{Figure of Merit}} \begin{array}{*{20}c} { = \, \left( {{\text{True}} \cap {\text{ Simulated}}} \right) \, / \, ({\text{True}} \cup {\text{Simulated}})} \\ {{\text{ = Hits/(Misses}}\;{ + }\;{\text{Hits}}\;{ + }\;{\text{False}}\;{\text{Alarms)}}} \\ \end{array} \hfill \\ \hfill \\ \end{gathered}$$

In addition, using the WoE method applied in Dinamica, we mapped the probability of deforestation based on patterns observed in the 2011–2016 period in relationship to the suite of spatial predictor variables (Table 1). Using histogram equalization, we rescaled the probabilities such that the lowest probability pixel was set to zero and the highest set to 100. We then overlaid observed forest loss from the 2016 to 2020 period on to the rescaled probability map to assess whether the relationship to the spatial variables was stationary through time.

The special case of protected and restricted areas

Simulated deforestation was limited within several protected areas (Fig. 1). Land cover change maps generated by the Panama Canal Authority and the Ministry of the Environment show limited forest loss between 2000 and 2007 (Martinez 2011, also see Fig. 1) in several protected areas. A similar result was found by (Walker 2020) in her analysis of deforestation between 1990 and 2015 but where landslides resulting from the extreme rainfall event of La Purisima in 2010 are visible and considered deforestation. Thus, we set deforestation rates to zero for the protected areas where very little deforestation was observed (Soberania National Park, Camino de Cruces National Park, Metropolitano Park in Panama City, and restricted areas to the west of the canal with unexploded ordnances). We mapped protected and restricted areas using spatial data supplied by MiAmbiente. All other protected areas were included as a categorical driver variable. Protected areas with historically high rates of forest loss receive higher weights of evidence (W +) values than those with historically low rates of forest loss. This ensured that simulated transitions within these areas mimicked historic rates and patterns depending on the past effectiveness of their protection status.

Final carbon estimates

Final carbon estimates at each time step represent net of forest ecosystem growth and loss. Ecosystem carbon gain is described above. With the exception of our GE scenario, no new forest stands were initiated in any of our scenarios. Existing forests all grew in our GO scenario while the forest area was expanded to its maximum potential and grown under GE. Our RT and AD scenarios grew in the same manner but also included carbon loss. Here we used the deforestation model transitions from the RT and AD scenarios to project rates of carbon loss over time. Ecosystem carbon density for a given pixel at a given time step results from ecosystem carbon accumulation based on the increment estimated in growth from initial conditions.

The role of secondary forests

To illustrate the contribution of secondary forests to carbon accumulation in our scenarios, we identified forest areas with carbon values of < 10-year-old forest, 10 years ≤ age < 30-year-old forest, 30 years ≤ age < 50-year-old forest, and age ≥ 50-year-old forest. Pixel or stand age was determined from our forest growth equation (see above).

Results

Accuracy assessment

The model’s performance, as determined by FOM statistic, exceeds the conventional threshold of acceptability set by Pointius (2008), who states that the “FOM’s minimum percentage must be larger than the deforestation area in the reference region during the confirmation period expressed as a percentage of the forest area in the reference region at the start of the confirmation period”. Our deforestation model FOM is 1.29%, while the net observed change in the confirmation period 2016–2020 was 1.24% (see Table SI 2).

The median scaled probability of the true deforested pixels was 76.95, which means that half of the observed deforested pixels occurred in the 23.05% of the landscaped ranked with the highest probability of deforestation values. Given that our analyses are not intended to reproduce the precise location of deforestation events, but rather to emulate the overall landscape patterns, we feel the model performance is more than adequate for exploring plausible future land-use scenarios.

Deforestation

Rates of deforestation declined dramatically within our study are, including the PCW, from the period before 2000 to the present study (2016 to 2020). Whereas (Dale et al. 2003) reported forest loss rate of between 1.7 and 3.0 percent per year within the PCW between the 1980s and 1998, Walker’s PVCTS reveal a deforestation rate between 2016 and 2020 of 0.20 percent per year within this same area. Taking 2.35 percent as the historical deforestation midpoint in the PCW, this represents a 91 percent reduction in the deforestation rate. Forest loss rates outside of the PCW but inside our study area for the period of 2016–2020 averaged 0.56 percent. Interestingly, the watersheds with the highest annual rates of deforestation were immediately south (Caimito 0.88 percent) and west of the PCW (Miguel de la Borda 1.56 percent, Indio 1.12 percent, and Platanal 0.91 percent, see Fig. 1 for watershed locations). Projected future deforestation are shown in Table 2.

Table 2 Forest cover under recent trends, accelerated deforestation, grow only, and grow everything scenarios for central Panama through 2050

Correlates of change

The Weights of Evidence calculated from the historic training data shows the relative probability of forest loss in relation to a suite of spatial driver variables. The probability of forest loss was highest within 10 km of large city centers and within 1.5 km of smaller towns. Distance to roads was positively correlated with forest loss up to 1 km. Distance to rivers showed only weak association with deforestation at close distances however it had a negative correlation with forest loss past 500 m. All flat and moderate slopes showed a weak positive correlation that quickly became negative past 14 degrees. Lower elevation areas < 200 m were positively correlated with forest loss while areas > 200 m were negatively correlated (Fig. 2). While regional stratification often results in an improved parameterization of locally distinct drivers of change this would also have required confining the rates of change to specific sub-regions. Given the high rates of change in our AD scenario, regional stratification was not an option as it would have produced unrealistic spatial patterns at the boundaries between sub-regions.

Fig. 2

Weights of evidence linking deforestation with physical and social variables often correlated with deforestation. Weights from 0 to 0.5 are described as “weak”, 0.5–1.0 as “moderate” and > 1.0 as “strong”. Positive weights indicate higher than random chance for the presence of a deforestation transition. Negative weights indicate a higher than random chance for the absence of a deforestation transition. Weights at or near zero indicate no significant association between the driver variable at that bin range and the presence/absence of a transition

Aboveground carbon growth modeling.

The model with the lowest AIC_c (Table 3) lowest RMSE, highest R² (Fig. 3) was the Michaelis–Menten model (Fig. 4):

Table 3 Estimated parameters (95% lower and upper confidence intervals in parentheses) and $AI{C}_{c}$ of each candidate model

Fig. 3

Model performance from tenfold cross validation as judged by (a) the root mean square error (RMSE) and (b) the coefficient of determination (R²). Model names are sorted in decreasing performance from left to right

Fig. 4

Comparison of different secondary forest biomass accumulation models fitted to 10 years of growth data from 108 plots in the Agua Salud Project Secondary Forest Dynamics network (SFD) in central Panama. Grey lines show growth of individual plots over time with point being age at first measurement. Colored lines represent different growth models. The black dot and error bars are the mean and standard deviation of forest on Barro Colorado Island (BCI), Panama. Mascaro et al. (2011) report half of BCI forests are 80–130 years old and these forests maintaining 15% less carbon than forest > 400 years of age but that slope was main driver of differences in aboveground carbon density

AGB = (6.904 Age) / (1 + 0.031 Age) whereby AGB and carbon achieve the average biomass and carbon of Barro Colorado Island (BCI) in the Panama Canal Watershed in just over 300 years (Fig. 4; see (Mascaro et al. 2011) and (Asner et al. 2013).

Ecosystem and secondary forest carbon

Accounting more fully for ecosystem carbon added > 60 percent more to aboveground tree carbon in our central Panamanian forest system, whether it is viewed as carbon density or total carbon across the landscape (Tables 4 and 5). The initial study area for the RT, AD, and GO scenarios included 5,102,266 ha of forest estimated to be younger than 50 years old (Table 6). In the GO scenario these forests accrue 21.8 million Mg C to 2050 accounting for 88.9 percent of the carbon accrued across the region.

Table 4 Ecosystem carbon under recent trends, accelerated deforestation, grow only, and grow everything scenarios for central Panama through 2050

Table 5 Aboveground carbon under recent trends, accelerated deforestation, grow only, and grow everything scenarios for central Panama through 2050

Table 6 Land area and ecosystem carbon for forest age classes of < 10 years, 10 years to 30 years, 30 years to 50 years and > 50 years old in central Panama

Changes in forest cover and carbon

By design forest area was unchanged within the “Grow Only” scenario and forest growth resulted in forests gaining 10.2 million Mg C by 2030 and 24.5 million Mg C 2050 in forest ecosystem carbon. We focus on 2030 as the Intergovernmental Panel on Climate Change has highlighted the next 10-years as a time by which significant efforts need to be undertaken if we are to keep temperature increases at or below 1.5 degrees Celsius (IPCC 2019); 2050 is the midpoint through the century and a commonly used milestone for projecting changes, including targets set by the Panamanian government (see below). Under our Recent Trends and Accelerated Deforestation scenarios we estimated a forest loss of 36,707 ha (RT) and 177,035 ha (AD) by 2030 (Table 3). Owing to the capacity of secondary forest to rapidly accumulate carbon, we nevertheless projected a carbon gain of 7.6 million Mg C by 2030, (Table 4; Fig. 5) in our RT scenario. It is noteworthy that our AD scenario resulted in relatively little carbon loss (2.9 million Mg C) by 2030 but nevertheless is 10.4 million Mg C lower than the RT scenario or ten years into the future. The Grow Only scenario accrues approximately 2.5 million and 10.4 million Mg C more than the RT scenarios by 2030 and 2050, respectively. Were policy makers able to flip land use to only allow for forest recovery across the entire region, there is a theoretical possibility of accruing 36.1 million Mg C and 59.1 million Mg C by 2030 and 2050, respectively above the business-as-usual RT scenario (Table 4).

Fig. 5

Projected carbon density in forests of central Panama under Recent Trends, Accelerated Deforestation, Grow Only, and Grow Everything scenarios, showing initial conditions in 2020, 2030, and final 2050 landscape. Deep red color illustrated land outside of forest mask for RT, AD, and GO scenarios; all vegetated land included in GE scenario

Discussion and Conclusions

The land-use scenarios examined here demonstrate a wide range of potential trajectories for terrestrial carbon pools in central Panama, with total carbon pools in the year 2050, ranging from 60.9 to 154.1 million Mg. Panama is transitioning to a low carbon economy (Ministerio de Ambiente 2019b) with carbon sequestration through active and passive reforestation planned to account for approximately 337 million Mg CO2e taken out of the atmosphere by 2050 (Ministerio de Ambiente 2019a). Our finding suggests that policy makers’ decisions regarding land-use can be a significant part of Panama’s climate mitigation strategy. Maintaining recent trends in deforestation would sequester an additional 51.9 million Mg CO2e by 2050 or 15.4% of the national goal in an area representing 23% of the nation’s land area. Yet should deforestation be halted, and forests allowed to recover (GO) or all available vegetated land within the study region be protected and permitted to grow as forests (GE), central Panama could sequester between 89.7 and 188.6 million Mg CO2e or between 26.6% and 56.0% of its national goal. In contrast, the AD scenario would have devastating consequences for Panama’s land based carbon sequestration releasing an additional 73 million Mg CO2e by 2050, making it extremely difficult for Panama to achieve its planned land-based carbon sequestration objective.

Decisions made now regarding land use in Panama will have a profound impact on Panama’s ability to meet these targets, a fact not lost on the government. In October of 2020 the President of the Republic, Lorentino Cortizo signed a decree outlining and empowering the Ministry of the Environment to begin the steps necessary to create a country wide program for monitoring greenhouse gas emissions and towards reducing the national carbon footprint (Gaceta Oficial Digital de Panama, 2020). Further, the public comment period for a draft decree to establish a nationwide carbon trading program closed on 2 September 2021 (Ministerio de Ambiente 2021). Beyond these legal instruments, the Government of Panama has several large-scale reforestation projects in the pipeline covering 10 s of thousands of hectares (Ministerio de Ambiente 2020); (Environmental and Facility 2021). Time will tell whether these efforts will indeed result in the hoped-for transition to a low carbon economy.

The reason that central Panama’s forests can sequester copious amounts of carbon has to do with the very large area of naturally regenerating, low carbon forests (Table 6 and Fig. 5). In 2020, 5.1 million ha or 58.6 percent of forest is younger than 50 years old (Table 6) in our RT, AD, and GO forest mask. Yet these aggrading forests account for 88.9 percent of the carbon in the GO scenario in 2050, an astonishing number given that these forests held only 34.6 percent of the carbon in 2020. Over the next 30 years the additional 530,482 ha of forest in the GE vs GO scenario would gain 48.8 million more Mg C or almost 2 times more than the total gain of the GO scenario alone. Thus, these young secondary forests are the engine that drives the potential carbon benefits in the region.

One reason that our carbon scenarios differ from past projections relates to our improved ability to determine carbon stocks in relatively young stands within the forest. Early studies classified areas as either with or without forest (e.g., Aide et al. 2013; Hansen et al. 2013), unable to account for fine-scale differences among forest stands within a heterogeneous landscape (Tarbox et al. 2018; Walker 2020). Sloan and Pelletier (2012) wondered, given the state of the art at the time, whether carbon baselines determined with remote sensing were worthwhile. Sloan et al. (2018) subsequently used the same LiDAR derived carbon baseline (Asner et al. 2013) as used herein to provide an accurate and precise estimate of forest carbon heterogeneity at the 1-hectare scale (Asner et al. 2012). Further advances have been made in assessing carbon heterogeneity using high resolution Landsat imagery both in terms of detection (e.g., Baccini et al. 2016; Zarin et al. 2016) and in terms of allometric equations used to estimate biomass and carbon across the landscape (e.g., Chave et al. 2015). Yet these advances still suffer from lack or incorporation of other carbon stocks into forest carbon estimates (see, e.g., Houghton et al. 2000). By leveraging local studies of tree root, soil, liana, and coarse woody debris, our carbon assessment provides an estimate of forest ecosystem carbon and changes therein, consistently estimating over 60 percent more carbon in the ecosystem than that estimated by tree AGB models (Tables 4 and 5).

Until recently, estimates of changes in forest carbon completed with remote sensing have been imprecise, not accounting for heterogeneity in forest development and composition. While repeated LiDAR overflights can determine changes in carbon uptake by re-growing forest trees and loss due to degradation, in practice such studies are rare. Tang et al. (2020) extracted data from Colombian forests contained in Poorter et al. (2016) to estimate carbon gain through forest recovery. They further included a sensitivity analysis using additional data from the Poorter et al. (2016) study, a chronosequence study that while noteworthy for its spatial coverage across the Neotropics still suffers from the constraints of such studies. Notably, chronosequence studies compare forests of different ages and assume they follow the same successional trajectory, which means they do not account for spatial heterogeneity in local and landscape factors, for legacy effects on forest growth, or for shifts in forest dynamics under changing climate conditions (for further discussion see e.g., Foster and Tilman 2000; Johnson and Miyanishi 2008; Walker et al. 2010). Cook-Patton et al. (2020) discussed variability in carbon accumulation rates as related to environmental variables at a global scale. We overcame these constraints by using dynamic data from a landscape scale study of secondary forest dynamics (Fig. 4). We recognize that climate change (Habu and Lewis 2020; Sullivan et al. 2020); and other forces of change may impact forest carbon trajectories during the time period of our study simulations. Our longitudinal study of secondary forest dynamics spans a period of repeated droughts, including the record drought of 2015–2016 when precipitation was only 55 percent of the annual average (Bretfeld et al. 2018; Sinacore et al. 2020) and is thus buffered against the modest changes in rainfall predicted under the more severe climate change predictions such as RCP scenario 8.5 (CHATOLAC 2015).

Deforestation trends

Several authors have raised concerns about the high rates of deforestation in central Panama (Condit et al. 2001; Ibanez et al. 2002; Dale et al. 2003) essentially stating that, given the growing population within the Panama Canal Watershed, it would take a miracle to stop or slow deforestation. Yet our analysis suggests that the rate of deforestation was reduced by some 91 percent within the Panama Canal Watershed between 2016 and 2020. The remarkable result of declining deforestation here is on the order of the highest reduction of deforestation rates observed in the Amazon Basin in 2017 when it was 76 percent lower than in 2004 (Amazon Fund Activity Report 2017) and occurred as the human population remained stable within the Panama Canal Watershed (Instituto Nacional de Estadistica y Censo de Panama 2019). Just outside of the PCW, Panama City and adjacent areas have experienced a virtual population explosion in the last two decades resulting from both Panamanians moving to the city and immigration from neighboring countries (Instituto Nacional de Estadistica y Censo de Panama 2019).

Scenario planning

By design, our GO scenario maintained the 2020 forest extent delineated using (Walker 2020) but grew young regenerating forests. Here we show the regenerative capacity of these forests with sustained and significant carbon gains through 2050 for our RT, GO, and GE scenarios (Table 4, Fig. 4). Yet the picture that emerged from our AD model is grim. By 2050 the model predicted a forest loss of over 430,000 ha or almost half of all forest found in 2020. Forest loss will be concentrated west of the Panama Canal and watershed and will likely result in an irreversible severance of forest connectivity across our region (Fig. 5). An estimated 2.9 million Mg C will be lost by 2030 under the AD scenario or 3.5 percent of forest carbon from our 2020 baseline. The apparent disconnect between results from forest and carbon loss is the result of the loss of low carbon or young secondary forest (Fig. 5). Yet by 2050, 19.9 Mg C or 25% the carbon baseline will be lost under this scenario. While this scenario may appear to be an unrealistic extreme, it is grounded in historical data and we believe is plausible due to recent developments. The government of Panama has completed a bridge over the Panama Canal near Colon with plans of opening a new highway in the north along the Caribbean coast linking Colon and Bocas del Toro to the west (URS Holdings and Inc. 2011). In addition to this, the government has negotiated with the government of China to secure contracts for Panamanian beef exports (CentralAmericaData.com 2019),Gobierno de la Republica de Panama 2019, also see Huang 2016). Secure markets for beef could help foster conditions that would encourage cattle production and deforestation. Indeed, the government of Panama has long recognized the need to improve agricultural production to achieve food security (Oxford Business Group 2019). The government’s past willingness to manipulate protected area boundaries in favor of mining could also lead to large, desecrate areas of mature froest being deforested (see Fig. 1 and above). Finally, as suggested for the forest transition in Puerto Rico (Yackulic et al. 2011) and as projected along the Pacific coast around and north of Panama City (Fig. 5), suburbanization may also reverse any trend in forest regrowth.

These types of impactful yet unpredictable events underscore the value of scenario planning—it gives us the opportunity to learn about the consequence of multiple alternative pathways, which will help land managers and decision makers prepare for uncertain futures. It is worth reiterating that none of the scenarios examined here are intended to serve as predictions, but rather they bound a range of potential outcomes and spur “out of the box” thinking. Recent and very dramatic changes in deforestation rates in the Brazilian Amazon (Ferrante and Fearnside 2020; Oliveira et al. 2020) illustrate how quickly forest policy changes can impact forests. While our AD scenario might seem extreme, it is not as extreme as actual socio-ecological changes occurring throughout the world.

Scenario implications for water provisioning ecosystem services.

The Panama Canal Watershed is managed first and foremost for abundant fresh water. Ogden et al. (2013) showed the role of mature and old secondary forests in regulating stream flow. While forests lose more water than pastures through the process of evapotranspiration (Zhang et al. 2001), the soils of these forests can absorb water during the wet season and release it as stream flow during the dry season, defined as the sponge effect (Ogden et al. 2013; Adamowicz et al. 2019). Ogden et al. (2013) have also shown how forests can dramatically reduce the risk and impacts of flooding and Birch et al. (2021) show ten year old regenerating forests in their study site had water flow paths down to 30 cm depth that were similar to those or mature forests. As the government of Panama contemplates where to find new sources of water (e.g., Rio Indio, Fig. 1) for the Panama Canal and the watershed’s other users, they would do well to consider the full potential of the regenerating secondary and mature forests of the region to help regulate stream flow.