Landscape composition mediates movement and habitat selection in bobcats (Lynx rufus): implications for conservation planning

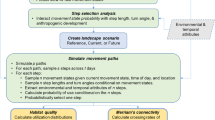
Abstract

Context

The analysis of individual movement choices can be used to better understand population-level resource selection and inform management.

Objectives

We investigated movements and habitat selection of 13 bobcats in Vermont, USA, under the assumption individuals makes choices based upon their current location. Results were used to identify “movement-defined” corridors.

Methods

We used GPS-collars and GIS to estimate bobcat movement paths, and extracted statistics on land cover proportions, topography, fine-scale vegetation, roads, and streams within “used” and “available” space surrounding each movement path. Compositional analyses were used to determine habitat preferences with respect to landcover and topography; ratio tests were used to determine if used versus available ratios for vegetation, roads, and streams differed from 1. Results were used to create travel cost maps, a primary input for corridor analysis.

Results

Forested and scrub-rock land cover were most preferred for movement, while developed land cover was least preferred. Preference depended on the composition of the “available” landscape: Bobcats moved > 3 times more quickly through forest and scrub-rock habitat when these habitats were surrounded by agriculture or development than when the available buffer was similarly composed. Overall, forest edge, wetland edge and higher stream densities were selected, while deep forest core and high road densities were not selected. Landscape-scale connectivity maps differed depending on whether habitat suitability, preference, or selection informed the travel cost map.

Conclusions

Both local and landscape scale land cover characteristics affect habitat preferences and travel speed of bobcats, which in turn can inform management and conservation activities.

Introduction

Maintaining and restoring the status of wide-ranging carnivore populations are among the most pressing conservation issues we face today (Weber and Rabinowitz 1996; Kareiva 2002; Beier et al. 2008; McRae et al. 2008). Individual movement choices affect habitat use, dispersal patterns, mating systems, reproductive success and territorial interactions, which in turn can influence population viability (Turchin 1998). Conservation planners have long recognized that corridors have the capacity to facilitate animal movement and population persistence in landscapes that are increasingly threatened by habitat loss and fragmentation (Beier and Noss 1998; Palomeres 2001; LaPoint et al. 2013). To achieve these goals, a fundamental understanding of how animals move through their environment is needed (Allen and Singh 2016).

A variety of modeling methods have been used to identify and map potential corridors within a landscape (e.g., Beier and Noss 1998; Tewksbury et al. 2002; McRae et al. 2008; Chetkiewicz and Boyce 2009; Rabinowitz and Zeller 2010). Such models often rely on habitat suitability indices that define habitat quality across the landscape for a given species. These indices can then be used to inform corridor planning. For instance, least cost path analysis has been frequently used to identify potential corridor locations, where the primary input is a resistance map in which resistance of a pixel (a measure of travel difficulty) is inversely related to its habitat suitability index (e.g., Adrianensen et al. 2003; Sawyer et al. 2011). Circuit theory likewise has been used to identify corridors and movement pinch points (McRae et al. 2008).

Because landscape-scale management is costly, it behooves planners to have the most relevant information for identifying habitat suitability across a landscape with respect to movement (Hodgson, et al. 2011). The first consideration is to be mindful that the primary goal of corridors is to facilitate individual movement. However, many habitat suitability models often include data pooled from all behavioral states (e.g., moving, resting, foraging) and do not estimate suitability based solely on moving individuals (Klar et al. 2008; Chetkiewicz and Boyce 2009). Such practices may obscure the actual suitability of an area for facilitating movement (LaPoint et al. 2013).

The second consideration is to ensure that corridors are designed based on a species’ habitat preferences. For the purposes of this analysis and discussion, we will distinguish the terms habitat use, habitat availability, habitat selection and habitat preference via the following definitions. Habitat use is the proportion of time animals spends in a given habitat type (Beyer et al. 2010). Habitat availability, or the habitat animals have access to, is both spatially and temporally dependent. Here, we define it as an area delineated by the fine-scale movements of the animal as they travel through a subset of their home range (Aebischer et al. 1993). Habitat selection is the process by which an animal selects or chooses to utilize a certain habitat type (Johnson 1980). Importantly, selection of a habitat type by animals may be the result of limited choice set or may be the result of animals preferring that habitat types over other, available habitat types. To differentiate these two alternatives, the proportion of the selected habitat must be compared to the proportion of other available habitat types available to animals (Aebischer et al. 1993; Aarts et al. 2008). For any given habitat, if the proportion selected exceeds the proportion available, habitat preference may be inferred, even when other habitats are available in equal or greater proportions. In contrast, if proportion selected is less than the proportion available, habitat non-reference or habitat avoidance may be inferred. Such analyses can help inform whether an individual is choosing a particular habitat, or whether that individual was simply constrained in some way to that habitat. By conducting a compositional analysis, which is an analysis of log-ratios and utilizes proportional habitat use relative to habitat availability, we can discern a measure of preference (Aebischer et al. 1993; Horne et al. 2007). In addition to utilizing habitat use in the context of habitat availability as a predictor of habitat preference, Dickson et al. (2005) suggest that speed can be a secondary predictor of habitat preference because individuals tend to move quickly through least preferred habitats and slowly through most preferred habitat. Incorporating habitat preference is important when allocating resources to design wildlife corridors that are attractive to wildlife species of interest.

Third, the structure and composition of the surrounding landscape may shape both habitat use and habitat selection. That is, habitat preference may vary depending on the surrounding landscape. The landscape ecology literature is replete with examples demonstrating that landscape patterns affect local ecological processes (e.g., Turner et al. 2001). In the context of movement, the preference of a particular habitat type may vary depending on the landscape matrix in which that habitat is embedded. For example, a linear forest feature that is surrounded by human development may be functionally different than a linear forest feature that is surrounded largely by natural land cover. This topic has received very little attention to date, and yet provides important information regarding the value of land parcels for conservation and management.

In recent years, advances in the field of movement ecology (Nathan et al. 2009) have shed light on the importance of “animal-defined corridors”, that is, corridors identified by incorporating information from moving animals. For example, LaPoint et al. (2013) used GPS technology to identify cost-surface maps for individual fishers (Martes pennanti) based on the individual’s habitat preferences when moving from one resting location to another. At a landscape or ecoregional scale, the central challenge is how to scale up from individually collared animals to the population as a whole, with an ultimate goal of defining corridors that connect conserved areas and provide dispersal opportunities between subpopulations.

Here, we build on these recent advances to determine the characteristics of bobcat (Lynx rufus) movement and habitat selection, and the environmental covariates that influence these characteristics. We further illustrate how this information can be used to identify movement corridors for this species. Our specific objectives were to (1) Quantify the characteristics of bobcat movement by calculating basic movement metrics, including step length and speed of travel as a function of sex and time of day; (2) Within a movement path (a series of consecutive observations for an individual), use compositional analysis (Aebischer et al. 1993) to rank land cover types and topographic types from “most preferred” to “least preferred”; (3) Determine if the ratio of used versus available habitat for forest edge, wetland edge, forest core and slope, as well as linear features (road and stream density), deviates from 1.0; (4) Investigate travel speed as an indicator of habitat preference, and evaluate how landscape composition affects travel speed; and (5) Compare four alternative landscape scale corridor designs that link two protected areas within the study area, one based on a more traditional habitat suitability index (resource selection functions that did not incorporate information on habitat preference derived from animal location data), and the remaining three based on animal movement-defined indices based on results from Objectives 2 and 3.

Methods

Study species

The bobcat is a wide-ranging carnivore in North America, occupies relatively large home ranges, and exhibits low reproductive rates, territoriality, and male-biased dispersal (Knowles 1985; Hansen 2007). Bobcats move long distances within their home ranges and travel mostly by night, with males traveling farther and faster than females (Chamberlain et al. 2003). Bobcats use a variety of land cover types for travel, including stream valleys and associated ridgelines (Woolf and Nielsen 2002), thick understories (Litvaitis et al. 1986), and rocky ledges (Anderson 1990; Hansen 2007). Despite tolerance of habitat fragmentation, it has been suggested that maintaining corridors for travel between habitat fragments is necessary for bobcat population persistence (Tigas et al. 2002; Litvaitis et al. 2015). Although habitat use in this species has been well-documented, habitat selection by individuals as they move and how landscape context affects habitat selection are topics that have received little attention.

Field methods

To obtain data on the trajectories of individuals through space and time, 41 bobcats were captured and GPS-collared between 2005 and 2007 in areas representing the Champlain Valley lowlands and higher elevation regions in the Green Mountains of Vermont, USA (University of Vermont IACUC 05-036). Bobcat home ranges were distributed in Chittenden, Washington, Lamoille and Addison counties. This large study area was comprised of the following land cover types based on National Land Cover Database (NLCD, Homer et al. 2007) categories: forest (62.4%), agriculture (24.5%), scrub and shrub/rock (5.4%), wetland (4.2%), and development (3.5%). These five land cover categories were created by combining relatively similar land cover classes from the original NLCD dataset, which is comprised of 16 land cover classes. For example, the forest category used in this analysis was created by combining the deciduous forest, evergreen forest and mixed forest categories delineated in the original NLCD dataset. Within forested land cover, 10.0% was forest edge and 22.6% was deep forest core (300 m from a forest edge). The remaining forested land cover was comprised of superficial forest core (30–300 m from a forest edge). Forest edge was defined as the transition between two habitat types by the scale of the data available. The NLCD data set is available in 30 m resolution, allowing the delineation of core and edge habitat in 30 m increments. Forest edge is defined as the interface between forest habitat and a different ecosystem type (Harper et al. 2005), and has long been perceived to have higher abundance and diversity of game species (Leopold 1933), including bobcat prey. In contrast, forest interior is defined as habitat that show no detectable edge influence, defined by alterations in biophysical processes and ecosystem composition and structure. Harper et al. (2005) suggest that edge effects on primary forest processes (e.g. tree mortality) and structure can extend up to ~ 300 m. The topographic landscape contained ridges (5.3%), slopes (56.9%), flat areas (31.3%) and valleys (6.5%). The average slope was 8.3˚.

Due to the seasonal variation in environmental conditions and bobcat behavior, two capture methods were used (Donovan et al. 2011, University of Vermont Animal Care and Use Protocol 05-036). During warmer months, bobcats were captured using padded foot-hold traps (Victor Soft Catch no. 3, Woodstream Corporation, Lititz, Pennsylvania, USA) and sedated via pole injection. During cooler months, as well as in areas with a high probability of human presence, bobcats were captured using cage traps (91 × 28 × 30 cm wire mesh, Safeguard, New Holland, Pennsylvania, USA) that were baited with meat. Traps were distributed widely across the study area in locations that would increase the likelihood of capturing the species of interest. All captured individuals were anesthetized according to body weight with ketamine and xylazine at a ratio of 5 to 1. Both foot-hold traps and cage traps were checked once every 24-h (Donovan et al. 2011).

Bobcats were then outfitted with a GPS collar (model 3300S, Lotek Wireless, Newmarket, Ontario, Canada or model G2400, Advanced Telemetry Systems, Isanti, Minnesota, USA). To avoid effects that might negatively alter natural survival, movement and reproduction, collars did not exceed 2% of the total body weight of a captured individual (Withey and Boloxton 2001). Collars collected temporal data and spatial data in the form of x,y location points. All data were stored on-board the GPS collars.

Bobcats are most active during dawn, dusk and evening hours (Anderson and Lovallo 2003). GPS collars recorded location data every 20 min during these periods (1600–930 h) on alternate days. During off days and all diurnal periods, location fixes were attempted every 5 h in a 24-h period for home range analyses. Data were collected at 20-min intervals periodically during daytime hours. Collars were programmed to actively collect data for 130 days. When this time period expired, collars self-released and were retrieved by technicians (Donovan et al. 2011).

The data were screened such that only those trajectories containing consecutive location points less than 20–25 min apart were used in movement analysis. Using a relatively short time interval reduced the risk that trajectories recreated from discrete point data differed from the true path of the individual. This strict screening resulted in 13 collared bobcats suitable for movement analysis (Table 1).

Table 1 Summary of movement path data for bobcats tracked in the Champlain Valley of Vermont, USA

Movement metrics analysis (objective 1)

We used the x,y location data in the Universal Transverse Mercator projected coordinated system (Zone 18 N, North American Datum 1983) to generate a point feature class for each individual bobcat in a GIS (Geographic Information System) environment (ArcGIS 9.3, ESRI, Redlands, California, USA). We used the Hawth’s Tools analysis package (Beyer 2004) to create continuous movement paths from the input point data. The distance between one point to the next created a movement segment. An example of a single movement path consisting of multiple segments is shown in Fig. 1; each bobcat had multiple movement paths.

Fig. 1

Diurnal travel path of adult male bobcat B1 headed south in the Champlain Valley, Vermont, USA. The area shaded in dark green consists of deciduous, mixed and coniferous forest. Actual GPS location data, re-created movement path, 60-m used space buffer and variable width available space buffer based on the mean Euclidian distance traveled within the movement segment are shown

Hawth’s Tools movement tools were used to calculate movement metrics, including step length and speed of travel. Step length was the Euclidean distance from the current point to the next point (Fig. 1). As points were, on average, 20 min apart, step length was the distance (m) traveled in a 20-min period. We calculated average step length and average speed for each bobcat. Then, we used two sample t-tests with unequal variances (α = 0.1) to analyze the effect of sex and time of day on step length (the distance traveled in a 20-min period) and speed of travel (meters/minute), where the individual was the sample unit. We used a paired t test to test for differences in mean step length and speed by time of day, where day and night designations were determined by using sunrise and sunset times for each 24-h period.

Resource selection via compositional analysis (objective 2)

To determine habitat selection and preference as it related to movement paths, we compared the habitat compositions of “used” movement space to those of “available” movement space. Used movement space was defined as the space through which an animal chose to travel from one point to the next. Available movement space was defined as the space through which an animal could have chosen to travel (see Used Space Buffer and Available Space Buffer in Fig. 1). The available movement space included used movement space.

In this analysis, recreated trajectories, or the movement paths, were encapsulated by a 60 m buffer to provide an estimate of used movement space. We chose this buffer size based on the activity sensor embedded within GPS collars, and because this buffer liberally encompassed GPS error and uncertainty of the exact movement path between discrete points (Dickson et al. 2005). Only movement segments > 60 m were used in this analysis. Location data were buffered by the Euclidean distance traveled between consecutive points to create “available” movement space for each observation (Fig. 1). This method assumes that individuals make choices based upon the space it currently occupies (Aebischer et al. 1993).

We used Python 2.4.1 (Van Rossum 2005) in conjunction with ArcGIS 9.3 to extract statistics on land cover proportions (agriculture, forest, development, scrub-rock, wetlands), vegetation (forest edge, wetland edge, and deep forest core), topography (ridge, slope, flat, valley), stream density, degree slope, and road density within used and available space. The original NLCD (Homer et al. 2007) was comprised of 16 land cover classes in the state of Vermont. Based on the land cover classes believed to be of significance to bobcats (Berg 1979; Sunquist and Sunquist 2002; Hansen 2007; Donovan et al. 2011), and to facilitate clear land cover comparisons (Dickson et al. 2005), we reclassified the original NLCD 2001 into the following five categories: forest, wetlands, developed, agriculture, scrub-rock. By combining classes in this way, we were able to maximize our sample size because individuals that did not have a habitat type available were eliminated from the analysis as they provided no information on use or availability (Aebischer et al. 1993).

We used compositional analysis to test for habitat preference among the five different land cover types (Aebischer et al. 1993). In this movement study, the composition of land cover types in a given space, be it used or available, summed to 1.0. However, being a proportion, the proportion of landcover type 1 (x₁) is dependent on the proportion of landcover type 2 (x₂). Additionally, proportions make it difficult to determine individual preference and avoidance, as the total habitat is constrained such that a preference for landcover type “1” will automatically lead to an avoidance of landcover type “2.” Aebischer et al. (1993) solved this challenge by using log-ratio transformations, which ensures linear independence of the proportions and allows the use of multivariate compositional analysis to determine preference for one landcover type over another (Aitchison 1986; Aebischer et al. 1993; Zar 2010).

Following Aebischer et al. (1993), the log-ratios of the average used space (x_i,u) to available space (x_i,a) for each land cover type were computed for each bobcat. Then, a “difference matrix” was created for each landcover type separately, in which the difference between the log-ratios of each landcover type was compared to the reference type on a bobcat-by-bobcat basis (Aebischer et al. 1993). For example, with ‘forest’ as a reference type, the difference (d) between the log-ratios of forest and the log-ratios of every other landtype (agriculture, development, wetland, shrub-scrub) were computed for each bobcat. In each of the 5 d matrices, positive d scores indicated preference, and negative scores indicated avoidance for a given land cover type relative to other land cover types. We used a MANOVA on the forest-reference d score matrix to test the omnibus null hypothesis of no difference in d scores between the alternative land types. Additionally, the scores for each d matrix were then averaged across individuals in the population, and were used to rank land cover types from most preferred to least preferred. Due to the large variance in the locations contributed by each bobcat, it was necessary to implement a weighting structure to account for the variation in available data per individual.

Similarly, we used compositional analysis to evaluate the effects of topography on movement. Elevation data were extracted from a 1:24,000-scale Digital Elevation Model (DEM) for the Vermont portion of the United States Geological Survey National Elevation Dataset (raster with 30 m × 30 m pixel size). We created a topographic position index map, which categorized the state of Vermont into valley, flat, sloped and ridge topographies based on change in elevation. This resulted in 4 categories whose proportions summed to 1 within a used or available space. Using this topographic position index, we performed a compositional analysis to test for preference as described for the landcover analysis.

Resource selection via paired tests (objective 3)

In addition to the compositional analysis of landcover types and topographic position, we also tested for selection in the form of slope, forest edge, forest core, and wetland edge vegetation (variables that are not proportions). Average slope encountered for used and available space was calculated using ArcGIS 9.3. Edge habitat existed where two habitats of contrasting composition met in the landscape. Forest edge (30 m) and wetland edge (30 m) consisted of forested and wetland habitats within 30 m of a contrasting habitat type. Core habitats were those habitats that were surrounded by habitat of like composition. Forest core (30 m) represented superficial core forest that was 30 m or more in distance from a habitat of contrasting type. Forest core (300 m), a measure of deep core, represented forest that was 300 m or more in distance away from a habitat of contrasting type. These edge and core categorizations were imposed by the use of a 30 m pixel landcover raster. We used the svyratio function in the R package, survey (Lumley 2004) to determine if the ratio of used to available significantly differed from 1 for slope, core habitats, and edge habitats, where the statistical sample was an individual’s average used and available score. Ratios > 1 indicate resource selection, and ratios < 1 indicate non-selection.

The effects of linear features, including streams and roads, on bobcat movement were similarly evaluated. The most accurate road data available for Vermont was the Emergency 911 roads centerline feature class data (McMullen 2008). This GIS layer was created from 1:5000 scale orthophotos. Both paved and dirt road densities were calculated using ArcGIS 9.3 for available and used movement space. Stream density was calculated and used as an indicator of riparian zones, which are thought to be of importance to bobcats in Vermont (Hansen 2007). We used the svyratio function in the R package, survey (Lumley 2004) to determine if the used to available ratio for road density and stream density differed from 1, where the average used and available scores for each individual constituted a data point for statistical analysis.

Effects of landscape composition on travel speed (objective 4)

We assessed travel speed as a function of proportion of used forest and as a function of used scrub-rock landcover types, with the expectation that speed would decline as these proportions increased if bobcats preferred these habitats. However, because speed through these habitats may be shaped by the landscape composition of the “available” habitat, our analysis included the main effect of used habitat (proportion of forest or scrub-rock), the main effect of available habitat (proportion of forest, scrub-rock, agriculture, and development), and the interaction between used and available habitat proportions. As such, we evaluated eight GEE models with an autoregressive correlation structure, and used QIC to rank models. The general model framework was speed = used_i + available habitat_j + used_i * available_j, where i was either the proportion of used forest or the proportion of used scrub rock, and j was the proportion of available forest, scrub-rock, development, or agriculture. The model included a repeated measurement by individuals to account for multiple observations per individual.

Comparison of corridor designs (objective 5)

We used least cost path analysis (Adrianensen et al. 2003) and circuit theory analysis (McRae et al. 2008) to map the potential corridors between two state management areas in a region within the bobcat study area (Little Otter Creek Wildlife Management Area and Huntington Gap Wildlife Management Area; focal region = ~ 34 × 16 km). We chose these areas because bobcats have been recorded in both and the region between them was heterogeneous and contained several landcover types. Both corridor design approaches require a cost map (the inverse of habitat suitability) which identifies each pixel’s resistance to animal movement. We evaluated four corridor designs based on four alternative habitat suitability maps. For the first map alternative (‘Resource Selection Function’), we used a habitat suitability map inferred from analysis of all GPS locations, regardless of behavioral state (moving or non-moving). The suitability score for each pixel was obtained by calculating the proportion of scrub, deciduous forest, mixed forest, evergreen forest, wetlands, and road density within 1 km of each pixel, multiplying each factor by its corresponding resource selection linear coefficient (see Donovan et al. 2011, Table 5), and then summing the scores; scores were positively related to habitat suitability. This suitability map was based on habitat use with no regard for habitat preference.

For the second suitability map alternative (‘Compositional Analysis’), we created a suitability map based on the habitat preferences of moving bobcats revealed by compositional analysis in Objective 2 (Aebischer et al. 1993). In this approach, the suitability score for each pixel was obtained by calculating the proportion of agriculture, forest, development, scrub-rock, and wetlands within a 161 m radius of each pixel (the average step distance for a moving bobcat; see “Results”), multiplied by their corresponding average d score, and then summed; scores were positively related to habitat suitability. This suitability map was based on habitat preferences by moving animals (highly weighted forested pixels and strongly penalized developed pixels; see Results), but was restricted to the subset of landcover variables analyzed in the compositional analysis.

The third suitability map alternative (‘Use-to-Available Ratios’) was based on the used versus available ratio results from Objective 3. In this approach, we used the used-to-available ratios to determine which variables were selected (ratio significantly greater than 1) and which were non-selected (ratio significantly less than 1). For each pixel, we used a moving window analysis to calculate the average score of each variable within a 161 m radius. We then determined the minimum (min) and maximum (max) value for each variable in the focal region. For each pixel in the focal region, each variable was scaled from 0 to 1: variables that were selected were scaled with the equation scaled score = (score − min)/(max − min), whereas variables that were non-selected were scaled with the equation scaled scored = (score − max)/(min − max). Consequently, a variable score of 1 represented the “ideal” condition for a moving bobcat. For example, if forest cover was preferred, a score of 1 indicated the highest level of forest cover in the focal region. In contrast, if roads were not preferred, a score of 1 indicated the lowest level of road density in the focal region. The total suitability of each pixel was then calculated by summing the scaled scores. The resulting suitability map was based on habitats selected by moving animals and based on multiple variables; however, each variable contributed equally to the resulting map.

The final suitability map (‘Weighted Used-to-Available Ratios’) incorporated a slight modification to the third method, in which the scaled scores were weighted by how far the use:availability ratios deviated from 1.0. For example, variables with a ratios of 0.8 or 1.2 would be weighted by 1.2, while variables with ratios of 0.9 or 1.1 would be weighted by 1.1, and variables with ratios of 1 would be unweighted. This suitability map was based on habitat preferences by moving animals and based on multiple variables, with each variable weighted based on the preference of moving bobcats.

For each of the four alternative suitability inputs, we evaluated connectivity between the two management areas with a three-step process. The first step involved converting the habitat suitability map to a cost map between the two areas. For each design, we first converted the habitat suitability raster to a cost raster by dividing the raster by its maximum value, and then subtracted the result from 1.0. Values were then rescaled from 1 (pixel with minimal cost) to 100 (pixel with maximal cost). Thus, pixels with a low score had low travel cost.

The second step involved creating a cost-weighted distance map and least-cost corridor map between the two areas. In a cost-weighted distance map, the value of a pixel is function of its resistance value and distance to a core area. We created a cost-weighted distance map for each management area. We then created a least-cost corridor map by adding, normalizing, and mosaicking the cost-distance maps, and truncated this final map by removing all cost-distance values > 25 km. We chose this value based on observations of bobcats and information on movement and dispersal elsewhere. The remaining pixels represented corridors where bobcats could be expected to travel between management areas. We used Linkage Mapper v. 1.1.0 (McRae and Kavanagh 2011) to create cost-weighted distance and least-cost corridor maps, and calculate least-cost paths between areas.

The third step involved estimating movement flow through the least-cost corridor map. We estimated flow using a circuit theory approach, which treats movement like the flow electrical current through a circuit with varying resistances (McRae et al. 2008). We used Pinchpoint Mapper (McRae 2012) to pass current from one management area to another through the least-cost corridor map, which consisted of pixels with varying resistances (or cost-weighted distance values). The resulting map showed the distribution of movement flow within the corridor.

Results

Movement metrics analysis (objective 1)

Movement analysis was based on 13 bobcats (5 females and 8 males), in which 12 individuals recorded movements in both diurnal and nocturnal periods. All analyses were conducted on the average movement statistics per individual. Across individuals, bobcats traveled at a mean speed of 6.28 m/min (SD = 2.86) and the average distance traveled in a 20-minute period was 125.7 m (SD = 57.27). Mean step length for females (n = 5) was 85.6 m (SD = 24.1) and 150.7 m (SD = 58.52) for males (n = 8). Males traveled an average of ~ 65 meters more than females within a 20-minute period (t = -2.79, P < 0.019, n = 5 females and 8 males). Consequently, on average, males traveled ~ 4.7 km more than females in a 24-hour period. Mean speed of travel for females was 4.28 m/min (SD = 1.20) and for males was 7.53 m/min (SD = 2.92). Males traveled an average of 3.26 m/min (or 0.2 km/h) faster than females (t = -2.7938, P < 0.0189, n = 5 females and 8 males). Individual bobcats on average travelled 107.1 m more per hour during night time hours (SD = 194.1). Mean speed of travel for day time hours was 5.30 m/min (SD = 3.00) and 7.09 m (SD = 3.62) for nighttime hours; nighttime travel was 33% faster than daytime travel on average. These differences were marginally significant (paired t = − 1.9113, P < 0.082, n = 12 bobcats).

Resource selection via compositional analysis (objective 2)

The land cover comprising used movement space differed from that of available movement space across all individuals (Wilks’ Lambda = 0.2055, P < 0.0149, numerator df = 4, denominator df = 7, n = 11 bobcats). Compositional ranking analyses revealed that, for movement purposes, forested land cover and scrub-rock land cover were most preferred while developed land cover types were least preferred (Table 2). However, wide variation in land cover preferences was observed among individuals (Fig. 2).

Table 2 Matrix used to construct weighted land cover habitat rankings for bobcats (n = 11) in the Champlain Valley of Vermont, USA

Fig. 2

Graphical depiction of the variation in individual habitat preferences displayed by bobcats (n = 11) in the Champlain Valley of Vermont, USA. The y-axis depicts the percent of individuals that displayed the following rankings for each land cover type. For example, approximately 48% of individuals preferred development the least (rank = 5) and almost 40% of individuals most preferred forest (rank = 1) when compared to all other land cover types

Using a multivariate compositional analysis, we found the topographic position index (valley, flat, sloped and ridge) comprising used movement space did not differ significantly than that of available movement space (Wilks’ Lambda = 0.643, P < 0.2908, numerator df = 3, denominator df = 8, n = 10 bobcats). Individual B11 was removed from this analysis because not all topography types were available to this bobcat and, therefore, this individual provided no information on use or availability. Although a ranking matrix was not constructed, the used to available ratio for flat topography was significantly lower than 1, and the used to available ratio for sloped topography was significantly greater than 1 (Fig. 3).

Fig. 3

Ratios of used movement space topography to available movement space topography for bobcats (n = 11) in the Champlain Valley of Vermont, USA. Error bars are 95% confidence intervals based on a t distribution with 10 degrees of freedom. Flat topography was not selected, while sloped topography was selected (ratios significantly differed from 1)

Resource selection via ratio tests (objective 3)

To investigate the effect of slope on movement choices (selection), mean degree slope was calculated for used and available movement space. Average slope used by bobcats was 5.0% steeper than available slope (SE = 0.016, n = 11 bobcats; Fig. 4). Mean forest edge (30 m) was 18.9% higher in used movement space as compared to available movement space (SE = 0.021, n = 11 bobcats; Fig. 4). Used wetland edge (30 m) was 10.2% more than available wetland edge (SE = 0.023, n = 11 bobcats; Fig. 4). Bobcats used superficial forest core (forest > 30 m from an edge) slightly more than it was available, with 3.1% more superficial forest core in used space when compared to available space (SE = 0.017, n = 11 bobcats). Deep forest core (forest > 300 m from an edge) was used 10.4% less than was available; however, this difference was not significant (SE = 0.126, n = 11 bobcats; Fig. 4).

Fig. 4

Ratios of used to available habitat for 7 covariate classes for bobcats (n = 11) in the Champlain Valley of Vermont, USA. The value “1” represents no effect. Values above “1” convey a higher usage given availability for a particular habitat. Values below “1” convey a lower usage given availability for a particular habitat. Error bars are 95% confidence intervals based on a t distribution with 10 degrees of freedom

Bobcats also used roads and streams disproportionately to their availability. Paved road density was 18.1% lower in used space when compared to available space (SE = 0.067, n = 11 bobcats; Fig. 4). Used dirt roads density was 5.7% lower than available dirt road density (SE = 0.045, n = 11 bobcats). Stream density was 11.2% higher in used movement space (SE = 0.032, n = 11 bobcats; Fig. 4).

Effects of composition of available habitat on travel speed (objective 4)

Bobcat travel speed through forest or scrub-rock used habitats was strongly influenced by the composition of the “available” habitat (Table 3). Regarding the use of forested habitat for travel, speed increased when that forested strip was surrounded by non-forested habitat, suggesting that linear forest features, such as hedgerows, were not preferred habitat. However, speed decreased when the used forested strip was surrounded by a significant amount of additional forest in the available buffer. These results suggest that bobcats preferred to use forested habitats for travel, but this preference was highly influenced by landscape-scale forest cover (Fig. 5a). When the surrounding landscape consisted of high levels of agriculture or development, speeds of travel through forested habitats increased dramatically, suggesting these areas were used strictly for traversing through inhospitable matrices (Fig. 5b, c). Similar results were found regarding the use of scrub-rock habitat for travel (Table 3). Speeds were lowest when used scrub-rock habitat was high and the available forest was moderate to high. Speeds were highest when the used scrub-rock habitat was low and the available forest was low (i.e., development or agriculture was high).

Table 3 Descriptions and analysis of the 8 generalized estimating equations (GEEs) created to explore the relationship between travel speed and habitat preference among bobcats in the Champlain Valley of Vermont, USA

Fig. 5

Relationship between highly preferred used habitat (forest), least preferred available habitat (agriculture and development) and their effect on predicted travel speed for bobcats (n = 11) in the Champlain Valley of Vermont, USA. Bobcats moved slowest when used forest was high and the surrounding available development and agriculture were low, illustrating the effect of the surrounding habitat matrix on travel speed through used habitat

Corridor design (objective 5)

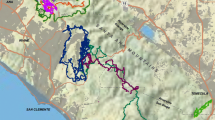
The Euclidean distance between the two focal wildlife management areas was 22.9 km (Fig. 6a). Corridor designs to link the units varied depending on which of the four methodologies were used to compute the habitat suitability map (Table 4, Fig. 6a–e). In the first method (in which the habitat suitability map was based on resource selection functions from GPS analysis with no regard for habitat preference), the least-cost path distance was the shortest among methods and nearly a straight line through a broad linear corridor (Table 4, Fig. 6b). This result is largely due to the fact that the resource selection function in Donovan et al. (2011) heavily weighted shrub and wetland habitat, rare landcover types within this landscape. Corridor designs for each of the three remaining methods were based on analysis of moving bobcats and different in pattern and configuration (Fig. 6c–e). The second method, (based on d scores from the compositional analysis of landcover types; Table 2) resulted in a more dispersed pattern of movement corridors between areas that heavily followed forested pixels. The remaining methods (based on use-to-availability ratios) resulted in single, relatively discrete corridors (Fig. 6b–e). The least cost path was longest in the second method, and shorter, but nearly the same in length and route for the third and fourth methods (Table 4, Fig. 6c–e).

Fig. 6

Estimated movement flow through least-cost corridors between two wildlife management areas in the Champlain Valley of Vermont, USA. a shows the geographic extent of the analysis, location of areas, and distribution of major habitat types. The remaining panels show expected movement flow between areas based on different maps of habitat suitability: b suitability based on resource selection functions that did not incorporate information on preference, c suitability based on compositional analysis, d suitability based on use-to-available ratios, and e suitability based on use-to-availability ratios weighted by how far the use to availability ratios deviated from 1.0. Movement flow estimated using a circuit theory approach

Table 4 Measures of distance and corridor quality between two wildlife management areas (Little Otter Creek WMA and Huntington Gap WMA) in the Champlain Valley of Vermont, USA

The ratio of cost-weighted to Euclidean distance values, which reflects a measure of corridor quality, was lowest for the second method, indicating the highest quality relative to the other three methods, which had ratios between 4.8 and 5.7 times greater (Table 4). The ratio of cost-weighted to least cost path distance values followed a similar pattern (Table 4). Movement flow was fairly uniform in the first method, but revealed distinctive pinch-points in the other three methods (Fig. 6b–e).

Discussion

Through compositional analysis, we identified strong preferences for forest and scrub and rock land cover types. We further documented that bobcats select forest edge, wetland edge, and areas with high stream density during movement. In spite of our low sample size of collared bobcats, combined with the requirement that consecutive GPS locations exceed 60 m to constitute movement, these results are fairly consistent with other studies on bobcats (Woolf and Nielsen 2002; Chamberlain et al. 2003; Hansen 2007; Litvaitis et al. 2015; Reed et al. 2016). Preferences for forest and scrub habitats are consistent with high prey densities and this species’ role as an obligate carnivore, which may explain why movement paths were selected in these areas (Hansen 2007). Rock habitat may provide refuges from predators and competitors, as well as denning habitat which would serve as a target destination for moving females (Hansen 2007). Bobcats avoided areas characterized by moderate to high anthropogenic influence, including developed and agricultural areas, agricultural land, and did not select areas with high road density for movement.

Like all wildlife GPS studies, there are limitations to this study. Most pressing is the potential bias that arises when the success or failure of GPS location fixes depends on the habitat in which the animal occurs (collar bias). For example, location fixes may have a low probability of success when animals occupy thickly vegetated areas which block satellite reception (e.g., thick, coniferous forest). These absences result in collar bias, which can significantly affect conclusions from a habitat selection analysis (Frair et al. 2010). We were not able to directly test for collar bias, but Friar et al. (2010) demonstrated that non-fixes were most closely associated with closed conifer habitat, a habitat type that is not often included in bobcat home ranges in this area (Donovan et al. 2011). We believe this potential bias may be small for our study, however, due to the fact that forest consistently emerged as a preferred habitat compared to non-forest habitats—a pattern that would not be evident if collar bias was severe.

Our results demonstrate the role of spatial scale interactions on habitat selection in a wide-ranging carnivore. When coupled with complementary analysis on habitat preference, such as compositional analysis, travel speed may provide an additional indicator of habitat preference in wild felids (Dickson et al. 2005). Bobcats traveled at greater speeds through habitat types that were least preferred in the compositional analysis and traveled at slower speeds through habitat types that were most preferred. Travel speed was influenced not only by the land cover composition of the movement path, but also by the composition of the landscape matrix which encompassed the movement path. Bobcats traveled more slowly through forested corridors surrounded by good quality habitat (forest, scrub and rock) and traveled more quickly through those same forested corridors when they were encompassed by a developed matrix. While this trend does not support a causal relationship between habitat preference and travel speed, it does provide an additional indicator of preference, when considered in the context of compositional analysis, or other analyses that establish preference based on used versus available habitat.

These results have important implications for conservation planning and corridor delineation. Beier et al. (2008) reviewed the use of models for identifying lands that will best maintain the ability of focal wildlife species to move between wildland blocks when the adjoining matrix is inhospitable. Generally speaking, and given a set of biological goals, an analyst develops an algorithm to estimate the resistance of each pixel in the landscape as a function of pixel attributes, where resistance refers to “the difficulty of moving through a pixel.” The analyst produces a travel cost map for the landscape, and then identifies the swath of pixels with the lowest cumulative travel cost.

This process introduces a number of challenges that must be addressed. Beier et al. (2008) noted that in most cases, information about movement or habitat use is unknown for many focal species and that most corridor designs rely on expert opinion. Additionally, for any given attribute analyzed, the scale at which organisms assess resources is usually unknown, and these scaling issues also influence the resulting resistance score of a given pixel. Moreover, to estimate the overall resistance of a pixel, the analyst must combine resistance due to land cover with resistance due to anthropogenic disturbance and other factors. To do so, the analyst must choose an arithmetic operation, standardize the attribute metrics if the metrics occur on different scales, and assign a weight to each factor, which are most often assigned solely by expert opinion.

Almost a decade after Beier et al.’s (2008) seminal paper, the age of the Anthropocene has been declared, ushered by the impact of humans on Earth’s ecosystems (Waters et al. 2016). As species’ distributions change, now, more than ever, there is a pressing need to link movement ecology with wildlife management and conservation (Allen and Singh 2016). Facilitating movement and landscape connectivity within disturbed landscapes is particularly relevant, in light of increasing rates of development at both international and local scales. Developed urban land cover comprised 3.1% of the United States in 2000 and is projected to increase to 8.1% in 2050; a 161% increase (Nowak and Walton 2005). Between 2000 and 2050, 392,400 km² will be converted to urban areas, with about 30% of the development replacing forest; an area roughly equal to the size of Pennsylvania (Nowak and Walton 2005). This indicates that as human populations increase, more land per capita is being converted from forest (the most preferred habitat of bobcats) to development (the least preferred). Such land use change patterns which produce increasingly human-altered landscapes are exhibited globally, cause habitat loss and fragmentation, and are the primary drivers of reductions in biodiversity (Plieninger 2006; Sala et al. 2000).

Despite these potential pitfalls for bobcat populations, present-day conservation planning can mediate some of these negative effects in the future. In this paper, we have introduced novel approaches addressing some of the challenges raised by Beier et al. (2008). First, the scale at which moving organisms utilize their environment is clearly related to both local and landscape characteristics (Objective 4), and that corridor designs differ depending on whether movement behavior is considered or not (Objective 5). With respect to assigning resistance due to landcover or topography, the compositional analysis d-scores provide a standardized measure of preference across all habitats, regardless of their wide variance in availability in the landscape. With respect to assigning weights to different pixel attributes, the ratios of used to proportion available provides a metric that is common across different resource attributes and therefore can be used to aid in weighting. These comparisons would not be meaningful otherwise due to differences in scale and wide variation in landscape availability. By shifting the basis of corridor design from expert opinions to empirical data, and using the above-described quantitative methods to derive pixel resistance, the resulting corridor will become more reflective of true focal species behavior (Reed et al. 2016). In addition, the process by which corridor design is accomplished will be more objective, as well as transparent to managers (Allen and Singh 2016).

Each corridor approach resulted in a different depiction of least-cost corridors and paths of movement. The differences reflect the quantitative approach used to estimate resistance, and managers should carefully consider which may be best for a given species and landscape. The resource selection function approach resulted in a nearly straight line corridor between areas, which is mainly due to the relatively coarse scale of the resource selection functions used to estimate resistance (e.g., model betas applied to habitats like forest cover at the 1 km radius scale; Donovan et al. 2011). The resource selection function model also did not include an agriculture covariate, so under this model, movement through the landscape would not be impacted by agriculture unlike other models. The compositional analysis approach resulted in the most distinct corridor and movement map. This approach applied d-scores for several variables to each pixel, and the convoluted pattern of corridors and movement reflected the relatively high d-score for forest. Areas with forest were generally lower in resistance and so multiple paths of movement emerged in large forested regions of the landscape (east side of map), and movement elsewhere (west side of the map) followed forest patches. The other two approaches (use-to-available and weighted use-to-available) resulted in similar depictions of corridors and movement, suggesting that the weighting had little appreciable effect on landscape resistance. However, weighting may result in different representations of resistance for other species and landscapes. The compositional analysis approach yields a result which better reflects species behavior and, as such, may yield a corridor more likely to facilitate the movement of species of interest. However, real world corridor design may be heavily driven by the resources available to wildlife managers accomplish conservation objectives. If a geographically complex corridor which is the result of incorporating detailed species preference information is difficult to conserve, a less complex corridor designed via coarse scale resource selection function information may be a more feasible option.

Corridor and movement flow maps provide depictions of the landscape that can be used to inform conservation planning. For example, maps of corridors and movement flow could be used to identify areas where bobcats may be more likely to cross roads. These areas could then be targeted for mitigation activities like wildlife crossing structures and warning signs, which have been employed in Vermont (e.g., underpasses for amphibians and signs warning motorists of moose and bear crossings). Maps could also be used to identify corridors across large spatial scales that may help identify key linkages between ecosystems. For example, the Staying Connected Initiative is an international effort that seeks to conserve, restore, and enhance wildlife connectivity across the Northern Appalachian/Acadian region of the eastern US and Canada (Trombulak et al. 2012). Our quantitative approach complements this effort by providing species-specific information on movement that could improve assessments of corridor location, quality, and importance to connectivity. Lastly, our approach revealed pinch-points of movement (i.e., constriction points or bottlenecks) within corridors, which represent a conservation concern as landscape change at these locations could disproportionally impair bobcat movement at multiple spatial scales.