Abstract
Assessing landscape connectivity is important to understand the ecology of landscapes and to evaluate alternative conservation strategies. The question is though, how to quantify connectivity appropriately, especially when the information available about the suitability of the matrix surrounding habitat is limited. Our goal here was to investigate the effects of matrix representation on assessments of the connectivity among habitat patches and of the relative importance of individual patches for the connectivity within a habitat network. We evaluated a set of 50 × 50 km2 test areas in the Carpathian Mountains and considered three different matrix representations (binary, categorical and continuous) using two types of connections among habitat patches (shortest lines and least-cost paths). We compared connections, and the importance of patches, based on (1) isolation, (2) incidence-functional, and (3) graph measures. Our results showed that matrix representation can greatly affect assessments of connections (i.e., connection length, effective distance, and spatial location), but not patch prioritization. Although patch importance was not much affected by matrix representation, it was influenced by the connectivity measure and its parameterization. We found the biggest differences in the case of the integral index of connectivity and equally weighted patches, but no consistent pattern in response to changing dispersal distance. Connectivity assessments in more fragmented landscapes were more sensitive to the selection of matrix representation. Although we recommend using continuous matrix representation whenever possible, our results indicated that simpler matrix representations can be also used as a proxy to delineate those patches that are important for overall connectivity, but not to identify connections among habitat patches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In today’s increasingly human-dominated landscapes, many species can only survive in the long run if habitat patches are well-connected (Fischer and Lindenmayer 2007). Quantifying habitat connectivity, i.e., the degree to which a landscape promotes or hinders movements among habitat patches for a given species (Taylor et al. 1993) is therefore essential for conservation decisions (Luque et al. 2012). However, how to quantify connectivity appropriately is often vague, partly because of the plethora of methods that have been proposed to measure connectivity, but also because of limitations in the available input data (Kool et al. 2012). Specifically, there is often only limited information about the suitability of the matrix surrounding habitat patches to facilitate species’ movement, and that raises the question to what degree this imperfect matrix information renders connectivity assessments useless or even misleading.
One useful classification scheme to assess connectivity distinguishes two major groups: structural and functional connectivity. Structural connectivity measures are solely based on landscape structure (e.g., size, shape and configuration of habitat) with no direct link to species’ behavior, while functional connectivity measures are based on the ecological responses of organisms to individual landscape elements (e.g., patches) and the ability of individuals to move in the matrix (Tischendorf and Fahrig 2000). Connectivity assessments are typically conducted in stages that include selection and definition of environmental variables and biological (field) data, definition of habitat and land area among habitat patches, and selection and application of connectivity measures. Decisions taken at each of these stages are driven by the availability of input data and knowledge on species’ habitat requirements and dispersal abilities, and are crucial for the final connectivity assessment. Therefore, it is important to highlight sources of possible uncertainties (including data and software uncertainties; Lehman and Ramil 2002; Lechner et al. 2013; de Rigo 2013) in connectivity assessments and their consequences in order to give practitioners more guidance on how to assess connectivity to inform conservation planning. Uncertainties in connectivity assessments focused on connectivity measures and their behavior in response to variation in landscape structure were widely discussed (e.g., Goodwin and Fahrig 2002; Pascual-Hortal and Saura 2006; Saura and Pascual-Hortal 2007a; Baranyi et al. 2011). As a result, limitations of many available connectivity measures have been indicated, together with practical solutions and recommendations on best performing ones.
Although proper selection and application of connectivity measures is undeniably important for evaluation of connectivity, how the landscape is represented in terms of habitat suitability and resistance for a given species may be equally important (Zeller et al. 2012; Trainor et al. 2013). Landscape structure clearly influences dispersal and habitat connectivity (e.g., Goodwin and Fahrig 2002; Uezu et al. 2005; Pflüger and Balkenhol 2014), making it crucial to represent landscape structure appropriately in connectivity analyses. Most connectivity analyses are based on a patch-mosaic model of landscape structure, in which landscapes are seen as mosaics of discrete habitat patches embedded in a background matrix (Forman 1995; Bender et al. 2003). The simplest assumption about the matrix is that it is homogeneous and does not influence the movement of organisms among habitat patches. This was a common approach in early connectivity studies (Fahrig and Merriam 1985; Henein and Merriam 1990), and it is also the most parsimonious approach for species for which knowledge about their response to different matrix elements is scarce, or for broad-scale assessments concerning a wide range of target species (e.g., Saura et al. 2011; Opermanis et al. 2012). However, in reality the matrix is rarely homogeneous in terms of its suitability for dispersal of a given species, and the composition of the matrix influences movement behavior and movement risk (Pflüger and Balkenhol 2014).
One way to better represent matrix heterogeneity is to estimate the resistance to movement among habitat patches. This is typically done by analyzing environmental variables that can be converted into a ‘resistance’ or ‘cost’ surface, i.e., a raster that depicts a travel cost in each cell (Rayfield et al. 2010; Zeller et al. 2012). Depending on the available information about the matrix and a species’ dispersal ability, this resistance surface can either be of categorical or continuous representation (Bender et al. 2003; Zeller et al. 2012). In categorical resistance surfaces, a limited number of classes represent different resistance levels to movement (e.g., Chardon et al. 2003; Rabinowitz and Zeller 2010; Magrach et al. 2012; Rubio et al. 2012). Alternatively, each cell in the matrix can be assigned a continuous resistance value (e.g., Kuemmerle et al. 2011; Ziółkowska et al. 2012; Trainor et al. 2013). In practice, the decision how to represent matrix resistance in a given connectivity analysis often depends on data availability for a given species (Beier et al. 2008; Sawyer et al. 2011; Zeller et al. 2012). Resistance surfaces based on land cover maps, maybe in conjunction with data on linear barriers (e.g., roads, rivers), are typically categorical, and the definition of cost values often relies on expert opinion. On the other hand, resistance maps based on habitat suitability models typically result in continuous resistance maps, where resistance is highest where habitat suitability is lowest (Zeller et al. 2012; Trainor et al. 2013).
An important question therefore is how different matrix representations may affect connectivity analyses. Most prior comparative studies of connectivity measures assessed either only binary (i.e., habitat vs. non-habitat) matrix representations (e.g., Moilanen and Nieminen 2002; Bender et al. 2003; Schooley and Branch 2011; Laita et al. 2011; Baranyi et al. 2011; Rubio and Saura 2012) or categorical matrix representations (e.g., Visconti and Elkin 2009). Only a few studies evaluated the influence of different matrix representations on connectivity analyses itself, and these compared only categorical matrix representations (Rayfield et al. 2010), or binary and continuous matrix representations (Szabó et al. 2012). More detailed and comprehensive studies in this matter are lacking, especially in terms of analyzing different aspects of connectivity assessments (delineation of corridors, selection and parameterization of connectivity measures, importance of habitat patches) in landscapes with different spatial patterns.
Our main goal here was to examine how different matrix representations affect connectivity assessments. For a set of landscapes, we compared three different matrix representations: (1) binary (where the matrix is considered as homogeneous in terms of its influence on species’ movement among habitat patches), (2) categorical (where different movement costs are assigned based on land-cover categories), and (3) continuous (where travel costs are derived from a habitat suitability map). Specifically, we addressed the following questions:
-
(1)
What is the influence of different matrix representations on the delineation of corridors, i.e., the connections among habitat patches?
-
(2)
What is the influence of different matrix representations on the importance and ranking of individual patches, according to different connectivity measures, for the overall connectivity of the habitat network?
-
(3)
To what extent does the effect of different matrix representations and measures on connectivity depend on landscape structure (i.e., the shape and spatial arrangements of habitat patches)?
Materials and methods
Study area
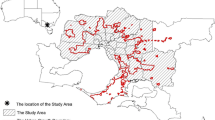
We evaluated the effect of different matrix representations on habitat connectivity assessments for a set of landscapes in the Carpathian Mountains. The Carpathians are Europe’s largest mountain range, stretching in an arc across Austria, Slovakia, the Czech Republic, Hungary, Poland, Ukraine, Romania, and Serbia (Fig. 1). Elevation ranges from around 100–2655 m a.s.l. Climate is moderately cool and humid. Forests cover approximately half of the Carpathians (up to 90 % between 1,000 and 1,500 m a.s.l.; Kozak et al. 2008). The region is critically important for biodiversity conservation in Europe, hosting vast semi-natural forests, unique traditional farming landscapes, and many endemic species. The Carpathians are also crucial for large carnivore and herbivore conservation, harboring Europe’s largest wolf and brown bear populations, and some of the largest free-ranging populations of European bison (UNEP 2007; Kozak et al. 2013).
Data
To create different matrix representations, we used a land cover map and a continuous habitat suitability map for European bison (Bison bonasus) that covered all of our study landscapes (Kuemmerle et al. 2010). Both maps had 100-m resolution. The land cover map was derived from the CORINE Land Cover 2000 database (http://dataservice.eea.europa.eu) and a land cover classification of Landsat TM/ETM+ images for Ukraine (overall accuracy >90 %; Kuemmerle et al. 2009, 2010), and included eight land cover classes: coniferous forest, mixed forest, broadleaved forest, grassland, cropland, open settlements, dense settlements, and water (Kuemmerle et al. 2010). The habitat suitability map, with suitability values ranging from 0 (the lowest suitability) to 100 (the highest suitability), was derived from actual observations and herd range maps using maximum entropy modeling and a set of predictor variables including land cover (land cover categories from the land cover map described above, forest fragmentation, and distance to forest), human disturbance (distance to roads, distance to settlements), and topography (aspect, slope; Kuemmerle et al. 2010). The habitat suitability map showed that bison select forest-dominated habitats with a preference for complex mosaics of forests and grassland patches in areas of low human disturbance (Kuemmerle et al. 2010).
We delineated six test areas (subsets of 50 × 50 km2) for further analyses (Fig. 1). We selected the test areas so that they had different proportions and patterns of high and low quality habitat. All data processing (including the definition of habitat networks) was done in ArcGIS 10.0 (ESRI 2011) with scripts written in Python 2.6 (Python Software Foundation 2013).
Habitat patches and matrix representations
We defined habitat patches as groups of at least 100 pixels (i.e., >1 km2) with a habitat suitability index above a certain threshold. We applied three different thresholds (50, 60, and 70) to produce maps with different spatial patterns (Fig. 1; Table 1). Depending on the threshold, habitat patches covered from 0.5 to 34.5 % of each test area. The resulting maps also differed in terms of the number of habitat patches (1–42), mean patch size (1–52 km2), and mean distance between neighboring patches (3–19 km).
For each test area and habitat patch delineation threshold, we considered three matrix representations to describe the resistance to movement defined as the physiological cost of moving through a particular environment (Zeller et al. 2012):
-
Binary: the landscape was only separated into habitat and non-habitat, reflecting the assumption that the matrix is homogeneous in terms of its influence on species movement.
-
Categorical: each land cover class was assigned a certain resistance to movement. The resistance for each land cover class was defined as a mean resistance for this class according to the continuous representation (Table 2).
Table 2 Resistance values for the categorical matrix representation -
Continuous: the matrix was defined as a continuous resistance surface, i.e., the inverse of the habitat suitability (cost = 100 − habitat suitability). Cost values ranged from 0.45 to 100, with a mean value of 80.95.
Since land cover was an important variable to determine habitat suitability, the categorical and continuous matrices were correlated (coefficients of determination varied from 0.63 to 0.78 among the test areas).
Connections among habitat patches
We delineated a connection between two given habitat patches either as the shortest line (binary matrix representation), or as a least-cost path (categorical and continuous matrix representations) connecting edges of patches. Least-cost paths were determined using the Cost Path tool available in ArcGIS Desktop 10.0 (ESRI 2011). For each connection, we calculated its length, and effective distance defined as the sum of cost values along the path multiplied by the grid cell dimensions (vertical/horizontal, or diagonal). To obtain effective distances for binary matrix representations, we calculated the sum of cost values (based on categorical or continuous representation) along each connection multiplied by the grid cells dimensions.
First, we compared the connections for different matrix representations visually in the maps. Second, we analyzed distributions of connection lengths and effective distances depicted in box plots. Based on this, we applied linear regression and the Wilcoxon rank-sum test to determinate the significance of differences among the lengths and effective distances of connections for different matrix representations. All statistical analysis were conducted in R 3.0 (R Core Team 2013).
Selection of connectivity measures
Various connectivity measures have been proposed in the literature (e.g., Goodwin and Fahrig 2002; Calabrese and Fagan 2004; Kindlmann and Burel 2008; Rayfield et al. 2011). Based on revision of studies discussing shortcomings and advantages of connectivity measures (e.g. Goodwin and Fahrig 2002; Moilanen and Nieminen 2002; Pascual-Hortal and Saura 2006; Moilanen 2011), we considered three types of measures to estimate patch importance: (1) isolation, (2) incidence-functional, and (3) graph theory measures (Table 3). Our choice of measures included best-performing and most-often-applied ones, and was also informed by the possibility of incorporating information on matrix resistance into measure’s calculation allowing for assessment of both structural and potential connectivity (measure’s ‘flexibility’), as well as by our primary focus on habitat network design (designation of key patches and connections).
Patch isolation measures the inaccessibility of a habitat patch for migrants from other patches. The inaccessibility is a function of the configuration of habitat patches, patch characteristics (e.g., shape or size), and matrix characteristics between habitat patches (Bender et al. 2003). Patch isolation is thus inverse to connectivity. We calculated two commonly used isolation measures: nearest-neighbor distance, and area-weighted nearest-neighbor distance (Table 3).
Incidence-functional measures take into account distances to all possible source populations (i.e., patches), and are based on negative exponential dispersal kernels. Especially in highly fragmented landscapes, incidence functional measures are a good predictor of colonization events (Moilanen and Nieminen 2002). We used the area-weighted version of the incidence functional measure (Moilanen and Nieminen 2002), assuming equal scaling parameters of emigration and immigration (i.e., b = c = 0.3; Table 3).
Graph theory provides a powerful way to represent complex landscape patterns and perform advanced connectivity analyses. In graph theory, habitat patches are considered as nodes, and connections among them as edges, allowing investigations of a habitat network using graph techniques (Urban and Keitt 2001; Pascual-Hortal and Saura 2006). Connectivity measures based on graph theory can assess both structural and functional connectivity. We calculated the integral index of connectivity, and the probability of connectivity index, because these perform best among graph connectivity measures and provide jointly a more complete view on the role of landscape elements for maintaining overall landscape connectivity (Saura and Pascual-Hortal 2007a; Baranyi et al. 2011; Table 3). When calculating graph measures, we defined the habitat patch attribute (weight) either as (1) habitat patch area (assuming that larger patches have more immigrants), or as (2) equal for all habitat patches (all patches have the same number of immigrants).
To test the influence of dispersal distance on our connectivity measures, we considered six maximum dispersal distances beyond which a pair of habitat patches was considered as unconnected (5, 10, 20, 30, 40, and 50 km). For the probability of connectivity index, we used a dispersal probability of 0.05 to match the maximum dispersal probability that we used in the analyses of the binary graph measure. To calculate the incidence-functional measure, we defined the mean dispersal distance (1/α) as distance corresponding to the probability of 0.5.
Importance of patches in the habitat network
To assess the importance of individual patches for maintaining overall connectivity, we ranked habitat patches. We assumed that the least-isolated patch is of highest importance for overall connectivity. We used Conefor Sensinode 2.6 (Saura and Pascual-Hortal 2007b; Pascual-Hortal and Saura 2007; Saura and Torne 2009, 2012) to evaluate the importance of habitat patches based on graph measures. To assess habitat patch (node) importance, Conefor Sensinode performs nodes removal operations (Urban and Keitt 2001). Node importance D was computed as the percentage change in a connectivity measure when removing a given node from the graph (Saura and Torne 2009):
where X corresponds to the overall connectivity value calculated for the landscape (considering all habitat patches) and X’ corresponds to the value of the same measure calculated after removing patch i.
Lastly, we compared the distributions of the differences in patch importance among the three matrix representations for different connectivity measures, dispersal distances, and habitat patch attributes using box plots. We also compared the position of individual habitat patches in the rankings, with special emphasis on the top-ranked patches.
Sensitivity of differences in patch importance to spatial patterns of habitat
Because the habitat maps differed in terms of their spatial patterns (see Table 1), we examined the influence of number of habitat patches, amount of habitat (%), and mean distance between neighboring habitat patches on the patch importance calculated based on different matrix representations. We plotted these relationships for each connectivity measure (nearest-neighbor distance, incidence-functional measure, integral index of connectivity, and probability of connectivity), dispersal distance (from 5 to 50 km) and for different weights assigned to habitat patches (patches weighted by the area and patches equally weighted). For selected examples, we confirmed the observed response patterns via a linear and nonlinear regression analysis (exponential and power regression models).
Results
Connections among habitat patches
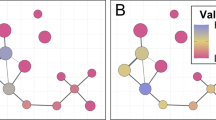
The number of connections varied strongly among the analyzed landscapes (from 1 to 861), primarily due to varying numbers of habitat patches. For a given set of patches, the spatial location of connections differed greatly among matrix representations, particularly between binary representation, which had the shortest paths connecting habitat patches, and continuous representation, where the least-cost paths were generally the longest (Fig. 2). Connections delineated based on categorical and continuous representations tended to overlap, since many connections between distant habitat patches passed through other patches that acted as stepping stones (Fig. 2).
Connections delineated based on binary matrix representation (dashed grey lines), categorical matrix representation (dashed black lines), and continuous matrix representation (black lines) for exemplary landscapes with different number of habitat patches and amount of habitat: (A) test area 3, habitat suitability index above 70; (B) test area 1, habitat suitability index above 60, (C) test area 2, habitat suitability index above 50; (D) test area 4, habitat suitability index above 50
We found the biggest differences between binary and continuous matrix representations in terms of the absolute lengths and the effective distances of connections, (mean difference around 4 km, maximum up to 40 km). Differences in the lengths of connections between binary and categorical on one hand, and categorical and continuous representations on the other, were much smaller (mean difference around 2 km; Fig. 3). Differences in connection lengths were substantially larger for more distant patches, especially between binary and continuous representations, but the correlations between inter-patch distances and differences in connection lengths were not very strong (R2 = 0.44 for binary and continuous representations, and only R2 = 0.17 for categorical and continuous representations; p < 0.01), except for differences between binary and categorical representations (R2 = 0.62; p < 0.01). We observed similar trends for effective distances, but differences between different matrix representations were smaller (Fig. 3), and correlations between inter-patch distances and differences in effective distances weaker (R2 = 0.35 for binary and categorical representations, R2 = 0.40 for binary and continuous representations, and R2 = 0.38 for categorical and continuous representations; p < 0.01). In general, connections delineated based on categorical and continuous representations were much longer than those based on binary representations, whereas the opposite was true for effective distances.
Importance of patches in the habitat network
Confirming our expectations, the influence of matrix representation on habitat patch rankings based on nearest-neighbor measures was small, since differences in the values of these measures were on average small among matrix representations (mean differences did not exceed 250 m for nearest-neighbor distance). The matrix representation had a bigger influence on the determination of the most isolated patches, than the most connected ones.
Contrary to our expectations, matrix representation had only a limited influence on patch importance based on incidence-functional (Fig. 4) and graph measures (Figs. 5, 6). For graph measures, the difference in patch importance for all landscapes did not, on average, exceed 1.1 % (binary vs. categorical, and binary vs. continuous matrix representations), and 0.4 % (categorical vs. continuous representations; Figs. 5, 6). We observed the biggest differences in patch importance for the incidence-functional measure between binary and continuous representations, regardless of the dispersal distance. For graph theory measures, comparisons between binary and categorical, and binary and continuous representations showed similar results. For both-incidence functional and graph measures, we noted the smallest differences in patch importance when we compared categorical and continuous matrix representations. While mean differences in patch importance were low, we observed outliers, especially for lower dispersal distances, and the integral index of connectivity. Maximum differences in patch importance for probability of connectivity did not exceed 5 %, but reached 24 % for the integral index of connectivity for some habitat patches.
(A) Distribution of differences in patch importance (without outliers) between different matrix representations for incidence functional measure, dots represent mean values; (B) relationship between mean difference in patch importance for incidence functional measure and maximum dispersal distance; MR1 - binary matrix representation, MR2 - categorical matrix representation, MR3 - continuous matrix representation
Distribution of differences in patch importance (without outliers) between different matrix representations for integral index of connectivity (IIC) for (A) patches weighted by the area, and (B) patches equally weighted (dots represent mean values); and relationship between mean difference in patch importance and maximum dispersal distance, for (C) patches weighted by the area, and (D) patches equally weighted; MR1 - binary matrix representation, MR2 - categorical matrix representation, MR3 - continuous matrix representation
Distribution of differences in patch importance (without outliers) between different matrix representations for probability of connectivity index (PC) for (A) patches weighted by the area, and (B) patches equally weighted (dots represent mean values); and relationship between mean difference in patch importance and maximum dispersal distance, for (C) patches weighted by the area, and (D) patches equally weighted; MR1 - binary matrix representation, MR2 - categorical matrix representation, MR3 - continuous matrix representation
While matrix representation had in general little effect on patch importance, patch importance was quite substantially affected by the connectivity measure that was used, the definition of habitat patch attribute, and the maximum dispersal distance. We observed bigger differences for the integral index of connectivity and equally weighted patches (for all matrix representations; Figs. 5, 6). Differences in patch importance between matrix representations based on the incidence-functional measure increased significantly with increasing dispersal distance (Fig. 4). For the integral index of connectivity and probability of connectivity, mean differences in patch importance decreased considerably with dispersal distance, but only when comparing binary and categorical, and binary and continuous matrix representations (Figs. 5, 6). For the incidence-functional measure, the integral index of connectivity, and the probability of connectivity, the mean differences between binary and continuous representations were generally larger than between binary and categorical representations.
Similar to the nearest-neighbor measures, matrix representation also had a small effect on the relative patch importance rankings for incidence-functional and graph measures. The only exceptions occurred in the case of the integral index of connectivity, when patch attribute was equal for all habitat patches, and dispersal distances were small. Differences between the importance of top-ranked habitat patches and other patches were much bigger when patch area was used as a patch attribute, especially for landscapes with several dominant big patches. When habitat patches were equally weighted, more habitat patches were similarly important for overall connectivity. Although the same patches were often highlighted as important for overall landscape connectivity regardless of patch weights, among the less-important habitat patches substantial differences in prioritization occurred.
Sensitivity of differences in patch importance to spatial patterns of habitat
Because differences in patch importance between categorical and continuous matrix representations were in most cases small, we analyzed in detail only the response patterns derived for differences in patch importance between binary and categorical, and binary and continuous representations. We noted that differences in patch importance changed considerably with increasing number of habitat patches, amount of habitat, and mean distance between neighboring habitat patches-regardless of the matrix representations used (Fig. 7). In other words, we observed the same trends for differences between binary and categorical, and binary and continuous matrix representations.
Relationships between mean difference in patch importance for binary and categorical matrix representations (black crosses), and binary and continuous matrix representations (black dots) computed for (A) nearest-neighbor distance; (B) and (C) incidence functional measure (IFM), integral index of connectivity (IIC), and probability of connectivity (PC) for patches equally weighted, and for different dispersal distances: (B) 10 km, and (C) 50 km
As number of habitat patches and habitat area within a landscape increased, differences in patch importance calculated based on nearest-neighbor measures showed an exponentially decreasing trend, and as the mean distance between neighboring habitat patches increased, an exponentially increasing trend. We observed reverse trends for differences in patch importance calculated based on the incidence-functional measure. These trends were not dependent on dispersal distance, but the strength of the relationship varied with changing dispersal distance (Fig. 7).
Response patterns observed for graph measures differed among dispersal distances. In general, they showed similar trends for longer dispersal distances (>10–20 km) as the nearest-neighbor measures, and the strength of the relationship increased with dispersal distance. For smaller dispersal distances (<10–20 km) the observed response patterns were either erratic or, in some cases, reversed. For all dispersal distances, we observed stronger dependences for probability of connectivity, and when patches were equally weighted (Fig. 7).
Discussion
Connectivity is a fundamental property of a landscape, crucial for the long-term survival of species, making the appropriate assessment of connectivity crucial for conservation decisions. Here we assessed the extent to which incomplete information about the resistance of the matrix for movement may mislead conservation efforts. Our results showed that different matrix representations can greatly affect assessments of connections, including their lengths, effective distances, and spatial locations, especially for more distant patches (Table 4). Connections delineated based on continuous representation of matrix resistance were much longer than those delineated based on binary representation, but their effective distances were shorter. Our findings thus coincide with the results obtained by Szabó et al. (2012).
Contrary to our expectations, we did not find major differences in patch prioritizations when using different matrix representations (Table 4), and this is a promising result for conservation practitioners working in landscapes similar to ones that we analyzed. We noted the biggest differences in patch importance between binary and continuous, and binary and categorical matrix representations regardless of the considered connectivity measure. However, while the influence of matrix representation on patch importance was generally small, it varied according to the connectivity measure, definition of patch attribute and dispersal distance (Table 4). In general matrix representation mattered more for smaller dispersal distances, which is intuitive, as species with relatively limited dispersal abilities are more sensitive to the changes in matrix resistance (Saura et al. 2011).
The bigger variations in patch importance that we found when calculating importance using the integral index of connectivity compared to probability of connectivity are a consequence of different connection models considered by each of these metrics (binary and probabilistic, respectively). A small change in the lengths of connections between habitat patches caused by the use of different matrix representation can sharply modify the connections among habitat patches, removing or adding those that are shorter or longer than the defined dispersal distance threshold. The corresponding change would cause only a comparatively small variation in the dispersal probabilities for the probability of connectivity index (see Bodin and Saura 2010).
When we used habitat patch area-weighting, the importance of patches was closely related to their size, but when the patches were equally-weighted, the influence of matrix representation and dispersal distance on patch prioritizations increased. This is generally consistent with results obtained by Ferrari et al. (2007), Laita et al. (2011), and Szabó et al. (2012). Connectivity analyses only based on distance estimators (either Euclidean or functional) tend to overestimate the role of small patches (Laita et al. 2011), but these patches can be critical network elements, acting as stepping stones between larger, but more distant, patches (Rubio and Saura 2012). On the other hand, when patch size is included in a connectivity measure as a patch weight, the overall value of the measure may be more sensitive to the intra-patch connectivity than to the matrix resistance itself (Estreguil et al. 2014). Possible solutions to this issue allowing to account for intra- and inter-patch connectivity separately were proposed by Saura and Rubio (2010) and Estreguil et al. (2014). Our research is complementary to these studies in that it addresses the impact of the matrix representation on the connectivity assessment in general, and key patches and connections in particular, while referring to the problem of the sensitivity of graph measures through investigation of different weights assigned to habitat patches.
Patch size is commonly used in connectivity analyses as a proxy for the number of individuals occupying patches, especially if detailed population data is not available. However, often the patch quality or effective area, i.e., weighted by habitat quality, may be a better proxy for population size and dispersal potential than unadjusted patch area (Visconti and Elkin 2009; Schooley and Branch 2011). The best compromise for most studies is probably to measure patch quality as a key resources that are likely to play a role in determining species survival, fecundity, and density (Mortelliti et al. 2010). The simplest way to include patch quality in connectivity measures would be to assess habitat suitability values for each patch, and then to weight patches using mean habitat suitability values, or the effective area calculated based on such statistics. Additional investigations of this issue are needed, especially given that our results showed that the parameterization of connectivity measures is critical for the assessment of patch importance.
In terms of different landscapes types, we found that matrix representation had a greater effect for landscapes with a low number of small and dispersed habitat patches, than for landscapes with high number of large, less-dispersed habitat patches (Fig. 8). This is an intuitive result, since the matrix should matter more in more fragmented landscapes where movement distances are longer and the probability of crossing inhospitable areas is higher. Surprisingly, for incidence-functional measure we observed the opposite, i.e., mean differences in patch importance were higher for landscapes with a high number of bigger habitat patches located close to each other. Furthermore, this response pattern was robust to changing dispersal distance, inferred from the graph measures which showed different trends for small and large dispersal distances (Fig. 8). We presume that the unusual behavior of the incidence functional measure may result from the definition of parameter α scaling the effect of distance to migration. Inaccurate estimates of α could easily lead to the false conclusion that increasing connectivity decreases the likelihood of occupancy (Prugh 2009). Although we investigated different dispersal distances, additional tests involving bigger range of α values, as well as landscape characteristics, might better explain the effect of this measure. These additional tests, by using neutral landscape models (i.e., fractal landscapes and fractional Brownian motion; Keitt 2000; Chipperfield et al. 2011) would also substantiate our findings regarding the influence of landscape structure on connectivity assessments under different matrix representations.
The change of response pattern of graph measures with the change of dispersal distance confirmed that the scale of analysis is, besides the definition of matrix resistance values and the selection of connectivity measure, critical in connectivity assessments (Kool et al. 2012). Furthermore, species can respond at different scales to different landscapes features indicating the possible need to examine a continuum of scales when estimating the resistance to movement (Zeller et al. 2014).
We did not consider alternative cost assignments for the different land cover classes in categorical representation, but least-cost route delineation is certainly sensitive to cost values assignment to land cover types (Rayfield et al. 2010). We decided to test only one categorical representation where weight of each land cover class was defined as the mean cost derived from continuous representation, in order to make those two representations more comparable. Indeed, even though we found a strong correlation between categorical and continuous representations, connections delineated based on them differed substantially. This confirmed that the least-cost analyses are quite sensitive to the parameterization of the cost surface. In addition, individuals rarely use a single optimum route, and connectivity analyses focusing on least-cost paths fail to incorporate variation in individual behavior (Bélisle 2005). Uncertainty analysis of least-cost modeling (Beier et al. 2009), and alternative methods for delineation of connections between habitat patches based on cost surface, such as conditional minimum transit cost, multiple shortest paths (Pinto and Keitt 2009), or circuit theory (McRae et al. 2008; Carroll et al. 2011), may ultimately be better suited to assess connectivity, but we suspect that these methods will be similarly sensitive to matrix representation.
To obtain a continuous resistance surface we applied a linear transformation of the habitat suitability map. This is a commonly used approach, partly because of the lack of adequate data on species movements and hence the actual resistance of different habitat types to movement (Richard and Armstrong 2010; Zeller et al. 2012). However, the relationship between habitat suitability and dispersal possibilities of species may not be so simple and can lead to underestimation of the population’s connectivity (Trainor et al. 2013), especially for far-ranging species. Since different transformation functions may yield different resistance surfaces, and thus affect connectivity estimates, identifying the biologically most relevant function is an important step in connectivity assessments (Trainor et al. 2013).
Although we compared both lengths and effective distances for connections based on different matrix representations, we used only the length of connections to calculate connectivity measures and habitat patches importance. Length of connection could easily be compared with dispersal abilities of species to evaluate potential corridors, but does not provide information on the quality of connection, as in the case of effective distance (Etherington and Holland 2013). Further research is required to incorporate effective distances in calculation of connectivity measures, in particular to find a way to determine the relationship between effective distances and species’ dispersal abilities. We assume that the influence of matrix representation on patch importance could be more pronounced if effective distances were used in calculations.
Conclusions
In order to be useful for conservationists and land use planners, connectivity assessments need to identify the key corridors and habitat patches that maintain overall connectivity of a landscape for a given species. An important question thus is how robust connectivity assessments are when data on matrix resistance to movement is imperfect, either because dispersal behavior of a given species is unknown, the relevant matrix information is unavailable, or the study covers large area and/or wide range of species with diverse dispersal abilities (e.g., in impact modeling of policy scenarios, land cover or/and climate change scenarios; Rubio et al. 2012; Mubareka et al. 2013). In such cases it is generally not possible to represent the resistance of the matrix to movement as a continuous surface, and binary or categorical representations may be all that is feasible. In general, connectivity assessments that are based on matrix representations incorporating resistance to movement, are better predictors of animal movements and colonization probabilities than the simple Euclidean approaches (Bender et al. 2003; Gebauer et al. 2013). This is intuitive, and we recommend using continuous matrix representation whenever possible. All stages of dispersal including emigration, transience and immigration are influenced by environmental heterogeneity, which is typically continuous (e.g. food availability, temperature, soil pH; Pflüger and Balkenhol 2014). This is why a continuous representation of matrix resistance to movement will likely reflect more accurately how an organism experiences the landscape (Stoddard 2010). However, an accurate continuous representation is often not feasible because of limited input data or knowledge about species’ habitat use and dispersal behavior. Our results showed that as long as the main goal of a connectivity assessment is to identify the most important habitat patches for overall connectivity, then the matrix representation may not be all that crucial. Indeed, in our study landscapes, the influence of matrix representation on the relative rankings of patch importance was negligible, especially when large habitat patches were present and connectivity measures were weighted according to patch size. Generally, we found that the selection and parameterization of connectivity measures (i.e., definition of patch attribute and dispersal distance) had a much stronger effect on the calculation of patch importance than matrix representation. On the contrary, the delineation of connections in the landscape was greatly affected by the type of matrix representation. Therefore we urge to proceed with great caution if information about a species dispersal behavior or the matrix resistance to movement is either lacking at all or only available for broad categories.
References
Baranyi G, Saura S, Podani J, Jordán F (2011) Contribution of habitat patches to network connectivity: redundancy and uniqueness of topological indices. Ecol Indic 11:1301–1310
Beier P, Majka DR, Spencer WD (2008) Forks in the road: choices in procedures for designing wildland linkages. Conserv Biol 22:836–851
Beier P, Majka DR, Newell SL (2009) Uncertainty analysis of least-cost modeling for designing wildlife linkages. Ecol Appl 19:2067–2077
Bélisle M (2005) Measuring landscape connectivity: the challenge of behavioral landscape ecology. Ecology 86:1988–1995
Bender DJ, Tischendorf L, Fahrig L (2003) Using patch isolation metrics to predict animal movement in binary landscapes. Landscape Ecol 18:17–40
Bodin O, Saura S (2010) Ranking individual habitat patches as connectivity providers: Integrating network analysis and patch removal experiments. Ecol Model 221:2393–2405
Calabrese JM, Fagan WF (2004) A comparison-shopper’s guide to connectivity metrics. Front Ecol Environ 2:529–536
Carroll C, McRae BH, Brookes A (2011) Use of linkage mapping and centrality analysis across habitat gradients to conserve connectivity of gray wolf populations in western North America. Conserv Biol 26:78–87
Chardon JP, Adriaensen F, Matthysen E (2003) Incorporating landscape elements into a connectivity measure: a case study for the Speckled wood butterfly (Pararge aegeria L.). Landscape Ecol 18:561–573
Chipperfield JD, Dytham C, Hovestadt T (2011) An updated algorithm for the generation of neutral landscapes by spectral synthesis. PLoS One 6:e17040. doi:10.1371/journal.pone.0017040
De Rigo D (2013) Software uncertainty in integrated environmental modelling: the role of semantics and open science. Geophys Res Abstr 15:13292
ESRI [Environmental Systems Resource Institute] (2011) ArcMap 10.0. ESRI, Redlands, California
Estreguil C, De Rigo D, Caudullo G (2014) A proposal for an integrated modelling framework to characterise habitat pattern. Environ Model Softw 52:176–191
Etherington TR, Holland EP (2013) Least-cost path length versus accumulated-cost as connectivity measures. Landscape Ecol 28:1223–1229
Fahrig L, Merriam G (1985) Habitat patch connectivity and population survival. Ecology 66:1762–1768
Ferrari JR, Lookingbill TR, Neel MC (2007) Two measures of landscape-graph connectivity: assessment across gradients in area and configuration. Landscape Ecol 22:1315–1323
Fischer J, Lindenmayer DB (2007) Landscape modification and habitat fragmentation: a synthesis. Glob Ecol Biogeogr 16:265–280
Forman RTT (1995) Land mosaics: the ecology of landscapes and regions. University Press Cambridge, Cambridge
Gebauer K, Dickinson KJM, Whigham PA, Seddon PJ (2013) Matrix matters: differences of grand skink metapopulation parameters in native tussock grasslands and exotic pasture grasslands. PLoS One 8:e76076. doi:10.1371/journal.pone.0076076
Goodwin BJ, Fahrig L (2002) How does landscape structure influence landscape connectivity? Oikos 99:552–570
Henein K, Merriam G (1990) The elements of connectivity where corridor quality is variable. Landscape Ecol 4:157–170
Keitt TH (2000) Spectral representation of neutral landscapes. Landscape Ecol 15:479–493
Kindlmann P, Burel F (2008) Connectivity measures: a review. Landscape Ecol 23:879–890
Kool JT, Moilanen A, Treml EA (2012) Population connectivity: recent advances and new perspectives. Landscape Ecol 28:165–185
Kozak J, Estreguil C, Ostapowicz K (2008) European forest cover mapping with high resolution satellite data: the Carpathians case study. Int J Appl Earth Obs Geoinform 10:44–55
Kozak J, Ostapowicz K, Bytnerowicz A, Wyżga B (2013) The Carpathians: integrating nature and society towards sustainability, environmental science and engineering. Springer-Verlag, Berlin Heidelberg
Kuemmerle T, Chaskovskyy O, Knorn J, Radeloff VC, Kruhlov I, Keeton WS, Hostert P (2009) Forest cover change and illegal logging in the Ukrainian Carpathians in the transition period from 1988 to 2007. Remote Sens Environ 113:1194–1207
Kuemmerle T, Perzanowski K, Chaskovskyy O, Ostapowicz K, Halada L, Bashta A-T, Kruhlov I, Hostert P, Waller D, Radeloff VC (2010) European Bison habitat in the Carpathian Mountains. Biol Conserv 143:908–916
Kuemmerle T, Perzanowski K, Akçakaya HR, Beaudry F, Van Deelen TR, Parnikoza I, Khoyetskyy P, Waller DM, Radeloff VC (2011) Cost-effectiveness of strategies to establish a European bison metapopulation in the Carpathians. J Appl Ecol 48:317–329
Laita A, Kotiaho JS, Mönkkönen M (2011) Graph-theoretic connectivity measures: what do they tell us about connectivity? Landscape Ecol 26:951–967
Lechner AM, Reinke KJ, Wang Y, Bastin L (2013) Interactions between landcover pattern and geospatial processing methods: effects on landscape metrics and classification accuracy. Ecol Complex 15:71–82
Lehman MM, Ramil JF (2002) Software uncertainty. In: Bustard D, Liu W, Sterritt R (eds) Soft-Ware 2002. Computing in an imperfect World, vol 2311. Springer, Berlin Heidelberg, pp 477–514
Luque S, Saura S, Fortin M-J (2012) Landscape connectivity analysis for conservation: insights from combining new methods with ecological and genetic data. Landscape Ecol 27:153–157
Magrach A, Larrinaga AR, Santamaría L (2012) Effects of matrix characteristics and interpatch distance on functional connectivity in fragmented temperate rainforests. Conserv Biol 26:238–247
McRae BH, Dickson BG, Keitt TH, Shah VB (2008) Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology 89:2712–2724
Moilanen A (2011) On the limitations of graph-theoretic connectivity in spatial ecology and conservation. J Appl Ecol 48:1543–1547
Moilanen A, Nieminen M (2002) Simple connectivity measures in spatial ecology. Ecology 83:1131–1145
Mortelliti A, Amori G, Boitani L (2010) The role of habitat quality in fragmented landscapes: a conceptual overview and prospectus for future research. Oecologia 163:535–547
Mubareka S, Estreguil C, Baranzelli C, Gomes CR, Lavalle C, Hofer B (2013) A land-use-based modelling chain to assess the impacts of natural water retention measures on Europe’s green infrastructure. Int J Geogr Inform Sci 27:1740–1763
Opermanis O, MacSharry B, Aunins A, Sipkova Z (2012) Connectedness and connectivity of the Natura 2000 network of protected areas across country borders in the European Union. Biol Conserv 153:227–238
Pascual-Hortal L, Saura S (2006) Comparison and development of new graph-based landscape connectivity indices: towards the priorization of habitat patches and corridors for conservation. Landscape Ecol 21:959–967
Pascual-Hortal L, Saura S (2007) Integrating landscape connectivity in broad-scale forest planning through a new graph-based habitat availability methodology: application to capercaillie (Tetrao urogallus) in Catalonia (NE Spain). Eur J For Res 127:23–31
Pflüger FJ, Balkenhol N (2014) A plea for simultaneously considering matrix quality and local environmental conditions when analyzing landscape impacts on effective dispersal. Mol Ecol 23:2146–2156
Pinto N, Keitt TH (2009) Beyond the least-cost path: evaluating corridor redundancy using a graph-theoretic approach. Landscape Ecol 24:253–266
Prugh LR (2009) An evaluation of patch connectivity measures. Ecol Appl 19:1300–1310
Python Software Foundation (2013) Python Language Reference, version 2.7. Python Software Foundation. Available from http://www.python.org. Accessed March 2014
R Core Team (2013) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available from www.R-project.org. Accessed March 2014
Rabinowitz A, Zeller KA (2010) A range-wide model of landscape connectivity and conservation for the jaguar, Panthera onca. Biol Conserv 143:939–945
Rayfield B, Fortin M-J, Fall A (2010) The sensitivity of least-cost habitat graphs to relative cost surface values. Landscape Ecol 25:519–532
Rayfield B, Fortin M-J, Fall A (2011) Connectivity for conservation: a framework to classify network measures. Ecology 92:847–858
Richard Y, Armstrong DP (2010) Cost distance modelling of landscape connectivity and gap-crossing ability using radio-tracking data. J Appl Ecol 47:603–610
Rubio L, Saura S (2012) Assessing the importance of individual habitat patches as irreplaceable connecting elements: an analysis of simulated and real landscape data. Ecol Complex 11:28–37
Rubio L, Rodríguez-Freire M, Mateo-Sánchez M, Estreguil C, Saura S (2012) Sustaining forest landscape connectivity under different land cover change scenarios. For Syst 21:223–235
Saura S, Pascual-Hortal L (2007a) A new habitat availability index to integrate connectivity in landscape conservation planning: comparison with existing indices and application to a case study. Landscape Urban Plan 83:91–103
Saura S, Pascual-Hortal L (2007b) Conefor Sensinode 2.2 User’s Manual: Software for quantifying the importance of habitat patches for maintaining landscape connectivity through graphs and habitat availability indices. Available from www.conefor.org. Accessed March 2014
Saura S, Rubio L (2010) A common currency for the different ways in which patches and links can contribute to habitat availability and connectivity in the landscape. Ecography 33:523–537
Saura S, Torne J (2009) Conefor Sensinode 2.2: a software package for quantifying the importance of habitat patches for landscape connectivity. Environ Model Softw 24:135–139
Saura S, Torne J (2012) Conefor 2.6 user manual. Available from www.conefor.org. Accessed March 2014
Saura S, Estreguil C, Mouton C, Rodríguez-Freire M (2011) Network analysis to assess landscape connectivity trends: application to European forests (1990–2000). Ecol Indic 11:407–416
Sawyer SC, Epps CW, Brashares JS (2011) Placing linkages among fragmented habitats: do least-cost models reflect how animals use landscapes? J Appl Ecol 48:668–678
Schooley RL, Branch LC (2011) Habitat quality of source patches and connectivity in fragmented landscapes. Biodivers Conserv 20:1611–1623
Stoddard ST (2010) Continuous versus binary representations of landscape heterogeneity in spatially-explicit models of mobile populations. Ecol Model 221:2409–2414
Szabó S, Novák T, Elek Z (2012) Distance models in ecological network management: a case study of patch connectivity in a grassland network. J Nat Conserv 20:293–300
Taylor PD, Fahrig L, Merriam G (1993) Connectivity is a vital element of landscape structure. Oikos 68:571–573
Tischendorf L, Fahrig L (2000) How should we measure landscape connectivity? Landscape Ecol 15:633–641
Trainor AM, Walters JR, Morris WF, Sexton J, Moody A (2013) Empirical estimation of dispersal resistance surfaces: a case study with red-cockaded woodpeckers. Landscape Ecol 28:755–767
Uezu A, Metzger JP, Vielliard JME (2005) Effects of structural and functional connectivity and patch size on the abundance of seven Atlantic forest bird species. Biol Conserv 123:507–519
UNEP [United Nations Environment Programme] (2007) Carpathians environment outlook. United Nations Environment Programme, Geneva
Urban D, Keitt T (2001) Landscape connectivity: a graph-theoretic perspective. Ecology 82:1205–1218
Visconti P, Elkin C (2009) Using connectivity metrics in conservation planning: when does habitat quality matter? Divers Distrib 15:602–612
Zeller KA, McGarigal K, Whiteley AR (2012) Estimating landscape resistance to movement: a review. Landscape Ecol 27:777–797
Zeller KA, McGarigal K, Beier P, Cushman SA, Vickers TW, Boyce WM (2014) Sensitivity of landscape resistance estimates based on point selection functions to scale and behavioral state: pumas as a case study. Landscape Ecol 29:541–557
Ziółkowska E, Ostapowicz K, Kuemmerle T, Perzanowski K, Radeloff VC, Kozak J (2012) Potential habitat connectivity of European bison (Bison bonasus) in the Carpathians. Biol Conserv 146:188–196
Acknowledgments
We thank J. Kozak for extremely helpful conversations, suggestions and assistance. We also thank coordinating editor B. Goodwin and two anonymous reviewers for their helpful comments on the manuscript. We gratefully acknowledge support by the National Science Centre [program SONATA, project no 2011/03/D/ST10/05568 (EZ, KO)], the Doctus (doctoral scholarship) program (EZ), the European Commission [Integrated Project VOLANTE FP7-ENV-2010-265104 (TK)], the Einstein Foundation Berlin, Germany (TK), and the NASA Land Cover and Land Use Program (VCR).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Ziółkowska, E., Ostapowicz, K., Radeloff, V.C. et al. Effects of different matrix representations and connectivity measures on habitat network assessments. Landscape Ecol 29, 1551–1570 (2014). https://doi.org/10.1007/s10980-014-0075-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-014-0075-2