Abstract
We studied the effects of landscape structure, habitat loss and fragmentation on genetic differentiation of Moor frog populations in two landscapes in The Netherlands (Drenthe and Noord-Brabant). Microsatellite data of eight loci showed small to moderate genetic differentiation among populations in both landscapes (F ST values 0.022 and 0.060, respectively). Both heterozygosity and population differentiation indicate a lower level of gene flow among populations in Noord-Brabant, where populations were further apart and have experienced a higher degree of fragmentation for a longer period of time as compared to populations in Drenthe. A significant isolation-by-distance pattern was found in Drenthe, indicating a limitation in dispersal among populations due to geographic distance. In Noord-Brabant a similar positive correlation was obtained only after the exclusion of a single long-time isolated population. After randomised exclusion of populations a significant additional negative effect of roads was found but not of other landscape elements. These results are discussed in view of improving methodology of assessing the effects of landscape elements on connectivity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Habitat fragmentation is a threat to the survival of wildlife populations, as isolated populations are more susceptible to demographic and genetic stochasticity. This can be compensated by dispersal of individuals among populations, as long as there is sufficient connectivity between habitat patches. Such a habitat network may effectively form a meta-population. Therefore, quantifying dispersal and the degree to which different parts of the landscape matrix between suitable habitat patches facilitate or impede movements (Ricketts 2001), has a high research priority in conservation biology (Wiens 1997; Rickets 2001). Dispersal may be measured by direct field methods, but this is costly and time-consuming and suffers from a number of limitations (Crochet 1996; Vos et al. 2002). In particular long-distance dispersal, which is an important factor determining extinction rate and recolonisation success, is difficult to measure directly. Dispersal can also be estimated from population genetic analyses (Neigel 1997), although these estimates may reflect the historical rather than the present day situation. Nevertheless, assessment of population genetic structure and especially combined population genetics with landscape ecology in a landscape genetic approach (Manel et al. 2003; Holderegger and Wagner 2006), can improve our understanding of the effects of habitat fragmentation.
In The Netherlands, habitat fragmentation for small ground-dwelling animal species with limited dispersal capacity is relatively recent. An example of such a species is the Moor frog (Rana arvalis Nilsson). The aquatic habitat of the Moor frog consists of moorland ponds and swamps. Its terrestrial habitat consists mainly of moorlands but also includes hedgerows and mixed woods with a well-developed herb layer. Moor frogs occur mainly in moorlands in the southern and eastern parts of The Netherlands. Habitat loss, fragmentation and intensification of land use in these areas started in the first half of the previous century. As Moor frogs become adult in their third year of life, a relatively low number of 30 to 40 (overlapping) generations has passed since habitats became fragmented. Due to the time lag involved in genetic differentiation through drift, a new equilibrium between migration and genetic drift may not have been reached yet. Consequently, overall population differentiation might still be low even if habitat fragmentation at present is severe (Bossart and Prowell 1998).
Nevertheless using a permeability model, Vos et al. (2001) showed that genetic effects of fragmentation on small spatial scales and in a short time span (65 years) could already be detected in Rana arvalis. Although overall population differentiation was low, barriers (roads and railways) between populations emerged as a distinct factor that reduced gene flow among populations. In the present study, we set out to test whether this approach is broadly useful and whether a significant correlation between genetic differentiation of populations and landscape elements depends on specific properties (scale and topology) of the studied landscape. We used two study landscapes (Drenthe and Noord-Brabant) that differ in landscape scale and degree of landscape fragmentation.
Material and methods
General description of study areas
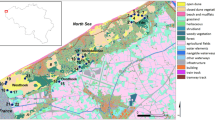
The study was conducted in Drenthe and Noord-Brabant, two provinces in The Netherlands (Fig. 1) that formerly contained large, continuous areas of Moor frog suitable habitat. Currently, Moor frog habitat has been strongly reduced in area and increased in fragmentation. Noord-Brabant and Drenthe differ in their extent of habitat fragmentation. The average distance among ponds in Noord-Brabant (8629 m) is almost twice the distance among ponds in Drenthe (4612 m). In addition, matrix permeability is lower in Noord-Brabant because of higher farming intensity, urbanisation, road density and traffic intensity (Van der Sluis and Vos 1997). Furthermore, reproductive sites in Noord-Brabant have become less favourable for Moor frogs due to water pollution as a result of intensive agriculture (Hoogerwerf and Crombaghs 1993).
The timing and speed of habitat fragmentation in both study areas was derived from historic maps (Historische atlas Drenthe/Noord-Brabant 1989). Until the mid-19th century, Noord-Brabant formed a vast plain, with heathlands, moors and forests, often grazed by sheep. By 1922, some 55% of the area was cultivated. By the 1950s, only 10% of the area remained natural. At present, land use is a mixture of livestock grazing and arable farming, and less than 10% of the surface area is still natural habitat. Hence, the transition of largely natural habitat to cultivated land in Noord-Brabant took place in the early 20th century, in a period of about 50 years. The study area in Drenthe was still unfragmented until 1932. The only infrastructure was a railway running through the area; otherwise, heathlands and moors were well connected. However, the map from 1950 showed that about 50% of the area had been converted into agricultural land. In 1957, the landscape had almost reached its present shape and land use was predominantly arable farming. Many of the remaining ponds are nowadays situated in small patches of natural areas of a few hectares, with the exception of ponds 310, 312 and 365, which are located in extensive moorland complexes (Fig. 1). This means that land transformation in Drenthe took place between 1930 and 1950, in a relative short period of 20 years and is more recent than in Noord-Brabant.
Geographical distance and matrix permeability
The spatial configuration of the Moor frog habitat, the habitat types in the matrix between suitable habitat patches and linear elements such as roads, railroads and ditches were recorded from a topographical map 1:25,000 using a Geographic Information System. Distances between all ponds were calculated from pond border to pond border. To correct for the relative permeability of the landscape mosaic, area and length of habitat types and linear landscape elements were calculated in a 200 m wide strip between ponds (Vos et al. 2001). Area types that are avoided by Moor frogs, such as dry and open areas (Hartung 1991), agricultural land and developed areas, or those that form potential barriers, such as roads and railroads, were considered negative landscape elements reducing permeability of the landscape. Four road types were distinguished: four lane motorways, secondary roads (>7 m wide), tertiary roads (4–7 m wide) and quaternary roads (paved roads <4 m wide). To aggregate the effects of all road types, road lengths were multiplied with a factor (mean traffic volume) to correct for traffic intensity as compared to quaternary roads (Vos and Chardon 1998; Van der Sluis and Vos 1997). Habitat types preferred by Moor frogs (Hartung 1991) were regarded as positive landscape elements improving matrix permeability (Forman 1995). These included deciduous forest, mixed forest, hedgerows and ditches. Three permeability variables were calculated (Table 1) as in Vos (1999) and Vos et al. (2001). Furthermore, positive and negative landscape elements were incorporated into one variable (D*R INT).
Sampling and DNA extraction
All ponds in the study area were surveyed for Moor frog presence and all occupied ponds were sampled in 1999 (Table 2). Preferably 20 to 30 samples per ponds were taken. Part of the area in Drenthe encompasses that studied by Vos et al. (2001). Seven populations were included in both studies, but for this study, populations were re-sampled four years later. In the other three ponds studied by Vos et al. (2001) no egg-clumps were found. These populations may have gone extinct during two unfavourable breeding seasons between 1995 and 1999. In the present study, four new populations (300, 330, 340 and 365) at larger distances were included, more samples per population and more genetic markers were used as compared with Vos et al. (2001). In Drenthe, two population samples were taken from adjacent ponds (pond 310 and 312; Fig. 1) only 346 m apart in continuous moorland. All other Drenthe populations were sampled from moorland ponds separated from other ponds by agricultural landscape. In Noord-Brabant, four small clusters of moorland ponds (2602 and 2603; 2302, 2303 and 2306; 1502 and 1503; 1201 and 1203; Fig. 1) were sampled in which ponds were 1–2 km apart with only moorland and/or forest in between them. All other sampled ponds in Noord-Brabant were separated at large distances by agricultural landscape.
Since females lay a single egg clump, the number of egg clumps in a pond was determined and taken as an estimate for reproductive population size (Schlüpmann 1988; Griffiths and Raper 1994). From each pond all egg clumps found were sampled. From each single egg clump, a small number of eggs were sampled and risen in the laboratory. Species-specific characteristics were checked at the tadpole stage. From each Moor frog egg clump one tadpole was used for DNA extraction. Remaining tadpoles were returned to their pond of origin. Due to small population sizes, mortality during raising and misidentification of egg clumps, the sample size of some populations dropped to less than 20 tadpoles (Table 2). DNA was extracted using standard proteinase K treatment (Knopp et al. 2007). In total, 440 individuals were sampled from eleven populations in Drenthe (n = 232) and twelve populations in Noord-Brabant (n = 208).
Microsatellite development
Four easily scorable microsatellite loci (RRD590, RECALQ, RCIDII and RC08604d) were available from Vos et al. (2001). In addition, microsatellite-enriched libraries were produced by a selective hybridisation procedure (Karagyozov et al. 1993) as described by Arens et al. (2000). A total of 292 positive clones (19%) were obtained, of which 100 clones were sequenced using a Taq DyeDeoxy Terminator Cycle Sequencing Kit and an ABI 377 sequencer (Applied Biosystems). About 30% of the sequences contained long compound microsatellites interspersed with stretches of non-repeat DNA, forming minisatellite arrays. For microsatellite repeat-containing sequences, primers were designed using Primer 0.5 (Whitehead Institute for Biomedical Research, Cambridge). Twenty primer pairs were tested on a set of twelve randomly chosen individuals from different populations using silver staining detection as described by Arens et al (2000). Four newly developed SSR loci (Table 3), deposited on the EMBL database, were used together with the four above mentioned loci to genotype all samples.
Statistical analysis
Unless stated otherwise, analyses were performed using TFPGA 1.3 (Miller 1997; http://herb.bio.nau.edu/∼miller/tfpga.htm), permutations were performed using at least 1000 randomisations. Evidence of linkage disequilibrium was assessed using Markov chain approximations (Guo and Thompson 1992). Similarly, deviations from Hardy–Weinberg equilibrium were tested for each locus and population separately with sequential Bonferroni correction (Rice 1989). Weir and Cockerham’s (1984) F-statistics were applied to the data. Significance of pairwise population differentiation was tested using the log-likelihood statistic G (Goudet et al. 1996). Genetic distance among populations was estimated by Nei’s (1978) genetic distance using POPGENE 1.31 (Yeh et al. 1999, http://www.ualberta.ca/∼fyeh/info.htm). The fraction of observed (H O) and expected (H E) heterozygotes, the effective number of alleles per locus (AE) and inbreeding coefficient (F IS) were calculated as measures of genetic diversity within populations (Cockerham 1973). Comparisons of genetic diversity between the two study areas were performed using Mann–Whitney tests. Tests for population structure and assignment of individuals to populations were performed using STRUCTURE 2.0 (Pritchard et al. 2000). The possible number of clusters (K) ranged from 1 to 12. Final runs were performed using the admixture model at burn-in length of 20,000 and MCMC of 300,000 (5 runs per K). Assignment results from STRUCTURE were compared with assignments from DOH (http://www2.biology.ualberta.ca/jbrzusto/Doh.php).
In addition to the geographical distance among ponds, distances corrected for the relative permeability of the landscape between ponds (Table 1) were tested, both separately and in a multiple Mantel test (Mantel 1967), which employs the randomisation distribution of the t-statistics obtained by means of multiple regression (Manly 1997). First, geographical distance was used in the model. Subsequently the model was extended with the relative permeability variables D*R L, D*R NA, D*C L and D*R INT (Table 1) to test whether permeability variables significantly contributed to the model in addition to geographical distance. Stability of the relationship was tested by jack-knifing over SSR loci whereas jack-knifing over populations was performed to test for departures from the correlations with geographic or relative distance measures due to specific populations. All Mantel tests were performed using GENSTAT 5 (Payne et al. 1993) with 10,000 randomisations per run. Population 2306 was not included in the IBD analyses because its small population size may increase the variance in genetic structure that is not explained by distance due its likely sensitivity to genetic drift compared with the other populations.
Results
Marker development
The newly developed microsatellite markers for R. arvalis exhibited a higher level of polymorphism (11–61 alleles per locus compared to 5–12) than the than the Rana sp. microsatellite markers from Vos et al. (2001), in agreement with the general finding that heterologous microsatellites tend to have lower numbers of alleles compared to their species of origin. The number of alleles per population was high given the estimated population sizes (Table 3). For instance in population 340, estimated at 25 breeding females, we found 18 different alleles at the most polymorphic marker (WRA1-160) in a sample of 20 individuals. No indications for linkage disequilibrium among loci were found. Deviations from Hardy–Weinberg proportions were detected in Drenthe and Noord-Brabant for a number of populations at loci WRA6-8 and RECALQ, showing a minor deficiency of heterozygotes. It is thus possible that these loci contained null-alleles although individuals without any amplification product did not occur in Noord-Brabant and were found only twice in Drenthe. Similar to Knopp et al. (2007), who analysed four progenies with these two markers, we found no evidence for null-alleles in an analysis of 20 offspring from one egg clump. This indicates that the frequency of null-alleles, if they occur, is low.
Genetic variation and population differentiation
All loci were highly polymorphic in Drenthe, with a mean number of effective alleles of 7.2. Observed heterozygosity varied across populations (0.48–0.70). There was a slight overall heterozygote deficit (H o = 0.60, H e = 0.68) indicating some local inbreeding (F IS = 0.096, 95% C.I. 0.029–0.183). The overall F ST value in Drenthe was 0.022 (95% C.I. 0.014–0.034) showing low but significant population differentiation. Pairwise F ST values between populations ranged from −0.011 to 0.061. The two ponds within the same moorland (populations 310 and 312) had a pairwise F ST value of −0.011, consistent with unrestricted gene flow.
Genetic variation in Noord-Brabant was lower, as observed heterozygosities (0.45–0.69) and effective number of alleles in Noord-Brabant (mean 5.9) were significantly lower than in Drenthe (Mann–Whitney tests; P < 0.01). Eight populations were fixed for the same allele at the RRD590a locus. There was again a small heterozygote deficit (H o = 0.51, H e = 0.59) and slight inbreeding (F IS = 0.086, 95% C.I. 0.027–0.180). The level of population differentiation in Noord-Brabant was higher with a F ST value of 0.060 (95% C.I. 0.041–0.091). Pairwise F ST values ranged from 0 to 0.175 indicating that some individual populations were considerably differentiated. Some populations in Drenthe and Noord-Brabant were not significantly differentiated from each other and formed population complexes of two or three ponds situated within natural areas of Noord-Brabant (Fig. 1; pond codes starting with 12, 23 or 26) or of neighbouring populations in close proximity within the southern part of Drenthe (310/312 + 330, 330 + 322), with the exception of two populations (330 + 319), which were 4 km apart.
Another way to evaluate the relative isolation of populations is the use of assignment tests. As predicted by Pritchard and Wen (Documentation for STRUCTURE software; http://pritch.bsd.uchicago.edu/structure.html) for populations showing isolation-by-distance (see below), most individuals in our study areas were assigned to various clusters with almost equal probabilities. In Drenthe, no clear results could be obtained with respect to the number of inferred clusters K. Similarly assignments by DOH showed that for none of the populations more than 50% of the individuals were assigned to their original population, and for all populations, individuals were assigned to at least six different populations. For Noord-Brabant, likelihoods suggested that four clusters could be identified (k = 3, Ln = −4404; k = 4, Ln = −4401; k = 5, Ln = −4451; k = 6, Ln = −4467; k = 7, Ln = −4586; average result of five runs), even though many individuals had admixed assignment to the inferred clusters. Individuals from population 0901 formed a clearly separate group with all individuals from this population assigned with high probabilities to one cluster. The remaining individuals were largely split into three clusters; (1) individuals from population 1301; (2) individuals from population complexes 12 and 15; (3) individuals from population complexes 23 and 26 (see Supplementary Figure 1S). DOH also exclusively assigned individuals from 0901 to their original population, whereas it assigned individuals from the other populations to various populations but mainly within the clusters described above.
Permeability model analysis
Among populations in Drenthe, a highly significant correlation was found with geographical distance (D), which explained 42.2% of the total variance (Table 4). Besides geographical distance, also the geographical distances corrected for negative area D*R NA, for negative linear elements D*R L and for positive linear elements D*C L as well as the integrated D*R INT showed a significant correlation with genetic distance. However in multiple Mantel tests, none of these permeability-adjusted distances had a significant additional effect (P > 0.24) on top of geographical distance D.
In Noord-Brabant, at first no significant correlation was found between the pairwise genetic and geographic distances across all populations. Examination of the scatter plot indicated that points largely deviating from the expected increase of genetic distance with geographic distance were all associated with population 0501 (Fig. 2). Inspection of historic maps showed that population 0501, the most eastern one in our study, was already poorly connected to other populations in 1850 and was separated from the rest of the study area by the construction of a canal between 1906 and 1923 and a four-lane motorway next to the canal later on. Reanalyses of the correlation between genetic and geographic distances without population 0501 resulted in significant correlations with all distance measures (Table 4), explaining between 37.6 (D*R NA) and 48.1% (D*C L) of the variation. In multiple Mantel tests, none of the permeability-adjusted distances added to a model with geographical distance alone (P > 0.22).
Scatter plot of genetic (Nei 1978) versus geographical distances between pairs of populations in Drenthe (a) and Noord-Brabant (b). Data points are indicated by filled diamonds, data points involving population 0501 in Noord-Brabant are indicated by open triangles
As observed for population 0501, permeability correlations may be obscured by single populations. On the other hand, correlations may also be associated with single populations at the edge of a study area (Bossart and Prowell 1998). To check for this, re-analyses of the Mantel tests were performed by systematically excluding one population per analysis. For Drenthe, the results of these analyses were similar to the original one, with all distance measures significantly related to genetic distance but none of the permeability-adjusted distances significant in the multiple Mantel tests. In Noord-Brabant, all distance measures were significant in each of the tests as well, but here the distance corrected for negative linear elements D*R L added significantly to a model with geographical distance in the multiple Mantel test only if population 0901 was excluded. Exclusion of any of the other populations did not change the Mantel test results.
Discussion
Genetic variation
We found small to moderate (F ST = 0.022 in Drenthe; F ST = 0.060 in Noord-Brabant) population differentiation in the two study areas in The Netherlands. The relatively longer time-span and higher level of habitat fragmentation (including increased interpond distances) for Noord-Brabant could be the cause of the higher F ST-values among its Moor frog populations. The higher degree of population isolation in Noord-Brabant, compared to Drenthe, can also be discerned from the lower numbers of alleles, the fixation of locus RRD590a in eight out of twelve populations, and the significantly lower degree of heterozygosity. A different recolonisation history of the two areas causing different basic population differentiation seems unlikely because both areas are only 150 km apart. Furthermore, the range of allele sizes was comparable in both areas.
Population genetic studies in amphibians have mainly focused on large geographic scales and consequently observed higher levels of population differentiation than found in our study (Newman and Squire 2001). For R. arvalis, genetic data on population differentiation are only available from Knopp et al. (2007), who found moderate to high population differentiation levels (F ST = 0.06 to 0.40) in Sweden among populations 110–660 km apart. Fine-scale studies in amphibians employing microsatellite markers (Scribner et al. 1994; Call 1997; Call et al. 1998; Newman and Squire 2001) found levels of differentiation comparable to our study, in Bufo bufo (F ST = 0.016 at 5.5–14.5 km distances), Rana luteiventris (F ST = 0.04 at 16 km; F ST = 0.07 at 3–34 km) and R. sylvatica (F ST = 0.014 at 0.05–21 km). Furthermore, R. arvalis exhibits comparable levels of genetic variation to other pond-breeding anurans (Brede and Beebee 2004; Scribner et al. 2001; Palo et al. 2004). Assessments of landscape history and matrix permeability in these studies are lacking, precluding further comparison.
Population differentiation and landscape change
Until 1850, the two studied landscapes formed large areas of unfragmented habitat with many ponds as potential breeding sites for the Moor frog. Since then, habitat loss and fragmentation has been more pronounced in Noord-Brabant. For instance, a study on water retention in Noord-Brabant showed that the surface area of ponds has decreased by almost 97% due to direct loss of ponds and lowered water tables (http://www.levenmetwater.nl). Currently, breeding ponds are on average 8.6 km apart, compared to 4.6 km in Drenthe. Dispersal distances of individual Moor frogs have been estimated to be 1–3 km, with a strong reduction in pond occupancy by roads (Hartung 1991; Vos and Chardon 1998). This would imply that both study areas, but especially Noord-Brabant, can be presently considered to be fragmented. Whereas the level of population differentiation is still low, the current permeability of the landscape matrix suggests that this genetic structure is unlikely to reflect present day gene flow levels although a definitive conclusion can not be drawn based on the present data. Nevertheless, we feel that our assumption of the genetic structure reflecting an intermediate situation between the historic situation in 1850 and the current landscape (Broughton and Harrison 2003) is a safe one. If the time since separation has been insufficient for complete divergence due to drift or to accumulation of mutations, populations will still resemble each other even in the absence of present-day gene flow (Bossart and Prowell 1998). Fragmentation started around 1910 in Noord-Brabant but only after 1932 in Drenthe. Because Moor frogs become adult in the third year of life (Hartung 1991), relatively few generations (max. 40) have passed since habitat fragmentation started. The species’ life history characteristics may to some extent counteract drift. The occurrence of overlapping generations and the possibility of multiple paternities (found in the single egg clump tested and is also observed in the related R. temporaria; Vieites et al. 2004), may contribute to the maintenance of genetic diversity in Moor frog populations. Alternatively, the numbers of alleles found in the populations may indicate that current population sizes are higher than estimated based on egg clump counts. Population differentiation and assignment tests indicated that several populations belong to the same population complex. If populations encompass more than a single breeding pond, drift and local loss of genetic diversity would be diminished.
The magnitude of the effect of drift for a relatively low number of generations on the level of population differentiation can be estimated in simulation models. We performed such simulations of the process of population differentiation starting with randomly assigned alleles to populations, mimicking severe fragmentation of a panmictic population using EASYPOP 1.8 (Balloux 2001). In these simulations, an island model with equal migration to all populations was assumed, in which the effective number of alleles for the overall area, the estimated population sizes and the number of populations, from either Drenthe or Noord-Brabant were used. Simulations of F ST values during 200 generations were performed using gene flow (Nm) values of 0.5 or 1.0 (Whitlock and McCauley 1998), thus mimicking a situation of limited gene flow after severe fragmentation. The simulations indicated that, even with such a low level of gene flow, F ST values of 0.06 (as found in our study) are only reached after approximately 30 and 40 generations. Equilibrium F ST levels were only attained after more than 100 generations irrespectively of the population model used (island or 2-D stepping stone; data not shown). Hence, it is likely that the populations in our study were not in migration-drift equilibrium, and that inferences about current gene flow cannot be drawn.
Matrix permeability and dispersal
For an isolation by distance (IBD) relation to establish between populations, dispersal between neighbouring ponds has to be possible but is restricted, so that populations differentiate from each other with increasing distance (Hutchinson and Templeton 1999). Both in Drenthe and in Noord-Brabant, an IBD pattern was found between populations separated by maximum distances of 10.0 and 18.6 km, respectively. For Noord-Brabant, the model including population 0501, for which historic data indicated that it was effectively isolated from the other populations in the early 1900’s, was not significant. Once 0501 was excluded, all IBD relationships became significant. According to Bossart and Prowell (1998), it can be concluded that this population is not connected by gene flow, even if its absolute level of differentiation is low. Although seemingly counterintuitive, populations with an absolute barrier to gene flow between them can actually show low levels of differentiation because genetic drift is undirected (Hutchinson and Templeton 1999). In the same time, if a population is large, the level of genetic drift is very low, and the population would not differentiate from other ones. This may actually be the case for population 0501, because a comparison of historic maps showed that 17% of its habitat in 1850 is still present today, compared to only 1–2% for other populations. Because the population differentiation of 0501 to most populations is low the latter explanation seems the most likely one.
In order to identify present-day landscape elements affecting gene flow, their effect has to be strong. Negative landscape elements like roads and canals are formidable barriers and were often present for a longer time period. Hence, they are more likely to be identified as gene flow barriers then other landscape elements. Nevertheless, effects of these negative landscape elements can also be concealed. In Noord-Brabant, population 0901 is situated in a military training area for tanks and, thus consisting of a high proportion of unsuitable land not accounted for in the landscape permeability measures. The fact that this population had the largest geographic distance to other populations and was also genetically different as shown in the assignment test obscured the effect of roads in this study area. The probability of the presence of populations such as 0501 and 0901 with a different population history and/or associated with an unequal distribution of certain landscape elements is likely to increase in larger and thus less homogeneous study areas. This may explain why in Drenthe, in contrast to the study of Vos et al. (2001), none of the landscape features had an effect in multiple Mantel tests. However, without population 0901, the distance corrected for negative linear elements D*R L (including roads) did significantly add to the genetic differentiation in the permeability model.
We have not been able to show any effects of other landscape elements. It may be that the positive and/or negative effects are too weak to have become significant after a limited number of generations. However, it may also be that the way in which we have calculated a type of structural connectivity measure, along 200-m strips through the landscape, does not accurately reflect the landscape as experienced by Moor frogs. For a more functional connectivity measure for R. arvalis, research on movement behaviour of frogs within landscapes is needed, so that real movement tracks can be modelled (Opdam et al. 2003). Such a permeability analysis (Chardon et al. 2003; Stevens et al. 2006), based on empirical data of current dispersal or gene flow may be less sensitive to landscape heterogeneity and populations differing in history.
References
Arens P, Van‘t Westende W, Bugter R, Smulders MJM, Vosman B (2000) Microsatellite markers for the European tree frog Hyla arborea. Molecular Ecology 9:1944–1946
Balloux F (2001) A computer program for the simulation of population genetics EASYPOP (version 1.7). J Heredity 92:301–302
Bossart JL, Prowell DP (1998) Genetic estimates of population structure and gene flow: limitations, lessons and new directions. Trends Ecol Evol 13:202–206
Brede EG, Beebee TJC (2004) Contrasting population structures in two sympatric anurans: implications for species conservation. Heredity 92:110–117
Broughton RE, Harrison RG (2003) Nuclear gene genealogies reveal historical, demographic and selective factors associated with speciation in field crickets. Genetics 163:1389–1401
Call DR (1997) Microsatellite characteristics and population structure for two anurans (Rana luteiventris and Hyla regilla). PhD Dissertation, Washington State University, Pullman
Call DR, Hallett JG, Mech SG, Evans M (1998) Considerations for measuring genetic variation and population structure with multilocus fingerprinting. Mol Ecol 7:1337–1346
Chardon JP, Adriaensen F, Matthysen E (2003) Incorporating landscape elements into a connectivity measure: a case study for the speckled wood butterfly (Pararge aegeria L.). Landsc Ecol 18:561–573
Cockerham CC (1973) Analysis of gene frequencies. Genetics 74:679–700
Crochet PA (1996) Can measures of gene flow help to evaluate bird dispersal? Acta Oecologica 17:459–474
Forman RTT (1995) Land mosaics; the ecology of landscapes and regions. Cambridge University Press, Cambridge
Goudet J, Raymond M, Demeeus T, Rousset F (1996) Testing differentiation in diploid populations. Genetics 144:1933–1940
Griffiths RA, Raper SJ (1994) How many clumps are there in a mass of frog spawn? British Herpetol Bull 50:14–17
Guo SW, Thompson EA (1992) Performing the exact test of Hardy–Weinberg proportion for multiple alleles. Biometrics 48:361–372
Hartung H (1991) Untersuchungen zur terrestrischen Biologie von Populationen des Moorfrosches (Rana arvalis Nilsson 1842) unter besonderer Berücksichtigung der Jahresmobilität. PhD thesis, University of Hamburg, Hamburg
Historische atlas Drenthe en Noord-Brabant (1989) Robas producties, Den Ilp
Holderegger R, Wagner HH (2006) A brief guide to landscape genetics. Landsc Ecol 21:793–796
Hoogerwerf G, Crombaghs B (1993) Herpetofauna onderzoek. Voorkomen en verspreiding van herpetofauna en kwaliteit van leefgebieden in het zuiden en oosten van Noord-Brabant. Limes Divergens adviesbureau voor Natuur and Landschap, Nijmegen
Hutchinson DW, Templeton AR (1999) Correlation of pairwise genetic and geographic distance measures: inferring the relative influences of gene flow and drift on distribution of genetic variability. Evolution 53:1898–1914
Karagyozov L, Kalcheva ID, Chapman M (1993) Construction of random small-insert genomic libraries highly enriched for simple sequence repeats. Nucleic Acids Res 21:3911–3912
Knopp T, Cano JM, Crochet PA, Merilä J (2007) Contrasting levels of variation in neutral and quantitative genetic loci on island populations of Moor frogs (Rana arvalis). Conserv Genet 8:45–56
Manel S, Schwartz MK, Luikart G, Taberlet P (2003) Landscape genetics: Combining landscape ecology and population genetics. Trends in Ecol Evol 18:189–197
Mantel N (1967) The detection of disease clustering and a generalized regression approach. Cancer Res 27:209–220
Manly BFJ (1997) Randomization, bootstrap and Monte Carlo methods in biology. Chapman and Hall, New York
Nei M (1978) Estimation of average heterozygosity and genetic distance from a small number of individuals. Genetics 89:583–590
Neigel JE (1997) A comparison of alternative strategies for estimating dispersal and gene flow from genetic markers. Ann Rev Ecol Systemat 28:105–128
Newman RA, Squire T (2001) Microsatellite variation and fine-scale population structure of wood frogs (Rana sylvatica). Mol Ecol 10:1087–1100
Opdam P, Verboom J, Pouwels R (2003) Landscape cohesion: an index for the conservation potential of landscapes for biodiversity. Landsc Ecol 18:113–126
Palo JU, Schmeller DS, Laurila A, Primmer CR, Kuzmin SL, Merilä J (2004) High degree of population subdivision in a widespread amphibian. Mol Ecol 13:2631–2644
Payne RW, Lane PW, Baird DB, Gilmour AR, Harding SA, Morgan GW, Murray DA, Thompson R, Todd AD, Tunnicliffe Wilson G, Webster R, Welham SJ (1993) Genstat 5, release 3, reference manual. Clarendon Press, Oxford
Pritchard JK, Stephens M, Donnelly P (2000) Inference of population structure using multilocus genotype data. Genetics 155:945–959
Rice WR (1989) Analyzing tables of statistical tests. Evolution 43:223–225
Ricketts TH (2001) The matrix matters: effective isolation in fragmented landscapes. The American Naturalist 158:87–99
Schlüpmann M (1988) Ziele und Methoden der Grasfrosch-Laichballen-Zählung in Westfalen. Jahrbuch für Feldherpetologie 2:67–88
Scribner KT, Arntzen JW, Burke T (1994) Comparative analysis of intra- and interpopulation genetic diversity in Bufo bufo, using allozyme, single-locus microsatellite, minisatellite and multilocus minisatellite data. Mol Biol Evol 11:737–748
Scribner KT, Arntzen JW, Cruddace N, Oldham RS, Burke T (2001) Environmental correlates of toad abundance and population genetic diversity. Biol Conserv 98:201–210
Stevens VM, Verkenne C, Vandewoestijne S, Wesselingh RA, Baguette M (2006) Gene flow and functional connectivity in the natterjack toad. Mol Ecol 15:2333–2344
Van der Sluis T, Vos CC (1997) Scenario studie verstoring heikikker door wegverkeer Noord-Brabant. In: Farjon H, Hazendonk NFC, Hoefnagel WJC (eds) Verkenningen natuur en verstedelijking 1995–2020. SC-DLO, IKC-Natuurbeheer, IBN-DLO, Wageningen, pp 1–27
Vieites DR, Nieto-Roman S, Barluenga M, Palanca A, Vences M, Meyer A (2004) Post-mating clutch piracy in an amphibian. Nature 431:305–308
Vos CC (1999) A frog’s-eye view of the landscape. Quantifying connectivity for fragmented amphibian populations. Ph.D. thesis Wageningen University, Wageningen
Vos CC, Chardon JP (1998) Effects of habitat fragmentation and road density on the distribution pattern of the Moor frog Rana arvalis. J Appl Ecol 35:44–56
Vos CC, Antonisse-De Jong AG, Goedhart PW, Smulders MJM (2001) Genetic similarity as a measure for connectivity between fragmented moor frog (Rana arvalis) populations. Heredity 86:598–608
Vos CC, Baveco H, Grashof-Bokdam CJ (2002) Corridors and species dispersal. In: Gutzwiller KJ (ed) Applying landscape ecology in biological conservation. Springer, New York, pp 84–104
Weir BS, Cockerham CC (1984) Estimating F-statistics for the analysis of population-structure. Evolution 38:1358–1370
Whitlock MC, McCauley DE (1998) Indirect measures of gene flow and migration: Fst≠1/(4Nm + 1). Heredity 82:117–125
Wiens JA (1997) Metapopulation dynamics and landscape ecology. In: Hanski I, Gilpin ME (eds) Metapopulation biology: ecology, genetics and evolution. Academic Press, San Diego, pp 43–68
Acknowledgements
We kindly acknowledged private landowners and nature conservation organisations (SBB, Natuurmonumenten, Drents Landschap, Brabants Landschap, Landgoed De Utrecht) for their permission to access fens and ponds. We want to thank H. Houweling and H. Meeuwsen for their assistance in the spatial modelling and GIS applications, R. Snep for the historical analysis and all people who participated in the field work. W. van Delden, R. Holderegger and two anonymous reviewers are kindly acknowledged for their helpful comments on an earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
10980_2007_9132_MOESM1_ESM.doc
Bar plot showing a visual representation of the proportion of membership of each individual in each of the 4 inferred clusters by STRUCTURE analysis of Noord-Brabant. Dataset used is subset without population 0501. Numbers above bar plot refer to sample locations. (DOC 52 kb)
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Arens, P., van der Sluis, T., van’t Westende, W.P.C. et al. Genetic population differentiation and connectivity among fragmented Moor frog (Rana arvalis) populations in The Netherlands. Landscape Ecol 22, 1489–1500 (2007). https://doi.org/10.1007/s10980-007-9132-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-007-9132-4