Introduction

Natural convection flows phenomena happen broadly in nature and are generally significant in solar energy collectors, purification processes, atmospheric, refrigeration of nuclear reactors, and oceanic circulation that occur in fluid mechanics if the temperature does vary density differences, leading to buoyant effects that affect its motion. Insights on utilizing natural convective flows may be seen in [1,2,3,4]

Akram et al. [6] investigated the impacts of MHD NF flow on peristaltic waves along with viscous dissipation as well as convection produced by slip effects through a channel, by employing the extensive wavelength and little but finite Reynold number estimation process. Sadia et al. [7] discussed a second-grade fluid motion produced by employing a permeable disc taking partial slip character. Thermal transmission made by heating the disc surface as well as by ohmic and viscous heating effects are evaluated and modelled with a thermal slip state. Associated mass transmission phenomena with thermophoretic distribution are also articulated. Further, the implementation of velocity slip supposition encourages non-linearity in the boundary situations in velocity mechanisms. Abidin et al. [8] studied a Carreau NF flow in a channel by Bvp4c technique of MATLAB. The concentration as well as energy equations is supposed by employing conservation and Navier–Stokes equations utilizing the revised Buongiorno model. They proved that temperature distribution rises along with heat source, thermal radiation, nanoscale effects, and Brinkman number. The fractional Oldroyd-B HNF with important impacts like wall slip condition, constant concentration, and Newtonian heating which further categorizes the behaviour of HNF flow and thermal transmission phenomena in a good manner was examined by the Laplace method. They also studied fractionalized Oldroyd-B HNF and second-grade NF based on AB and Prabhakar fractional techniques [9, 10]. A fractionalized MHD as well as the thermal transfer of a Brinkman tri-HNF in a porous medium with ramped conditions and generalized velocity in a vertical plate was discussed by utilizing AB differentiation and the Laplace approach. Further, a convection flow of a fractional HNF in a microchannel containing two parallel plates separately was considered with Newtonian heating impacts with the Caputo–Fabrizio (CF) and Laplace's approach by Amir et al. [11, 12].

The effects of Newtonian heating constraint with free convection fluid flowing were examined by Vieru et al. [13]. The problems for an incompressible flow with chemical reactions for some different fluids over a plate were considered in [14]. Viscous dissoluteness as well as the effect of the Joule heating scheme is investigated in [15]. The Newtonian heating impacts for the three-dimensional MHD flow with a special form of pressure were studied in [16]. A particular form of movement with Newtonian heating effect and power-law NF was discussed by Hayat et al. [17].

Free convective MHD flow with slip condition was investigated in [18]. They considered the Newtonian heating impacts with a nonlinear elastic plate in their research. Kamran et al. [19] discoursed Newtonian heating with the convective flow by using chemical reactions and boundary slip conditions. The characteristics of Newtonian heating were deliberated in [20] because of the motion of a micropolar fluid with a flexible plate. The spectral relaxation technique was used to discuss the NF for MHD flow through a channel flow in [21]. The consequences of Newtonian heating, heat generation, and organic response were studied [22] by considering Casson fluid flow on a moving plate placed with a permeable media. The flow of non-Newtonian fluid by taking into mind the viscosity and Newtonian heating effect was examined by Ahmad et al. [23].

The perception of fractional order and integral operators has suggestively affected several areas of applied sciences, engineering, and technology. In 1967, the perception of fractional calculus was developed from Caputo’s research work [24] in the year of 1967 and projected a characterization of the fractional derivative. This description helps use the integral transform method with an initial condition.

Moreover, this method was useful to find the solution to numerous physical mathematical problems. However, Caputo and Fabrizio studied that this non-integer technique has few drawbacks that yield indeterminate outcomes mostly for the structure and explanation of applied models. Hereafter, some well-known investigators appealed that such ambiguous consequences are due to singularity in the complicated integral. Their suggestion was useful and attentive. Subsequently, Caputo and Fabrizio proposed an innovative fractional derivative lacking a singularity [25].

Numerous researchers efficiently applied the Caputo-Fabrizio operator method in their work [26]. After this, a novel fractional order derivative also acknowledged oppositions due to the non-local kernel. So, Atangana and Baleanu presented an innovative non-integer operator involving a non-singular as well as non-local kernel [27]. Newly, many researchers are applying these non-integer operators having the Mittag-Leffler function. However, a more systematic and comprehensive investigation of these recent techniques is still compulsory. Lin et al. [28] used the Laplace technique to study a Casson fluid fractional model that included two parallel plates subjected to magnetic force. El-Zahar et al. [29] solved a fractionalized convection–diffusion system with a modified residual power series approach. Demir et al. [30] investigated a proportional Caputo-hybrid technique with a novel feature for this operator. Furthermore, they demonstrated how results build on and improve on prior findings in the system of integral inequalities. Chu et al. [31] examined a fractional third-order dispersive system using a variational iteration transform approach and the Shehu decomposition method. Raza et al. [32] used a nonlinear fractional system with the AB derivative to define COVID-19. They used the Toufik-Atangana approach to provide numerical solutions for the fractional model. Majeed et al. studied Newtonian and non-Newtonian fluids with different circumstances i.e. viscous fluid flow between two discs, with a hexagonal cavity, Maxwell fluid flow with Keller box-scheme, flow and thermal transfer over a pair of heated bluff bodies through a channel and presented important results in the literature [33,34,35]. Different researchers discussed flow in a channel; in a wavy trapezoidal cavity, MHD flows with slip conditions and periodic flow in no-Newtonian fluid [37,38,39].

The study of MHD fractionalized viscous fluids with thermal memory, slip, and Newtonian heating effects is very important in many scientific and engineering disciplines. Understanding these complex fluid dynamics is critical for optimizing heat transfer operations in industrial systems, increasing the performance of energy conversion devices, and designing innovative cooling systems. Further, the proposed fractional model, which employs the Atangana-Baleanu time-fractional approach and the Mittag-Leffler kernel, advances mathematical modelling methods to describe phenomena involving non-local and memory-dependent effects, providing a valuable tool for investigators in fluid dynamics as well as applied mathematics. This study's findings are poised to manipulate diverse fields, including materials science and environmental engineering, by giving insights into the complicated interplay of magnetic fields, thermal memory, and fractional calculus in fluid systems [41,42,43,44,45].

In the above literature, we see that the investigation of the Newtonian heating influence in numerous sceneries is a substantial practical as well as theoretical study for the solution of significant problems based on the non-integer derivative. After receiving inspiration from these facts, our main goal is to examine the influences of Newtonian heating on incompressible natural convection unsteady and viscous flow over an oscillating infinite inclined plate with an inclined magnetic field by employing fractional operator with Mittag-Leffler memory. The Laplace transform is invoked for the numerical and fractional simulations. To accomplish the Laplace inversion, two different approaches, Tzou technique and Stehfest are used. Finally, a graphical investigation of fractional and flow parameters is done by employing MathCad15 and discussed.

Problem statement based on Atangana-Balenau-time-fractional derivative

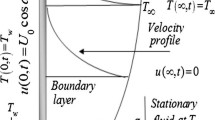
We consider unsteady and free convection viscous flow over an oscillating inclined plate with an inclined magnetic field having a strength \({B}_{{\text{o}}}\). Initially, fluid and the inclined plate having an ambient medium temperature \({\phi }_{\infty }\) and concentration value of \({\psi }_{\infty }\). At \(t>{0}^{+}\), the fixed plate starts oscillating through velocity \({U}_{{\text{o}}}{\text{cos}}\left(\omega t\right)\). The values of thermal as well as concentration also increase over time as revealed in Fig. 1. With the above conditions and using Boussinseq's estimation, the governing equations for this problem are [5]

$$\frac{{\partial w\left( {y,t} \right)}}{{\partial t}} = \nu \frac{{\partial ^{2} w\left( {y,t} \right)}}{{\partial y^{2} }} - \frac{{\sigma B_{{\text{o}}}^{2} }}{\rho }\sin \left( {\theta _{1} } \right)w\left( {y,t} \right) + g\beta _{\phi } \left( {\phi \left( {y,t} \right) - \phi _{\infty } } \right){\text{Cos}}\left( {\theta _{2} } \right) + g\beta _{\psi } \left( {\psi \left( {y,t} \right) - \psi _{\infty } } \right){\text{Cos}}\left( {\theta _{2} } \right).$$
(1)
$$\rho C_{{\text{p}}} \frac{{\partial \phi \left( {y,t} \right)}}{\partial t} = - \frac{{\partial \xi \left( {y,t} \right)}}{\partial y}.$$
(2)
$$\xi \left( {y,t} \right) = - K\frac{{\partial \phi \left( {y,t} \right)}}{\partial y}.$$
(3)
$$\frac{{\partial \psi \left( {y,t} \right)}}{\partial t} = - \frac{{\partial \eta \left( {y,t} \right)}}{\partial y} - K\left( {\psi \left( {y,t} \right) - \psi_{\infty } } \right).$$
(4)
$$\eta \left( {y,t} \right) = - D\frac{{\partial \psi \left( {y,t} \right)}}{\partial y}.$$
(5)

where \(\xi \left(y,t\right), \eta \left(y,t\right)\) indicates the thermal and mass fluxes by Fourier as well as Fick’s law.

Fig. 1
figure 1

Flow geometry

Full size image

The following are the supposed physical initial boundary conditions

$$w\left( {y,0} \right) = 0, \phi \left( {y,0} \right) = \phi_{\infty } , \psi \left( {y,0} \right) = \psi_{\infty } ; \;\;y \ge 0$$
(6)
$$w\left( {0,t} \right) - h\left. {\frac{{\partial w\left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = U_{{\text{o}}} \cos \left( {\omega t} \right), \left. {\frac{{\partial \phi \left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - \frac{h}{k} \phi \left( {0,t} \right), \;\;\psi \left( {0,t} \right) = \psi_{w} ; \;\;t > 0$$
(7)
$$w\left( {y,t} \right) \to 0,\;\;\; \;\phi \left( {y,t} \right) \to \phi_{\infty } , \;\;\;\; \psi \left( {y,t} \right) \to \psi_{\infty } \;{\text{as}}\;y \to \infty$$
(8)

By introducing the following dimensionless parameters and functional values

$$w^{*} = \frac{K}{\nu h}w, \; y^{*} = \frac{h}{K}y, \; t^{*} = \frac{Kg}{{h\nu }}t, \; \phi^{*} = \frac{{ \phi \left( {y,t} \right) - \phi_{\infty } }}{{\phi_{{\text{w}}} - \phi_{\infty } }}, \;\;{\text{Re}} = \left( \frac{h}{K} \right)^{3} \frac{{\nu^{2} }}{g}$$
$$\psi^{*} = \frac{{w\left( {y,t} \right) - \psi_{\infty } }}{{\psi_{{\text{w}}} - \psi_{\infty } }}, \; k^{*} = k\frac{\nu }{g}\left( \frac{h}{K} \right), \; \xi^{*} = \frac{\xi }{{\xi_{{\text{o}}} }}, \; \eta^{*} = \frac{\eta }{{\eta_{{\text{o}}} }}.$$

Into Eqs. (1–8) and ignore the steric notation. We have

$$\frac{{\partial w\left( {y,t} \right)}}{\partial t} = {\text{Re}} \frac{{\partial^{2} w\left( {y,t} \right)}}{{\partial y^{2} }} - M \sin \left( {\theta_{1} } \right) w\left( {y,t} \right) + {\text{Gr}} {\text{Cos}} \left( {\theta_{2} } \right)\phi \left( {y,t} \right) + {\text{Gm}} {\text{Cos}} \left( {\theta_{2} } \right)\psi \left( {y,t} \right).$$
(9)
$$\Pr _{{{\text{eff}}}} \frac{{\partial \phi }}{{\partial t}} = - \frac{{\partial \xi }}{{\partial y}}.$$
(10)
$$\xi \left( {y,t} \right) = - k\frac{\partial \phi }{{\partial y}}.$$
(11)
$${\text{Sc}}_{{{\text{eff}}}} \frac{{\partial \psi \left( {y,t} \right)}}{\partial t} = - \frac{{\partial \eta \left( {y,t} \right)}}{\partial y} - k {\text{Sc}}_{{{\text{eff}}}} \psi \left( {y,t} \right).$$
(12)
$$\eta \left( {y,t} \right) = - \frac{{\partial \psi \left( {y,t} \right)}}{\partial y}.$$
(13)
$$w\left( {y,0} \right) = 0, \phi \left( {y,0} \right) = 0, \psi \left( {y,0} \right) = 0; \;\;y \ge 0,$$
(14)
$$w\left( {0,t} \right) - h\left. {\frac{{\partial w\left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = \cos \left( {\omega t} \right), \;\left. {\frac{{\partial \phi \left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - \left( {1 + \phi \left( {0,t} \right)} \right),\;\psi \left( {0,t} \right) = 1,$$
(15)
$$w\left( {y,t} \right) \to 0,\;\;\phi \left( {y,t} \right) \to 0,\;\psi \left( {y,t} \right) \to 0\;{\text{as}}\;y \to \infty .$$
(16)

where

$$\Pr = \frac{{\mu C_{{\text{p}}} }}{K}, {\text{Gr}} = \frac{{g\left( {\upsilon \beta_{\phi } } \right)_{{\text{f}}} \left( {\phi_{{\text{w}}} - \phi_{\infty } } \right)}}{{\nu_{o}^{2} }}, \;{\text{Sc}} = \frac{\nu }{D},\;\Pr_{{{\text{eff}}}} = \frac{\Pr }{{\text{Re}}}, \;{\text{Sc}}_{{{\text{eff}}}} = \frac{{{\text{Sc}}}}{{{\text{Re}}}}.$$

Formulation of fractional model by using AB fractional derivative

To construct a fractional model recently introduced fractional derivative i.e. AB derivative is utilized, which is stated as [32, 33] for the function η \(\left(\xi ,t\right)\).

$${}^{AB}{\mathfrak{D}}_{t}^{\gamma } \eta \left(\xi ,t\right)=\frac{1}{1-\upgamma }{\int }_{0}^{t}{E}_{\upgamma }\left[\frac{\gamma {\left(t-z\right)}^{\gamma }}{1-\upgamma }\right]{ \eta }^{\mathrm{^{\prime}}}\left(\xi ,t\right){\text{d}}t; \; 0<\upgamma <1$$
(17)

and \({E}_{\upgamma }\left(z\right)\) is a Mittage-Lefflerr function demarcated as

$${E}_{\upgamma }\left(z\right)=\sum_{{\text{i}}=0}^{\infty }\frac{{z}^{\gamma }}{\Gamma \left(i\gamma +1\right)}; \; 0< \gamma <1, z\in {\mathbb{C}}.$$
(18)
$$\mathcal{L}\left\{{}_{ }{}^{AB}{\mathfrak{D}}_{t}^{\gamma }\upeta \left(\xi ,t\right)\right\}=\frac{{q}^{\gamma }\mathcal{L}\left[\eta \left(\xi ,t\right)\right]-{q}^{\upgamma -1}\eta \left(\xi ,0\right)}{\left(1-\upeta \right){q}^{\gamma }+\upgamma },$$
(19)

with

$$\underset{\gamma \to 1}{{\text{Lim}}}{}_{ }{}^{AB}{\mathfrak{D}}_{t}^{\gamma }\eta \left(\xi ,t\right)=\frac{\partial \eta (\xi ,t)}{\partial t}.$$
(20)

In this investigation, we have used an effective fractional approach i.e. AB time-fractional operator to investigate the thermal memory in view of generalized Fourier and Fick's law [32, 33]

$$\xi \left(y,t\right)=-{}_{ }{}^{AB}{\mathfrak{D}}_\text{t}^{\gamma } \frac{\partial \phi \left(y,t\right)}{\partial y}.$$
(21)
$$\eta \left(y,t\right)=-{}_{ }{}^{AB}{\mathfrak{D}}_\text{t}^{\gamma }\frac{\partial \psi \left(y,t\right)}{\partial y}.$$
(22)

Solution of the problem

Temperature field

Applying the Laplace transform on Eqs. (10 and 21) and conditions (14)2–(16)2, we get

$$\Pr _{{{\text{eff}}}} q\bar{\phi }\left( {y,q} \right) = \frac{{q^{\gamma } }}{{\left( {1 - \gamma } \right)q^{\gamma } + \gamma }}\frac{{\partial ^{2} \bar{\phi }\left( {y,q} \right)}}{{\partial y^{2} }},$$
(23)
$$\left. {\frac{{\partial \overline{\phi }\left( {y,q} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - \left( {\frac{1}{q} + \overline{\phi }\left( {0,q} \right)} \right), \overline{\phi }\left( {y,q} \right) \to 0; \; y \to \infty .$$
(24)

The solution of Eq. (23) with transformed conditions in Eq. (24) will be yielded as

$$\overline{\phi }\left( {y,q} \right) = \frac{{\sqrt {q^{\gamma } } }}{{\sqrt {\Pr_{{{\text{eff}}}} \left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]q} - \sqrt {q^{\gamma } } }} \frac{{e^{{ - y\sqrt {\frac{{\Pr_{{{\text{eff}}}} q\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}} }} }}{q}.$$
(25)

To obtain the Laplace transform inversion of Eq. (25), we utilized the Stehfest and Tzou numerical methods as in Table 1. In this subsection, we have found the solution for temperature distribution based on the AB fractional derivative by employing the Laplace method.

Table 1 Numerical results of concentration, temperature, and momentum profile through Stehfest as well as Tzou’s technique
Full size table

Concentration profile

Taking Laplace transform on Eqs. (12 and 22) and conforming conditions (14)3–(16)3, we get

$$\frac{{\partial^{2} \overline{\psi }\left( {y,q} \right)}}{{\partial y^{2} }} - {\text{Sc}}_{{{\text{eff}}}} \left( {q + k} \right)\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }} \overline{\psi }\left( {y,q} \right) = 0,$$
(26)
$$\overline{\psi }\left( {y,q} \right) = \frac{1}{q}, \overline{\psi }\left( {y,q} \right) \to 0; y \to \infty .$$
(27)

By employing the above conditions of Eq. (27) and after simplification, Eq. (26) gives the concentration field

$$\overline{\psi }\left( {y,q} \right) = \frac{{e^{{ - y\sqrt {{\text{Sc}}_{{{\text{eff}}}} \left( {q + k} \right)\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}} }} }}{q}.$$
(28)

The Laplace inverse of Eq. (28) will be examined in Table 1 numerically. In this subsection, we have found the solution for the concentration profile based on the AB fractional derivative by employing the Laplace technique.

Velocity field

Taking the Laplace transform on Eq. (9) and corresponding conditions (14)1–(16)1, we get

$${\text{Re}} \frac{{\partial^{2 } \overline{w}\left( {y,q} \right)}}{{\partial y^{2} }} - q\overline{w}\left( {y,q} \right) - M \sin \left( {\theta_{1} } \right) \overline{w}\left( {y,q} \right) = - {\text{Gr}} {\text{Cos}} \left( {\theta_{2} } \right)\overline{\phi }\left( {y,q} \right) - {\text{Gm }}{\text{Cos}} \left( {\theta_{2} } \right)\overline{\psi }\left( {y,q} \right),$$
(29)
$$\overline{w}\left( {0,q} \right) - h\left. {\frac{{\partial \overline{w}\left( {y,q} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = \frac{q}{{q^{2} + \omega^{2} }}, \overline{w}\left( {y,q} \right) \to 0; y \to \infty .$$
(30)

By using the conditions of Eq. (30) and temperature solution from Eq. (25) and the concentration value from Eq. (28), the solution of the momentum Eq. (29) is

$$\bar{w}\left( {y,q} \right) = {\text{ }}\left( {\begin{array}{*{20}l} {\frac{q}{{q^{2} + \omega ^{2} }} + \frac{{{\text{Gr}}\;{\text{cos}}\left( {\theta _{2} } \right)}}{{q{\text{Re}}}}\frac{{\sqrt {q^{\gamma } } }}{{\sqrt {q{\text{Pr}}_{{{\text{eff}}}} \left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]} }}\frac{{1 + h\sqrt {{\text{Pr}}_{{{\text{eff}}}} \frac{{q\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}} }}{{\frac{{ - \sqrt {q^{\gamma } } \left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]q{\text{Pr}}_{{{\text{eff}}}} }}{{q^{\gamma } }} - \frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}}}} \hfill \\ {\quad + \frac{{{\text{Gm}}\;{\text{cos}}\left( {\theta _{2} } \right)}}{{{\text{Re}}q}}\frac{{1 + h\sqrt {{\text{Sc}}_{{{\text{eff}}}} \left( {q + k} \right)\frac{{q\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}} }}{{{\text{Sc}}_{{{\text{eff}}}} \left( {k + q} \right)\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }} - \frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}}}} \hfill \\ \end{array} } \right)\frac{1}{{1 + h\sqrt {\frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}} }}e^{{ - y\sqrt {\frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}} }} {\text{ }}\quad - \frac{{{\text{Gr}}\;{\text{cos}}\left( {\theta _{2} } \right)}}{{{\text{Re}}q}}\frac{{\sqrt {q^{\gamma } } }}{{\sqrt {q{\text{Pr}}_{{{\text{eff}}}} \left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]} - \sqrt {q^{\gamma } } }}\frac{{e^{{ - y\sqrt {{\text{Pr}}_{{{\text{eff}}}} \frac{{q\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}} }} }}{{\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]q{\text{Pr}}_{{{\text{eff}}}} }}{{q^{\gamma } }} - \frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}}}{\text{ }} \quad - \frac{{{\text{Gm}}\;{\text{cos}}\left( {\theta _{2} } \right)}}{{{\text{Re}}q}}\frac{{e^{{ - y\sqrt {\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }}{\text{Sc}}_{{{\text{eff}}}} \left( {k + q} \right)} }} }}{{{\text{Sc}}_{{{\text{eff}}}} \left( {k + q} \right)\frac{{\left[ {\left( {1 - \gamma } \right)q^{\gamma } + \gamma } \right]}}{{q^{\gamma } }} - \frac{{q + M{\text{sin}}\left( {\theta _{1} } \right)}}{{{\text{Re}}}}}}.$$
(31)

The Laplace inversion of above Eq. (31) will be examined in Table 1 numerically.

Gradients

The present research also addresses the three essential variables of engineering curiosity: the Nusselt number, the Sherwood number, and shear stress. The aforementioned gradients can be expressed mathematically as:

Nusselt number

$${\text{Nu}} = - \left. {\frac{{\partial \phi \left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - {\mathcal{L}}^{ - 1} \left\{ {\frac{{\partial \overline{\phi }\left( {0,q} \right)}}{\partial y}} \right\}.$$

Sherwood number

$${\text{Sh}} = - \left. {\frac{{\partial \psi \left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - {\mathcal{L}}^{ - 1} \left\{ {\frac{{\partial \overline{\psi }\left( {0,q} \right)}}{\partial y}} \right\}.$$

Skin friction

$$C_{{\text{f}}} = - \left. {\frac{{\partial w\left( {y,t} \right)}}{\partial y}} \right|_{{{\text{y}} = 0}} = - {\mathcal{L}}^{ - 1} \left\{ {\frac{{\partial \overline{w}\left( {0,q} \right)}}{\partial y}} \right\}.$$

For the Laplace inversion, numerous investigators have used diverse numerical inverse approaches. So, here, we will also utilize the Stehfest technique [47] to investigate the solution of thermal, concentration, and momentum profiles numerically. Gaver-Stehfest method [47] mathematically may be simulated as

$$w\left(y,t\right)=\frac{{\text{ln}}\left(2\right)}{t} \sum_{{\text{m}}=1}^{P}{u}_{{\text{m}}} \overline{w}\left(y,m\frac{{\text{ln}}\left(2\right)}{t}\right)$$
(32)

where \(P\) is a positive integer, and

$${u}_{{\text{m}}}={\left(-1\right)}^{\text{m}+\frac{\text{P}}{2}}\sum_{i=\left[\frac{q+1}{2}\right]}^{{\text{min}}\left(q,\frac{P}{2}\right)}\frac{{i}^\frac{\text{P}}{2} \left(2i\right)!}{\left(\frac{P}{2}-i\right)!i! \left(i-1\right)! \left(q-i\right)! \left(2i-q\right)!}$$

Nevertheless, we have also hired another approximation to find the solution of concentration, energy, and momentum profile, Tzou’s method for the validity and comparison of our attained numerical consequences by the Stehfest method. Tzou’s technique [48] can be demarcated as

$$w\left(y,t\right)=\frac{{e}^{4.7}}{t} \left[\frac{1}{2}\overline{w }\left(i,\frac{4.7}{t}\right)+{\text{Re}} \left\{\sum_{j=1}^{P}{\left(-1\right)}^\text{k} \overline{w}\left(i,\frac{4.7+k\pi l}{t}\right)\right\}\right]$$
(33)

where \(l\) is an imaginary unit and \({\text{Re}}\left(.\right)\) is the real part and \(P>1\) is the natural number.

In this subsection, we have found the solution for velocity distribution based on the AB fractional derivative by employing the Laplace technique. Furthermore, we also found the three essential variables of engineering curiosity i.e. Nusselt number, Sherwood number, and Skin friction. In the end, we included a comparison for the validation of the codes for the Gaver–Stehfest method [47] and Tzou’s technique [48].

Results with discussion

The physical characteristics of the MHD free convective fractionalized viscous fluid model based on the AB derivative having a non-singular and non-local kernel to investigate the slip and Newtonian heating effect are studied. Furthermore, the joint effect of thermal, mass, and velocity transfer has been taken into our study by demonstrating graphs for diverse estimations of the time. The graphical analysis illustrates the impacts of different fractional and flow parameters i.e. \(\gamma\), \({\text{Gr}}\), \({\text{Gm}}\), \({{\text{Pr}}}_{{\text{eff}}}\), \({\text{Re}}\), \({{\text{Sc}}}_{{\text{eff}}}\), \(M\), and the angle of magnetic fields’ inclination (\({\theta }_{1}\)) for the physical understanding of the found results for energy, momentum, and concentration profiles on the MHD fluid flowing over an inclined oscillating plate in Figs. 2–14 through Mathcad15

Fig. 2
figure 2

Simulation for temperature with a variation of \(\gamma\) when \({\text{Pr}}=2.2\), \({\text{Re}}=0.5\)

Full size image

Figure 2 is organized to examine the impacts of \(\gamma\) on the temperature distribution. By increasing the estimation of \(\gamma\), the heat shows increasing behaviour for a small time and the fractional parameter shows the opposite behaviour for the temperature at a large time. This specifies the significance of the AB fractional operator (a non-singular and non-local kernel) that assures to illustration of the extensive generalized memory and hereditary characteristics. Figure 3 is planned to display the consequence of effective Prandtl number \({{\text{Pr}}}_{{\text{eff}}}\) on the energy profile. The effective Prandtl number is the ratio of Prandtl number \({\text{Pr}}\) and Reynolds number \({\text{Re}}\). The \({\text{Pr}}\) is a dimensionless measure that clarifies the connection between the energy as well as velocity boundary layer thickness. The higher the values of \({{\text{Pr}}}_{{\text{eff}}}\) results from the higher values of \({\text{Pr}}\). In heat transfer problems, the thinner energy boundary layer in comparison with the velocity boundary layer is due to greater \({\text{Pr}}\), which outcomes in a lessening in the energy profile at small and large times. Hence, \({\text{Pr}}\) may be applied to increase the rate of cooling.

Fig. 3
figure 3

Simulation for temperature with the variation of \({{\text{Pr}}}_{{\text{eff}}}\) when \(\gamma =0.5\)

Full size image

Figure 4 displays the influence of \(\gamma\) on the concentration. A gradual increase (at a small time) and decreasing behaviour (at a large time) can be observed as \(\gamma\) rises. This is also due to the significance of the AB fractional operator (a non-singular and non-local kernel) that assures to illustration of the extensive generalized memory and hereditary characteristics. Figure 5 exposes the result of \({{\text{Sc}}}_{{\text{eff}}}\) on the concentration. The effective Schmidt number \({{\text{Sc}}}_{{\text{eff}}}\) resulted from the dimensionless numbers i.e. Schmidt \({\text{Sc}}\) and Reynolds \({\text{Re}}\). It is found that at small and larger times values-enhancing \({{\text{Sc}}}_{{\text{eff}}}\) which makes concentration levels fall. This may be enlightened by the detail that \({\text{Sc}}\) is the ratio among viscous forces as well as mass diffusivity, so an intensification in \({\text{Sc}}\) raises the viscous forces, and therefore, the concentration declines.

Fig. 4
figure 4

Simulation for concentration with the variation of \(\gamma\) when \({\text{Sc}}=0.22\), \(K={\text{Re}}=0.5\)

Full size image
Fig. 5
figure 5

Simulation for concentration with the variation of \({{\text{Sc}}}_{{\text{eff}}}\) when \(\gamma =0.5\), \(K=2\)

Full size image

Figure 6 exposes the effects of \(\gamma\) on the momentum profile. This can be detected that at a smaller time growing, the estimation of \(\gamma\) leads to enhancing and declining (at a larger time) the velocity profile. This is also due to the implication of the AB fractional operator (a non-singular and non-local kernel) that assures to illustration of the extensive generalized memory and hereditary characteristics. Also, velocity decreases away from the plate as well as asymptotically rises in \(y\)-direction, which is also denoting the considered conditions. The effects of \({{\text{Pr}}}_{{\text{eff}}}\) on the rate of velocity are studied in Fig. 7. The velocity decreases by growing \({{\text{Pr}}}_{{\text{eff}}}\). An increase in \({{\text{Pr}}}_{{\text{eff}}}\) leads from increasing \({\text{Pr}}\) which decreases the energy boundary layer thickness. The \({\text{Pr}}\) denotes the ratio of momentum diffusivity to energy diffusivity. The increasing value of \({\text{Pr}}\) raises the thickening of the momentum boundary layer compared to thermal boundary layers. That’s why velocity declines for growing estimation of \({{\text{Pr}}}_{{\text{eff}}}\) for different times.

Fig. 6
figure 6

Simulation for velocity with the variation of \(\gamma\) when \({\text{Pr}}=2.2, {\text{Sc}}=0.22, {\text{Re}}=1.0, {\text{Gr}}=8, {\text{Gm}}=4.5, K=0.5, M=1, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2\)

Full size image
Fig. 7
figure 7

Simulation for the velocity at changing \({{\text{Pr}}}_{{\text{eff}}}\) when \(\gamma =0.5, {\text{Sc}}=0.5, {\text{Re}}=1.5, {\text{Gr}}=5, {\text{Gm}}=6.5, K=1, M=0.5, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2\)

Full size image

The Grashof number is significant for the reason that it depicts the ratio of resistive forces arising from fluid viscosity to buoyant forces coming from spatial variation as well as fluid density. Figures 8 and 9 illustrate velocity profiles for various values of \({\text{Gr}}\) and \({\text{Gm}}\). Increased values of these parameters produce forces of buoyancy, leading to higher induced flows. As \({\text{Gr}}\) and \({\text{Gm}}\) are increased, the fluid's velocity improves as a result.

Fig. 8
figure 8

Simulation for velocity with variation of \({\text{Gr}}\) when \(\gamma =0.5, {\text{Sc}}=0.22,\mathrm{ Pr}=2.2, {\text{Re}}=1.5, {\text{Gm}}=4.5, K=2.5, M=1, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2\)

Full size image
Fig. 9
figure 9

Simulation of velocity for variation of \({\text{Gm}}\) when \(\gamma =0.5, {\text{Sc}}=0.22, {\text{Pr}}=2.2, {\text{Re}}=1.5, K=2.5, M=1, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2, {\text{Gr}}=5\)

Full size image

Figure 10 determines the result of \({{\text{Sc}}}_{{\text{eff}}}\) on the velocity. It is exposed that growing the estimation of \({{\text{Sc}}}_{{\text{eff}}}\) declines the velocity. This is clarified by the element that \({\text{Sc}}\) is the ratio of viscous forces as well as mass diffusivity, so growth in \({\text{Sc}}\) grows the viscous forces and therefore declines the velocity. Figure 11 exhibited that the reduction in velocity profile resulted from enhancing the value of \({\text{Re}}\). \({\text{Re}}\) is the ratio of inertial forces and viscous forces (friction forces of two fluid elements moving to each other). An increasing value of \(Re\) decreases the viscous forces, so velocity is enhanced.

Fig. 10
figure 10

Simulation of velocity for variation of \({{\text{Sc}}}_{{\text{eff}}}\) when \(\gamma =0.5, {\text{Gr}}=5,\mathrm{ Pr}=2.5, \mathrm{ Re}=1.5, {\text{Gm}}=6.5, K=1, M=0.5, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2\)

Full size image
Fig. 11
figure 11

Simulation of velocity with a variation of \({\text{Re}}\) when \(\gamma =0.5,\mathrm{ Sc}=0.5, \mathrm{ Gr}=5, {\text{Gm}}=6.5, K=1, M=0.5, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2, {\text{Pr}}=2.2\)

Full size image

Figure 12 and 13 reveal the impact of magnetic parameter \(M\) and angle \({\theta }_{1}\) of magnetic effect on the velocity profile. \(M\) is a dimensionless number that is rendered with Lorentz force that counters fluid velocity. The advanced value of \(M\) leads to a higher Lorentz force, which opposes movement. So, velocity is reduced with growing \(M\). Likewise, the angle of a magnetic field \({\theta }_{1}\) stronger the stimulus of \(M\) which is transferred by the Lorentz force. For \({\theta }_{1}=\pi /2\) (normal magnetic field), the effect of the Lorentz force is maximum, so lowers the velocity. Figure 14 is plotted for comparing two diverse numerical methods, Stehfest as well as Tzou for thermal, concentration, and velocity curves. The obtained results from diverse profile curves have overlapped with each other, signifying this research work's validity. (Table 2)

Fig. 12
figure 12

Simulation for velocity with the variation of \(M\) when \(\gamma =0.5, {\text{Gr}}=5,\mathrm{ Pr}=2.2, {\text{Re}}=1.5, {\text{Sc}}=0.22, {\text{Gm}}=6.5, K=1, {\theta }_{1}=\phi =\frac{\pi }{4}, h=0.2\)

Full size image
Fig. 13
figure 13

Simulation for the velocity at changed values of \({\theta }_{1}\) when \(\gamma =0.5, {\text{Gr}}=5, {\text{Pr}}=2.2,\mathrm{ Re}=1.5, {\text{Sc}}=0.22, {\text{Gm}}=6.5, K=1, \phi =\frac{\pi }{4}, h=0.2, M=1\)

Full size image
Fig. 14
figure 14

Comparison of the velocity, concentration, and temperature profiles with different numerical algorithms

Full size image
Table 2 Numerical results of Nusselt number and Sherwood number, as well as skin friction
Full size table

Conclusions

In this attempt, the flow of unsteady, viscous, MHD flow over an infinite inclined oscillating plate along with an AB fractional derivative (having a non-singular and non-local kernel) with the Mittag-Leffler function is invoked for developing the fractional model to study the memory effects. The effects of Newtonian heating as well as slip conditions are also taken to be under consideration. The Laplace approach is employed to obtain the solution for governing equations of energy and concentration, as well as velocity. The main key points are enumerated below:

  • The profiles of concentration and temperature, as well as velocity increased for a small time by enhancing \(\gamma\) and asymptotically declined at a large time.

  • The effective Prandtl and Schmidt numbers decrease the thermal and concentration, as well as velocity levels of the fluid.

  • Velocity profiles are boosted by enhancing the value of \({\text{Gr}}\) and \({\text{Gm}}\) because of the growth in the buoyancy effect.

  • The velocity profile shows a trend of increasing and declining by improving the estimations of the Reynolds number and magnetic parameter, respectively.

  • The solution curves of temperature, momentum, and concentration fields with numerical techniques i.e. Stehfest and Tzou coincided with each other which assures the validation of our achieved results.

Consequently, our claimed results offer significant insights into industrial and engineering systems. These findings guide the development of thermal transfer technologies, assisting in the optimization of processes for better efficiency in applications such as cooling mechanisms and power generation. The research advances heat transfer processes, increasing the overall efficiency of industrial systems.

Future recommendations

To extend the problem addressed in this paper, we propose the following ideas based on the analysis, geometries, methodologies, and expansions stated below:

  • The Prabhakar and Caputo-Fabrizio fractional operators may be used to study the same problem in channel flow with a permeable medium.

  • The same problem may also be explored using the fractional natural decomposition method (FNDM) and the Keller Box approach.

  • A comparison investigation of this fractional model may also be performed by using the natural and Laplace transforms.