Introduction

Global warming is one of the most significant challenges that the world faces today, and this is closely linked to the world’s increasing energy demand. This challenge has led to considerable interest in developing new technologies that can improve energy efficiency. One such technology is the use of nanofluids, which are engineered fluids that contain nanoscale particles dispersed in a base fluid. These fluids have shown promising results in improving energy efficiency in various applications such as heat exchangers, refrigeration systems, and solar collectors [1, 2].

The unique properties of nanofluids arise from the addition of nanoparticles, which have a high surface area to volume ratio and can enhance heat transfer by increasing the fluid’s thermal conductivity (TC). Several researchers have investigated the thermophysical properties of different types of nanofluids, including metallic, oxide [3,4,5], and carbon-based nanoparticles [6,7,8]. Despite the ability of these nanofluids to enhance TC, the majority of them exhibit unfavorable rheological properties and low stability [9]. Conversely, some nanofluids exhibit better rheological properties but at a high cost, with moderate TC and poor stability. This led to the formation of a hybrid nanofluid (HNF), whose studies have been growing over the past decade. Numerous reports have shown that the combination of two or more nanomaterials to form HNFs can enhance both TC and offer favorable rheological properties or stability.

Ghafouri and Toghraie [10] studied the TC of a SiC–ZnO/ethylene glycol (EG) HNF in their experimental study. They developed the HNF using a two-step method with an equal mixture of SiC and ZnO nanoparticles within the EG base fluid. The authors found that the TC increased with an increase in solid volume fraction and temperature or a decrease in nanoparticle diameter. The study also found that the TC enhancement of the hybrid SiC–ZnO/EG nanofluid was greater than that of the ZnO/EG and SiC/EG single-nanofluids. At a temperature of 50 °C, the TC intensification was raised to 15.91% with a nanomaterial volume loading of 1%.

The study conducted by Shelton et al. [11] aimed to investigate the rheological properties of hybrid Al2O3–TiO2/mineral oil nanofluids. The results showed that the ratio of the hybrid nanoparticle mixture affected the rheological characteristics, with a 50%-Al2O3/50%-TiO2 composition presenting a peak value relative to other hybrid compositions and an overall decline in flow behavior index with a rising ratio of TiO2 in the Al2O3/TiO2 hybrid mixture. These results suggest that using HNFs would be preferred over traditional nanofluids in thermofluids applications.

Wanatasanappan et al. [12] investigated the effect of Al2O3–Fe2O3 nanomaterial composition on the viscosity (µ) of water/EG-based HNF at steady volume loading. The combination of Al2O3 and Fe2O3 in a 40:60 ratio resulted in the most significant increase in µ, with a maximum increase of 4.69 times higher than water/EG at a temperature of 100 °C. The impact of temperature on µ was found to be much more significant than the effect of the mixing ratio of nanomaterials. The highest increase in µ caused by changes in the Al2O3–Fe2O3 ratio was around 4.94%; while, the increase in µ due to temperature changes was around 57.16%. An artificial neural network (ANN) was used to create a framework for the experimental study’s data, resulting in a high correlation value of more than 99.99%.

Several studies have investigated the effect of temperature and concentration on the TC of various HNFs. Shahsavar et al. [13] found that a HNF containing Fe3O4–CNTs/water exhibited the highest TC improvement with the maximum concentration of CNTs and Fe3O4 at a 25–55 °C temperature range. Nabil et al. [14] reported a 22.8% increase in TC by incorporating TiO2–SiO2 nanoparticles into the base fluid. Afrand [15] observed that the TC of a HNF (MgO–FMWCNTs/ethyl glycol) increased at lower concentrations of nanoparticles and proposed a new correlation for estimating TC. Madhesh and Kalaiselvam [16] found that the TC of a Cu–TiO2/water HNF increased with the addition of nanoparticles and raised the temperature of the fluid. Hamid et al. [17] investigated the effects of different ratios of TiO2–SiO2 nanoparticles on the heat transfer rate and thermophysical properties. They found that the 20:80 ratio showed the highest enhancement in TC. Yarmand et al. [18] reported the highest TC of a graphene (nanoplatelets-platinum/water) HNF at the highest concentration and temperature. Qing et al. [19] studied the thermophysical and electrical properties of a SiO2–graphene/naphthenic oil HNF. They found that pH level affected the stability and TC, with the highest enhancement observed at 0.04 mass% and 100 °C. Jana et al. [20] compared the TC enhancement of mono and HNFs and found that mono-nanofluids showed higher enhancement, with the highest value observed for Cu/water nanofluids. Nadooshan et al. [21] investigated the rheological behavior of a Fe3O4–MWCNTs/ethylene glycol HNF and found that the µ increased with the volume fraction and temperature range. Overall, these studies demonstrate the potential of HNFs for enhancing TC in various applications.

Recently, the study by Alsangur et al. [22] delves into the investigation of magnetic hybrid nanofluids, mainly focusing on Fe3O4/CNT–water and Fe3O4/Graphene–water compositions and their TC under the influence of an external magnetic field. Through meticulous experimentation using a 3ω method and a 3D Helmholtz coil system to generate a uniform magnetic field, samples ranging from 1 to 5 mass% were prepared and analyzed. The results unveil a notable increase in thermal conductivity with both magnetic field strength and particle concentration, with Fe3O4/Graphene–water exhibiting up to three times higher enhancement than Fe3O4/CNT–water. Under the application of an external magnetic field, thermal conductivity enhancements of up to approximately 12% and 51% were observed for Fe3O4/CNT–water and Fe3O4/Graphene–water, respectively, with the parallel direction yielding more significant enhancements than the perpendicular direction. The study’s findings underscore the potential of magnetic hybrid nanofluids, especially those incorporating graphenes and CNTs, to revolutionize thermal management systems by offering substantially enhanced thermal conductivity and responsiveness to magnetic fields.

Ajeena et al. [23] delve into the dynamic viscosity of a hybrid nanofluid composed of ZrO2 and SiC dispersed in distilled water. Employing a two-step method for nanoparticle dispersion, they conducted experiments to measure dynamic viscosity at solid volume fractions ranging from 0.025 to 0.1% and temperatures from 20 to 60 °C using a Brookfield digital viscometer. Characterization tests confirmed the stability of the nanoparticles in the base fluid. Results revealed increased dynamic viscosity with higher solid concentrations and lower temperatures. Notably, a 29.6% and 64.2% rise in viscosity was observed at 20 °C and 60 °C, respectively, with 0.025% nanoparticle concentration. Conclusions drawn from the experiment highlight the significant impact of solid concentration and temperature on viscosity, with concentration changes exhibiting a greater effect. The hybrid nanofluid showcased a maximum viscosity increase of 169.47% at 0.1% solid volume fraction and 60 °C temperature.

Notably, among the various nanofluids, ferrofluids and carbon-based nanofluids offer an interesting and promising hybrid combination for thermal management applications due to their unique properties and synergistic effects. Ferrofluids are colloidal suspensions of magnetic nanoparticles in a liquid carrier; while, carbon-based nanofluids contain carbon-based nanoparticles dispersed in a liquid carrier.

Ferrofluids possess unique properties such as high TC and magnetization, making them attractive for thermal management applications [24]. On the other hand, carbon-based nanofluids offer a high surface area-to-volume ratio, which enhances heat transfer capabilities [9]. By combining these two types of nanofluids, a HNF can be created that not only enhances TC but also offers favorable rheological properties or stability. The synergistic effects of combining ferrofluids and carbon-based nanofluids in a HNF can offer improved heat transfer and stability, making them a promising solution for thermal management applications.

Among the numerous ferromagnetic and carbon-based nanoparticles, this study will focus on the application of Fe2O3 nanoparticles and GNPs for the HNF preparation. The selection of nanomaterials for this experimental investigation was based on their unique properties and potential benefits for enhancing the thermophysical properties of the nanofluid. Individually, GNPs [25] and Fe2O3 [26] have both shown promise in improving the TC of nanofluids. GNPs are known for their high TC, excellent mechanical properties, and large surface area, making them suitable for enhancing the heat transfer capabilities of fluids [25]. Fe2O3 nanoparticles, on the other hand, are inexpensive and have been shown to have high thermal stability and TC, as well as unique magnetic properties that could be useful in applications such as magnetic cooling [24, 27].

Furthermore, combining GNPs and Fe2O3 nanoparticles in HNFs can potentially result in synergistic effects that improve the thermophysical properties beyond what each individual nanomaterial can achieve on its own. Therefore, selecting these nanomaterials for the experimental investigation is a reasonable choice based on their unique properties and potential benefits for enhancing the thermophysical properties of the nanofluid.

However, to further improve the performance of nanofluids, it is essential to understand the influence of parameters such as the mixing ratio of nanoparticles, temperature, and concentration on their thermophysical properties. In this regard, experimental investigations are crucial for obtaining reliable data and optimizing the performance of nanofluids. Also, it is noteworthy to state that, to the authors’ knowledge, no studies have investigated the effect of mixing different types of GNP–Fe2O3 hybrid nanoparticles in a base fluid. Therefore, this study aims to fill this gap by examining the effects of different mass fractions of the nanoparticles on the thermophysical properties of the resulting nanofluid.

Also, numerous studies have shown that traditional models cannot explain the behavior of nanofluids, and the experimental results often show poor agreement with well-known models [28, 29]. This limitation highlights the need for advanced modeling techniques to capture nanoparticles’ complex interactions in the fluid. With the inadequacy of conventional models in explaining the behavior of HNFs, the use of sophisticated modeling techniques, including adaptive neuro-fuzzy inference system, ANN, and response surface methodology (RSM), has emerged as a topic of significant research interest [30, 31]. These techniques have proven to be effective in predicting the properties of nanofluids, as demonstrated by various studies. Esfe et al. [32,33,34] conducted numerous studies on the TC of HNFs and utilized the ANN technique to model the experimental data. They compared the experimental correlation with the ANN model and found that the latter could predict TC with greater efficiency. This suggests that the ANN model can be a more effective tool in modeling the thermophysical properties of nanofluids. Afrand et al. [35] showed that using ANN reduced the time and cost required for measuring the rheological properties of iron-ethylene glycol nanofluid. Pare and Ghosh [36] also achieved good agreement between their ANN model and experimental data in predicting the TC of metal-oxide/water-based nanofluids. Esfe et al. [37] compared the performance of ANN and RSM in modeling the TC of titania-water nanofluid and found that ANN exhibited higher accuracy. These studies collectively suggest that this advanced modeling is a promising approach for predicting the properties of nanofluids.

Therefore, in this study, we aim to investigate the effects of temperature and the mixing ratio of GNPs and Fe2O3 nanoparticles on the thermophysical properties of GNP–Fe2O3 HNFs. To achieve this goal, the study uses both experimental and modeling approaches. RSM and ANN modeling techniques are applied to the experimental data to determine the relationships between the variables and the thermophysical properties. The results of this study are expected to provide valuable insights into the use of these HNFs in energy-efficient applications.

Notably, the motivation behind this research study stems from the growing interest in enhancing the thermophysical properties of nanofluids for various industrial applications, particularly in heat transfer and thermal management systems. This study addresses existing limitations in conventional nanofluid formulations by exploring the synergistic effects of GNP and Fe2O3 nanoparticles in a HNF matrix. This approach represents a novel contribution to the field, as it offers a unique opportunity to leverage the individual strengths of both nanoparticle types while mitigating their respective drawbacks. By carefully characterizing the thermophysical properties of the HNF and employing advanced modeling techniques such as ANN and RSM, this study aims to provide valuable insights into the behavior and performance of these innovative nanofluid formulations. The significance of this research lies in its potential to advance the understanding of nanofluid science and pave the way for developing highly efficient and tailored nanofluid systems with superior TC, µ, and EC properties. Ultimately, this study’s findings could have far-reaching implications for diverse applications ranging from electronics cooling to solar thermal energy conversion, offering significant energy efficiency and sustainability benefits.

In conclusion, this research provides a comprehensive overview of the investigation into the thermophysical properties of the HNFs, focusing on their TC, µ, and EC. The experimental procedures involved the production of HNFs with different mass ratios of GNPs and Fe2O3 dispersed in deionized water, stabilized with a surfactant. The stability of the HNFs was assessed through µ measurements and TEM imaging. Various instruments were used to measure TC, µ, and EC over specific temperature ranges. Finally, ANN modelling was employed to simulate the thermophysical properties of the HNFs through iterative adjustments of neuron numbers to fine-tune and obtain the optimal ANN architecture.

Overall, the study provides valuable insights into the design and optimization of HNFs for various applications, with ANN and RSM modelling offering a robust approach for predicting their thermophysical properties accurately.

Materials and methods

Experimental

In this research, deionized water was chosen as the base fluid because of its higher TC and lower µ in comparison with other base fluids like ethylene glycol and engine oil. The HNF with 0.1 vol% was produced by mixing GNP (15 nm) and Fe2O3 (ϕ 10–20 nm) at various mass percent ratios (0:100, 25:75, 50:50 and 75:25). The GNPs and Fe2O3 were obtained from Sigma Aldrich (DE), and MKnano Company (CA), respectively. To stabilize the HNFs, SDS surfactant (Sigma Aldrich, DE) was added at a nanoparticle-surfactant ratio of 1:1. The nanomaterials mass was estimated using Eq. (1).

$$\varphi = \frac{{\omega_{{{\text{GNP}}}} \left( {\frac{m}{\rho }} \right)_{{{\text{GNP}}}} + \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} \left( {\frac{m}{\rho }} \right)_{{{\text{Fe}}_{2} {\text{O}}_{3} }} }}{{\omega_{{{\text{GNP}}}} \left( {\frac{m}{\rho }} \right)_{{{\text{GNP}}}} + \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} \left( {\frac{m}{\rho }} \right)_{{{\text{Fe}}_{2} {\text{O}}_{3} }} + \left( {\frac{m}{\rho }} \right)_{{{\text{water}}}} }}$$
(1)

The GNP–Fe2O3 HNFs were prepared using a two-step method. To prepare the HNFs, the nanoparticles and surfactant were initially dispersed in deionized water using an ultrasonic agitator for 45 min to achieve proper suspension. While the agitation process was taking place, the nanofluid was submerged in a water bath with a specific temperature of 20 °C to avoid excessive heat and vaporization. The stability of the nanofluid was subsequently assessed by monitoring HNF viscosity over 24 h and through transmission electron microscopy (TEM) imaging.

To analyze the HNFs, their µ, TC, and EC were measured using various instruments, including a Vibro-viscometer (SV-10), KD-2 Pro meter, and EUTECH electrical conductivity (EC) meter (CON700). Measurements of µ and EC were taken between the temperatures of 20 °C and 55 °C, whereas measurements of TC were taken within a temperature range of 15 °C to 40 °C. The temperature was regulated using a water bath (LAUDA ECO). The EC meter was calibrated with the calibration fluid provided by the manufacturer, and the average value of measurement was in proximity to the value specified by the manufacturer with a residual of + 1 µS m−1. Various factors that could result in inaccuracies, such as determining the mass (m) of nanomaterials and surfactants, measuring the volume of water (V), and considering the temperature (T) were recognized, and Equation (2)was utilized to assess the corresponding uncertainty in the thermophysical properties (P).

$$u = \pm \sqrt{{\left(\frac{\partial P}{P}\right)}^{2}+{\left(\frac{\partial m}{m}\right)}^{2}+{\left(\frac{\partial V}{V}\right)}^{2}+{\left(\frac{\partial T}{T}\right)}^{2}}$$
(2)

The measurement of EC has an associated degree of uncertainty (u) of ± 2.06%; while, the measurement of TC and µ have an associated degree of uncertainty of ± 2.12% and ± 2.07%, respectively.

Artificial neural network

Using MATLAB software, an ANN was constructed to simulate the thermophysical properties of a HNF. The ANN model was fine-tuned by adjusting the number of neurons and then trained with 70% of the experimental data. The remaining 30% of the data was split into a 15% testing set and a 15% validation set. To determine the accuracy of the ANN model, the predicted values were compared against the experimental data, and the MSE was computed as a measure of effectiveness. Equation (4) outlines the MSE formula [38], which quantifies the disparity between the actual data and the predicted values generated by the ANN.

$${\text{MSE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} ({\text{Actual}}\;{\text{Value}}_{\rm i} - {\text{Preducted}}\;{\text{value}}_{\rm i} )^{2} .$$
(3)

ANNs are a machine-learning algorithm that imitates the structure and functionality of the human brain [39]. ANNs comprise interconnected artificial neurons that process and analyze data. Each neuron receives input signals from its neighboring neurons, applies an activation function to process the information, and sends the output to other neurons in the network. ANNs learn by adjusting the strengths of the connections between the neurons to optimize the network’s ability to make accurate predictions or classifications. Neurons are represented as mathematical functions that take input values (xj), multiply them by corresponding mass (wij), add a bias term (bi), and then apply an activation function (f) to produce an output, Pi. The equation for a neuron is shown in Eq. (4) [40]. To evaluate the precision of the ANN model in forecasting Phnf, the MSE was calculated by comparing the predicted and actual values of Phnf. Here, ‘n’ denotes the total number of data points.

$$P_{\rm i} = f\left( {\mathop \sum \limits_{j = 1}^{n} \left( {w_{\rm ij} x_{\rm j} + b_{\rm i} } \right)} \right).$$
(4)

Several factors must be considered when developing a practical ANN, including the learning algorithm, number of neurons, and activation function. For this study, the Levenberg–Marquardt algorithm was selected as the learning algorithm. This algorithm minimizes the difference between the predicted and actual outputs through an iterative approach. The ANN used in this study was a two-layer feedforward network, with tansig as the activation function for the hidden layer and purelin for the output layer. The mathematical formulas for tansig and purelin are presented in Eqs. (5) and (6), respectively [41].

$${\text{tansig}}\left(n\right)= \frac{2}{1+{e}^{-2\text{n}}}-1.$$
(5)
$$f\left( x \right) = \frac{1}{{1 + \exp \left( { - x} \right)}}.$$
(6)

The number of neurons in the ANN was fine-tuned to improve and optimize the network’s performance. The process involved testing various numbers of neurons in the hidden layer to find the optimal configuration that resulted in the lowest MSE value. In this study, the ANN was trained with various numbers of neurons ranging from 2 to 20, and the MSE was calculated for each configuration. As the process of generating mass and biases for the network is randomized, the network was executed multiple times with each neuron number, and the average performance was taken as the standard. The configuration that produced the lowest MSE was selected as the optimal number of neurons.

Response surface methodology

The Phnf of the HNF was modelled using the statistical method of RSM through the Design of Experiments (DoE). This involved fitting a response surface to experimental data with the software. Design Expert 13 is used for this purpose. Furthermore, input parameters ωGNP, \(\omega_{{{\text{Fe}}_{{2}} {\text{O}}_{{3}} }}\) and T, and output P (TC, µ and EC) were used to propose several polynomial functions resembling first or second-order equations as depicted in Eqs. (7) and (8), respectively [42]. The optimal polynomial function was selected based on mathematical criteria. The software then calculated the coefficients of the quadratic equation using multiple regression analysis of the experimental results. The strength of the regression equation was evaluated using R2; while, graphical techniques were used to visualize the model’s capacity to fit the actual data. The significance of the model was assessed using ANOVA. The details of the RSM analysis code and factor definition are provided in Tables 1 and 2.

$$P_{{{\text{hnf}}}} = \alpha_{0} + \alpha_{1} \omega_{{{\text{GNP}}}} + \alpha_{2} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} + \alpha_{3} T.$$
(7)
$$\begin{aligned} P_{{{\text{hnf}}}} & = \beta_{0} + \beta_{1} \omega_{{{\text{GNP}}}} + \beta_{2} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} + \beta_{3} T + \beta_{4} \omega_{{{\text{GNP}}}}^{2} + \beta_{5} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }}^{2} + \beta_{6} T^{2} + \beta_{7} \omega_{{{\text{GNP}}}} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} \\ & \quad + \beta_{8} \omega_{{{\text{GNP}}}} T + \beta_{9} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} T \\ \end{aligned}$$
(8)
Table 1 Code and factors for the RSM architecture for thermal conductivity
Full size table
Table 2 Code and factors for the RSM architecture for viscosity and electrical conductivity
Full size table

Correlation model comparison

The research analyzed and compared the effectiveness of different models, including ANFIS, ANN, RSM, and linear regression analysis. Performance evaluation was conducted using various metrics such as prediction accuracy, correlation coefficient, and absolute error. The models’ performances were further evaluated using MOD, MAPE, MAE, and RMSE, which were calculated using specific Eqs. (9)–(12) [43, 44].

$${\text{MOD}} = \frac{{{\text{actual}}\;{\text{value}} - {\text{predicted}}\;{\text{ value}}}}{{{\text{actual}}\;{\text{value}}}} \times 100.$$
(9)
$${\text{MAPE}} = \frac{1}{n} \mathop \sum \limits_{i = 1}^{n} \left| {{\text{MOD}}_{{\text{I}}} } \right|.$$
(10)
$${\text{MAE}} = \frac{1}{n} \mathop \sum \limits_{i = 1}^{n} \left| {{\text{actual}}\;{\text{value}}_{\rm i} - {\text{Predicted }}\;{\text{value}}_{\rm i} } \right|.$$
(11)
$${\text{RSME}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {{\text{Actual }}\;{\text{value}}_{\rm i} - {\text{Predicted}}\;{\text{ value}}_{\rm i} } \right)^{2} } .$$
(12)

where n represents the number of data points.

Results and discussions

Nanofluid stability

Figure 1a, b presents TEM images of nanofluids, Fe2O3 and GNP–Fe2O3 hybrid nanofluids. In Fig. 1a, the TEM image shows the Fe2O3 nanofluid, where small, uniform, and spherical nanoparticles can be observed. The nanoparticles appear well dispersed in the liquid medium, indicating good nanofluid stability.

Fig. 1
figure 1

TEM images of a Fe2O3 and b GNP–Fe2O3 hybrid nanofluids

Full size image

In Fig. 1b, the TEM image shows the GNP–Fe2O3 hybrid nanofluid, which contains both Fe2O3 nanoparticles and GNPs. The image reveals that the Fe2O3 nanoparticles in the hybrid nanofluid have a similar size and shape to those in the Fe2O3 nanofluid (Fig. 1a). However, the GNPs can also be seen as small, dark flakes dispersed within the liquid medium. The GNPs appear well distributed throughout the nanofluid and form a network-like structure with the Fe2O3 nanoparticles. This structure suggests that the GNPs may act as a stabilizing agent, preventing the aggregation of Fe2O3 nanoparticles and improving the overall stability of the hybrid nanofluid.

Figure 2 shows the changes in viscosity over time for four different nanofluids: Fe2O3, GNP–Fe2O3 (25:75), GNP–Fe2O3 (50:50), and GNP–Fe2O3 (75:25). The viscosity of each nanofluid was measured at different time intervals. The graph indicates that the viscosity of all four nanofluids remains relatively constant over time, with only minor fluctuations. This stability is important because it suggests that the nanofluids would not experience significant changes in their properties during use, which is essential for practical applications.

Fig. 2
figure 2

Viscosity stability of Fe2O3 and GNP–Fe2O3 nanofluids over time

Full size image

Thermal conductivity

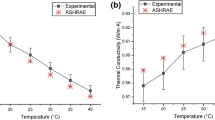
Figure 3a, b shows the effect of temperature and nanoparticle mixing percent ratio on the TC of the HNF compared to that of water. The graph in Fig. 3a shows a curve that increases with temperature, indicating that the TC of the HNF increases as the temperature increases. The increase in TC with temperature can be explained by the increase in the mean free path of the heat-carrying particles (such as electrons, phonons, and photons) as temperature increases. At higher temperatures, the particles in the material gain kinetic energy due to Brownian motion and move faster, leading to more frequent collisions between particles. However, the increased energy also means that the particles can travel farther before colliding with other particles or defects in the material, which increases the mean free path. This increased mean free path allows the particles to carry heat more efficiently through the material, resulting in higher TC. In addition, as temperature increases, the lattice vibrations in the material become stronger and more intense, leading to a higher frequency of phonon scattering events. This can also contribute to an increase in TC. Similar observations can be found in the literature [45,46,47].

Fig. 3
figure 3

Thermal conductivity of the HNF in relation to a temperature and b the mixing ratio

Full size image

Figure 3b indicates that the TC of the HNF changes with different mixing percent ratios. The graph shows that the TC increases with an increase in the mixing percent ratio, indicating that the TC of the HNF is dependent on the amount of nanoparticles present in the mixture. This shows that the TC of nanofluids is influenced by the type and concentration of nanoparticles, and the hybrid nanoparticles may have synergistic or antagonistic effects on the TC of nanofluids. In the case of this study, the TC of the HNF is enhanced with an increasing mass fraction of GNP. This could be attributed to GNPs having high TC due to their two-dimensional structure, which allows for efficient heat transfer along their surface. As the mass fraction of GNP increases in the HNF, more GNPs are available to transfer heat, thereby increasing TC. Also, the presence of Fe2O3 nanoparticles in the HNF can increase the interfacial thermal resistance between the GNP and the fluid, which could reduce the effective TC. However, as the mass fraction of GNP increases, the number of GNP–Fe2O3 interfaces also increases, which may lead to improved thermal contact between the particles and the fluid and, thus, a higher TC. The TC enhancement due to the increased mass percent of GNP could also be attributed to the Brownian motion of the nanoparticles. As the mass fraction of GNP increases, the Brownian motion of the GNP–Fe2O3 nanoparticles becomes more pronounced, leading to increased particle–particle interactions and thermal transport through the fluid.

Figure 4 shows the thermal conductivity ratio (TCR) of various nanofluids containing different mass mixing ratios of Fe2O3 and GNP at different temperatures ranging from 15 to 40 °C. The TCR is defined as the ratio of the TC of the HNF to the TC of the base fluid (in this case, water). Generally, the TCR of all the nanofluids is higher than 1, indicating enhancement. This could be ascribed to the addition of nanoparticles to the base fluid, which enhances the TC by providing an additional heat transfer pathway through interfacial thermal resistance.

Fig. 4
figure 4

TCR of the HNF in relation to the NP mass mixing ratio at various temperatures

Full size image

Further observation shows that the TCR generally increases with increasing temperature for all the nanofluids. This is because at higher temperatures, the Brownian motion of nanoparticles is increased, and they become more dispersed in the base fluid, which leads to enhanced TC. It was also noticed that HNFs with GNP have higher TCR than that of single Fe2O3 nanofluid. This could be attributed to the GNP nanomaterial’s higher TC compared to Fe2O3.

However, it is interesting to note that the TCR of GNP–Fe2O3 (75:25) nanofluid is not always the highest among the three GNP–Fe2O3 HNFs tested, as depicted in the figure. At lower temperatures (15 °C and 20 °C), the TCR of GNP–Fe2O3 (50:50) is higher than that of GNP–Fe2O3 (25:75) and GNP–Fe2O3 (75:25). This could be because the 50:50 mass mixing ratio provides the optimal balance between the TC enhancement due to GNPs and Fe2O3 nanoparticles. At higher temperatures, however, the TCR of GNP–Fe2O3 (75:25) becomes the highest, indicating that adding more GNPs is more effective in enhancing the TC at higher temperatures.

Viscosity

Figure 5a, b show the effect of temperature and nanoparticle mixing percent ratio on the µ of the HNF compared to that of water. The figures indicate that water has the lowest µ across all temperatures, while the Fe2O3 and GNP–Fe2O3 nanofluids have higher viscosities. This could be attributed to the fact that adding nanoparticles increases the particle concentration in water, consequently increasing its µ. This is because the particles can interact with each other and with the base fluid molecules, creating more resistance to flow. Also, the size of the particles in HNFs is generally smaller than that of the base fluid, which can also contribute to the increased µ. Smaller particles have a larger surface area to volume ratio, meaning they can interact more strongly with the fluid molecules, leading to higher resistance to flow. The nanoparticle shape is another factor which also plays an important role in increasing the µ of the HNF. Particles with irregular shapes can create more turbulence in the fluid, increasing the resistance to flow. Furthermore, the nanoparticles in HNFs also tend to aggregate, forming clusters or agglomerates. These clusters can further increase the resistance to flow, leading to higher µ.

Fig. 5
figure 5

Viscosity of the HNF in relation to a temperature and b the mixing ratio

Full size image

Further, Fig. 5a suggests that the µ of each nanofluid generally decreases with increasing temperature. This could be attributed to the increase in the kinetic energy of the molecules in the nanofluid, which leads to increased molecular motion. As a result, the intermolecular forces between the molecules weaken, and the fluid becomes less viscous. This increased kinetic energy of molecules also weakens the intermolecular forces and makes it easier for the molecules to slide past one another, reducing µ. In addition, the freer movement of molecules reduces the frictional forces between the fluid molecules and the walls of the container or the surface over which it flows are reduced. This could also lead to a reduction in the µ of HNF. The observed trend in Fig. 5a is supported by existing scientific knowledge [7, 25, 46].

Figure 5b indicates that the µ of the HNF is influenced by the variation in the mixing percent ratios of the nanoparticles. The graph shows that the µ of the nanofluids reduces with an increase in the mixing percent ratio. This means the µ of the HNF declines with increasing mass percent of GNP. The result suggests that the hybridization of Fe2O3 nanofluid with GNP creates a synergistic effect, which reduces the nanofluid’s µ. This is because the GNP can act as spacers between the Fe2O3 nanoparticles, thereby reducing their tendency to aggregate and increasing the fluidity of the nanofluid. Also, due to the size and shape of GNP and its consequent tendency to move more freely in the base fluid, its increased addition creates more Brownian motion, which helps to break up and disperse agglomerates of Fe2O3 nanoparticles, subsequently reducing the µ of HNF.

Figure 6 shows the relative viscosity (RV) of various nanofluids containing different mass mixing ratios of nanoparticles at different temperatures ranging from 20 to 55 °C. Relative viscosity is the ratio of the µ of the HNF to the µ of the base fluid (water) at the same temperature and shear rate. It is a measure of the resistance to flow of a fluid due to the presence of suspended particles.

Fig. 6
figure 6

RV of the HNF in relation to the NP mass mixing ratio at various temperatures

Full size image

It can be observed that the RV generally is greater than 1, which indicates µ increase with the addition of nanoparticles. This further confirms that the nanoparticles in the base fluid increased the effective volume fraction of the suspended particles and caused an increase in the resistance to the flow of the nanofluid. Also, at higher temperatures, the Brownian motion of nanoparticles increases, and they become more dispersed in the base fluid, which leads to an increase in RV.

Interestingly, the RV of nanofluids containing GNP is generally lower than that of nanofluids containing only Fe2O3 nanoparticles. This could be because GNP has a more planar shape and a larger aspect ratio than Fe2O3 nanoparticles, making them less likely to agglomerate and settle. As a result, the RV of GNP–containing nanofluids is lower.

Electrical conductivity

Figure 7a, b shows the effect of temperature and nanoparticle mixing percent ratio on the EC of the HNF compared to that of water. The figures indicate that the EC of all the nanofluids is higher than that of water, which suggests that the EC of water is elevated with the addition of nanoparticles. This is because when nanoparticles (mono or hybrid) are dispersed in the base fluid, they create a large interface area between the nanoparticle and the fluid. The increased surface area of the nanoparticles increases the number of ions present at the interface, which in turn increases the EC of the fluid. Nanoparticles also adsorb to the surface of ions present in water [48, 49], which can increase their mobility and lead to an increase in EC. Also, nanoparticles can form a percolation network in the fluid. A percolation network is a connected pathway of nanoparticles through which electric current can flow [50]. Therefore, when sufficient nanoparticles are present, they can form a percolation network, which leads to an increase in EC.

Fig. 7
figure 7

Electrical conductivity of the HNF in relation to a temperature and b the mixing ratio

Full size image

The graph in Fig. 7a shows a curve that increases with temperature, indicating that the EC of the HNF increases as the temperature increases. Similar observations have been reported in the literature [45, 51]. Much like the TC, this EC enhancement can be attributed to the intensification in Brownian motion at elevated temperatures, intensifying the mobility of ions and electrons in the HNF. When the Brownian motion of nanoparticles increases, fluid particles tend to move toward each other, which can lead to the formation of clusters. These clusters can increase the percolation network of nanoparticles and enhance the HNF’s EC. This EC augmentation also corresponds to the diminution in µ of the HNF, which suggests that the mobility of ions and electrons is enhanced due to reduced resistance to fluid flow at elevated temperatures.

Figure 7b indicates that the variation in the mixing percent ratios of the nanoparticles influences the EC of the HNF. The graph shows that the EC of the nanofluids reduces with an increase in the mixing percent ratio. This indicates that the increased presence of GNPs at a higher mixing percent ratio causes the electron transfer efficiency of the HNF to decline. This can be explained by the higher electron mobility of GNPs compared to Fe2O3 nanoparticles, which means that the electrons can transfer more efficiently between GNPs compared to Fe2O3 nanoparticles. However, as the concentration of GNPs in the HNF increases, the transfer of electrons from Fe2O3 nanoparticles to GNPs becomes less efficient. This leads to a decrease in the number of charge carriers available to conduct electricity, thus lower EC.

Figure 8 shows the electrical conductivity ratio (ECR) of the HNFs at different temperatures and nanoparticle mass mixing ratios. The ECR is the ratio of the EC of the HNF to the EC of the base fluid. The figure indicates that at each temperature, the ECR decreases with an increase in the mass mixing ratio (\(\omega_{{{\text{GNP}}}} {/}\omega_{{{\text{Fe}}_{{2}} {\text{O}}_{{3}} }}\)) of the nanoparticles. This indicates that the addition of GNP to the HNF reduces the EC of the resulting HNF.

Fig. 8
figure 8

ECR of the HNF in relation to the NP mass mixing ratio at various temperatures

Full size image

Moreover, the ECR generally increases with an increase in temperature for each mass mixing ratio of the nanoparticles. This trend is consistent with the fact that the EC of most materials increases with an increase in temperature [45, 51].

Modelling and correlation

Artificial neural network

Tables 3–5 summarize the performance of a neural network model for predicting the TC, µ and EC of the HNF, respectively. The tables show the optimal sorting of the mean squared error (MSE) performance for each property. The neural network model was trained with different numbers of neurons, and the MSE performance was calculated for training, validation, testing, and overall datasets. The tables show the number of neurons used in the neural network model, the MSE performance for training, validation, testing, and overall datasets, and the correlation coefficient for each dataset. The MSE performance is sorted based on the overall dataset, with the best-performing model at the top of the table.

Table 3 Optimal sorting of the MSE performance for the thermal conductivity
Full size table
Table 4 Optimal sorting of the MSE performance for the viscosity
Full size table
Table 5 Optimal sorting of the MSE performance for the electrical conductivity
Full size table

For the TC, as shown in Table 3, the model with 6 neurons achieved the best overall MSE performance of 1.50E−05, with the highest overall correlation coefficient. Similar to Table 3, for the µ data presented in Table 4, the model with 10 neurons achieved the best overall MSE performance of 8.77E−06, with the highest overall correlation coefficient. In the case of the EC, as shown in Table 5, the model with 18 neurons achieved the best overall MSE performance with the highest correlation coefficients for the overall datasets. Further, Fig. 9a, b displays the ANN design that includes the ideal number of neurons.

Fig. 9
figure 9

ANN optimal architecture for the a thermal conductivity, b viscosity, and c electrical conductivity

Full size image

Figures 10–12 show a graph representing the linear fitting of the training, validation, testing and overall datasets predicted values generated by the optimal ANN model for the TC, µ and EC, respectively. These graphs are useful for assessing the accuracy of the model’s prediction and estimating its correlation parameters. The study found a high degree of correlation between the predicted and actual values for all the modelled parameters, indicating a strong correlation with minimal deviations. For instance, the overall dataset has a coefficient correlation of 0.99427, 0.99979 and 0.99997 for the TC, µ and EC, respectively. The slope of the fitted line was close to 1, which indicates that the ANN model accurately predicted the TC, µ and EC of the HNFs. The result suggests that the ANN model of EC fits the data better than that of µ with negligible deviations, followed by TC, which has more visible deviations than the other properties. This indicates that the ANN model for EC and µ will likely be more accurate and reliable in predicting future observations.

Fig. 10
figure 10

ANN fitting of the predicted versus the experimental data for the thermal conductivity

Full size image
Fig. 11
figure 11

ANN fitting of the predicted versus the experimental data for the viscosity

Full size image
Fig. 12
figure 12

ANN fitting of the predicted versus the experimental data for the electrical conductivity

Full size image

Response surface methodology

The RSM is a statistical technique used to analyze the relationship between independent variables (factors) and dependent variables (response). Table 6 presents the results of the RSM model optimization for three properties: TC, µ, and EC. The table presents the p values, Adjusted R2, and Predicted R2 values for the linear, two-factor interaction (2FI), and quadratic terms of the RSM model. The p value indicates the significance of each term in the model, with a value less than 0.05 considered significant. The Adjusted R2 value represents the proportion of the variation in the response variable that is explained by the model, adjusted for the number of terms in the model. The Predicted R2 value represents the proportion of the variation in the response variable that the model can predict.

Table 6 RSM model optimization
Full size table

Table 6 shows that the linear and 2FI models for the TC are significant, with p values less than 0.05. However, the 2FI model has the highest Adjusted R2 and Predicted R2 values, indicating that it is the most important factor for optimizing the TC. Further, the linear and quadratic models were shown to be significant (p value less than 0.05), but the linear term has the highest Adjusted R2 and Predicted R2 values, indicating that it is the most significant factor for optimizing the µ. In the case of EC, all three terms (linear, 2FI, and quadratic) are significant (p value less than 0.05), with an Adjusted R2 of 0.9964, 0.9988, and 0.9995, respectively. Notwithstanding, the 2FI term has the highest Adjusted R2 and Predicted R2 values, indicating that it is the most significant factor for optimizing the EC. The models with significant factors for optimization of the different properties have been highlighted in bold within the table.

Table 7 provides the ANOVA properties for the optimal model. It shows the sources of variation, the sum of squares, degrees of freedom, mean square, F value, and p value for each of the three properties: TC, µ, and EC. For TC, the model is significant (p value < 0.0001), indicating that it can explain the observed variation in the response variable. Among the six factors considered (A, B, C, AB, AC, BC), only factors A, B, C, and AC are significant (p value < 0.05). Factor C has the highest mean square value and F-value, indicating it exhibits the greatest effect on the response variable. The residual sum of squares is small, suggesting that the model fits the data well

Table 7 ANOVA properties of the optimal model
Full size table

For µ, the model is also significant (p value < 0.0001), and only factors A, B, and C are significant (p value < 0.05). Factor C has the highest mean square value and F-value, indicating that it has the most significant effect on the response variable. The residual sum of squares is small, suggesting that the model fits the data well. In the case of EC, the model is highly significant (p value < 0.0001), and all six factors are significant (p value < 0.05). Factors A, B, and C have the highest mean square values and F-values, indicating they significantly affect the response variable. The residual sum of squares is relatively large compared to the sum of squares for the model, indicating that there may be some unexplained variation in the data.

The equations for the TC, µ, and EC of the HNF in terms of coded factors are presented in Eqs. (13), (14) and (15). These equations can be used to predict the response of the HNF system based on the levels of factors A, B, and C. This approach helps identify the factors that have the most significant effect on the response, as it allows for a direct comparison of the factor coefficients. By examining the coefficients, which represent the change in response for a unit change in the coded value of each factor, one can determine which factors have a stronger or weaker impact on the response and use this information to optimize the system or make predictions about future outcomes.

The coded equation uses + 1 to represent the high levels of the factors and − 1 to represent the low levels. This enables a comparison of the relative impact of the factors by examining the size and direction of the factor coefficients. For example, in Eq. (13), a unit increase in factor A would change 0.0252 units in TC, assuming all other factors remain constant. The interaction terms, such as AB, AC, and BC, represent the combined impact of two factors on the response.

The intercept term, which is 0.6480 for TC, represents the baseline value of the response when all factors are set to their midpoint value. It is important to note that the coded equation is unsuitable for determining the actual impact of the factors since the coefficients are scaled to accommodate the units of each factor, and the intercept is not at the center of the design space. The final equation for the TC, µ and EC of the HNF in terms of actual factors are presented in Eqs. (16), (17) and (18), respectively. These resulting equations can predict the system’s response to different levels of the independent variables in their original units.

$${\text{TC}}_{{{\text{hnf}}}} = 0.6480 + 0.0252{\text{A}} + 0.0191{\text{B}} + 0.0426{\text{C}} - 0.0016{\text{AB}} + 0.0119{\text{AC}} + 0.0081{\text{BC}}.$$
(13)
$$\mu_{{{\text{hnf}}}} = 0.8044 + 0.0070{\text{A}} + 0.0311{\text{B}} - 0.2080{\text{C}}.$$
(14)
$${\text{EC}}_{{{\text{hnf}}}} = 1105.10 + 145.90{\text{A}} + 430.02{\text{B}} + 53.30{\text{C}} + 11.81{\text{AB}} + 12.84{\text{AC}} + 29.71{\text{BC}}.$$
(15)
$${\text{TC}}_{{{\text{nf}}}} = 0.552352 + 0.001485\omega _{{{\text{GNP}}}} + 0.005865\omega _{{{\text{Fe}}_{2} {\text{O}}_{3} }} + 0.001811{\text{T}} - 0.008440\omega _{{{\text{GNP}}}} \omega _{{{\text{Fe}}_{2} {\text{O}}_{3} }} + 0.002543\omega _{{{\text{GNP}}}} {\text{T}} + 0.001290\omega _{{{\text{Fe}}_{2} {\text{O}}_{3} }} {\text{T}}.$$
(16)
$$\mu_{{{\text{hnf}}}} = 1.21196 + 0.018750{\text{R}} + 0.062250{\text{T}} - 0.011886{\text{T}}.$$
(17)
$${\text{EC}}_{{{\text{hnf}}}} = 517.96429 + 284.16964\omega_{{{\text{GNP}}}} + 709.09107\omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} + 0.614286{\text{T}} + 63.0000\omega_{{{\text{GNP}}}} \omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} + 1.95714\omega_{{{\text{GNP}}}} {\text{T}} + 3.39524\omega_{{{\text{Fe}}_{2} {\text{O}}_{3} }} {\text{T}}{.}$$
(18)

where ω is the nanoparticle mass fraction, ranging between 0 and 1.

Figure 13a–c presents a perturbation plot that demonstrates how the three factors affect the response of all the evaluated thermoelectric properties. This type of plot visually represents the relationship between the factors and the system’s response. To generate this plot, one factor is modified at a time while keeping the other factors constant, and the resulting changes in the response are observed. This approach allows the curvature of the response surface to be observed and the identification of any interactions between the factors. The slope of a line on the plot reflects the sensitivity of the response to a particular factor; while, the curvature of the line indicates the presence of interactions with other factors [52]. Based on the findings, it can be inferred that factor C (temperature) has a more significant impact on both TC and µhnf compared to factor A (mass of GNP) and B (mass of Fe2O3), which has the least impact on µ and TC, respectively. However, in the case of EC, factor B has the most significant impact on the EC of the HNF, followed by factor A, while factor C has the least impact.

Fig. 13
figure 13

Perturbation plot for a TC, b viscosity and c EC

Full size image

Figure 14a–c displays a graph that compares predicted values with actual values for all the thermophysical properties. This graph is a useful tool for evaluating the accuracy of the RSM predictive model. The graphs show that the data points of all the properties are tightly clustered on and around the linear fitting diagonal line, with only that of TC in Fig. 14a having some minor outliers. Figure 14a–c indicates a strong correlation between the fitted response values and actual values, thus indicating a satisfactory signal for the RSM models.

Fig. 14
figure 14

Linear fitting of the predicted and actual values of the a TC, b viscosity and c EC of the HNF

Full size image

In Fig. 15a–c, the external residuals are plotted against the run order of the TC, µ and EC, showing no outliers in the residual plot, with all residuals evenly distributed across the run number. This is evident as all the data points of all the properties fall within the control limits (red lines), demonstrating the validity of the models. Figure 16a–c further confirms the accuracy and suitability of the RSM models with the normal probability plot of the studentized residuals for the TC, µ and EC, respectively. Based on the results, it can be inferred that the data are normally distributed, as evidenced by the data points falling closely along the diagonal line.

Fig. 15
figure 15

Residual plot for the a TC, b viscosity and c EC of the HNF

Full size image
Fig. 16
figure 16

Normal Probability plot for the a TC, b viscosity and c EC of the HNF

Full size image

Figure 17a–c displays a contour plot illustrating the combined effects of the mass fraction of Fe2O3 and GNP on the TC, µ and EC, respectively. The contour pattern reveals the relationship between the two factors; while, the surface response graph shows the optimal process parameters that yield the highest or lowest response values. The study found that an increase in the mass fraction of the individual nanomaterials increases both the TC, µ and EC. However, the impact in more pronounced in the case of EC, compared to TC and µ, which is not impacted significantly.

Fig. 17
figure 17

Contour plot of the a TC, b viscosity and c EC of the HNF in relation to mass fraction of the GNP and Fe2O3

Full size image

Figure 18a–c displays a contour plot illustrating the combined effects of temperature and mass fraction of GNP on the TC, µ and EC, respectively. The figures show that the TC and EC of the HNF is enhanced with an increase in temperature while the µ declines. Overall, Fig. 17 and Fig. 18 indicate that the optimal TC and EC were achieved when all the factors were increased. Conversely, since a lower µ is beneficial for heat transfer [45], an optimal µ was achieved at a higher temperature and mass fraction of GNP with a lower mass fraction of Fe2O3.

Fig. 18
figure 18

Contour plot of the a TC, b viscosity and c EC of the HNF in relation to the mass fraction of the GNP and temperature

Full size image

ANN and RSM comparison

Table 8 compares the ANN and RSM models for the thermophysical properties of the HNF. The table includes three different properties: TC, µ, and EC. The table shows the values of several evaluation metrics for each property for both models. These metrics are used to assess the accuracy and reliability of the models. The table includes five different metrics used to evaluate the performance of the models. The R2 value measures the proportion of variance in the data that is explained by the model, with higher values indicating better performance. The margin-of-deviation (MOD) is the range of values that the model predictions deviate from the actual values, with smaller ranges indicating better performance. The RSME value measures the difference between the predicted and actual values, with smaller values indicating better performance. The MAE value measures the average absolute difference between the predicted and actual values, with smaller values indicating better performance. Finally, the MAPE value measures the average percentage difference between the predicted and actual values, with smaller values indicating better performance. The ANN model generally outperforms the RSM model for all three properties, as indicated by the higher R2 values and smaller values of RSME, MAE, and MAPE. Additionally, the margin-of-deviation range is smaller for the ANN models, further supporting its superiority over the RSM model.

Table 8 ANN and RSM model comparison for the thermophysical properties
Full size table

This result is similar to findings from previous studies in the literature [30, 37, 53] that have reported higher R2 values for ANN models compared to RSM models in predicting various properties.

Conclusions

This study explored the effect of temperature and nanoparticle mixing ratio on the thermophysical properties of GNP–Fe2O3 HNFs. The results showed that the TC and the EC of the HNF intensified with an increase in the temperature while the µ of the HNF declined. Additionally, an increase in nanoparticle mixing, which indicates a higher GNP than Fe2O3, causes augmentation in the TC while the EC and µ decrease. This clearly indicates that the 2D-dimensional structure of GNP, coupled with its higher TC, is beneficial in improving the thermophysical properties of the HNF and its potential for heat transfer application.

Furthermore, ANN and RSM were used to model and correlate the thermophysical properties of HNFs. The results of the ANN modelling showed that the optimal number of neurons varied for each nanofluid property. For TC, the model with 6 neurons achieved the best overall performance, while for µ, the model with 10 neurons had the best overall performance. In the case of EC, the model with 18 neurons performed the best. The optimal ANN models showed a high degree of correlation between the predicted and actual values for all three properties, with negligible deviations. The RSM results indicated that the 2FI term was the most significant factor for optimizing the TC and EC properties; while, the linear term was the most significant for optimizing the µ. The ANOVA properties for the optimal model showed that factors A, B, C, and AC were significant for TC; while, factors A, B, and AB were significant for µ. For EC, all three terms (linear, 2FI, and quadratic) were significant, with the 2FI term being the most significant. In general, the ANN models for all the properties performed better than the RSM models.

Overall, this study demonstrates the potential for using ANN and RSM models to accurately predict the thermophysical properties of HNFs based on different factors. The findings provide insights into the factors that affect the TC, µ, and EC of HNFs, which can be useful for developing better heat transfer fluids in various industrial applications.