Introduction

The polymer industry has recently seen increased interest in rubber composites, which contain natural organic fillers from renewable sources [1, 2]. In traditional rubber vulcanisation processing, carbon black or silica is commonly used as fillers; they are non-degradable and their production is energy-intensive. Both natural rubber (NR) and cellulose (CEL) are natural biodegradable materials, and their composites can be considered new-generation materials.

To date, research has focused mainly on the extraction of CEL from various bio-sources and the bonding of CEL and NR rubber in the preparation of composites [3,4,5,6] and on the mechanical, chemical, physical, and thermal properties of NR–CEL composites [7,8,9,10,11]. However, until now, almost no attention has been paid to the thermal decomposition kinetics of these NR–CEL composites.

Kinetic analysis is very important for understanding the thermal behaviour of newly designed composites [12], establishing the right processing conditions in composite production and properly managing biomass [13, 14] and wastes [15].

Thermogravimetric (TG) analysis is an essential technique for studying the kinetic mechanism during thermally affected processes. According to the Kinetics Committee of the International Confederation for Thermal Analysis and Calorimetry (ICTAC), only such temperature programmes should be applied for kinetic calculations allowing a series of experiments under different temperature regimes [16].

Although there is a lack of publications that deal with the kinetics of thermal decomposition of NR-CEL composites, there are studies on the decomposition kinetics of the individual components, i.e. NR and CEL.

TG analysis, sometimes coupled with gas chromatography or FTIR, has shown that the pyrolysis of NR is complex and does not occur in one step. The thermal decomposition process of NR (a depolymerisation/condensation and degradation reactions) takes place by the radical mechanism with the formation of isoprene, dipentene, and other compounds [17]. Power-law models are commonly used to describe the kinetics of rubber degradation, as in works [18, 19]. Some authors describe the kinetics of pyrolytic decomposition of NR in the form of two steps. In [20], the Friedman model and the nth-order model were used for kinetic analysis with formal kinetic parameters, the activation energy Ea = 215 kJ mol–1, the pre-exponential factor log A = 15.3 s–1, and the kinetic exponent n = 0.89 for the first zone and Ea = 434 kJ mol–1, log A = 32.2 s–1, and n = 4.79 for the second zone. In [21], the authors described the individual steps using the truncated Šestak–Berggren function, i.e. f1(α) = (1 – α)1.34 α0.27 and f2(α) = (1 – α)1.16 α–1.83, with apparent Ea1 = (205.2 ± 5.3) kJ mol–1 and Ea2 = (318.9 ± 7.2) kJ mol–1, respectively, and cA1 = (4.20·1016 ± 0.6·1016) min–1 and cA2 = (4.50·1016 ± 1.1·1016) min–1, respectively.

In terms of cellulose, various investigations of pyrolysis have been performed, and a relatively large number of kinetic models and mechanisms can be found in the literature. The thermal degradation of cellulose is often studied using thermogravimetric experiments in different temperature regimes. The mechanism of cellulose pyrolytic decomposition is mainly based on the basic Broido–Shafizadeh scheme [22, 23], which assumes the decomposition of cellulose into active cellulose and its subsequent decomposition into volatiles and light gases and char. The thermal degradation mechanism of cellulose is very complex in terms of its chemical nature; therefore, power-law models, especially the first–order model, are often used to simplify the kinetic analysis [22, 24, 25]. In [26], a new kinetic model was presented involving a chain scission mechanism in the form of f(α) = (1 – α)1.3 α0.392 with apparent Ea = (193 ± 0.4) kJ mol–1 and A = (5.9·1016 ± 0.5·1016) min–1. The random scission model assumes a random cleavage of the polymer backbone that gradually breaks down into shorter fragments of molecules, and if they are small enough, they evaporate [27]. In [28], the main stage of cellulose decomposition was described by the random scission reaction mechanism f(α) = (1 – α)1.1991 α0.3112 with Ea = 199.66 kJ mol–1. The random scission reaction mechanism was also applied in [29], where the authors proposed a new mechanism of cellulose pyrolysis consisting of two parallel pathways that form active cellulose (Ea = 137 kJ mol–1), and dehydrocellulose (Ea = 91.3 kJ mol–1). Active cellulose then degrades through two parallel pathways to form levoglucosan (Ea = 159.2 kJ mol–1) and some volatiles (Ea = 203.5 kJ mol–1). In addition to the random scission kinetic model, the authors also allow using the first-order model in the case of heat and mass transfer dominance. In [30], the basic kinetic model of cellulose decomposition similar to that of [29] was presented. Cellulose decomposed by parallel reactions to active cellulose (Ea = 233.25 kJ mol–1) and char and water (Ea = 251.21 kJ mol–1), while active cellulose decomposes by parallel pathways to levoglucosan (Ea = 83.74 kJ mol–1) and other volatile compounds and char (Ea = 104.67 kJ mol–1). In [31, 32], model-free methods were applied for the kinetic analysis; these methods assume that the reaction rate is a function of temperature at constant conversion and are applicable to the one-step mechanism.

However, the results of kinetic analyses of the individual components of the composite cannot be taken to describe the kinetics of the thermal decomposition of the composite. The thermal decomposition of NR–CEL composites is a complex multi-step process, and the kinetic analysis of these processes is quite challenging, as evidenced by two recent articles by the ICTAC Kinetics Committee [33, 34].

The motivation for writing this paper was to fill the research gap on the thermal decomposition kinetics of NR–CEL composites by presenting original results and new findings. The main objective of the presented study is the kinetic analysis and determination of formal kinetic parameters for the pyrolytic decomposition of three types of NR–CEL composites (differing in the amount of filler). For these purposes, an experimental TG analysis of neat NR, neat CEL, and NR–CEL composites was first performed for one heating rate, and based on the TG and DTG curves, the degradation behaviour of the neat components and composites was described and compared with the previously reported findings. Subsequently, TG analysis was performed for NR–CEL composites with graduated heating rates from 2 to 20 °C min–1. The apparent activation energy was determined using two different model-free isoconversional methods. Subsequently, model-based methods were applied, and the formal kinetic parameters of the individual decomposition steps were determined. Finally, master plots were constructed, and the kinetic degradation mechanism of the individual steps was estimated based on theoretical physico-geometrical or physico-chemical models.

Experimental

Materials and preparation of NR-CEL composites

Natural rubber SMR 10 (NR) was purchased from Kuala Lumpur Malaysia. Cellulose fibres (CEL) containing 99.5% cellulose, bulk density 90–110 g cm–3, were supplied from Greencel, Ltd. Hencovce, Slovak Republic.

Cellulose fibres were melt-blended with NR in Brabender Plasti–Corder PLE 331 (Brabender GmbH&Co. KG, Germany). The mixing was carried out at 80 °C, 90 °C, and 50 rpm. The CEL contents were 0 phr (NR–CEL 0 sample), 30 phr (NR–CEL 30 sample), 45 phr (NR–CEL 45 sample), and 55 phr (NR–CEL 55 sample), respectively. Compounds were vulcanised with the following formula: stearic acid, ZnO, plasticiser, N-tert-Butyl-2-benzothiazolesulfenamide, and sulphur. The temperature of vulcanisation was 150 °C.

Scanning electron microscopy (SEM)

All samples were broken at liquid nitrogen temperature, and the fracture surfaces were coated with an ultrathin gold layer using high–vacuum evaporation. The micromorphology of the samples was studied with SEM analysis using the VEGA TC scanning electron microscope (Tescan, Brno, Czech Republic); the acceleration voltage was 20 kV. All micrographs are backscattered electron (BSE) images. The measure distance application included in the measurement module (a part of the Vega TC software) was used to measure the 2-D geometric parameters of cellulose agglomerates and surface micromorphology.

Thermogravimetric analysis

Experimental measurements were made using the Setaram Setsys 18TM instrument using simultaneous TG/DTA analysis. The samples for analysis were approximately 10.5 mg in mass and analysed in corundum cups. The measurements were carried out at heating rates of 2, 4, 6, 8, 10, and 20 °C min–1 in the temperature interval 20–600 °C. An inert Ar (6N) atmosphere was maintained throughout the experiment. To minimise the noise of the experimental data, a blank DTA run with an empty sample cup was first performed under conditions identical to those in the following sample measurement. Then, the resulting blank DTA curve was subtracted from the sample DTA curve. This procedure was performed for each sample.

Theoretical background of kinetic modelling

In order to describe the kinetics of condensed phases, it is generally assumed that the process rate is a function of only temperature T and degree of conversion α:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\left( T \right)\,f\left( \alpha \right)$$
(1)

where k(T) presents the temperature dependence of the rate constant and f(α) is the reaction model.

The extent of conversion (or simple conversion) in the form of mass is defined as:

$$\alpha \left( t \right) = \frac{{m_{{\text{i}}} - m\left( t \right)}}{{m_{{\text{i}}} - m_{{\text{f}}} }}$$
(2)

where mi and mf are the initial and the final mass of the sample, respectively, and m(t) is the mass at a given moment of time t. The α value varies from 0 to 1.

Table 1 presents typical functions of the kinetic model for the thermal degradation of solids. Based on physico-geometric or physico-chemical assumptions, the models can be expressed as empirical models using the non-integral values of the kinetic exponents [21, 34]. All kinetic models are included in the empirical Šestak–Berggren model (SB) with three kinetic exponents m, n, p [35]:

$$f\left( \alpha \right) = \alpha^\text{m} \left( {1 - \alpha } \right)^\text{n} \left[ { - {\text{ln}}\left( {1 - \alpha } \right)} \right]^\text{p}$$
(3)
Table 1 Common kinetics models f(α)
Full size table

With a specific combination of the parameters m, n, and p, the SB model can describe different types of kinetic behaviour. Sometimes, a truncated form of the SB model (with p set to zero) is used:

$$f\left( \alpha \right) = c\alpha^\text{m} \left( {1 - \alpha } \right)^\text{n}$$
(4)

Parameter c often becomes part of the pre-exponential factor A when fitting the model to the experimental kinetic data. With c set to one (c = 1), this model transitions to the extended Prout–Tompkins model (see Table 1), where the parameters n and m are the orders of reaction and autocatalysis, respectively.

The dependence of the rate constant k(T) on temperature is expressed by the Arrhenius equation:

$$k\left( T \right) = A {\text{exp}} \left( {\frac{{ - E_{{\text{a}}} }}{RT}} \right)$$
(5)

where A is the pre-exponential factor, Ea is the activation energy, and R is the gas constant.

When a non-isothermal temperature programme is used at a constant heating rate β

$$\beta = \frac{{{\text{d}}T}}{{{\text{d}}t}} = {\text{const}}.,$$
(6)

Then by combining Eqs. (1), (5), and (6), the resulting Eq. (7) is obtained, which forms the basis of differential kinetic methods for constant heating rate [16]:

$$\beta \frac{{{\text{d}}\alpha }}{{{\text{d}}T}} = A {\text{exp}}\left( {\frac{{ - E_{{\text{a}}} }}{RT}} \right){\text{f}}\left( \alpha \right)$$
(7)

Integration of Eq. (7) leads to the basis of integral kinetic methods [16]:

$$g\left( \alpha \right) = \frac{A}{\beta }\mathop \smallint \limits_{0}^{T} \exp \left( {\frac{{ - E_{{\text{a}}} }}{RT}} \right){\text{d}}T$$
(8)

Isoconversional kinetics

All isoconversion methods assume that the rate of the process is only a function of the temperature at a constant degree of conversion [16]. Under this assumption, the derivation of the logarithmic form of Eq. (1) leads to the following relation:

$$\left[ {\frac{{\partial \ln \left( {{\text{d}}\alpha /{\text{d}}t} \right)}}{\partial T}} \right]_{\upalpha } = - \frac{{E_{\upalpha } }}{R}$$
(9)

Equation (9) makes it possible to determine Eα for selected values of conversion α without considering the specific reaction model (model-free methods). However, even if no model is explicitly stated, the existence of some model f(α) is implicitly assumed [16].

In this paper, two model-free methods that are often used for pyrolysis decomposition have been chosen to determine the apparent activation energy: the differential Friedman method and the integral Kissinger–Akahira–Sunose (KAS) method.

Here, only the principal equation of the Friedman method [36] is given:

$${\text{ln}}\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{{\upalpha ,{\text{i}}}} = {\text{ln}}\left[ {f\left( \alpha \right)A_{\upalpha } } \right] - \frac{{E_{\upalpha } }}{{RT_{{\upalpha ,{\text{i}}}} }}$$
(10)

The isoconversional integral methods are based on an approximation of Eq. (8) that does not have an analytical solution. The KAS method [37] is expressed as

$${\text{ln}}\left( {\frac{{\beta_{{\text{i}}} }}{{T_{{\upalpha ,{\text{i}}}}^{2} }}} \right) = {\text{const}} - \frac{{E_{\upalpha } }}{{RT_{{\upalpha ,{\text{i}}}} }}$$
(11)

The value of Eα in Eqs. (10) and (11) can be determined from the slope of the left side of the equation against 1/Tα,i for each value α. The index i expresses an individual heating rate for a non-isothermal linear programme.

Note that model-free methods are applicable to single-step processes (reactions), where the reaction mechanism does not change significantly during the step. In case of multi-step kinetic analysis, it is assumed that the whole process takes place in several steps, which can be independent, competitive, consecutive, separate, or overlapping. Each step of the process has its own degree of conversion α, reaction rate dα/dt, and a so-called kinetic triplet: the apparent activation energy Ea, the apparent pre-exponential factor A, and the reaction model f(α) [16].

Results and discussion

Interfaces/morphologies of NR–CEL composites

SEM analysis was performed to study filler distribution and compatibility between the filler and the matrix. SEM images for the filler (CEL) and the NR–CEL 30 and NR–CEL 55 composites are shown in Figs. 1 and 2. Cellulose agglomerates ranged from 2.70 to 6.37 μm in thickness and from 19.24 to 28.33 μm in length. The cellulose particles have a fibrous structure with a smooth surface.

Fig. 1 
figure 1

SEM images of cellulose fibres at different magnifications

Full size image
Fig. 2
figure 2

SEM images of NR–CEL composites with different filler content CEL a fracture surface, b section

Full size image

Figure 2 presents SEM images of a fracture surface (Fig. 2a) and a section (Fig. 2b) of NR–CEL composites. In the detailed image of the section of the NR–CEL 30 composite, black spots (cavities) can be observed. Poor filler dispersion in the matrix caused a sharp interfacial adhesion between the matrix (NR) and the filler. Relatively poor filler incorporation can be observed in the NR–CEL 55 composite section. The weak interfacial adhesion and compatibility between the filler and the matrix are caused by cellulose being inherently hydrophilic and the matrix being hydrophobic. Abundant hydrogen bonding allows the cellulosic filler to stick together and resist wetting by the matrix, resulting in poor filler dispersion and bonding [38]. The aggregation of the filler on the surface of the composite, the uneven distribution of the filler in the matrix, and impaired interfacial adhesion and bonding in composites in which more filler was formulated were also confirmed by studies [39, 40].

TG/DTG analysis

TG analysis was performed to investigate the thermal behaviour of the samples analysed. Figure 3 presents the TGA and DTG curves of samples NR, CEL, NR–CEL 0, NR–CEL 30, NR–CEL 45, and NR–CEL 55 measured at a heating rate of 10 °C min–1. It can be seen from these figures that the pyrolysis trends of NR and CEL are the same, although the pyrolysis temperatures are different. As a polysaccharide, CEL has thermal stability much lower than that of NR, and its residual char after pyrolysis is higher. As shown in Fig. 3, the main temperature range of NR pyrolysis is from 310 to 470 °C, where the highest mass loss occurs. The temperature of the significant peak is 377 °C with a maximum mass loss rate of 17.7% min–1. The typical shoulder for NR is visible at higher temperatures on the DTG curve. The results are comparable to previously reported TG/DGT curves for NR, e.g. [18, 20, 41, 42]. In the case of CEL (Fig. 3), the main pyrolysis zone ranges from 270 to 380 °C with a peak at 348 °C and a maximum loss rate of 15.4% min–1. These findings are also consistent with previous studies [28, 29, 43, 44]. The slight mass loss at lower temperatures (before 270 °C) is caused by the evaporation of physically adsorbed water and light volatiles [43, 45].

Fig. 3
figure 3

TG curves (left) and DTG curves (right) of NR, CEL, and NR–CEL composites, heating rate 10 °C min−1

Full size image

Figure 3 also presents the TG and DTG curves of the sample NR–CEL 0. Compared with the NR curve, a slight shift to lower temperature and a slight reduction in the mass loss rate can be found at the maximum peak temperature. The shoulder at higher temperatures (DTG curve) is straighter than that of the NR curve. Vulcanisation reduced the degree of polymerisation because the polymer chains are partially broken by heating and cross-linking processes. According to [18] and [46], these slight changes in the DTG curve were caused by the addition of sulphur during vulcanisation. The TG curve in Fig. 3 shows that the vulcanisation process also results in an increased proportion of residual char compared to pure NR. According to [41], during vulcanisation, the structure of the network formed by the cross-linking reactions increased the thermal stability of the residuals of char and thus weakened the secondary reactions in the residuals. This increased the char yield.

In NR–CEL composite systems, the degradation mechanism is rather complex. The addition of a filler (CEL) to NR reduces its thermal stability and shifts the pyrolysis temperature interval (reaction zone) to lower temperatures, while the initial degradation temperature is affected more than the termination temperature; see Fig. 3. If we compare the composites NR–CEL 30, NR–CEL 45, and NR–CEL 55, there is a slight shift to lower temperature values (by 3–4 °C) in the initial decomposition temperature for the applied filler range. This agrees with the authors [47], who analysed NR/regenerated CEL in the range of 10–100 phr CEL. A significant effect of the addition of fillers on the shift of the pyrolysis temperature interval towards lower temperatures was demonstrated in a study [10] on NR/CEL blends with 25, 50, and 75 mass% cellulose. The authors in [8] found that the degradation temperature of the NR/nanocellulose blend with 2.5 mass% nanocellulose is somewhat higher than that of the unfilled NR; however, with a higher percentage of filler, it shifts to a lower temperature. It follows from the above–mentioned observations that the exact relationship between the CEL content and the pyrolysis temperature shift cannot simply be determined for NR–CEL composites. The effect of CEL in NR–CEL composites on the temperature interval of pyrolysis depends on the amount and type of CEL, the modification of CEL to increase the compatibility between hydrophilic CEL and the hydrophobic rubber matrix, and the method of processing NR–CEL composites [1].

The thermal behaviour of NR–based composites reflects the thermal nature of their constituents. It is evident from Fig. 3 when comparing the DTG curves for NR, and CEL, and the composites. The DTG curves of the NR–CEL composites show two maximum peaks at temperatures of about 360 and 380 °C. When the DTG curves of three composites are compared, it is clear that, for the peak at a lower temperature, the mass loss rate increases with increasing CEL contents and for the peak at a higher temperature, the mass loss rate decreases with increasing CEL contents. Thus, it can be assumed that the first DTG peak located at a lower temperature corresponds to a cellulosic fraction, and the second peak corresponds to an NR fraction. The shape of the DTG curves (the existence of two maximum peaks) suggests that the structure of the NR–CEL polymers studied could be formed by an interpenetrating polymer network (see Fig. 2), as also presented in [47].

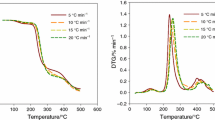
Figures 4–6 present the TG and DTG curves for the pyrolysis of NR–CEL composites measured at graduated heating rates of 2–20 °C min–1. As the heating temperature increases, there is generally a shift of the mass loss (and thus the reaction zone) to a higher temperature region (Figs. 4a, 5a and 6a). At the lowest heating rate (2 °C min–1), the pyrolysis interval is approximately from 230 to 440 °C, while at the highest heating rate (20 °C min–1), the pyrolysis interval is approximately from 280 to 470 °C. The increasing heating rate affects the thermal gradients in the sample and thus the heat transfer, which is less effective inside the sample at higher heating rates.

Fig. 4 
figure 4

NR–CEL 30, graduated heating rates from 2 to 20 °C min–1, a TG curves, b DTG curves

Full size image
Fig. 5 
figure 5

NR–CEL 45, graduated heating rates from 2 to 20 °C min–1, a TG curves, b DTG curves

Full size image
Fig. 6 
figure 6

NR–CEL 55, graduated heating rates from 2 to 20 °C min–1, a TG curves, b DTG curves

Full size image

The DTG curves show two main peaks (Figs. 4b, 5b, and 6b). Peak temperatures for the given heating rate were found to be near the same for the three NR–CEL systems, see Table 2. For a heating rate of 2 °C min–1, the first peak temperatures (Tp1) are 332 °C, 354 °C, and 332 °C; for the second peak temperatures (Tp2) are 357 °C, 353 °C, and 357 °C. At the highest heating rate of 20 °C min–1, the peak temperatures are 375 °C, 371 °C, and 371 °C for the first peak and 393 °C, 391 °C, and 391 °C for the second peak. For the other heating rates, the peak temperatures lie within the given range. Thus, the amount of filler (CEL) does not affect the peak temperatures. For a given heating rate, the Tp1 temperatures are almost identical for all three composites. The same is true for the Tp2 temperatures. However, the amount of filler affects the rate of mass loss at peak temperatures (Vp), as shown in Table 2. Increasing the filler content increases the mass loss rate of the peak at lower temperatures (Vp1) and decreases the mass loss rate of the peak at higher temperatures (Vp2). For a given heating rate, the values of mass loss rate Vp1 have an increasing tendency with increasing CEL content in the composites, and for values of Vp2 the tendency is the opposite. This trend can also be seen in Figs. 4b, 5b, and 6b). It indicates that the amount of filler affects the thermal degradation mechanism of the NR-CEL system.

Table 2 Approximate values of temperature T (°C) and the rate of mass lost V (mass% min–1) for two peaks in Figs. 4b, 5b and 6b
Full size table

Kinetic analysis

NETZSCH Kinetics Neo software was used for kinetic computations.

Model-free methods

In this study, model-free methods were used only to calculate the apparent activation energies Ea. The dependence of Ea on the conversion calculated according to the Friedman and KAS methods for the NR–CEL composites is shown in Fig. 7. The values of apparent Ea were calculated for α = 0.01–0.99 with a step of 0.01. The low values of Ea for α < 0.1 are probably related to the moisture release process. The sharp increase in the Ea values for α > 0.95 may be related to reactions in the ash residue. In order to exclude initial and final effects, it is recommended to determine Ea values in a range of α = 0.05–0.95 [16]. Tables S1–S3 in the Supplementary information section present selected values of the apparent activation energy, including their errors. The following conclusions can be drawn from Fig. 7 and Tables S1–S3: The trend of the dependence of Ea on conversion is the same for both models; the value of Ea gradually increases until it reaches a maximum at conversion values between 0.7 and 0.8 and then decreases. The increase in the Ea values to the maximum for the Friedman model is steeper than for the KAS model. The influence of the amount of filler on the behaviour of Ea cannot be unambiguously formulated from these curves. The calculated coefficients of determination R2 for the NR–CEL 30, NR–CEL 45, and NR–CEL 55 components are as follows: Friedman model: 0.99988, 0.99978, and 0.99993; KAS model: 0.99284, 0.99288, and 0.99305, respectively.

Fig. 7
figure 7

The apparent activation energy Ea as a function of conversion α calculated according to the Friedman and KAS methods

Full size image

Figure 8 (and Figs. S1 and S2) shows the simulated conversion versus temperature curves and conversion rate versus temperature curves according to the Friedman and KAS models compared to the experimental data for the NR–CEL composites. It can be seen from Fig. 8 (and Figs. S1 and S2) that the Friedman model fits the experimental curves better than the KAS model. The KAS model is unable to distinguish the two peaks on the conversion rate versus temperature curves.

Fig. 8
figure 8

Simulated α–T curves (left) and conversion rate – T curves (right) according to the Friedman model (top figures) and the KAS model (bottom figures) compared to experimental data for the NR–CEL 30 composite. Squares—experimental data, lines—model

Full size image

Although the correlation between the experimental data and the Friedman model is excellent (see the high values of the determination coefficients above and Figs. 8, S1, and S2), it is evident from Fig. 7 that the pyrolytic decomposition of the NR–CEL composite does not occur in one step. This statement is consistent with the conclusions of the works [4, 8, 10].

The multi-step kinetic modelling

The multi-step decomposition kinetics of the NR–CEL composites studied in this work was modelled using an extended Prout–Tompkins model (Table 1). The model-fitting procedure was used for the optimal multi-step kinetic model determination; the procedure was based on the calculated statistical parameters (the coefficient of determination R2, the residual sum of squares RSS, and F-test).

The resulting optimal model consists of two kinetically independent parallel processes, each with two consecutive steps. The proposed scheme of the multi-step kinetic model is as follows:

A → B → C.

D → E → F.

It is assumed that these steps overlap each other. This assumption is based on TG/DTG analyses, where it was found that the temperature intervals of active pyrolysis of NR and CEL overlap (for a heating rate of 10 °C min–1, the pyrolysis temperature interval of NR is 310–470 °C and of CEL is 270–380 °C). Furthermore, the individual components of the NR–CEL composite pyrolyse in overlapping steps, as was demonstrated for NR in [21] and for CEL in [29, 30]. The model of kinetically independent processes is consistent with [34] for “a mixture of different materials that react in partially overlapping temperature regions (typically co-precipitates and composites)”.

The overall rate of pyrolytic decomposition of individual NR-CEL composites can be expressed by a general equation [34]:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \mathop \sum \limits_{{{\text{i}} = 1}}^{N} c_{{\text{i}}} A_{{\text{i}}} {\text{exp}}\left( { - \frac{{E_{{{\text{a}},{\text{i}}}} }}{RT}} \right)f_{{\text{i}}} \left( {\alpha_{{\text{i}}} } \right)$$
(12)

with \(\mathop \sum \limits_{{{\text{i}} = 1}}^{N} c_{{\text{i}}} = 1\) and \(\mathop \sum \limits_{{{\text{i}} = 1}}^{N} c_{{\text{i}}} \alpha_{{\text{i}}} = 1\), where ci is the contribution of the ith step and N is the total number of steps (four in this case).

Values of all the kinetic parameters in Eq. (12) had to be calculated employing the optimisation method via nonlinear least-squares analysis to minimise RSS:

$${\text{RSS}} = \mathop \sum \limits_{{{\text{k}} = 1}}^{L} \mathop \sum \limits_{{{\text{j}} = 1}}^{M} \left[ {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{{{\text{exp}}, {\text{k}}, {\text{j}}}} - \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{{{\text{cal}}, {\text{k}}, {\text{j}}}} } \right]^{2}$$
(13)

where L denotes the total number of experimental curves and M the total number of data points in the individual curve, k identifies the kinetic curve and j each data point in the curve. The subscripts exp and cal mean experimental and calculated data, respectively [34].

The calculated values of the formal kinetic parameters, that is, the apparent activation energy Ea, the apparent pre-exponential factor A, and the kinetic exponents n and m, are given in Table 3. The calculated coefficient of determination R2 for the entire model is as follows: NR–CEL 30: R2 = 0.99983; NR–CEL 45: R2 = 0.99978 and NR–CEL 55: R2 = 0.99995. The value of R2 characterises the goodness of fit of the model to the experimental data. Figures S3–S5 show the simulated α–T curves and the conversion rate– T curves according to the proposed multi-step model compared to the experimental data for the NR–CEL composites analysed. It follows from the calculated values of the R2 parameters and from Figs.S3 to S5 that the proposed multi-step model fits the experimental data relatively well and is able to distinguish two peaks on the conversion rate – T curves. Furthermore, it can be seen from Figs. S3 to S5 that as the heating rate increases, the conformity of the experimental data with the proposed model decreases.

Table 3 Calculated values of the apparent activation energy Ea (kJ mol–1), the apparent pre-exponential factor log A (log s–1), and the exponents n and m for the individual steps
Full size table

Because the pyrolytic decomposition of NR–CEL composites is a complex process, the steps presented here are assumed to be the main steps; however, they may not be the only steps or all the steps. These steps also do not represent individual chemical reactions; they are assumed to include a series of consecutive and/or competitive reactions.

To better understand the thermal decomposition kinetic mechanism of the NR-CEL composites, the individual steps of the proposed model were compared with some of the theoretical models listed in Table 1 using the method of master plots; see Fig. 9.

Fig. 9
figure 9

Comparison of the kinetic function f(α) = (1–α)n αm for individual steps of the composites analysed with theoretical models

Full size image

Step A → B has the shape of an nth-order model for the entire range of conversion α for the three composites. The order of autocatalysis m is very low for the A → B and B → C steps (see Table 3). As the amount of CEL increases, the value of Ea increases in the A → B step; therefore, it affects the kinetics of the decomposition of this step. The value of Ea is higher for the B → C step than for the A → B step for all composites. The B → C step follows an nth-order model up to α = 0.5; at higher values of α (α > 0.5) it is difficult to distinguish the curves of the F2, F3, and D3 models. Due to the relatively high values of Ea (302–349 kJ mol–1), it is probable that this step obeys the diffusion mechanism at higher conversion values. Perejón et al. [21] have found that the pyrolytic decomposition of NR occurs in two non-independent overlapping stages, where the second stage follows a diffusion kinetic model (D3). The authors in [48] also explained the high value of Ea in the second step by a diffusion mechanism; moreover, they specified the diffusion of pyrolysis products not only from the surface but also from the bulk polymer to the surface. The amount of CEL influences the decomposition kinetics in the B → C step; the value of Ea is the highest in the NR–CEL 55 composite. Higher Ea values in the B → C step may also be related reactions that occur in the char residue. As mentioned in the TG/DTG analysis section, the residual char of CEL is higher than that of NR; thus, in the composite with the highest amount of CEL NR–CEL 55, char will form in more significant amounts than in the other two composites.

By comparing the calculated kinetic parameters in Table 3 and the estimated decomposition mechanism in the A → B and B → C steps with the data from the literature discussed in the Introduction section, it can be assumed that the steps A → B and B → C mainly correspond to the thermal decomposition of a NR fraction.

The decomposition mechanism of the D → E step is strongly affected by the amount of cellulose in the analysed composites. In the conversion interval up to α = 0.5, this step has the shape of a random scission mechanism with a minor deviation for the NR–CEL 30 composite, some type of autocatalytic reaction (nucleation mechanism) and/or chain scission mechanism with large deviations for the NR–CEL 45 composite and the shape of a model of the nth-order for the NR–CEL 55 composite. With the increase in proportion of cellulose, the decomposition mechanism of this step is transferred from sigmoidal models involving various combinations of nucleation and random scission of polymer chains to the mechanism of deceleration model, where the consumption of reactant molecules is taken as the only factor influencing the reaction rate. The different behaviour of the NR–CEL 55 sample in step D → E may be related to the agglomeration of CEL during sample preparation (see the explanation in the Interfaces/morphologies of NR–CEL composites section), which results in a different internal structure and therefore different heat and mass transfer inside the sample, resulting in different kinetics of decomposition. The authors in [29] allow the use of the nth-order model in the case of heat and mass transfer dominance instead of the random scission model for the kinetic description of CEL pyrolysis. Step E → F follows the chain scission mechanism for the entire range of conversion α; for the NR–CEL 30 composite, it has exactly the shape of the L2 model, and for the other two composites, there are small deviations. With increasing amounts of CEL, the value of Ea increases in this step, which is a consequence of the higher amount of char in samples with higher amounts of CEL.

From the comparison of the calculated formal kinetic parameters (see Table 3) with those of the literature discussed in the Introduction section, it could be hypothesised that the steps D → E and E → F mainly belong to the pyrolysis of a cellulosic fraction.

The above kinetic analysis indicates that the thermal decomposition mechanism of the investigated NR-CEL composite is dominated by the decomposition of individual components, NR and CEL, which is expressed by the kinetic model of two independent parallel processes. The cause of this behaviour may be the weak compatibility between NR and CEL, which is visible from the SEM photographs as an interpenetrating polymer network (see Interfaces/morphologies of NR-CEL composites section). The cellulose fibres were not surface modified to improve the compatibility between the non-polar and hydrophobic matrix (NR) and the polar and hydrophilic filler (CEL). The interpenetrating polymer network manifested itself in the thermal analysis as two separate peaks on the DTG curves and in the kinetic analysis as the mechanism of two kinetically independent parallel processes.

For a deeper and more detailed description of the thermal decomposition of the analysed composites in terms of the formation of individual chemical species and compounds, another experimental technique (FTIR, gas chromatography, mass spectrometry, etc.) would have to be used, which is beyond the scope of this work.

Conclusions

A detailed kinetic study of the pyrolysis of NR–CEL composites with different amounts of filler was presented based on thermogravimetric data. The main findings are summarised as follows:

  • The DTG curves of the NR–CEL composites show two maximum peaks; the first DTG peak located at lower temperature corresponds to a cellulosic fraction, and the second peak corresponds to an NR fraction.

  • The amount of CEL does not affect the DTG peak temperatures; however, the amount of CEL affects the rate of mass loss at peak temperatures. Therefore, the amount of CEL affects the thermal degradation mechanism of the NR–CEL composites.

  • The Friedman model fits the experimental data better than the KAS model. However, model-free methods cannot be recommended because the pyrolytic decomposition of the NR–CEL composite does not occur in one step.

  • The extended empirical Prout–Tompkins model and the NETZSCH Kinetics Neo software with the model–fitting procedure were used to find the optimal multi-step kinetic model. The proposed model consists of two parallel processes that are kinetically independent: A → B → C and D → E → F.

  • For each step of all analysed NR–CEL composites, the formal kinetic parameters (Ea, A, and the kinetic exponents n and m) were calculated. For NR–CEL 30, NR–CEL 45 and NR–CEL 55 are calculated values of apparent Ea as follows (in kJ mol−1), step A → B: 163, 174, and 230; step B → C: 320, 302, and 349; step D → E 260, 271, and 161; step E → F: 249, 268, and 296, respectively.

  • By comparing the empirical model with theoretical models based on geometrical-physical and physico-chemical assumptions, it was found that step A → B has the shape of nth-order model, step B → C follows mainly diffusion model, the mechanism of step D → E transfers from a random scission kinetics model to nth-order model with increasing amount of CEL, and step E → F obeys the chain scission mechanism.

  • The amount of filler (CEL) affects the kinetic behaviour of the studied composites in all four steps.