Abstract
A wide range of studies was conducted to increase the heat transfer rate and reduce the size and cost of shell and tube heat exchangers (STHE). The paper’s contributions lie in its ability to provide a comprehensive, up-to-date, and systematic overview of the various methods available for heat transfer enhancement in STHEs, making it an essential resource for researchers, engineers, and practitioners in the field of heat transfer. The studies that researched the overall heat transfer coefficient (U), number of transfer units, exergy efficiency, pressure drop, and thermal–hydraulic performance were reviewed. There are some advantages of the passive method such as no external needed power and lower operating cost compared to the active methods. The studies broadly support the view that heat transfer enhancement in STHE is heading toward considerable progress. A total of 47.8% of studies have focused on the passive approach, the air injection method, enhancing heat transfer utilizing nanofluids, and compound methods have percentages of studies 20.2, 22.3, and 9.7%, respectively. The air bubble injection causes the rise of the U ratio where the maximum value was indicated at 452% compared to only water flow. Swirl vane, corrugated tube, and wire coil insert have U ratio values of 130, 161, and 264%, respectively. Nanofluid results in a growth in the heat transfer where the TiO2 has the maximum U ratio (175.9%) compared to traditional fluid. The combination of air injection and passive heat augmentation methods, which was shown to be a substantial solution to several issues, needs to be the focus of more work in the future. Geometrical changes in tube surfaces in STHE are too required in the future with the use of materials coating to enhance heat transfer. The theoretical analysis of heat transfer techniques still needs to be improved, especially for pertinent empirical formulations. Also, since there aren’t many relevant numerical simulations, more attention is required.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
A shell and tube heat exchanger (STHE) is a device that transfers heat between two or more fluids and is used to gain or reject heat in a system. Most chemical and mechanical systems use STHEs. Ventilation, heating and air conditioning, radiators, condensers, boilers, preheaters, and fluid coolers are some of the most typical uses. HEs are a key component of efficient energy generation. HEs have an impact on the overall efficiency and size of a system. To achieve the preferred tradeoff between size and efficiency of the system, heat exchangers (HE) shapes are required to reach a consensus between HE effectiveness and pressure drop (∆P) [1]. With every system of energy conversion, the trade-off between system efficiency and system size will be different. Many factors determine how HEs are categorized, including the transfer process, surface compactness, flow arrangement, the mass of fluids, transfer mechanisms, kind of service, and structure. Tubular exchangers, plate exchangers, extended surface exchangers, and regenerative HEs are the four main types of HEs based on construction. Tubular HEs are made up of circular tubes and are further divided into three types: double pipe, spiral tube, and STHEs [2].
Heat exchangers
A heat exchanger is a device used to transfer heat from one fluid to another, without the fluids coming into direct contact with each other. HEs are widely used in industrial, commercial, and residential settings, and can be found in a variety of applications, including refrigeration and air conditioning systems, power generation, chemical processing, and food and beverage production.
Heat exchangers classification
Heat exchangers can be classified in various ways, based on their construction, working principle, or application. The type of HE used in a particular application will depend on various factors, including the required heat transfer rate, the types of fluids involved, and the available space and resources. HEs can be classified based on their construction into several types, including [3].
-
Shell and tube heat exchangers
This is the most common type of HE. It consists of a cylindrical shell with a bundle of tubes inside. One fluid flows through the tubes, while the other fluid flows around the outside of the tubes in the shell.
-
Plate heat exchangers
Plate heat exchangers consist of a series of plates arranged in a stack. The plates have channels through which the fluids flow. The plates are typically corrugated to increase the surface area available for heat transfer.
-
Spiral heat exchangers
Spiral heat exchangers consist of two long, coiled metal strips, one of which is wound around the other to create two separate channels for the fluids to flow through.
-
Finned tube heat exchangers
Finned tube heat exchangers have fins attached to the outer surface of the tubes to increase the surface area available for heat transfer.
-
Plate-fin heat exchangers
Plate-fin heat exchangers consist of alternating layers of corrugated fins and flat plates. The fluids flow through channels formed by the fins and plates.
-
Regenerative heat exchangers
Regenerative heat exchangers use a matrix of solid material to absorb and release heat as the fluids flow through it. The matrix can be made of ceramic, metal, or other materials. There are many systematic effects of HE. The HEs can improve the energy efficiency of systems by transferring heat from waste streams to incoming streams, thereby reducing energy consumption and operating costs. HEs can help maintain consistent product quality by controlling the temperature of processed fluids, which can affect product characteristics such as taste, texture, and appearance. HEs can reduce wear and tear on equipment by maintaining optimal operating temperatures, thereby reducing the risk of breakdowns, and prolonging the life of machinery. HEs can reduce the environmental impact of systems by reducing the energy required to operate them, which can reduce greenhouse gas emissions and other pollutants.
STHEs structures and geometry
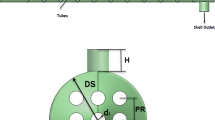
Numerous tubes make up STHEs, which contain either heated or cooled fluid. To supply or absorb heat as required, a second fluid circulates through the tubes that are being heated or cooled. The term "tube bundle" refers to a group of tubes, which may comprise plain, longitudinally finned, and other kinds of tubes. Because of their toughness, STHEs are commonly utilized in high-pressure applications. To promote efficiency, HEs are designed to maximize the surface area of the wall separating the two fluids while lowering flow resistance. STHE maintenance and cleaning methods are critical aspects of HE designs and development. The efficiency of the exchanger is impacted by the inclusion of fins or corrugations in many directions, which increase surface area and can guide fluid flow or create turbulence [4]. Fouling is a natural occurrence that leads to decreased heat transmission and efficacy, as well as higher production costs. This necessitates a yearly cleaning and maintenance routine for STHEs. Fouling can be caused in a variety of ways, and water pollution can have a negative impact [5] (Fig. 1).
Limiting requirements for STHE
In the design of a STHE, several limiting requirements need to be considered to ensure efficient and safe operation. Overall, a successful design of a STHE will require careful consideration of limiting requirements such as pressure, temperature, flow rate, fouling, and material limitations. Some of these requirements can be concluded in those points [6]:
-
The STHE must be designed to withstand the maximum pressure it will be exposed to during operation. This includes both the internal pressure of the fluid being heated or cooled, as well as any external pressure from the surrounding environment.
-
The materials used in the construction of the HE must be able to withstand the highest temperature of the fluid being heated or cooled. This is particularly important for high-temperature applications, where failure to account for temperature limitations can result in equipment failure and safety hazards.
-
The flow rate of the fluid through the HE must be within a specified range to ensure efficient heat transfer. If the flow rate is too low, heat transfer will be slow, while if the flow rate is too high, it can lead to excessive pressure drop and reduced heat transfer efficiency.
-
Fouling is the buildup of material on the heat transfer surface, which can reduce the heat transfer efficiency of the HE. The design of the HE must consider the expected fouling characteristics of the fluid being processed and include measures to prevent or reduce fouling.
-
The materials used in the construction of the HE must be compatible with the fluids being processed. This includes considerations such as corrosion resistance, chemical compatibility, and thermal expansion properties.
Heat transfer enhancement method’s overall view
Heat transfer enhancement has been developed and widely used in HE applications throughout the last decade. Accommodating high heat fluxes is the goal of augmentative heat transfer (h). Attempts to lower the size and expense of the HE, as well as energy usage, have been made to date. Decreasing the temperature driving force, which boosts second law efficiency and lowers entropy generation, is the most important variable in reducing the size and cost of the HE, which typically leads to lower capital costs. The use of various strategies to boost the q by obligatory force convection is a tremendous effort [7]. Meanwhile, it has been discovered that this method may lower the size of the HE device while also conserving energy. The importance of using different methods of heat transfer enhancement in STHE can be concluded in those points [8]:
-
Reducing the size of the equipment.
-
Maximizing heat transfer.
-
Reducing the pumping power.
-
Minimizing the cost of energy and materials.
-
Improving system and process efficiency.
-
Creating the ideal HE size.
-
Transferring the necessary quantity of heat efficiently.
There are three techniques for increasing the q within STHEs, which reflect the responsibility of all HEs (passive, active, and combined passive and active) methods. Geometrical or surface adjustments without external power, for example, treated surfaces, twisted tapes, abrasive surfaces, expanded surfaces, or the use of different inserts, are used in the passive approach. Enhancement devices, wire coils, twisted tape, coiled tubes, swirl flow generation, surface tension devices, and gas and liquid additives are examples of such inserts seen in Fig. 2. The active approach, which employs external power, includes magnetic field reciprocating plungers, fluid suction for flow disruption, surface or flow vibration, and the use of electromagnetic fields. The compound approach, which combines active and passive procedures, is the third option. Using solely the passive or active methods yields appealing outcomes.
The advantages of passive techniques
There are some advantages of the passive method such as no external needed power and lower operating cost compared to the active method. Many configurations of active methods can be added for the HE without modification in HE designs. Some passive techniques can be inserted into the HE, but the major modifications need to change the design or build a new one. The advantages of passive methods can be concluded in those points:
-
These techniques generally use simple surface or geometrical modifications to the flow channel by incorporating inserts or additional devices.
-
It does not need any external power input.
-
The insert manufacturing process is simple, and these techniques can be easily employed in an existing HE.
-
Passive insert configuration can be selected according to the HE working condition.
-
It can be used in the design of compact HEs.
Thermal–hydraulic parameters
The thermal performance parameters of STHE for example effectiveness (ε), overall heat transfer coefficient (U), number of transfer units (NTU), exergy efficiency (ηex), hydraulic parameters like pressure drop and friction factor thermal, and hydraulic performance parameter (\(\upeta \)) are listed in this section.
Effectiveness (ε)
In a steady state, the STHE’s ε is calculated by dividing the actual heat transfer by the maximal heat transfer [9] \(\varepsilon = \frac{{\dot{Q}}}{{\dot{Q}_{\max } }}\):
where \(\dot{m}_{{\text{h}}}\) is the mass flow rate of hot fluid, \(c_{{{\text{p}},{\text{ h}}}}\) is the specific heat of hot fluid, \(T_{{{\text{h}},{\text{ in}}}}\) is the temperature at the inlet of the hot side and, \(T_{{{\text{h}},{\text{ out}}}}\) is the temperature at the outlet of the hot side. The mass flow rate of cold fluid is expressed in \(\dot{m}_{{\text{c}}}\), \(c_{{{\text{p}},{\text{ c}}}}\) is the specific heat of cold fluid, \(T_{{{\text{c}},{\text{ in}}}}\) is the temperature at the inlet of the cold side and, \(T_{{\text{C, out}}}\) is the temperature at the outlet of the cold side.
Overall heat transfer coefficient (U)
At first, the STHE's average heat transfer rate (\(\dot{Q}_{{{\text{ave}}}}\)) may be calculated by using the following formulas:
where \(\dot{Q}_{{\text{c}}} = \dot{m}_{{\text{c}}} c_{{\text{p,c}}} \left( {T_{{\text{c,out}}} - T_{{\text{c,in}}} } \right)\) and \(\dot{Q}_{{\text{h}}} = \dot{m}_{{\text{h}}} c_{{\text{p,h}}} \left( {T_{{\text{h,in}}} - T_{{\text{h,out}}} } \right)\).
The average value of (U) may then be determined by using this relationship [10]:
where ΔTLMTD is the logarithmic mean temperature difference between the hot fluid and cold-fluid flow rates, F is the correlation factor of the logarithmic mean temperature difference that is determined by the HE's geometry and the temperatures at the hot and cold fluid streams' input and output [11], and Aout is the surface area where heat transfer occurs cross.
Number of transfer units (NTU)
The number of transfer units (NTU) is defined as a percentage of the total thermal sizing (UA) and the minimum storage capacity \(\left( {\dot{m}c_{{\text{p}}} } \right)_{\min }\). The formula for this non-dimensional term is [12]:
Thermal performance factor (TPF)
Many modifications in STHE lead to enhancing the heat transfer at the expense of hydraulic performance so it is required to indicate the relation between thermal and hydraulic performance. TPF specifies the comparison of the heat transfer development for a STHE with modification to a plain tube (without modification) for the same pump power requirements and fully developed turbulence flow. It is described as the ratio of the improved heat transfer ratio (Nu/Nup) to the increased friction ratio (f/fp), where the subscript p denotes the scenario in which the heat transfer is not boosted. This may be written as [13].
It is indicated that the value of this factor should be more than unity for enhancing HE performance.
Exergy efficiency
The second law efficiency principle states that the ratio of the actual thermal efficiency to the highest potential (reversible) thermal efficiency under the same condition applies to thermal steady-state systems such as HEs. The temperature fluctuation and flow resistance of a HE are explanations for energy losses. The exergy analysis uses the irreversibility of heat transmission. The exergy loss for an open system in the steady state may be computed as follows [14]:
Ec and Eh stand for the exergy change of cold and hot fluids, respectively. Each of these may be determined using the two equations below.
The S expresses the entropy parameter and Tsur is the surrounding temperature where the exergy loss is determined as:
Dimensionless exergy (the second-law efficiency) can be determined based on the hot fluid stream in tube side availability:
The exergy loss is expressed in E and h is the hot side in the STHE, where ψ is the availability in J kg-1 and it can be used to analyze the efficiency of the heat transfer process and identify opportunities for optimization. The equation relates the exergy of the hot and cold streams entering the HE to the exergy of the mixed stream leaving the HE, as well as the temperature and pressure of the environment. The availability equation can be used in conjunction with the dimensionless exergy ratio to identify opportunities for improving the efficiency of the heat transfer process. For example, increasing the temperature or pressure of one or both streams entering the HE can increase the exergy of those streams, which in turn can increase the dimensionless exergy ratio and the overall efficiency of the heat transfer process and Δψ is calculated by.
The exergy efficiency can be calculated as:
where To is the surrounding environmental temperature. Exergy analysis can be applied to STHEs to evaluate their thermodynamic performance and identify opportunities for improving their efficiency. In a STHE, the exergy of the hot fluid entering the exchanger is partly transferred to the cold fluid and partly lost due to irreversibilities such as fluid friction and heat transfer across temperature gradients. The exergy efficiency of a STHEs can be defined as the ratio of the exergy transferred to the cold fluid to the exergy of the hot fluid entering the exchanger. Exergy analysis can be used to identify the sources of irreversibility in the HE, such as pressure drops, temperature differences, and fluid mixing. By minimizing these irreversibilities, the exergy efficiency of the HE can be improved. For example, one way to improve the exergy efficiency of a STHEs is to increase the surface area of the heat transfer surfaces, which can reduce the temperature difference between the hot and cold fluids and thereby reduce the exergy losses due to temperature gradients. Another approach is to improve the fluid flow patterns within the HE, such as by using baffles or other flow control devices, to reduce the pressure drops and fluid mixing that can cause irreversibilities. Overall, exergy analysis can be a valuable tool for optimizing the design and operation of STHEs, and for improving the overall efficiency and sustainability of energy systems [15].
Work justification
The designs of HEs are reviewed in many studies [16,17,18,19,20]. Double tube heat exchangers [21,22,23,24,25], plate heat exchangers [26,27,28,29,30,31,32], finned heat exchangers [33,34,35,36,37,38], and helical heat exchangers [39,40,41,42,43,44,45] are studied and reviewed. Fewer studies reviewed the STHE such as [15, 40] that performed a review of helical baffles and exergy analysis in STHE. So, the authors tend to carry out a comprehensive review of heat transfer enhancement methods in STHE. The work justification of this review can be summarized as follows:
-
STHEs are widely used in industrial applications for heat transfer between two fluids. The efficient operation of these HEs is essential for process optimization, energy efficiency, and cost-effectiveness. Therefore, there is a need to enhance the heat transfer rate of these HEs.
-
Although there are several research papers available on the methods of heat transfer enhancement in STHEs, there is a lack of a comprehensive review that covers all the available methods. This paper aims to fill this gap by providing a comprehensive and systematic review of the various methods available for heat transfer enhancement in STHEs.
-
The paper compares and evaluates the different methods of heat transfer enhancement, which helps in selecting the most effective method for a specific application. This comparison is important as it provides a comprehensive understanding of the advantages and limitations of each method.
-
The paper includes recent advances in the field of heat transfer enhancement, which makes it an up-to-date resource for researchers and practitioners. This information is important for researchers and engineers who need to stay updated with the latest developments in the field.
-
The paper provides practical implications for engineers and designers who need to select the most appropriate method for a specific application. This information can help in improving the energy efficiency and cost-effectiveness of STHEs, which is of practical importance to industries.
Objectives of the present review
Because of the inexpensive cost of design and maintenance of STHEs, many companies also employ them. Consequently, it is concluded that the earlier studies done on this sort of HE should be classified to remove the confusion associated with selecting the most suitable techniques of heat transfer enhancement. To the authors’ knowledge, no review papers concerning STHEs have been published so far and this fact is one of the main objectives of this review. The history of publications regarding STHE was traced beginning 2000s. The studies broadly support the view that heat transfer enhancement in STHE is heading toward considerable progress. Through these years, many studies that fall into various categories have been carried out. In some cases, passive methods for heat transfer improvement were studied, and some studies investigated active methods, air injection, nanofluids, and compound methods. This review is a follow-up to several articles by earlier authors; it summarizes the findings of previous studies to assist academics in better understanding the most recent advancements in this field; and this thorough evaluation may help related specialists make greater advancements. The writers also put up a few issues and ideas that they believe should be researched further in the future. This paper can provide insights into the latest developments in enhanced STHE design and optimization. Engineers can use this information to improve the efficiency and performance of enhanced STHEs in various applications. It can help engineers select the most appropriate type of enhanced heat transfer technique for a given application. Comparing the performance of different techniques such as fins, inserts, and twisted tapes, and providing guidance on when to use each technique can be introduced. Insights into the latest techniques and strategies for improving the energy efficiency of STHEs can be provided. This can help engineers reduce energy consumption and save costs in various applications. It can provide examples of the use of enhanced STHEs in different industries and applications, such as petrochemical, power generation, and refrigeration. This can help engineers identify new opportunities for the use of enhanced STHEs in their applications.
Passive method
Active methods often include adding inserts or other devices to the flow channel's surface or changing its geometry. It does not require any outside power sources. These approaches are simple to use in an existing HE, and the insert production process is very straightforward. Surface or geometrical adjustments without external power, for example, treated surfaces, twisted tapes, abrasive surfaces, expanded surfaces, or the utilizing of different inserts, are used in the passive approach. Enhancement devices, twisted tape, wire coil, swirl flow generator coiled tubes, and surface tension devices were examples of such inserts as seen in Table 1. Son and Shin [46] studied the effects of spiral baffle plates on the performance of a conventional STHE numerical. Fluid interactions with tubes flowing rotationally in the shell were indicated. Because stagnation areas in the shell could be eliminated, it could increase HE performance. In terms of heat transmission, the STHE with spiral baffle plates has been proven to be superior to the standard HE. Heat transmission and exergy loss along both sides of a circular DPHE with a snail intake were explored by Durmuş et al. [47]. Working fluids in the inner and outer tubes were cold air and hot water, respectively. Due to the quick rotation of the air, the effect of the snail vortex generator on heat transfer was also observed to be reduced for low Re. That snail entrance, which was inserted in the intake area of the inner tube, may promote heat transmission by producing a whirling flow. The results verified that the Nu for counterflow rose from 85 to 200% on both sides of the HE, with the values mostly impacted by swirling angles. When assuming an equivalent whirling angle, the estimations were often around 20% higher than the observed parallel flow data. In parallel and counter flows, ∆P was found to be around 110% greater than in the smooth tube. The counterflow was shown to be the best choice in terms of exergy loss. Saffar-Avval et al. [48] studied the suitable baffle spacing in the design process in STHE. For segmentally baffled shell and tube condensers, computer software was created that allows designers to find the best baffle spacing. To accomplish the target function, total expenses of heat transfer area and pumping power were involved, with a mass factor based on the economic conditions of the desired site. Consequently, a set of correlations was offered to identify the best baffle spacing, which may be used in conjunction with HE designs suggestions. Andrews and Master [49] evaluated the performance of a helically baffled HE using three-dimensional CFD modeling by the HEATX program. The simulation considers the leakages, complicated baffles helical geometry, and exit entrance nozzles. There were three examples, each with a helix angle of 10°, 25°, or 40° given concerning the radial axis. The simulated streams have separate internal and external portions, with the outer part displaying a plug flow feature, which was extremely desirable. Back mixing at the small helix angle generates recirculation zones in the inner region, signaling potential vibration issues while also achieving the necessary temperature uniformity. The fluid turn ratio of the helically baffled HE was 0.64, 0.78, and 0.77 for the 10th, 25th, and 40th helix angles, respectively, indicating that the higher helix angles had greater overall plug-like flow. Characteristics of heat transfer and ∆P of the horizontal standard DPHE and DPHE with twisted tape in tubes were analyzed by Naphon [50]. The twisted tape insert improves q significantly, albeit at the expense of increased ∆P. Two nusslet number (Nu) and friction factor (f) connections were proposed. Figure 3 depicts the fluctuation of average tube-side h with tube-side Re under the same conditions. No text on the page matches the requested style. The (U) and the Re number were related in three ways. As one might assume, the average tube-side h rises as the Re number rises. This was because the h was completely proportional to the heat quantity (q). Furthermore, the hs in the tube side for tube twisted tape inserts were larger than those for plain tubes. The twisted tape insert’s h was greater than those for plain tubes as seen in Fig. 3.
Relation between the U and Re [50]
Akpinar [51] employed helical wires within tubes and found that the Nu increased by up to 2.64 times and the f increased by up to 2.74 times compared with the smooth pipe. The rise in f was approximately 2.74 times that of the empty pipe, based on Re and pitch or helical range. In the helical arrangement, the dimensionless exergy loss increased by up to 1.16 times as compared to the empty pipe. The results were also expressed in empirical correlations, which were calculated and discussed. Peng et al. [52] used continuous helical baffles in two STHEs. The tube bundles of the two STHEs in development were identical, but the shell designs were not. The shape of the continuous helical baffles forced the flow pattern on the shell side of the HE to be rotating and helical, leading to a significant increase in h per unit ∆P. Continuous helical baffles may lessen fouling on the shell side while also preventing flow-induced vibration with the right design. Based on findings, using continuous helical baffles increases the h by around 10% for the same ∆P on the shell side. Based on experimental data for the suggested continuous helical baffle HEs with various shell configurations, nondimensional correlations for hand ∆P were created. Costa and Queiroz [53] studied the design optimization of STHEs. The defined issue involves discrete choice variables and consists of minimizing the thermal surface area for a specific service. Extra constraints were geometrical characteristics and velocity criteria that must be satisfied to get an added realistic process task solution. The optimization technique was established on an examination near the tube count table, using the given restrictions and examined design candidates to remove nonoptimal options and reduce the number of rating runs. Two design examples were used to investigate the algorithm's and its individual components' performance. Yadav [54] investigated experimentally h, ∆P, and TPF in DPHE with an insert of half-length twisted. It was found that inserts boost performance by 40%–60%, raise the ∆P by 0.09–0.27 bar, and lower the TPF by 66%–78%. Eiamsa-ard et al. [55] studied the effects of twisted tapes (oblique and straight delta winglet, O-DWT, and S-DWT) on the heat transfer of HE. For all Res tested, Nu and f improve with reducing and rising wing cut ratio depth, as seen in Fig. 4. The O-DWT also produces a greater Nu and f than the S-DWT. The performance factor in tubes fitted with the O-DWT and S-DWT was determined to be roughly 0.92–1.24 and 0.88–1.21, respectively, across the range, examined. The DWT outperforms ordinary twisted tape when it comes to heat transfer improvement. It means that a HE equipped with DWT was more condensed than one equipped with traditional twisted tape. Again, the DWT may be efficiently replaced by any of the TT to lower the HE's size.
Relation between Nu and Re number [55]
Wang et al. [56] used a novel baffle type in the STHE where the experiments were applied for the novel baffle and the SB. The two HEs' operation performances were also compared. According to the findings, the improved model's overall performance was 20–30% greater efficiency than the SB in HE with similar circumstances. The testing findings revealed that as the Re number in the tube and shell sides was the same, the Nu for flower baffles was approximately half that of SBs, and the ∆P of the former was about a third that of the latter. The heat transfer improvement and flow friction growth would be considered when constructing HEs to save energy. In comparison with the standard SBs, the heat transfer and ∆P performance of the flower baffles may be enhanced by appropriately designing them. Bhatta et.al [57] looked at how CFD may be used in different forms of HEs and looked at fluid flow, ∆P, heat transfer, and existing turbulence models for HEs. They discovered that the k-turbulence model was the most often utilized for HE simulation, and they proposed a method for comparing the experimental and numerical findings of the research. Under turbulent flow conditions, You et al. [58] evaluated the shell-side thermal and hydraulic analysis of a STHE with trefoil hole baffles. The q on the shell side was effectively enhanced; however, the flow resistance increased dramatically, according to the test findings. Furthermore, the heat transfer performance and ∆P both improve as the Re rises. As a result, the q has improved greatly, and the flow resistance has increased significantly. According to a numerical simulation of the unit channel, the trefoil-hole baffle might cause a high-speed flush against the downflow tube wall, intense recirculating flow, and a high level of turbulence intensity. Consequently, the temperature boundary thickness near the wall was greatly reduced, and the q was significantly improved, with a corresponding increase in flow resistance. STHEs with trefoil-hole baffles were simple to manufacture and less prone to foul, making them a good contender for several applications. Gowthaman and Sathish [59] quantitatively studied two distinct baffles in a STHE. HEs that meet certain criteria have a high hand and a low ∆P. Helical baffles minimize shell side ∆P, pumping cost, mass, fouling, and other factors when compared to a SB for a new installation. In comparison with a SB, the ratio of heat to the increased cross-flow area results in a lesser mass flux across the shell, resulting in a bigger ∆P. The helical baffle was significantly greater than the SB due to the decreased bypass impact and less shell side fouling. Gao et al. [60] investigated the friction factor and heat transfer enhancement of different STHEs with discontinuous helical baffles. The results showed that the HE with a lower helix angle has a higher shell-side ∆P and h than those with a greater helix angle. The irreversibility of a HE was calculated in second-law thermodynamic comparisons using entropy production and entrance dissipation theories. The STHE with lower helix angle baffles generates reduced irreversibility in the heat exchange procedure in the same heat transfer area and under the same operating circumstances, according to an experimental study. Furthermore, HEs with helical baffles were extra efficient under specific shell-side Re circumstances. Salahuddin et al. [40] presented a summary of the key work that was performed on helical baffles to enhance the performance. There was also a comparing between helical as well as SBs, which showed that helical baffles were preferable to SBs. Continuous helical baffles reduce dead zones, whereas sextant-helical baffles, inclination angle (40°), and small baffle spacing offer the best results when employed together. Wen et.al [61] investigated the THP and revised the construction of the ladders pattern fold baffle to prevent the triangle leakage regions in the original STHE. The outcomes demonstrated that axial short circuit flow was eliminated, and the fluid velocity and temperature distribution inside the shell were more uniform in the improved HE. Yehia et al. [62] simulated the fluid flow fields through HEs for a large range of temperatures, Res, and geometry configurations. The tube side Nu and tube side f rose as the MFR grows, whereas the thermal enhancement factor falls marginally. The tube side Nu and f rise as the diameter of the inserted vane swirlers decreases with the reduction in blade angle, but the tube side thermal enhancement factor drops. The resulting Nu, f, and thermal enhancement factor were 2.3, 19.02, and 0.86, respectively, when compared to the plain tube’s scenario. Improving the number of swirl vanes improves heat transmission and the thermal enhancement factor, resulting in a more effective HE with less heat transfer area and volume, and hence cheaper costs. Wang et al. [63] employed CFD to investigate the influence of rod baffle on thermal performance and ∆P in a double-shell side rod baffle HE (DS-RBHX). The outcomes showed that the DS-RBHX has a larger q and ∆P than the SS-RBHX by 34.5–42.7% and 41.6–40.6%, respectively. Furthermore, at the identical MFR, the DS-RBHX has a better complete performance index h/Dp than the SS-RBHX by up to 8.9%. In this study, the efficiency estimation criterion, which was the ratio of the increase in q to the cost of power consumption, was used to assess the overall performance. Gomaa et al. [64] investigated the triple concentric tube HE with inserted ribs' THP parameters. Both experimental and numerical methods were used. Based on dimensionless design parameters, correlations for Nu, f, and efficacy were also derived. The Nu and efficacy of the triple tube HE with ribs were greater than those of the triple tube HE without ribs at various flow configurations. By 21.48% and 16.74%, respectively, without ribs. The Nu and HE efficacy were higher when the flow pattern was countercurrent. Lei and Jing [65] examined two types of reformed STHEs with louver baffles to reduce pumping power and increase overall shell performance compared to STHEs with traditional SBs. The h per ∆P of the STHE-LV1 and STHE-LV2 were found to be around 94.6–118.2% and 73.3–89.7% greater than the STHE-SG, respectively. Louvre baffles on the shell side of HEs generate a gentler flow pattern than SBs on the shell side of HEs. Heat transfer efficiency was improved because the new STHEs have fewer dead areas and recirculation zones than HEs with SBs. Acute changes in flow direction were avoided on the shell side of the two new STHEs, resulting in a smaller ∆P. Labbadlia et al. [66] looked at four possible tube arrangement types in STHE numerical. The results indicated that the tube characteristics had a considerable effect on the flow pattern. The flow distribution of a 60° design was found to be 21% more homogeneous than that of a 90° configuration. The 45° layout, in comparison with the other designs, provides superior pressure distribution homogeneity. Mellal et al. [67] looked at 3D numerical simulations of turbulent water stream and heat transfer in an STHE's shell. Baffle spacings of 106.6, 80, and 64 mm, as well as six orientation orientations of 45, 60, 90, 120, 150, and 180°, were studied. The simulation was conducted using the COMSOL package and the finite element procedure for Re varying from 3000 to 10,000. Many numerical outcomes were compared to the experimental data and preserved in close proximity. When compared to STHE without baffles, the findings demonstrated the relevance of the examined parameters in enhancing shell-side thermal performance, with the 180° baffle arrangement at 64 mm baffle spacing being the optimum that guarantees mixing flow, producing a thermal performance criteria of 3.55. Dizaji et al. [68] used corrugated shell and orrugated tube in a STHE. The researchers studied a variety of concave and convex corrugated tube configurations. According to the data, corrugations cause growth in NTU as well as exergy loss. The exergy loss, as well as NTU, increased by around 17–81 and 34–60%, respectively, when both the tube and the shell were corrugated. Exergy loss was largest in the HE with the convex corrugated tube and concave corrugated shell. Shinde and Chavan [69] utilized computational and experimental approaches to examine the THP of a STHE attached with helical baffles and several helix angles. The difference in ∆P and h between stainless steel and FRP materials was 3–5% and 10–12%, respectively. Because the difference was small, the FRP material can be an excellent prospective replacement for the present material, lowering the HE's initial and operating costs significantly. For a 25° helix angle, numerical and experimental findings were compared to forecast FCHB-STHE thermal performance. In the FCHB-STHE and single baffle STHE experimental results, ∆P was smaller than hat lower flow rates, but the inverse was true at higher flow rates. When continuous helical baffle HEs were utilized in the industry, energy costs can be reduced by 15–20%. Amini and Amini [70] investigated the influence of tube fins in STHE calculations using both the parameters fin pitch and fin height, as well as a study of helical continuous fins. They discovered that segmented vertical fins increased q and efficiency due to vortex production and that although increasing fin height improves q, increasing fin pitch has the opposite effect. Heat transmission was improved as Re was raised to a certain surface roughness. The heat transmission rate was increased by using segmented vertical fins, which increase the vortex formation. Finned tubes have a far faster q and consequently a higher Nu number than plain tubes without fins. While the height of the fins grows q, Fin pitch increases have a detrimental impact on it. Furthermore, increasing pitch causes less ∆P than increased height, therefore finding the optimal fin pitch and height can result in maximal heat transfer with the least amount of ∆P. When helical fins were used, the HE's thermal performance was improved even more. For example, helical fins have a 35% higher Nu number than segmented vertical fins under the same circumstances, making them more desirable. Ayub et al. [71] investigated a unique STHE with twisted tape insert and the working fluid is a solution of propylene glycol and water. For both HEs, Nu and Darcy f correlations were presented. The TPF of the baffled HE (A) was better, while the bundle ∆P of the HE with twist tapes on the shell side (B) was substantially lower. As a result, HE B's thermal enhancement index was determined to be roughly 20% higher than HE A's. These findings suggest that such HEs could be used in situations where a low ∆P penalty was a primary need, such as viscous hydrocarbons and oil cooling and heating. Empirical correlations for determining Nu and Darcy f for both HEs were reported based on experimental data. This research can be expanded to include testing with a variety of additional H/W twist ratios as well as other very viscous fluids. Bichkar et al. [72] looked into thermal performance and ∆P as significant aspects. Thermal performance and ∆P were both affected by the direction of fluid flow and the kinds of baffles used in various orientations. While comparing with single SBs, double SBs reduce vibrational damage. Because dead zones were eliminated when helical baffles were used, ∆P was reduced. Heat transfer was improved when there were fewer dead zones. Smaller pumping power was required because of the lower ∆P, which improves total efficiency. The outcomes reveal that helical baffles outperform the other two types of baffles. He and Li [73] used simulation methods to investigate the thermo-hydraulic performance of STHEs with different baffle shapes. From the standpoint of exergy analysis, a double-tube-pass (DTP-STHE) was presented in this study to increase the recovered heat quality. The helical, flower, and helical baffles were all compared under identical conditions. Flower baffles generate the lowest ∆P and h, according to the results. The q per efficient pumping energy was presented to help evaluate the economic performance of these three forms of HEs. The q per efficient pumping energy of the floral baffle was the greatest, while the q per efficient pumping energy of the SB was the shortest, according to the simulation findings. Wen et al. [74] studied the entrance theory and the genetic algorithm was merged into an optimization technique. The reliability of performance evaluation criteria (PEC) and entransy dissipation concept depending on investigational data was used to demonstrate the application of entransy theory on STHEs with helical baffles. The change in entransy dissipation thermal resistance was almost unaffected by the overlapped degree. According to the sensitivity study, the shell-side velocity has the greatest impact on thermal resistance, followed by the helix angle. Yu et al. [75] created a brand-new kind of curve rod baffle-inspired hexagon clamping anti-vibration baffle STHE (HCB) to address the vibration susceptibility of round rod baffle STHEs. The findings revealed that HCB was more rigid than CRB, making it best placed for heavy and massive tube bundles. HCB has a higher heat transfer augmentation but performs worse overall compared to CRB. Baffle spacing had a massive influence on THP, but the baffle width had less effect. The structure of the CRB characteristic was exceptional to that of the HCB when it comes to PEC where the baffle in perpendicular configuration could improve the heat transfer. El-Said and Abou Alsood [76] investigated the influence of many baffles in STHEs with four distinct baffle designs (CSSB, SSSB, FSB, and HSB), with THP analysis as seen in Fig. 5. When comparing with CSSB shape, the HSB design improves the HE's U, ε, and NTU by 185–248%, 134–149%, and 148.9–189%, respectively.
Four distinct baffle designs a CSSB, b SSSB, c FSB, and d HSB [76]
Wang et al. [77] examined the efficiency of rod baffles in a double-shell HE in terms of heat transfer and flow (DSRBHX). According to experimental findings, the h of the DSRBHX was greater overall than the SSRBHX for all measures. When looking at the overall performance, the DS-shell-side RBHX’s h was 14.4–24.3% greater than the SS-under RBHX's identical shell side ∆P. It was demonstrated that the DS-RBHX performs more comprehensively than the SS-RBHX. Numerical results were obtained on the behaviors of DSRBHX with guide shells. The three guide shells enhance the shell side output zone's capacity for heat transmission, especially on the outer side. Saffarian et al. [78] investigated tubes at various cross sections such as circular, elliptical at 90° attack angle, and elliptical with zero attack angle in STHE. For each of the five situations in this investigation, the ∆P in the tube and shell was examined. The influence of tube placement on heat transmission was looked at. When comparing tubes near the shell to tubes in the middle of the shell, it was discovered that tubes close to the shell had a stronger influence on heat transmission. Chen et al. [79] investigated the STHE’s new unilateral ladder-type helical baffle construction (ULHB). Compared to the STHE-SB, the ∆P of the ULHB was 12.1–45.9% lower. Overall, ULHB's side h per unit ∆P was 151.9–176.4% greater than STHE-SB's. The ULHB TEF values increase from 161.3 to 178.9%, with an average value of 171.2%. The findings demonstrate that the STHE-all-around ULHB's performance was excellent compared to the STHE-SB's. In a STHE with a wavy tube bundle and cosine corrugated wall, Shirvan et al. [80] investigated the impacts of wavy surface features on HE efficacy, U, and energetic sustainability index. The focus was on the ε of the HE optimization technique and the total enhancement caused by effective parameters. The efficacy of the HE and the U improve as the cold-water flow rate increases. The HE's efficacy and U were reduced as the wavy beginning lengths were increased. The HE's efficacy was negatively and consistently affected by wavy beginning lengths and hot water flow rates. The HE's sensitivity to cold water flow rates, on the other hand, was positive and continuous. The U was negative and consistent in its sensitivity to the wavy beginning lengths. Mohammadi [81] studied the heat transfer and ∆P along a STHE with six porous baffles. The maximum heat transmission was achieved with low baffle cuts, but a significant quantity of ∆P was also produced. Even if the porosity of 0.2 was better at transferring heat, a larger ∆P at a smaller baffle cut makes it difficult to consider it the ideal value. The artificial neural network was trained on the data to describe the STHE and carry out the sensitivity analysis. The baffle cut had the most influence on heat transmission and ∆P, while the porosity had the least influence on both, contributing 5% less to both. The best parameters for permeability, porosity, and baffle cut were then determined using a genetic algorithm to maximize heat transmission and minimize system ∆P. Mahendran [82] investigated the STHE performance with a typical single plate and a novel type of baffles. Baffle plate HEs and traditional single plate HEs were compared for investigation and performance. With Solid Works Flow Simulation software, modify the baffle plate to increase the HE's cooling ε. The outcomes will imply that the traditional model performs more effectively overall than the SB plate HE. The pathlines, pressure distribution, and temperature distribution were all numerically investigated. Utilizing flow modeling, the HE was accurately analyzed. Marzouk et al. [83] studied a STHE equipped with anew insert (circular rod welded with wired nails) on the side of the tube performed thermally, hydraulically, and thermodynamically. While the words U, ε, and NTU were used to describe thermal performance, tube-side ∆P and exergy efficiency were used to describe hydraulic and thermodynamic performance, respectively. The experimental findings showed that the proposed insertion designs have a disadvantage in hydraulic performance but a considerable increase in HE thermal and thermodynamic performances. Biçer et al. [84] investigated various baffle forms by simulating and visualizing a 3D turbulent flow environment on the shell side. The results revealed that a three-zonal baffle outperformed the other designs tested. The ∆P in the shell was reduced by 49% when the temperature differential increased by 7%. The CFD simulations of the improved STHE were conducted under boundary conditions, and the findings were compared to experimental results. The three zonal baffles enhanced the STHE performance in terms of q and ∆P. Yu et al. [85] studied a novel compound parallel flow STHE using longitudinal vortex generators (LVG) and a clamping plate baffle experimentally and numerically. THP and flow formation of five various arrangements were examined. The LVG improved heat transfer effectively where the NuLVG/NuRRB was in the range of 1.2265–2.0076; the fLVG/fRRB was in the range of 5.457–15.859; the PECLVT/PECRRB was in the range of 0.6457–0.7574.
Kallannavar et al. [86] looked at the tube layouts to comprehend how the STHEs' design attributes were affected by the process settings. It was clear from the experimental investigation that the rate of heat transfer reduces as MFR increases. It was shown that heat transmission under situations of counterflow was superior to those of parallel flow. Additionally, it was shown that, when compared to parallel flow HEs, counterflow HEs were up to 26.7% more effective at a flow rate of 0.024 kg s-1 with a 45° tube configuration. The least percentage change, on the other hand, was 0.14% with a 0.045 kg s-1 flow rate and 60° tube architecture. Additionally, it should be noted that the heat transmission rate in the 30-degree tube configuration was higher than it was in other tube layouts. Chen et al. [87] investigated a brand-new STHE design with three-blade triple-layer floral baffles. Cold water was used in the tube and hot water was used in the shell as the experiment was conducted in a counter-flow design. According to testing results, the STHEs with triple and double-layer flower baffles had shell side h that are, respectively, 31.7% and 14.3% greater than those of conventional SBs. The STHE with triple-layer flower baffles achieved a complete performance that was 23.7% better than the STHE with double-layer flower baffles thanks to the addition of more blades. Abbasian and Uosofvand [88] studied the influence of the SB, SPHB, DPHB, and the different elliptical tube bundles along with the double pass combination helical segmental baffle (DPCHSB). The impacts of various tube bundle arrangements, including vertical, horizontal, and angled ones, were investigated. Compared to the suggested baffle and tube bundle configurations' efficiency evaluation coefficient (EEC), the angled elliptical tube bundle performed better than the other tube bundle layouts under study. In comparison with horizontal elliptical and vertical elliptical configurations, the EEC of angled elliptical improved models for the DPCHSB was 30.3 and 14.8%, respectively. Miansari et al. [89] studied the thermal efficiency of helical STHE models (standard, circular fins, and circular fins chopped into V shapes) as seen in Fig. 6. It was discovered that moving hot water across the coil enhances heat transfer while moving cold water in the shell improves the velocity. In comparison with the circular fins, the impacts of the cut circular fins on the helical STHE efficiency and heat transmission were negligible.
Helical STHE without a fin, with circular fins, and with circular fins [89]
Al-Obaidi and Chaer [90] presented the results of a study that used computational fluid dynamics to examine the effects of various ball tabulators inserts (BTI) diameters on the three-dimensional flow pattern and heat transfer properties within a circular tube. The performance assessment findings showed a strong correlation between the BTI configurations and the features of flow behavior and velocity field contour fluctuations. The performance of the rate of heat transfer may be improved by BTI by more than 46%. Also, it is discovered that the PEC's maximum value exceeds 1.03. pipe. Al‐Obaidi et al. [91] investigated the properties of heat transmission and fluid flow in the circular pipe using various axial groove geometrical designs and axial groove numbers. The flow alteration takes place close to and around the axial groove parameters. Nu values for groove turbulators ranged from 14.5 to 21% higher than average. The groove turbulators' friction factor (f) value was roughly 7.5–24% greater than average. Because there are larger viscous losses near the wall surfaces, dynamic pressure dissipation is what causes most friction losses. With this style of passing approach, heat performance was improved by more than 1.2%. Li et al. [92] investigated the properties of twisted oval tubes used alone and in combination with circular tubes in double tube HEs with Re between 2700 and 22,000 to enhance shell-side heat transfer. On the shell side performance convection heat transfer and hydrodynamic resistance, the impacts of the aspect ratio, twist pitch length, twisting directions, and the ratio of inner tube radius to external radius were also investigated. In twin-tube HE made of twisted oval tubes, the rotating motions brought on by these motions result in secondary flow and spiral flow, which intensify shell-side heat transfer and erode the boundary layer Fig. 7. The performance of the shell side comprehensive heat transmission may be considerably enhanced by simultaneously lowering the twist pitch length and raising the aspect ratio of the inner tube. The maximum heat transfer performance was demonstrated by case ten, which has the shortest twist pitch length and the biggest inner tube aspect ratio. The use of twisted oval tubes as inner tubes can improve heat transmission performance by 24.0–39.0%. The increase of shell side heat transfer was unaffected by the inner twisted oval tubes' leftward or rightward twisting orientations.
Distribution of streamlines of velocity flow for various tube configurations [92]
For the analysis and improvement of THP, El-Said et al. [93] studied STHE using three arrangements of novel segmental curved baffles. In contrast, STHE with traditional SB was also numerically analyzed. Depending on the U, and NTU, each baffle layout was examined at various Re in the shell side. To assess the system's energy loss because of the recommended design, ∆P over the shell side was also computed. Also evaluated, examined, and addressed where the effects of the input cold fluid temperature, the ratio of baffle cutting, and the spacing of the baffle. The findings demonstrated that, in comparison with the other two designs, the CB3 configuration significantly improves HE performance for all scenarios examined. To examine the impact of mini-channels on the THP of a STHE, Ünverdi [94] used the CFD approach. According to the findings, h and ∆P increase in correlation with Re. The differences in h per unit of ∆P were what make up the performance benchmark (ψ). The findings indicated that the decreased ψ with increasing Re. Using numerical solutions, the flow in the mini-channel tube achieved its ideal circumstances at Re 5900, including thermally and hydrodynamically. While there was a 13–13% difference between the calculated and experimental f, there was a 15–20% difference between the numerical and investigational h (Fig. 8).
Contours of temperature in mini-channel for different Re [94]
Al-Obaidi and Alhamid [95] evaluated the thermal–hydraulic performance of the circular pipe heat exchanger with different twisted tape inserts. Twisted tape inserts can raise the flow resistance in pipes, which raises the pressure differential. The twisted tapes inside the pipe also increased the amount of vortex motion (swirl flows), which led to a variety of radial velocities. The numerical findings demonstrated that when the different twisted tape inserts were increased from 1 to 5, the temperature difference increases to 38.1, 46.11, and 50.52% in comparison with the temperature difference in a smooth pipe. Al‐Obaidi [96] quantitatively investigated the impact of various twisted tape designs on thermal performance, flow patterns, and heat transmission. The average percentages discrepancy between the experimental and computational fluid dynamics findings for Nu number and friction factor were recorded at roughly 6.5 and 4.5%. The highest value of temperature differential and friction factor was for model 13. Al-Obaidi [97] investigated the impact of various tube geometrical features on the analysis of its flow field and the efficiency of its thermal heat transfer. The optimization findings showed that the corrugated diameter had the highest value of pressure difference. When compared to a smooth pipe, the numerical technique employing offers a faster rate of heat transmission. The results showed that when the geometry of the corrugated pipe changed and the PEC value climbed above 1.3, the PEC ratio of the corrugated pipe changed and increased. Al-Obaidi et al. [98] investigated the impact of various corrugation interruption settings on the thermodynamic properties and heat transmission performance of a three-dimensional corrugated tube. The outcome showed that the Nu tends to rise when the Re rises. Higher corrugated geometrical arrangements resulted in a rise in the Nu value. Because the PEC value is greater than unity, using different corrugated geometric layouts can produce a performance that is superior to that of smooth pipes. The PEF value, Re increments, and PEF value all showed a decreasing trend. Al-Obaidi and Alhamid [99] investigated how different corrugated pipe shapes affected the thermo-hydraulic flow and improved heat transfer efficiency while creating varied correlations. The numerical results and observations showed that the pressure loss increased significantly with the number of corrugated designs. At a Re of 12,021.9, the Nu values for all configurations of corrugated ring diameters were around 32.2, 40.5, and 45.6% higher than for the smooth pipe. The Nu values for the smooth pipe were 17.5, 29.3, and 49.6% lower than those for the value parameters for the corrugated ring angles.
Siddiqui et al. [100] showed the ability of conventional finned tube heat exchangers, employed in active atmospheric water generating systems, to capture moisture. Plots of several factors versus the yield of water on a per unit frontal area basis were used to represent the results. The increase in water yield was the largest and lowest for increasing row count and fin density, respectively. Marzouk et al. [101] investigated many unique tube designs to investigate both experimentally and numerically the thermal and hydraulic performance of a helical tube HE. The results demonstrated that the novel configurations have a higher overall heat transfer coefficient than the uniform tube distribution. It was found that when the Reynolds number grows, the pressure decreases also. Although changes in pressure drop and pumping power were only marginally impacted, the innovative tube layouts significantly enhanced the performance of heat transmission. Ikhtiar et al. [102] conducted numerical research on the lamella HE for cooling engine intake charge air. The findings demonstrated that all parameters, except LMTD, were inversely related to the lamella's internal openness and directly proportional to the lamella's aspect ratio. The lamella's smaller internal hole increased heat transmission, temperature decrease, the number of transfer units, and pressure drop. Kücük [103] conducted an experimental investigation on how mini-channel STHEs affected a STHE's performance in terms of pressure drop and U for five distinct thermal and hydrodynamic operating conditions. The U of the mini-channels STHE was 1.1–6.6 times higher than that of the traditional HEs. Moreover, the mini-channels raised the STHE's U to 6700 W/m2 K and produced a pressure drop that was greater than 14,000 psi than macro-tube HEs.
The biggest heat transfer improvement when using the passive approach is when baffles are added; trefoil hole baffles outperformed smooth tubes by 450% in terms of U ratio [58]. Twisted tape provides the best value of 325% for the U ratio out of all the tapes utilized for heat augmentation. U ratio values for wire coil insert, corrugated tube, and swirl vane are 130, 161, and 264%, respectively, as seen in Table 1. It is indicated exergy efficiency is a crucial factor for STHE performance and many studies investigated exergy efficiency [47, 51, 68, 76, 104] with passive methods of heat transfer enhancement. It is observed that the maximum exergy efficiency is achieved with the corrugated shell and tube modification in STHE. It is indicated that many modifications in passive methods enhance heat transfer but on the other hand they increase the pressure drop. It is recommended to study the thermal and hydraulic performance of STHE to show the effect of modifications on pressure drop. Passive modifications that lead to fewer pressure losses are recommended. The reasons behind the heat enhancement by using various passive techniques can be boundary layer interruption, swirl flow, displaced flow, secondary flow promotion, and hydraulic diameter reduction.to reduce the heat transfer surface area required for a given application and thus reduces the size and cost as well as increase the heat duty of the STHE.
Active method
This approach deals with the problem of speeding up heat transfer by applying an outside force. The use of reciprocating plungers, electromagnetic fields, surface or flow vibration, and magnetic fields to interrupt flows were some common examples. It was mentioned that this strategy was the subject of various studies in HTHEs.
Air injection
The use of air injection requires external power such as an air compressor. Many studied the effects of ABIs inside the tube and shell sides in STHE for various Re number ranges as seen in Table 2. Kitagawa et al. [106] experimented to see how sub-millimeter bubble injections affected water’s Natural laminar convection on a heated vertical plate. The temperature measurements revealed that the ratios of the h with submillimeter bubble injection to that without injection increased, ranging from 1.35 to 1.85, as the bubble flow rate or the wall heat flux increased. Additionally, measurements of both temperature and velocity simultaneously showed that the flow alteration brought on by bubbles forming close to the warmed vertical plate directly affected the improvement of heat transfer. Sadikin et al. [107] researched two-phase flow on the shell side of a STHE. Donnelly et al. [108] used a sliding bubble flow to determine the amount of heat that would be transferred from a heated coated surface. The impact of the air bubble placed on the test plate’s base surface and allowed to float down its length was observed using two different methods. A 2D temperature map of the test surface was created using a high-speed camera and thermochromic liquid crystals. At 10°, 20°, and 30° angles from the horizontal, the tests were conducted. The angle established between the heated surface and the horizontal controls heat transfer by varying the speed of the bubble. When the angle was steeper, a higher bubble velocity enhances heat transfer. Fsadni et al. [109] examined the bubble-detaching diameters in this system concerning several operational factors, such as system flow rate, pressure, heating load, and saturation ratio. The test results for forecasting bubble detachment diameters in supersaturated fluids were compared to the Winterton models for zero and finite contact angles. Accurate results have been obtained using the method for forecasting bubble detaching diameters in round tubes at finite contact angles. The Winterton model did not account for the effects of pressure and heat flow on bubble characteristics, thus a new correlation was proposed to do so. Dizaji and Jafarmadar [110] added air to a liquid solution to speed up the q of a horizontal twin pipe HE. Air bubbles move about inside the liquid fluid because of the buoyancy effect, significantly mixing and tubulating the fluid. This approach has the potential to be developed into a workable heat transfer enhancement strategy for radiators that use water or other liquid fluids in automotive cooling systems. The bubbles were injected using a particular technique. There has never been researching on this type of ABI or using this mechanism for a twin tube HE. Dizaji and Jafarmadar [111] examined the impacts of ABI on q, the NTUs, and effectiveness. He injected air bubbles both in the tube and in the shell of a horizontal double pipe HE. Because of the rise in Re, ABI was identified as a possible way to speed up heat transfer through exchangers. Nandan and Singh [112] examined the use of ABI to improve STHEs. Their findings demonstrated that inserting air bubbles at various Re ranges [5000–20000] increased the q by 25–40% as seen in Fig. 9. Additionally, heat transfer as well as the exergy loss have been impacted.
Dimensionless exergy Loss versus Re [112]
Moosavi et al. [113] looked for an ideal state by injecting air bubbles inside the shell or coil side of the HE at various air flow rates. The airflow rate changed from (1–5) LPM. The water coil side flow rate was held constant at 1 LPM (inlet temperature of 40 °C), while the water flow rate in the shell was changed between 1 and 5 LPM (inlet temperature of 15 °C). In addition, ∆P due to ABI was assessed as a novel parameter in this research for the HEs. The results show that the effect of ABI on HEs was significantly influenced by the airflow rate and injection side (shell and coil). The findings show that increasing air flow enhances the h. Air injection into the HE’s shell side increased the U by 6–187% depending on the airflow rate. Khorasani and Dadvand [114] researched the experimental ABI in a HE with a horizontal helical shell and coiled tubes. According to their findings, the HE's efficiency and NTU rose when air bubbles were injected. Additionally, it can speed up the shell side flow. These were the primary findings' descriptions. It was discovered that the air bubbles' injection considerably improved the HE's efficiency. There was a 1.3–4.3 times increase in the values. The greatest increase happened in the counter-flow arrangement with the shell side water flow rate of 1 LPM and air flow rate of 5 LPM. Zavaragh et al. [115] examined the air–water mixture in the cooling circuit. A constant pressure air injection system was built at the point of the coolant inlet to the engine, which can be regulated at the appropriate flow rate by a computer. The air injection method had two key advantages. By creating air layers around the cylinder, additional air injection into the coolant fluid during the warm-up stage accelerated the heating of engine components. In the post-warm-up condition, however, to create turbulent flow for improving heat transmission and cooling, air injection was decreased to a certain level. A specific method for periodic air injection can improve fuel efficiency while simultaneously reducing the engine's harmful emissions. To boost the q of a vertical shell and coiled tube HE, Panahi [116] injected air bubbles. The HE’s coil and shell sides were supplied with hot and cold water, respectively, and the shell side’s air bubbles were injected using a programmable method. The rate of heat transfer can be increased by mixing the thermal boundary layers, growing the fluid flow's turbulence, and increasing the fluid Re on the shell side of the HE. Thakur et al. [117] investigated the STHE’s heat transfer properties by injecting air bubbles into the tube's intake and through it using water-based Al2O3 nanofluids at (0.1 and 0.2%v/v) concentrations. The results presented that the volumetric concentrations of nanoparticles and the injection of air bubbles improved the heat transmission characteristics. The situation in which air bubbles were injected into the entire tube produced the greatest improvement, followed by situations in which air bubbles were injected only at the tube's intake and not at all. With ABI inside the tube, the q increased by about 25–40% and the exergy loss increased by around 33–43%. Additionally, it was discovered that the hot fluid temperature improved the heat transfer features while maintaining a constant flow rate for both heat transfer fluids. El-Said and Abou Alsood [118] completed studies to look into ways to improve thermal performance. To determine the ideal performance conditions, the air was pumped within the HE shells using two distinct methods (parallel ABI inside the front of the shell and cross injection from the shell wall). To enhance the heat transfer into the shell side of STHE using the enhancement approach, ∆P between the shell side exit and intake produced by ABI was also assessed. The effects of ABI on ε, U, and NTU of HE in the first method on heat transfer performance were obvious compared to the second method as in Fig. 10.
The effects of airflow injection on ε of cross-air injection [118]
Heyhat et al. [119] researched the impact of ABI as an active technique in a double pipe HE's thermal performance. Through various injectors, air bubbles were introduced into the annulus side. Many flow rates inside the tubes and annulus sides were the subjects of experimental data collection. Along with the energetic analysis, the impacts of air flow rate and HE is positioning angle on its thermal performance were examined. Results obtained indicate that ABI can increase the h overall by 10.3–149.5%. Khorasani et al. [120] injected air inside the coil of a shell and coiled tube HE. An exterior piece of equipment was employed to inject air bubbles. With this approach, there was no requirement to modify the HE's initial design. Investigated were the effects of various air VFR on the ∆P and NTU. The second rule of thermodynamics was also used to analyze the impact of ABI. The results demonstrated that adding air bubbles to the HE's coil side improved its thermal characteristics. It was also discovered that the volume fraction should be tuned to achieve the optimum results. Furthermore, a second law study reveals that injecting air bubbles into the coil side was a more efficient way for HEs with high liquid flow rates. In a vertical counter-current coiled tube HE. Baqir et al. [121] injected air bubbles in a vertical coiled tube HE's. The applied shell flow, airflow, and coil side flow rates varied from 2 to 10, 0–10, and 1–2 LPM, respectively, with three temperature variations. They thoroughly assessed the thermal performance of the HE as well as the NTU. With no visible impact on the temperature differential, the injected air flow, shell, and coil side flow rates all have a sizable impact on the NTU and efficacy. Furthermore, the beneficial impact of the air flow rates was lessened, and there was no additional improvement in NTU and efficacy. The greatest NTU and ε augmentations were 1.93 and 0.83, respectively, whereas the minimum NTU and ε augmentations were 0.66 and 0.63, respectively. Pourhedayat et al. [122] looked into the effect of ABI on the thermal and energy properties of a vertical double-tube HE. Through holes in a ring tube, bubbles were introduced through the annulus side of a HE. Air bubbles enhanced energy destruction, which was to be expected. However, bubbles used less energy than the turbulators, which caused resistance to flow moving. The Nu improvement and exergy destruction increased by around 57 and 30%, respectively. The efficient design of holes on a plastic tube, as well as the rational selection of their number and diameter, can increase HE performance. Subesh et al. [123] investigated the effects of two air injection techniques on the performance of single-pass and double-segmental baffled multi-tube shell HEs. The U, efficacy, NTU, and ∆P of a STHE increased as the size of the air bubble increased. ABI was introduced into the shell side and cross-flowed to the cold water at varied air flow rates to identify the ideal performance conditions. Airflow rates of 1–6 LPM and shell side water flow rates of 10–20 LPM were converted using a constant tube-side hot water flow rate. Sokhal et al. [124] investigated the thermal performance and energy consumption of a STHE using ABI. The experiment included several factors, such as flow rate, fluid input temperature, and several air injection methods. Air was fed into the pipe at the intake, at various points along the pipe, and in the outer pipe of the HE. The findings demonstrate that improved HE performance arises from raising the fluid input temperature and flow rate. As a result of adding air bubbles to the HE, it was demonstrated that the temperature difference increased, and the energy loss increased. The lowest dimensionless exergy when air bubbles were introduced throughout the tube part was 27.49%. Ghashim and Flayh [125] experimentally inspected the effects of inserting air bubbles on the rate of heat transfer and the ∆P brought on by turbulent flow. The HE had two helical coils. With a turbulent flow having a Re of and hot water flowing at a constant MFR of 0.0331 kg s-1 (9000–50,000). The journey has come to an end. Air bubbles were injected into hot water at a rate of (1.5, 2.5, and 3.5) LPM. According to data, air bubbles in hot water increased the Nu from 64 to 126% and the f in the Re ranged from 66 to 85% (9000 to 50,000). Due to air bubbles, the NTU and ε significantly increased. Moreover, exergy loss in the case of ABI was greater than without ABI. Sinaga et al. [126] looked into the heat transfer performance of an experimentally streamed air/water two-phase flow using an inner tube HE. Hot water and air were joined in a T-junction on the outside of the HE before flowing inside the inner tube. Two LPM was the specified water flow rate, which was maintained constant. For the hot flow rate, three various flow rates 3, 4, 5, and 6 LPM were considered. Air volumetric fraction ranged from 0.14 to 0.62. Several energetic and exergetic parameters, such as ∆P, effectiveness, NTU, h, dimensionless exergy loss, and Witte-Shamsundar efficiency factor, were used to examine the results. The results presented an increase in the h and NTU of 33 and 38%, respectively. Talib et al. [127] performed an examination of energy using various air injection sites in a STHE and the efficiency of heat transmission. Nu was administered to the HE with ABI than to the HE without ABI, ranging from 2.41 to 25.5%. When air bubbles were injected into the shell and tube at a high level of Re around 15,000, the maximum NTU was experienced. In comparison with the case of no ABI, the improvements in q for air injection through the shell, tube, and both shell and tube were 4.45, 8.42, and 13.63%, respectively. El-Said et al. [128] studied the THP of STHE with baffles and air injection into the shell at various flow rates during the injection process. The outcomes showed the random vector functional link model's strong capacity to identify the nonlinear relationship between operating conditions and process responses. Zarei et al. [129] investigated the effects of ABI on Nu, temperature variations in the storage tank, energy deprivation in the evaporator, and COP. Airflow rates (3–11 LPM) were used to inject the bubbles into four distinct geometries from the bottom of the storage tank. The geometry and flow rate of the ABI had a significant impact on this increase. The outcomes showed that the ABI had an ideal flow rate, which in this case was 9 LPM.
In STHEs, when the active enhancement technique for improving heat transfer was used, it is believed that the authors should pay particular attention to this strategy. The U ratio increases because of the injection of air bubbles; the greatest value was 452% as compared to merely water flow. It is indicated the most studies carried out in air injection methods for heat transfer improvement are experimental ones. It is required more numerical explanations for the reasons for enhancing heat transfer by air bubbles injections inside the tube and shell of STHE.
Nanofluids
One of the significant techniques for speeding up heat transfer in HEs in latest years was the addition of solid particles to heat transfer streams. Despite receiving a lot of attention, they have drawbacks, for example, significant pressure drops, abrasion, clogging, and sedimentation. However, compared to solid particles, the usage of nanofluids generates a substantially larger increase in heat transmission. Nanofluids were employed with solid particles that were in very tiny sizes and low concentrations to address the issues. Many researchers investigated the nanofluid utilized for heat transfer improvement as seen in Table 3. In a fluidized bed vertical shell and tube type, HE with counterflow, Ahn et al. [131] examined how fluid flow and heat transfer qualities were affected by moving solid particles. The current study discovered that heat transmission increased in the order of sand, copper, steel, aluminum, and glass and that greater-density solid particles had a higher flow velocity range for particle impacts with the tube wall. Farajollahi et al. [132] investigated the heat transfer properties of nanofluids made of -Al2O3/water and -TiO2/water in a STHE with turbulent flow. Investigated were the impacts of Peclet number, suspended nanoparticle VC, and particle type on the thermal properties. According to the findings, adding nanoparticles to the base fluid significantly improves the properties of heat transmission. There were two distinct optimal nanoparticle concentrations for both types of nanofluids. Huminic and Huminic [133] used nanofluids in a computational study to examine the heat transfer properties of twin-tube helical HEs with laminar flow. As the working fluid, 24 nm-sized CuO and TiO2 nanoparticles were dispersed in water at VCs of 0.5–3 vol%. The De and the nanoparticle concentration level's effects on the qs and hs were provided. The results demonstrate that the nanofluid's q was roughly 14% bigger than that of pure water for 2% CuO concentration with similar MFR inside internal and annulus sides and that it was approximately 19% greater than for the scenario where water flowed inside the internal and annulus sides. The findings further demonstrate that the MFR and De were positively correlated with the convective h of water and nanofluids. By contrasting simulations with the data derived using empirical equations, the results have been validated. Lotfi et al. [134] investigated experimentally how MWNT/water nanofluid may improve heat transfer in a horizontal STHE. The Co–Mo/MgO nanocatalyst was used in the catalytic chemical vapor deposition process to create carbon nanotubes. A three-step process was used to purify the obtained MWNTs. The addition of COOH functional groups made the nano-tubes hydrophilic and improved nanofluid stability. The outcomes showed that, in contrast to the base fluid, heat transport was enhanced with the adding of multi-walled nanotubes. Elias et al. [135] studied the impact of various nanoparticle forms, including cylindrical, brick-like, blade-like, plate-like, and spherical ones, on the performance of a STHE using nanofluid. Differently shaped boehmite alumina (γ-AlOOH) nanoparticles were distributed in a water/ethylene glycol nanofluid. The q and entropy production were utilized to analyze the thermodynamic performance of the STHE that was employed in a waste heat recovery system. The thermal conductivity, h, rate, and entropy production of nanofluid were measured using established correlations. The outcomes demonstrate an improvement in the system's heat transport and thermodynamic performance. Entropy generation, however, was larger for nanofluids including cylindrical nanoparticles than for those containing other types of nanoparticles. Entropy did increase, but only by less than 1%. Therefore, it might be concluded that this increased entropy generation was minor, and cylindrically shaped nanoparticles were advised to be used in HE systems using nanofluids. Aly [136] examined the effects of VCs water-based Al2O3 nano-fluid of the nanofluids and the curvature ratio of the helical tube on the heat transfer and ∆P. The findings demonstrated that coil diameter and nanofluid volumetric flow rates both affect a HE's efficiency and that the 3D realizable k–e model was crucial for turbulence modeling. Rach and Dipak [137] investigated the enhancement of heat transfer by nanofluids with fixed heat flux in both laminar and transition streams. A novel strategy for improving heat transmission was the use of inserts containing nanofluids. In the experiment, water was utilized as the base fluid and iron oxide nanofluid was combined with it at various VCs. After that, using nanofluid and comparing it to ordinary water, measure the change in the convective h. The experiment's findings showed that the value of convective h increased as the MFR raised and provided improvements ranging from 2 to 48%. Additionally, it increased with rising nanofluid VC, although just about 4% concentration. Once more, it will begin to decline at about 4% concentration.
Dharmalingam et al. [138] investigated in an experimental setting the forced h and flow properties of a nanofluid made up of water and 1% volume-concentrated Al2O3 nanoparticles that were running in parallel, counter, and STHEs under laminar flow conditions. This study shows that at the same MFR and input temperature, the U and dimensionless Nu of the nanofluid were marginally greater than those of the base liquid. It was evident from the experimental data that as MFR increases, the nanofluid's U increases. It demonstrates that regardless of flow direction, as MFR rises, so do the U and Nu. Additionally, it was discovered that regardless of flow direction, LMTD value finally declines as MFR increases. However, due to the multiple pass flow of nanofluid, STHEs offer higher heat transfer properties than parallel and counter-flow HEs. Azad and Vahdat [139] investigated the use of alumina-nanofluid to improve the efficiency of HEs. The Nu and, consequently, the h of STHEs were both increased by alumina nanofluid. The ∆P can be decreased by up to 94% thanks to increased hs since they shorten the length of the tubes that must be used, which reduces the pressure inside them. As a result, the HE's overall cost decreased by more than 55%. Shahrul et al. [140] studied the performance of a STHE by adding Al2O3, SiO2, and ZnO nanofluids experimentally examined. Al2O3 and SiO2 nanofluids were prepared without using any surfactant. ZnO and Fe3O4 nanofluids were stabilized using the polyvinylpyrrolidone (PVP) surfactant. ZnO has the highest h, U, and real heat transfer q, while SiO2 exhibits the lowest h, U, and q. ZnO, Al2O3, and SiO2 nanofluids, respectively, were reported to improve h by about 50, 15, and 9%. When the nanofluids were used, U was enhanced by about 35, 26, and 12%, respectively. When compared to water, q was improved by about 51, 32, and 26%. Using 0.3 vol.% of ZnO nanofluid, the best performance was obtained at 6 LPM. Similarly, utilizing 0.5 vol.% of Al2O3 and SiO2 the greatest performance was attained at 7 LPM. Adding ZnO nanofluids boosted the STHE's overall performance by roughly 35%. Kumar and Sonawane [141] studied Fe2O3/water and Fe2O3/EG nanofluids' heat transfer properties were examined in a STHE with laminar to turbulent flow conditions. The Fe2O3 nanofluids with volume fractions of 0.02, 0.04, 0.06, and 0.08% were employed in the STHE as working fluids with varying nanofluid flow rates. Investigations into how to increase heat transfer considered many variables, including fluid temperatures, base fluid kinds, nanoparticle concentrations, and sonication times. Due to more particle contact, thermal conductivity and heat transfer significantly improved as nanoparticle concentration rose. Additionally, it was found that when the temperature rose, the base fluid thermal conductivity improved. The tests also revealed that, under a regime of turbulent flow, the ∆P of the nanofluid was greater than that of the base fluid. However, the ∆P during laminar flow did not significantly increase. Aghabozorg et al. [142] investigated the influences of flow types (laminar, transient, and turbulent) flows with three distinct heat fluxes on the amplification of Fe2O3-CNT magnetic nanoparticles within a horizontal STHE. The h of hybrid Fe2O3-CNT magnetic nanofluids was found to be greater than that of the base fluid. The outcomes showed that at 0.1% mass concentration (ϕ), the h for turbulent and laminar flow was augmented by 13.54 and 27.69%, respectively. Additionally, laminar, and turbulent flow enhancement was 34.02 and 37.50% at 0.2% mass concentration compared to pure water. Esfahani and Languri [143] investigated how the STHE performance was impacted by graphene oxide nanofluid. The concentrations of the graphene oxide nanofluids were 0.01 and 0.1 mass %. Exergy research revealed that growing the content of graphene-oxide from 0.01 mass % to 0.1 weight % led to growth in thermal conductivity of 8.7 and 18.9% at 25 and 40 °C, respectively. The findings demonstrated that the STHE had decreased energy loss when employing graphene oxide nanofluids, both in laminar and turbulent settings. In contrast to laminar circumstances, distilled water induced an exergy loss that was 22 and 109% more than that of graphene oxide nanofluids. Barzegarian et al. [144] investigated the effects of SB in STHE on the thermal performance experimentally. By increasing Re, the results showed a significant increase in Nu and U the HE's. At a given Re, the HE's heat transfer characteristics increase as the VC of nanoparticles rises. Results of the heat transfer assessment showed that substituting nanofluids for base fluid increase the Nu by up to 9.7, 20.9, and 29.8% at 0.03, 0.14, and 0.3 vol %, respectively. Additionally, it was demonstrated that U of HE improves by approximately 5.4, 10.3, and 19.1% at the nanoparticle volume fractions. The use of nanofluid in the test section was found to have a minor negative impact on ∆P.
Rambabu et al. [145] investigated the q between water and TiO2. In a STHE with turbulent flow, nanofluids were detected. Even a little concentration of nanoparticles in the base fluids improves h. The TiO2 has a higher q than water when its nanoparticle concentration was optimal. TiO2 nanoparticles were chosen to improve heat transfer capabilities, disperse them in water, and compare them to the merely pure base fluid. Finding the U and the degree of heat transfer amplification at various flow rates was another extension of the study. The results of the experiment reveal, with the addition of nanoparticles, the properties of heat transmission were improved at various flow rates and VCs (0.05, 0.1, 0.15, and 0.2%). Naik and Vinod [146] investigated the present inquiry, which studies heat transmission utilizing three distinct non-Newtonian nanofluids made up of aqueous carboxymethyl cellulose (CMC) base fluids including Fe2O3, Al2O3, and CuO nanoparticles. The findings demonstrated that the Nu increases with increasing fluid temperature in the shell side, nanofluid concentration, De in the coil side water flow rate, and stirrer speeds. Somasekhar et al. [147] studied the ∆P and heat transfer properties of the Al2O3–H2O nanofluid under turbulent flow conditions using computational fluid dynamics software. Instead of using distilled water as a cooling medium, nanofluids such as Al2O3 were employed. The findings of the CFD simulation and the experimental data were then compared. According to the outcomes, mixing nanoparticles with the base fluid significantly improves the properties of heat transmission. Said et al. [148] looked at the thermophysical characteristics, and heat transfer efficiency of a STHE using a CuO and water nanofluid. They employed concentrations of 0.05, 0.1, and 0.3 vol% of nanoparticles. To support the findings of the experimental investigation, a theoretical model was also created. According to the results, while operating with nanofluid at similar fluid input temperatures and mass flow rates as base fluid, the convective h was somewhat greater. Results from experiments demonstrate how nanofluids increase heat transfer. Convective heat transmission rose by 11.39%, the U improved by 7%, and the area was reduced by 6.81%. Anitha et al. [149] researched how the VC and fraction of nanoparticles affected the efficiency of heat transfer of an Al2O3 and Cu hybrid nanofluid in a STHE. The outcomes presented that the HTP of the hybrid nanofluid was dominated by enhanced nanoparticle VC. In comparison with water and Cu/water nanofluid, the hybrid nanofluid's h increases by 139 and 25%, respectively. Compared with Al2O3 nanofluid, hybrid nanofluid exhibits a maximum enhancement in Nu of over 90%. Consequently, hybrid nanofluid systems achieve the best heat transfer performance. Utilizing a hybrid nanofluid enhances HE efficiency by about 124%. They demonstrated that it was also greater than water. Results were anticipated to be useful in furthering the industrial-level implementation of nanofluids, a field that was now pertinent for continuing activities worldwide in academia-industry partnerships. Fares et al. [150] investigated how graphene nanofluids affected convective heat transfer in an experimental vertical STHE. As a starting point, graphite foam made of sugar was used to create graphene flakes. The impacts of several factors on the h and thermal efficiency, for example, the nanofluid concentration, the flow rate, and the inlet temperatures were investigated. The findings demonstrated that the vertical STHE's thermal performance was improved using graphene/water nanofluids. Using 0.2% graphene/water nanofluids, a maximum increase in the h of 29% was accomplished. Additionally, the use of graphene/water nanofluid increased the HE's mean thermal efficiency by 13.7%. Karimi et al. [151] investigated the effects of silicon carbide nanofluid in tubes of the STHE. There were four distinct levels of nanofluid concentration: 0.25, 0.5, 0.75, and 1 vol.%. At 35, 45, and 55 °C. The findings demonstrate that as MFR and volume percentage of nanoparticles rise, so do heat transmission and pressure decrease. Incorporating nanoparticles causes a 19.8% increase in heat transfer. Sridhar et al. [152] examined the efficiency of an experimental STHE using tin nanoparticles such as SnO2 and silver Ag nanofluids. The effects of nanoparticle VCs on ∆P, thermal conductivity, h, viscosity, f, and Nu. Due to the special intrinsic feature of the nanoparticles, the results demonstrated that adding 0.1 mass % of SnO2 or Ag nanoparticles enhanced the thermal conductivity of nanofluids by 29 or 39%, respectively. Additionally, the two-phase mixture's improved thermal conductivity raised the convective h, and the F rose because of the nanofluids' higher viscosity and density. Perumal et al. [153] increased the U while decreasing the ∆P in STHEs to improve their efficiency. To create nanofluids, this work considered a variety of nanoparticles, including aluminum oxide (Al2O3), silicon dioxide (SiO2), titanium oxide (TiO2), and zirconium dioxide (ZrO2). The use of these nanofluids, which have excellent thermal conductivity, accelerates heat transfer in STHEs. Based on their features for both heat transmission and thermophysics, the chosen nanofluids were contrasted with base fluid. By utilizing nanofluids, all heat transfer properties were enhanced, although TiO2 and Al2O3 provide much better results than SiO2 and ZrO2. Mixing of nanoparticles increased in terms of volume percentage it will be increases all Heat transfer characteristics as well as performance of the HE. Bahiraei and Monavari [154] looked into how different nanoparticle shapes affected the THP of a boehmite nanofluid (BNF) in a small STHE, both with and without fins. Five different nanoparticle forms were taken into consideration, each with an intake temperature of 90 °C at a Re of 500 for the warm fluid side and an inlet temperature of 20 °C at four different Res of 500, 1000, 1500, and 2000 for the cold fluid side. While normal water was the cold fluid within the shell side, the heated fluid was the nanofluid that travels inside the tube side. Pressure decreases as Re increases, as does the q, U, effectiveness, and NTU growth, though declining the performance index. The performance index decreases by 21.7% and then increases by 20% when the Re in the nanofluid containing the oblate spheroid nanoparticles was increased from 500 to 2000. The BNF with the platelet additives produces the highest q, while the Os-shaped additives produce the lowest ∆P. Additionally, the small STHE with fin has higher q, U, effectiveness, NTU, performance index, and ∆P than the small STHE without fin. Rios et al. [155] proposed that stable nanofluids with the appropriate nanoparticle selection at the best VC may be used in a thermal system to provide beneficial economic and environmental outcomes.
Based on the type and size of the utilized nanoparticles, the type of base fluid, and their thermophysical characteristics, the examined nanofluids are described and categorized as seen in Table 3. Also, the findings of the research about the improvement of heat transfer are reported together with the experimental and numerical techniques used in the inquiry on the performance of nanofluids through HEs. In most earlier studies, using nanofluids in place of conventional fluids resulted in a significant increase in STHE's thermal performance when compared to using its base fluid. Increased nanoparticle volume fraction, Re, and pressure drop were shown to boost heat transfer. It is indicated that nanoparticles enhanced the thermal conductivity of nanofluids. According to the research, heat transfer increases while using nanofluids, with TiO2 having the highest U ratio (175.9%) when compared to conventional fluid.
Compound method
This technique for improving heat transmission combines active and passive techniques. The simultaneous use of fluid vibration and wire coils was an excellent illustration of this technique, which has been the subject of several investigations in HEs as seen in Table 4. Raja et al. [157] investigated how a coil insert and an alumina/water nanofluid affected an STHE’s heat transmission properties. On heat transfer and pumping power parameters, the effects of the Peclet number and the concentration of the alumina/water nanofluid were examined. The base fluid's overall thermal characteristics were improved when the VC of nanoparticles was increased as compared to water. For a given peclet number, the U rose even more with the addition of a wire coil insert. Increased heat transmission resulted from the thermal dispersion influence's flattening of the temperature distribution and subsequent steepening of the temperature difference between the fluid and tube wall. Elias et al. [158] investigated the impact of several particle types (cylindrical, bricks, blades, and platelets) on the U, the q, and the creation of entropy in a STHE with various baffle angles and SBs. Nanofluids were employed to calculate the HE's characteristics using established correlations. In terms of U and q, cylindrical shape nanoparticles outperformed other shapes for various baffle angles, along with SBs. When Boehmite alumina (γ-AlOOH) was present in concentrations of 1 vol.%, the augmentation of U for cylindrical form particles with a 20° baffle angle was found to be 12, 19.9, 28.23, and 17.85% higher than that for 30°, 40°, and 50° baffle angles, respectively. Compared to other baffle angles and a SB, Q was likewise found to be higher for cylindrical shapes at a 20° baffle angle. However, for all baffle angles and SBs, entropy generation falls as VC rises. Bahiraei et al. [159] studied the heat transfer performance of a water-Al2O3 nanofluid in the shell of a STHE using helical baffles. As the volume percentage and Re grew, both heat transmission and ∆P were accelerated. When the Re was decreased, the f increased, but when the volume fraction was increased at the same Re, there was no discernible change in the friction factor. The volume percentage of the particles was shown to be more important for the nanofluid’s heat transfer at a lower Re number. A neural network was used to build models of the Nu and f in the HE in terms of Re and volume percentage. Thakur and Singh [117] examined the heat transfer properties of STHE with the ABI at the entrance and over the tube using Al2O3 nanofluids such as 0.1 and 0.2% v/v. The results showed that ABI and nanoparticle volumetric concentration improved the heat transfer properties. The largest improvement was obtained when ABI was performed throughout the tube, and it was followed by situations in which no air bubbles were injected and cases in which air bubbles were injected only at the tube's intake. Additionally, it was discovered that an increase in the hot fluid's temperature, while maintaining a constant flow rate for both heat transfer fluids led to an improvement in the properties of heat transfer. Heydari et al. [160] looked at how adding various nanoparticles to the fluid might affect the efficiency of a baffled STHE. The impact of various nano-fluids at varying volume fractions applied in a baffled STHE was examined using a three-dimensional modeling technique. They obtained q, ∆P, outlet shell temperature, and exchanger efficacy for various volume fractions and particle sizes of various nano-fluids after confirming the grid independence and results. Al2O3, CuO, Fe2O3, Cu, Fe, SiO2, and Au were among the nanoparticles under investigation. Ethylene glycol and water were used as the basic fluids. The results showed that adding nanoparticles had decreased the h in all scenarios with constant mass flow rate, ∆P, and the rate of heat transfer through the shell, even though it had increased outlet shell temperature. In other words, considering a constant q, the presence of nano-fluids in a baffled STHE was likely to be associated with increased outlet shell temperature. Another consequence presents that using ethylene glycol as a base fluid led to higher ε compared with water as a base fluid in the exchanger. Kareemullah et al. [161] examined the heat transfer analysis of an experimental STHE that used helical baffles and zinc oxide as a nanofluid. While the MFR was maintained constantly on the shell side, it was changed on the tube side. They looked at several heat transfer characteristics, including LMTD, h, q, and ε. As soon as the steady state was attained under forced flow circumstances, the experimental values were recorded. It was discovered that, when compared to base fluid, the efficacy of nanofluids increases with mass flow rate. The acquired data led to the conclusion that nanofluids can enhance heat transfer and efficiency, albeit at the expense of pumping power. Jafarzad and Heyhat [162] investigated the energy, exergy, and hydrodynamic characteristics of an Annulus-side combined method-affected vertical double-pipe HE. Finally, to determine the optimal performance based on HE efficiency and energy performance, multi-objective optimization using artificial neural network metamodeling and evolutionary algorithms was conducted. The combined strategy has a promising potential for improving performance, according to the results. Goldanlou et al. [156] studied the Fe3O4/CNT/water hybrid nanofluid’s (HNF) turbulent forced convection heat transfer in a HE fitted with blade-shaped turbulators. The control volume method and the simplex algorithm were used to numerically solve the 3D governing equations (CVM). On the performance characteristics of HE, the effects of Re, VCs of Fe3O4 nanoparticles (φM) and CNTs (φCNT), and blade rod span were assessed. The findings demonstrated that increasing Re and φM causes the PEC of HNF to increase, but increasing dr causes the PEC to rise initially before declining. Bahiraei et al. [163] conducted research on the THP for the nanofluid streams including different particles forms, with cylinder, blade, brick, platelet, and oblate spheroid STHE. The helical unilateral ladder baffles were installed on the STHE to create spiral streams inside the shell side. The heated fluid that flows within the tube side was thought to be nanofluid. Water was used as the cold fluid with Res ranging from 5000 to 20,000 that flows within the shell side. The STHE performance was significantly impacted by the flow pattern the baffles created. By increasing the q, U, efficiency, and NTU, as well as the Re of the shell side, and ∆P increase. Nevertheless, the performance index falls. The presence of the new baffles, particularly at high Res, completely reveals the strong cross and secondary flows on the shell side. Bahiraei et al. [164] investigated how the form of nanoparticles affected the rate of entropy generation in the case of boehmite nanofluid in a STHE equipped with trapezoidal oblique baffles. Cold fluid flows at the side of the shell, whereas hot fluid flows at the side of the tube. The thermal and friction entropies creations rise in the warm fluid when the Re was raised, whereas the Bejan Number falls. The thermal EGR decreased and the frictional EGR increased as the Re was raised in a cold fluid. The cold fluid exhibits the greatest thermal and friction entropies creation in the Os-shaped nanofluid. Overall, the platelet-shaped particles were the ideal ones to be used in the HE since they have the lowest irreversibility when the HE was considered in terms of the second law of thermodynamics. Bahiraei et al. [165] studied the features of unilateral ladder-type helical baffles equipped in STHE. The heated fluid in the tube side uses a boehmite nanofluid with various nanoparticle morphologies and a constant Re. The cold fluid, which enters the shell with varying Re number, was given clean water to use. The Re was amplified, leading to a rise in both thermal and friction entropy in both fluids. The multiple entropy generation rates of the hot and cool fluids, respectively, showed 8.4–20.9% increased by the Re range (5000–20,000) under the scenario of utilizing platelet nanoparticles. The creation of thermal entropy was highest in the nanofluid containing platelet nanoparticles. Bellahcene et al. [166] studied the Al2O3 nanofluid fluid flows and forced convective heat transfer phenomena in the baffled STHE. Al2O3 nanofluids move as a cooling fluid on the shell-side and water as a hot fluid on the side of the tubes. The findings were reported using several physical parameters that represent a volumetric fraction of nanoparticles (1 and 3%) as well as the average Nu, streamlines, and isotherms. The findings show that as inflow velocity and volume % increase, so does heat transmission. Additionally, the inclusion of baffles inside tubular HEs helps improve the fluid mix, which improves heat transmission performance. To improve heat transmission as much as possible while using the least amount of entropy possible, these parameters must be carefully chosen. Ahmadi and Toghraie [167] conducted a three-dimensional study of nanofluid flow and heat transmission in a STHE. The coolant was thought of as the outer layer of pure water, seawater, and CuO nanofluid with φ = 2–4%. This research examined the velocity of the hot gases, the coolant fluid depending on Res, different fluids, and the volume fraction of the nanofluid (φ). Compared to pure water, the ∆P caused by seawater was 16% higher. The findings show that twisted tape has a greater impact than baffles in enhancing thermal performance. The findings showed that even if heat transfer was increased when using nanoparticles with the insert of twisted tape, thermal performance was decreased. While using nanoparticles in seawater improves heat transmission, it also significantly raises friction. Marzouk et al. [168] injected the air using a straightforward technique into the tube sides where wired nails-circular rod inserts (WNCR) were presented as seen in Fig. 11. On thermal parameters (such as NTU, ε, and U) and hydraulic performance (∆P), the effects of inserts alone, inserts in combination with air injection, and air injection alone were examined and analyzed. Also discussed and examined were exergy efficiency and thermal–hydraulic parameters. The findings showed that for all performance criteria, inserts were more noticeable than air injection. Furthermore, insert B (the second variety) has a greater impact than insert A. (insert A). The ranges of the performance parameter percentage improvements for inserts A and B were 31–131%, 43–177%, 33–143%, 44–184%, 2–19%, and 1–23%, respectively, as seen in Fig. 12. For air injection alone with insert A, the ranges were 2–19% and 1–23%, respectively. Air injection had a negligible impact on HE performance measures including NTU, p, and thermal–hydraulic parameters (less than 5%).
The description of ABI inside tubes with inserts [168]
The THP parameter for insert of type A and type B versus TSFR at various AFR [168]
Pourahmad et al. [169] used a twin twisted tape turbulator and introduced ABI into the working water. When used together, the effects of these two techniques on the ∆P and Nu were assessed. The outcomes demonstrated that the Nu was improved with a rise in cold water flow rate, ABI flow rate, and Re as well as a drop in turbulator ratio. The results also demonstrated that the Nu could be increased by 98–114%, 3–14%, and 20–39%, respectively, when the two methods were used simultaneously instead of a simple tube HE, a turbulator-equipped HE (without ABI), and a HE with ABI (without a turbulator). Hussein et al. [170] stated that the total performance of STHE was achieved when a fin was presented in a soft tube. In addition, using a vortex generator, which was a well-known passive approach, considerably accelerates heat transfer and lowers ∆P. Additionally, it appears that additional heat transfer techniques, for example, vortex generators, structural tube design, interior, and exterior HE structures and dimensions, and additive nanofluids improved the HE's overall performance.
Basit Shafiq et al. [171] numerically examined how combining two passive approaches improved the thermal performance of a shell and helical coil tube HEs. Coiled tubes were employed in addition to MWCNT/water nanofluids. The findings showed that when coil Reynolds number and nanofluid volume concentration rose, the Nusselt number of the fluid flowing through the coil increased. Also determined was the thermal performance factor, which acts as an index for HE performance. Tavakoli, Soufivand [172] numerically investigated the THP and entropy formation of a hybrid nanofluid in a STHE with two various cross-sectional baffles. Baffle 1 is more suitable, according to the numerical data found in terms of pressure drop, total entropy production, and performance evaluation criteria (PEC). Baffle 2 is better suited in terms of heat transfer rate and average Nu number values. When the baffle type was switched from the second type to the first type, the PEC maximum change was 5.13% at Re = 45,000 and φ = 0%. When φ = 0% for the first type of baffles, the overall entropy generation increased to its highest level by 73.68%.
Challenges and future scope
It is indicated that many researches that fall into various methods of heat transfer enhancement in STHE have been carried out. Geometrical or surface adjustments without external power, for example, treated surfaces, twisted tapes, abrasive surfaces, and expanded surfaces, or the use of different inserts, are used in the passive approach. Enhancement devices, wire coils, twisted tape, coiled tubes, swirl flow generation, surface tension devices, and gas and liquid additives are examples of such inserts [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104]. The active approach, which employs external power, includes magnetic field reciprocating plungers, fluid suction for flow disruption, surface or flow vibration, and the use of electromagnetic fields was studied. The air injection methods [107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130] and enhancing heat transfer by using nanofluids [132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156] were introduced. The compound approach, which combines active and passive procedures, is the third option. Using solely the passive or active methods yields appealing outcomes [158,159,160,161,162,163,164,165,166,167,168,169,170,171,172].
Figure 13 explains the percentages of the number of papers carried on each method of heat transfer enhancement. The passive method, air injection method, heat transfer improving by using nanofluids, and compound methods have percentages of researches 47.8, 20.2, 22.3, 9.7%, respectively. The active heat transfer enhancement technique has the highest attention from scientists compared to other methods. Less attention was observed to the compound method so more research about this method is necessary.
Geometrical changes in tube surfaces in STHE are too required in the future with the use of materials coating to enhance heat transfer. In addition to other aspects like the cost of the nanoparticle type, the negative effects on pressure drop of the flow, and the overall energy efficiency of STHE, it is prudent to examine the pollution and toxicity implications of the nanoparticles on the environment and health. Secondary flow has a substantial impact on raising the q in several of these experiments. It is still necessary to enhance the theoretical analysis for heat transfer methods, particularly for relevant empirical formulations. To forecast the outcomes as precisely as possible, it is required to present some formulae for methods of heat transfer improvement. Also, since there aren’t many relevant numerical simulations, greater attention is required.
Conclusions
Nowadays, STHE heat transfer technologies are a popular issue in energy-related sectors. Industrial and technical applications frequently utilize this kind of heat exchanger (HE). The HEs have an impact on the overall efficiency and size of a system. Although there are research papers available on the methods of heat transfer enhancement in STHEs, there is a lack of a comprehensive review that covers all the available methods. The work justification of the paper lies in its ability to provide a comprehensive, up-to-date, and systematic review of the various methods (Active, Passive, and Compounds) available for heat transfer enhancement in STHEs. The paper’s findings have practical implications for industries, researchers, and engineers, making it an essential resource for the field of heat transfer. The paper compares and evaluates the different methods of heat transfer enhancement, which helps in selecting the most effective method for a specific application. This comparison is important as it provides a comprehensive understanding of the advantages and limitations of each method.
-
In order to help academics better comprehend the most recent developments in the STHE area, this review, which is a follow-up to many papers by prior writers, summarizes the results of past investigations. This in-depth analysis might aid associated experts in developing their work more. The authors also provide a few issues and ideas that, in their opinion, need additional investigation in the future.
-
There have been 47.8% of studies on the passive approach and the air injection method, increasing heat transfer using nanofluids, and compound methods have percentages of previous studies near 20.2, 22.3, and 9.7%, correspondingly.
-
In the current review, the experimental and numerical studies mostly related to U and exergy efficiency in STHE are introduced. In the case of the passive method, adding baffles has the best heat transfer enhancement where trefoil hole baffles achieved 450% for U ratio compared to smooth tubes. Many different tapes are used for heat augmentation where twisted tape has the best value of 325% for the U ratio. Swirl vane, corrugated tube, and wire coil insert have U ratio values of 130, 161, and 264%, respectively.
-
The active enhancement technique for heat transfer enhancement was employed in STHEs where it is thought that the authors should focus especially on this approach. The air bubble injection causes the rise of the U ratio where the maximum value was indicated at 452% compared to only water flow. It is indicated that nanofluid results in a growth in heat transfer where the TiO2 has the maximum U ratio (175.9%) compared to traditional fluid.
-
For the compound method, utilizing the blade-shaped turbulators with Fe3O4 leads to the maximum U ratio. The combination of air injection and passive heat augmentation techniques, which was shown to be a substantial solution to several issues, needs to be the focus of more work in the future.
-
The cost of the nanoparticle type, the negative effects on pressure drop of the flow, the toxicity implications of the nanoparticles on the environment. Geometrical designs for surfaces in STHE are mandatory in the future with the use of materials coating to improve heat transfer.
-
The theoretical analysis for heat transfer methods in relevant empirical formulations is required. Also, since there aren’t many relevant numerical simulations, greater attention is required.
Data availability
Data will be made available on request.
Abbreviations
- CFD:
-
Computational fluid dynamics
- PT:
-
Plain tube
- STHE:
-
Shell and tube heat exchanger
- HE:
-
Heat exchanger
- LPM:
-
Liter per minute
- MFR:
-
Mass flow rate
- THP:
-
Thermal and hydraulic performance
- NTU:
-
Number of transfer units
- COP:
-
Coefficient of performance
- VFL:
-
Volumetric flow rate
- DWT:
-
Delta winglet tape
- DTP:
-
Double tube pass
- STP:
-
Single tube pass
- SB:
-
Segmental baffle
- SPHB:
-
Single pass helical baffle
- DPHB:
-
Double pass helical baffle
- DPCHSB:
-
Double pass helical segmental baffle
- ABI:
-
Air bubbles injection
- CV:
-
Volume concentration
- PEF:
-
Performance evaluation factor
- S-ODW:
-
Single-oblique delta winglet
- D-ODW:
-
Dingle-oblique delta winglet
- LVG:
-
Longitudinal vortex generators
- BTI:
-
Ball tabulators insert
- MWCNT:
-
Multiwall carbon nanotube
- LMTD:
-
Logarithmic mean temperature difference
- PEC:
-
Performance evaluation criteria
- HNF:
-
Hybrid nanofluid
- A :
-
Area, m2
- Nu:
-
Nusselt number
- De:
-
Dean number
- \(\dot{m}\) :
-
Mass flow rate, kg s-1
- V :
-
Volume, m3
- Re:
-
Reynolds number
- T :
-
Temperature, °C
- h :
-
Enthalpy, J kg-1
- E :
-
Exergy loss
- Q :
-
Heat transfer rate, W
- g :
-
Gravity acceleration, m/s2
- C p :
-
Specific heat, J kg-1 K
- ∆P :
-
Pressure drop
- U :
-
Overall heat transfer coefficient, W m-2 K
- u :
-
Velocity, m s-1
- f :
-
Friction factor
- s :
-
Entropy, J kg-1 K-1
- z :
-
Potential, m
- ϕ :
-
Mass concentration
- d/w :
-
Perforation hole diameter ratio
- y/w :
-
Twist ratio of the twisted tape
- η :
-
Efficiency, %
- ε :
-
Effectiveness
- ψ :
-
Availability, J/kg
- ave:
-
Average
- out:
-
Out
- o :
-
Environment
- ex:
-
Exergy
- c :
-
Cold
- h :
-
Hot
- in:
-
In
- c :
-
Conventional
References
Babu BV, Munawar SA. Differential evolution strategies for optimal design of shell-and-tube heat exchangers. Chem Eng Sci. 2007;62(14):3720–39. https://doi.org/10.1016/j.ces.2007.03.039.
Zheng W, Jiang Y, Wang Y. The sloshing effects on distribution characteristics of gas–liquid mixture in spiral-wound heat exchanger. J Therm Anal Calorim. 2020;141(1):599–612. https://doi.org/10.1007/s10973-020-09423-2.
Zohuri B. Retracted chapter: heat exchanger types and classifications. In: Zohuri B, editor. Retracted book: compact heat exchangers: selection, application, design and evaluation. Cham: Springer International Publishing; 2017. p. 19–56.
Targui N, Kahalerras H. Analysis of fluid flow and heat transfer in a double pipe heat exchanger with porous structures. Energy Convers Manag. 2008;49(11):3217–29. https://doi.org/10.1016/j.enconman.2008.02.010.
Genić SB, Jaćimović BM, Mandić D, Petrović D. Experimental determination of fouling factor on plate heat exchangers in district heating system. Energy Build. 2012;50:204–11. https://doi.org/10.1016/j.enbuild.2012.03.039.
Vengateson U. Design of multiple shell and tube heat exchangers in series: E shell and F shell. Chem Eng Res Des. 2010;88(5–6):725–36. https://doi.org/10.1016/j.cherd.2009.10.005.
Masoud Hosseini S, Safaei MR, Estellé P, Hadi JS. Heat transfer of water-based carbon nanotube nanofluids in the shell and tube cooling heat exchangers of the gasoline product of the residue fluid catalytic cracking unit. J Therm Anal Calorim. 2019;140(1):351–62. https://doi.org/10.1007/s10973-019-08813-5.
Serth RW, Lestina TG. Design of shell-and-tube heat exchangers. In: Serth RW, Lestina TG, editors. Process heat transfer. Boston: Academic Press; 2014. p. 151–97.
Marzouk SA, Al-Sood MMA, El-Fakharany MK, El-Said EMS. A comparative numerical study of shell and multi-tube heat exchanger performance with different baffles configurations. Int J Therm Sci. 2022;179:107655. https://doi.org/10.1016/j.ijthermalsci.2022.107655.
Marzouk SA, Abou Al-Sood MM, El-Said EMS, Younes MM, El-Fakharany MK. Experimental and numerical investigation of a novel fractal tube configuration in helically tube heat exchanger. Int J Therm Sci. 2023;187:108175. https://doi.org/10.1016/j.ijthermalsci.2023.108175.
Çengel YA. Heat and mass transfer: a practical approach. 3rd ed. New York: McGraw-Hill; 2007.
Venkata Rao R, Majethia M. Design optimization of shell-and-tube heat exchanger using Rao algorithms and their variants. Therm Sci Eng Prog. 2022;36:101520. https://doi.org/10.1016/j.tsep.2022.101520.
Afzal A, Islam MT, Kaladgi AR, Manokar AM, Samuel OD, Mujtaba MA, et al. Experimental investigation on the thermal performance of inserted helical tube three-fluid heat exchanger using graphene/water nanofluid. J Therm Anal Calorim. 2021;147(8):5087–100. https://doi.org/10.1007/s10973-021-10869-1.
Kapicioglu A. Energy and exergy analysis of a ground source heat pump system with a slinky ground heat exchanger supported by nanofluid. J Therm Anal Calorim. 2021;147(2):1455–68. https://doi.org/10.1007/s10973-020-10498-0.
Rashidi MM, Mahariq I, Alhuyi Nazari M, Accouche O, Bhatti MM. Comprehensive review on exergy analysis of shell and tube heat exchangers. J Therm Anal Calorim. 2022;147(22):12301–11. https://doi.org/10.1007/s10973-022-11478-2.
Mehendale S, Jacobi A, Shah R. Fluid flow and heat transfer at micro-and meso-scales with application to heat exchanger design. Appl Mech Rev. 2000.
Hatami M, Ganji D, Gorji-Bandpy M. A review of different heat exchangers designs for increasing the diesel exhaust waste heat recovery. Renew Sustain Energy Rev. 2014;37:168–81.
Aresti L, Christodoulides P, Florides G. A review of the design aspects of ground heat exchangers. Renew Sustain Energy Rev. 2018;92:757–73.
Kalapala L, Devanuri JK. Influence of operational and design parameters on the performance of a PCM based heat exchanger for thermal energy storage–a review. J Energy Storage. 2018;20:497–519.
Azeez Mohammed Hussein H, Zulkifli R, Faizal Bin Wan Mahmood WM, Ajeel RK. Structure parameters and designs and their impact on performance of different heat exchangers: a review. Renew Sustain Energy Rev. 2022;154(C).
Omidi M, Farhadi M, Jafari M. A comprehensive review on double pipe heat exchangers. Appl Therm Eng. 2017;110:1075–90.
Thejaraju R, Girish K. A comprehensive review on design and analysis of passive enhancement techniques in double pipe heat exchanger. Power. 2019;2:2.
Gabir MM, Alkhafaji D (eds). Comprehensive review on double pipe heat exchanger techniques. In: Journal of physics: conference series. IOP Publishing; 2021.
Louis SP, Ushak S, Milian Y, Nems M, Nems A. Application of nanofluids in improving the performance of double-pipe heat exchangers-a critical review. Materials. 2022;15(19):6879. https://doi.org/10.3390/ma15196879.
Singh SK, Chauhan MK, Shukla AK (eds). Heat transfer enhancement in double-pipe heat exchanger: a review. In: Journal of physics: conference series. IOP Publishing; 2022.
Kumar V, Tiwari AK, Ghosh SK. Application of nanofluids in plate heat exchanger: a review. Energy Convers Manag. 2015;105:1017–36. https://doi.org/10.1016/j.enconman.2015.08.053.
Tao X, Nuijten MP, Infante Ferreira CA. Two-phase vertical downward flow in plate heat exchangers: flow patterns and condensation mechanisms. Int J Refrig. 2018;85:489–510. https://doi.org/10.1016/j.ijrefrig.2017.10.008.
Tao X, Infante Ferreira CA. Heat transfer and frictional pressure drop during condensation in plate heat exchangers: assessment of correlations and a new method. Int J Heat Mass Transf. 2019;135:996–1012. https://doi.org/10.1016/j.ijheatmasstransfer.2019.01.132.
Zhang J, Zhu X, Mondejar ME, Haglind F. A review of heat transfer enhancement techniques in plate heat exchangers. Renew Sustain Energy Rev. 2019;101:305–28. https://doi.org/10.1016/j.rser.2018.11.017.
Pandya NS, Shah H, Molana M, Tiwari AK. Heat transfer enhancement with nanofluids in plate heat exchangers: a comprehensive review. Eur J Mech B Fluids. 2020;81:173–90. https://doi.org/10.1016/j.euromechflu.2020.02.004.
Indumathy M, Sobana S, Panda B, Panda RC. Modelling and control of plate heat exchanger with continuous high-temperature short time milk pasteurization process—a review. Chem Eng J Adv. 2022;11:100305. https://doi.org/10.1016/j.ceja.2022.100305.
Mastani Joybari M, Selvnes H, Sevault A, Hafner A. Potentials and challenges for pillow-plate heat exchangers: state-of-the-art review. Appl Therm Eng. 2022;214:118739. https://doi.org/10.1016/j.applthermaleng.2022.118739.
Pongsoi P, Pikulkajorn S, Wongwises S. Heat transfer and flow characteristics of spiral fin-and-tube heat exchangers: a review. Int J Heat Mass Transf. 2014;79:417–31. https://doi.org/10.1016/j.ijheatmasstransfer.2014.07.072.
Bhuiyan AA, Islam AKMS. Thermal and hydraulic performance of finned-tube heat exchangers under different flow ranges: a review on modeling and experiment. Int J Heat Mass Transf. 2016;101:38–59. https://doi.org/10.1016/j.ijheatmasstransfer.2016.05.022.
Sadeghianjahromi A, Wang C-C. Heat transfer enhancement in fin-and-tube heat exchangers—a review on different mechanisms. Renew Sustain Energy Rev. 2021;137:110470. https://doi.org/10.1016/j.rser.2020.110470.
Al-Askaree EH, Al-Muhsen NFO. Experimental investigation on thermal performance of solar water heater equipped with Serpentine fin core heat exchanger. Cleaner Eng Technol. 2023;12:100593. https://doi.org/10.1016/j.clet.2022.100593.
Inamdar HV, Groll EA, Weibel JA, Garimella SV. Air-side fouling of finned heat exchangers: part 1, review and proposed test protocol. Int J Refrig. 2023. https://doi.org/10.1016/j.ijrefrig.2023.02.017.
Marzouk SA, El-Fakharany MK, Baz FB. Heat transfer performance of particle solar receiver: numerical study. Heat Transf Res. 2022;53(13):1–19.
Dehankar P, Patil N. Heat transfer augmentation-a review for helical tape insert. Int J Sci Eng Technol. 2014;3(10):1236–8.
Salahuddin U, Bilal M, Ejaz H. A review of the advancements made in helical baffles used in shell and tube heat exchangers. Int Commun Heat Mass Transf. 2015;67:104–8. https://doi.org/10.1016/j.icheatmasstransfer.2015.07.005.
Fsadni AM, Whitty JP. A review on the two-phase heat transfer characteristics in helically coiled tube heat exchangers. Int J Heat Mass Transf. 2016;95:551–65.
Bhuvaneswari S, Elatharasan G (eds). A study of the literature review on heat transfer in a helically coiled heat exchanger. In: RTICCT-2019 conference proceedings; 2019.
Kumar PM, Chandrasekar M. A review on helically coiled tube heat exchanger using nanofluids. Mater Today Proc. 2020;21:137–41.
Rafi S, Sivarajan C, Ch M (eds). Optimization of helical coil tube heat exchanger: a systematic review. In IOP conference series: materials science and engineering. IOP Publishing; 2020.
Rashidi S, Bakhshi N, Rafee R. Progress and challenges of helical-shaped geothermal heat exchangers. Environ Sci Pollut Res Int. 2021;28(23):28965–92. https://doi.org/10.1007/s11356-021-13766-0.
Son Y-S, Shin J-Y. Performance of a shell-and-tube heat exchanger with spiral baffle plates. KSME Int J. 2001;15(11):1555–62. https://doi.org/10.1007/bf03185746.
Durmuş A, Durmuş A, Esen M. Investigation of heat transfer and pressure drop in a concentric heat exchanger with snail entrance. Appl Therm Eng. 2002;22(3):321–32. https://doi.org/10.1016/s1359-4311(01)00078-3.
Khalifeh Soltan B, Saffar-Avval M, Damangir E. Minimizing capital and operating costs of shell and tube condensers using optimum baffle spacing. Appl Therm Eng. 2004;24(17–18):2801–10. https://doi.org/10.1016/j.applthermaleng.2004.04.005.
Andrews MJ, Master BI. Three-dimensional modeling of a helixchanger® heat exchanger using CFD. Heat Transf Eng. 2005;26(6):22–31. https://doi.org/10.1080/01457630590950871.
Naphon P. Heat transfer and pressure drop in the horizontal double pipes with and without twisted tape insert. Int Commun Heat Mass Transf. 2006;33(2):166–75. https://doi.org/10.1016/j.icheatmasstransfer.2005.09.007.
Akpinar EK. Evaluation of heat transfer and exergy loss in a concentric double pipe exchanger equipped with helical wires. Energy Convers Manag. 2006;47(18):3473–86. https://doi.org/10.1016/j.enconman.2005.12.014.
Peng B, Wang QW, Zhang C, Xie GN, Luo LQ, Chen QY, et al. An experimental study of shell-and-tube heat exchangers with continuous helical baffles. J Heat Transf. 2007;129(10):1425–31. https://doi.org/10.1115/1.2754878.
Costa ALH, Queiroz EM. Design optimization of shell-and-tube heat exchangers. Appl Therm Eng. 2008;28(14–15):1798–805. https://doi.org/10.1016/j.applthermaleng.2007.11.009.
Yadav AS. Effect of half length twisted-tape turbulators on heat transfer and pressure drop characteristics inside a double pipe u-bend heat exchanger. Jordan J Mech Ind. 2009;3(1):17–22.
Eiamsa-ard S, Wongcharee K, Eiamsa-ard P, Thianpong C. Heat transfer enhancement in a tube using delta-winglet twisted tape inserts. Appl Therm Eng. 2010;30(4):310–8. https://doi.org/10.1016/j.applthermaleng.2009.09.006.
Wang Y, Liu Z, Huang S, Liu W, Li W. Experimental investigation of shell-and-tube heat exchanger with a new type of baffles. Int J Heat Mass Transf. 2011;47(7):833–9. https://doi.org/10.1007/s00231-010-0590-x.
Aslam Bhutta MM, Hayat N, Bashir MH, Khan AR, Ahmad KN, Khan S. CFD applications in various heat exchangers design: a review. Appl Therm Eng. 2012;32:1–12. https://doi.org/10.1016/j.applthermaleng.2011.09.001.
You Y, Fan A, Lai X, Huang S, Liu W. Experimental and numerical investigations of shell-side thermo-hydraulic performances for shell-and-tube heat exchanger with trefoil-hole baffles. Appl Therm Eng. 2013;50(1):950–6. https://doi.org/10.1016/j.applthermaleng.2012.08.034.
Gowthaman PS, Sathish S. Analysis of segmental and helical baffle in shell and tube heat exchanger. Int J Curr Eng Technol. 2014;2:625–8. https://doi.org/10.14741/ijcet/spl.2.2014.119.
Gao B, Bi Q, Nie Z, Wu J. Experimental study of effects of baffle helix angle on shell-side performance of shell-and-tube heat exchangers with discontinuous helical baffles. Exp Therm Fluid Sci. 2015;68:48–57. https://doi.org/10.1016/j.expthermflusci.2015.04.011.
Wen J, Yang H, Wang S, Xue Y, Tong X. Experimental investigation on performance comparison for shell-and-tube heat exchangers with different baffles. Int J Heat Mass Transf. 2015;84:990–7. https://doi.org/10.1016/j.ijheatmasstransfer.2014.12.071.
Yehia MG, Attia AAA, Abdelatif OE, Khalil EE. Heat transfer and friction characteristics of shell and tube heat exchanger with multi inserted swirl vanes. Appl Therm Eng. 2016;102:1481–91. https://doi.org/10.1016/j.applthermaleng.2016.03.095.
Wang X, Zheng N, Liu P, Liu Z, Liu W. Numerical investigation of shell side performance of a double shell side rod baffle heat exchanger. Int J Heat Mass Transf. 2017;108:2029–39. https://doi.org/10.1016/j.ijheatmasstransfer.2017.01.055.
Gomaa A, Halim MA, Elsaid AM. Enhancement of cooling characteristics and optimization of a triple concentric-tube heat exchanger with inserted ribs. Int J Therm Sci. 2017;120:106–20. https://doi.org/10.1016/j.ijthermalsci.2017.06.002.
Lei Y, Li Y, Jing S, Song C, Lyu Y, Wang F. Design and performance analysis of the novel shell-and-tube heat exchangers with louver baffles. Appl Therm Eng. 2017;125:870–9. https://doi.org/10.1016/j.applthermaleng.2017.07.081.
Labbadlia O, Laribi B, Chetti B, Hendrick P. Numerical study of the influence of tube arrangement on the flow distribution in the header of shell and tube heat exchangers. Appl Therm Eng. 2017;126:315–21. https://doi.org/10.1016/j.applthermaleng.2017.07.184.
Mellal M, Benzeguir R, Sahel D, Ameur H. Hydro-thermal shell-side performance evaluation of a shell and tube heat exchanger under different baffle arrangement and orientation. Int J Therm Sci. 2017;121:138–49. https://doi.org/10.1016/j.ijthermalsci.2017.07.011.
Sadighi Dizaji H, Jafarmadar S, Asaadi S. Experimental exergy analysis for shell and tube heat exchanger made of corrugated shell and corrugated tube. Exp Therm Fluid Sci. 2017;81:475–81. https://doi.org/10.1016/j.expthermflusci.2016.09.007.
Shinde S, Chavan U. Numerical and experimental analysis on shell side thermo-hydraulic performance of shell and tube heat exchanger with continuous helical FRP baffles. Therm Sci Eng Prog. 2018;5:158–71. https://doi.org/10.1016/j.tsep.2017.11.006.
Amini R, Amini M, Jafarinia A, Kashfi M. Numerical investigation on effects of using segmented and helical tube fins on thermal performance and efficiency of a shell and tube heat exchanger. Appl Therm Eng. 2018;138:750–60. https://doi.org/10.1016/j.applthermaleng.2018.03.004.
Ayub ZH, Yang D, Khan TS, Al-Hajri E, Ayub AH. Performance characteristics of a novel shell and tube heat exchanger with shell side interstitial twisted tapes for viscous fluids application. Appl Therm Eng. 2018;134:248–55. https://doi.org/10.1016/j.applthermaleng.2018.01.054.
Bichkar P, Dandgaval O, Dalvi P, Godase R, Dey T. Study of shell and tube heat exchanger with the effect of types of baffles. Procedia Manuf. 2018;20:195–200. https://doi.org/10.1016/j.promfg.2018.02.028.
He L, Li P. Numerical investigation on double tube-pass shell-and-tube heat exchangers with different baffle configurations. Appl Therm Eng. 2018;143:561–9. https://doi.org/10.1016/j.applthermaleng.2018.07.098.
Wen J, Gu X, Wang M, Liu Y, Wang S. Multi-parameter optimization of shell-and-tube heat exchanger with helical baffles based on entransy theory. Appl Therm Eng. 2018;130:804–13. https://doi.org/10.1016/j.applthermaleng.2017.10.164.
Yu C, Ren Z, Zeng M. Numerical investigation of shell-side performance for shell and tube heat exchangers with two different clamping type anti-vibration baffles. Appl Therm Eng. 2018;133:125–36. https://doi.org/10.1016/j.applthermaleng.2018.01.029.
El-Said EMS, Abou Al-Sood MM. Shell and tube heat exchanger with new segmental baffles configurations: a comparative experimental investigation. Appl Therm Eng. 2019;150:803–10. https://doi.org/10.1016/j.applthermaleng.2019.01.039.
Wang X, Liang Y, Sun Y, Liu Z, Liu W. Experimental and numerical investigation on shell-side performance of a double shell-pass rod baffle heat exchanger. Int J Heat Mass Transf. 2019;132:631–42. https://doi.org/10.1016/j.ijheatmasstransfer.2018.12.046.
Saffarian MR, Fazelpour F, Sham M. Numerical study of shell and tube heat exchanger with different cross-section tubes and combined tubes. Int J Energy Environ Eng. 2019;10(1):33–46.
Chen J, Lu X, Wang Q, Zeng M. Experimental investigation on thermal-hydraulic performance of a novel shell-and-tube heat exchanger with unilateral ladder type helical baffles. Appl Therm Eng. 2019;161:114099. https://doi.org/10.1016/j.applthermaleng.2019.114099.
Milani Shirvan K, Mamourian M, Abolfazli EJ. Experimental study on thermal analysis of a novel shell and tube heat exchanger with corrugated tubes. J Therm Anal Calorim. 2019;138(2):1583–606. https://doi.org/10.1007/s10973-019-08308-3.
Mohammadi MH, Abbasi HR, Yavarinasab A, Pourrahmani H. Thermal optimization of shell and tube heat exchanger using porous baffles. Appl Therm Eng. 2020;170:115005. https://doi.org/10.1016/j.applthermaleng.2020.115005.
Mahendran J. Experimental analysis of shell and tube heat exchanger using flower baffle plate configuration. Mater Today Proc. 2020;21:419–24. https://doi.org/10.1016/j.matpr.2019.06.380.
Marzouk SA, Abou Al-Sood MM, El-Said EMS, El-Fakharany MK. Effect of wired nails circular–rod inserts on tube side performance of shell and tube heat exchanger: Experimental study. Appl Therm Eng. 2020;167:114696. https://doi.org/10.1016/j.applthermaleng.2019.114696.
Biçer N, Engin T, Yaşar H, Büyükkaya E, Aydın A, Topuz A. Design optimization of a shell-and-tube heat exchanger with novel three-zonal baffle by using CFD and taguchi method. Int J Therm Sci. 2020;155:106417. https://doi.org/10.1016/j.ijthermalsci.2020.106417.
Yu C, Zhang H, Zeng M, Wang R, Gao B. Numerical study on turbulent heat transfer performance of a new compound parallel flow shell and tube heat exchanger with longitudinal vortex generator. Appl Therm Eng. 2020;164:114449. https://doi.org/10.1016/j.applthermaleng.2019.114449.
Kallannavar S, Mashyal S, Rajangale M. Effect of tube layout on the performance of shell and tube heat exchangers. Mater Today Proc. 2020;27:263–7. https://doi.org/10.1016/j.matpr.2019.10.151.
Chen J, Zhao P, Wang Q, Zeng M. Experimental investigation of shell-side performance and optimal design of shell-and-tube heat exchanger with different flower baffles. Heat Transf Eng. 2020;42(7):613–26. https://doi.org/10.1080/01457632.2020.1716485.
Abbasian Arani AA, Uosofvand H. Double-pass shell-and-tube heat exchanger performance enhancement with new combined baffle and elliptical tube bundle arrangement. Int J Therm Sci. 2021;167:106999. https://doi.org/10.1016/j.ijthermalsci.2021.106999.
Miansari M, Jafarzadeh A, Arasteh H, Toghraie D. Thermal performance of a helical shell and tube heat exchanger without fin, with circular fins, and with V-shaped circular fins applying on the coil. J Therm Anal Calorim. 2020;143(6):4273–85. https://doi.org/10.1007/s10973-020-09395-3.
Al-Obaidi AR, Chaer I. Flow field structure, characteristics of thermo-hydraulic and heat transfer performance analysis in a three dimensions circular tube with different ball turbulators configurations. Arab J Sci Eng. 2021;46(12):12253–82.
Al-Obaidi AR, Alhamid J, Saleh Q. Analysis on flow structure and improvement of heat transfer in 3D circular tube with varying axial groove turbulator configurations. Heat Transf. 2021;50(7):7333–48.
Li X, Wang L, Feng R, Wang Z, Liu S, Zhu D. Study on shell side heat transport enhancement of double tube heat exchangers by twisted oval tubes. Int Commun Heat Mass Transf. 2021;124:105273. https://doi.org/10.1016/j.icheatmasstransfer.2021.105273.
El-Said EMS, Elsheikh AH, El-Tahan HR. Effect of curved segmental baffle on a shell and tube heat exchanger thermohydraulic performance: numerical investigation. Int J Therm Sci. 2021;165:106922. https://doi.org/10.1016/j.ijthermalsci.2021.106922.
Ünverdi M. Prediction of heat transfer coefficient and friction factor of mini channel shell and tube heat exchanger using numerical analysis and experimental validation. Int J Therm Sci. 2022;171:107182. https://doi.org/10.1016/j.ijthermalsci.2021.107182.
Al-Obaidi AR, Alhamid J. The effect of different twisted tape inserts configurations on fluid flow characteristics, pressure drop, thermo-hydraulic performance and heat transfer enhancement in the 3D circular tube. Int J Ambient Energy. 2023;44(1):57–72. https://doi.org/10.1080/01430750.2022.2091023.
Al-Obaidi AR. Thermal flow and heat performance analyses in circular pipe using different twisted tape parameters based on design of experiments. Heat Transf. 2022;51(8):7202–32.
Al-Obaidi AR. Characterization of internal thermohydraulic flow and heat transfer improvement in a three-dimensional circular corrugated tube surfaces based on numerical simulation and design of experiment. Heat Transf. 2022;51(5):4688–713.
Al-Obaidi AR, Alhamid J, Khalaf HA. Effect of different corrugation interruptions Parameters on thermohydrodynamic characteristics and heat transfer performance of 3D Three-dimensional corrugated tube. Case Stud Therm Eng. 2022;32:101879. https://doi.org/10.1016/j.csite.2022.101879.
Al-Obaidi AR, Alhamid J. Investigation of the effect of various corrugated pipe configurations on thermo-hydraulic flow and enhancement of heat transfer performance with the development of different correlations. Int J Therm Sci. 2022;176:107528. https://doi.org/10.1016/j.ijthermalsci.2022.107528.
Siddiqui M, Azam MA, Ali HM. Parametric evaluation of condensate water yield from plain finned tube heat exchangers in atmospheric water generation. Arab J Sci Eng. 2022;47(12):16251–71. https://doi.org/10.1007/s13369-022-06832-3.
Marzouk SA, Abou Al-Sood MM, El-Said EMS, El-Fakharany MK, Younes MM. Study of heat transfer and pressure drop for novel configurations of helical tube heat exchanger: a numerical and experimental approach. J Therm Anal Calorim. 2023. https://doi.org/10.1007/s10973-023-12067-7.
Ikhtiar U, Hairuddin AAB, Asarry AB, Rezali KABM, Ali HM. Numerical investigation of lamella heat exchanger for engine intake charge air cooling utilizing refrigerant as coolant medium. Alex Eng J. 2023;65:661–73. https://doi.org/10.1016/j.aej.2022.10.008.
Kücük H. The effect of minichannels on the overall heat transfer coefficient and pressure drop of a shell and tube heat exchanger: experimental performance comparison. Int J Therm Sci. 2023;188:108217. https://doi.org/10.1016/j.ijthermalsci.2023.108217.
Wang S, Wen J, Li Y. An experimental investigation of heat transfer enhancement for a shell-and-tube heat exchanger. Appl Therm Eng. 2009;29(11–12):2433–8. https://doi.org/10.1016/j.applthermaleng.2008.12.008.
Abbasian Arani AA, Moradi R. Shell and tube heat exchanger optimization using new baffle and tube configuration. Appl Therm Eng. 2019. https://doi.org/10.1016/j.applthermaleng.2019.113736.
Kitagawa A, Kosuge K, Uchida K, Hagiwara Y. Heat transfer enhancement for laminar natural convection along a vertical plate due to sub-millimeter-bubble injection. Exp Fluids. 2008;45(3):473–84. https://doi.org/10.1007/s00348-008-0490-8.
Sadikin A, McNeil DA, Barmadouf KH (eds). Two-phase flow on the shell side of a shell and tube heat exchanger. In: 2010 14th international heat transfer conference 2010.
Donnelly B, O’Donovan TS, Murray DB. Surface heat transfer due to sliding bubble motion. Appl Therm Eng. 2009;29(7):1319–26. https://doi.org/10.1016/j.applthermaleng.2008.09.002.
Fsadni AM, Ge YT, Lamers AG. Measurement of bubble detachment diameters from the surface of the boiler heat exchanger in a domestic central heating system. Appl Therm Eng. 2011;31(14–15):2808–18. https://doi.org/10.1016/j.applthermaleng.2011.05.006.
Dizaji HS, Jafarmadar S. Heat transfer enhancement due to air bubble injection into a horizontal double pipe heat exchanger. J Automot Eng. 2014;4(4):902–10.
Sadighi Dizaji H, Jafarmadar S, Abbasalizadeh M, Khorasani S. Experiments on air bubbles injection into a vertical shell and coiled tube heat exchanger; exergy and NTU analysis. Energy Convers Manag. 2015;103:973–80. https://doi.org/10.1016/j.enconman.2015.07.044.
Nandan A, Singh G. Experimental study of heat transfer rate in a shell and tube heat exchanger with air bubble injection. Int J Eng. 2016. https://doi.org/10.5829/idosi.ije.2016.29.08b.16.
Moosavi A, Abbasalizadeh M, Sadighi DH. Optimization of heat transfer and pressure drop characteristics via air bubble injection inside a shell and coiled tube heat exchanger. Exp Therm Fluid Sci. 2016;78:1–9. https://doi.org/10.1016/j.expthermflusci.2016.05.011.
Khorasani S, Dadvand A. Effect of air bubble injection on the performance of a horizontal helical shell and coiled tube heat exchanger: an experimental study. Appl Therm Eng. 2017;111:676–83. https://doi.org/10.1016/j.applthermaleng.2016.09.101.
Ghasemi Zavaragh H, Kaleli A, Afshari F, Amini A. Optimization of heat transfer and efficiency of engine via air bubble injection inside engine cooling system. Appl Therm Eng. 2017;123:390–402. https://doi.org/10.1016/j.applthermaleng.2017.04.164.
Panahi D. Evaluation of Nusselt number and effectiveness for a vertical shell-coiled tube heat exchanger with air bubble injection into shell side. Exp Heat Transf. 2016;30(3):179–91. https://doi.org/10.1080/08916152.2016.1233145.
Thakur G, Singh G. An experimental investigation of heat transfer characteristics of water based Al2O3 nanofluid operated shell and tube heat exchanger with air bubble injection technique. Int J Eng Technol. 2017;6(4):83–90. https://doi.org/10.14419/ijet.v6i4.7881.
El-Said EMS, Alsood MMA. Experimental investigation of air injection effect on the performance of horizontal shell and multi-tube heat exchanger with baffles. Appl Therm Eng. 2018;134:238–47. https://doi.org/10.1016/j.applthermaleng.2018.02.001.
Mahdi Heyhat M, Abdi A, Jafarzad A. Performance evaluation and exergy analysis of a double pipe heat exchanger under air bubble injection. Appl Therm Eng. 2018;143:582–93. https://doi.org/10.1016/j.applthermaleng.2018.07.129.
Khorasani S, Moosavi A, Dadvand A, Hashemian M. A comprehensive second law analysis of coil side air injection in the shell and coiled tube heat exchanger: An experimental study. Appl Therm Eng. 2019;150:80–7. https://doi.org/10.1016/j.applthermaleng.2018.12.163.
Baqir AS, Mahood HB, Kareem AR. Optimisation and evaluation of NTU and effectiveness of a helical coil tube heat exchanger with air injection. Therm Sci Eng Prog. 2019;14:100420. https://doi.org/10.1016/j.tsep.2019.100420.
Pourhedayat S, Sadighi Dizaji H, Jafarmadar S. Thermal-exergetic behavior of a vertical double-tube heat exchanger with bubble injection. Exp Heat Transf. 2018;32(5):455–68. https://doi.org/10.1080/08916152.2018.1540504.
Subesh T, Dilip Raja N, Logesh K, Ramesh V, Venkatasudhahar M, Surrya PD. Study on performance of horizontal single pass shell and multi-tube heat exchanger with baffles by air bubble injection. Int J Ambient Energy. 2018;41(6):641–51. https://doi.org/10.1080/01430750.2018.1484808.
Sokhal GS, Dhindsa GS, Sokhal KS, Ghazvini M, Sharifpur M, Sadeghzadeh M. Experimental investigation of heat transfer and exergy loss in heat exchanger with air bubble injection technique. J Therm Anal Calorim. 2020;145(3):727–37. https://doi.org/10.1007/s10973-020-10192-1.
Ghashim SL, Flayh AM. Experimental investigation of heat transfer enhancement in heat exchanger due to air bubbles injection. J King Saud Univ Eng Sci. 2021;33(7):517–24. https://doi.org/10.1016/j.jksues.2020.06.006.
Sinaga N, Khorasani S, Sooppy Nisar K, Kaood A. Second law efficiency analysis of air injection into inner tube of double tube heat exchanger. Alex Eng J. 2021;60(1):1465–76. https://doi.org/10.1016/j.aej.2020.10.064.
Talib SM, Rashid FL, Eleiwi MA. The effect of air injection in a shell and tube heat exchanger. J Mech Eng Res Dev. 2021;44:305–17.
El-Said EMS, Abd Elaziz M, Elsheikh AH. Machine learning algorithms for improving the prediction of air injection effect on the thermohydraulic performance of shell and tube heat exchanger. Appl Therm Eng. 2021;185:116471. https://doi.org/10.1016/j.applthermaleng.2020.116471.
Zarei A, Seddighi S, Elahi S, Örlü R. Experimental investigation of the heat transfer from the helical coil heat exchanger using bubble injection for cold thermal energy storage system. Appl Therm Eng. 2022;200:117559. https://doi.org/10.1016/j.applthermaleng.2021.117559.
Thakur G, Singh G, Thakur M, Kajla S. An experimental study of nanofluids operated shell and tube heat exchanger with air bubble injection. Int J Eng. 2018;31(1):136–43.
Ahn SW, Bae ST, Lee BC, Kim WC, Bae MW. Fluid flow and heat transfer in fluidized bed vertical shell and tube type heat exchanger. Int Commun Heat Mass Transf. 2005;32(1–2):224–32. https://doi.org/10.1016/j.icheatmasstransfer.2004.03.017.
Farajollahi B, Etemad SG, Hojjat M. Heat transfer of nanofluids in a shell and tube heat exchanger. Int J Heat Mass Transf. 2010;53(1–3):12–7. https://doi.org/10.1016/j.ijheatmasstransfer.2009.10.019.
Huminic G, Huminic A. Heat transfer characteristics in double tube helical heat exchangers using nanofluids. Int J Heat Mass Transf. 2011;54(19–20):4280–7. https://doi.org/10.1016/j.ijheatmasstransfer.2011.05.017.
Lotfi R, Rashidi AM, Amrollahi A. Experimental study on the heat transfer enhancement of MWNT-water nanofluid in a shell and tube heat exchanger. Int Commun Heat Mass Transf. 2012;39(1):108–11. https://doi.org/10.1016/j.icheatmasstransfer.2011.10.002.
Elias MM, Miqdad M, Mahbubul IM, Saidur R, Kamalisarvestani M, Sohel MR, et al. Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger. Int Commun Heat Mass Transf. 2013;44:93–9. https://doi.org/10.1016/j.icheatmasstransfer.2013.03.014.
Aly WIA. Numerical study on turbulent heat transfer and pressure drop of nanofluid in coiled tube-in-tube heat exchangers. Energy Convers Manag. 2014;79:304–16. https://doi.org/10.1016/j.enconman.2013.12.031.
Rach S, Patel P, Deore D. Heat transfer enhancement in shell and tube heat exchanger by using iron oxide nanofluid. Int J Eng Res. 2014;2(2):2422–32.
Dharmalingam R, Sivagnanaprabhu KK, Yogaraja J, Gunasekaran S, Mohan R. Experimental investigation of heat transfer characteristics of nanofluid using parallel flow, counter flow and shell and tube heat exchanger. Arch Mech Eng. 2015;62(4):509–22. https://doi.org/10.1515/meceng-2015-0028.
Vahdat Azad A, Vahdat AN. Application of nanofluids for the optimal design of shell and tube heat exchangers using genetic algorithm. Case Stud Therm Eng. 2016;8:198–206. https://doi.org/10.1016/j.csite.2016.07.004.
Shahrul IM, Mahbubul IM, Saidur R, Sabri MFM. Experimental investigation on Al2O3–W, SiO2–W and ZnO–W nanofluids and their application in a shell and tube heat exchanger. Int J Heat Mass Transf. 2016;97:547–58. https://doi.org/10.1016/j.ijheatmasstransfer.2016.02.016.
Kumar N, Sonawane SS. Experimental study of Fe2O3/water and Fe2O3/ethylene glycol nanofluid heat transfer enhancement in a shell and tube heat exchanger. Int Commun Heat Mass Transf. 2016;78:277–84. https://doi.org/10.1016/j.icheatmasstransfer.2016.09.009.
Aghabozorg MH, Rashidi A, Mohammadi S. Experimental investigation of heat transfer enhancement of Fe2O3-CNT/water magnetic nanofluids under laminar, transient and turbulent flow inside a horizontal shell and tube heat exchanger. Exp Therm Fluid Sci. 2016;72:182–9. https://doi.org/10.1016/j.expthermflusci.2015.11.011.
Esfahani MR, Languri EM. Exergy analysis of a shell-and-tube heat exchanger using graphene oxide nanofluids. Exp Therm Fluid Sci. 2017;83:100–6. https://doi.org/10.1016/j.expthermflusci.2016.12.004.
Barzegarian R, Aloueyan A, Yousefi T. Thermal performance augmentation using water based Al2O3 -gamma nanofluid in a horizontal shell and tube heat exchanger under forced circulation. Int Commun Heat Mass Transf. 2017;86:52–9. https://doi.org/10.1016/j.icheatmasstransfer.2017.05.021.
Rambabu V, Ramarao J, Babu SR. Enhancement of Heat transfer in Shell and Tube heat exchanger by using nano fluid. Int J Mech Prod Eng. 2017;7(5):191–8.
Naik BAK, Vinod AV. Heat transfer enhancement using non-Newtonian nanofluids in a shell and helical coil heat exchanger. Exp Therm Fluid Sci. 2018;90:132–42. https://doi.org/10.1016/j.expthermflusci.2017.09.013.
Somasekhar K, Malleswara Rao KND, Sankararao V, Mohammed R, Veerendra M, Venkateswararao T. A CFD investigation of heat transfer enhancement of shell and tube heat exchanger using Al2O3-water nanofluid. Mater Today Proc. 2018;5(1):1057–62. https://doi.org/10.1016/j.matpr.2017.11.182.
Said Z, Rahman SMA, El Haj AM, Alami AH. Heat transfer enhancement and life cycle analysis of a Shell-and-Tube Heat Exchanger using stable CuO/water nanofluid. Sustain Energy Technol Assess. 2019;31:306–17. https://doi.org/10.1016/j.seta.2018.12.020.
Anitha S, Thomas T, Parthiban V, Pichumani M. What dominates heat transfer performance of hybrid nanofluid in single pass shell and tube heat exchanger? Adv Powder Technol. 2019;30(12):3107–17. https://doi.org/10.1016/j.apt.2019.09.018.
Fares M, Al-Mayyahi M, Al-Saad M. Heat transfer analysis of a shell and tube heat exchanger operated with graphene nanofluids. Case Stud Therm Eng. 2020;18:100584. https://doi.org/10.1016/j.csite.2020.100584.
Karimi S, Heyhat MM, Isfahani AHM, Hosseinian A. Experimental investigation of convective heat transfer and pressure drop of SiC/water nanofluid in a shell and tube heat exchanger. Int J Heat Mass Transf. 2020;56(8):2325–31. https://doi.org/10.1007/s00231-020-02844-7.
Sridhar SV, Karuppasamy R, Sivakumar GD. Experimental investigation of heat transfer enhancement of shell and tube heat exchanger using SnO2-water and Ag-water nanofluids. J Therm Sci Eng Appl. 2020;12(4):041016. https://doi.org/10.1115/1.4045699.
Perumal S, Venkatraman V, Sivanraju R, Mekonnen A, Thanikodi S, Chinnappan R. Effects of nanofluids on heat transfer characteristics in shell and tube heat exchanger. Therm Sci. 2022;26(2 Part A):835–41. https://doi.org/10.2298/tsci200426076p.
Bahiraei M, Monavari A. Thermohydraulic performance and effectiveness of a mini shell and tube heat exchanger working with a nanofluid regarding effects of fins and nanoparticle shape. Adv Powder Technol. 2021;32(12):4468–80. https://doi.org/10.1016/j.apt.2021.09.042.
Bretado-de los Rios MS, Rivera-Solorio CI, Nigam KDP. An overview of sustainability of heat exchangers and solar thermal applications with nanofluids: a review. Renew Sustain Energy Rev. 2021;142:110855. https://doi.org/10.1016/j.rser.2021.110855.
Shahsavar Goldanlou A, Sepehrirad M, Papi M, Hussein AK, Afrand M, Rostami S. Heat transfer of hybrid nanofluid in a shell and tube heat exchanger equipped with blade-shape turbulators. J Therm Anal Calorim. 2020;143(2):1689–700. https://doi.org/10.1007/s10973-020-09893-4.
Raja M, Arunachalam R, Suresh S. Experimental studies on heat transfer of alumina/water nanofluid in a shell and tube heat exchanger with wire coil insert. Int J Mech Mater Eng. 2012;7(1):16–23.
Elias MM, Shahrul IM, Mahbubul IM, Saidur R, Rahim NA. Effect of different nanoparticle shapes on shell and tube heat exchanger using different baffle angles and operated with nanofluid. Int J Heat Mass Transf. 2014;70:289–97. https://doi.org/10.1016/j.ijheatmasstransfer.2013.11.018.
Bahiraei M, Hosseinalipour SM, Saeedan M. Prediction of Nusselt number and friction factor of water-Al2O3 nanofluid flow in shell-and-tube heat exchanger with helical baffles. Chem Eng Commun. 2014;202(2):260–8. https://doi.org/10.1080/00986445.2013.840828.
Heydari A, Shateri M, Sanjari S. Numerical analysis of a small size baffled shell-and-tube heat exchanger using different nano-fluids. Heat Transf Eng. 2018;39(2):141–53.
Kareemullah M, Chethan KM, Fouzan MK, Darshan BV, Kaladgi AR, Prashanth MBH, et al. Heat transfer analysis of shell and tube heat exchanger cooled using nanofluids. Recent Pat Mech Eng. 2019;12(4):350–6. https://doi.org/10.2174/2212797612666190924183251.
Jafarzad A, Heyhat MM. Thermal and exergy analysis of air- nanofluid bubbly flow in a double-pipe heat exchanger. Powder Technol. 2020;372:563–77. https://doi.org/10.1016/j.powtec.2020.06.046.
Bahiraei M, Naseri M, Monavari A. A CFD study on thermohydraulic characteristics of a nanofluid in a shell-and-tube heat exchanger fitted with new unilateral ladder type helical baffles. Int Commun Heat Mass Transf. 2021;124:105248. https://doi.org/10.1016/j.icheatmasstransfer.2021.105248.
Bahiraei M, Naseri M, Monavari A. Irreversibility features of a shell-and-tube heat exchanger fitted with novel trapezoidal oblique baffles: application of a nanofluid with different particle shapes. Int Commun Heat Mass Transf. 2021;126:105352. https://doi.org/10.1016/j.icheatmasstransfer.2021.105352.
Bahiraei M, Naseri M, Monavari A. A second law analysis on flow of a nanofluid in a shell-and-tube heat exchanger equipped with new unilateral ladder type helical baffles. Powder Technol. 2021;394:234–49. https://doi.org/10.1016/j.powtec.2021.08.040.
Bellahcene L, Sahel D, Yousfi A. Numerical study of shell and tube heat exchanger performance enhancement using nanofluids and baffling technique. J Adv Res Fluid Mech. 2021;80(2):42–55. https://doi.org/10.37934/arfmts.80.2.4255.
Ahmadi MR, Toghraie D. Numerical analysis of flow and heat transfer in a shell and tube heat exchanger in the gas recirculation cooling system of a diesel engine and the effect of nanofluid on its performance. J Therm Anal Calorim. 2021;147(7):4853–71. https://doi.org/10.1007/s10973-021-10831-1.
Marzouk SA, Abou Al-Sood MM, El-Fakharany MK, El-Said EMS. Thermo-hydraulic study in a shell and tube heat exchanger using rod inserts consisting of wire-nails with air injection: experimental study. Int J Therm Sci. 2021;161:106742. https://doi.org/10.1016/j.ijthermalsci.2020.106742.
Pourahmad S, Pesteei SM, Ravaeei H, Khorasani S. Experimental study of heat transfer and pressure drop analysis of the air/water two-phase flow in a double tube heat exchanger equipped with dual twisted tape turbulator: simultaneous usage of active and passive methods. J Energy Storage. 2021;44:103408. https://doi.org/10.1016/j.est.2021.103408.
Azeez Mohammed Hussein H, Zulkifli R, Faizal Bin Wan Mahmood WM, Ajeel RK. Structure parameters and designs and their impact on performance of different heat exchangers: a review. Renew Sustain Energy Rev. 2022;154:111842. https://doi.org/10.1016/j.rser.2021.111842.
Basit Shafiq M, Allauddin U, Qaisrani MA, Rehman T-U, Ahmed N, Usman Mushtaq M, et al. Thermal performance enhancement of shell and helical coil heat exchanger using MWCNTs/water nanofluid. J Therm Anal Calorim. 2022;147(21):12111–26. https://doi.org/10.1007/s10973-022-11405-5.
Tavakoli M, Soufivand MR. Performance evaluation criteria and entropy generation of hybrid nanofluid in a shell-and-tube heat exchanger with two different types of cross-sectional baffles. Eng Anal Bound Elem. 2023;150:272–84. https://doi.org/10.1016/j.enganabound.2023.01.024.
Acknowledgements
The authors are grateful to the mechanical engineering staff in Kafrelsheikh University, Faculty of Engineering for helping with the study by offering guidance, recommendations, and advice.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors affirm that they have no known financial or interpersonal conflicts that would have seemed to have an impact on the research presented in this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marzouk, S.A., Abou Al-Sood, M.M., El-Said, E.M.S. et al. A comprehensive review of methods of heat transfer enhancement in shell and tube heat exchangers. J Therm Anal Calorim 148, 7539–7578 (2023). https://doi.org/10.1007/s10973-023-12265-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10973-023-12265-3