Introduction

The idea of improving heat transfer within tubes, one of the most significant engineering applications where heat transfer coefficients are minimal, has received considerable attention. Pulsating is one of several techniques used to produce separation in the flow and increase the coefficient of heat transfer in internal flows. Creating time-varying flow, or pulsating flow, is thought to be an active method for enhancing convective heat transfer. In this work, two distinct techniques for enhancing heat transfer (pulsating flow and conically coiled tubes) are combined to improve heat transfer.

Widespread uses for coiled tubes include heating systems, chilled water systems, ground water systems, and residential usage. These applications are prevalent in several industries, including the chemical, biological, petrochemical, mechanical, and medicinal sectors. This extensive use of coiled tubes is a result of their compactness and shape, which promotes effective fluid mixing and increases heat transfer coefficients. Due to the considerable usage of coiled tubes in these applications, it is crucial to understand their heat transfer and pressure drop characteristics. Sheeba et al. [1] investigated experimentally and numerically the heat transfer characteristics and flow parameters of fully developed flow in a conical coiled tube heat exchanger in counter flow mode. Dean number and cone angle have a significant impact on heat transfer. The research drew the following conclusions: (i) the inner Nu is impacted by the inner and outer Dean numbers, and (ii) the ratios of mass flow rates of hot and cold fluids have a substantial effect on heat transfer and hence the efficacy of the heat exchanger. Purandare et al. [2] investigated pressure drop and the heat transfer properties of the CCT heat exchanger with varying cone angles, tube diameters, and mass flow rates. The findings demonstrated that the Nu rises as the Re within the tube increases. In addition, the findings demonstrated that when cone angle rises, f increases for a given Re.

Heyhat et al. [3] examined the effect of nanofluids and CCT geometric parameters on pressure drop and heat transfer. Experiments were conducted with various concentrations of SiO2/water under laminar conditions. As geometric variables, several cone angles and coil pitches were used. According to the results, increasing the coil pitch enhances the heat transfer rate. Moreover, cone angle variation enhances heat transfer more effectively than coil pitch change. Abdelmagied [4] performed experimental and numerical analysis of the thermal performance of a triple CCT heat exchanger. In all studies, the triple CCT heat exchanger performed better in terms of Nu than the double CCT heat exchanger by 127.5% when they were both set up to work in a counter-flow configuration. Results also showed that raising the temperature of the water coming in makes the system more efficient while lowering the Nu. Abdelghany et al. [5, 6] studied experimentally two tube geometries, CCT and HCT, utilizing a variety of coil torsions while preserving the same curvature ratio. According to the findings, the Nu and h rise when the coil's torsion decreases. Al-Salem et al. [7] investigated steady-state heat transfer and fluid flow in the annulus portion of a tube-in-tube conically coiled heat exchanger. The findings permitted the development of two correlations for estimating the annulus section exergy efficiency and exergy performance coefficient. Furthermore, the thermal and hydraulic properties of coiled tubes have been the subject of several investigations [8,9,10,11,12,13,14,15,16]. Some correlations were reported in these research' outcomes for forecasting the Nusselt number, friction factor, total heat transfer coefficient, and so on.

Khosravi-Bizhaem et al. [17] conducted an experiment to study the effects of pulsating flow on heat transfer and friction factor in HCT. Experiments were conducted for a range of Re between 2000 and 9500 and Womersley numbers between 16 and 40. They evaluated the Nusselt number and fanning friction factor in constant flow with the known correlations in the literature and found an exceptional degree of agreement. Zohir et al. [18] examined the effects of pulsation with varied amplitudes on rates of heat transfer in a double-pipe heat exchanger with a coiled wire positioned on the outside surface of the inner tube. Experiments are conducted for Re values between 4000 and 12,000. The experimental findings revealed that heat transfer rates rise as the pitch of coiled wire increases.

Pan et al. [19, 20] have determined the mechanism by which sinusoidal pulsing flow enhances heat transfer in HCT. Compared to continuous flow, the volume average field synergy angle was 2.45% lower for pulsed flow. Zhang et al. [21] observed that square wave pulsing flow produced greater fluid disturbance and promoted fluid mixing more easily. Therefore, it may be desirable to boost heat transfer. Using computational techniques, Yu et al. [22] studied the flow and heat transfer properties of pulsating laminar flow within a heated square cylinder. The results were analyzed at a Reynolds number of 100, which was kept constant. The amplitude of the pulsation varied between 0.2 and 0.8, while the frequency ranged from 0 to 20 Hz. The findings revealed that the heat transfer enhancement increased with the increment of the flow pulsation amplitude. The heat transfer enhancement factor peaks when the pulsing frequency is inside the lock-on regime. This is caused by the narrowing of the vortex forming region.

Li et al. [23, 24] examined numerically the effect of square-wave pulsing flow in a HCT on heat transfer enhancement. The numerical results agree with the experimental outcomes. Results indicate that both the Nusselt number and the flow resistance coefficient increase as amplitude and Womersley number values rise. Guo et al. [25] conducted a numerical analysis of nanofluid heat transfer performance in a helical coil under pulsation, detailing the impact of frequency of pulsation and Re on heat transfer performance. Regarding the purview of Re, the findings demonstrated an optimal pulsation frequency for enhancing heat transfer. Under pulsation, the secondary flow created in the cross area and the counter-rotating vortex produced axially contribute to the enhancement of the helical coil's heat transfer. Moreover, the subject of pulsating flow has been the focus of a lot of previous research [26,27,28,29,30]. The recent literature on heat transfer and pressure drop in coiled tubes is summarized in Table 1.

Table 1 An overview of recent research on heat transfer and pressure drop in coiled tubes
Full size table

The literature reviews show that there hasn't been enough research done on the flow field and heat transfer characteristics of the square wave pulsating flow in the conical coiled tubes (CCTs) [23]. Consequently, the objective of this work is to investigate the effects of pulsating flow phenomena on pressure drop and heat transfer characteristics in CCTs. Pulsation frequency, Womersley number, coil torsion, Dean number, and tube side flow rate are all aspects of better heat transfer that have been investigated for their potential implications.

Experimental setup and procedures

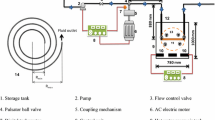
Figure 1 depicts a photograph of the experimental setup and its schematic diagram. As the testing fluid in a closed loop, water maintained at a temperature of 25 °C was employed. The main cycle includes a water tank, a centrifugal pump, a solenoid valve, an accumulator, a cooling system, and CCT. The following is the technique for setting up. The water was pumped from the tank using a centrifugal pump, cycled through the CCT, and then returned to the tank. The solenoid valve was connected to the Arduino Uno board through a relay module to create the square wave pulsation. The solenoid valve can open and close automatically at a regular time interval, and this is done through code written on the Arduino IDE program, and the same square-wave pulsating mechanism was used in recent work by Khosravi-Bizhaem et al. [17] and Li et al. [23, 24]. In a square wave with a 4 Hz pulsation frequency, the solenoid valve opens and closes four times per second. Therefore, a square wave with an opening and closing period of 0.125 s was formed. An accumulator was placed in front of the solenoid valve so that pressure variations brought on by flow pulsations would no longer occur, as well as to protect the pump from being damaged. An electrical heater that was well insulated and looped around a CCT was used to provide a heat flux that was uniform throughout. In order to remove heat from the water in the cooling tank, a cooling system with a horsepower rating of 0.5 is used. In order to keep the temperature of the cold water input constant, a system that is regulated by a thermostat is used.

Fig. 1
figure 1

Experimental setup, a photograph view, and b schematic diagram

Full size image

During the experiment, three test sections consisting of 45° angle conical coiled tubes were used. In Table 2, geometrical characteristics of CCTs are outlined. Copper M-type tubes were used in the process of manufacturing the CCTs. K-type thermocouples were installed at various intervals along the CCTs in order to determine the temperature of the wall surface in parts that were thermally developing and regions that were thermally completely formed. Thermocouples were connected to data acquisition equipment, and LabVIEW software was used to transport temperature data from the equipment to a laptop. In order to achieve steady-state conditions, an experiment must be run for nearly half an hour at the beginning, followed by another 10 min during which the flow rate is varied. After the system has reached a steady state, all of the parameters will have been measured and written down. After that, the flow rate was altered to achieve the new needed value, and the procedure that came before it was carried out once again.

Table 2 CCTs' geometrical characteristics
Full size table

This study has some important definitions of some parameters that have an important impact. The coil curvature (\(\delta\)) is defined as the ratio of the inner diameter of the CCT (\({d}_{\text{t},\text{i}}\)) to the mean diameter of the coil curvature (\({D}_{\mathrm{c}}\)), and the coil torsion (λ) is the ratio of the coil pitch to the length of one completed turn.

$$\delta =\frac{{\mathrm{d}}_{\mathrm{t,i}}}{{\mathrm{D}}_{\mathrm{c}}}$$
(1)
$$\lambda =\frac{{\mathrm{P}}_{\mathrm{c}}}{\pi {\mathrm{D}}_{\mathrm{c}}}$$
(2)

Non-dimensional parameter Dean number (De) is used to describe the fluid flow in a CCT and is represented as

$$\mathrm{De}=\mathrm{Re}\sqrt{\delta }$$
(3)

Womersley number (\(\mathrm{Wo}\)) is used to describe the pulsating flow and is defined as follows:

$$\mathrm{Wo}=\frac{{\mathrm{d}}_{\mathrm{t}}}{2}\sqrt{\frac{2\pi F\rho }{\mu }}$$
(4)

where F is the pulsating frequency and μ is the fluid's dynamic viscosity. In the current investigation, the value of F varies from 4 to 10 Hz.

Figure 2 depicts the stages involved in the fabrication of CCTs in which a uniform heat flux was supplied using an electrical heater wrapped around a CCT and well insulated by glass fiber and cermic fiber. Twelve thermocouples of the K type were used to measure and record the temperatures after being checked for accuracy. The flow rate was measured using a water flow sensor (YF-S201) connected to an Arduino board and placed after the solenoid valve to know the flow pattern after the pulsation process. Two pressure sensors were connected to an Arduino board, and the LabVIEW Interface for Arduino (LIFA) was used to connect the Arduino board to the LabVIEW software. We have built a code that can read both sensors simultaneously and measure the pressure drop without the need to read each sensor separately. Table 3 describes the apparatus used in the experimental setup.

Fig. 2
figure 2

CCTs during fabrication process

Full size image
Table 3 Detailed descriptions of measurement equipment
Full size table

Methodology for data analysis

The following is how the Nu and friction factor were calculated in order to measure the rate of heat transfer and the drop in pressure that occurred in the CCTs. As a first step, the overall heat transfer rate and the heat flux in the CCTs were determined as follows:

$$Q^{\circ} = \dot{m} {C}_{\rm p}{(T}_{\rm o} - {T}_{\rm i}),\quad {\hbox{and}}\quad Q^{\circ} = VI$$
(5)
$$\dot{q}= \frac{Q^{\circ}}{\mathrm{Area}}$$
(6)

The outlet and inlet of the tube are denoted by the subscripts 'o' and 'i,' respectively, while Q° symbolizes the heat transfer rate, q° represents the heat flux, m˚ denotes the mass flow rate, Cp is the specific heat capacity, and T represents the temperature. The thermo-physical properties of water were measured at its mean temperature to establish a friction factor and heat transfer coefficient.

$${T}_{\rm m}=\frac{{T}_{\rm i}+{T}_{\rm o}}{2}$$
(7)

Here's how the local heat transfer coefficient and the local Nusselt number were found [34].

$${h}_{\rm x}=\frac{\dot{q}}{{T}_{\rm w,x}-{T}_{\rm m,x}}$$
(8)
$${\mathrm{Nu}}_{\rm x}=\frac{{h}_{\rm x} d}{K}$$
(9)

\({T}_{\mathrm{w},\mathrm{x}}\) is the local wall temperature, which was recorded at the tube's outer wall surface using thermocouples installed on the coil wall, and \({T}_{\mathrm{m},\mathrm{x}}\) is the local mean fluid temperature, which was calculated using the given formula:

$${T}_{\rm m,x}={T}_{\rm i}+ \frac{\dot{q} P}{\dot{m }{C}_{\rm p} }x$$
(10)

where P is the tube's perimeter. The average heat transfer coefficient was computed numerically (using the trapezoidal rule) by integrating the local values across the tube's length as shown [35, 36]:

$${h}_{\rm avg}=\frac{1}{L}{\int }_{0}^{L}{h}_{({\rm x})}\mathrm{d}x$$
(11)

where L is the le le test segment. The average Nusselt number was calculated as follows [36].

$${\mathrm{Nu}}_{\rm avg}=\frac{\dot{q} {d}_{\rm t}}{K \Delta {T}_{\rm avg}}, \Delta {T}_{\rm avg}=[\frac{1}{x}{\int }_{0}^{x}\frac{dx}{{T}_{\rm w,x}-{T}_{\rm m,x}}{]}^{-1}$$
(12)

The fanning friction factor was calculated as follows [34, 37]:

$$f=\frac{{\Delta {P}}_{\mathrm{c}} {{d}}_{\mathrm{t},\mathrm{ i}}}{2{{L}}_{\mathrm{t}} {{\rho }_{\mathrm{t}}{U}}_{\mathrm{t}}^{2}}=\frac{{\Delta {P}}_{\mathrm{c}} {\pi }^{2} {\rho }_{\mathrm{t}} {{d}}_{\mathrm{t},\mathrm{ i}}^{5}}{32 {{L}}_{\mathrm{t}} {\dot{{m}}}_{\mathrm{t}}^{2}}$$
(13)

Uncertainty analysis

Holman [38] describes Kline and McClintock's more accurate approach for measuring experimental uncertainty. The approach is based on a detailed definition of the uncertainties associated with the basic experimental data. Assume that R is a given function of the independent variables \({{x}}_{1},{{x}}_{2},{{x}}_{3},\dots ,{{x}}_{\mathrm{n}}\). Thus \({R}={R}\left({{x}}_{1},{{x}}_{2},{{x}}_{3},\dots ,{{x}}_{\mathrm{n}}\right)\). Let \({u}_{\rm R}\) represent the result's uncertainty and \({{u}}_{1},{{u}}_{2},{{u}}_{3},\dots ,{{u}}_{\mathrm{n}}\) represent the uncertainties in the independent variables. The result's uncertainty is expressed as:

$${u}_{\rm R}=\sqrt{{\left(\frac{\partial R}{\partial {x}_{1}}{u}_{1}\right)}^{2}+{\left(\frac{\partial R}{\partial {x}_{2}}{u}_{2}\right)}^{2}+\dots +{\left(\frac{\partial R}{\partial {x}_{\rm n}}{u}_{\rm n}\right)}^{2}}$$
(14)

The maximum uncertainties of De, Nu and f for all experimental runs are around 1.4%, 4.3%, and 3.5%, respectively.

Results and discussions

Studies were performed on three distinct CCTS, each of which had a different coil torsion (0.0202 ≤ λ ≤ 0.052) but the same curvature ratio (δ = 0.0564). This was done so that the results of the experiments could be compared. In the present research, the pulsing frequency (F) of the square wave pulsating flow is found to be between 4 and 10 Hz, and Wo that corresponds to this frequency range is predicted to be between 30 and 48. For the purpose of this comparison, the average flow rate of CCT during the pulsating flow condition is the same as that during the steady flow state. The pulsating flow velocity profiles were all square waves. Moreover, the solenoid valve was manipulated to get the desired velocity profile. Figure 3 shows how the inlet velocity changes over time for a 4 Hz frequency as an example. According to Li et al. [23, 24], the changing inlet velocity is either the mean velocity plus the amplitude (the maximum velocity) or the mean velocity minus the amplitude (the minimum velocity), as shown in Fig. 3.

Fig. 3
figure 3

The pulsation inlet velocity pattern [23, 24]

Full size image

Here, Umax and Umin are the maximum and minimum velocities in the conical tube in a pulsing condition. To begin, the experimental apparatus and procedures were validated by comparing Nu for pulsating flow through the CCT to Nu published in the literature. According to the literature research, there is a lack of correlations needed to estimate the Nu for pulsating flow in CCTs. The Nu for steady flow in CCTs, on the other hand, has a number of correlations in the literature. The current experimental data for steady flow in CCTs were validated using data from Abdelmagied [4] and Ali et al.[39].

The results of the comparison of experimental values of Nu with the correlated values of Nu are shown in Fig. 4. This figure shows how the experimental results for heat transfer and friction factor calculations agree well with earlier research.

Fig. 4
figure 4

Validation of the experimental data for steady flow in CCT (λ = 0.036)

Full size image

Heat transfer results

A group of experiments were carried out on CCTs in which the mass flow rate ranged from 0.03 to 0.09 kg s−1, the fluid temperature at the coil inlet was kept at 25 °C, and the pulsation frequency ranged from 4 to 10 Hz. The corresponding dimensionless parameters are 0.02 ≤ λ ≤ 0.052, 1148 ≤ De ≤ 2983 and 30 ≤ Wo ≤ 48. Experiments were conducted with Re ranging from 4836 to 12,562. The critical Re for coiled tubes is displayed in Tables 4 and 5 of Appendix B, which are based on several published correlations. The relationship between the average Nu and the Dean number is seen in Fig. 5. It is clear from looking at Fig. 5 that the Nu values that are obtained under conditions of pulsing flow are higher than those that are obtained under conditions of steady flow (Wo = 0) when the same value of De is used. This demonstrates that the square wave pulsating flow may further enhance the performance of the CCT with regard to heat transfer; nevertheless, it will also raise the flow resistance. It is important to keep in mind that in the pulsating condition, the influence that Wo has on Nu is more substantial when the De is large.

Table 4 Critical Reynolds number correlations
Full size table
Table 5 Critical Reynolds number for coiled tubes
Full size table
Fig. 5
figure 5

Variation of average Nusselt number with Dean number for a λ = 0.02, b λ = 0.036 and c λ = 0.052

Full size image

When the Wo was increased from 30 to 48 Hz while maintaining the same De, the increase in Nu was 36% for a CCT with λ = 0.02. Furthermore, the increase in Nu was 32% for λ = 0.036 and 26% for λ = 0.052. This is mostly due to the fact that the action of secondary flow is primarily responsible for the enhancement in heat transfer that conical tubes provide [1,2,3,4]. The findings of previous studies [23, 40, 41] indicate that the secondary flow is responsible for a main role in the improvement of heat transfer even when the De is low.

Within the scope of this investigation, the condition of Wo = 30 (F = 4 Hz) represents the best possible outcome. When F is more than 4 Hz, there is a gradual drop in the average Nu value. This is due to the fact that the enhancement and expansion of secondary flow not only contribute to the enhancement of heat transfer but also increase flow resistance under situations that include pulsating flow. The construction of the vortex, its growth, and its expansion can only be achieved with the greatest possible balance by using the pulsating frequency that is ideal. This is necessary to ensure that the fluid is well mixed and to maximize the rate at which heat may be transferred [25]. As shown in Fig. 11 of Appendix A, every data point's error bar indicates the experimental uncertainty of the average Nu.

Pressure drop results

Two high-precision pressure sensors were attached to an Arduino circuit in order to detect the pressure drop through the conically coiled tubes at a variety of mass flow rates. The values of the friction coefficient are presented in Fig. 6 for a variety of pulsating flows ranging from 4 to 10 Hz, as well as for constant flow. Experiments were performed on CCTs in which the mass flow rate varied between 0.03 and 0.09 kg s−1 and the fluid temperature at the coil inlet was maintained at 25 °C throughout all of the tests. The dimensionless parameters that correspond to these ranges are as follows: 0.02 ≤ λ ≤ 0.052, 1148 ≤ De ≤ 2983 and 30 ≤ Wo ≤ 48.

Fig. 6
figure 6

Variation of friction factor with Dean number for a λ = 0.02, b λ = 0.036 and c λ = 0.052

Full size image

Figure 6 depicts the relationship between the average ƒ and De. Figure 6 demonstrates that the friction factor values with the pulsating flow are better than those under steady flow (Wo = 0) while maintaining the same De, and this demonstrates that the square wave pulsating flow increases the heat transfer performance of the conical tube. Within the limits of this study, the Wo = 30 (F = 4 Hz) condition reflects the best result. The friction factor tends to decrease as the De increases. When the Wo was increased from 30 to 48 Hz, the rise in ƒ for a CCT with λ = 0.02 was 22% at the same De. The increase of Nu was 23% when λ = 0.036, and it was about 22% λ = 0.052, this is due to an increase in centrifugal force and the consequent formation of vortices as a result of decreasing the torsion or rotational effect [41]. As shown in Fig. 12 of Appendix A, every data point's error bar indicates the experimental uncertainty of the friction factor.

Correlation for average Nusselt number and friction factor

Correlations were developed using the current experimental data to predict the average Nu and the Fanning friction factor inside the CCT. Using the least squares method, a correlation for the average Nusselt number was presented on the basis of experimental data. The correlation estimates the steady-state Nusselt number when the Womersley number tends toward infinite, as also confirmed by Khosravi-Bizhaem [17]. The average Nusselt number is correlated as a function of Womersley, Dean, and Prandtl numbers and coil torsion.

$$\mathrm{Nu}_{\rm avg}=\left(0.43- 0.82 {\mathrm{Wo}}^{-0.6277}\right)\mathrm{De}^{0.658} { \lambda }^{-0.2344} \mathrm{Pr}^{0.012}$$
(15)

Equation (15) is applicable for 0.02≤ λ ≤ 0.052, 5.5 ≤ Pr ≤ 6, 1148 ≤ De ≤ 2983 and 30 ≤ Wo ≤ 48.

Figure 7 compares the experimental Nu to the correlated Nu, and it is obvious that the suggested correlations are in excellent agreement with the current experimental data, with a maximum deviation of 12%.

Fig. 7
figure 7

Comparison of experimental values for average Nu with that correlated by Eq. (15)

Full size image

The friction factor is correlated as a function of Womersley, Dean numbers and coil torsion.

$$f= 42.97 {\mathrm{Wo}}^{-0.3616} \mathrm{De}^{-0.8705} { \lambda }^{-0.2218}$$
(16)

Equation (16) is applicable for 0.02≤ λ ≤ 0.052, 1148 ≤ De ≤ 2983 and 30 ≤ Wo ≤ 48.

Figure 8 compares the experimental ƒ to the correlated ƒ, and it is obvious that the suggested correlations are in excellent agreement with the current experimental data, with a maximum deviation of 15%.

Fig. 8
figure 8

Comparison of experimental values for friction factor with that correlated by Eq. (16)

Full size image

Performance evaluation criteria (PEC)

Performance evaluation criterion (PEC) of pulsating flow is the ratio of the Nusselt number ratio to the friction factor ratio at the same Dean number, as defined by Eq. (17). This ratio is used to assess the complete heat transfer improvement performance of square wave pulsating flow in a CCT.

$$\mathrm{PEC}=\frac{\left(\frac{{\mathrm{Nu}}_{\rm p}}{{\mathrm{Nu}}_{\rm s}}\right)}{ {\left(\frac{{f}_{\rm p}}{{f}_{\rm s}}\right)}^\frac{1}{3}}$$
(17)

where \({\mathrm{Nu}}_{\mathrm{p}}\) and \({{f}}_{\mathrm{p}}\) represent the pulsating state's values. \({\mathrm{Nu}}_{\mathrm{s}}\) and \({{f}}_{\mathrm{s}}\) represent the steady-flow state values. Figure 9 illustrates the experimental outcomes of the PEC of pulsating flow versus Womersley number for different coil torsion values. As shown in Fig. 9, PEC improves by lowering the Wo. This is due to the fact that when there is pulsating flow, both the flow resistance and heat transfer increase, as the secondary flow becomes increasingly powerful. The PEC increased by 37% when the Womersley number was decreased from 48 to 30 for a CCT of λ = 0.02 (coil #1) with the same De value. For λ = 0.036 (coil #2), the PEC increased by 35%. Additionally, for λ = 0.052 (coil #3), the PEC increased by 28%.

Fig. 9
figure 9

The variations of PEC with Womersley number at different coil torsions

Full size image

Figure 10 depicts the relationship between performance evaluation criteria (PEC) and Dean number for a variety of pulsating frequencies. It is clear that the PEC values in the analysed scope are all bigger than unity, demonstrating the importance of using square wave pulsing flow to improve fluid heat transfer in conical tubes. Furthermore, it can be seen that in the range under study, the situation of Wo = 30 is ideal. When Wo exceeds 30, the PEC value steadily decreases.

Fig. 10
figure 10

Variation of PEC with Dean number for a λ = 0.02, b λ = 0.036 and c λ = 0.052

Full size image
Fig. 11
figure 11

Average Nu results with error bars for a λ = 0.02, b λ = 0.036 and c λ = 0.052

Full size image
Fig. 12
figure 12

Friction factor results with error bars for a λ = 0.02, b λ = 0.036 and c λ = 0.052

Full size image

Conclusions

The effects of pulsating flow on heat transfer and pressure drop in conical coiled tubes (CCTs) are the focus of this research. Three CCTs with various coil torsions (0.02 ≤ λ ≤ 0.052) but the same curvature ratio (δ = 0.0564) were used in the experiments. The pulsating frequency (F) of pulsating flow is between 4 and 10 Hz, and the corresponding Womersley number (Wo) is estimated to be between 30 and 48 Hz. Moreover, the following conclusions might be drawn:

  • Reducing the coil's torsion increases the heat transfer rate under similar operating conditions, whether the flow is constant or pulsating. This is because heat transfer is more efficient when secondary flows begin rapidly.

  • The results demonstrate that the CCT-friction factor increases as the coil torsion decreases.

  • The average Nusselt number increases as Dean number increases, although the friction factor typically decreases.

  • The findings show that decreasing the pulsating frequency increases the heat transfer characteristics.

  • A pulsating flow at 4 Hz (Wo = 30) was shown to promote heat transfer the most compared to all other frequencies investigated.

  • The average Nu is increased by 23% at a frequency of 4 Hz (Wo = 30) and by decreasing coil torsion from 0.052 to 0.02 while the friction factor increased by 30%.

  • Based on the Womersley, Dean, and Prandtl numbers and the coil torsion, the proposed correlations can accurately predict the average Nu and friction factor.

  • Performance evaluation criteria (PEC) increased when the coil torsion decreased from 0.052 to 0.02.