Structural and thermal characteristics of Ge_30−xSb_xTe₁₀Se₆₀ (0 ≤ x ≤ 20) glasses for electronic devices

Abstract

Thermal characterization of different compositions of Ge_30−xSb_xTe₁₀Se₆₀ (x = 0, 5, 10, 15, 20 at.%) glassy materials has been investigated through differential scanning calorimetry (DSC). The tested glasses have been synthesized by melt-quench technique. Glassy materials display compositional phase separation at x = 0, 5, 10, 15 at.%. For additional increase in Sb content at x = 20 at.%, the separation of phases combines in the glass matrix. The glass transition temperature (T_g), initial temperature of crystallization (T_c), peak crystallization temperature (T_p) and melting temperature (T_m) were found to be affected by both heating rate and composition. It is noticed that the increasing of antimony mass percentage in the glassy matrix is leading to decrease in T_g, T_c, T_p and T_m values. The melting temperature (T_m) of these glasses was found in the range 733–746 K for the first phase and in the range 740–792 K for the second phase. The activation energy of glass transition (E_g), activation energy for crystallization (E_c), Avrami index (n) and fragility index (F_i) were calculated using these specific temperatures. E_g decreases with increasing Sb content in all studied samples, but E_g is increasing in the sample with Sb content of 20%, and hence, it varies between 102.7 and 110.6 kJ approximately, whereas (E_c) decreases with the increase in the Sb content in all the tested samples and varies between 283 and 339 kJ. The fragility index varies between 10 and 26 indicating that the melts of these glasses are strong, and the fragility is minimum. The results were discussed in terms of the average coordination number N_C and chemical bond approach.

Introduction

Chalcogenides have received a significant interest in recent decades due to their vast variety of scientific and technological applications [1,2,3,4]. As glass modifiers, various metals are utilized to improve the thermal stability and the glass-forming ability (GFA). The glass-forming ability of amorphous Se makes it a suitable host material to examine glassy chalcogenides. However, its' pure form has some drawbacks such as the short lifetime and the low sensitivity. To address these issues, multiple additives such as Ge, Te, As, Bi, Ga and others are used. Ge–Se binary glass has simple requirements for synthesis, highly stable chemically, quickly glass forming [5, 6], and the Sb doping as a third component to the Ge–Se glassy system improves the modification of material properties and structural stability [7]. The Ge–Sb–Te (GST) family are highly promising systems for phase transformation devices due to their quick reversible transition from crystalline to amorphous states at optimal temperatures for the device applications [8], Germanium telluride and Sb₂Te₃ are two major components in this class that serve as the foundation for GST ternary alloys [9,10,11]. In this study, Sb was introduced into the quaternary system Ge_30−xSb_xTe₁₀Se₆₀ (where x = 0, 5, 10, 15, 20 at.%) to examine the implications of Sb addition on crystallization kinetics. The evaluation of glass’s crystallization behavior is essential to assess its glass-forming ability, thermal stability (GFA), and eventually to determining the optimal operating temperature range. Thermal analysis (TA) technique is a useful instrument for investigating the material's features which being influenced by temperature [12], DSC is one of TA techniques which provides information about physical changes induce by endothermic or exothermic processes and variations in heat capacity. In this study, non-isothermal DSC data have been utilized in investigating the kinetics of the phase transformation of glass; four theoretical models were used to interpret the activation energy: Kissinger, Augis–Bennett, Ozawa and Matusita–Sakka.

Experimental

The melt quenching technique was used to synthesize the bulk glassy materials of the Ge _30−xSb_xTe₁₀ Se₆₀ where (x = 0, 5, 10, 15, 20 at.%). Firstly, silica ampoules of 20 cm length and 1.5 cm diameter were soaked in chromic acid for 24 h, then washed by deionized water and were dried in a dryer furnace at 60 °C. Secondly, an appropriate amount of highly pure germanium, antimony, tellurium and selenium have been weighted using sensitive electrical balance (Shimadzu AW220), and the masses of the materials were placed into previously cleaned silica tubes. The tubes were sealed under vacuum of about 10^–5 torr, which was obtained by oil diffusion pump, followed by mixing the components in the ampoules, each one was individually heated in an electrical muffle furnace, the temperature was raised up to 1000 °C for 9 h. The ampoules were shaken on a regular basis to ensure that the compositions are homogeneous, and then the melted components were promptly quenched in a mix of ice and cold water while these ampoules were holding horizontally. Finally, after cooling, the ingots were taken out of the tubes by breaking the silica ampoules and were kept in a dry a T_m osphere at room temperature.

The DSC (Shimadzu 50) was used to study the thermal characteristic of the prepared samples with an accuracy of ± 0.1 K. The DSC for each heating rate was calibrated by using reference materials of zinc and indium supplied with the instrument, and the studied samples were used in a powder form and compressed 20 mg of the sample into aluminum pans. One can distinguish four characteristic temperatures, namely T_g the glass transition temperature, T_c, initial temperature of crystallization, T_p the peak crystallization temperature and T_m the melting temperature. The temperature is simultaneously recorded as a solid line on the recorder chart where non-isothermal DSC curves were obtained at 5, 10, 20, 30 and 40 K/min heating rates.

Results and discussion

Distinguish the four characteristic temperatures

Figure 1a–e shows DSC curves for Ge _30−xSb_xTe₁₀Se₆₀ glassy alloys where x is the Sb mass percentage (x = 0, 5, 10, 15, 20 at.%) at 5, 10, 20, 30, 40 Kmin⁻¹ heating rates. From these figures, T_g, T_c, T_p and T_m can be identified, and the distinctive characters of endothermic and exothermic peaks are evidence in the DSC curves at the investigated temperature region. There are three separate portions to these curves. The first zone, the glass transition area, is distinguished by an endothermic reaction at T_g. The second zone, which is represented by exothermic peaks, is connected to the crystallization process. All the tested glass samples in these two locations exhibit single T_g and T_p values. The third zone, endothermic reactions on the DSC curves which show the melting zone, in this region the glass sample Ge₂₀Sb₁₀Te₁₀Se_60, exhibits just one melting temperature, whereas the glasses (Ge_30−xSb_xTe₁₀Se₆₀), where Sb mass percentage is 0, 5, 10, 15 at.%, exhibit two melting temperatures. That is attributed to the formation of additional phases in Ge_30−xSb_xTe₁₀Se₆₀ (with Sb doping = 0, 5, 10, 15 at.%) beyond the melting region. As we will see later, theses phases will be identified according XRD of the annealed samples at temperatures beyond the melting temperatures. These additional phases disappear at Sb doping rate = 20 at.% which may be explained by the fact that increasing antimony (Sb) can lead to the formation of new defects, an increase in network disorders and an impact on the short- and medium-range order in the glass network [13,14,15] and that at temperatures beyond the melting point, these defects and disorders may absorb thermal energy to maintain more stable single phase instead of creating further phases.

Fig. 1

a–e DSC curves for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15, 20 at.%) at different heating rates (5, 10, 20, 30, 40 K min⁻¹)

The values of T_g, T_c, T_p and T_m for Ge _30−xSb_xTe₁₀Se₆₀ glassy alloys (x = 0, 5, 10, 15, 20 at.%) at various heating rates (α) are listed in Table 1. The table demonstrates that both T_g and T_p are increasing with the heating rate. The increase in T_p with heating rate indicates a reduction in the crystal growth or nucleation process, which could happen due to the high heating rate leaves the system with insufficient time for nucleation and crystallization. The variation of (T_g) with (α) as well as with Sb doping mass percentage is shown in Fig. 2.

Table 1 The values of glass transition temperature T_g/K, crystallization temperature T_c/K, the peak temperature of crystallization T_p/K, melting temperature T_m/K and T_rg for Ge_30−xSb_xTe₁₀Se₆₀ glassy alloys where (x = 0, 5, 10, 15, 20 at.%) at different heating rates (α)

Fig. 2

The variation of glass transition temperature T_g at different heating rates versus Sb mass contents

As listed in Table 1, it is noticed that the increasing antimony mass percentage in the glassy matrix leads to decrease in T_g, T_c, T_p and T_m values.

The value of T_g is determined by various factors such as band gap, bond energy, cohesive energy and average heat of atomization. It is possible to explain the decrease in (T_g) by considering the structural modification brought on by the addition of Sb atoms. The increasing Sb concentration may break the Se–Se bond, which has a bond energy of 44.04 kcal/mol and be replaced by Sb–Se which has a bond energy of 43.981 kcal/mol, or mixed rings to meet the bond's valency and create a more cross-linked structure [16]. The introduction of Sb reduces the concentration of Se₈ rings while increasing chain length in the glass matrix [17,18,19].

X-ray diffraction (XRD) for crystalline phase identification of the annealed samples

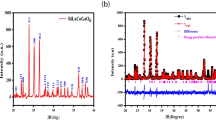
Figure 3a–d shows the patterns formed by XRD of the glassy samples of Sb mass percentage (0, 5, 10, 15 at.%) of Ge_30−xSb_xTe₁₀Se₆₀ composition, and the samples were annealed at temperatures beyond the melting temperatures at 670 K for one hour. After crystallization, the altered materials' diffractograms reveal the presence of microcrystallites. Using the JCPDS files, these peaks can be classified as different phases of binary Sb–Te and Ge–Te, ternary phase of Se–Sb–Te exists only in the sample Ge_30−xSb_xTe₁₀Se₆₀ (x = 15 at.%), and Sb crystallites exist in Ge_30−xSb_xTe₁₀Se₆₀ (x = 10, 15 at.%). The chains of Se₈ appear in all the tested compositions (the coded phases are represented in each figure for each distinct sample), while the amorphous phases represented by the remaining two large humps are shown in Fig. 3a–d for Ge_30−xSb_xTe₁₀Se₆₀(x = 0, 5, 10, 15 at.%) respectively.

Fig. 3

a–d XRD patterns for the annealed samples (Ge_30−xSb_xTe₁₀Se₆₀) where Sb mass percentage (0, 5, 10, 15 at.%)

Glass transition activation energy

T_g denotes the strength and stiffness of the glass network and may be calculated from the endothermic reaction generated by network breaking. It is defined as the commencement of endothermic DSC occurrence; empirical equation was used to examine T_g’s heating rate dependence [20, 21].

$$T_{{\text{g}}} = A + B\ln \left( \alpha \right)$$

(1)

where α is the heating rate for the prepared samples and A and B are constants. The values of A represent the glass transition temperature for the heating rate of 1 K min⁻¹, and the value of B depends upon the heating rate used during the preparation of samples [22]. The plot of T_g against lnα is shown in Fig. 4, and the Eq. (1) seems to be applicable for the current system as shown in Fig. 4. The estimated values of A and B are listed in Table 2, and the values of A have been found to decrease with rising Sb doping percent.

Fig. 4

Plot of T_g/K against (lnα) for evaluation of A and B constants for the present system

Table 2 Values of the parameters A, B, E_g, C and α_o as mentioned in text for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where (x = 0, 5, 10, 15, 20 at.%)

The Kissinger formula has been applied to analyze the value of the glass transition activation.

$$\ln \left( {\frac{{T_{{\text{g}}}^{2} }}{ \propto }} \right) = \frac{{E_{{\text{g}}} }}{{{\text{RT}}_{{\text{g}}} }} + {\text{Constant}}$$

(2)

R is the gas constant. The plot ln (T_g²/α) versus (1000/T_g) produces a straight line whose slope gives the value of E_g as shown in Fig. 5, and the evaluated values of E_g are listed in Table 2. E_g values are within the normal range for chalcogenide glasses [23,24,25] and decrease with increasing Sb content in all samples, but E_g is increasing in the sample with Sb content of 20%.

Fig. 5

Plot of ln (T_g²/α) against 1000/T_g (K⁻¹) for evaluation of glass transition activation energy for the present system

That may be understood in terms of the variation of the average coordination number N_C as we will see below.

Hence, N_C, the average coordination number of Ge_αSb_βTeγSe_ζ quaternary composition $\left( {\rho + \beta + \gamma + \zeta = 100} \right)$, $\left( {{\upalpha } + {\upbeta } + {\upgamma } + {\upzeta } = 100} \right)$ can be assessed by the subsequent procedure as [26]:

$$N_{{\text{C}}} = \frac{{\left[ {\left( {\rho \cdot N_{{{\text{Ge}}}} } \right) + \left( {\beta \cdot N_{{{\text{Sb}}}} } \right) + \left( {\gamma \cdot N_{{{\text{Te}}}} } \right) + \left( {\zeta \cdot N_{{{\text{Se}}}} } \right)} \right]}}{{\left( {\rho + \beta + \gamma + \zeta } \right)}}$$

(3)

Here ρ, β, γ and $\zeta$ are the atomic percentage of Ge, Sb, Te and Se which equal to _30−x, x, 10 and 60 with (x = 0, 5, 10, 15 and 20 at.%), respectively; N_Ge, N_Sb, N_Te and N_Se correspond to their respective coordination numbers and equivalent to 4, 3, 2 and 2, respectively. The determined values N_c of the investigated glasses are listed in Table 3. It is undoubtedly displayed that the coordination number increases with increasing the Sb content within these compositions.As Sb doping increases from 0 to 20%, the average coordination number varies between 2.6 and 2.4. The value of 2.4 is a crucial value in chalcogenides; at this value, a shift from floppy to more rigid occurs [27] and this could explain the increase in E_g at Sb = 20%. According to Phillips theory [27], when the entire number of constraints equals the total number of degrees of freedom, the production of glass is improved; this is achievable when the average coordination number N_C is equal to 2.4, which is known as the rigidity percolation threshold. At N_C = 2.4, the number of inter atomic force-field constraints per atom ma T_c has the number of vector degrees of freedom per atom; ideal mechanical stability is realized. The network is under-constrained for N_C ˂ 2.4 (floppy or spongy). However, when N_C > 2.4, the network is over-constrained (rigid). The floppy-to-rigid transition occurs when N_C = 2.4, and properties display anomalous behavior.

Table 3 Average coordination number N_c, the average heat of atomization H_s, the cohesive energy CE, numbers of lone-pair electrons L and single bond strength S_bt as a function of Sb content of the Ge_30−xSb_xTe₁₀Se₆₀ (0 ≤ x ≤ 20 at.%) glassy compositions

According to the chemical bond approximation, bonds made up of different atoms are preferable to those made up of the same kind of atoms for glass structures [28]. Using the following formula, the heteronuclear bond energies D_(A–B) have been calculated [29]:

$$D_{{\left( {{\text{A}} - {\text{B}}} \right)}} = \sqrt {D_{{\left( {{\text{A}} - {\text{A}}} \right)}} \times D_{{\left( {{\text{B}} - {\text{B}}} \right)}} } + 30\left( {\chi_{{\text{A}}} - \chi_{{\text{B}}} } \right)^{2}$$

(4)

In this case, x_A and x_B are the electronegativities of the associated elements, and D_(A–A) and D_(B–B) are the energies of the homonuclear bonds. By adding the bond energies of all the bonds anticipated in the tested system, the cohesive energy (CE) has been calculated:

$${\text{CE}} = \frac{{\sum {C_{{\text{i}}} D_{{\text{i}}} } }}{100}$$

(5)

C_i and D_i stand for the anticipated number of chemical bonds and the energy of each corresponding bond, respectively. Table 3 includes the estimated CE values. The distribution of likely chemical bonds may be used to estimate the CE. Ge–Se bonds are formed first and have a high bond energy, followed by Te–Se and Sb–Se links, which have somewhat lower bond energies, and finally unsaturated Se–Se bonds [30]. The likelihood of Ge–Se bond formation is reduced when Sb is used in lieu of Ge, which increases the production of Te–Se and Sb–Se bonds. Sb addition results in a drop in the system's (CE) as shown in Table 3. As another way to define cohesive energy, the average heat of atomization H_s (kcal/mole) and single bond strength S_bt can be calculated as [31].

$$H_{{\text{s}}} = \frac{{\left[ {\left( {\rho \cdot H_{{{\text{Ge}}}} } \right) + \left( {\beta \cdot H_{{{\text{Sb}}}} } \right) + \left( {\gamma \cdot H_{{{\text{Te}}}} } \right) + \left( {\zeta \cdot H_{{{\text{Se}}}} } \right)} \right]}}{{\left( {\rho + \beta + \gamma + \zeta } \right)}} ,$$

(6)

$$S_{{{\text{bt}}}} = \frac{{H_{{\text{s}}} }}{{N_{{\text{C}}} }}$$

(7)

The heat of atomization for the constituent elements (Ge, Sb, Te and Se) of the investigated chalcogenide glass are given here as H_Ge, H_Sb, H_Te, H_Se respectively. Table 3 lists the estimated values of H_s and S_bt for the Ge–Sb–Te–Se glass compositions.

The following relation was used to calculate the lone-pair electron numbers, L, of the compositions that were tested [32]:

$$L = V - N_{{\text{C}}}$$

(8)

where V is the valence electrons, also known as unshared lone-pair electrons, and is represented by the following formula [32]:

$$V = \frac{{\left[ {\left( {\rho \cdot V_{{{\text{Ge}}}} } \right) + \left( {\beta \cdot V_{{{\text{Sb}}}} } \right) + \left( {\gamma \cdot V_{{{\text{Te}}}} } \right) + \left( {\zeta \cdot V_{{{\text{Se}}}} } \right)} \right]}}{{\left( {\rho + \beta + \gamma + \zeta } \right)}}$$

(9)

The estimated values of lone-pair electrons are listed in Table 3 where V_Ge, V_Sb, V_Te, V_Se represent the valence for Ge, Sb, Te and Se, which are 4, 5, 6 and 6 respectively. The value of L rises as Sb doping level increases in the compositions under examination.

The free volume theory-based approach, in which the relationship between T_g and heating rate takes the following form [33, 34]:

$$\propto = \propto_{^\circ } \exp \left\lfloor { - 1/C\left( {\frac{1}{{T_{{\text{g}}} }} - \frac{1}{{T_{{\text{m}}} }}} \right)} \right\rfloor$$

(10)

where α_o and C are constants. Figure 6 represents a plot of lnα against (1/T_g−1/T_m). The estimated values of α_o and C are listed in Table 2. Figure 6a represents the first peak of melting for (Ge_30−xSb_xTe₁₀ Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15 at.%) and the plot in (Fig. 6b) correspond to the second peak of melting for Ge_30−xSb_xTe₁₀Se₆₀ glassy alloys where Sb mass percentage was 0, 5, 10, 15, 20 at.%.

Fig. 6

Plot of (lnα) against (1/T_g−1/T_m) for estimation of the constants C and α_o

Activation energy for crystallization and crystallization behavior

The activation energy of amorphous–crystalline transformation (E_c), the Avrami exponent (n) and the frequency factor (K_o) for all prepared samples have been deduced by three different approaches: Kissinger, Augis–Bennett, Ozawa and Matusita–Sakkaas, and they will be explained further down.

DSC has been used to investigate the non-isothermal transformation kinetics of crystallization (amorphous–crystalline transformation), and the heat flow (γ) evolved during crystallization is given by [35, 36]:

$$\gamma = \Delta H\frac{{{\text{d}}\chi }}{{{\text{d}}t}}$$

(11)

where ΔH is the heat of crystallization and χ is the crystallization fraction. This fraction can be represented as a function of time using the formula Johnson–Mehl–Avrami (JMA) transformation equation [24, 25]:

$$\chi \left( t \right) = 1 - \exp \left\lfloor { - \left( {kt} \right)^{{\text{n}}} } \right\rfloor$$

(12)

where n is the Avrami index and K is the reaction rate constant which is given by:

$$K = K_{{\text{o}}} \exp \left( {\frac{{E_{{\text{c}}} }}{{{\text{RT}}}}} \right)$$

(13)

where K_o is the frequency factor and E_c is the effective activation energy. Equations (12) and (13) can be used to justify practically all the experimental treatments in DSC.

The first way to calculate E_c is Kissinger's peak shift method [23], which uses the following equation to connect peak temperature (T_p) with heating rate (α):

$$\ln \left( {T_{{\text{p}}}^{2} /\alpha } \right) = \left( {E_{{\text{c}}} /{\text{RT}}_{{\text{p}}} } \right) + {\text{Constant}}$$

(14)

Figure 7 shows the plot of ln (T_p²/α) against (1000/T_p) for the present system, the slopes of the lines give the values of (Eb_c) for all the studied compositions, and the values of the calculated (E_c) are given in Table 4.

Fig. 7

Plot of ln (T_p²/α) against 1000/T_p (K⁻¹) for evaluation of activation energy of crystallization E_c for the present system

Table 4 Activation energies of the crystallization (E_c), Avrami exponent (n) and frequency factor of crystallization (K_o) for Ge_30−xSb_xTe₁₀Se₆₀ glassy alloys where (x = 0, 5, 10, 15, 20 at.%)

The second approach to evaluate (E_c) and the frequency factor K_o is by using Augis& Bennett method [37], which relates the peak temperature and T_p with the heating rate (α) via the equation:

$$\ln \left( {T_{{\text{p}}} /\alpha } \right) = \left( {E_{{\text{c}}} /{\text{RT}}_{{\text{p}}} } \right) + \ln K_{0}$$

(15)

The plot of ln (T_p/α) versus (1000/T_p) in Fig. 8 provides a straight line, the activation energy (E_c) is given by the slope, and the interceptions give the frequency factor K_o. The values of E_c and K_o are given in Table 4.

Fig. 8

Plot of ln (T_p/α) against 1000/T_p (K⁻¹) for evaluation of activation energy of crystallization E_c and the frequency factor K_o for the present system

The third approach to evaluate E_c is by using Matusita–Sakka’s peak shift method [38], which relates the peak temperature T_p, with the heating rate (α) according to the next formula:

$$\ln \left( \alpha \right) = - \left( {\frac{{E_{{\text{c}}} }}{{{\text{RT}}_{{\text{p}}} }}} \right) + {\text{Constant}}$$

(16)

As represented by Fig. 9, the plot of ln(α) against (1000/T_p) gives a straight line, the E_c is given by the slope, the values of E_c are given in Table 4, and the values of (E_c) calculated from the three methods are well aligned with one another.

Fig. 9

Plot of ln α against 1000/T_p (K⁻¹) for evaluation of activation energy of crystallization E_c for the present system

As the amount of Sb increases during the phase change, the (E_c) value declines (Table 4), which may be interpreted in terms of cohesive energy (CE). Sb addition results in a drop in the system's (CE) (Table 3). E_c may have decreased because to the nucleation and growth processes needed for devitrification. It is worth mentioning that the decreasing (E_c) in the investigated system with the doping of Sb enhances the phase change possibility, which is a good property in phase change memory applications.

By using the following equation, the volume fraction of crystals precipitated in a glass heated at a consistent rate (α) is directly linked to (E_c) of the amorphous-crystalline transition [39]:

$$\ln \left[ { - \ln \left( {1 - \chi } \right)} \right] = - n\ln \ln \propto - \frac{{1.052\;{\text{mE}}_{{\text{c}}} }}{{{\text{RT}}}} + {\text{Constant}}$$

(17)

where m and n are constants and depend on the morphology of the crystal growth. The crystallized fraction χ at a temperature T is deduced by $\chi = \phi_{{\text{T}}} /\phi$, where $\phi$ is the total area of the exothermic peak and $\phi_{{\text{T}}}$ is the area among T_c and T. The crystallized volume fraction χ was plotted as a function of temperature for all the samples as shown in Fig. 10a–e. To determine m, a relation between $\ln \left[ { - \ln \left( {1 - \chi } \right)} \right]$ and 1000/T at different heating rates was plotted, where straight lines were obtained over the used temperature range as shown in Fig. 11a–e. From the slope of each straight line, the m value was calculated and is listed in Table 4.

Fig. 10

a–e The crystallized fraction χ as a function of temperature for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15, 20 at.%) at different heating rates

Fig. 11

a–e Plot of ln [−ln (1−χ)] against 1000/T (K⁻¹) at different heating rates for (Ge_30−xSb_xTe₁₀Se₆₀) where Sb mass percentage (0, 5, 10, 15, 20 at.%)

As the values of E_c were before estimated applying three distinct ways, the mean value could be obtained. Avrami exponent n has been evaluated from the slopes of the straight lines of plotting $\ln \left[ { - \ln \left( {1 - \chi } \right)} \right]$ and ln (α) relation at a fixed temperature; the values of n are listed in Table 4. According to Mahadevan et al. [40], the values of n can be 4, 3, 2, or 1 and are related to the various glass-crystal transformation mechanisms: n = 4 corresponds to volume nucleation, which results in three-dimensional growth; n = 3 corresponds to volume nucleation, which results in two-dimensional growth; n = 2 corresponds to volume nucleation, which results in one-dimensional growth; and n = 1 represents surface nucleation, one-dimensional growth from surface to the interior. In light of the aforementioned mean value, the examined samples' n should be 2, 3, or 4. When n is not an integer, it is discovered that more than one growth process is operating concurrently during the amorphous to crystalline transition [41]. The nucleation activation energy (E_n) and the crystal growth activation energy (E_G) are added to create the activation energy (E_c), which was calculated using thermal analysis [42,43,44,45,46]. The crystallization exotherm characterizes the growth of the crystalline phase from the amorphous state, and nucleation calorimetrically is unobservable at temperatures below the crystallization exotherm, and it has been noted [47] in non-isothermal measurements owing to a rapid increase in temperature and great differences in the latent heats of nucleation and growth. Therefore, it may be assumed that the E_c values obtained represent the activation energy of growth E_G in the system at hand.

Glass-forming ability, thermal stability and glass fragility

Glass-forming ability (GFA) is essential for knowledge the causes of glass formation; the thermal stability of the material is utilized to determine its technical applications. GFA is evaluated according to the reduced glass transition temperature established by Kauzmann [48, 49] (T_rg = T_g/T_m), and the calculated value (T_rg) is listed in Table 1. For a good glass, the value of (T_rg) is nearly about 2/3 [48]. The studied glasses have good fit with this value.

A parameter H_r that may be used as the GFA index was developed by Hruby [50]:

$$H_{{\text{r}}} = \frac{{T_{{\text{c}}} - T_{{\text{g}}} }}{{T_{{\text{m}}} - T_{{\text{c}}} }}$$

(18)

On the other hand, two characteristics were suggested as a sign of a glass's thermal stability [51], and they are as follows:

$$H^{/} = \frac{{T_{{\text{c}}} - T_{{\text{g}}} }}{{T_{{\text{g}}} }}$$

(19)

$$S = \frac{{\left( {T_{{\text{p}}} - T_{{\text{c}}} } \right)\left( {T_{{\text{c}}} - T_{{\text{g}}} } \right)}}{{T_{{\text{g}}} }}$$

(20)

The values H_r, H^/ and S are listed in Table 5 as function of heating rate and composition. The variation of the H^/ and S for the studied glasses at different heating rates as a function of Sb content is shown in Figs. 12 and 13 respectively. It can be observed from this table that the adding of Sb to the Ge–Se–Te ternary glass reduces the stability of the examined glasses. The fragility (F_i) characterizes and quantifies the anomalous non-Arrhenius transport behavior of glassy materials near the ergodicity breaking glass transition region. Fragile glasses are substances with non-directional interatomic/intermolecular bonds. Strong glasses are those which show resistance to structural degradation. Fragility (F_i) is calculated using the following relation [52]:

$$F_{{\text{i}}} = \frac{{E_{{\text{g}}} }}{{{\text{RT}}_{{\text{g}}} \ln \alpha }}$$

(21)

Table 5 Characteristic parameters for the thermal stability and glass fragility for Ge_30−xSb_xTe₁₀Se₆₀ glassy alloys where (x = 0, 5, 10, 15, 20 at.%)

Fig. 12

The thermal stability parameter H^/ as a function of heating rate for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15, 20 at.%) at different heating rates

Fig. 13

The thermal stability parameter S as a function of heating rate for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15, 20 at.%) at different heating rates

The glasses with lower values of (F_i) are classified as strong, whereas the glasses with higher value of (F_i) are classified as fragile. As seen from Fig. 14, the fragility index of the present glasses decreased with the increase in the heating rate, the glass with x = 20 at.% shows the highest value for fragility index indicating that the melt at x = 20 (N_c = 2.40) is characterized by maximum fragility among the tested glasses.

Fig. 14

Glass fragility (F_i) as a function of heating rate for (Ge_30−xSb_xTe₁₀Se₆₀) glassy alloys where Sb mass percentage (0, 5, 10, 15, 20 at.%) at different heating rates

Strong glass-forming liquids are indicated by a low value of F_i (F_i ≈ 16) [53], whereas fragile glass-forming liquids are indicated by a high value of F_i (F_i ≈ 200) [54]. F_i values for the current system at various heating rates are shown in Table 5. The findings demonstrate that this system was built from powerful liquids capable of producing glass.

Conclusions

DSC curves of the bulk glassy materials of Ge_30−xSb_xTe₁₀Se₆₀ where (x = 0, 5, 10, 15, 20 at.%) reveal that each sample has one glass transition and crystallization temperature and two melting stages, except for the sample with Sb content 20% which has just one melting temperature. The detected phase separation in Ge_30−xSb_xTe₁₀Se₆₀ (x = 0, 5, 10, 15 at.%) was identified by XRD for annealed sampled at temperature beyond the melting temperatures at 670 K. The characteristic temperatures T_g, T_c and T_p of Ge_30−xSb_xTe₁₀Se₆₀ (x = 0, 5, 10, 15, 20 at.%) glasses tend to a downward, and this can be used in applications that require just low thermal deformation. The glass-forming ability decreases with increasing Sb content. The glass transition activation energy decreased with increasing content of Sb for all the samples and back to increasing again in the sample which has Sb content 20% which discussed in terms of average coordination number. The decreased activation energies for crystallization due to Sb doping are explained by cohesive energy, which decreases with rising Sb doping. The decrease in activation energy of crystallization in Ge_30−xSb_xTe₁₀Se₆₀ system on the addition of Sb enhances the phase change possibility and subsequently improves their usage in phase change memory applications. In accordance with the Avrami concept of nucleation, the estimated values of the Avrami index ‹n› indicate that ‹n› = 2, 3, 4 for the investigated sample, which refer to volume nucleation with different mechanisms of growth.