Introduction

Air travel is an essential part of people's lives all over the world. It boosts national economies, international trade, and tourism. It contributes to the improvement of the living standards in developing nations. It brings people together, allows them to explore new horizons and cultures and provides access to career and educational opportunities [1]. In the aviation industry, total market is anticipated to achieve 61% as before 2019 levels in 2022. In the coming years, the potential is estimated to be higher than market, achieving 67% of pre-Covid-19 grades until 2022 [2]. The growth of the aviation industry has provided significant perks to several sectors of the economy around worldwide. The aviation outperforms other modes of transportation in terms of mobility and speed [3]. The increased demand will necessitate the use of more natural and financial assets. Air transportation not only conveys quickly and easily goods and people but also does not necessitate substructure as many other modes of transportation. Furthermore, physical barriers do not constraint for aviation as many other modes of transportation [4, 5]. Beyond all of these advantages, the aviation activities have a broad and serious environmental impact. Since aviation growth rates are so rapid that technical improvements may not keep abreast of demand growth, the environmental consequences can be more severe for our world. For instance, the aviation contributes 1–2% of GHG pollutants. However, by the year of 2050, the aviation will have anticipated to contribute to 15% within global climatic changes [6]. On the other hand, the aviation industry generates CO2 emissions around 600 million tonnes into the environment each year [7]. Besides, as air traffic and passenger numbers have increased, so has the number of people exposed to aircraft-induced noise [8, 9]. Because of the increase in air traffic over the years, there is growing concern about the emissions caused by airport operations. Future air traffic motions are anticipated to rise at a 5 to 7% annualized rate [10, 11]. In the coming years, aviation-induced global carbon dioxide gas releases are expected to rise at almost four percent per year. As a result, global aviation carriers attempt to implement remedies in order to enhance environmental performance [12]. In the aviation industry, one of the main reasons for aircraft-induced emissions is propellant group in aircraft, namely the engine and fuel absorbed by the engine. Initially, kerosene basis of fuel was used to power jets in the aviation industry. Even though various types of fuel are used in aviation jets, the most frequent ones are aviation turbine fuel, jet fuel, and kerosene type of traditional aviation fuels. Jet fuels are used extensively in military and commercial fields. Jet fuels are classified various types for instance Jet-B, Jet-A-1, and Jet-A. In recent years, alternative additives have been incorporated to these fuels to augment thrust while decreasing gas emissions. As a result, to meet the need for fossil fuels, the usage of alternative fuels is expanding [13]. At this point, bio-based fuels or biomass are a viable resource with growing hopes for meeting requirements of energy with lower pollutants, as well as tremendous utility of the biofuels in transport industry, in which they can be generated at large amounts and utilized first-hand within engines to reduce hazardous pollutants [14, 15]. Jet fuel and diesel will be the principal fuels required for the expansion of the aviation industry. Recently, developing efficient and sustainable techniques for producing renewable diesel and renewable aviation fuel has a tremendous attentiveness [16]. As far as alternative fuel solutions are concerned, it can be said that among the prominent ones are biofuels, biodiesel derivatives, and biofuel blends, namely the bio-based fuels. Biofuels have also been discussed and promoted as a low-carbon alternative to fossil-fueled jet fuel. For example, the aviation industry-led SAFUG (Sustainable Aviation Fuel Users Group), for example, has centered on speeding the advancement of sustainable aviation biofuels [17].

When considering the open literature, alternative fuel initiatives and their possible consequences on aircraft engines have been undertaken by dealing with various sustainable bio-based fuels.

Gawron et al. [18] investigated a miniature type of turbojet engine fueled with pure Jet A-1 and Jet A-1/butanol blends. They observed the engine’s emission and performance characteristics. They concluded specific fuel consumption and fuel consumption of the engine are lightly higher compared to pure Jet A-1 utilization case, while the NOx (nitrogen oxides), CO2 (carbon dioxide) and CO (carbon monoxide) emission values emitted by the engine are lower compared to the pure Jet A-1 case. Yakovlieva et al. [19] studied and tested the traditional jet fuel and a new alternative developed bio-additive jet fuel. It was obtained that there was not a notable difference in the engine's performance. Also, it was stated that the proposed bio-based fuel developed by the authors was completely satisfied exploitation norms. In another study, Arkoudeas et al. [20] researched the JP-8 type of aviation fuel on CI engines. They argued that the two varieties of biodiesel appeared to work similarly and regardless of raw material used in their synthesis, its addition to JP -8 aviation fuel reduced particulate matter emissions. Badami et al. [21] reported findings of a numerical and experimental study on the effect of alternative fuels on emissions performance on the small scale turbojet engine at 80,000 rpm and 80 N of thrust. Fawal and Kodal [22] investigated performance assessments of turbojet engine under various operation conditions. The authors mentioned that the design parameters at maximum Ecological Function and maximum Ecological Coefficient of Performance conditions may result in turbojet engines that are smaller, more efficient, and consume less fuel than those at maximum power and maximum power density.

Moreover, Zhang et al. [23] and Braun-Unkhoff and Riedel [24] were centered on the bio-based jet fuels in terms of combustion characteristics. Gutiérrez-Antonio et al. [16] examined scientific and technologic advancements in thermochemical routes, hydroprocessing and alcohol to jet processes. Mendez et al. [25] examined emissions and performance behaviors of a small-scale gas turbine engine powered by ethanol and Jet-A blend. They highlighted that the ethanol mixtures reduced the maximum operational RPM by 10,000 to 20,000 rpm when comparing the Jet-A. Wei et al. [26] reviewed production of bio- based jet fuels for the aviation industry. Vela-Garcia et al. [27] investigated the flight performance, life cycle and thermoeconomic analyses of a bio-jet fuel. Apart from this, Liu et al. [28] and Chiaramonti et al. [29] investigated several jet fuel generation routes.

Abu Talib et al. [30] monitored some performance characteristics of Armfield CM4 type of turbojet engine fueled by Palm oil methyl ester biodiesel (PME). They concluded that the PME was a feasible for microturbine applications in both power generation and UAVs. Leitner et al. [31] investigated a systematic approach to energy efficiency and bio-jet fuels synthesis by taking an integrative view of turbine engine combustion and bio jet fuel synthesis.

In another study, using a life cycle GHC model, Lokesh et al. [32] estimated the "cradle-grave" carbon intensity of different bio jet fuel. Their findings showed that bio-jet fuels sourced from camelina, micro-algae, and jatropha save 70%, 58% and 64% of life cycle emissions, when compared to Jet A 1. On the other hand, they argued that there was a several downsides to bio jet fuels, such as low energy density, poor high-temperature thermal stability, storage instability, and so on. Gawron and Bialecki [33] investigated the performance and emissions of the light turbojet engine fueled with jet-fuel containing synthetic paraffinic kerosene (SPK). At the end of study, the authors stated that the greatest variances in running parameters were found in fuel efficiency. Also, it was determined individual fuel usage and these parameters are lower for a Jet-A-1 /HEFA blend fuel than for a Jet-A 1. What is more, emission indices of exhaust gases are also lower as comparing the Jet-A-1. Gabriel et al. [34] investigated technoeconomic of bio jet fuels derived from various feed stocks. But, the bio-jet advancements are rapidly evolving and new conversion advancements for instance lignin to jet, have yet to be studied.

Beyond all of these studies, there are some studies which are also undertaking the thermodynamically based energetic and exergetic behaviors of bio-based alternative fuels on aircraft engines in the open literature.

Akdeniz and Balli [35] observed the energetic and exergetic performances of alternative fuels usage in aero-turbojet engine for the concept of sustainable aviation. The authors determined the biofuel and hydrogen as alternative fuels. Then, they conducted separately the energy and exergy analyses for biofuel, hydrogen and conventional kerosene usages. They stated that the biofuel fuel absorbing of engine was slightly higher than conventional one, while hydrogen absorbing of the engine was slightly lower than the conventional fuel. Also, when the biofuel was chosen for the operation of the engine, they found that the engine’s thermal efficiency incremented from 16.39% to 16.43%, comparing conventional fuel. At the end of their study, when the biofuel was chosen for the operation of the engine, it was concluded the efficiency of exergy was estimated as 15.25%. Manigandan et al. [13] discussed emission, performance and combustion behavior for both JET-A and various ratios of additives with biofuel on a micro-gas-turbine engine. They underlined at the end of their study that these fuel mixes emit fewer environmentally unfavorable toxic gases, such as NOx, CO, and HC, when comparing the straight Jet A fuel. Coban et al. [36] conducted an exergy-based assessment of an experimental turbojet engine running on biodiesel and conventional aviation fuel. As a result of this study, the exergy efficiency of air compressor, combustion chamber and gas turbine components were estimated as 74.52%, 47.68% and 99.00%, respectively, in the biofuel operating conditions. What is more, while system is operated by aviation-fuel, exergy efficiency of air compressor, combustion chamber and gas turbine components was computed to be 75.22%, 48.34% and 98.44%. Coban et al. [37] investigated the exergoeconomic and exergy performance of turbojet type of aircraft propulsion system powered with biodiesel and standard gasoline. According to study's outputs, with the usage of biofuel, efficiency of exergy for turbine unit increased but compressor and combustion unit's exergetic efficiency decreased. They also noticed that there was a rise stream of cost of the thrust. Gurbuz et al. [38] investigated the impacts of hydrogen and euro diesel dual fuel utilization in a small-scale turbojet type of aircraft engine used for unmanned aerial vehicles. They monitored some environmental and economic performance metrics. With the usage of hydrogen and euro diesel dual fuel, it was mentioned that there was a declining fuel consumption, whereas it was an increased combustion performance up to a 15% density of hydrogen. They found that the CO2 emissions had a greater influence on reducing environmental impact, energy emissions index, and environmental costs than other emissions, while the CO emissions had a greater impact on reducing environmental and social cost.

Previous studies explained that bio-based fuels are one of the efficient source of energy and feasible candidate to standard conventional ones. The prime goals of this study are to observe and benchmark thermodynamics behaviors of bio-based fueled and jet kerosene-fueled aircraft turbojet engine by using energy, exergy, thermoecological, environmental, enviroeconomic and sustainability analyses. These extensive analyses are firstly applied to the jet kerosene and a bio-based fueled aircraft turbojet engine. This study also intends to gather extensive findings on the enviroeconomic implications of a jet type of aviation engine to ensure of our sustainability. In addition, the results of this research can be a helpful guide and spearhead for researchers and stakeholders who are interested in the concept of sustainable and cleaner aviation.

System description

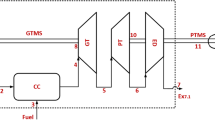
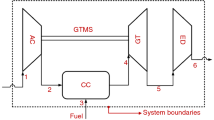
The engine, which is modeled as a thermodynamic system in this study, is a member of medium-scale family of turbojet engines. This type of aircraft engines is a kind of jet engines that is widely used for aircraft propulsion systems in the aviation industry. The system is made up of five major sub-components. These are an air compressor (AC), a combustion chamber (CC), a gas turbine (GT), an exhaust duct (ED) and a single spool gas turbine mechanical shaft (GTMS). Thermodynamic specifications of the engine are summarized as below [39]:

  • The jet kerosene fuel mass stream is 0.084 kg s−1, while inlet air mass stream is 4.45 kg s−1. Additionally, AFR (Air to fuel ratio) value is 52.976.

  • The gas turbine inlet pressure (GTIP) is 388.63 kPa, whereas the gas turbine inlet temperature (GTIT) is 1082.35 K.

  • The air compressor outlet pressure (ACOP) is 411.25 kPa, while the air compressor outlet temperature (ACOT) is 450.75 K. Finally, the velocity of the exhaust duct outlet value is 538.65 m/s.

The control volume, system boundaries, and designated stations of the system is visualized as a schematic layout in Fig. 1.

Fig. 1
figure 1

Cutaway view of the engine (a) and schematic layout of the engine’s sub-components and stations designated (b)

Full size image

To better analyze each sub-component and each station, the necessary assumptions regarding this study are as below:

  • Engine is considered under the steady state; the dead state’s pressure (P0) and temperature (T0) are 101.33 kPa and 288.15 K.

  • The system parts excluding the combustor (CC) are assumed as adiabatic. Also, there is a completed combustion stage and exhaust pollutants as well as air gases have ideal behavior [40, 41].

  • A static condition test is considered for the air entrance.

  • The aviation jet fuel is a kerosene type of jet fuel (C12H23), and the lower heating value (LHV) of the fuel is 43124 kJ kg−1 [42, 43].

  • The bio-based fuel is biofuel (C19H36O2), and the LHV of this fuel is 37400 kJ kg−1 [37].

When utilization the standard aviation jet fuel in the engine, the combustion balance function based on the engine's AFR value, which is mentioned above, is determined as follows:

$$\begin{aligned} {\text{C}}_{{{\text{12}}}} {\text{H}}_{{{\text{23}}}} & + 309.3894\left( {\begin{array}{*{20}l} {0.7748{\text{N}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.2059{\text{O}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.0003{\text{CO}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.019{\text{H}}_{{\text{2}}} {\text{O}}} \hfill \\ \end{array} } \right) \to 12.0928\left( {{\text{CO}}_{{\text{2}}} } \right) \\ & + 17.3784\left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right) + 45.9533\left( {{\text{O}}_{{\text{2}}} } \right) + 239.7149\left( {{\text{N}}_{{\text{2}}} } \right) \\ \end{aligned}$$
(1)

Upon the combustion reaction, 5.89% CO2 with 0.267 kg s−1, 3.47% H2O with 0.157 kg s−1, 16.28% O2 with 0.738 kg s−1 and 74.36% N2 with 3.371 kg s−1 of a mass composition of emissions are obtained. The ideal gas constant of these pollutants is found as Reg = 0.290126535 kJ kg−1 K−1. The cp value of the exhaust gases can be measured in that the temperature and created as below:

$$c_{\rm P,eg} { (}T) = { 0}{\text{.988612 + }}\frac{0.011943}{{10^{2} }}\left( T \right) + \frac{0.015151}{{10^{5} }}\left( {T^{2} } \right) - \frac{0.066501}{{10^{9} }}\left( {T^{3} } \right)$$
(2)

In view of the constant combustion energy principle at the combustion chamber, which is depending on the design requirements of the combustion chamber unit, there is an equal input fuel energy rate value to the engine for both jet kerosene utilization and biofuel utilization cases [43, 44]. Accordingly, for the biofuel utilization case, the biofuel fuel flow absorbed by the engine is calculated as 0.097 kg s−1, while the value of AFR is determined to be 45.944. Also, the combustion balance function based on this AFR is estimated as follows:

$$\begin{aligned} {\text{C}}_{{{\text{19}}}} {\text{H}}_{{{\text{36}}}} {\text{O}}_{{\text{2}}} & + 475.4580\left( {\begin{array}{*{20}l} {0.7748{\text{N}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.2059{\text{O}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.0003{\text{CO}}_{{\text{2}}} {\mkern 1mu} + } \hfill \\ {0.019{\text{H}}_{{\text{2}}} {\text{O}}} \hfill \\ \end{array} } \right) \to 12.1426\left( {{\text{CO}}_{{\text{2}}} } \right) + 20.5337\left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right) \\ & + 80.1468\left( {{\text{O}}_{{\text{2}}} } \right) + 368.3849\left( {{\text{N}}_{{\text{2}}} } \right) \\ \end{aligned}$$
(3)

Once the combustion reaction, 3.88% CO2 with 0.177 kg/s, 2.68% H2O with 0.122 kg s−1, 18.60% O2 with 0.846 kg s−1 and 74.84% N2 with 3.403 kg s−1 of a mass composition of emissions are obtained. The ideal gas constant of these pollutants is found as Reg = 0.290154969 kJ kg−1 K−1. The cp value of the exhaust gases can be measured in that the temperature and created as below:

$$c_{\rm P,eg} { (}T) = { 0}{\text{.987826 + }}\frac{0.010191}{{10^{2} }}\left( T \right) + \frac{0.015919}{{10^{5} }}\left( {T^{2} } \right) - \frac{0.067907}{{10^{9} }}\left( {T^{3} } \right)$$
(4)

For the air, specific heat capacity can be written by the temperature as follows [45, 46]:

$$c_{\rm P,air} { (}T) = \, 1.04841 - \left( {\frac{3.83719}{{10^{4} }}T} \right) + \left( {\frac{9.45378}{{10^{7} }}T^{2} } \right) - \left( {\frac{5.49031}{{10^{10} }}T^{3} } \right) + \left( {\frac{7.92981}{{10^{14} }}T^{4} } \right)$$
(5)

Analyses

The extensive energy and exergy, thermoecologic, environmental, enviroeconomic and sustainability level analyses of the turbojet type of aircraft engine are described step by step in subsequent subsections.

Extensive energy and exergy analyses

In this study, to deeply observe thermodynamic performance of turbojet engine and to reach as exact results as possible, the energy and exergy analyses is conducted not only to the engine as a system level, but also to the submodules of the engine as a component level. Furthermore, to observe clearer results in performance benchmarks for both jet fuel utilization case and biofuel utilization case, both the engine’s design features are evaluated in their original values and the dead state conditions are taken as the same during all analyses covered this study.

To assign the energy efficiency of the engine and to estimate the heat, work, and mass conservation, the energy analysis is conducted. In this regard, the general mass and general energy balance equations are given as below [47,48,49,50]:

$$\sum {\dot{m}_{\rm in} } = \sum {\dot{m}_{\rm out} }$$
(6)
$$\sum {\dot{E}_{\rm in} } = \sum {\dot{E}_{\rm out} }$$
(7)
$$\dot{Q} - \dot{W} + \sum\limits_{\rm in}^{{}} {\dot{E}_{\rm in} } - \sum\limits_{\rm out}^{{}} {\dot{E}_{\rm out} } = 0$$
(8)

where \(\dot{Q}\) represents stream of energy by heat, \(\dot{E}\) denotes the stream of energy, and \(\dot{W}\) indicates stream of energy by work.

The statement of general exergy is found as follows [51, 52]:

$$\sum\limits_{\rm {}}^{{}} {\left( {1 - \frac{{T_{\rm o} }}{{T_{\rm k} }}} \right)} \dot{Q}_{\rm k} - \dot{W} + \sum\limits_{\rm in}^{{}} {\dot{E}x_{\rm in} } - \sum\limits_{\rm out}^{{}} {\dot{E}x_{\rm out} } - \dot{E}x_{\rm D} = 0$$
(9)

Energy balance relations and governing equations

The equilibrium of energy in terms of the rule of fuel-product (F-Pr) and inlet–outlet streams can be described as below [40]:

$$\dot{E}_{\rm F} = \dot{E}_{\Pr } + \dot{E}_{\rm L}$$
(10)

where \(\dot{E}_{\rm L}\), \(\dot{E}_{\Pr }\) and \(\dot{E}_{\rm F}\) denote the heat loss rate, product energy rate and fuel energy rate, respectively.

For components:

  • Air Compressor (AC):

    $$T_{\rm 2} = T_{\rm 1} \left\{ {1 + \frac{1}{{\eta_{\rm AC} }}\left[ {\left( {\frac{{P_{\rm 2} }}{{P_{\rm 1} }}} \right)^{{\frac{{\mu_{\rm air} - 1}}{{\mu_{\rm air} }}}} - 1} \right]} \right\}$$
    (11)
    $$\dot{m}_{\rm 1} = \dot{m}_{\rm 2} = \dot{m}_{\rm air}$$
    (12)
    $$\dot{W}_{\rm AC} = \dot{m}_{\rm air} \left( {c_{\rm P,2} T_{\rm 2} - c_{\rm P,1} T_{\rm 1} } \right)$$
    (13)
    $$\mu_{\rm air} = \frac{1}{{1 - \frac{{R_{\rm air} }}{{c_{\rm P,air} }}}}$$
    (14)

  • Combustion Chamber (CC):

    $$\dot{m}_{\rm 2} c_{\rm P,2} T_{\rm 2} + \eta_{\rm CC} \dot{m}_{\rm 3} LHV = \dot{m}_{\rm 4} c_{\rm P,4} T_{\rm 4}$$
    (15)
    $$\dot{m}_{\rm 2} + \dot{m}_{\rm 3} = \dot{m}_{\rm 4}$$
    (16)

  • Gas Turbine (GT):

    $$T_{\rm 5} = T_{\rm 4} \left\{ {1 - \eta_{\rm GT} \left[ {1 - \left( {\frac{{P_{\rm 4} }}{{P_{\rm 5} }}} \right)^{{\frac{{1 - \mu_{\rm eg} }}{{\mu_{\rm eg} }}}} } \right]} \right\}$$
    (17)
    $$\dot{m}_{\rm 4} = \dot{m}_{\rm 5} = \dot{m}_{\rm eg}$$
    (18)
    $$\dot{W}_{\rm GT} = \dot{m}_{\rm eg} \left( {c_{\rm P,4} T_{\rm 4} - c_{\rm P,5} T_{\rm 5} } \right)$$
    (19)
    $$\mu_{\rm eg} = \frac{1}{{1 - \frac{{R_{\rm eg} }}{{c_{\rm P,eg} }}}}$$
    (20)

  • Exhaust Duct (ED):

    $$\dot{Q}_{\rm 6} = \eta_{\rm ED} \dot{Q}_{\rm 5}$$
    (21)

  • Gas turbine mechanical shaft (GTMS):

    $$\dot{W}_{\rm AC} = \eta_{\rm GTMS} \dot{W}_{\rm GT}$$
    (22)

Performance indicators for energy perspective

The engine and its sub-modules are subjected to widely used useful equations for measuring aircraft engine systems based on the first law of thermodynamic [53,54,55,56]:

  • First law efficiency: the energy efficiency \(\left( \eta \right)\):

    $$\eta = \frac{{\dot{E}_{\Pr } }}{{\dot{E}_{\rm F} }} = \eta_{\rm TJE} = \frac{{\dot{E}_{\rm kn} }}{{\dot{m}_{\rm F} {\rm LHV}}}$$
    (23)

  • Specific fuel consumption (SFC):

    $${\rm SFC} = \frac{{\dot{m}_{\rm F} }}{{ET_{\rm TJE} }}$$
    (24)

  • Specific thrust (ST):

    $${\rm ST} = \frac{{ET_{\rm TJE} }}{{\dot{m}_{\rm a} }}$$
    (25)

  • Thermal limit ratio (TLR):

    $${\rm TLR} = \frac{{T_{\rm TIT} }}{{T_{\rm ref} }} = \frac{{T_{\rm 4} }}{{T_{\rm 0} }}$$
    (26)

  • Fuel heating value ratio (FHVR):

    $${\rm FHVR} = \frac{{{\rm LHV}_{\rm F} }}{{h_{\rm 0} }} = \frac{{{\rm LHV}_{\rm F} }}{{c_{\rm Pair,0} T_{\rm 0} }}$$
    (27)

  • Enthalpy ratio (ER):

    $${\rm ER} = \frac{{h_{\rm out,CC} }}{{h_{\rm 0} }}$$
    (28)

Exergy balance relations and governing equations

The equilibrium of exergy in terms of the rule of fuel-product (F-Pr) and inlet–outlet streams can be described as below [40]:

  • For overall system:

    $$\begin{aligned} \sum {\dot{E}x_{{{\text{D}},{\text{TJE}}}} = } & \dot{E}x_{{{\text{D}},{\text{AC}}}} + \dot{E}x_{{{\text{D}},{\text{CC}}}} + \dot{E}x_{{{\text{D}},{\text{GT}}}} \\ & + \dot{E}x_{{{\text{D}},{\text{ED}}}} + \dot{E}x_{{{\text{D}},{\text{GTMS}}}} \\ \end{aligned}$$
    (29)
    $$\dot{E}x_{\rm L,TJE} = \dot{E}x_{\rm 6} - \dot{E}x_{\rm 7}$$
    (30)
    $$\dot{E}x_{\rm WE} = \sum {\dot{E}x_{\rm D} } + \dot{E}x_{\rm L}$$
    (31)
    $$\dot{E}x_{\rm WE,TJE} = \left( {\dot{E}x_{\rm 1} + \dot{E}x_{\rm 3} } \right) - \dot{E}x_{7,\Pr }$$
    (32)
    $$\dot{E}x_{\Pr ,{\rm TJE}} = \dot{E}x_{\rm 7,KN} = \dot{m}_{\rm 7} \frac{{\dot{V}_{7}^{2} }}{2000}\left( {kW} \right)$$
    (33)

  • For components:

  • Air compressor (AC):

    $$\psi_{\rm AC} = \frac{{\dot{E}x_{\rm 2} - \dot{E}x_{\rm 1} }}{{\dot{W}_{\rm 9} }}$$
    (34)
    $$\dot{E}x_{\rm D,AC} = \dot{W}_{\rm 9} - \left( {\dot{E}x_{\rm 2} - \dot{E}x_{\rm 1} } \right)$$
    (35)

  • Combustion chamber (CC):

    $$\psi_{\rm CC} = \frac{{\dot{E}x_{\rm 4} - \dot{E}x_{\rm 2} }}{{\dot{E}x_{\rm 3} }}$$
    (36)
    $$\dot{E}x_{\rm D,CC} = \dot{E}x_{\rm 3} - \left( {\dot{E}x_{\rm 4} - \dot{E}x_{\rm 2} } \right)$$
    (37)

  • Gas turbine (GT):

    $$\psi_{\rm GT} = \frac{{\dot{W}_{\rm 8} }}{{\dot{E}x_{\rm 4} - \dot{E}x_{\rm 5} }}$$
    (38)
    $$\dot{E}x_{\rm D,GT} = \left( {\dot{E}x_{4} - \dot{E}x_{5} } \right) - \dot{W}_{\rm 8}$$
    (39)

  • Exhaust duct (ED):

    $$\psi_{\rm ED} = \frac{{\dot{E}x_{\rm 6} }}{{\dot{E}x_{\rm 5} }}$$
    (40)
    $$\dot{E}x_{\rm D,ED} = \left( {\dot{E}x_{\rm 5} - \dot{E}x_{\rm 6} } \right)$$
    (41)

  • Gas turbine mechanical shaft (GTMS):

    $$\psi_{\rm GTMS} = \frac{{\dot{W}_{\rm 9} }}{{\dot{W}_{\rm 8} }}$$
    (42)
    $$\dot{E}x_{\rm D,GTMS} = \left( {\dot{W}_{\rm 8} - \dot{W}_{\rm 9} } \right)$$
    (43)

Performance indicators for exergy perspective

It is subjected to widely used useful equations for measuring aircraft engine systems [57,58,59,60,61,62]:

  • Second law efficiency: the exergy efficiency \(\left( \psi \right)\):

    $${\text{For }}\,{\text{components}}:\psi_{\rm k} = \frac{{\dot{E}x_{\Pr ,{\rm k}} }}{{\dot{E}x_{\rm F,k} }} = 1 - \frac{{\dot{E}x_{\rm D,k} }}{{\dot{E}x_{\rm F,k} }}$$
    (44)
    $${\text{For overall system}}:\,\psi_{\rm TJE} = \frac{{\dot{E}x_{\Pr ,{\rm TJE}} }}{{\dot{E}x_{\rm F,TJE} }} = 1 - \frac{{\dot{E}x_{\rm WE,TJE} }}{{\dot{E}x_{\rm F,TJE} }} = 1 - \frac{{\sum {\dot{E}x_{\rm D,TJE} } + \sum {\dot{E}x_{\rm L,TJE} } }}{{\dot{E}x_{\rm F,TJE} }}$$
    (45)

  • Irreversibility (exergy destruction ratio):

    $${\rm ExDR}_{\rm k} = \frac{{\dot{E}x_{\rm D,k} }}{{\dot{E}x_{\rm D,tot,TPE} }}$$
    (46)

  • Waste exergy ratio:

    $${\rm WExR}_{\rm k} = \frac{{\dot{E}x_{\rm WE,k} }}{{\dot{E}x_{\rm WE,TJE} }} = \frac{{\dot{E}x_{\rm D,k} + \dot{E}x_{\rm L,k} }}{{\dot{E}x_{\rm WE,TJE} }}$$
    (47)

  • System-level fuel exergy waste ratio:

    $${\rm SFExWR}_{\rm k} = \frac{{\dot{E}x_{\rm WE,k} }}{{\dot{E}x_{\rm F,TJE} }} = \frac{{\dot{E}x_{\rm D,k} + \dot{E}x_{\rm L,k} }}{{\dot{E}x_{\rm F,TJE} }}$$
    (48)

  • Component-level fuel exergy waste ratio:

    $${\rm CFExWR}_{\rm k} = \frac{{\dot{E}x_{\rm WE,k} }}{{\dot{E}x_{\rm F,k} }} = \frac{{\dot{E}x_{\rm D,k} + \dot{E}x_{\rm L,k} }}{{\dot{E}x_{\rm F,k} }}$$
    (49)

  • System-level productivity lack ratio:

    $${\rm SPLR}_{\rm k} = \frac{{\dot{E}x_{\rm WE,k} }}{{\dot{E}x_{\Pr ,{\rm TJE}} }} = \frac{{\dot{E}x_{\rm D,k} + \dot{E}x_{\rm L,k} }}{{\dot{E}x_{\Pr ,{\rm TJE}} }}$$
    (50)

  • Component-level productivity lack ratio:

    $${\rm CPLR}_{\rm k} = \frac{{\dot{E}x_{\rm WE,k} }}{{\dot{E}x_{\Pr ,{\rm k}} }} = \frac{{\dot{E}x_{\rm D,k} + \dot{E}x_{\rm L,k} }}{{\dot{E}x_{\Pr ,{\rm k}} }}$$
    (51)

  • Exergetic improvement potential:

    $$\dot{E}xIP = \left( {1 - \psi } \right)\dot{E}x_{\rm D}$$
    (52)

Thermoecologic analysis

Thermoecological analysis can be determined by the ecological performance indicator (ECOP). This is found as the ratio of the net useful exergy output of the system to the exergy destruction [51, 63, 64].

$${\rm ECOP} = \frac{{\Delta \dot{E}x_{\rm W} }}{{\dot{E}x_{\rm D} }}$$
(53)

Environmental analysis

As far as exergy-based environmental analysis for aircraft engines is concerned, the performance tools of environmental effect factor, ecological effect factor and ecological objection function can be helpful to measure both system-level and its sub-components. In this manner, these indicators can be given as follows [35, 41, 42, 62]:

  • Environmental effect factor (EEF):

For components:

$${\rm EEF}_{\rm k} = \frac{{CFExWR_{\rm k} }}{{\psi_{\rm k} }}$$
(54)

For overall system:

$${\rm EEF}_{\rm TJE} = \frac{{SFExWR_{\rm TJE} }}{{\psi_{\rm TJE} }}$$
(55)

  • Ecological effect factor (EcoEF):

For components:

$${\rm EcoEF}_{\rm k} = \frac{{\dot{E}x_{\rm F,k} }}{{\dot{E}x_{\Pr ,{\rm k}} }} = \frac{1}{{\psi_{\rm k} }}$$
(56)

For overall system:

$${\rm EcoEF}_{\rm TJE} = \frac{{\dot{E}x_{\rm F,TJE} }}{{\dot{E}x_{\Pr ,{\rm TJE}} }} = \frac{1}{{\psi_{\rm TJE} }}$$
(57)

  • Ecological objection function (EOF):

For components:

$${\rm EOF}_{\rm k} = \dot{E}x_{\Pr ,{\rm k}} - \dot{E}x_{\rm D,k}$$
(58)

For overall system:

$${\rm EOF}_{\rm TJE} = \dot{E}x_{\Pr ,{\rm TJE}} - \left( {\dot{E}x_{\rm D,TJE} + \dot{E}x_{\rm L,TJE} } \right)$$
(59)

Enviroeconomic analysis

The enviroeconomic analysis provides to observe the economic aspects of environmental information obtained from the aircraft engine systems. In this study, the environmental damage cost approach developed by Caliskan [65] is chosen as the enviroeconomic perspective. In this study, only carbon dioxide emission is taken into consideration as a main environmental pollutant. Enviroeconomic analysis is determined by the enviroeconomic factor as follows [65]:

$$\dot{C}_{\rm env} = c_{{\rm CO}_{2} } x_{{\rm CO}_{2} }$$
(60)

where the \(\dot{C}_{\rm env}\) (enviroeconomic factor) specifies the environmental damage cost rate of CO2 emission in a year (€ year−1 or $ year−1), the \(c_{{\rm CO}_{2} }\) and \(x_{ {\rm CO}_{2} }\) are indicate that the specific cost of CO2 emission (0.135 € kg−1 or 0.176 $ kg−1) and the CO2 emissions emitting in a year ( kg year−1), respectively [65,66,67,68].

Sustainability level analysis

The performance indicators of exergetic sustainability index and the sustainable efficiency factor can be used to observe sustainability level of aircraft engines and sub-components. These are as below [35, 41, 42, 62]:

  • Exergetic sustainability Index:

For components:

$${\rm ESI}_{\rm k} = \frac{1}{{{\rm EEF}_{\rm k} }}$$
(61)

For overall system:

$${\rm ESI}_{\rm TJE} = \frac{1}{{{\rm EEF}_{\rm TJE} }}$$
(62)

  • Sustainable efficiency factor:

For components:

$${\rm SEF}_{\rm k} = \frac{1}{{1 - \psi_{\rm k} }}$$
(63)

For overall system:

$${\rm SEF}_{\rm TJE} = \frac{1}{{1 - \psi_{\rm TJE} }}$$
(64)

Results and discussion

The jet kerosene- and biofuel-fueled turbojet engine is examined using extensive energy and exergy, thermoecologic, environmental, enviroeconomic and sustainability level research methods. The engine cycle data for jet kerosene and biofuel usage conditions are listed in Tables 1 and 2, respectively.

Table 1 Engine cycle data for jet kerosene utilization
Full size table
Table 2 Engine cycle data for biofuel utilization
Full size table

Results of extensive energy and exergy analyses

Extensive energy and exergy assessments are carried out for both the engine and its key subcomponents, with the engine running on both jet kerosene and biofuel fuels. Also, various useful performance indicators are used to benchmark the performance of the fuels. The comparative assessment results of each analysis and each performance indicator are discussed separately in their own subsequent sections.

Firstly, the results of energy analysis with various performance indicators of the engine for both cases are given in Table 3.

Table 3 Energy analysis results of the engine for both jet kerosene and biofuel cases
Full size table

As per Table 3, if the system is fueled by jet kerosene, energy efficiency of engine is obtained to be 18.16%. This parameter is found to be 18.18% for biofuel-powered case. The specific fuel consumption and the specific thrust are determined as 0.13 kg kN−1 s−1 and 147.81 kNs kg−1 for jet kerosene-powered case, while they are calculated as 0.15 kg kN−1 s−1 and 148.23 kNs kg−1 for biofuel-powered condition. Moreover, the thermal limit ratio, fuel heating ratio and enthalpy ratio results of jet kerosene case are computed to be 3.76, 149.10 and 4.53, respectively, besides, these energetic performance indicators are found to be 3.78, 129.31 and 4.51 for biofuel case, respectively. The results of exergy analysis of the engine and its sub-modules for jet kerosene utilization and biofuel utilization cases are displayed in Tables 4 and 5.

Table 4 Exergy analysis results of the engine and submodules for jet kerosene utilization
Full size table
Table 5 Exergy analysis results of the engine and submodules for biofuel utilization
Full size table

When Tables 4 and 5 are reviewed together, when the engine is fueled with biofuel, it has been revealed that although it has higher fuel, product, exergy destruction and waste exergy rates than jet kerosene, it has a lower loss exergy rate. On the other hand, it is observed that the component of CC has higher results than the utilization of jet kerosene in all of these exergetic values. The results of exergetic performance for both cases are listed in Table 6.

Table 6 The exergetic performance results in terms of performance indicators of the engine and its sub-modules for both cases
Full size table

In Table 6, if the system is powered with biofuel, exergy efficiency of GT, CC and ED decreases from 90.71% to 90.43%, from 54.49% to 54.22% and from 99.27% to 98.23%, respectively, while no significant change is observed in other components. Also, the relative exergy destruction ratios of AC and CC drop from 4.68% to 4.56% and drop from 90.00% to 89.09%, respectively. Waste exergy ratios of the CC, GT, and ED increment from 54.83% to 55.07%, 2.46% to 2.51% and 0.44% to 1.06%, respectively. When it comes to the system-level and component-level fuel exergy waste ratios of jet kerosene and biofuel cases, an increase is seen that the performances of GT and ED are from 2.04% to 2.09% and 0.36% to 0.88%, 9.29% to 9.57% and 0.73% to 1.77%, respectively. A similar trend is observed in the SPLR and CPLR performances of these components. Namely, a rise is observed that the results of SPLR and CPLR, which rises from 12.00% to 12.38%, from 2.14 to 5.20% and from 10.24% to 10.58% and from 0.74% to 1.81%, respectively. On the other hand, ESI results of GT, ED, CC and GTMS are higher compared to the jet kerosene case. As such, these values are estimated to be 7.33 kW, 0.10 kW, 801.09 kW and 0.16 kW for jet kerosene case, while they are determined as 7.82 kW, 0.61 kW, 818.94 kW and 0.17 kW for biofuel case, respectively. As far as system-level exergetic performance is concerned, with the utilization of biofuel, it is measured that whereas the exergy efficiency of the engine decreases from 17.00% to 16.88%, the system level fuel exergy waste ratio, the system level productivity lack ratio and exergetic improvement potential values rise from 83.00% to 83.12, 488.11% to 492.53% and 1623.44 kW to 1669.19 kW, respectively. When the engine is powered with biofuel and jet kerosene fuels, the exergy efficiency performances of the engine and its sub-modules are depicted in Fig. 2.

Fig. 2
figure 2

Comparison of exergy efficiencies of the jet kerosene and biofuel cases

Full size image

Figure 2 depicts with the biofuel usage, it is seen the efficiency of exergy of the other components except for AC and the engine's exergy efficiency decreases by a small amount. Besides, the CC is the minimum exergy efficient component among the other ones for both cases. When the engine is powered with biofuel and jet kerosene fuels, the exergy destruction ratio performances of system’s sub-modules are plotted in Fig. 3.

Fig. 3
figure 3

Comparing the exergy destruction results for jet kerosene and biofuel cases

Full size image

Figure 3 demonstrates when system is operated by biofuel, while exergy destruction ratios of ED, CC and AC reduces, it is seen that there is an opposite trend for GT and GTMS. When the engine is powered with biofuel and jet kerosene fuels, the waste exergy ratio performances of the of the sub-modules of the engine are illustrated in Fig. 4.

Fig. 4
figure 4

Comparison of waste exergy ratios of the jet kerosene and biofuel cases

Full size image

Figure 4 implies that the highest waste exergy ratio is estimated as 54.83% and 55.07% via the CC for jet kerosene and biofuel cases because the CC has the highest value of exergy waste flows among the other components. Furthermore, the CC is followed by the AC with values of 2.85% and 2.82% for jet kerosene and biofuel utilization cases. The system level fuel exergy waste ratio performance results are graphed in Fig. 5.

Fig. 5
figure 5

Comparison of system-level fuel exergy waste ratios of the jet kerosene and biofuel cases

Full size image

Figure 5 points out that the GTMS has the minimum value of system-level fuel exergy waste ratio for both cases with a value of 0.29%. Unlike this, the CC has the maximum value of this performance indicator with values of 45.51% and 45.77% for jet kerosene utilization and biofuel utilization cases. One of the reasons for this result is because the component with occurs maximum depletion rate of exergy is the CC. On the other hand, it is seen that an increase within the other components except for the AC for this performance parameter, as far as biofuel usage is concerned. When the engine is powered with biofuel and jet kerosene fuels, the component level fuel exergy waste ratios are visualized in Fig. 6.

Figure 6 indicates that the component with the minimum component level fuel exergy waste ratio is ED, which has 0.73% for jet kerosene case and 1.77% for biofuel case. When the engine is fueled by biofuel, it is seen that this parameter rises from 45.51% to 45.77% for CC when comparing the jet kerosene usage condition. When the engine is powered with biofuel and jet kerosene fuels, the system level productivity lack ratio performances are plotted in Fig. 7.

Fig. 6
figure 6

Comparison of component level fuel exergy waste ratio values for jet kerosene and biofuel cases

Full size image
Fig. 7
figure 7

Comparison of system level fuel productivity lack ratio values for jet kerosene and biofuel cases

Full size image

Figure 7 specifies that the system-level productivity lack ratio of the engine is determined to be 488.11% for jet kerosene utilization case, while it is obtained as 492.53% for biofuel utilization case. Additionally, when the biofuel is preferred instead of jet kerosene fuel, system-level PLR of CC, GT, ED and GTMS components rise. These are computed to be 13.87%, 271.22%, 12.38%, 5.20% and 1.75%, respectively. When the engine is powered with biofuel and jet kerosene fuels, the component-level productivity lack ratio performances of the sub-modules of the engine are shown in Fig. 8.

Fig. 8
figure 8

Comparison of component level productivity lack ratio values for jet kerosene and biofuel cases

Full size image

Figure 8 indicates that it is observed that other components except for the CC increase the component-level PLR value, as far as biofuel usage is concerned. The CC has the highest PLRs for both cases. These values are estimated as 83.51% in case of jet kerosene utilization case and 84.41% for biofuel utilization case. One of the possible causes for this result is that the waste exergy values of the CC is higher than the other components for both cases. In opposite to this, the ED has the lowest waste exergy ratios for both cases. When the engine is powered with biofuel and jet kerosene fuels, the ExIP performances are demonstrated in Fig. 9.

Fig. 9
figure 9

Comparing the ExIP results for jet kerosene and biofuel cases

Full size image

Figure 9 illustrates that when the engine is powered by biofuel instead of jet kerosene, while the ExIP of CC, GT, ED and GTMS components increase, it is observed that there is no change within the components of the AC for this performance parameter.

Results of thermoecologic analysis

The results of thermoecologic performance of the engine for both cases are designated in Table 7.

Table 7 Thermoecologic performance results of the engine for both cases
Full size table

In Table 7, it is observed that the thermoecologic performance indicator value of the engine increments from 0.34 to 0.35, as far as biofuel usage instead of jet kerosene.

Results of environmental analysis

The results of environmental performance of the engine and its sub-modules for both cases are given in Table 8.

Table 8 Environmental performance results of the engine and its sub-modules for both cases
Full size table

In Table 8, the engine’s EEF is computed to be 4.88 for jet kerosene usage condition, while it is calculated to be 4.93 for biofuel utilization case. As a similar trend, the engine’s EcoEF is higher compared to the jet kerosene utilization case. On the other hand, whereas the ecological objection function values of the CC, GT, ED and GTMS components fall down from 347.61 kW to 330.35 kW, from 692.18 kW to 689.79, from 1898.25 kW to 1866.13 kW and from 748.73 kW to 748.40 kW. When the engine is powered with biofuel and jet kerosene fuels, the environmental performance results are graphed in Fig. 10.

Fig. 10
figure 10

Comparison of the environmental effect factor and ecological effect factor values of the jet kerosene and biofuel cases

Full size image

Figure 10 declares that the component with the maximum environmental effect factor and ecological effect factor for both cases is the CC. These are 0.84 and 1.84 for environmental effect factor for jet kerosene utilization case and 0.84 and 1.84 for ecological effect factor for biofuel usage condition. Moreover, as far as biofuel usage is concerned, it is seen that there is no change for the environmental performance parameters of EEF and EcoEF.

Results of enviroeconomic analysis

The results of enviroeconomic performance of the engine for both cases are given in Table 9.

Table 9 Enviroeconomic performance results of the engine for both cases
Full size table

According to Table 9, even though the total amount of emitted CO2 emissions is calculated to be 336,672 kg-CO2 year−1 in the case of jet kerosene usage, it is estimated as 222,012 kg-CO2 year−1 for the biofuel utilization case. Additionally, when the biofuel is preferred instead of jet-kerosene, environmental damage cost stream, namely the enviroeconomic parameter of the engine, falls from 59,254.27 US$ year−1 to 39,074.11 US$ year−1.

Results of sustainability level analysis

The results of sustainability performance of the engine and its sub-modules for both cases are given in Table 10.

Table 10 Sustainability performance results of the engine and its sub-modules for both conditions
Full size table

As per the sustainability level findings in Table 10, exergetic sustainability index and sustainable efficiency factor of engine drop from 0.21 to 0.20 and decrease from 1.21 to 1.20, respectively. Also, it is observed that the exergetic sustainability index and sustainable efficiency factor values of the AC are the same for jet fuel utilization and biofuel utilization cases, which are 7.31 and 8.31, respectively. On the other hand, with the usage of biofuel utilization, the exergetic sustainability indexes for CC, GT, ED and GTMS components fall from 1.20 to 1.18, from 9.77 to 9.45, from 136.03 to 55.36 and from 67.91 to 65.95, respectively. As a same tendency with the results of the exergetic sustainability index, the sustainable efficiency factor values of these components reduce from 2.20 to 2.18, from 10.77 to 10.45, from 137.03 to 56.36 and from 68.91 to 66.95. Exergetic sustainability index and sustainable efficiency factor results are depicted in Fig. 11.

Fig. 11
figure 11

Comparison of the exergetic sustainability index and sustainable efficiency factor values of the jet kerosene and biofuel cases

Full size image

Figure 11 points out that the component with the highest exergetic sustainability index and sustainable efficiency factor is the ED with values of 136.03 and 137.03 for jet kerosene utilization case, while the component with the highest exergetic sustainability index and sustainable efficiency factor is the GTMS with values of 66.95 and 67.95 for biofuel utilization case.

Conclusions

In this study, utilization of a bio-based fuel as an alternative to jet kerosene fuel used in aircraft engines in the aviation sector has been extensively observed with adapting various useful indicators for the scope of the study based on thermodynamic principles. Within this framework, a turbojet engine, which is fueled by both jet kerosene and biofuel, is examined using the extensive energy and exergy, thermoecologic, environmental, enviroeconomic and sustainability level research methods. Some comparative results are as below:

  • The mass stream of combustion emissions is measured to be 4.547 kg s−1, when the engine is powered by biofuel. The specific fuel consumption and the specific thrust are determined as 0.13 kg kN−1 s−1 and 147.81 kNs kg−1 for jet kerosene-powered case, while they are calculated as 0.15 kg kN−1 s−1 and 148.23 kNs kg−1 for biofuel-powered case.

  • When biofuel is selected instead of jet kerosene, it has been observed that the engine has better energy efficiency performance by 18.18%, while it is 18.16% for the jet kerosene utilization case. Also, engine’s exergy efficiency drops from 17.00 to 16.88% while the engine's exergy efficiency decreases by a small amount. Besides, the combustion chamber is the minimum exergy efficient component among the other ones for both cases. What is more, the relative exergy destruction ratios of air compressor and combustion chamber drop from 4.68% to 4.56% and drop from 90.00% to 89.09%, respectively. Waste exergy ratios of the combustion chamber, gas turbine, and exhaust duct increment from 54.83% to 55.07%, 2.46% to 2.51% and 0.44% to 1.06%, respectively. As far as system-level exergetic performance is concerned, with the utilization of biofuel, the system level fuel exergy waste ratio, the system level productivity lack ratio and exergetic improvement potential values rise from 83.00% to 83.12, 488.11% to 492.53% and 1623.44 kW to 1669.19 kW, respectively.

  • When engine is powered by biofuel instead of jet kerosene, it is observed that the thermoecologic performance indicator value of the engine increments from 0.34 to 0.35.

  • The environmental effect factor of the engine is computed to be 4.88 for jet kerosene utilization case, while it is calculated to be 4.93 for biofuel utilization case.

  • Total amount of emitted CO2 emissions is determined as 336,672 kg-CO2 year−1 for jet-kerosene usage, while it is estimated as 222,012 kg-CO2 year−1 for the biofuel utilization case. Also, the environmental damage cost stream, namely the enviroeconomic parameter of the engine, falls from 59,254.27 US$ year−1 to 39,074.11 US$ year−1.

  • The exergetic sustainability index and sustainable efficiency factor values of the air compressor are the same for jet fuel utilization and biofuel utilization cases, which are 7.31 and 8.31, respectively.

  • As may be observed from the extensive findings shown above, the results of extensive energy and exergy, thermoecologic, environmental, enviroeconomic and sustainability level performances of the fuels examined are too close to the jet-kerosene. As such, it can be said that the biofuels can be solutions to traditional fossil fuels in aircraft engines. Also, biofuels can be a feasible option to offset CO2-equivalent emissions for sustainable aviation.

  • The outputs of this study can be a helpful guide and spearhead for researchers and stakeholders who are interested in the concept of sustainable and cleaner aviation.

  • The authors suggest that alternative fuel efforts like biofuels and hydrogen be evaluated whether parametrically or empirically for other aircraft engines too.

  • For a future work, advanced exergoenvironmental and damage-cost assessments of this study under operated two fuel conditions are considered.