Introduction

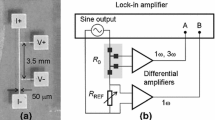
Currently, thermal management and flexible thermoelectric devices in the fields of micro, power, and flexible electronics are being actively studied [1,2,3,4]. When wire samples are used to fabricate such heat-utilizing devices, a method for accurately measuring the thermal conductivity of conductive wires with diameters of 1–100 μm is extremely important. Therefore, a number of measurement methods have been developed for such purposes [5,6,7,8,9,10,11]. Among them, the 3ω method for wire samples [11] is superior to others because thermal, electrical, and thermoelectric properties can be measured in the same direction of the same sample and by the similar sample setup. In the 3ω method, the 3ω component of voltage signal induced by the self-heating of wire under an AC current flow is analyzed to obtain the thermal conductivity of the wire. A typical measurement setup requires a pair of current application electrodes and another pair of voltage measurement ones as seen in Fig. 1. The wire sample is usually bonded to the four electrodes by conductive adhesive to ensure good electrical and thermal contacts.

Fig. 1
figure 1

a Schematic diagram of the measurement setup. b photograph of the electrodes–substrate and the sample configuration used in this work. The substrate has 4 electrodes for the 4-terminal measurement and 2 thermocouples to measure the temperatures at the voltage measurement electrodes

Full size image

In order to obtain the correct thermal conductivity of the wire sample using the 3ω method, it is necessary to understand and reduce the error factors that occur during the measurement. From the measurement principle of the 3ω methods, the following 4 factors could be the causes of uncertainty in the measured values:

  1. (1)

    Stability of electrical resistance of the sample and its temperature dependence, which are important for measuring temperature rise of the sample,

  2. (2)

    Heat loss caused by radiation and conduction to surrounding gas molecules,

  3. (3)

    Uncertainty of electrical resistance and 3ω voltage due to the ambiguity of the voltage measurement points, and

  4. (4)

    Non-ideal distribution of current and temperature at around the voltage measurement electrodes due to the finite size of the conductive adhesive which connects the sample to the electrodes.

Among these four factors, factor (1) is excluded from this study because it depends only on the sample used. We have to avoid using electrically unstable samples for any of the direct heating methods. In factor (2), the radiation heat loss is also excluded from this study because the influence of the radiation heat loss has been already well-explained in other works [11, 12] and is easily estimated from the measurement results. In the case of a wire with circular cross section, it is not so difficult to avoid a significant error of the measurement by the radiation heat loss when we use relatively shorter sample length. In fact, the influence of the radiation heat loss was not observed in this study, as mentioned later. The influence of convection heat loss under an atmospheric condition has been also considered and reported [13,14,15,16]. However, the error caused by heat loss due to conduction to the residual gas on the measurement has not been sufficiently examined. Most of the measurements are performed under a certain degree of reduced pressure because the large influence of convection heat loss under an atmospheric pressure is well known and its influence on the measurement can be easily predicted. On the other hand, the extent to which ambient gas in the medium-to-high vacuum range affects the measurement has not been investigated in detail. When the pressure is in the medium-to-high vacuum range, which corresponds to the transition region to the molecular flow, the heat loss cannot be quantified by assuming convection but by considering the direct heat transfer by gaseous molecules from the sample to other objects in the measurement chamber. Therefore, it is necessary to establish another quantification method that quantitatively explains the effect of the gas conduction heat loss in the medium-to-high vacuum range and to estimate a maximum pressure that can prevent errors in the thermal conductivity measurements.

Factors (3) and (4) have not been quantitatively studied so far but were found to also induce significant error in thermal conductivity measurements. If the voltage measurement point is ambiguous, it indicates that the actual sample length is ambiguous, causing errors in the measurement results. One may suppose that reduction of the size of conductive adhesive is an easy solution to suppress such uncertainty. However, its size cannot be small enough to ensure thermal connection to the heat sink. Furthermore, it is also difficult to make the sample length long enough to ignore the size of conductive adhesive because of the significant increase of heat loss as explained later. Under such circumstances, it can be easily inferred that the current and temperature distribution at the voltage measuring electrode section will dissociate from the ideal state assumed by the analytical model, resulting in measurement errors. Therefore, it is practically important to evaluate the effects of these factors and determine an upper limit for the size of the conductive adhesive in order to perform accurate thermal conductivity measurements.

In this study, we conducted two series of experiments for factors (2), (3), and (4) in order to clarify the conditions necessary for the high-accuracy measurement of thermal conductivity of the wire samples by the 3ω methods. First, for consideration of factor (2), we measured apparent thermal conductivity of an Au wire under a wide range of ambient pressures, approximately from 10–3 to 105 Pa. As a result, we found that measured thermal conductivity increases rapidly with increasing pressure in the medium vacuum region. The pressure dependence of the measured value was analyzed using a model of gas heat conduction, and a practical limit of the ambient pressure was determined for the accurate measurement. Second, regarding factors (3) and (4), dependences of the measured sample resistance and thermal conductivity on the length of the conductive adhesive along the sample wire were investigated by measuring the thermal conductivity of the Au wire with the ratio of conductive adhesive to sample length ranging approximately from 7 to 50%. As a result, the measured thermal conductivity increased with increasing length of the conductive adhesive, even though the measured electrical resistance remained almost constant. The error caused by the length was considered to be due to the spreading electrical current in the conductive adhesive and complicated distribution of the heat generation around the contact regions. The practical limit of the length ratio between the adhesive and wire was proposed by considering the experimental results.

Influence of ambient pressure on the measurement of thermal conductivity

Experimental details and results

In the 3ω method, an AC current (amplitude: I0, angular frequency: ω) applied to a sample producing temperature oscillation with a frequency of 2ω, and as a result, the resistance oscillation appears. This resistance oscillation induces the third harmonic component in the sample voltage, V3ω, which is used for the estimation of thermal conductivity. V3ω is expressed by the following equation [11]:

$${V}_{3\omega }=\frac{4{I}^{3}{LRR}^{\mathrm{^{\prime}}}}{{\pi }^{4}\kappa S}\left[\frac{1}{\sqrt{1+{\left(2\gamma \omega \right)}^{2}}}\right]+{V}_{\mathrm{offset}},$$
(1)

where I is the effective value of the AC current, L is the length of the sample, R is the electrical resistance of the sample, R' is the temperature derivative of resistance, κ is the thermal conductivity of the sample, S is the cross-sectional area of the sample, γ is the thermal time constant of the sample which is defined as \(\gamma ={L}^{2}/{\pi }^{2}\alpha\), then α is thermal diffusivity of the sample, and Voffset, which is not used in ref. 11, is a small offset signal derived from the instrument due to, for example, a harmonic noise due to the distortion of AC current generator and amplifier.

An Au wire with 30 μm in diameter (Nilaco, AU-171095) was used as a test sample. The true diameter of the Au wire used in this experiment was measured by a calibrated optical microscope and was estimated to be 29.9 μm. Figure 1a, b shows the schematic diagram of the measurement setup and a photograph of an actual sample, respectively. For the substrate, a sapphire was used because of the high thermal conductivity and electrical insulation. Au-coated Cu blocks were used for the electrodes. This substrate with electrodes is designed also for Seebeck coefficient measurements. The sample Au wire was bonded on the electrodes using Ag paste (Chemtronics, CW2401) as conductive adhesive. The substrate was then placed on a temperature-controlled stage in a vacuum chamber. During the measurement, the stage temperature was maintained at 298 K, which is approximately the same as room temperature, to minimize the radiation heat loss from sample to the chamber wall. The pressure in the chamber was controlled from 1.0 × 10−4 to 1.0 × 105 Pa by varying conductance of the vacuum pumping line and N2 gas introduced from a variable leak valve. The sample length was defined as the distance between the centers of two mounds of conductive adhesive on the electrodes for voltage measurement, unless otherwise noticed. In the case of Fig. 1b, the sample length was 7.15 mm. A Keithley 6221 was used as the current source to apply an AC current to sample. A Keithley 2000 was used to monitor the temperature of voltage measurement electrodes. An AD converter, National Instruments USB-6281, was used to measure the AC voltage. V1ω, which is the fundamental component of the sample voltage, and V3ω were obtained by the fast fourier transform (FFT) of the AC voltage signal measured by the AD converter. All of the electrical instruments and the measurement chamber were grounded to suppress electrical noises.

Figure 2 shows the dependence of measured thermal conductivity on the chamber pressure. In the molecular flow region, the thermal conductivity is almost constant, but starts increasing when the pressure approaches to the transition region. In the transition region, the thermal conductivity obviously increases as the pressure increases and the increasing rate becomes slower in the viscous flow region. Below 1.0 × 10−2 Pa, the average thermal conductivity is estimated to be 295 ± 3 Wm−1 K−1, of which deviation is about 7% from the reference value (317 Wm−1 K−1) [17] or the average value of the round robin test which is measured by several methods and judged to be reliable (318 W m−1 K−1) [18]. We can, therefore, say that the measurement results in this pressure region are sufficiently accurate.

Fig. 2
figure 2

Dependence of measured thermal conductivity of the Au wire on the pressure of the measurement chamber. To decide the boundary of each flow region, N2 and the diameter of Au wire were assumed as atmospheric gas and the representative length and the Knudsen numbers of 0.01 and 3 were used for the left- and right-side boundary of the transition region, respectively. The solid line is the fitting curve drawn by the fitting function Eq. (18)

Full size image

Figure 3a, b shows the dependence of R and temperature coefficient of resistance (TCR) on pressure. The average of R is 0.252 ± 0.001 Ω and the average of TCR is (3.50 ± 0.03) × 10−3 K−1 within the pressure range of the experiments. Each standard deviation is less than 1% of the average value, and thus the dependences of R and TCR on pressure are concluded not to influence the error in the thermal conductivity measurement. Moreover, judging from this minor change in the sample resistance, the thermal conductivity of Au, which is a typical noble metal following the Wiedemann–Franz law, must not be changed by the chamber pressure. The large variation of the measured thermal conductivity is, therefore, considered not to be due to an artifact of the electrical measurement for resistance or TCR.

Fig. 3
figure 3

a Dependence of electrical resistance of Au wire on chamber pressure. b dependence of TCR of Au wire on chamber pressure

Full size image

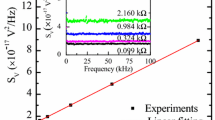
Figure 4 shows the dependence of V3ω on frequency at several different pressures. As pressure increases, the value of V3ω saturating at low frequency tends to decrease. From Eq. (1), one may notice that the thermal conductivity is estimated higher when the V3ω becomes lower. According to the measurement principal of the 3ω method, V3ω also decreases when the heat loss from the sample increases. A noteworthy fact is that the theoretical curve can be perfectly fitted on all of the measured values as seen in Fig. 4, which makes this artifact difficult to distinguish from the correct measurement result.

Fig. 4
figure 4

Frequency dependence of V3ω at each pressure. The marks are experimental values, and the curve connecting them is the result of fitting Eq. (1) to the experimental values

Full size image

Analysis and discussion

First, let us follow how Lu et al. derived Eq. (1) [11] and introduce the influence of gas heat conduction later. Considering an AC current of amplitude I0 and angular frequency ω flowing through a rod-like sample of diameter D and length L, the following one-dimensional heat conduction equation was used to derive the thermal conductivity:

$$\rho {C}_{\mathrm{p}}\frac{\partial }{\partial t}T\left(x,t\right)-\kappa \frac{{\partial }^{2}}{\partial {x}^{2}}T\left(x,t\right)=\frac{{I}_{0}^{2}{\mathrm{sin}}^{2}\omega t}{LS}\left[R+{R}^{^{\prime}}\left(T\left(x,t\right)-{T}_{0}\right)\right],$$
(2)

where ρ is the mass density of the sample, Cp is the specific heat of the sample, T(x, t) is the temperature on the sample at a given position, x, and time, t, and T0 is the temperature of the substrate. The boundary condition of Eq. (2) is as follows:

$$\left\{\begin{array}{c}T\left(0,t\right)\,={{T}}_{0}\\ T(L ,t)\,={{T}}_{0}\\ T(x,-\infty )\,={{T}}_{0}\end{array} \right..$$
(3)

Since Eq. (2) does not include the heat loss by radiation and heat transfer to gas, we here introduce both effects to Eq. (2). Assuming that the ambient and substrate temperatures are equal, the radiation heat loss from the sample per unit length to the ambient temperature, \({W}_{\mathrm{r}}\left(x,t\right)\), is expressed by the following equation:

$${W}_{\mathrm{r}}\left(x,t\right)=\pi \epsilon {\sigma }_{\mathrm{SB}}D\left[{T}^{4}\left(x,t\right)-{T}_{0}^{4}\right]\approx 4\pi \varepsilon {\sigma }_{\mathrm{SB}}D{T}_{0}^{3}\Delta T\left(x, t\right),$$
(4)

where \(\Delta T\left(x,t\right)=T\left(x,t\right)-{T}_{0}\), ε is the emissivity of the sample, and σSB is the Stefan-Boltzmann constant. In this work, we additionally introduce the heat loss due to the conduction to gas according to the analyzing model of the Pirani vacuum gauge [19]. The conduction to gas per unit length, \({W}_{\mathrm{g}}\left(x,t\right)\), is expressed by the following equation:

$${W}_{\mathrm{g}}\left(x,t\right)=\pi DkP\left(\frac{{P}_{\mathrm{t}}}{P+{P}_{\mathrm{t}}}\right)\Delta T\left(x,t\right),$$
(5)

where P is the gas pressure, Pt is the transition pressure, and k is a constant expressed as:

$$k=\frac{\varphi }{2-\varphi }{\Lambda }_{0}{\left(\frac{273.2}{{T}_{\mathrm{a}}}\right)}^\frac{1}{2},$$
(6)

where φ is the accommodation coefficient of the gas, Λ0 is the free molecular conductivity at 273 K, and Ta is the heat sink temperature. On the other hand, amount of heat transmitted through the side of the sample, dQsur, denoting the amount of heat escaping from the side face of the sample can be expressed by the second derivative of the temperature distribution as:

$$\mathrm{d}{Q}_{\mathrm{sur}}=\kappa {\pi \left(\frac{D}{2}\right)}^{2}\frac{{\mathrm{d}}^{2}T\left(x.t\right)}{{\mathrm{d}x}^{2}}\mathrm{d}x.$$
(7)

Since dQsur must be equal to the sum of \({W}_{\mathrm{r}}\left(x,t\right)\) and \({W}_{\mathrm{g}}\left(x,t\right)\), the heat balance in the section dx is described as:

$${W}_{\mathrm{r}}\left(x,t\right)\mathrm{d}x+{W}_{\mathrm{g}}\left(x,t\right)\mathrm{d}x=\kappa \pi {\left(\frac{D}{2}\right)}^{2}\frac{{\mathrm{d}}^{2}T\left(x,t\right)}{{\mathrm{d}x}^{2}}\mathrm{d}x.$$
(8)

Thus, the heat loss by radiation and gas conduction are expressed as follows:

$$\kappa \frac{{\partial }^{2}T(x,t)}{\partial {x}^{2}}=\frac{1}{\pi }{\left(\frac{2}{D}\right)}^{2}\left\{{W}_{\mathrm{r}}\left(x,t\right)+{W}_{\mathrm{g}}\left(x,t\right)\right\}.$$
(9)

Adding Eq. (9) to Eq. (2), the heat conduction equation becomes:

$$\frac{\partial }{\partial t}\Delta T\left(x,t\right)-\alpha \frac{{\partial }^{2}}{\partial {x}^{2}}\Delta T\left(x,t\right)+\left(g-{\mathit{c }\mathrm{sin}}^{2}\omega t\right)\Delta T\left(x,t\right)=b{\mathrm{sin}}^{2}\omega t,$$
(10)
$$g=\frac{16\varepsilon {\sigma }_{\mathrm{SB}}{T}_{0}^{3}}{\rho {C}_\mathrm{p}D}+\frac{4k}{\rho {C}_\mathrm{p}D}P\left(\frac{{P}_\mathrm{t}}{P+{P}_\mathrm{t}}\right),$$
(11)
$$b=\frac{{I}_{0}^{2}{R}}{\rho {C}_{\text{p}}LS},$$
(12)
$$c=\frac{{I}_{0}^{2}{R}^{^{\prime}}}{\rho {C}_{\text{p}}LS}.$$
(13)

Using impulse theorem and Fourier expansion, Eq. (10) becomes:

$$\sum_{\text{n}=1}^{\infty }\left[\frac{\text{d}{U}_\text{n}}{\text{d}t}+\left(\frac{{n}^{2}}{\gamma }+g-{\mathit{c }\mathrm{sin}}^{2}\omega t\right){U}_\text{n}\right]\mathrm{sin}\frac{n\pi x}{L}=0,$$
(14)

where n is natural number. In Eq. (14), when \({n}^{2}/\gamma +g\gg c\), the term c sin2ωt can be ignored. Then, defining the apparent thermal time constant γap to satisfy \({n}^{2}/\gamma +g={n}^{2}/{\gamma }_{\mathrm{ap}}\), the following condition is obtained when \({n}^{2}/{\gamma }_{\mathrm{ap}}\gg c\):

$$\frac{{I}_{0}^{2}{R}^{^{\prime}}L}{{{n}^{2}\pi }^{2}{\kappa }_{\mathrm{ap}}S}\ll 1,$$
(15)

where κap is apparent thermal conductivity expressed as \({\kappa }_{\mathrm{ap}}=\kappa (1+g\gamma )\). From that, the condition to ignore the influence of radiation and gas conduction heat loss is \(\mathrm{g}\gamma \ll 1\). When n = 1, which is the strictest condition of Eq. (16), V3ω is expressed as:

$${V}_{3\omega }\approx \frac{{4I}_{0}^{3}{LRR}^{\mathrm{^{\prime}}}}{{\pi }^{4}{\kappa }_{\mathrm{ap}}S\sqrt{1+{\left(2\omega {\gamma }_{\mathrm{ap}}\right)}^{2}}}.$$
(16)

And then, since γ is defined as \(\gamma ={L}^{2}/{\pi }^{2}\alpha\), \({\kappa }_{\mathrm{ap}}=\kappa (1+g\gamma )\) is expressed as:

$${\kappa }_{\mathrm{ap}}=\kappa +\frac{16\varepsilon \sigma {{L}^{2}T}_{0}^{3}}{{\pi }^{2}D}+\frac{4{L}^{2}}{D}kP\left(\frac{{P}_{\mathrm{t}}}{P+{P}_{\mathrm{t}}}\right).$$
(17)

As one may recognize, Eq. (16) has the same form of function as Eq. (1) except that \(\kappa\) and \(\gamma\) are replaced with corresponding apparent values. This is the reason why it is impossible to notice the influence of heat losses only by the fitting results shown in Fig. 4. The second and third terms in Eq. (17) represent the influence of radiation heat loss and heat loss to gas, respectively. Therefore, when there is a heat loss to the gas, the apparent thermal conductivity obtained by the 3ω method always becomes larger than the true value.

An important point is that both of the heat losses are proportional to L2/D. In the case of a typical centimeter-sized sample, such as a metallic material for mechanical engineering, the L2/D is on the order of 10−2 m, assuming a typical sample geometry of a few centimeters in length and a few centimeters in diameter. On the other hand, for micrometer-sized wire samples as discussed in this work, a typical size is a few millimeters in length, considering the attachment to electrodes, and a few tens of micrometers in diameter, resulting in the L2/D of the order of 10–1 m. In the case of thermal conductivity measurement of nanometer-sized samples, such as a single CNT, a typical size is several hundred nanometers in length and several nanometers in diameter, resulting in an L2/D of the order of 10−5 m. Therefore, it should be noted that thermal conductivity measurements of micrometer-sized wires are the most susceptible to heat losses in most practical cases. This fact makes the accurate thermal conductivity measurement of micrometer-sized wire the most difficult although the nanometer-sized samples come with another problem with sampling.

So, why is the influence of the radiation heat loss negligible in this work? The ratio between the radiation heat loss and thermal conductivity of the sample can be estimated by calculating the term expressed as \(16\varepsilon {\sigma }_{\mathrm{SB}}{L}^{2}{T}_{0}^{3}/{\pi }^{2}\kappa D\). The calculated value of this term for the experiment at lowest pressure was 0.016 and much lower than 1. Therefore, the influence of radiation heat loss can be ignored in this work, and Eq. (18) can be further simplified as:

$${\kappa }_{\mathrm{ap}}^{^{\prime}}=\kappa +\frac{4{L}^{2}}{D}kP\left(\frac{{P}_{\mathrm{t}}}{P+{P}_{\mathrm{t}}}\right).$$
(18)

This equation was fitted to the pressure dependence of the measured thermal conductivity using \(\frac{4{L}^{2}}{D}k\) and \({P}_{\mathrm{t}}\) as fitting parameters (a solid curve in Fig. 2). The fitting curve by Eq. (18) reproduces the pressure dependence of the apparent thermal conductivity well in the molecular and transition flow regions, which indicate that it is reasonable to apply the analytical model used in the Pirani vacuum gauge [19] to this experiment. Therefore, we concluded the increase in apparent thermal conductivity due to high gas pressure to be mainly caused by the heat conduction from the wire-like sample to the ambient gas. In the viscous flow region, the fitting by Eq. (18) becomes constant which is somewhat inconsistent with the continuous increase in the experimental results. This is because convective heat loss is dominant in the viscous flow region. Under the viscous flow condition, the heat transfer coefficient is known to be proportional to the temperature gradient of the boundary layer and the convective heat loss increases with increasing pressure [20], hence the measured thermal conductivity in the viscous flow region increases with pressure. Since the thermal conductivity measurement will not be performed under such a high pressure condition, this part is not further discussed in this paper.

Having been able to reproduce the experimental results by Eq. (18), we would now use Eq. (18) to examine how the measured thermal conductivity of the wire-like sample and its ambient pressure dependence are affected by the thermal conductivity and size of the sample.

First, variation of the curve by the thermal conductivity of the sample is shown in Fig. 5. The larger the thermal conductivity of the sample is, the lower the influence of the heat loss by gas on the measured value becomes, and the upper pressure limit at which the thermal conductivity starts deviating from the true value becomes higher. For the sample with a thermal conductivity of 0.1 Wm−1 K−1, which will be the lower limit of thermal conductivity for non-porous materials, the thermal conductivity needs to be measured under a pressure of < 1.0 × 10−2 Pa. In many cases where the thermal conductivity of electrically conducting wires, of which value will be in a range of several-hundreds of Wm−1 K−1, is to be measured, higher pressure is acceptable but, even so, the upper limit of chamber pressure should be less than around 1.0 Pa.

Fig. 5
figure 5

Variation of the apparent thermal conductivity vs pressure curve by true thermal conductivity of the sample. For this calculation, the sample size was fixed for 7.51 mm in length and 30 μm in diameter

Full size image

Next, the variation by the sample size is considered. Figure 6a, b shows variation of the measured thermal conductivity vs pressure curve by sample diameter. Here, the sample length was fixed to 7.51 mm and the thermal conductivity to 295 Wm−1 K−1. One may notice that the measurement of a very thin wire of which a diameter is around 10 μm or less is very sensitive to gas pressure. This is the reason why we use a-few-tens-of-micrometer-thick platinum hot wire for the Pirani vacuum gauge. The smaller the sample diameter is, the larger the influence of the of gas conduction heat loss on the measured value becomes, and the upper pressure limit to avoid the deviation from the true value becomes lower. These results are expected from the construction of Eq. (18) because the term of the influence of gas conduction heat loss depend on the diameter of the sample. From Fig. 6b, the practical upper limit of pressure was estimated. The pressure should be < 1.0 × 10−2 Pa for a sample diameter of 1 μm, and < 1.0 × 10−1 Pa for 10 μm, which is the lower limit of the generally available self-standing wires. Note that these results are calculated by assuming the thermal conductivity of gold. For a considerably worst sample among practical ones, of which thermal conductivity is a few Wm−1 K−1 and diameter is 10 μm, we can conclude that the chamber pressure should be < 1.0 × 10−2 Pa. This pressure would be a good reference for designing a general-purpose instrument with a safety margin.

Fig. 6
figure 6

Variation of the apparent thermal conductivity vs pressure curve by sample diameter: a the entire graph and b a magnified view for the thermal conductivity ranging 280–360 Wm−1 K−1. For this calculation, the sample length was fixed to 7.51 mm and the thermal conductivity to 294.78 Wm−1 K−1

Full size image

Influence of the length of conductive adhesive on the measurement of thermal conductivity

Experimental details and results

From the electrical point of view, it is obvious that the size of the conductive adhesive which is used to fix the sample to the voltage electrodes should be as small as possible. However, its size cannot be small enough to ensure the boundary condition of Eq. (3) because it also serves as a heat conductor to the heat sink. In addition, the error in measured thermal conductivity due to radiation and gas heat conduction is proportional to the square of the length as in Eq. (17), which suggests that the sample cannot be too long to make the size of conductive adhesive negligible. In this section, we therefore examine the influence of the length of the conductive adhesive along the sample experimentally.

The experimental method is schematically shown in Fig. 7. First, an Au wire was fixed at the outermost ends of the two voltage electrodes by conductive adhesive—Ag paste in this work. Here, a narrow space was kept between the wire and the electrodes so that the wire contacts to the electrodes only through the conductive adhesive. Then, the adhesive was added to the inside of the electrodes step-by-step after each measurement to obtain the dependence of the measured value on the length of the conductive adhesive. The Au wire and the conductive adhesive used in this experiment were the same as those used for the pressure dependence experiments. The true diameter of the Au wire used in this experiment was measured by the same method as in the first experiment and was estimated to be 30.0 μm. The conditions for the measurement were a pressure of less than 3.0 × 10−3 Pa and a substrate temperature of 298 K. Totally, five different lengths of conductive adhesive were used, namely stages 1–5. Measurements were performed three times for each stage of sample using the same measurement routine as for the pressure dependence measurements. Equation (1) was used for fitting to the frequency dependence of the 3ω voltage.

Fig. 7
figure 7

Schematic diagram of the experiments investigating the influence of the length of conducive adhesive. Conductive adhesive was added step-by-step after each measurement. a, b and c are the example of first, second and third measurements, respectively. wl and wr are the lengths of left- and right-side conductive adhesive, respectively. l is the length of Au wire defined as the distance between inside edges of two mounds of conductive adhesive

Full size image

Table 1 shows measured values of wl, wr, l and the ratio of conductive adhesive to sample length, which is defined by \(\left({w}_{\mathrm{l}}+{w}_{\mathrm{r}}\right)/\left(l+ {w}_{\mathrm{l}}+{w}_{\mathrm{r}}\right)\). The frequency dependence of V3ω for each sample is shown in Fig. 8a–e. The numbers written in the figures are the magnitudes of the current amplitudes used for the measurements. As seen in these graphs, all of the experimental curves are well fitted by Eq. (1).

Table 1 Measured length of each part of the sample at stage 1–5: lengths of the left- and right-side conductive adhesive (wl and wr, respectively), length of the bare Au wire between the conductive adhesive (l), and the ratio of conductive adhesive to sample length
Full size table
Fig. 8
figure 8

a–e Dependence of V3ω on frequency at stage 1–5, respectively. Opaque circles indicate the raw data obtained by three-times measurements, filled circles average values of them, and solid line fitting results using Eq. (1)

Full size image

Analysis and discussion

In order to calculate the electrical and thermal conductivities of a sample, the accurate length of the sample, L, is necessary. However, considering the possibility of non-negligible current flowing through the conductive adhesive and the uncertainty of the position of the measured potential, there are several practical choices for the definition of L. The first is that between the inner edges of the two mounds of conductive adhesive (Inside, \(L=l\)), the second is between the centers of them (Center, \(L=l+\frac{{w}_{\mathrm{l}}+{w}_{\mathrm{r}}}{2}\)), and the last is between the outer edges of them (Outside, \(L=l+{w}_{\mathrm{l}}+{w}_{\mathrm{r}}\)). To determine a reasonable length, these three definitions of length were tested to calculate the electrical conductivity of Au wires at the 5 stages and the length dependence of the calculated values were compared.

Figure 9 shows the wire length dependence of the apparent conductivity calculated for the three different definitions of length. Essentially, electrical conductivity should be independent of length. However, apparent conductivity increases by decreasing length when the Outside is used and decreases when the Inside is used. Apparent conductivity shows only a slight increase as the length decreases but is almost constant when the Center is used. Thus, the measured voltage seems to be indicating the potential difference approximately between the centers of the two mounds of conductive adhesive. This result indicates that the electrical potential in the conductive adhesive is not constant and there is an unexpected potential gradient within the conductive adhesive. This possibly happens when the conductivity of the conductive adhesive is lower than that of the sample wire. Based on these results, the Center definition was adopted as L in the following experiments for the calculation of thermal conductivity.

Fig. 9
figure 9

Dependence of the calculated electrical conductivity on the length of Au wire. “Inside” denote the calculation using \(L=l\), “Center” using \(L=l+\frac{{w}_{\mathrm{l}}+{w}_{\mathrm{r}}}{2}\), and “Outside” using \(L=l+{w}_{\mathrm{l}}+{w}_{\mathrm{r}}\). (See the main text and Table. 1.)

Full size image

This experiment was performed under the condition which the electrical conductivity of the sample is higher than that of the conductive adhesive. But if the wire sample has a significantly lower electrical conductivity than that of the conductive adhesive, the potential gradient surrounded by the conductive adhesive will be extremely small under the condition of continuous current, and the definition of \(L=l\) should give a more accurate conductivity. Therefore, if the ratio of the conductive adhesive to the sample length cannot be less than a few percent, the decision on the definition of length should be made by performing a similar length dependence experiment as this work.

Next, the influence of conductive adhesive on the measured thermal conductivity is evaluated. Figure 10 shows the change in the measured thermal conductivity as a function of the ratio of conductive adhesive length. As the ratio increases, the measured thermal conductivity tends to increase.

Fig. 10
figure 10

Variation of measured thermal conductivity by the ratio of the length of conductive adhesive (Ag paste) against that of the Au wire

Full size image

At 7.25%, the smallest percentage in this experiment, the measured value was 321 Wm−1 K−1, and at 17.1%, the next smallest, the measured value was 335.9 Wm−1 K−1, both of which are within ± 6% of the reference value [17, 18]. This result indicates that reducing the amount of conductive adhesive is important in order to measure the thermal conductivity accurately using the 3ω method and, in the case of the combination of Ag paste and gold wire used in this study, it is necessary to reduce it to less than around 20%. As in the experiment of pressure dependence, the influence of radiation heat loss was estimated. The radiation heat loss at low ratio of Ag paste width was 0.029 which was much lower than 1. Therefore, the influence of radiation heat loss can be ignored in these results.

Here, let us consider the cause of the increase in the measured thermal conductivity with the increase in the conductive adhesive length. The contact heat resistance of the Ag bond between the sample and the voltage measured electrode is not considered to be main factor for the increase in apparent thermal conductivity because we found that the apparent thermal conductivity didn’t have significant dependence on the thickness of Ag layer between sample and electrode [18]. Putting the factor \(\frac{4{I}^{3}{LRR}^{\mathrm{^{\prime}}}}{{\pi }^{4}\kappa S}\) in Eq. (1) as A, V3ω converges to A at the low-frequency limit. Then, if sample length L, resistance R, and its temperature derivative R’ are wrong, a wrong thermal conductivity is obtained. In this work, L and R are expected to represent the potential distribution of the Au mostly correct, because they have been chosen based on the evaluation in Fig. 9. To examine in which parameter the artifact is originally incorporated, A/LR2, in which the contribution of L and R is removed, is plotted against the ratio of the conductive adhesive length in Fig. 11. A/LR2 tends to decrease as the ratio of conductive adhesive increases. Even though I, S, and TCR (R'/R) are the only experimental parameters left in A/LR2, the value is far from constant against the ratio. From this result, it is suspected that the error factor caused by the wider conductive adhesive length is not purely electrical, but more related to a thermal phenomenon. We, therefore, focus on TCR which is a kind of thermal parameter remaining in A/LR2.

Fig. 11
figure 11

Variation of A/LR2 by the ratio of the length of conductive adhesive (Ag paste) against that of the Au wire. A is a factor in Eq. (1) and defined as \(A=\frac{4{I}^{3}{LRR}^{\mathrm{^{\prime}}}}{{\pi }^{4}\kappa S}\)

Full size image

A plot of TCR against the ratio of conductive adhesive length is shown in Fig. 12. This value should be invariant for the same Au wire. The TCR obtained is nearly constant up to about 20% of the conductive adhesive length, but increases monotonically as the ratio increases beyond 20%. What is important is that TCR varied with the conductive adhesive length even though the electrical conductivity was measured correctly, as shown in Fig. 9. As mentioned above, a potential gradient must exist in the conductive adhesive, from which an electrical current must extend to the conductive adhesive around the sample as well as to the electrodes underneath. As a result, the measured TCR of the sample must be affected by the TCR of the surrounding conductors.

Fig. 12
figure 12

Variation of TCR by the ratio of the length of conductive adhesive (Ag paste) against that of the Au wire

Full size image

It is assumed that the average of the measured values when the ratio is less than 20% is reliable because they are constant against the ratio and measured thermal conductivity in this range is close to the reference value (Fig. 10). The TCR value obtained here is also close to that of gold near room temperature in a relatively reliable database [21], 0.00340 K−1. This value is also in good agreement with the obtained TCR of 0.00350 K−1 in the pressure dependence experiments (Fig. 3b). Since the ratio of conductive adhesive length in the pressure dependence experiment is about 10%, which is within the recommended range in this section, the influence of conductive adhesive is also considered negligible.

What we should point out here is that only the increase in the apparent TCR (Fig. 12) to about 127% in this range does not fully explain the significant decrease in A/LR2 to about 10.7% with increasing conductive adhesive length (Fig. 11). The remaining error factors are considered to be due to the discrepancies in the thermal boundary conditions at the electrodes (Eq. (3)) and the electrical boundary conditions, such as DC and AC potentials. In the state where the current spreads to the conductive adhesive, Joule heating due to AC current also occurs in the conductive adhesive, and 3ω voltages are thought to be generated there as well. In the conductive adhesive, the current flows mainly in the horizontal direction, while the heat flows mainly in the vertical direction, and the interfacial resistance is also different between electric and thermal ones. It is quite possible that the 3ω voltage generated in such a complicated three-dimensional situation does not match Eq. (1).

So far, only the increase in the length of the conductive adhesive along the sample has been considered as a cause of measurement error. Increases in other directions, or that in volume may have similar influence. However, there is a critical difference between the length direction and others. Increase in length direction increases unexpected spreading of electrical current also to the electrodes but others do not. Therefore, the length of the conductive adhesive along the sample is considered to be the most effective indicator to minimize the measurement error.

In summary, it was revealed that the length of the conductive adhesive along the sample should be sufficiently small compared to the sample length between the voltage measurement electrodes. In the case of the combination of gold wire and Ag paste, it was found that the accuracy of the thermal conductivity was sufficiently high at about less than 20% of the ratio. In the case of a material with a smaller electrical conductivity than Ag paste (1000 Scm−1 for the one used in this study), the ratio of the current spreading to the conductive adhesive side becomes higher. Even so, the influence of the conductive adhesive part on the measured DC and AC voltages will not increase much because the resistance of the bare wire part between the voltage electrodes will also increase. However, in the case of a wire with a high thermal conductivity, it would be necessary to attach it to the electrodes considering the thermal conductance so that the temperature of the voltage measurement part becomes equal to that of the electrode/heat sink. This will limit the length of the conductive adhesive shortened and further optimization is needed when extremely high accuracy is required.

Conclusions

We quantitatively studied the major factors causing error in the thermal conductivity measurements with the 3ω method for wire samples. An Au wire with a diameter of 30 μm was used as a test sample to evaluate the dependence of the measured thermal conductivity on the chamber pressure and the conductive adhesive length.

The pressure dependence of thermal conductivity revealed that the measured value tends to increase with increasing pressure. The conductivity–pressure curve was explained well by the theoretical equation incorporating the gas heat conduction (Eq. (18)). Based on the theoretical equation, we calculated the variation of the measured conductivity and its pressure dependence by changing the thermal conductivity and size of the sample. The results indicated that the chamber pressure should be kept below 1.0 × 10−2 Pa in order to perform accurate thermal conductivity measurements for conductive wires with realistic range of size and thermal conductivity.

Experiments for the influence of the ratio of conductive adhesive length against that of the Au wire suggested that two error factors, electrical and thermal, appear as conductive adhesive length increases. First, the dependence of electrical conductivity on wire length showed that increasing the ratio enhanced an electrical error factor due to the uncertainty of the position where the voltage is being measured. Upon the thermal conductivity measurement using the 3ω method, this uncertainty is a critical problem because the value of the sample length in the part where the voltage is being measured is necessary for the analysis as it appears in Eq. (1). In order to determine the proper sample length which gives more reliable results, it is useful to examine the relationship between measured electrical conductivity and lengths according to several possible definitions of the length.

Even when the electrically proper sample length was used, the thermal conductivity tended to be largely overestimated as the ratio of conductive adhesive length increased. The variations of TCR and A/LR2 against the length ratio suggested that the current flows not only through the sample but also through the conductive adhesive and electrodes, causing unexpected Joule heating, and that the thermal and electrical boundary conditions, which are the premises of the 3ω methods, may no longer be valid. In the case of a combination of 30 μm Au wire and Ag paste, it was shown that the ratio of conductive adhesive should be less than 20% in length.

In addition to elucidating the error factors due to ambient pressure and conductive adhesive length, this study provided guidelines for avoiding these errors which have not been reported. These will be useful information for all researchers and engineers who need to precisely measure thermal conductivity of micrometer-scale wires.