Introduction

Compounds of divalent europium, samarium and ytterbium form an attractive group of activators in inorganic phosphors. Divalent ytterbium in halides may be a promising alternative to Eu2+ for scintillation materials and phosphors for light-emitting diodes (LEDs) [1, 2]. Ions of Yb2+ are interesting doping material because their 4f-shell is completely filled and no disturbing 4f–4f transitions influence on the luminescence due to the 5d ↔ 4f transition is observed. Yb2+ as doping material was first investigated in alkaline earth halides and alkali halides and YbCl2 was used as doping compound [3, 4].

Despite scientific and technological interest in divalent ytterbium chloride, still only few investigations were carried out on this compound and based on its halide systems. That’s why we decided to fill this gap and perform investigations of YbCl2–MCl binary systems (M = Li, Na, K). When work was started only data on pure YbCl2 and phase diagram of YbCl2-KCl binary system were existing in the literature. Melting temperature of YbCl2 was reported as 975 K [5], 994 K [6], and 1000 K [7], and molar melting enthalpy as 20.6 kJ mol−1 [8] or 23.7 kJ mol−1 [6]. The heat capacity of YbCl2 was determined by Tolmach et al. [9, 10] in the temperature range of 8–310 K by adiabatic calorimetry, and by Rycerz [6] in the temperature range of 300–1100 K with use of DSC. The only data on ytterbium(II) chloride—based systems were phase diagram of YbCl2-KCl binary system presented in graphic form only [11].

The present paper reports the YbCl2–LiCl and YbCl2–NaCl phase diagrams, and the mixing enthalpies of YbCl2–NaCl and YbCl2–KCl liquid mixtures, determined experimentally for the first time. All the experimental results along with the available literature data were used to optimize the thermodynamic properties of the investigated systems by CALPHAD method.

Experimental

Chemicals

The main reagents used in this study are presented in Table 1.

Table 1 Reagent description table
Full size table

Ytterbium dichloride was synthesized from Yb2O3 (Johnson Matthey, 99.9%) according to the description given in reference [6]. Ytterbium oxide was dissolved in a hot concentrated hydrochloric acid and YbCl3·6H2O hydrates were crystallized. These hydrates were dried in the atmosphere of gaseous HCl during 12 h, when temperature was slowly increased from ambient to 650 K. Obtained in this way YbCl3 was reduced to dichloride with zinc (in a double excess to the stoichiometry). YbCl3 and Zn were put into a quartz ampoule inside a quartz vessel, under reduced pressure (~ 1 Pa). The temperature was gradually increased up to 773 K, maintained for 3 h, then increased up to 900 K and kept during 5 h, all the time under static vacuum. Finally, dynamic vacuum was established in order to purify the YbC12 compound from Zn by distillation at 1193 K. Chemical analysis of the prepared YbC12 was performed by complexometric (ethylenediaminetetraacetic acid, EDTA, in presence of xylenole orange—ytterbium) and mercurometric (chloride) methods, obtaining the following results: Yb = 70.95 ± 0.09% (70.93% theoretical); Cl = 29.05 ± 0.10% (29.07% theoretical). Due to high hygroscopicity, YbC12 was stored in sealed glass ampoules. All further operations with ytterbium dichloride were performed in a glove box filled with argon (6N purity, Messer).

Lithium, sodium and potassium chlorides were additionally dehydrated by heating above the melting point in a stream of gaseous HCl.

Sample preparation

Mixtures of YbCl2 and LiCl or NaCl for DSC measurements were prepared by weighing out the appropriate amounts of the individual salts, which were then sealed under vacuum in quartz ampoules, melted and homogenized. Then the samples were ground in a mortar, placed in special quartz ampoules for DSC measurements and sealed under a vacuum. The masses of individual samples ranged from 0.100 to 0.400 g.

The samples for mixing enthalpy measurements were prepared in such a way that the more hygroscopic compound (YbCl2) was placed in a quartz (bubble-shaped) ampoule to be broken. The ampoule was then sealed under vacuum and attached to a quartz tube. The second component was placed in a quartz crucible with a bottom in the form of a cone (facilitates breaking). Preparation of both components was carried out in a glove box under argon atmosphere. Masses of all compounds were determined with an accuracy of 10–4 g.

Measurements

Phase diagrams of the YbCl2–LiCl and YbCl2–NaCl systems were constructed on the basis of DSC measurements performed with DSC 121 SETARAM differential scanning calorimeter equipped with a unique 3D DSC sensor. The advantages of this calorimeter, as well as the procedure for calibrating the apparatus and measurements, were presented in earlier papers [6, 12].

The mixing enthalpy measurements were carried out using the Calvet-type high temperature microcalorimeter over the whole composition range at 1085 K. The mixing experiments were all of the simple liquid–liquid type, performed under pure argon at atmospheric pressure. Directly after experiment, the calibration of the calorimeter was performed with α-alumina (NIST, USA). All points were obtained from separate experiments (one composition − one experiment + 4 calibrations). Detailed description of the calorimeter, mixing device and the “break-off bubble” method, as well as calibration of the calorimeter and evaluation of uncertainty, is given elsewhere [13, 14]. Standard uncertainty of mixing enthalpy determination was estimated as 6–8%.

Experimental uncertainty

The standard uncertainty in mole fraction of composition was estimated using Eq. (1)

$${u}^{2}\left({x}_{{\mathrm{YbCl}}_{2}}\right)=\left[{x}_{{\mathrm{YbCl}}_{2}}\cdot \left(1-{x}_{{\mathrm{YbCl}}_{2}}\right)\right]\cdot \left[{u}_{\mathrm{r}}^{2}\left({n}_{{\mathrm{YbCl}}_{2}}\right)+{u}_{\mathrm{r}}^{2}\left({n}_{\mathrm{MCl}}\right)\right]$$
(1)

The standard uncertainty in nYbCl2 and nMCl was estimated by combining the squared uncertainty of the YbCl2 and MCl (M = Li, Na, K) mass measurement and the purity of these compounds as specified in Table 1.

The standard uncertainty of the temperature measurements was estimated by combining in quadrature the standard deviation of five repeat measurements performed with high-purity metals (0.8 K) with the standard uncertainty of the thermocouple calibration (0.6 K).

The relative uncertainty of mixing enthalpy determination (ur(ΔHMIX) = 0.08) was discussed in detail in our previous work [13].

Results

Phase diagrams determination on the basis of DSC measurements

DSC heating and cooling curves for some samples from the systems under investigation are shown in Fig. 1. In all cases supercooling was observed on cooling curves. Therefore, all the temperature and enthalpy values used for phase diagrams construction were determined from heating curves. Temperature of the liquidus and temperature of other effects were determined as peak maximum temperature (Tpeak), and onset extrapolated temperature (Tonset), respectively.

Fig. 1
figure 1

SC heating (solid lines) and cooling (dashed lines) curves for YbCl2–LiCl mixtures with \({x}_{{\mathrm{YbCl}}_{2}} \)= 0.255 (a), 0.585 (b) 0.945 (c); and YbCl2–NaCl mixtures with \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.239 (d), 0.552 (e) 0.855 (f). Heating rate: 5 K min−1

Full size image

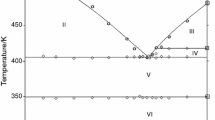
All heating curves for YbCl2–LiCl system revealed a presence of two or three pronounced thermal effects. In the composition range 0 < \({x}_{{\mathrm{YbCl}}_{2}}\) ≤ 0.400 two endothermic peaks were present (Fig. 1a). The second effect, occurred at the highest temperature, corresponds to the liquidus temperature. The first one, in the temperature range 723–736 K, was observable in all curves up to mole fraction of YbCl2 equal to 0.632. Then it disappeared, thus suggesting the existence of a compound with the stoichiometry LiYb2Cl5. This suggestion is confirmed by the lack of effect for the samples with \({x}_{{\mathrm{YbCl}}_{2}}\) > 0.668. This thermal effect was ascribed to the LiCl–LiYb2Cl5 eutectic. Its contribution to the enthalpy of fusion (calculated per mole of mixture) is plotted against composition in Fig. 2 (bottom, (A)). This Tammann plot allows to determine the composition of the eutectic from the intercept of the two linear parts as \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.415 ± 0.022. The eutectic mixture melts with the enthalpy, ΔHFUS, of about 15.56 ± 1.06 kJ mol−1 at the temperature T = 733 ± 4 K. This diagram gives also information about the formation of solid solutions in the LiCl-rich side since the straight line obtained for mixtures beyond the eutectic composition did not intercept the composition axis at \({x}_{{\mathrm{YbCl}}_{2}}\) = 0. The molar fractions at which solid solutions may exist at 733 K were found (Fig. 2, bottom (A)) as \({x}_{{\mathrm{YbCl}}_{2}}\hspace{0.17em}\)≤ 0.027 ± 0.024.

Fig. 2
figure 2

Phase diagram of the YbCl2–LiCl binary system (top) determined from DSC measurements and respective Tamman plots (bottom). Circles, crosses, squares and triangles—experimental data, solid lines (top)—phase equilibria, dotted lines (bottom)—enthalpy measurements error. Values in brackets—determined by CALPHAD calculations

Full size image

In the composition range 0.467 ≤ \({x}_{{\mathrm{YbCl}}_{2}}\) < 1 one or two endothermic peaks followed by a third thermal event related to the liquidus (Fig. 1b) were observed on curves. The first one (appearing only in samples with \({x}_{{\mathrm{YbCl}}_{2}}\)˂ 0.666, at T = 733 ± 4 K, as discussed above, is ascribed to the LiCl–LiYb2Cl5 eutectic. The second effect, occurring at T = 734–746 K, is observable in the samples with mole fraction of YbCl2 up to 1.000. The Tammann diagram i.e., enthalpy related to this effect (calculated per mole of the mixture) versus composition (Fig. 2, bottom (B)) confirmed the existence of stoichiometric compound in the system. The intersection of two straight lines gives value \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.692 ± 0.021. This value corresponds to the stoichiometry Li3Yb7Cl17 (theoretical value \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.700) or LiYb2Cl5 (\({x}_{{\mathrm{YbCl}}_{2}}\) = 0.666) compound, which melts incongruently. The stoichiometry of the first compound seems unusual and it does not appear in the systems based on divalent europium chloride and bromide [12,13,14,15]. At the same time compounds with stoichiometry MEu2Cl5 and MEu2Br5 (M = K, Rb) were found to exist in these systems. Therefore, taking into account the similarity of divalent europium and ytterbium, we assume that the stoichiometry of the compound under discussion corresponds to LiYb2Cl5. Moreover, the existence of LiYb2Cl5 compound was reported in the literature [16].

Additional thermal effects of very low intensity (marked as crosses in Fig. 2) were observed for most samples at temperatures around 700–714 K. Their enthalpy was several J‧mol−1 and showed no dependence on the molar fraction. Continued discussions about that can be found in the “Calculations by CALPHAD method” section.

The phase diagram of YbCl2–LiCl system is presented in Fig. 2 (top), and all the experimental data are given in Table 2.

Table 2 Characteristic temperatures and enthalpy values of thermal effects in the YbCl2–LiCl system derived from heating DSC curves
Full size table

Preliminary results of the YbCl2–NaCl phase diagram determination were presented previously [6]. Now this system was reinvestigated, and the complete phase diagram of YbCl2–NaCl binary system have been determined. This system was found to be of eutectic type. Three endothermic effects were observed in almost all heating curves. The effect at the highest temperature was undoubtedly related to liquidus. The second large effect occuring in whole composition range at T = 758–767 K was ascribed to the NaCl–YbCl2 eutectic. Eutectic composition was determined from Tammann plot (Fig. 3 bottom, left) as \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.559 ± 0.035. The eutectic mixture melts with the enthalpy, ΔHFUS, of about 14.81 ± 1.16 kJ mol−1 at the temperature T = 764 ± 2 K. This Tammann plot also informs about formation of solid solutions of YbCl2 in NaCl. Limit of solubility at eutectic temperature corresponds to mole fraction of YbCl2 equal to \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.116 ± 0.026.

Fig. 3
figure 3

Phase diagram of the YbCl2–NaCl binary system (top) determined from DSC measurements and respective Tamman plots (bottom). Circles, squares and crosses—experimental data, crosses in circles (bottom)—experimental data taken for calculations. Solid lines (top)—phase equilibria, solid lines (bottom, A)—Tamman diagram for the enthalpy scale on the left, solid lines (bottom, B)—Tamman diagram for the enthalpy scale on the right; dotted lines (bottom)—enthalpy measurements error. Values in brackets—determined by CALPHAD calculations

Full size image

The third endothermic effect was observed at T = 739–745 K (in whole composition range, but not in all samples). It was marked as “ × ” in Fig. 3. The enthalpy of this effect (calculated per mole of the mixture) is plotted against composition in Fig. 3 (bottom, right). It is worth emphasizing that it is very small (more than 10 times smaller) compared to eutectic enthalpy, with a maximum value of about 1.29 ± 0.06 kJ mol−1. The mole fraction of YbCl2 corresponding to the intersection of straight lines on the Tammann plot is equal to 0.525 ± 0.023. This may suggest the presence of a NaYbCl3 compound, which decomposes in the solid phase. However, it must be pointed out that it is only supposition because enthalpy related to this effect for some samples was totally different and it was not taken into account in the calculation. Continued discussions can be found in the “Calculations by CALPHAD method” section.

The complete phase diagram of the YbCl2–NaCl system is presented in Fig. 3 (top), and all experimental data are given in Table 3.

Table 3 Characteristic temperatures and enthalpy values of thermal effects in the YbCl2–NaCl systems derived from heating DSC curves
Full size table
Table 4 Molar enthalpy of mixing, ΔHMIX, of the YbCl2–NaCl and YbCl2–KCl liquid systems at T = 1085 K
Full size table

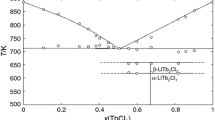
The only phase diagram of the system with YbCl2 published so far is the work of Novikov et al. [11]. Unfortunately, it was published only in a graphic form, so the coordinates of the points have been digitized. The authors found the existence of one stoichiometric compound, KYbCl3, which melts congruently at around T = 916 K. They also determined the mole fraction of two eutectic points as \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.33 (T = 839 K) and \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.73 (T = 831 K). Complete phase diagram constructed on the basis of digitalization and CALPHAD calculation is showed in Fig. 4.

Fig. 4
figure 4

Phase diagram of the YbCl2–KCl binary system: open circles—values digitized from Novikow et al. [11] solid lines and values in brackets—determined by CALPHAD calculations

Full size image

Determination of the mixing enthalpy

The mixing enthalpies of the YbCl2–NaCl and YbCl2–KCl liquid binary systems were determined for the first time in this work. The calorimetric experiments were performed at 1085 K on samples with different compositions in the whole \({x}_{{\mathrm{YbCl}}_{2}}\) range. The results are presented in Table 3 and are plotted against composition in Fig. 5.

Fig. 5
figure 5

Molar enthalpies of mixing ΔHMIX for YbCl2–MCl (M = Li, Na, K) liquid systems at T = 1085 K: open and black circles—experimental results, lines—calculated by CALPHAD method

Full size image

A negative value of mixing enthalpy was observed for all melts. The minimum value was of approximately: − 2.5, and − 7.5 kJ mol−1, for systems with NaCl and KCl, respectively. The mixing enthalpies become more negative with increasing radius of the alkali ion (from sodium to potassium). On the other hand, the composition at the minimum of the enthalpy is nearly the same for both systems. This composition (\({x}_{{\mathrm{YbCl}}_{2}}\) ~ 0.5), similar like in the case of EuCl2–MCl liquid mixtures [15], evidences the difference between the behavior of alkali systems with divalent lanthanide chlorides and those with trivalent lanthanide chlorides which have been examined earlier [6], where a minimum enthalpy was also observed, but it was far more exothermic and occurred at compositions more shifted toward the alkali-rich side (\({x}_{{\mathrm{LnCl}}_{3}}\) ~ 0.3–0.4).

Calculations by CALPHAD method

All calculations were made by CALPHAD method using the BINGSS and BINFKT programs of Lukas [17, 18]. For the calculations we used our experimental data and phase diagram of YbCl2–KCl system determined by Novikow et al. [11]. Thermodynamic data for solid and liquid pure components of the systems were taken from Kubaschewski [19] (LiCl, NaCl, KCl), Rycerz [6] (YbCl2) and Tolmach [9, 10] (YbCl2).

The temperature dependence of Gibbs free energy of pure system components was presented in form of the SGTE description:

$${\{{G}^{0}\left(T\right)-{H}^{\mathrm{SER}}\left(298.15 K\right)\}}_{\mathrm{i}}={a}_{\mathrm{i}}+{b}_{\mathrm{i}}\cdot T+{c}_{\mathrm{i}}\cdot T\cdot \mathrm{ln}T+{d}_{\mathrm{i}}\cdot {T}^{2}+{e}_{\mathrm{i}}\cdot {T}^{-1}$$
(2)

where ai…ei are the coefficients presented in Table 5.

Table 5 The coefficients of Eq. (2) describing {G°(T) − HSER}/J mol−1 of pure systems components
Full size table

The Redlich–Kister model [20, 21] was used to describe the liquid and solid phases. It is a typical mathematical model describing the thermodynamic properties of the phases, which assumes the development of a subregular solution model. The interaction energies change with the composition in a nonlinear manner, and the Gibbs energy of mixing is described as follows:

$${G}^{\mathrm{MIX}}=R\cdot T\cdot \left[{x}_{\mathrm{MCl}}\cdot \mathrm{ln}\left({x}_{\mathrm{MCl}}\right)+{x}_{{\mathrm{YbCl}}_{2}}\cdot \mathrm{ln}\left({x}_{{\mathrm{YbCl}}_{2}}\right)\right] +{x}_{\mathrm{MCl}}\cdot {x}_{{\mathrm{YbCl}}_{2}}\cdot \sum \left({\mathrm{A}}_{\mathrm{i}}-{\mathrm{B}}_{\mathrm{i}}\cdot T\right)\cdot {\left({x}_{\mathrm{MCl}}-{x}_{{\mathrm{YbCl}}_{2}}\right)}^{i-1} $$
(3)

where Ai and Bi are calculated coefficients. The standard deviation of the fit of liquidus line and standard deviation of the fit of mixing enthalpy (Table 6) were used as the criterion of adequacy. The optimized coefficients of Eq. (3) are also presented in Table 6.

Table 6 The coefficients of Eq. (3) describing mixing enthalpies of liquid and solid phases at 1085 K calculated from YbCl2–MCl (M = Li, Na, K) phase diagrams and standard deviation calculated from the unbiased estimator of the population variance of liquidus (ΔT)
Full size table

The molar enthalpies of mixing ΔHMIX for the YbCl2–MCl (M = Li, Na, K) liquid systems at T = 1085 K calculated by CALPHAD method are presented in Fig. 5. The calculated molar enthalpy of mixing of liquid for YbCl2–LiCl is almost ideal with a small minimum around the mole fraction \({x}_{{\mathrm{YbCl}}_{2}}\)= 0.5. As the ionic radius of alkali metal kation increases, the ΔHMIX is more negative, while the minimum is still around the molar fraction \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.5 (in YbCl2–NaCl system is slightly shifted to the left, but this may be due to the accuracy of the measurements).

The calculated phase diagrams (lines in Figs. 2–4) are in a good agreement with the measured one (open circles in Figs. 2–4). Only the solidus and solvus lines calculated by the CALPHAD method for YCl2–LiCl and YCl2–NaCl systems, in the composition range where solid solutions are formed, differ significantly from experimental results (Fig. 2–3). Such a phenomenon was previously discussed by Pelton [22]. He stated that for systems that do not deviate too much from ideality, the calculation can be made with the assumption that the entropy of the solid is ideal. Then a satisfactory compliance of the solidus with the measured values is obtained. In the case of irregular systems, where there is no complete solubility of the solids, the calculations may differ significantly from the experimental data. We suspect that the same situation may occur in the case of solvus.

The less accurate fit was obtained for the YbCl2–KCl system in the ytterbium chloride-rich region (Fig. 4). This is due to the different melting temperature of pure YbCl2 used in the calculations, which was taken from Rycerz [6] (990 K compared to 982 K determined experimentally by Novikow [11]). The difference between liquidus calculated and determined experimentally decreases successively with increasing KCl mole fraction.

To verify whether the LiYb2Cl5, NaYbCl3 and KYbCl3 compounds are formed in the examined systems, we calculated the Gibbs free energy of their formation.

  • For LiYb2Cl5 the GFORM from chlorides in their standard states is estimated as − 1000 J mol−1 K−1 at 746 K. Taking into account literature information on LiYb2Cl5 [16] it is evident that it exists in temperature range between 298 and 746 K.

  • For NaYbCl3 the \({G}^{\mathrm{FORM}}=-525\) J mol−1 K−1 (T = 764 K) which limits the probability of existence of this compound. However, the effect at T = 739–746 K is clearly visible on all DSC curves, therefore we allow its existence in the YbCl2–NaCl system, but probably in a small temperature range.

  • For KYbCl3 the \({G}^{\mathrm{FORM}}=-11 000-10.0\cdot T\)(J mol−1 K−1). Significantly negative values may indicate the existence of this compound, moreover, it is more stable than the LiYb2Cl5 and NaYbCl3. We treat this result as strongly estimated due to inadequacies of liquidus temperatures for mole fractions of YbCl2 greater than 0.5.

Conclusions

  • The phase diagram of YbCl2–LiCl binary system is eutectic type (\({x}_{{\mathrm{YbCl}}_{2}}\) = 0.415 ± 0.022 T = 733 ± 4 K) with one stoichiometric compound, LiYb2Cl5.

  • The phase diagram of YbCl2–NaCl binary system is eutectic type (\({x}_{{\mathrm{YbCl}}_{2}}\hspace{0.17em}\)= 0.559 ± 0.035 T = 764 ± 2 K). It is likely that a stoichiometric compound, NaYbCl3, may exist in this system, but its scope of existence is limited.

  • In the YbCl2–KCl binary system two eutectic points at mole fractions \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.33 (T = 839 K) and \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.73 (T = 831 K) occurs. Also the existence of one stoichiometric compound, KYbCl3, which melts congruently at around T = 916 K.

  • All the melts are characterized by negative enthalpies of mixing with the minimum around the mole fraction \({x}_{{\mathrm{YbCl}}_{2}}\) = 0.5. For the liquid YbCl2–LiCl it is almost ideal, and later it grows slightly with increasing ionic radius of alkali metal kation and reaches values of approximately: − 2.5 and − 7.5 kJ mol−1 for systems with NaCl and KCl, respectively.