Introduction

Temperature is the magnitude of major interest in the study of the thermal behavior of the human body. This magnitude relates the physiology of the human body to environmental conditions [1]. In addition, febrile states [2] and pathologies such as allergies [3], inflammations [4], skin cancer [5] or infections [6] produce detectable changes in temperature, which allow non-invasive monitoring. The human body can regulate its own temperature through energy exchange mechanisms [7].

The energy dissipated by the human body is also a magnitude of interest. Heat flux sensors can be used to directly measure the heat dissipation of the human body in localized areas. However, the most common technology is indirect calorimetry [8], which consists of measuring the volume of O2 absorbed and CO2 released by a subject to assess the metabolic rate at rest [9,10,11] or during an activity [12, 13]. The energy response of the human body is variable. Heat flux can vary between 4 and 77 mWcm−2 depending on the subject and the activity performed [14, 15].

Calorimetry also includes the study of various thermal properties, such as heat capacity, thermal diffusivity or thermal conductivity. This work deals with the measurement of heat capacity, which is usually determined by in vitro procedures. Until the 1980s [16], several studies measured in vivo the thermal inertia of the skin (a quantity that depends on the heat capacity), with the aim of finding its thermal conductivity. Later, differential scanning calorimetry (DSC) techniques were used to measure heat capacity in vitro [17]. DSC measurements have been efficient, so in vivo measurement of heat capacity has not been developed much.

In the mid-1990s, the use of the 3ω method for measuring heat capacities of solids and liquids became popular [18, 19]. In the following decade, the use of this method to measure the thermal conductivity of skin in vivo was discussed [20]. In the last decade, sensors based on 3ω technology have been developed to measure the thermal conductivity of skin [21]. This technology is also able to determine the heat capacity of the skin in vivo with an appropriate signal processing [22]. In 2013, Webb R.C. began to investigate the application of ultra-thin conformal arrays for skin thermal characterization [23]. In 2014, photonic devices were used to perform these measurements [24]. Later, devices consisting of arrays of metallic filamentary structures, constructed with gold and chromium conductors, which function as both sensor and actuator (technology very similar to the 3ω method), were used. Initially, the work of Webb et al. focused on the determination of thermal conductivity and thermal diffusivity, but in 2015 they presented results of heat capacities measured in vivo. From thermal diffusivity, they determined the heat capacity in different areas of the human body [22], with a thermal penetration depth of approximately 0.5 mm. In one of the latest works of this research group, the 3ω method was used [25]. These methods resulted in a patent in 2017 [26].

The calorimetric sensor used in this work has been built in our laboratory [27]. This sensor consists of a thermopile equipped with a programmable thermostat. The principle of operation consists of a linear variation of the temperature of the sensor thermostat, while the device is applied to the skin. By means of an appropriate treatment of the signals given by the sensor, we can determine the skin heat dissipation (W), the heat capacity (JK−1) and the thermal resistance (in KW−1) of a skin area of 4 cm2. The thermal penetration depth of these measurements varies from 3 to 4 mm. This paper begins with a brief description of the sensor and the measurement method. Heat capacity obtained in different areas of the skin in some subjects is presented in specific and absolute form, and our results are compared with those obtained by other authors. This sensor has the advantage of allowing non-invasive in vivo measurements. In addition, the possibility of programming the thermostat at the researcher criteria makes it possible to determine several thermal magnitudes of the skin simultaneously, and to study the thermal response of the skin to different excitations.

Materials and methods

Calorimetric sensor

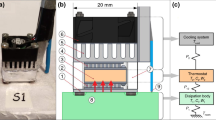
The calorimetric sensor consists of a measuring thermopile (part 2 in Fig. 1), located between an aluminum plate (part 1 in Fig. 1) and a thermostat (part 3 in Fig. 1). The measuring thermopile provides the calorimetric signal by Seebeck effect. The aluminum plate rests on the area where the heat capacity is measured: the skin of the human body, or a calibration surface. The thermostat consists of an aluminum block that contains a heating resistor and an RTD sensor (resistance temperature detector). The cooling system is based on a Peltier element, a heatsink and a fan (parts 4, 5 and 6 in Fig. 1). The perimeter of the sensor is surrounded by a thermal insulation of expanded polystyrene (part 7 in Fig. 1) which reduces external disturbances. For sensor calibration, a calibration base is used. This base consists of a block of insulating material (part 8 in Fig. 1) which has a copper plate with a resistor for Joule calibrations (part 9 in Fig. 1). In addition, the calibration base has a magnetic holding system (part 10 in Fig. 1) for easy handling of the sensor. A thermistor on the outside of the sensor (part 11 in Fig. 1) allows measuring the skin temperature in the vicinity of the sensor. The operation of the calorimetric sensor and its calibration is described in previous works [27].

Fig. 1
figure 1

Calorimetric sensor scheme: (1) measuring plate, 2() measurement thermopile, (3) thermostat, (4) Peltier element, (5) heat sink, (6) fan, (7) thermal insulation, 8) calibration base, (9) calibration surface, (10) magnetic holding, (11) thermistor

Full size image

Heat capacity measurement

To measure the heat capacity, the calorimetric sensor is operated as a scanning calorimeter. While the measurement is performed, the device is applied on the skin as shown in Fig. 2. The measurement procedure is as follows. Initially, the sensor is on the calibration base, and the thermostat is set at 26 °C (Fig. 1). When the sensor reaches the steady state, it is applied on the skin (Fig. 2) and the thermostat temperature is maintained at 26 ºC for 300 s. Next, a linear variation of the thermostat temperature from 26 to 36  ºC in 150 s (rate of 4 Kmin−1) is programmed. Then, the thermostat temperature is maintained at 36  ºC for 300 s. Finally, the sensor is returned to the calibration base, keeping the thermostat temperature constant at 36 ºC.

Fig. 2
figure 2

Application of the sensor on the temple of a 26-year-old male subject: a manual holding, b adaptable attachment holding

Full size image

Figure 3 shows an experimental measurement on the temple of a healthy 26-year-old male subject, seated and at rest. The thermostat temperature programming is shown in Fig. 3a. By applying this temperature variation on the skin, the calorimetric signal (Fig. 3b) captures the response of the human body. Using an error minimization method described in a previous work [27], the heat power (Fig. 3c) and the heat capacity of the skin, C1, are determined. This method reconstructs the calorimetric signal and the thermostat temperature (Fig. 3a,b). For this purpose, a two-body RC model is used. This model is based on two heat capacities, connected to each other and to the outside, by thermal couplings of given thermal conductance. The first element represents the place where the heat dissipation occurs and the second one represents the sensor thermostat. The Joule calibrations performed on the calibration base allow the determination of all the parameters of this model.

Fig. 3
figure 3

Experimental measurement on the skin of the temple of a 26-year-old male subject. a Thermostat temperature, experimental (T2exp) and reconstructed by model (T2cal), b calorimetric signal, experimental (yexp) and reconstructed by model (ycal) with baseline corrected, c heat power calculated (W1)

Full size image

To test the validity of the method for the heat capacity determination, five aluminum blocks of 4-mm thickness and known masses (0.67, 1.11, 1.56, 2.00 and 2.44 g) have been used. These blocks were placed between the calibration base and the sensor, programming a measurement similar to the one shown in Fig. 3, for each aluminum block. Figure 4 shows the relationship between the heat capacity (C1) obtained with the calculation method and the real capacity of the aluminum blocks (C).

Fig. 4
figure 4

Validation experiment: heat capacity measurement of 0.67, 1.11, 1.56, 2.00 y 2.44 g aluminum blocks

Full size image

As we can see, the heat capacity obtained follows the expression C1 = 2.9 + C (JK−1), where C is the real capacity of the aluminum block and 2.9 JK−1 is the heat capacity of the calibration base. In calibrations performed on the calibration base in the ordinary way (without placing any aluminum block) this value, C1 = 2.9 JK−1, is obtained. The error in the adjustment is ± 0.03 JK−1. Aluminum blocks have been used because of their high thermal conductivity. Thus, the identified model only changes in the heat capacity C1.

Results and discussion

Heat capacity

Using the procedure described in the previous section, measurements were made on 6 subjects, whose anthropometric characteristics are shown in Table 1. The measurements were made on 6 different areas of the skin. The heat capacity measured by the calorimetric sensor varies between 4.1 and 6.6 JK−1. Figure 5 shows the results obtained in each zone, as mean ± standard deviation. In all the zones the standard deviation is similar (≈ 5%). The thermal properties measured by the sensor are a combination of the properties of the tissues affected by the measurement. Therefore, each zone has a different heat capacity. The lowest heat capacity values were obtained in the heel. The volar area of the wrist and the abdomen present a higher heat capacity. This is possibly related with a higher perfusion in these zones. The temperature variation of the sensor thermostat was linear from 26 to 36 °C.

Table 1 Anthropometric characteristics of subjects
Full size table
Fig. 5
figure 5

Mean heat capacity of different zones, obtained with the calorimetric sensor in the subjects of Table 1

Full size image

All measurements were performed with the subjects seated, at rest and under the same conditions of humidity and ambient temperature (55% RH, 23 °C). Before and after each measurement, the subjects' heart rate and blood pressure were measured to check their resting state. The skin area studied was dry, untreated, and no creams were applied. The sensor was attached to the skin in two ways: manually or with an adapted attachment (see Fig. 2). The pressure applied on the skin is the minimum necessary to ensure good contact between the sensor and the skin, but without disturbing the blood circulation. The results were similar with the two types of holding, although with the adapted attachment the experimental curves show less oscillations.

Thermal penetration depth

Heat capacity obtained with our calorimetric sensor is an absolute magnitude. In order to compare our results with those of other authors, a dimensional modelling of the heat-affected zone must be carried out. This volume is usually modelled by considering a thermal penetration depth. Each author considers this magnitude in a different way. Limei [25] used the expression of David [28], obtaining a maximum depth of 0.1 mm. Webb [22]. characterized the depth with the expression of Silas [29], obtaining a value of 0.5 mm. The expression used by him is as follows:

$$\Delta p = \beta \sqrt {\alpha {t_{\max }}} = \beta \sqrt {\frac{\lambda }{{\rho {c_{\rm P}}}}{t_{\max }}}$$
(1)

where Δp is the thermal penetration depth, β is a constant (in this case β = 1), α is the thermal diffusivity, tmax is the transient time (of temperature change), ρ is the density, cp is the specific heat capacity and λ is the thermal conductivity.

In our case, we define the thermal penetration depth by considering a prismatic heat-affected zone. Considering the average values of density, thermal conductivity and heat capacity of the skin, and the results of our measurements, we obtain a thermal penetration depth of 3–4 mm. If we use Eq. 1, we obtain a value of approximately 3 mm. In the calculation we associate the time tmax with the time constant of the final part of the calorimetric signal (see Fig. 6). This time constant corresponds to the stabilization of the calorimetric signal at the end of the linear variation of the sensor thermostat temperature. Figure 6 shows the adjustment on this section of the calorimetric curve (red), obtained considering a time constant of 90 s. Note that the method for determining the heat capacity performs a better reconstruction as it considers a two-body model, i.e., two time constants.

Fig. 6
figure 6

Exponential fitting of the final part of the calorimetric signal (red). Value of the time constant = 90 s

Full size image

Thermal penetration depth is not invariant: it depends on the properties of the tissue on which the measurement is made, and also on the characteristics of the thermal excitation produced by the sensor. We have studied how the thermostat temperature change affects the thermal penetration depth. Figure 7 shows several experimental measurements on the left wrist of subject 1; as a function of the thermostat temperature change (2.5, 5.0, 7.0 and 9.0 ºC). Note that there is proportionality between the magnitude of the thermostat temperature change and the heat capacity measured by the sensor. As the magnitude of the temperature change increases, the excitation produced by the calorimetric sensor on the human tissue also increases, leading to an increase in the volume of the heat-affected zone. Correlations shown in the figure intend to illustrate this increasing trend. On the other hand, we have detected no relationship between the measured heat capacity and the heating rates used (1–4 Kmin−1).

Fig. 7
figure 7

Dependency of the heat capacity with thermostat temperature increment, in the left wrist of subject 1

Full size image

Specific heat capacity

Direct measurement of the heat capacity and its treatment as an absolute quantity (Fig. 5) simplifies the interpretation of the results obtained. However, we consider convenient to contrast the results in specific quantities. Table 2 shows the results of Fig. 5, but expressed in specific form. Results obtained by other authors are also shown. In 2014, Li et al. [24] used photonic devices to measure the thermal properties of skin in vivo, as a function of the degree of tissue hydration. The following year, Webb et al. [22] determined heat capacity from thermal diffusivity using ultrathin conformal arrays. In 2017, Limei et al. [25] measured the thermal diffusivity and thermal conductivity of different areas of the skin, which also allows to estimate the heat capacity. To unify the units of the data provided by the different authors, an average tissue density of 1.109 g cm−3 is considered [30]. We can observe the high standard deviation of the measurements, our case being the lowest. On the other hand, the specific heat capacity values obtained by our sensor are higher, due to the greater thermal penetration depth of our measurements.

Table 2 In vivo specific heat capacity measurements (results expressed as min ~ max, mean ± standard deviation %)
Full size table

Figure 8 shows the heat capacity obtained in the works referenced in Table 2. Each point corresponds to a mean value, and the line through it to its standard deviation. Grey rectangles are bounded by the maximum and minimum measured value. As we said before, measurement of the in vivo heat capacity is novel and this property is usually measured in vitro by DSC. For this reason, in Fig. 8, some specific heat capacity values measured in vitro are indicated in orange areas [30].

Fig. 8
figure 8

Specific heat capacity measured in vivo (grey rectangles) and in vitro (orange rectangles). Where D is dorsal and V volar

Full size image

All the results are coherent with the in vitro references shown in the orange areas in Fig. 8. However, there are significant differences between authors. This is consistent, given the difference between the thermal penetration depths of each instrument. Consequently, the tissues involved in the heat-affected zone are different for each work.

The skin is composed of several layers with different thermal properties. The epidermis thickness can vary between 0.1 and 1.0 mm, and it is also composed of different layers. On the other hand, the dermis can be several millimeters thick [31]. The first layer of the epidermis is the stratum corneum, whose heat capacity can be estimated at 2.2 JK−1 g−1 [32, 33]. The structure of the dermis consists of collagen and elastin fibers, with heat capacities of 2.0 [34] and 1.3 [35] JK−1 g−1, respectively. These heat capacities are low compared to water (4.18 JK−1 g−1). As we go deeper into the skin, the blood perfusion (and water content) of the tissues increase, leading to a higher heat capacity. Thus, the heat capacity measured is a function of thermal penetration depth, as shown in Fig. 8.

Webb investigated the correlation between heat capacity and the thickness of the epidermis and stratum corneum, and its water content [22]. He found negative correlations with thickness (the thicker the epidermis or stratum corneum, the lower the heat capacity) and positive correlations with water content (more water implies a higher heat capacity), which is consistent with the hypothesis set out in the previous paragraph. For example, the lowest heat capacity detected by Webb is in the heel area, which has a very thick stratum corneum and a very low degree of humidity compared to the rest of the tissues analyzed in his experiment. This observation also coincides with the lower heat capacity detected with our instrument in the heel. Li et al. [24] also detected an increase in heat capacity as a consequence of water content. The dependence between heat capacity and water content can also be studied by producing alterations in the skin. As an example, we can cite the experience of Limei: after artificially producing urticaria, heat capacity increased by 17%. With our sensor, we monitored a second-degree burn on the volar area of the right wrist of subject 1 (Table 1). This 2 × 1 cm2 lesion was caused by an unfortunate accident while doing the ironing. Figure 9 shows the variation of the heat capacity of the injured area compared to a nearby healthy area. We emphasize on the ability of the sensor to quantitatively monitor the recovery process of an injured tissue. Figure 9 shows a 25% heat capacity decrease, mainly due to dehydration of the injured area.

Fig. 9
figure 9

Heat capacity variation of a 2 × 1 cm2 second degree burn of in the right wrist volar area. Comparison of the injured skin (red) with the healthy skin (blue)

Full size image

Conclusions

We have developed a sensor that implements the principles of scanning calorimetry to measure in vivo the heat power and the heat capacity of a 2 × 2 (4) cm2 skin region. Its thermal penetration depth is up to 4 mm in the current configuration. The calorimetric sensor is a useful tool for the study of the human body physiology and can complement other technologies. Our sensor provides a numerical value of the physiological state of the skin area under study. The possible deviation from the normal values provides interesting information. In this paper we present measurements made with the calorimetric sensor. The order of magnitude of the results obtained have been evaluated in several subjects and different areas of the human body, and a comparison with the results provided by other authors is made.

Heat capacity at rest varies from 4.1 to 6.6 JK−1. It presents a different value in each area studied, which depends mainly on the composition of the tissue analyzed. The lowest heat capacities were found in the heel and the highest in the abdomen. There are only a few studies in which this magnitude is measured in vivo, and most of them are very recent. The differences between authors are consistent with the difference of thermal penetration depth of each instrument. As the thermal penetration depth is greater, the heat capacity is also greater, since the tissue distribution changes and the water content increases. This is the main variable that affects the in vivo heat capacity value.

This technology has three advantages: (1) the device measures heat power and heat capacity simultaneously, (2) heat capacity is measured as an absolute quantity, which simplifies the interpretation of the results obtained, and (3) it is possible to regulate its thermal penetration depth by programming the thermostat temperature. Although this procedure is working successfully, the duration of measurements with these sensors must be taken into account; they usually require more time than other techniques and the processing of the signals is more complex.