Introduction

Behaviour of steel at high temperatures

In case of a fire load, the physical properties of steel change as a result of the temperature increase, and it undergoes a phase transition in higher-temperature ranges. The rate of change is different for hot-rolled and cold-formed steels.

The thermal conductivity, specific heat, strength and stiffness of steel change continuously with the increasing temperature (Figs. 1–3).

Fig. 1
figure 1

Change of thermal conductivity of steel as a function of temperature [1]

Full size image
Fig. 2
figure 2

Change of specific heat of steel as a function of temperature [1]

Full size image
Fig. 3
figure 3

Variation of young-modulus and proof stress (yield) of steel as a function of temperature

Full size image

From a thermodynamical point of view, changes in thermal conductivity and specific heat are also very important. Concerning fire protection, the changes of these two characteristics are the most important, as they affect the rate of heating of steel and the amount of energy required for heating. Ultimately, they affect the extent to which strength and stiffness parameters change.

It can also be clearly seen in Fig. 1 that the thermal conductivity decreases more and more as the temperature increases and less and less as the heat passes through the unit cross-sectional area per unit time. This phenomenon has a positive effect on the thermal properties of steel from a fire protection point of view.

However, the other side of the process must also be observed. Figure 2 describes the change in specific heat, i.e. the amount of energy required to heat a unit amount of material by 1 °K. This hardly changes up to 735 °C, but there is an almost infinite amount of energy requirement to increase the temperature. This is due to the fact that at 723 °C (PSK line) the phase transformation of eutectoid (containing ferrite and cementite) starts and austenite appears in the alloy [2]. The energy is used for the chemical transformation and not for raising the temperature, and then, when the transformation process is complete, the specific heat decreases again around 800 °C.

These matches with Fig. 1, thus at the temperature at which the thermal conductivity factor already changes favourably from a fire protection point of view, the chemical transformation of the steel takes place. The advantageous change in the thermal conductivity cannot be used from an engineering point of view, as the strength of steel does not even reach 20% of the value measured at normal temperature [1].

For civil engineers, the most important of the changing physical factors are the development of the strength, stiffness and elastic modulus of steel at high temperatures. The yield strength of steels starts to decrease at 400 °C for structural steels (Ac) and at 300 °C for cold-formed steels (Ab), and this change can be considered linear up to 700–800 °C (Fig. 3). However, the decrease in the elastic modulus begins at 100 °C, at which point the steel begins to soften. The critical temperature is 500 °C for hot-rolled steels and 400 °C for cold-formed steels. The critical temperature is the temperature at which steel transitions from the linearly elastic range to the plastic range, i.e. it undergoes large deformations under relatively small load.

Behaviour of steel structures at high temperatures

Several examples have confirmed the fact that special attention is needed to the fire protection of steel structures. Ensuring proper fire resistance of structures, including steel structures, is a priority worldwide. With the introduction of Eurocodes in Europe, the fire resistance design of buildings became mandatory, so since 2011, in addition to the structural design of structures it also has to be carried out in Hungary.

To minimize the damage to the structure and to claim as few casualties as possible in the event of a fire, it is extremely important to know the fire behaviour of buildings.

On 15 October 2015, around 5 a.m., a fire broke out in the athletics hall of the University of Physical Education (Hungary). Firefighting lasted a long time as firefighters were unable to enter the building. The fire curve is similar to the normative (standard) fire curve.

The steel-roof structure of the athletics hall softened and broke relatively quickly (Fig. 4). Steel truss-girders in this case deform to a “bar-chain” shape, which may still be able to reach a stable state while maintaining enough load-bearing capacity for its self-mass, if the support of the girder is able to withstand the associated stresses and deformations. In the case of the athletics hall, the detachment of the steel support end plates from the fixing screws was observed in several cases (Fig. 5).

Fig. 4
figure 4

The steel-roof structure after fire (15.10. 2015)

Full size image
Fig. 5
figure 5

Detachment of endplates of steel stingers (15.10. 2015)

Full size image

In case of a fire, one of the characteristics of steel structures is that there is no clear sign of the failure of the structure, which can endanger rescue and extinguish. Unlike concrete, steel structures regain some of their strength after cooling, so if they do not suffer excessive deformation, collapse of the structure after cooling is not expected.

In several cases, the failure of welded joints was observed. It can be seen that at some nodes the welding seam was destroyed (Fig. 6), while in other cases (Fig. 7) in addition to the welding seam, the steel also ruptured.

Fig. 6
figure 6

Failure of welds (15.10. 2015)

Full size image
Fig. 7
figure 7

Failure of weld and steel material (15.10. 2015)

Full size image

Additional fire protection for steel structures

Fire protection of steel structures is playing an increasingly important role nowadays. The fire protection of steel structures can be solved with intumescent (thermally foaming) paint, mortar, fire protection coating and concrete coating.

However, it is an interesting question how effective the combined fire protection solutions are the combined use of fire protection sheets and thermal insulation. Several literature data are available on the mechanism of action of fire protection sheets and their effectiveness [3, 4]. However, little data are available on the effectiveness of insulation materials and fire protection coatings together [5, 6]. Within the present research, the thermal protection of a fire-resistant gypsum board combined with rock wool of different densities was examined.

Behaviour of gypsum boards at high temperatures

The manufacturers do not publish their own measurement results regarding fire performance of their gypsum boards, so the small number of experimental descriptions in the literature and their results was used to determine the thermal parameters of the gypsum board used in the simulation.

Gypsum decomposes in three stages under the influence of increasing temperature [4]. In the first stage (110–180 °C), 3/2 mol of gypsum crystalline water leaves and hemihydrate gypsum is formed. In the second stage (180–300 °C), the remaining 1/2 mol of crystalline water also leaves. In anhydrous calcium sulphate, anhydrite is formed. Anhydrite is unable to retain its strength in the absence of crystalline water. The crystal lattice and its material itself disintegrate. In the third stage (at 300–600 °C), the calcium sulphate crystal structure of the gypsum is transformed, and dead-burnt gypsum is formed. The three-step endothermic decomposition processes detailed above are those that cool their environment, thereby providing chemical protection for gypsum-containing sheets. With the exhaustion of this chemical protection, the thermal inertia of the materials comes to the fore. If fibre reinforcement is used, the gypsum-bonded fire protection sheets remain in one piece even after the gypsum has been transformed. Anhydrite cannot disintegrate, so the panel stands in the way of heat. Of the gypsum-bonded panels, refractory gypsum board and gypsum fibre board are mainly used for fire protection. Fireproof gypsum boards are similar to normal gypsum boards. Between two layers of paper is a layer of gypsum that is fiberglass-reinforced. The gypsum fibre board has no double-sided paper cover and contains 15–20% cellulose fibre instead of glass fibre [7].

The determination of the thermal technical parameters of gypsum board is dealt with only by a negligible number of papers. This makes it difficult to fully define the material characteristics used in the model.

Keerthan and Mahendra [8] investigated the fire resistance of board-mounted walls in their studies. The wall structure consisted of special sandwich panels mounted on aluminium profiles, where the “sandwich” structure was constructed of insulating material placed between two plasterboard sheets. For the numerical modelling of their studies, the changes in the density, specific heat and thermal conductivity of drywall under fire were measured. Thomas [9] has developed different methods to consider the thermal parameters of gypsum boards at high temperatures. Sultan [10] and then Mehaffey et al. [11] also investigated the fire resistance of a plasterboard-mounted wall structure, measuring the change in specific gravity, specific heat and thermal conductivity of drywall under fire. The results of the above experiments are summarized in Figs. 8–10. Keerthan and Mahendra [8] took 25 Wm−2·°K−1 for the value of the heat transfer coefficient on the side of fire and 10 W/m−2·°K−1 on the other side. The emission constant was supposed to have the value on both sides 0.9.

Fig. 8
figure 8

Thermal conductivity [Wm−1°K−1] as a function of temperature [°C]

Full size image
Fig. 9
figure 9

Specific heat values of drywall plates as a function of temperature

Full size image
Fig. 10
figure 10

Relative density of drywall plates as a function of temperature [°C]

Full size image

Behaviour of rockwool at high temperatures

The specific heat of rockwool can be regarded as a constant 900 J(kg·°K)−1 for the purpose of this research. The density of rockwool does not change with the temperature either in this range [6]. The variation of thermal conductivity with temperature is shown in Fig. 11.

Fig. 11
figure 11

Thermal conductivity of rockwool as a function of temperature [5]

Full size image

Applied materials and methods

Materials

Six different rockwool products (Table 1) were used to compare the behaviour of rockwool products of different bulk densities at high temperatures. Dependence of heat conductivity on bulk density is shown in Fig. 12.

Table 1 Summary of experimental measurements from rock wool products
Full size table
Fig. 12
figure 12

Heat conductivity of rockwool as a function of bulk density

Full size image

Measurement methods

Characteristics of the fire

During the test, the temperatures of the steel I80 profile (St500B) and the furnace were measured with thermocouples at time T = 0 and every 5 min thereafter until the temperature of the steel profile at the measured location had reached at least 650 °C at the time of reading. At 650 °C, the yield stress of the steel material reaches only 35% of its yield stress at normal temperature. This limit for the end of the test was taken based on an arbitrary decision.

The temperature of the furnace was set so that its maximum temperature was 1000 °C; thus, it did not fully follow the standard fire curve [12] either, but it approximated it well in the last stage of the tests. At the end of the experiments, the temperature of the steels was 658–841 °C, while the temperature of the furnace was between 951 and 1002 °C at the end of each experiment. The shortest test lasted 65 min, at which time the gas temperature in the heating chamber of the test furnace was 651 °C, at which time the gas temperature of the standard indoor fire curve is 657 °C.

$$\theta_{{\text{g}}} = 20 + 345 \cdot \log \left( {8 \cdot t + 1} \right) = 20 + 345 \cdot \log \left( {8 \cdot 65 + 1} \right) = 657 ^\circ {\text{C}}$$

In the above formula, θg is the gas temperature in °C for the given fire compartment, while t is the time in minutes since the fire started. At the end of the 110-min test, the furnace temperature is 1002 °C due to the set temperature limit of 1000 °C (then for 20 min continuously), while the temperature of the standard indoor fire after 110 min is:

$$\theta_{{\text{g}}} = 20 + 345 \cdot \log \left( {8 \cdot t + 1} \right) = 20 + 345 \cdot \log \left( {8 \cdot 110 + 1} \right) = 1036 ^\circ {\text{C,}}$$

that is, at the end of the test, there was no significant difference between the gas temperature of the furnace and the standard ISO 834-1 [12] fire curve. The majority of the tests (75%) ended in the range of 70–95 min; in this interval, the differences between the test and standard gas temperatures were even more favourable, only 1–13 °C. Based on the above, the furnace temperature differences between the tests were disregarded.

The examinations started with the closing of the furnace door at T = 0 min after the boxes were placed. The heating of the furnace should in principle have taken place by the standard fire curve according to ISO 834-1, but the temperature–time curve deviated from this, which is illustrated in Fig. 13. During the 12 experiments, the heating of the furnace did not differ significantly, with the exception of the data set marked “5” in the figure, which is explained by the fact that during the test the furnace temporarily overloaded the electrical network at ~ 15 and ~ 50 min. At these points, the heating slowed down slightly, resulting in a blue line, more different from the trend. Apart from this, it can be stated that although the furnace temperature–time diagram does not fit the standard (ISO 384-1) indoor fire curve, it behaves in a constant way throughout the series of tests, i.e. subjecting the samples to almost the same heat load at the same time (Fig. 13).

Fig. 13
figure 13

Heating curve of the furnace

Full size image

Measuring the mass loss

Mass loss was measured on cube-shaped samples of measures: 50*50*50 mm. The samples were measured after T = 20 °C, 150 °C, 300 °C, 500 °C and 800 °C heat load, and the losses were calculated in % by mass.

Investigation of downscaled models of real buildings

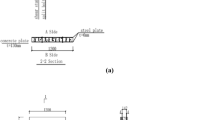
The models had identical structure to real building structures consisting of materials of light-structure covers: fireproof drywall plate having 12.5 mm thickness, 27 × 60 mm C-profile and self-pruning screws type 212 with measure of 3.5 × 25 mm [13]. We put in the covered structure one piece hot-rolled I80 steel profile having the length of 300 mm [14]. In cases of insulation materials with very low bulk density, we applied four pieces of hardboard screws for spacing to prop up the heavy profile and prevent the compression of the isolating material due to the mass (5.94 kgm−3) of the I80 steel. These spacing screws were holding the steel profile in the furnace, touching it only with the small peaks, having just negligible influence on the heat conduction and load of the steel item.

Experimental

Mass loss of rockwool as a function of temperature

Results are shown in Fig. 14. Based on these, the following can be said:

  • There is no mass loss up to 300 °C except in few cases: (max. 5%).

  • The mass loss is about 5% up to 500 °C except for the sample with a bulk density of 32 kgm−3.

  • Up to 800 °C, there is about 10% mass loss except for the sample with a bulk density of 32 kgm−3.

Fig. 14
figure 14

Mass loss of samples with different bulk densities

Full size image

The reason of this dissimilar behaviour of the sample with bulk density of 32 kgm−3 is probably due to the different binder materials applied for this insulation.

Examination of the construction element isolated with rockwool isolations material

The general results of the experiments for heat loading of samples filled with rockwool insulation materials are as follows:

  • Even the insulation material with the lowest bulk density of 32 kgm−3 had enough stiffness withstanding the compression rectangular to its plane. The melting point of rockwool is above 1000 °C (for a few types even above 1100 °C); for this reason, melting of the isolation material was not observed in the set temperature range (up to 1000 °C).

  • The spatial structure of insulation materials changed heavily; it became denser and more homogeneous, while the volume decreased inhomogeneously along the sample (Fig. 15)

  • The temperature–time diagrams for the steel samples have similar trends: starting horizontally due to the heat insulation at the beginning. The length of the horizontal part depends on the bulk density of the insulation material. Following this horizontal section, an increase in the temperature can be observed. The steepness of this temperature increase depends on the bulk density of the applied insulation as well. This phase of warming up stopped at 95–97 °C, and in some cases it slightly decreased. This effect showed a dependence on the bulk density of the insulation material again. After reaching a local minimum, the temperature increased up to the end of that 5-min period in which the sample temperature reached 650 °C and at this point the experiments were stopped.

  • During the heat loading, arising waste gases (smoke) and steam condensation was observed at furnace temperature of about 300 °C close to the leaks and window of the furnace. This effect stopped with the increasing temperature quite before reaching the end value of 650 °C.

  • Some of the rockwool became more compact and tighter in structure; other samples lost their cohesion and fell apart.

  • The higher was the bulk density of rockwool, the longer was the starting horizontal plateau of the temperature of the steel sample, i.e. the slower was the warming up of the insulated steel sample (see Figs. 16 and 17).

  • The graphs are parallel to each other after the constant-temperature plateau (Fig. 18).

Fig. 15
figure 15

Characteristic degradation of rockwool sample

Full size image
Fig. 16
figure 16

Change of steel-sample temperature in time

Full size image
Fig. 17
figure 17

Lengths of the plateaus

Full size image
Fig. 18
figure 18

Section following the plateau

Full size image

Modelling

The aim of the numerical investigation of models was to achieve a good approximation in describing the warming-up process of the examined structural elements.

For the numerical analysis, ANSYS 15 (nonlinear finite-element software) was used. The geometry of the numerical model was constructed with the included planning module (Design Modeller) and was identical to the laboratory test constructions.

The thermal parameters of the applied materials can be found in chapter 1.

In Fig. 19 the spatial temperature distribution, i.e. the isotherms, can be seen. A decreasing steepness of temperature growth can be observed, with the increasing bulk density. Figure 20 shows the varying temperatures of steel profile as a function of time, which looks very similar to the curve of real values measured at the laboratory.

Fig. 19
figure 19

Isotherms in the 100 min of the heat load

Full size image
Fig. 20
figure 20

Varying temperatures of the steel profile isolated with rockwool as a function of temperature (measured and VEM model)

Full size image

In Fig. 21 a direct comparison of data from numerical analysis and from experiment can be seen. There are two positions showing relevant differences: first at about 100 °C due to the phase transition of water and second at about temperature of 300 °C, which was caused probably by the phase transition of the applied binder material. These two phase transitions are of course not yet included in the FE model.

Fig. 21
figure 21

Comparison of temperature changes of the steel profile insulated with rockwool as a function of temperature from numerical analysis and from our experiment (measured and VEM model)

Full size image

With the data currently available from the literature, the early trends of the temperature–time curves from the models differ greatly from the measurements. Based on the results, further investigation of the thermal parameters (specific heat, thermal conductivity and bulk density) and the chemical changes is recommended in the lower temperature ranges (up to 300 °C) to resolve these issues. The differences most probably occurred due to the water content and the different binder materials, which the model did not have data for.

For other porous materials (concrete, timber), the standards define a peak in specific heat based on the water content. A similar solution could be used for the thermal insulation materials as well.

Conclusions

Fire protection of steel structures is playing an increasingly important role nowadays. The fire protection of steel structures can be achieved with intumescent (thermally foaming) paint, mortar, fire protection coating and concreting around it. In the present article, we examined the case of a combined fire protection solution consisting of fire-resistant drywall plate and rockwool heat isolation. Several literature data are available on the mechanism of action of fire protection sheets and their effectiveness [3, 4]. However, little data are available on the effectiveness of insulation materials and fire protection coatings together. For this reason, we examined the thermal protection provided by a refractory gypsum board combined with rock wool of different densities.

Six different types of rockwool isolation materials were examined. Thermal behaviours of these isolating materials of different bulk densities (32–152 kgm−3) were compared at high temperature. The models had identical structure to real building structures consisting of materials of light-structure covers: fireproof drywall plate having 12.5 mm thickness, 27 × 60 mm C-profile and self-pruning screws type 212 with measure of 3.5 × 25 mm. We put in the covered structure one piece hot-rolled I80 steel profile having the length of 300 mm. During the test, the temperatures of the steel I80 profile (St500B) and the furnace were measured with thermocouples at time T = 0 and every 5 min thereafter until the temperature of the steel profile at the measured location had reached at least 650 °C at the time of reading. At 650 °C, the yield stress of the steel material reaches only 35% of its yield stress at normal temperature. This limit for the end of the test was taken based on an arbitrary decision.

For isolating materials can be established a positive correlation between the bulk density and delay of warming up, i.e. the larger the bulk density (32–152 kgm−3) of the isolating material was, the longer time (60–80 min) elapsed until the starting of warming up of the steel sample.

A thermal finite element model was built using currently available data from the literature. When comparing the model data and the measurements, there are two positions showing relevant differences: first at about 100 °C due to the phase transition of water and second at about temperature of 300 °C which was caused probably by the phase transition of the applied binder material. These two phase transitions are of course not yet included in the FE model.

Based on the results, further investigation of the thermal parameters (specific heat, thermal conductivity and density) and the chemical changes is recommended in the lower temperature ranges (up to 300 °C) to resolve these issues. The differences most probably occurred due to the water content and the different binder materials, which the model did not have data for.