Introduction

The collection of vapor–liquid equilibrium (VLE) data is essential not only for the distillation design, but also to provide the inputs to many first-principle or semi-empirical models capable to calculate other properties [1, 2].

The long-established vaporization and condensation apparatuses, coupled to analytical techniques such as gas- and mass chromatography, have been continuously evolving [3,4,5] and providing valuable information [6, 7]. Other methods, such as thermogravimetric analysis (TGA) [8, 9] and differential scanning calorimetry (DSC), have been lately used as complementary tools, because they are much faster and employ very limited quantity of substance [10]. In particular, TGA has long been used to measure saturation pressures and latent heats for a broad range of mixtures (even ionic liquids and copolymers) [4, 11,12,13,14,15,16,17,18,19,20], also as a built-in feature in up-do-date equipment [21]. Machines dedicated to calorimetric assays only, on the other hand, feature a high-quality response and can provide critical temperatures and latent heats [5, 10, 22,23,24,25] with suitable analysis protocols [26], besides valuable insights on a mixture’s composition [27], and even highlight more complex phase-transition occurrences [28].

The scope of this work is to discuss the outcomes of TGA experiments performed placing the liquid sample in open crucibles that can reproduce at once the outcome of a bench-scale batch distillation with very little or no reflux at all. The approach of Coutinho [29] and Muller [30] is here applied to a vapor–liquid transition taking place as the evaporating liquid changes its composition and extended by the interplay of mass and heat signal considered together. A method to correct the errors affecting the heat signals of a combined TGA–DSC apparatus (with respect to that of a dedicated DSC-only one) is also proposed. For these explorative tests, the choice fell on acetonitrile–water and methanol–water binary mixtures, because:

  • They represent the cases of a non-azeotropic and azeotropic mixture;

  • They do not present liquid miscibility gaps;

  • Their latent heats (as pure) and boiling points (at atmospheric pressure) are not too similar, which helps to overcome sensitivity problems;

  • Their latent heats show little variation from ambient temperature to the boiling point, which makes easier the data analysis presented below;

  • The chosen low-boiling species have a high volatility respect to water (except near the acetonitrile–water azeotrope), which helps to distinguish between a short-term system behavior and a long-term experiment completion.

The vapor–liquid equilibrium compositions for: (a) acetonitrile–water (content from 15% by mass up to the azeotrope) and (b) methanol–water (20– 90% by mass), are put in relation to the TGA analysis, without need of any gas-phase separate analysis [9]. A parallel series of DSC tests is used to have a more complete picture of the thermal data.

Materials and methods

Acetonitrile HPLC-grade (> 99.9%) and methanol reagent-grade (> 99%) were obtained by Sigma-Aldrich and used without further purification. Demineralized milliQ water was obtained by ion exchange (conductivity < 2 μS). The liquids were mixed into vials by weighting using a Gibertini electronic scale precision balance and then sampled with a pipette. Several mixtures were also picked up to have a composition check via NMR analysis, using D2O as solvent and known quantities of purified ethanol (Sigma Aldrich, > 99.9%) as internal reference. The instrument was a Bruker-Avance.

All the TGA–DSC scans were performed by a Mettler-Toledo TGA/DSC/3 + 1100 (horizontal loading) unit with open crucibles (standard type, volume: 150 μL), with a purging flow of Nitrogen (5 mL min−1) and a temperature increase from 30 to 150 °C at the low heating speed of 5 °C min−1. The slow ramp maintains the analysis plus cooldown time within one-hour time lapse.

The pure substances, together with most samples, underwent also a DSC thermal-scan in a Mettler-Toledo DSC3/500 apparatus. In this case, the sample holders (standard type, volume: 40 μL) were covered with lids, manually pierced with the vendor-provided nails (yielding gaps with an approximate diameter of 0.5 mm). This choice was made in order to seek a compromise between the peculiar features of the evaporation from the open spot (back-pressures effects were not important) and the higher precision achievable when the boiling sample is kept within a semi-closed environment. The temperature ramp was the same of the TGA unit.

The bench-scale distillation was made loading acetonitrile and water (76% acetonitrile by mass) in a 250-mL round flask equipped with a horizontal condenser and a thermometer. The flask was heated on a thermo-mantle, and the distillate cuts were collected into plastic vials. The resulting samples were analyzed by the same TGA apparatus.

The TGA and DSC records (digitally collected and stored every 1 s) list the time, the sample and reference temperature, and the heat flow between the sample and reference pan, calculated by the equipment’s software with respect to the temperature values. The mass loss speed is also calculated automatically and printed in the reports. The data analysis consists in:

  1. (a)

    The subtraction of the mass-loss baseline and normalization from percentage to fractional basis;

  2. (b)

    The heat flow integration with respect to time.

    At this point, the data are furtherly treated as follows (all calculations performed with MicroCal Origin 8.5):

    1. 1.

      The differential signal \({\Delta w}/{\Delta t}\) (where w denotes the normalized mass) bears the information on the liquid saturation pressure, according to the evaporation kinetic analysis by Langmuir [31] compared to the Clausius–Clapeyron equation:

      $$\text{ln}\left( {\frac{{\Delta m}}{{\Delta t}}} \right) - 0.5\text{ln}\left( {\frac{1}{T}} \right) = A - 0.5\text{ln}\left( {2\pi R/M} \right) + \text{ln}\left( {\alpha S} \right) - \frac{{{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {273R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${273R}$}}}}{{1 + {\raise0.7ex\hbox{$\theta $} \!\mathord{\left/ {\vphantom {\theta {273}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${273}$}}}}$$
      (1)

      where A is a constant, M is the molar mass, S and \(\alpha\) are experimental parameters (see the Used Symbols Table below), \(\lambda\) is the latent heat, and \(\theta\) is the temperature which is in the Celsius scale employed by the instrument.

      Various authors [32, 33] pointed out that in many cases \(\alpha\) cannot be considered an experimental constant, due to the importance of diffusive phenomena; a convenient correction of Eq. (1) is then [32]:

      $$\text{ln}\left(\frac{\Delta m}{\Delta t}\right)-\text{ln}\left(\frac{1}{T}\right)=A-\text{ln}\left(zR/M\right)+\text{ln}\left(S\times D\right)- \frac{{{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {273R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${273R}$}}}}{{1 + {\raise0.7ex\hbox{$\theta $} \!\mathord{\left/ {\vphantom {\theta {273}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${273}$}}}}$$
      (2)

      where z and D are geometric dimensions of the evaporation crucible. In both cases, computing the left-hand quantity on the basis of the experimental results and fitting it to the second-hand rational function of temperature, the latent heat can be retrieved.

    2. 2.

      The latent heat can also be read directly from the data, considering that:

      $$\frac{\Delta h}{\Delta t}= \lambda \frac{\Delta w}{\Delta t}+ {w(t)c}_\text{p}\frac{\Delta \theta }{\Delta t}$$
      (3)

      where \(\frac{\Delta h}{\Delta t}\) denotes the instantaneous heat signal already normalized for the initial sample mass, as given directly by the instrument. Before the phase transition, the temperature derivative is essentially constant and fixed by the working protocol, so the term can be ruled out repeating the experiment with different ramps and extrapolating the behavior for \(\frac{\Delta \theta }{\Delta t}\to 0\) [16]. Anyway, for this work it was chosen the straightforward approach to perform a bi-linear regression over the \(\frac{\Delta w}{\Delta t}\) and \(w(t)\frac{\Delta \theta }{\Delta t}\) quantities for \(0.8<w\left(t\right)<1.0\) (i.e. when the sensible heat term is more important). To reduce the noise coming from the differential mass signal, Eq. (3) was also considered in its integral form:

      $$\int \frac{\Delta h}{\Delta t}\text{d}t= \Delta h(t)=\lambda w\left(t\right)+ {c}_{p}\int w\left(t\right)\theta (t)dt$$
      (4)

      If the specific heat contribution can be neglected, a deviation of the plot \(\Delta h/w\) from linearity indicates a contextual shift of the latent heat value, which means a change in the mixture composition (because acetonitrile, methanol and water display roughly constant latent heats from ambient temperature to their boiling points [34, 35]).

    3. 3.

      According to the Rayleigh formulas, the mass and thermal balances related to the low-boiling component of a binary mixture read:

      $$\begin{array}{c}\frac{\text{d}w}{w}=\frac{\text{d}x}{{y}^{*}-x}\end{array}$$
      (5)
      $$w \text{d}{h}_\text{l}+ \text{d}h=\text{d}w \lambda$$
      (6)

    where x and y* are the liquid mass fraction and pseudo-equilibrium vapor mass fraction of the volatile, and \(\text{d}{h}_\text{l}\) is the change in the specific enthalpy when the liquid composition changes from x to x-dx. The integration of Eq. (5) yields:

    $$\int\limits_{1}^{{w_\text{f} }} {\left( {\frac{{\text{d}w}}{w}} \right)} = \int\limits_{{x_\text{i} }}^{0} {\left( {\frac{{\text{d}x}}{{y^{*} - x}}} \right)} \Rightarrow ln\frac{1}{{w_\text{f} }} = \int\limits_{0}^{{x_\text{i} }} {\left( {\frac{{\text{d}x}}{{y^{*} - x}}} \right)} = F(x_\text{i} )$$
    (7)

    where \({w}_\text{f}\) is the liquid normalized mass remaining on the crucible when all the volatile component has been stripped and only water is evaporating, i.e. when the acetonitrile (or methanol) sample content passes form \({x}_\text{i}\) to 0. The value of \({w}_\text{f}\) can be identified, in the results logfile, as the mass fraction after which the \(\Delta h/w\) plot becomes linear with \(\lambda ={\lambda }_{\text{H}_{2}\text{O}}\), which corresponds to \(w\times \text{d}{h}_\text{l}=0\) in Eq. (6). The unknown curve y*(x) can be furtherly estimated observing that, if a mixture with xi initial mass fraction of the more volatile component yields a wf value, then:

    $${y}^{*}({x}_\text{i})={x}_\text{i}+{\left[\frac{1}{{y}^{*}({x}_\text{i})-{x}_\text{i}}\right]}^{-1}= {x}_\text{i}+ {\left[\frac{\text{d}F({x}_\text{i})}{\text{d}{x}_\text{i}}\right]}^{-1}={x}_\text{i}+{\left[\frac{\text{d}}{\text{d}{x}_\text{i}}ln\frac{1}{{w}_\text{f}({x}_\text{i})}\right]}^{-1}$$
    (8)

    The derivative and inverse operator can introduce an appreciable error, especially treating the experimental, discrete function \(ln\frac{1}{{w}_\text{f}({x}_\text{i})}\), so it is more reliable to perform previously a suitable interpolation \(ln\frac{1}{{w}_\text{f}({x}_\text{i})} \cong f(x)\), then getting the continuous function \({y}^{*}\left(x\right)=x+{\left[\frac{\text{d}}{\text{d}x}f(x)\right]}^{-1}\) (see also the Supporting File for details).

Results and discussion

Trends and latent heats

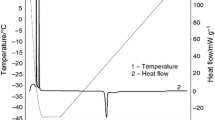
The adopted experimental conditions lead to discrimination of two evaporation and boiling regimes, for the binary mixtures under study, as shown in Figs. 1 and  2. The open environment let the overall composition of the sample vary, as the first vapors are richer in the low-boiling species, but before reaching the saturation temperature this loss is not too important, so the sample starts boiling still as a binary mixture. On the other hand, the temperature rise is slow enough to eliminate all the acetonitrile before the saturation condition for pure water is met; then a second-phase transition is eventually detected. This double regime can be suppressed if the heating ramps becomes faster.

Fig. 1
figure 1

Evaporation trends (points, left axis scale) and mass loss speed (lines, right axis) for several water-acetonitrile test samples. xi indicates the initial acetonitrile mass fraction

Full size image
Fig. 2
figure 2

Evaporation trends (points, left axis scale) and mass loss speed (lines, right axis) for several water–methanol samples (xi indicates the initial methanol mass fraction)

Full size image

This behavior is not clearly recognized when the acetonitrile and methanol initial contents are below 20–30%, though mass fractions down to the 15–20% can be retraced via the data analysis. Also over-azeotropic acetonitrile–water mixtures and methanol samples richer than 80% do not yield a clearly split mass-loss trend, because the pure acetonitrile and the azeotrope saturation temperatures are too close to be resolved in these conditions.

Analyzing the data with a \(\Delta h/\Delta t\) vs \(\Delta w/\Delta t\) graph (Figs. 3–5), the distinct evaporation regimes of the mixtures are all the more recognizable, and the first boiling transition appears as wide gap between two remarkably linear trends. Pure substances show the linear trend only. Mixtures with an acetonitrile content higher than 77–80% feature one latent heat trend like pure substances, because nearly all the sample evaporates as the azeotrope. The specific heat contribution is neglected, in the data analysis presented hereafter, because it is much less important than the latent heat: this can be seen, for example, in Table 1, showing the results of the data interpolation according to Eq. (3) for pure substances.

Fig. 3
figure 3

Normalized heat signal plotted versus the mass loss speed for pure ↔ samples

Full size image
Fig. 4
figure 4

Normalized heat signal with respect to the mass loss speed for binary mixtures of water and acetonitrile. The linear trends may have a nonzero offset, and the same substance can yield different slopes, as a consequence of the open-pan evaporation condition

Full size image
Fig. 5
figure 5

Normalized heat signal with respect to the mass loss speed for binary mixtures of water and methanol

Full size image
Table 1 Results of the bilinear interpolation of the heat signal for pure species according to Eq. (3). Least-Square fit, other reference values are in Table 3
Full size table

The graph of \(\Delta h\) vs \(\Delta w\) contains the same information but, while pure substances (or the azeotrope) still show a linear behavior (just on a different scale, see Fig. 6), the mixtures are recognized as convex curves followed by a more or less extended linear trend at low w values, that marks the evaporation of pure water (Figs. 7 and 8). This second way to represent data hides somehow the double regime and suppresses the peculiar λ-shift zone, but acts also as an effective noise-dumping technique, thanks to the low-pass filtering obtained applying the integral operator.

Fig. 6
figure 6

Integrated heat signal plotted against the corresponding residual mass fraction for pure species

Full size image
Fig. 7
figure 7

Integrated heat signal plotted against the corresponding residual mass fraction for acetonitrile–water mixtures

Full size image
Fig. 8
figure 8

Integrated heat signal plotted against the corresponding residual mass fraction for methanol–water mixtures

Full size image

Both the differential and integral data representation do not yield fully reproducible values of the latent heats that can actually vary from one experiment to the other: likely causes are variations in the gas-flow controller behavior and in the initial sample mass. The qualitative analysis is reproducible and mixtures of the same composition always show trends of the same shape, but quantitatively the enthalpy signal retrieved in these open-pan experiment is not as reliable as the mass measure (see for example the total heat content for the pure water evaporation in Fig. 6 and Table 1, amounting to a mere 67% of the expected value). The data treatment via Eq. (2), anyway, yields the correct value for the pure substances (Fig. 9, Table 3), so the actual latent heat of the species can be retrieved if treated as an activation barrier, by its indirect effect on the evaporative loss.

Fig. 9
figure 9

Data analysis according to Eq. (2), from where the latent heat of evaporation can be determined

Full size image

This means very likely that the thermogravimetric scan of a liquid sample in an open crucible presents reproducibility issues, when analyzing the heat signal, respect to the analysis of solids. The latent heat of an azeotropic acetonitrile–water mixture is also estimated with a good approximation (Fig. 10, Table 3).

Fig. 10
figure 10

Data analysis according to Eq. (2) for acetonitrile–water mixtures, together with examples of interpolation over the useful ranges

Full size image

If the constant and parameters appearing in Eq. (2) are adjusted using the known saturation pressure of water, then the same calibration yields the expected saturation pressure for acetonitrile and methanol (Fig. 9). When binary mixtures are analyzed (Fig. 10), it is the ‘broken’ signal trend itself that prevents a full-range recalibration, because:

  1. (a)

    The same values of \(\Delta w/\Delta t\) are repeated at different temperature ranges;

  2. (b)

    The molar mass varies from one region to the other: samples with less acetonitrile than 30–33% (by mass) cannot even establish a first evaporation as azeotropes.

Mass balance

Despite these shortcomings, the above described data treatment let it possible to identify the onset of the free-water evaporation both on the differential and integral heat signals.

To do this, the ranges attributable to pure water are linearly interpolated as: \(a+w\times {\lambda }_{\text{H}_{2}\text{O}}\) (for the integral signal); then the points \({w}_\text{f1}\) and \({w}_\text{f3}\) are calculated as the value of w for which the difference \(\left|\Delta h-{a-w\times \lambda }_{\text{H}_{2}\text{O}}\right| \ge 1\%\) or 3% (see also Eq. (4) and Figure S1). The same can be done on the differential signal, finding w: \(\left| {{\raise0.7ex\hbox{${\Delta h}$} \!\mathord{\left/ {\vphantom {{\Delta h} {\Delta t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\Delta t}$}} - a^{\prime} - {\raise0.7ex\hbox{${\Delta w}$} \!\mathord{\left/ {\vphantom {{\Delta w} {\Delta t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\Delta t}$}} \times \lambda _{{H_{2} O}} } \right| \ge 1\% ,3\%\). The average < wf > is calculated assigning to wf1 and wf3 a 33% and 67% mass, respectively; then after interpolating the values of −n(< wf >) with a suitable function, the values of y* are computed numerically over \(0 \le x \le 0.8\) (for acetonitrile) or \(0 \le x \le 1\) (for methanol) with \(\Delta x=0.01\) (see also the Supporting File). The results are presented in Table 2 and throughout Figs. 11–14.

Table 2 Residual water fractions for 1% and 3% deviation of the heat signal from the pure water reference, averaged between the integral and differential representation and then between themselves. The 3% value is weighted for the 67% in the mean, because it is a more robust indicator
Full size table
Fig. 11
figure 11

Interpolation (solid line) of the pure water residual quantities (in logarithmic scale) for acetonitrile–water mixtures. The dashed line is the function \(F({x}_\text{i})\), appearing in Eq. (7), as expected from the actual VLE data. Grayed-out points are excluded from the analysis

Full size image
Fig. 12
figure 12

Interpolation (solid line) of the pure water residual quantities (in logarithmic scale) for methanol–water mixtures

Full size image
Fig. 13
figure 13

Calculation of the xy curve of acetonitrile–water from the data of Table 2 interpolated as shown in Fig. 11. Acetonitrile mass fractions on axes. VLE data from Acosta et al. [34]

Full size image
Fig. 14
figure 14

Calculation of the xy curve of methanol–water from the data of Table 2 interpolated as shown in Fig. 12. Methanol mass fractions on axes. VLE data from Kurihara et al. [36]

Full size image

Comparison with DSC measures

One TGA run does not always yield the correct enthalpy contents of the samples, but as long as the free-water range is recognizable, then a self-calibration becomes possible. In Table 3 are listed the values for \({\lambda }_{\text{H}_{2}\text{O}}\) that can be extrapolated from the TGA data: supposing that the instrument response is linear, the absorbed heat calculated from Eq. (4) can be rescaled according to the ratio between water’s known latent heat (2260 - J g-1) and the value interpolated from a \(\Delta h\mathrm{ vs w}\) plot (some examples are reported in Table 4). If a sample is too rich in acetonitrile or methanol to yield a detectable water residue, the instrumental response can be calibrated analyzing a water-rich sample within the same day. In some cases, the latent heat values cannot be calculated according to all the approaches, i.e. via Eqs. (2)–(4) together. For example, at high water contents the volatile-related region may be limited to low-temperature values, where the noise affecting the heat and derivative signal is not negligible; the methanol samples, moreover, are quite difficult to treat via Eq. (2) because the molar mass of the evaporating liquid changes steadily for most of the experiment.

Table 3 Latent heat retrieved form samples for whom the evaporation regimes as volatile (the azeotrope when acetonitrile is used, or methanol) plus pure-water can be detected. Expected values are: 2260 (water), 1100 (methanol) and 960 (acetonitrile/water azeotrope) J g−1. (*) interpolation according to Eq. (3)
Full size table
Table 4 Total heat absorbed by a mixture’s evaporation: a) by TGA integrated and auto-calibrated signal; b) by DSC integrated signal; c) by NRTL-RK thermodynamic model. (*) Not calibrated; (**) calibration factors retrieved by a 50% CH3CN sample of the same day
Full size table

Since the total evaporation heat has to be read from the integrated signal of Eq. (4) and not from the differential value of Eq. (3), the calibration factor coming from the \({{\Delta {\text{h}}} \mathord{\left/ {\vphantom {{\Delta {\text{h}}} {\Delta {\text{t}}}}} \right. \kern-\nulldelimiterspace} {\Delta {\text{t}}}}\,vs.\,{{\Delta {\text{w}}} \mathord{\left/ {\vphantom {{\Delta {\text{w}}} {\Delta {\text{t}}}}} \right. \kern-\nulldelimiterspace} {\Delta {\text{t}}}}\) data analysis is not strictly consistent, but it can be used to provide an estimate of the error. A similar analysis is possible also for pure species and for the evaporation regime attributable to the azeotrope.

Some DSC tests used for the comparison are reported in Figure S2—Figure S3—Figure S4—Figure S5: it must be said that the adoption of pierced pans did not always yield very good results. Many analyses (not shown here) were affected from early evaporation (likely because of too large holes), split peaks and a poor reproducibility of the double-evaporation behavior outside the range 50–60% of initial volatile content; nevertheless, the integrated heat is always much nearer to the expected values without the need of recalibrations. The validity of this DSC use seems confirmed by the very similar trends observed in quite different mixtures that undergo dynamic analysis [12], interpreted by the authors in the same way as in our case. On the other hand, Troni et al. [37] pointed out that even closed-pan experiments (meant to yield a unique boiling point) can undisclosed the lighter component early evaporation, but not systematically nor at the expected temperature.

Comparison with a Batch distillation

The batch distillation of a sub-azeotropic mixture of water and acetonitrile (0.76 by mass) resulted in the recovery of distillate cuts richer in acetonitrile: all the samples were almost at the azeotropic composition, because this system presents very similar vapor y* values (above 0.75) for any liquid mass fraction x ≥ 0.25 of acetonitrile. Due to practical reasons, the experiment was stopped when the residue was still enough to contain some acetonitrile. Analyzing the distillates and the residue, it can be seen (Figs. 15 and 16) that the separation achieved by the bench-scale test is very similar to the acetonitrile stripping taking place on the open pan of the TGA apparatus. In fact, a liquid droplet with a very similar initial composition (0.74) produces a fraction of azeotrope comparable to the total distillate mass normalized on the starting batch (the distillate collection stopped just before the boiling temperature started increasing above 77–80 °C).

Fig. 15
figure 15

Acetonitrile contents of the cuts distillated at zero reflux. The samples were analyzed by TGA. Almost 80% of the starting batch (75% by mass) is collected as azeotrope

Full size image
Fig. 16
figure 16

TGA of on acetonitrile–water droplet (0.76 of CH3CN by mass): the quantity evaporated at azeotropic composition (first linear region of dh/dt) is about the 75%

Full size image

This confirms that the interpretation of the TGA data as a micro-batch distillation at zero reflux is essentially correct, despite some sensitivity problem of the technique in identifying the onset of the pure-water regime: the higher precision of the bench-scale procedure, anyway, comes from the larger amount of sample. On the other hand, the automated procedure looks as an interesting predictive test because it employs minimal quantities of a mixture to yield experimental (rather than just theoretical) results.

Composition assessment through TGA data

The procedure described to estimate the equilibrium compositions can be easily used in the reverse sense.

  1. 1.

    Having calculated the integral function F(x) that appears in Eq. (7) from a known x–y* series, then a TG experiment yielding a certain wf value must have started from a liquid mixture with composition\({x}_text{i} :F\left({x}_\text{i}\right)=-\mathrm{ln}{w}_\text{f}\).

  2. 2.

    The total heat required from the sample vaporization can be compared to known values, that can be obtained from precise DSC calibration measurements at known initial compositions, or by the numerical solution of Eq. (6) for several \({x}_\text{i}\) (if \({h}_\text{l}(x)\) and \(\lambda (x)\) are available).

Notice that, at least in principle, the second approach can be used also when only TGA data are available because, despite the lack of precision, the stripping of the volatile-rich vapors from the pure water residues makes it possible to calibrate each signal using its own \(\Delta h/w\) shape at low w values. This is shown by the values in Table 4. For a quick glance to the method capabilities, Figs. 17 and 18 report the compositions of the tested mixtures extrapolated by the calculated wf values, via the comparison with the function F(x) expected from literature data or fitted as described in the previous paragraphs.

Fig. 17
figure 17

Parity plot for the acetonitrile content of several sub-azeotropic samples. The experimental values are initially known by weighting, the calculated values are derived from the data analysis as represented in Fig. 11

Full size image
Fig. 18
figure 18

Parity plot for the methanol content of the tested mixtures

Full size image

Conclusions

Thermogravimetric experiments performed with open pans can split the evaporation regime of a binary mixture in two parts, which represent, respectively, the distillates and the residues that would be obtained with a batch distillation at null reflux ratio. This is true not only for the overall mass balance of the sample, but also for the thermal properties of the residual liquid. An azeotrope can be identified by its apparent behavior as a pure species in a range of compositions (in this case, 75–85% of acetonitrile by mass), while non-azeotropic mixtures produce a qualitatively different signal. According to this finding, the bias introduced in the calorimetric signal by the experiment conditions can be evaluated examining the data range belonging to a pure species, making any experiment also a calibration measure.

Since multiple evaporation behaviors coexist on the same velocity scale, an adjustment of the vapor tension values over the whole range was not possible—nevertheless, the kinetic interpolation of the data returned latent heat values more reliable than those calculated by the pseudo-equilibrium data analysis.

The presented technique can be extended to other mixtures characterized by appreciable differences in volatility, boiling point and latent heat between the pure species or their azeotropes. In particular, the very existence of an azeotrope can be spotted directly by the fact that the heat signal of a pure species is apparently missing, and substituted with a different, specific one.

The main drawbacks of the presented experiments are the anticipation of the boiling temperatures and its limited sensitivity. Mixtures with less acetonitrile or methanol than 0.15 by mass appear as pure water, while samples richer than 0.75–0.80 behave like azeotropes or pure methanol: it is worth noticing, anyway, that a bench-scale purification does not actually achieve a higher sensitivity by itself, because it employs several milliliters of samples instead of a droplet.

Closed-pan DSC can achieve a good analytical performance, but it cannot evaporate liquids with changing compositions within a single run: unfortunately, the use of lids with relatively large holes to seek a compromise between the two phenomena was not fully successful, mainly for reproducibility issues, but the enthalpy calculation was found just as reliable. More practically, both the instruments are critically affected by a correct and steady behavior of the gas-flow controller, while the microscale shows the higher reliability.

The extrapolation of the VLE curve from the water residuals analysis presents two criticalities: the relatively high uncertainty in quantifying the free-water mass, and the computational noise introduced by the derivative and inverse operations in Eq. (8). In principle, this approach would allow to obtain an indirect measure of the equilibrium vapor fractions resorting to a mass balance, without need of any gas-phase analysis, nor of thermodynamic models that estimate y*(x) from PTx critical points. In practice, however, the data collected so far show a limited predictive capability, which we deem could be improved by gathering more data to have more robust statistics. Better results are achieved using the technique to establish the mixtures’ composition.

In summary, even TGAs of liquid samples on open pans can yield reliable calorimetric data by a careful analysis and can provide useful complementary information related to the VLE behavior of the mixture. Even with the present limitations, it is possible to detect azeotropes and explore a substantial range of mixtures’ compositions with a great save of materials, in compact turnkey units, and without the need of any gas-phase condenser or analyzer. Improved calibration procedures and larger data collections will likely extend the method’s sensitivity and applicability. The qualitative and quantitative equivalence between the TGA of a binary mixture and its bench-scale distillation was verified both experimentally and analytically.