Introduction

The fluid flow and heat transfer in the enclosures have been already studied extensively [1,2,3]. In the meantime, heat transfer in enclosures with moving boundaries has received considerable attention in recent years because of its growing application in the industry. Electronics cooling, solar collectors manufacturing, furnace engineering, lubrication technology and chemical equipment are some practical examples in which the physics of lid-driven enclosure is of importance [4].

Developments in nanotechnology applications have led to synthesis of nanoparticles, featuring high thermal conductivity [5, 6]. Nanofluids, formed by uniformly dispersing nanoparticles through a pure base fluid, could significantly improve the heat transfer process in industrial equipment [7, 8] and therefore attracted a great deal of interest; see for example [9,10,11]. Applying the advantages of nanoparticles to intensification of forced convection, some limited studies have been carried out on lid-driven enclosures filled with a nanofluid. These are presented in the following.

Karimipour et al. [12] investigated laminar mixed convection of copper–water nanofluid in a shallow inclined lid-driven cavity. The upper hot wall moved with a constant velocity, while the other walls were maintained fixed and adiabatic. The governing equations were solved using lattice Boltzmann method (LBM). It was shown that higher Nusselt number could be achieved at higher inclined angles and volume fractions of nanoparticles mixed in the base fluid flow. This study demonstrated the excellent capability of LBM to simulate the problems including mixed convection of a nanofluid. LBM simulation of forced convection of water–Ag nanofluid in a square lid-driven cavity was analyzed by Dahani et al. [13]. The upper wall was pushed horizontally, while the other walls were fixed. The vertical walls held at a low temperature, while the horizontal walls were set adiabatic. A heated plate was fixed horizontally in the domain. The middle position of the heated plate was found to be the best location for optimizing the heat transfer.

A double lid-driven cavity containing a nanofluid of Cu–water was conducted using LBM by Rahmati et al. [14]. They considered mixed convection in the cavity with vertical wall, thermally sinusoidal heated. It was observed that the variation of the Richardson number and Nusselt number was in the opposite directions. Sheikholeslami et al. [15] studied nanofluid (alumina–water) convective heat transfer in a lid-driven cubic with hot obstacles in the presence of a magnetic field using LBM. These authors considered the effects of Darcy and Reynolds numbers on the thermal boundary layer.

Zhou et al. [16] tackled the problem of double lid-driven enclosure containing nanofluid of alumina–water through using 3D LBM. The effects of nanoparticle volume fraction, Reynolds number and Richardson number on mixed convective heat transfer were taken into account. The best heat transfer characteristics were found for the case of downward moving of cold wall and upward moving for hot wall. It was shown that different heat source distributions, such as constant and sinusoidal function, significantly influence the temperature field and Nusselt number.

Through applying LBM, Sheikholeslami et al. [17] numerically conducted convection of heat and mass transfer in a permeable, non-Darcy cubic. The lower horizontal wall was moved, and a magnetic field was imposed upon the nanofluid of alumina–water. The domain contained a hot elliptic obstacle. Permeability, Reynolds number and Lorentz force were reported to dominate the physics of the problem. Further, multi-relaxation time LBM was applied to simulate a three-dimensional enclosure with lid-driven walls by Ghasemi and Siavashi [18]. Nusselt number was observed to increase at higher volume fraction values or Reynolds number.

Karimipour et al. [19] investigated periodic combined convection in a lid-driven cavity filled with a nanofluid using the finite volume method and SIMPLE algorithm to couple the pressure and velocity field. These authors reported smaller oscillations of mean Nusselt number at higher values of Richardson number. This study is apparently the only work on the lid-driven cavity with sinusoidal wall velocity in the literature.

The above review clearly depicts the shortage of studies on the problem of lid-driven enclosures filled with nanofluids by means of LBM. Given the importance of such configuration in industry, more investigations are required for understanding and optimization of the problem. Further, novel numerical methods, like LBM, are gradually spreading throughout the general field of computational fluid dynamics [20, 21]. It follows that they should be used for classical problems, such as mixed convection in enclosures. Therefore, the current study aims to numerically investigate the mixed convection in a lid-driven enclosure filled with a nanofluid through using LBM. The rare boundary condition of sinusoidal motion of the wall is considered as a novel method of improving the thermohydraulic performance. Further, the power demand for the wall motion in periodic and constant velocity cases is compared to develop a comprehensive view of the problem.

Problem configuration and boundary conditions

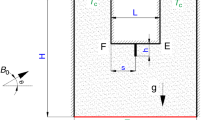
The schematic geometry for the current problem is shown in Fig. 1. The height and width of the enclosure are represented, respectively, by \(H\) and \(L\). The aspect ratio of the enclosure \({\text{AR}} = L/H\) is 3. Only the top wall moves, and the other walls are completely stationary. The top and bottom walls of the enclosure are correspondingly maintained at low (\(T_{\text{c}}\)) and high temperatures (\(T_{\text{h}}\)), while the vertical walls are assumed to be adiabatic. Gravitational acceleration is in the negative direction of \(y\) axis (Fig. 1).

Fig. 1
figure 1

The schematic view of the current configuration with the a sinusoidal or b constant top wall velocity

Full size image

Two distinct velocities for the top wall of the enclosure are assumed. These are a constant value, presented by \(u = u_{0}\), or a periodic sine function, shown as \(u = u_{0} \sin \left( {\omega t} \right)\) where \(u_{0}\) is the amplitude of oscillations, \(t\) is time and \(\omega\) denotes the angular frequency of motion. The physical problem and the corresponding numerical solution are therefore unsteady. This type of forcing has been already used to study nonlinear phenomena in many other fluid mechanical systems, such as low-density jets [22, 23] and thermoacoustic systems [24, 25].

The working fluid in the enclosure is water–Cu nanofluid, which is assumed Newtonian and incompressible. The flow is further considered laminar and single phase. The latter implies that the velocity of the fluid and solid particles is the same without any slip velocity. Boussinesq approximation is used to calculate the fluid density as a function of temperature [26, 27].

Numerical method

Governing equations

The lattice Boltzmann method has been derived from the statistical view of the transport phenomena in the physical domain and solves the governing equations without any discretization [28]. Introducing a structured pattern for particles moving through the computation domain, the governing equations are determined. LBM comprises some relevant steps, namely streaming and collision [29, 30], implemented in the current computational code, to solve the governing equations along with the boundary conditions. Once the convergence criterion is satisfied, the iterative process is terminated.

As Fig. 2 illustrates, D2Q9 [31] and D2Q5 [32] networks are applied in the current work for the calculation of velocity and temperature, respectively.

Fig. 2
figure 2

The schematic of a D2Q9 and b D2Q5 networks

Full size image

At each time step, the density and velocity values for the D2Q9 network and the temperature upon D2Q5 network can be obtained from the following equations:

$$\rho \left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{9} f_{\text{i}} \left( {x,t} \right),$$
(1)
$$V\left( {x,t} \right) = \frac{1}{{\rho \left( {x,t} \right)}}\mathop \sum \limits_{i = 1}^{9} c_{\text{i}} f_{\text{i}} \left( {x,t} \right),$$
(2)
$$T\left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{5} G_{\text{i}} \left( {x,t} \right),$$
(3)

in which \(c_{\text{i}}\) is determined by [28]

$$c_{\text{i}} = \left\{ {\begin{array}{*{20}l} {\left( {0,0} \right), } \hfill & { i = 1 } \hfill \\ {c\left\{ {\cos \left( {\left( {i - 2} \right)\frac{\pi }{2}} \right), \sin \left( {\left( {i - 2} \right)\frac{\pi }{2}} \right)} \right\},} \hfill & { i = 2,3,4,5} \hfill \\ {\sqrt 2 c\left\{ {\cos \left[ {\left( {\left( {i - 6} \right)\frac{\pi }{2}} \right) + \frac{\pi }{4}} \right], \sin \left[ {\left( {\left( {i - 6} \right)\frac{\pi }{2}} \right) + \frac{\pi }{4}} \right]} \right\},} \hfill & {i = 6,7,8,9} \hfill \\ \end{array} } \right.$$
(4)

In Eq. (4), \(c\) is the base speed of the lattice Boltzmann, which is equal to unity [33]. The value of the equilibrium distribution function for the flow field and temperature are also obtained from [33]

$$\begin{aligned} f_{\text{i}}^{\text{eq}} \left( x \right) = W_{\text{i}} \rho \left( x \right)\left[ {1 + 3\frac{{c_{\text{i}} \cdot V}}{{c^{2} }} + \frac{9}{2}\frac{{\left( {c_{\text{i}} \cdot V} \right)^{2} }}{{c^{4} }} - \frac{3}{2}\frac{{\left| V \right|^{2} }}{{c^{2} }}} \right], \\ G_{\text{i}}^{\text{eq}} \left( {x,t} \right) = W_{\text{i}} T\left( {x,t} \right)\left( {1 + 3c_{\text{i}} \cdot V} \right), \\ \end{aligned}$$
(5)

where \(V\) is the macroscopic velocity and \(W_{\text{i}}\) is the weighting factor. On the flow field domain, \(W_{\text{i}}\) takes the value of \(4/9\) for \(i = 1\), \(1/9\) for \(i = 2, 3, 4, 5\) and \(1/36\) at the other \(i\) values. However, the thermal field specifies the \(W_{\text{i}}\) value of \(1/3\) for \(i = 1\) and \(1/6\) when \(2 \le i \le 5\). Since this work deals with mixed convection, the volume force of free convection should be defined in \(y\)-axis using the following relation [34]:

$$F_{\text{iy}} \left( {x,t} \right) = 3W_{\text{i}} g\beta \left( {T\left( {x,t} \right) - T_{0} } \right)c_{\text{iy}} .$$
(6)

In Eq. (6), \(c_{\text{iy}}\) is the microscopic velocity of the particle in the \(y\) direction, \(g\) is the gravitational acceleration, \(\beta\) is the volume expansion coefficient and \(T_{0}\) is called the reference temperature, which equals the cold temperature (\(T_{\text{c}}\)).

Non-dimensionalizing of the variables

Aiding the reference parameters, the governing hydrodynamic and thermal variables are turned into those of non-dimensional form, by the following definitions. Next, the dimensionless parameters for more insightful physical analysis are stated in Table 1.

Table 1 Dimensionless parameters
Full size table

This process generalizes the results through reducing the wide variety of parameters and making the discussion more perceptive.

One of the most important non-dimensional variables is the Nusselt number. Therefore, spatially averaged Nusselt number is defined by

$$\overline{\text{Nu}} = \frac{1}{L}\mathop \int \limits_{0}^{L} {\text{Nu}}\left( x \right){\text{d}}x,$$
(7)

where \(L\) is the length of the non-adiabatic horizontal walls. Because the current problem is time-dependent, the temporal averaging should be also performed to have a fully averaged Nusselt number in this problem. Considering \(\lambda\) as a temporal period of moving lid wall, the average Nusselt number becomes

$$\overline{\text{Nu}}_{\text{avg}} = \frac{1}{\lambda }\mathop \int \limits_{0}^{\lambda } \overline{\text{Nu}} \;{\text{d}}t^{*} .$$
(8)

It should be pointed out that the Nusselt number is calculated after passing 50 temporal periods, due to wiping out of the probable irregular unsteadiness.

Mathematical description of boundary conditions

The boundary conditions are now presented in their non-dimensional form. Dirichlet boundary conditions [35] are employed on the walls for velocity. On the top wall, the nonzero lid velocity and in the other walls zero velocity of no-slip condition are applied. These are expressed as the following:

  • The left wall

    $$u^{*} = 0 ,\;v^{*} = 0\quad {\text{at }}x^{*} = 0,\;0 \le y^{*} \le 1$$
    (9)

  • The right wall

    $$u^{*} = 0 ,\;v^{*} = 0\quad {\text{at }}x^{*} = L/H ,\;0 \le y^{*} \le 1$$
    (10)

  • The bottom wall

    $$u^{*} = 0,\;v^{*} = 0\quad {\text{at }}y^{*} = 0 ,\;0 \le x^{*} \le L/H$$
    (11)

  • The top wall

    $$u^{*} = \sin \omega^{*} t^{*} , \;v^{*} = 0\quad {\text{at}}\quad y^{*} = 1,\;0 \le x^{*} \le L/H$$
    (12)

where \(\omega^{* }\) is the dimensionless frequency and it is defined as

$$\omega^{*} = \frac{\omega H}{{u_{0} }}.$$
(13)

Dirichlet boundary condition for the constant temperature walls and Neumann type [35] for those with zero heat flux are implemented, as follows:

  • The left wall

    $$\frac{{\partial T^{*} }}{{\partial x^{*} }} = 0 \quad {\text{at}}\quad x^{*} = 0,\; 0\le y^{*} \le 1$$
    (14)

  • The right wall

    $$\frac{{\partial T^{*} }}{{\partial x^{*} }} = 0\quad {\text{at }}x^{*} = L/H ,\; 0\le y^{*} \le 1$$
    (15)

  • The upper wall

    $$T^{*} = 0\quad {\text{at}}\quad y^{*} = 1,\;0 \le x^{*} \le L/H$$
    (16)

  • The bottom wall

    $$T^{*} = 1\quad {\text{at}}\quad y^{*} = 0,\;0 \le x^{*} \le L/H$$
    (17)

The boundary conditions should be treated for the LBM. All the hydrodynamic distributed functions should be, therefore, specified on the boundaries. However, the unknown ones are those toward the domain, required to calculate. For example, \(f_{6}\), \(f_{2}\) and \(f_{9}\) need to be determined on the west wall of D2Q9 network, as shown in Fig. 3. This figure illustrates the schematic view of the problem with the direction of distributed functions on the walls. On each wall, the equations of density, x and y momentum, should be considered, as presented in Eqs. (18) to (20):

Fig. 3
figure 3

Distribution functions on the a D2Q9 and b D2Q5 domain boundaries

Full size image
$$\rho = f_{1} + f_{2} + f_{3} + f_{4} + f_{5} + f_{6} + f_{7} + f_{8} + f_{9}$$
(18)
$$\rho u^{*} = \mathop \sum \limits_{i = 1}^{9} c_{ix} f_{i} \to \rho u^{*} = f_{2} + f_{6} + f_{9} - f_{8} - f_{4} - f_{7}$$
(19)
$$\rho v^{*} = \mathop \sum \limits_{i = 1}^{9} c_{iy} f_{i} \to \rho v^{*} = f_{3} + f_{6} + f_{7} - f_{9} - f_{5} - f_{8}$$
(20)

There are three distribution functions as well as density on every wall, which are undetermined, and therefore, another equation is required in addition to Eqs. (18) to (20). The system of finding boundary conditions is closed using the non-equilibrium part of particle distribution normal to the boundary [36]. In this case, Eqs. (21) and (22) are, respectively, appropriate for the vertical and horizontal walls:

$$f_{2} - f_{2}^{\text{eq}} = f_{4} - f_{4}^{\text{eq}} ,$$
(21)
$$f_{3} - f_{3}^{\text{eq}} = f_{5} - f_{5}^{\text{eq}}.$$
(22)

It should be pointed out that the dimensionless velocity of the boundaries, i.e., \(u^{*}\) and \(v^{*}\), is zero at all the walls except for the lid wall where it is determined by the constant or periodic functions, as stated earlier by Eq. (12).

Similar to what performed regarding hydrodynamic boundary conditions, unknown thermal distribution functions on the walls should be determined. However, as D2Q5 network is used for the energy equation, only a single unknown function, which is toward the domain, is required to be calculated. Aiding Eq. (3) and using the known temperature on the horizontal walls, the boundary condition equation is satisfied. On the vertical walls, all the distribution functions are assumed to be equal [33].

Nanofluid properties

As stated earlier, single phase assumption of nanofluid mixture is considered in the current study. This approach uses some mathematical relations to determine the thermo-physical properties of the nanofluid. Nanofluid density can be determined by the following equation [37]:

$$\rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{s}} ,$$
(23)

where subscribes f, s and nf denote fluid, solid and nanofluid, respectively. \(\phi\) and \(\rho\) are the volume fraction of the nanoparticles and density, correspondingly. The heat capacity, \(c_{\text{p}}\), and the volume expansion coefficient, \(\beta\), for the nanofluid are also defined as follows [37]:

$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho c_{\text{p}} } \right)_{\text{s}} ,$$
(24)
$$\left( {\rho \beta } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{\text{f}} + \phi \left( {\rho \beta } \right)_{\text{s}} .$$
(25)

The nanofluid dynamic viscosity, \(\mu_{\text{nf}}\), is calculated using the Brinkman model [38]:

$$\mu_{\text{nf}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \phi } \right)^{2.5} }}.$$
(26)

The effective conductivity coefficient of the nanofluid is defined by the Maxwell model [39], which is

$$\frac{{k_{\text{eff}} }}{{k_{\text{f}} }} = \frac{{k_{\text{s}} + 2k_{\text{f}} - 2\phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}{{k_{\text{s}} + 2k_{\text{f}} + \phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}.$$
(27)

The thermo-physical properties of the current nanofluid component (copper nanoparticles and pure water) at the reference temperature of 298 K are presented in Table 2.

Table 2 Thermo-physical properties of water fluid and copper nanoparticles [51]
Full size table

Grid independency

Grid independency test was performed to choose the optimal mesh size. The mesh used in the current study is structural with a uniform size in each direction. The parameters value applied during the grid independency test is presented in Table 3. Further, the non-dimensional time step, \(\Delta t^{*}\), was assumed to be unity, for restricting the CFLFootnote 1 number below those recommended for the similar problems [40].

Table 3 The value of parameters used for grid independency test
Full size table

Four mesh sizes of 40 × 120, 50 × 150, 60 × 180 and 70 × 210 on the x–y domain were examined. The non-dimensional temperature versus time at the midpoint of the enclosure, located at \(x^{*} = y^{*} = 0.5\), is presented in Fig. 4 for various mesh sizes. This figure shows that the mesh size of 60 × 180 is more precise and economic than the others and therefore was chosen for the rest of simulations.

Fig. 4
figure 4

Comparison of dimensionless temperature versus non-dimensional time at the midpoint of the enclosure (\(x^{*} = y^{*} = 0.5\)): a comparison among four mesh sizes

Full size image

Validation of the computational code

In order to validate the in-house computational code, the current results were compared to the other published results. The current results for dimensionless velocity and the local Nusselt number on the mid-vertical centerline of a two-sided lid-driven cavity filled with Cu–water nanofluid are compared with those of Ref. [38], respectively, as shown in Fig. 5a, b. Clearly, the two sets of data are in very good agreement.

Fig. 5
figure 5

Comparison between the current results and those of Tiwari et al. [38] at \({\text{Gr}} = 10^{4}\) and \({\text{Ri}} = 1\): a dimensionless velocity (\(\phi = 0\%\)) and b local Nusselt number (\(\phi = 8\%\))

Full size image

Finally, the current results are also compared with those of Karimipour et al. [19], as shown in Fig. 6. This figure includes the dimensionless temperature for the non-dimensional time that matches the temporal period of lid wall motion at the vertical centerline. A high degree of agreement is observed in this figure. These comparisons can potentially prove that the current in-house code can completely capture the physics of fluid flow and heat transfer in the transient lid-driven enclosure.

Fig. 6
figure 6

Dimensionless temperature at the temporal period of the lid wall moving: a comparison between the current results and those of Karimipour et al. [19] at \({\text{Gr}} = 10^{4}\), \({\text{Ri = }}0.1\), \(L/H = 3\) and \(\phi = 0\%\)

Full size image

Results and discussion

In this section, the results of mixed convection in a sinusoidal lid-driven enclosure filled with copper–water nanofluid are presented for \({\text{Gr}} = 10^{4}\) \({ \Pr } = 6.2\) and \(L/H = 3\). The time-dependent motion of the top wall causes the temporal variation of the parameters, as it will be shown in this section. Further, the effects of changes in Richardson number and nanoparticles volume fraction and the lid wall period on the fluid flow and heat transfer are investigated.

Figure 7 shows the influences of variations in Richardson number on the average Nusselt number. According to this figure, decreasing the numerical value of Richardson number leads to increases in the average Nusselt number, as the lid velocity rises. This figure shows that decrement of \(R\) from 10 to 0.1 makes the averaged Nu number increase by the factor of 1.8. At the lowest lid velocity (\({\text{Ri}} = 0.1\)), variation of the average Nu number demonstrates a decreasing trend with growing frequencies, representing a low-pass-filter trend in this problem. However, the average Nusselt number shows steady-like variation at the highest value of Ri, emanated from the lowest velocity of the lid wall.

Fig. 7
figure 7

The effect of the lid wall frequency on the average Nusselt number for \(\phi = 0\%\)

Full size image

The non-dimensional horizontal velocity at the vertical mid-centerline in one period of lid wall moving is illustrated for two values of Ri and zero nanoparticles volume fraction in Fig. 8. The top lid velocity is positive when the non-dimensional time is lower than \(\lambda /2\). In this case, the shear stress is applied in the positive direction of \(x^{*}\). However, this trend is reversed for the non-dimensional times greater than \(\lambda /2\). The velocity profile of non-dimensional time that is equal to \(0\) and \(\lambda /2\) and further \(\lambda /4\) and \(3\lambda /4\) is mirror image with respect to each other as the simulation is performed under a stationary unsteady condition. The variation of the velocity is negligible around the core of the enclosure compared to that in the vicinity of the wall regions. Farther away from the top wall, the lid velocity penetration becomes less significant. Yet, as the non-dimensional frequency of the lid oscillation decreases, the velocity effects of the lid penetrate deeper into the fluid. Lower velocity at the vicinity of the bottom wall zone renders a weaker shear stress at that region.

Fig. 8
figure 8

Non-dimensional horizontal velocity profile during a period of lid wall motion at the mid-vertical centerline for \(\phi = 0\) and a \({\text{Ri}} = 0.1\) and b \({\text{Ri}} = 10\)

Full size image

Figure 9, drawn for the same conditions as in Fig. 8, shows the non-dimensional temperature inside the enclosure. The temperature profile is varied between the minimum and maximum values, which is 1 and − 1. The symmetric profile at \({\text{Ri}} = 10\) shows the uniform free convection cell through the enclosure. Further, higher Richardson number makes the buoyancy effects stronger and this is the reason for the extension of the higher temperature zone close to the horizontal walls region. The temperature profile does not change by time passing after the beginning (\(t^{*} = 0\)). This shows a fast thermal response of the system, leading to stationary conditions for the temperature just after the lid motion.

Fig. 9
figure 9

Non-dimensional temperature profile during a period of lid wall motion at the mid-vertical centerline for \(\phi = 0\) and a \({\text{Ri}} = 0.1\) and b \({\text{Ri}} = 10\)

Full size image

Figures 10–13 show the streamline and isotherms for one period of lid wall oscillation and for various Richardson numbers and volume fractions. At the even quarters of temporal period and \({\text{Ri}} = 10\), most of the enclosure is filled with a large cell for zero concentration of nanoparticles. Further, one or two small cells may be found in the domain. However, this pattern changes by decreasing the Richardson number or increasing Reynolds number. In this case, the number of recirculating cells is increased. The different cells arrangement between the cases of \(\phi = 0\%\) and \(\phi = 4\%\) arises from the difference between dynamic viscosity. At odd quarters of time period, three recirculating cells occupy the enclosure at \({\text{Ri}} = 10\), while one big wake as well as another small cell covers the domain at \({\text{Ri}} = 0.1\). Isotherms show the conduction of heat on the non-adiabatic walls, represented by the dense and parallel lines. This type of heat transfer tends to magnify at higher Richardson numbers. The thickness of thermal boundary layer is found to be lower at lower \({\text{Ri}}\), as a result of intensification of forced convection by increasing the lid wall velocity. This also causes thickness reduction in the hydrodynamic boundary layer. The patterns of the isotherms and streamlines are similar at \(t^{*} = 0\), \(t^{*} = \lambda /2\) and \(t^{*} = \lambda\). Further, the distribution of the isotherms and streamlines of \(t^{*} = 3\lambda /4\) is the same as those of \(t^{*} = \lambda /4\), rendering a stationary temporal behavior.

Fig. 10
figure 10

Streamlines for \({\text{Ri}} = 10,\; \omega^{*} = 0.1050\) and volume fractions of 0 and 4% during a temporal period of lid wall moving

Full size image
Fig. 11
figure 11

Streamlines for \({\text{Ri}} = 0.1, \;\omega^{*} = 0.1256\) and volume fractions of 0 and 4% during a temporal period of lid wall moving

Full size image
Fig. 12
figure 12

Isotherms for \({\text{Ri}} = 10,\; \omega^{*} = 0.1050\) and volume fractions of 0 and 4% during a temporal period of lid wall moving

Full size image
Fig. 13
figure 13

Isotherms for \({\text{Ri}} = 10,\; \omega^{*} = 0.1050\) and volume fractions of 0 and 4% during a temporal period of lid wall moving

Full size image

Variations of Nusselt number versus three periods of lid wall motion at \({\text{Ri}} = 0.1\) and \(10\) and for various nanoparticles volume fractions are illustrated in Fig. 14. The Nusselt number is periodically changed due to the sinusoidal velocity of the lid wall. This clearly shows that the heat transfer behavior of the enclosure is time-dependent and varies according to the frequency of the wall moving. Interestingly, about two periods of Nusselt number variation is set on one period of lid wall motion. This is a clear manifestation of the nonlinear behavior of the system in which the frequency of the input forcing (lid oscillation) is different to that of the output (Nusselt number). Reducing Ri from 10 to 0.1 causes the Nusselt number increase by a factor of two. This is physically conceivable as the forced convection is stronger than the free convection. Increasing the volume fraction makes an increment in convection heat transfer [41]. However, its growth rate is not restricted by increasing Ri, in contrast to the previous studies [38]. Therefore, as an important result, wall oscillations can compensate this weakness in heat transfer.

Fig. 14
figure 14

Nusselt number for various nanoparticles volume fractions during three temporal periods of lid wall moving at a \({\text{Ri}} = 10\) and b \({\text{Ri}} = 0.1\)

Full size image

Figure 15 depicts a comparison of the average Nusselt number for different values of Ri and the volume fraction of nanoparticles. Clearly, a reduction in Ri results in higher rates of heat transfer. This could be readily explained by noting that forced convection of heat is strengthened at lower values of Ri. Enhancement of Nusselt number is also achieved by increasing the concentration of nanoparticles, as it boosts the thermo-physical properties of the nanofluid. This figure shows that heat transfer is partly subsided by imposing a sinusoidal motion on the lid wall, especially at lower Richardson numbers. It is inferred from Fig. 15 that throughout the considered range of the parameters, the effects of Ri are stronger than that of the volume fraction of nanoparticles. The non-dimensional frequencies in Fig. 15 are those that lead to obtaining the maximum Nusselt number. Intensifying the non-dimensional frequency of the lid oscillation for the cases with higher velocity (\({\text{Ri}} \le 1\)) may be another reason for the decline of Nusselt number. This behavior is further expected from the low-pass filter response of the system.

Fig. 15
figure 15

Variation of the average Nusselt number versus volume fraction for various Richardson number in the case of a constant and b sinusoidal wall velocity

Full size image

The mechanical power required to move the lid wall is calculated for constant or oscillatory wall velocity in this study. Importantly, it is noted that despite its practical importance, so far, this aspect of the problem has not been investigated in the literature. In practice, the power may be delivered by an electrical motor to the enclosure’s wall. The imposed force on the lid wall is computed using shear stress, \(\tau_{\text{w}}\), as the following relation shows:

$$F = \mathop \int \limits_{0}^{\lambda } \mathop \int \limits_{0}^{L} \tau_{\text{w}} {\text{d}}x{\text{d}}t,$$
(28)

where \(\lambda\) and \(L\) are correspondingly the moving time period and width of the lid wall. The power demand subsequently becomes

$$P = \int \int {\text{d}}F{\text{d}}V_{\text{w}} = \mathop \int \limits_{0}^{\lambda } \mathop \int \limits_{0}^{L} \tau_{\text{w}} U_{0} { \sin }\left( {\omega t} \right){\text{d}}x{\text{d}}t.$$
(29)

The average power on one oscillation period gives

$$\bar{P} = \frac{P}{\lambda }.$$
(30)

Figure 16 illustrates the average heat transfer rate out of the top wall against the average power demand to move the enclosure’s wall. As expected, increasing heat transfer magnifies the power consumption to drive the wall. The difference between two cases of constant and oscillatory velocity of the lid wall is small at lower power demands, while it grows to a higher extent as power input rises. Figure 16 shows that for a constant heat transfer rate, the enclosure with constant lid velocity needs more input power than that of the periodic velocity case. This indicates that for a specific thermal gain, the enclosure of the sinusoidal wall velocity is more efficient. Lower power demand for the oscillatory wall may be induced by lower average velocity in the temporal period compared to the constant lid velocity. The variation of heat transfer rate through the graph tends to decline by increasing the power demand. This implies that as the power input of the system increases, the heat transfer system takes farther distance from its optimal operation.

Fig. 16
figure 16

The average Nusselt number on the lid wall versus average non-dimensional power: a comparison between two cases of constant and oscillatory wall velocity

Full size image

The average rate of heat transfer versus power demand for two values of volume fraction for the case of periodic wall velocity is depicted in Fig. 17. The power demand for a constant heat transfer rate grows by increasing the volume fraction. This emanates from the fact that a nanofluid flow involves higher shear stress due to more dynamic viscosity in comparison with the base fluid flow. In keeping with the findings of other thermohydraulic studies of nanofluid flows [42,43,44,45,46] and those on other types of fluids [47,48,49,50], the power demand grows for the cases of higher heat transfer.

Fig. 17
figure 17

The average Nusselt number on the sinusoidal oscillatory lid wall against average non-dimensional power for various volume fractions of nanoparticles

Full size image

Conclusions

Using the lattice Boltzmann method, mixed heat convection in a two-dimensional lid-driven enclosure filled with nanofluid was simulated. The lid velocity was assumed to be oscillatory and sinusoidal. A range of Richardson number (\(0.1\) to \(10\)) and volume fraction of nanoparticle (\(0\) to \(4\%\)) was considered. For the first time in the literature, isotherms, streamlines and Nusselt number as well as the power demand to move the lid wall were studied. The main findings of this study are summarized as follows.

  • The enclosure with sinusoidal lid wall velocity was demonstrated to act as a classical low-pass filter, which responds most strongly to low-frequency oscillations and filters out higher frequencies. This was the reason for decline of Nusselt number as the non-dimensional frequency increased.

  • Assuming a constant heat transfer rate from the enclosure, the case with oscillatory lid wall velocity showed a lower demand of input power in comparison with that with constant lid wall speed.

  • The power required to oscillate the lid wall grew by increasing the concentration of nanoparticles, due to increases in the fluid viscosity.

  • Keeping Grashof number at a constant value, the Nusselt number increased with decreasing Richardson number, due to magnification of forced convection. Increasing the volume fraction of nanoparticles also appeared to boost the heat transfer rate.