Introduction

Catalytic porous microchannels, where catalytic channels of small sizes filled with porous media, have received increased interest in traditional and advanced chemical and energy technologies in the last decade. Featuring high surface-to-volume ratios, catalytic porous microchannels can readily achieve the desired performance on transport and chemical reactions [1,2,3]. Therefore, extensive studies have been reported in recent years on applications of catalytic porous microchannels [4,5,6,7]. However, due to the relatively complex natures in catalytic porous microchannels, our understanding of relevant fundamental mechanisms is still far from satisfactory and there are considerable voids for efficient utilization of catalytic porous microchannels. Thus, accurately quantifying the inherent characteristics in catalytic porous microchannels is the prerequisite for their subsequent efficient utilization and optimization. Among the massive aspects that require in-depth investigation for catalytic porous microchannels, transport processes and entropy generation are of vital importance as they are directly related to the overall performance of a catalytic porous microchannel.

Owing to the coupled complexities of multi-physics and geometrical topology in a typical catalytic porous microchannel, a comprehensive investigation of intrinsic characteristics and engineering principles through experiments may be too expensive [8,9,10]. Additionally, accurate measurements at the small spatiotemporal scales in catalytic porous microchannels pose great challenges to current measuring techniques [11, 12]. Considering the dramatical increase in computational power and rapid development of theoretical models, numerical modeling has played greater roles in scientific research and engineering optimization for catalytic porous microchannels. Although the general transport [13,14,15] and entropy generation [16,17,18] characteristics of microreactors have been investigated to some extent, their behavior under non-Newtonian fluids is still largely unknown. As a matter of fact, there is still a significant knowledge gap in understating convective heat and mass transfer in porous media and microchannels with non-Newtonian fluid flow [19,20,21]. In the following, some of the recent studies in these areas are briefly discussed.

Neffah et al. [22] conducted a numerical study of heat and mass transfer in a non-Newtonian fluid in a parallel-plate channel partly filled with an anisotropic porous medium. They investigated the effects of various parameters pertinent to the porous medium, the non-Newtonian fluid and the chemical reaction on the velocity, temperature and concentration distributions, as well as mean Nusselt and Sherwood numbers. Neffah et al. [22] showed that compared with the isotropic case, the anisotropy of a porous medium can lead to significant improvements in heat and mass transfer. The shear-thickening fluids exhibit the highest values of mean Nusselt and Sherwood numbers at large Darcy number values. The work of Neffah et al. [22] clarified that an increment in the chemical reaction parameters mitigates heat and mass transfer rates.

In a recent numerical work, Wang et al. [23] investigated entropy generation in thermal natural convection with differentially discrete heat boundary conditions at various Rayleigh numbers. This study showed that the thermal, viscous and total entropy generation increase with the increase in Rayleigh number. It also confirmed that the system’s availability improves in the presence of effective heat source at the bottom of the boundary.

Saeed et al. [24] analyzed the methods of biofuel processing in diesel engines to evaluate non-Newtonian biofuel flow in a magnetic microreactor. It was shown that variations in the magnetic field strength and the thermo-physical properties of the fluid could cause considerable temperature differences. It was also observed that the alterations in the properties of Casson fluid as well as the change in the magnitude and angle of the magnetic field could affect Nusselt number. It was further found that the extent of the variations is strongly dependent on the wall thickness.

Gholamalizadeh et al. [25] performed a two-dimensional numerical study of a convective flow in a nanofluid water/FMWCNT-coated microchannel. The slip velocity boundary condition was applied for the solid walls. The results showed that as compared to Reynolds number, Darcy number has a more pronounced effect upon the velocity profile. It was also found that increasing porosity did not affect the velocity profile growth in any way.

It has been already reported that working fluids have significant impact on the overall performance of a catalytic porous microchannel [1, 2, 7]. In a numerical study, Maleki et al. [26] investigated flow and heat transfer in non-Newtonian nanofluids over porous surfaces. They investigated the effects of parameters, such as power-law index, volume fraction of nanoparticles, nanoparticles type and permeability parameter on the flow and heat transfer of the desired nanofluid. The study found that the hydro-thermal properties of non-Newtonian nanofluid flows exhibited different behaviors as compared with the common working fluids. For instant, the injections and permeability in the plate showed higher heat transfer performance for non-Newtonian nanofluids in comparison with Newtonian nanofluids.

In their numerical work, Animasaun and Pop [27] considered the geometry and position of the surface for the study of the desired fluid flow in order to evaluate the flow performance on the target parameters. The results showed that the non-Newtonian fluid temperature distribution was higher than that of the Newtonian fluid. It was also found that by applying the non-Newtonian fluid, the rate of local heat transfer decreases more rapidly. The apparent disagreement of this finding with that reported by Maleki et al. [26] is a clear indication that the field of heat convection in non-Newtonian fluids has not settled yet.

Al-Rashed et al. [28] conducted a study to evaluate the thermal and entropic properties of a non-Newtonian nanofluid containing CuO particles in the substrate (MCHS). This article discusses the effects of concentration of nanoparticles, the Reynolds number as well as the geometric size intended for MCHS based on the first and second laws of thermodynamics. The results showed that increasing Reynolds number improves the performance of MCHS by increasing the fluid convection heat transfer coefficient of the working fluid, which in turn results in uniform temperature of the substrate. They further revealed that the use of non-Newtonian nanofluid instead of the base ordinary fluid leads to an increase in heat transfer efficiency against increasing the pressure drop. Also, by using non-Newtonian nanofluid, the least amount of entropy generation in the system can be achieved.

So far, most studies and applications of catalytic porous microchannels have used Newtonian fluids, while effects of non-Newtonian fluids on thermal transport and entropy generation have been seldomly touched [29, 30]. However, non-Newtonian fluids are more common in practice and our knowledge of their influences on performance of catalytic porous microchannels should be advanced. To partially close the gap of clarifying the effects of non-Newtonian fluids, a catalytic porous microchannel with power-law fluids has been studied in this study. The reasons to choose power-law fluids in this work are twofold. First, the mathematical description of power-law fluids is relatively simple, which can greatly benefit the formulation of conservation equations for modeling of thermal transport and entropy generation in porous microchannels. Second, as a widely encountered type of non-Newtonian fluids, power-law fluids are rather representative in the engineering.

In this work, numerical analysis of thermal transport and entropy generation of a typical catalytic porous microchannel filled with power-law fluids has been conducted. To focus on the effects of power-law fluids, catalytic reactions only happen at the sidewalls of channels and Soret effect is taken into consideration. In the following, governing equations of the studied system are described and discussed. Then, analytical solutions of relevant governing equations are derived and solved numerically. After validating the developed theoretical solution, the differences of thermal transport and entropy generation between Newtonian and power-law fluids are compared and discussed. Finally, a comprehensive parametric analysis was conducted to study the effects of physical properties of power-law fluids.

Theoretical and numerical methods

Assumptions

The assumptions considered in this study are presented as the following.

  • The flow is laminar, steady and hydrodynamically fully developed.

  • The fluid is non-Newtonian power law.

  • The flow regime is assumed to be continuous with Knudsen number lower than 0.3.

  • All chemical reactions on the catalyst are assumed to be of zeroth order.

  • The effect of temperature on the surface reactions is neglected.

  • The porous medium is isotropic, homogeneous, saturated with fluid and under thermally non-equilibrium conditions (LTNE).

Governing equations and boundary conditions

The rheological equation for an isotropic, incompressible flow of a power-law fluid is [31]

$$\mu = m\left| {\frac{\partial u}{\partial y}} \right|^{{\text{n}} - 1} ,$$
(1)

where m, u, y and n are the power-law consistency index, fluid velocity, dimensional transverse coordinate and power-law behavior index, respectively.

The Darcy–Brinkman equation for the momentum equation [2, 32, 33] is considered as the follows:

$$- \frac{\partial p}{\partial x} + \mu_{\text{eff}} \frac{{\partial u^{2} }}{{\partial y^{2} }} - \frac{\mu }{\kappa }u = 0\quad - h_{1} \le y < h_{1} .$$
(2)

The following equations represent the energy transfer in the solid and fluid phases:

$$k_{2} \frac{\partial }{\partial y}\left[ {\frac{{\partial T_{2} }}{\partial y}} \right] = 0,\quad h_{1} < y \le h_{2}$$
(3a)
$$k_{\text{ef}} \frac{{\partial^{2} T_{\text{f}} }}{{\partial y^{2} }} + h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) = \rho_{\text{f}} C_{\text{p,f}} u\frac{{\partial T_{\text{f}} }}{\partial x},\quad - h_{1} \le y < h_{1}$$
(3b)
$$k_{\text{es}} \frac{{\partial^{2} T_{\text{s}} }}{{\partial y^{2} }} - h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) = 0,\quad - h_{1} \le y < h_{1}$$
(3c)
$$k_{1} \frac{\partial }{\partial y}\left[ {\frac{{\partial T_{1} }}{\partial y}} \right] = 0\quad - h_{2} \le y < - h_{1} .$$
(3d)

The mass transfer involves the effect of thermal diffusion (Sorter effects) on the Fickian diffusion in the advective–diffusive system, as follows [1]:

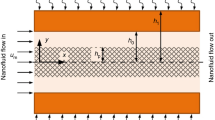
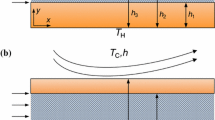
$$u\frac{\partial C}{\partial x} = D\frac{{\partial^{2} C}}{{\partial y^{2} }} - D_{\text{T}} \frac{{\partial^{2} T_{\text{f}} }}{{\partial y^{2} }}\quad - h_{1} \le y < h_{1} .$$
(4)

In Eqs. (2)–(4), \(p\) is thepressure, \(x\) is the dimensional axial coordinate, \(\mu\) and \(\mu_{\text{eff}}\) are the viscosity of the fluid and the effective viscosity of the porous medium, respectively, \(\kappa\) is the permeability of the porous insert, \(h_{1}\) and \(h_{2, }\) refer to the half-thickness and half-height of the microchannel. Further, \(k_{\text{ef}}\) and \(k_{\text{es}}\) are the effective thermal conductivity of the fluid phase and solid phase of the porous medium, \(k_{1}\) and \(k_{2}\) are the thermal conductivity of wall 1 and wall 2 (see Fig. 1), \(h_{\text{sf}}\) and \(a_{sf}\) are the interstitial heat transfer coefficient and interfacial area per unit volume of porous media. Furthermore, \(T_{\text{s}}\), \(T_{\text{f}}\), \(T_{1}\) and \(T_{2}\) denote the temperature of solid phase, fluid phase, lower and upper wall, respectively. Also, \(\rho_{\text{f}}\) and \(C_{\text{p,f}}\) show the density and specific heat capacity of the fluid, \(C\) is the mass species concentration, \(D\) denotes the effective mass diffusion coefficient and \(D_{T}\) represents the coefficient of thermal mass diffusion.

Fig. 1
figure 1

Schematic a isometric and b side view of the porous microchannel under investigation

Full size image

Although most solutes feature positive coefficients of thermal mass diffusion representing that the mass can be moved down the thermal gradient, the other have the negative coefficients and are able to be diffused up the thermal gradient. Therefore, the negative or positive sign of the last term in Eq. (4) is acceptable.

For energy and momentum equations, the boundary conditions are

$$y = h_{2} : k_{2} \left. {\frac{{\partial T_{2} }}{\partial y}} \right|_{{y = h_{2} }} = q_{2}^{{\prime \prime }} ,$$
(5a)
$$y = h_{1} : u_{\text{f}} = 0 , T_{2} = T_{\text{f}} = T_{\text{s}} = T_{\text{w2}} , q_{2}^{\prime \prime } = k_{\text{ef}} \left. {\frac{{\partial T_{\text{f}} }}{\partial y}} \right|_{{y = h_{1} }} + k_{\text{es}} \left. {\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{{y = h_{1} }}$$
(5b)
$$y = 0: \frac{{{\text{d}}u_{{\rm f}} }}{{{\text{d}}y}} = 0$$
(5c)
$$y = - h_{1} :\;u_{\text{f}} = 0 , T_{2} = T_{\text{f}} = T_{\text{s}} = T_{\text{w1}} ,\, q_{1}^{\prime \prime } = - k_{\text{ef}} \left. {\frac{{\partial T_{{\rm f}} }}{\partial y}} \right|_{{y = - h_{1} }} - k_{\text{es}} \left. {\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{{y = - h_{1} }}$$
(5d)
$$y = - h_{2} : k_{1} \left. {\frac{{\partial T_{1} }}{\partial y}} \right|_{{y = - h_{2} }} = q_{1}^{\prime \prime }$$
(5e)

The concentration boundary conditions are expressed as follows:

$$y = - h_{1} : C = C_{0}$$
(6a)
$$y = 0: D\frac{\partial C}{\partial y} = D_{\text{T}} \frac{{\partial T_{{\rm f}} }}{\partial y}.$$
(6b)

Next, the dimensionless parameters for better physical analysis are stated in Table 1.

Table 1 Dimensionless parameters
Full size table

The dimensionless temperature follows the given chain, i = 1, 2,s, f.

In Table 1, \(q_{1} ^{\prime \prime }\) and \(q_{1} ^{\prime \prime }\) are the lower and upper wall heat flux, \(\theta\) is the dimensionless temperature, \(k_{{\rm R}}\) is the reaction rate constant on the walls, \(X\) and \(Y\) are the dimensionless axial and transverse coordinates, Da, \(Bi\), \(\gamma\), Sr, Pr, Re and Pe are the Darcy, Biot, Damköhler, Soret, Prandtl, Reynolds and Peclet numbers, respectively. Also, \(Q\) represents the wall heat flux ratio, \(S\) is the shape factor of the porous medium, \(\xi\) shows the aspect ratio of the microchannel, \(\varepsilon\) is the porosity of the porous medium, \(\phi\) and \(U\) denote the dimensionless concentration and fluid velocity, respectively. Further, \(k_{\text{e1}}\) is the ratio of thermal conductivity of wall 1 and thermal conductivity of the porous solid, \(k_{\text{e2}}\) is the ratio of thermal conductivity of wall 2 and thermal conductivity of the porous solid and \(k\) refers to the effective thermal conductivity ratio of the fluid and the porous solid.

Analytical derivation of the dimensionless governing equations

Given the dimensionless equations defined in Table 1, Eq. (2) can be expressed as

$$n\frac{{{\text{d}}^{2} U}}{{{\text{d}}Y^{2} }} - \frac{U}{\text{Da}} + 1 = 0\quad - Y_{1} \le Y < Y_{1} .$$
(7)

Similarly, no-slip boundary conditions and axial symmetry conditions at \(Y = 0\) can be expressed as follows:

$$U\left( { \pm Y_{1} } \right) = 0,$$
(8a)
$$U ^{\prime } \left( 0 \right) = 0.$$
(8b)

Solution of Eq. (7) can be expressed with

$$U = {\text{Da}}\left( {1 - \frac{{\rm Cosh}(SY)}{{{\rm Cosh}(SY_{1} )}}} \right)\quad - Y_{1} \le Y < Y_{1} .$$
(9)

Using Eq. (8), the average dimensionless velocity across the channel equals

$$\bar{u} = {\text{Da}}\left( {1 - \frac{{\tanh (SY_{1} )}}{{SY_{1} }}} \right).$$
(10)

By combining Eqs. (9) and (10), the following ratio of absolute and mean is defined in Eq. (11):

$${\raise0.7ex\hbox{$u$} \!\mathord{\left/ {\vphantom {u {\bar{u}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\bar{u}}$}} = {\raise0.7ex\hbox{$U$} \!\mathord{\left/ {\vphantom {U {\bar{U}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\bar{U}}$}} = \frac{{SY_{1} \left( {{{\rm Cosh}}\left( {SY_{1} } \right) - {{\rm Cosh}}(SY)} \right)}}{{SY_{1} {{\rm Cosh}}\left( {SY_{1} } \right) - {{\rm Sinh}}(SY_{1} )}}.$$
(11)

Assuming the flow to be fully developed, as given the assumptions in Section “Assumptions”, the conditions stated are [1, 32]

$$\frac{{\partial T_{\text{f}} }}{\partial x} = \frac{{\partial \bar{T}_{\text{f}} }}{\partial x} = \frac{{\partial T_{\text{s}} }}{\partial x} = \frac{{\partial \bar{T}_{\text{s}} }}{\partial x} = \frac{{\partial T_{\text{w1}} }}{\partial x} = \frac{{\partial T_{\text{w2}} }}{\partial x} = \varOmega = {\text{Constant}}.$$
(12)

Subsequently, the temperature equation is [1]

$$T_{\text{i}} \left( {x,y} \right) = f_{\text{i}} \left( y \right) + \varOmega x\quad i = 1,2,s,f.$$
(13)

In Eq. (13), the function \(f_{\text{i}} \left( y \right)\) is obtained by solving Eq. (3a) with the resultant equation from combination of Eq. (3b) and (3c). By placing the heat flux boundary conditions in Eq. (5b) and (5d), we have

$$q_{1}^{\prime \prime } + q_{2}^{\prime \prime } = \rho_{\text{f}} C_{\text{p,f}} \mathop \int \limits_{{ - h_{1} }}^{{h_{1} }} u\frac{{\partial T_{\text{f}} }}{\partial x}{\text{d}}y.$$
(14)

Substituting the velocity from Eq. (11) into Eq. (14) and using the dimensionless parameters defined in Table 1, the following equation is taken:

$$\frac{{\partial \bar{T}_{{\rm f}} }}{\partial x} = \frac{1}{{2\rho_{{\rm f}} C_{{\text{p}},{\text{f}}} \bar{u}h_{1} h_{2} }}\left[ {h_{1} q_{1}^{\prime \prime } + h_{2} q_{2}^{\prime \prime } } \right] = \varOmega ,$$
(15)

where the average non-Newtonian fluid temperature is given as follows:

$$\bar{T}_{\text{f}} = \frac{1}{{2\bar{u}h_{1} }}\mathop \int \limits_{{ - h_{1} }}^{{h_{1} }} uT_{\text{f}} {\text{d}}y.$$
(16)

Using the dimensionless parameters of Table 1 and rearranging Eqs. (11) to (15), the dimensionless form of Eq. (3a) to (3d) is obtained.

$$k_{\text{e2}} \theta_{2}^ {\prime \prime} = 0, Y_{1} < Y \le 1$$
(17a)
$$k\theta_{\text{f}}^{\prime \prime } + {\text{Bi}}\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right) + D_{3} \text{Cosh} \left( {SY} \right) + D_{4} = 0, - Y_{1} \le Y < Y_{1}$$
(17b)
$$\theta_{\text{s}}^{\prime \prime } - Bi\left( {\theta_{{\rm s}} - \theta_{{\rm f}} } \right) = 0, - Y_{1} \le Y < Y_{1}$$
(17c)
$$k_{\text{e1}} \theta_{1}^{\prime \prime } = 0. - 1 \le Y < - Y_{1}$$
(17d)

Algebraic manipulating Eq. (17b) and (17c) gives

$$k\theta_{\text{f}}^{\prime \prime \prime \prime } - Bi\left( {1 + k} \right)\theta_{{\rm f}}^{\prime \prime \prime \prime } + \left( {S^{2} - Bi} \right)D_{3} \text{Cosh} \left( {SY} \right) - {\text{Bi}}D_{4} = 0,\quad - Y_{1} \le Y < Y_{1}$$
(18a)
$$k\theta_{\text{s}}^{\prime \prime \prime \prime } - {\text{Bi}}\left( {1 + k} \right)\theta_{\text{s}}^{\prime \prime } - {\text{Bi}}(D_{3} \text{Cosh} \left( {SY} \right) + D_{4} ) = 0\quad - Y_{1} \le Y < Y_{1} .$$
(18b)

The boundary conditions of Eq. (17a–17d) and Eq. (18a) and (18b) are expressed by the following relations.

$$\theta_{\text{f}} \left( { - Y_{1} } \right) = \theta_{\text{s}} \left( { - Y_{1} } \right) = 0, \theta_{\text{f}} \left( { - Y_{1} } \right) = \theta_{\text{s}} \left( { - Y_{1} } \right) = \theta_{\text{w2}}$$
(19a)
$$\theta_{\text{s}}^{\prime \prime } \left( { - Y_{1} } \right) = \theta_{\text{s}}^{\prime \prime } \left( {Y_{1} } \right) = 0,$$
(19b)
$$\theta_{{\rm f}}^{\prime \prime } \left( { - Y_{1} } \right) = \theta_{{\rm f}}^{\prime \prime } \left( {Y_{1} } \right) = - \frac{1}{k}\left( {D_{3} \text{Cosh} (SY) + D_{4} } \right),$$
(19c,d)
$$\theta_{1} \left( { - Y_{1} } \right) = 0, k_{\text{e1}} \theta_{1} \prime \left( 1 \right) = 2(1 - Q),$$
(19e,f)
$$\theta_{2} \left( {Y_{1} } \right) = \theta_{\text{w}2} , k_{\text{e}2} \theta_{2}^{{\prime }} \left( 1 \right) = 2Q,$$
(19g,h)

By applying Eq. (19a) to (19h), it is possible to solve analytically the dimensionless cross-sectional temperature profiles using Eqs. (17a), (17b) and (18a), as the following:

$$\theta_{2} \left( Y \right) = E_{1} + E_{2} Y, Y_{1} < Y \le 1,$$
(20a)
$$\theta_{{\rm f}} \left( Y \right) = E_{4} {{\rm Cosh}}\left( {SY} \right) + E_{5} {{\rm Cosh}}\left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{8} , - Y_{1} < Y \le Y_{1}$$
(20b)
$$\theta_{{\rm s}} \left( Y \right) = E_{10} {{\rm Cosh}}\left( {SY} \right) + E_{11} {{\rm Cosh}}\left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{12} , - Y_{1} < Y \le Y_{1}$$
(20c)
$$\theta_{1} \left( Y \right) = E_{13} + E_{14} Y. - 1 \le Y < - Y_{1}$$
(20d)

where alpha equals

$$\alpha = \sqrt {Bi(1 + k^{ - 1} )} .$$
(21)

By placing dimensionless cross-sectional temperature profiles of Eq. (20) inside Eq. (13), the final dimensionless temperature profiles are expressed by

$$\theta_{2} \left( {X,Y} \right) = \frac{2X}{{Re\Pr k Y_{1} \xi }} + E_{1} + E_{2} Y,Y_{1} < Y \le 1$$
(22a)
$$\theta_{{\rm f}} \left( {X,Y} \right) = \frac{2X}{{\text{Re} \,\Pr \,k Y_{1} \xi }} + E_{4} {{\rm Cosh}}\left( {SY} \right) + E_{5} {{\rm Cosh}}\left( {\alpha Y} \right) + E_{6} Y^{2} + E_{8} + E_{7} Y, - Y_{1} \le Y < Y_{1}$$
(22b)
$$\theta_{{\rm s}} \left( {X,Y} \right) = \frac{2X}{{\text{Re} \,\Pr \,k Y_{1} \xi }} + E_{10} {{\rm Cosh}}\left( {SY} \right) + E_{11} {{\rm Cosh}}\left( {\alpha Y} \right) + E_{6} Y^{2} + E_{12} + E_{7} Y, - Y_{1} \le Y < Y_{1}$$
(22c)
$$\theta_{1} \left( {X,Y} \right) = \frac{2X}{{\text{Re} \,\Pr \,k Y_{1} \xi }} + E_{13} + E_{14} Y. - 1 \le Y < Y_{1}$$
(22d)

The following equation is developed by applying Leibniz’s rule [34] on Eq. (4):

$$\left[ {\mathop \int \limits_{0}^{{h_{1} }} u\cdot C\cdot {\text{d}}y} \right] + K_{\text{R}} {\text{d}}x - \left[ {\mathop \int \limits_{0}^{{h_{1} }} u\cdot C\cdot {\text{d}}y + \frac{\partial }{\partial x}\left( {\mathop \int \limits_{0}^{{h_{1} }} u\cdot C\cdot {\text{d}}y} \right){\text{d}}x} \right] = 0.$$
(23)

The velocity profile along the microchannel is symmetrical, and therefore half of the channel is considered. The average velocity in half of the microchannel is given by

$$\mathop \int \limits_{0}^{{h_{1} }} u\cdot \frac{\partial C}{\partial x}\cdot {\text{d}}y = K_{\text{R}} .$$
(24)

The average flow velocity is defined as

$$\bar{u} = \frac{1}{{h_{1} }}\mathop \int \limits_{0}^{{h_{1} }} u.{\text{d}}y.$$
(25)

By setting \(C_{0}\) as the initial concentration, the following equation is revealed.

$$\frac{\partial C}{\partial x} = \frac{{K_{R} }}{{h_{1} \bar{u}}}.$$
(26)

Using the dimensionless parameters defined in Table 1, the concentration distribution yields

$$C\left( x \right) = \frac{{K_{\text{R}} x}}{{h_{1} \bar{u}}}.$$
(27)

Replacing Eq. (26) into Eq. (4), the distribution of dimensionless concentration function is given as

$$\phi \left( x \right) = \frac{\gamma X}{{PeY_{1} \xi }}.$$
(28)

Applying the dimensionless parameters of Table 1 and the ratio of velocity in Eq. (11), the dimensionless form of Eq. (4) is derived. That is

$$\frac{{uK_{R} }}{{h_{1} \bar{u}}} = D\frac{{\partial^{2} C}}{{\partial y^{2} }} - D_{T} \frac{{\partial^{2} T_{{\rm f}} }}{{\partial y^{2} }} .$$
(29)

Since the second derivative of the non-Newtonian, non-dimensional fluid temperature is determined from the form of Eq. (20b), only the dimensionless form of boundary conditions of Eq. (6a) and (6b) is required to solve Eq. (29). These are as follows:

$$\phi^{\prime \prime } \left( 0 \right) = \frac{Sr.k}{{Y_{1} .\varepsilon }}\theta_{\text{f}}^{\prime } \left( 0 \right),$$
(30a)
$$\phi \left( { - Y_{1} } \right) = 1.$$
(30b)

By applying parts (a) and (b) of Eq. (30), it is possible to determine analytically the second derivative of dimensionless concentration profiles on the cross section, which is

$$\phi^{\prime \prime } \left( Y \right) = \frac{Sr.k}{{Y_{1} .\varepsilon }}\theta_{\text{f}}^{\prime \prime } \left( Y \right) + \frac{{\gamma D_{1} \left( {{\text{Cosh}}\left( {SY_{1} } \right) - {\text{Cosh}}(SY)} \right)}}{{Y_{1}^{2} }}.$$
(31)

Finally, substituting Eq. (28) into Eq. (26), the dimensionless concentration equation, containing two transverse and axial cross sections, can be expressed as follows:

$$\phi \left( Y \right) = F_{1} + F_{2} Y + F_{3} Y^{2} + F_{4} {{\rm Cosh}}\left( {2SY} \right) + F_{5} {{\rm Cosh}}\left( {SY} \right) + F_{6} {{\rm Cosh}}(\alpha Y)$$
(32)
$$\phi \left( {X,Y} \right) = \frac{\gamma X}{{PeY_{1} \xi }} + F_{1} + F_{2} Y + F_{3} Y^{2} + F_{4} {{\rm Cosh}}\left( {2SY} \right) + F_{5} {{\rm Cosh}}\left( {SY} \right) + F_{6} {{\rm Cosh}}(\alpha Y)$$
(33)

Nusselt number

The heat convection coefficient on the upper and lower walls of the channel can be expressed by

$$H_{\text{w1}} = \frac{{q ^{\prime \prime }_{1} }}{{T_{\text{w1}} - \bar{T}_{\text{f}} }},$$
(34a)
$$H_{\text{w2}} = \frac{{q ^{\prime \prime }_{2} }}{{T_{\text{w2}} - \bar{T}_{\text{f}} }}$$
(34b)

Considering dimensionless parameters presented in Table 1, the Nusselt number is taken by

$${\text{Nu}}_{\text{w1}} = \frac{{2H_{\text{w1}} h_{1} }}{{k_{\text{ef}} }} = \frac{{4\left( {Q - 1} \right)Y_{1} }}{{k\bar{\theta }_{\text{f}} }},$$
(35a)
$${\text{Nu}}_{\text{w2}} = \frac{{2H_{\text{w2}} h_{1} }}{{k_{\text{ef}} }} = \frac{{4QY_{1} }}{{k\left( {\theta_{\text{w2}} - \bar{\theta }_{\text{f}} } \right)}}.$$
(35b)

The non-Newtonian fluid average temperature is obtained by the dimensionless form of Eq. (16) along the channel. That is

$$\bar{\theta }_{\text{f}} = \frac{{D_{1} }}{{2Y_{1} }}\mathop \int \limits_{{ - Y_{1} }}^{{Y_{1} }} \theta_{\text{f}} \left[ {{{\rm Cosh}}\left( {SY_{1} } \right) - Cos(SY)} \right]{\text{d}}Y.$$
(36)

Entropy generation

The entropy generation in the current system raises from various irreversible sources. The contribution of heat and mass transfer and friction between the fluid and solid surface to exergy destruction cause lower energy quality and weaker hydrothermal performance of the current system.

The potential sources of entropy generation in the typical microchannel are presented as the following:

$$\dot{S}_{\text{w2}}^{{{\prime \prime \prime }}} = \frac{{k_{2} }}{{T_{2}^{2} }}\left[ {\left( {\frac{{\partial T_{2} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{2} }}{\partial y}} \right)^{2} } \right],$$
(37a)
$$\dot{S}_{\text{S}}^{{{\prime \prime \prime }}} = \frac{{k_{\text{es}} }}{{T_{\text{S}}^{2} }}\left[ {\left( {\frac{{\partial T_{{\rm s}} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{{\rm s}} }}{\partial y}} \right)^{2} } \right] - \frac{{h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{S}} - T_{\text{f}} } \right)}}{{T_{\text{S}} }},$$
(37b)
$$\dot{S}_{\text{f}}^{{{\prime \prime \prime }}} = \frac{{k_{\text{ef}} }}{{T_{\text{f}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{f}} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{\text{f}} }}{\partial y}} \right)^{2} } \right] + \frac{{h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{S}} - T_{\text{f}} } \right)}}{{T_{\text{f}} }},$$
(37c)
$$\dot{S}_{\text{FF}}^{{{\prime \prime \prime }}} = \frac{{\mu_{\text{f}} }}{{\kappa T_{\text{f}} }}u^{2} + \frac{{\mu_{\text{eff}} }}{{T_{\text{f}} }}\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} ,$$
(37d)
$$\dot{S}_{\text{DI}}^{{{\prime \prime \prime }}} = \frac{R D}{C}\left[ {\left( {\frac{\partial C}{\partial x}} \right)^{2} + \left( {\frac{\partial C}{\partial y}} \right)^{2} } \right] + \frac{R D}{{T_{\text{f}} }}\left[ {\left( {\frac{\partial C}{\partial x}} \right)\left( {\frac{{\partial T_{\text{f}} }}{\partial x}} \right) + \left( {\frac{\partial C}{\partial y}} \right)\left( {\frac{{\partial T_{{\rm f}} }}{\partial y}} \right)} \right],$$
(37e)
$$\dot{S}_{\text{w1}}^{{{\prime \prime \prime }}} = \frac{{k_{1} }}{{T_{1}^{2} }}\left[ {\left( {\frac{{\partial T_{1} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{1} }}{\partial y}} \right)^{2} } \right].$$
(37f)

The dimensionless results of Eq. (37a–37f) are

$$N_{\text{i}} = \frac{{\dot{S}_{i}^{{{\prime \prime \prime }}} h_{2}^{2} }}{{k_{\text{es}} }},\quad i = w1, s, f, DI, w2$$
(38)
$$\omega = \frac{{\left( {q _{1}^{\prime \prime } + q _{2}^{\prime \prime } } \right)h_{2} }}{{2k_{\text{es}} T_{\text{w,in}} }},$$
(39)
$$\varphi = \frac{{RDC_{0} }}{{k_{\text{es}} }},$$
(40)

in which \(\dot{S}_{\text{w1}}^{{{\prime \prime \prime }}}\) and \(\dot{S}_{\text{w2}}^{{{\prime \prime \prime }}}\) are the volumetric entropy generation rate from the lower and upper walls. Further, \(\dot{S}_{\text{s}}^{{{\prime \prime \prime }}}\), \(\dot{S}_{\text{f}}^{{{\prime \prime \prime }}}\) and \(\dot{S}_{\text{DI}}^{{{\prime \prime \prime }}}\) are the volumetric entropy generation in the porous solid, fluid and due to mass transfer, respectively. Further, \(R\) denotes the specific gas constant, \(N\) refers to the dimensionless irreversibility, \(\omega\) is the dimensionless heat flux and \(\varphi\) is the irreversibility distribution ratio.

In order to provide a simple substrate for investigating the entropy generation and evaluating its distribution for different irreversible sources, the equations for the solid and fluid phases in the porous medium are described as follows:

$$N_{\text{w1}} = \frac{{k_{e1} \omega^{2} }}{{\left( {\omega \theta_{1} + 1} \right)^{2} }}\left[ {\left( {\frac{{\partial \theta_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{1} }}{\partial Y}} \right)^{2} } \right] , - 1 \le Y < - Y_{1}$$
(41a)
$$N_{{\rm s}} = \frac{{\omega^{2} }}{{\left( {\omega \theta_{{\rm s}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{{\rm s}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{{\rm s}} }}{\partial Y}} \right)^{2} } \right] - \frac{{Bi.\omega \left( {\theta_{{\rm s}} - \theta_{{\rm f}} } \right)}}{{\left( {\omega \theta_{{\rm s}} + 1} \right)}}, - Y_{1} \le Y < - Y_{1}$$
(41b)
$$N_{\text{f}} = \frac{{k\omega^{2} }}{{\left( {\omega \theta_{\text{f}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{f}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{{\rm f}} }}{\partial Y}} \right)^{2} } \right] + \frac{{{\text{Bi}}.\omega \left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)}}{{\left( {\omega \theta_{\text{f}} + 1} \right)}}, - Y_{1} \le Y < - Y_{1}$$
(41c)
$$N_{\text{DI}} = \frac{\varphi }{\phi }\left[ {\xi^{2} \left( {\frac{\partial \phi }{\partial X}} \right)^{2} + \left( {\frac{\partial \phi }{\partial Y}} \right)^{2} } \right] + \frac{\varphi .\omega }{{\left( {\omega \theta_{{\rm f}} + 1} \right)}}\left[ {\xi^{2} \left( {\frac{\partial \phi }{\partial X}} \right)\left( {\frac{{\partial \theta_{{\rm f}} }}{\partial X}} \right) + \left( {\frac{\partial \phi }{\partial Y}} \right)\left( {\frac{{\partial \theta_{\text{f}} }}{\partial Y}} \right)} \right], - Y_{1} \le Y < - Y_{1}$$
(41d)
$$N_{w2} = \frac{{k_{e2} \omega^{2} }}{{\left( {\omega \theta_{2} + 1} \right)^{2} }}\left[ {\left( {\frac{{\partial \theta_{2} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{2} }}{\partial Y}} \right)^{2} } \right] . Y_{1} \le Y < 1$$
(41e)

By adding Eqs. (41b) and (42c), the volumetric entropy generation expressions are defined as follows:

$$N_{\text{f, ht}} = \frac{{\omega^{2} }}{{\left( {\omega \theta_{\text{s}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{s}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{s}} }}{\partial Y}} \right)^{2} } \right],$$
(42a)
$$N_{\text{f, ht}} = \frac{{k\omega^{2} }}{{\left( {\omega \theta_{\text{f}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{f}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{f}} }}{\partial Y}} \right)^{2} } \right].$$
(42b)

The volumetric entropy generation in the porous media is equal to the sum of the equations applicable to the porous media.

$$N_{\text{int}} = \frac{{{\text{Bi}}.\omega^{2} \left( {\theta_{\text{f}} - \theta_{\text{s}} } \right)^{2} }}{{\left( {\omega \theta_{\text{s}} + 1} \right)\left( {\omega \theta_{\text{f}} + 1} \right)}}.$$
(43)

The total entropy generation defines the entropy produced by the heat transfer, viscous dissipative and concentration gradient for each point in the \(X\) and \(Y\) directions. That is

$$N_{\text{pm}} = N_{\text{s,ht}} + N_{\text{f, ht}} + N_{\text{int}} + N_{\text{DI}} .$$
(44)

The total entropy generation on the whole microchannel is obtained by sweeping two-segmental integration on the physical domain, which equals

$$N_{\text{Tot}} = \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{0}^{1} N_{\text{pm}} {\text{d}}X{\text{d}}Y.$$
(45)

Numerical simulation and validation

The equations derived analytically in Section “Theoretical and numerical methods” provide the general solution of the dimensionless governing equations. Although it is possible to derive fully analytical solutions for the current problem, the non-Newtonian nature of the considered fluid makes such solution immensely complicated and therefore of little use. Hence, to evaluate the unknown coefficients and find the particular solutions, a numerical approach was taken. The details of numerical methodology along with the specification of the system configuration are given in this section.

Description of the system configuration

Figure 1 shows a schematic of the geometry considered in the current study. The microchannel is fully filled with porous materials, with two thick walls, subjected to constant but non-equal heat fluxes with a catalytic layer on the inner microchannel surface. A non-Newtonian, power-law fluid flow enters the left side of the microchannel and, after passing through the porous media, leaves from the right side of the system.

The problem outlined in Section “Theoretical and numerical methods” was solved using various non-dimensional and dimensional parameters that are presented for quantitative analysis by the default values in Tables 2 and 3, respectively. It is noted that the values of parameters in Table 2 were chosen in a way that the results become comparable with the existing data in the literature for Newtonian fluids [1, 3].

Table 2 Default values of the dimensionless parameters
Full size table
Table 3 Default values of the dimensional parameters
Full size table

Grid independency and validation

The non-dimensionalized governing equations derived in Section “Theoretical and numerical methods” (Eqs. (7), (17a), (17b), (18a) and (18b) and (31) along with boundary conditions of Eq. (19)) were solved numerically through using a finite volume technique. Four mesh densities including 20 × 300, 30 × 400, 40 × 500 and 45 × 550 grids were tested. It was observed that the mesh sizes of 40 × 500 and 45 × 550 are perfectly consistent and have a relative error of 1.35% for Nusselt number. Thus, in the current study a mesh containing 40 × 500 cells was used (Fig. 2).

Fig. 2
figure 2

Grid independency test

Full size image

The present numerical data are compared with the closed-form analytical results of Hunt et al. [1] for Nusselt number and entropy generation (Figs. 3 and 4) in the limit case that power-law fluid approaches a Newtonian fluid at different values of wall thickness (Y1). Evidently, the two data sets exhibit very good agreement and thus the analytical solutions are deemed to be valid.

Fig. 3
figure 3

Comparison of Nusselt number between the present work and the results of Hunt et al. [1] in three different values of wall thickness, (Y1)

Full size image
Fig. 4
figure 4

Comparison of entropy generation between the present work and the results of Hunt et al. [1] in three different values of wall thickness, (Y1)

Full size image

Results and discussion

In this section, an emphasis is put on the influences of non-Newtonian fluid characteristics upon the thermal behavior of the micro-system. In the interest of brevity, other effects are not discussed.

Detailed comparison of transport phenomena and entropy generation between Newtonian and power-law fluids

Figure 5 shows the dimensionless temperature contours drawn for the solid and fluid phases of the porous medium for different values of power index. It should be noted that the dimensionless temperature in this figure can take negative or positive values. The temperature contours in Fig. 5 indicate that with increasing power index, as the fluid tends to thicken and increase the viscosity and thus increase the shear stress, the heat transfer rate decreases. This can be deduced from the fact that the fluid temperature takes larger values of dimensionless temperature at higher values of power index. Since the dimensionless temperature expresses the difference between the temperature of fluid and that of the wall, higher values of dimensionless temperature imply larger difference between fluid and wall temperature. For the current iso-flux problem, this means weakened convective heat transfer. This argument will be later supported by calculation of Nusselt number.

Fig. 5
figure 5

Contours of dimensionless temperature for varying values of the power-law index (n) at (\(Y_{1} = 0.7),\)a solid phase \(n = 0.5\), b fluid phase \(n = 0.5\), c solid phase \(n = 1.0\), d fluid phase \(n = 1.0\), e solid phase \(n = 1.5\), f fluid phase \(n = 1.5\)

Full size image

Figures 6 and 7 show the contours related to the local entropy generation inside the fluid phase of the microchannel. It is important to note that entropy generation is only calculated for the fluid phase and porous media and the solid wall are excluded from the analyses of local entropy generation. Also, as depicted by Eq. (41d) the mass transfer irreversibilities are included in the current analysis.

Fig. 6
figure 6

Contours of local entropy generation for the fluid phase for varying Damköhler number, \(\gamma\), a \(n = 1.0, \gamma = 0.8\), b \(n = 1.3, \gamma = 0.8\), c \(n = 1.0, \gamma = 1.2\), d \(n = 1.3, \gamma = 1.2.\)

Full size image
Fig. 7
figure 7

Contours of local entropy generation for the fluid phase for varying Soret number, \(Sr\), a \(Sr = 0.5 , n = 1.0\), b \(Sr = 0.7 , n = 1.3\), c \(Sr = 0.5 , n = 1.0\), d \(Sr = 0.7 , n = 1.3\)

Full size image

Figure 6 shows the total entropy variations for the two power-law indices with two different Damköhler numbers for the fluid phase. It is clarified that the value of Damköhler number influences the rate of mass transfer and thus can affect the irreversibility. As can be seen in this figure, for a value of Damköhler number less than one, an increment in the value of the power-law index intensifies the generation of entropy. This is due to the enhancement of friction irreversibilities at higher values of power-law index. More importantly, as shown earlier, the rate of heat transfer decreases at higher values of power-law index, which in turn strengthens the temperature gradients and thus increases the generation of entropy. Interestingly, this behavior is inversed at higher value of Damköhler number. This is because of the dominance of mass transfer in entropy generation in the current problem [1, 35, 36], which can overrule other effects.

Figure 7 illustrates the influences of changes in Soret number upon the local entropy generation in the fluid phase. This has been done for two different values of the power-law index corresponding to Newtonian and non-Newtonian fluids. Figure 7 indicates that for a constant power-law index, in either of Newtonian and non-Newtonian fluids, Soret number growth causes a reduction in the local irreversibility. This can be explained by noting that in the current problem irreversibility is dominated by that of mass transfer [34,35,36]. Magnifying the value of Soret number enhances the process of mass transfer and hence reduces the irreversibility associated with the transport of mass. Thus, the local entropy generation drops. Further, Fig. 7 shows that increasing the value of power-law index at a fixed Soret number leads to a slight intensification of the local entropy generation. As already discussed, this is mostly due to the magnification of thermal irreversibilities following the fluid temperature gradient strengthening.

According to Fig. 8, increasing the power-law index results in the reduction in Nusselt number. This reduction can be quite significant such that by increasing the power-law index from 0.4 to 1.8, a drop of around 50% is observed in Nusselt number for all the investigated cases. This is an important result and shows that deviation from the state of Newtonian fluid can majorly affect the rate of heat transfer. Hence, close attention should be paid to possible non-Newtonian behaviors of the working fluids in microchannels and microreactors. Figure 8 further shows the pronounced effects of the wall thickness upon Nusselt number. In keeping with the results reported in the literature [33, 34], it is shown that thicker walls act as thermal resistance and thus tend to reduce the Nusselt number. This figure clearly shows that alteration of wall thickness by around 30% can change the value of Nusselt number by more than 40%. Thus, wall thickness is an essential parameter dominating the rate of heat transfer in microchannels.

Fig. 8
figure 8

Nusselt Number against the power-law index (n) for different values of wall thickness, (Y1)

Full size image

Figure 9 illustrates the effects of power-law index on the total generation of entropy. Clearly, variations in the power-law index strongly affect the total entropy generation. According to this figure, an increase in the power-law index from 0.4 to 1.8 can boost the total entropy by more than 50%. As already discussed, decreasing Y1 (thickening the walls) also contributes to this increase. Once again, impediment of heat convection process by increases in the value of power-law index (as already discussed) is responsible for this trend.

Fig. 9
figure 9

Total entropy generation against the values of power-law index (n) for different values of wall thickness, (Y1)

Full size image

Parametric studies on the effects of physical properties of power-law fluids

In Fig. 10, temperature contours for non-Newtonian fluids for two different values of Y1 are depicted. The right-hand side contours correspond to the solid phase, and the left-hand side contours correspond to the fluid phase. It is observed that by increasingY1, that is by making the wall thinner, the deflection of temperature contours increases. Thus, at any cross section in the microchannel, the transversal temperature variation increases. As shown previously [1, 34, 35] and also further supported in the later sections, this causes an increase in the overall heat transfer rate of the system.

Fig. 10
figure 10

Contours of dimensionless temperature at \(n = 0.5\) for varying values of the wall thickness, Y1, a solid phase \(Y_{1} = 0.6\), b fluid, \(Y_{1} = 0.6\), c solid phase, \(Y1 = 0.9\), d fluid phase, \(Y_{1} = 0.9\)

Full size image

Figure 11 shows the distribution of dimensionless fluid temperature inside the porous microchannel for different values of Reynolds number and the power-law index. This figure essentially compares the case of Newtonian fluid to that of non-Newtonian fluid. Evidently, regardless of the value of Reynolds number, the axial temperature increase along the microchannel for the non-Newtonian fluid is larger than that of the Newtonian fluid. For the current constant heat flux problem, this implies smaller convection coefficient for the non-Newtonian fluid flow. This finding will be later verified by calculating the Nusselt number for the two types of fluid. Further, the increase in Nusselt number has resulted in a general drop of the dimensionless temperature at any given point inside the microchannel. This is to be expected, as in general, increases in Reynolds number (on the basis of the microchannel height) lead to improved heat convection coefficient and thus result in lower temperatures.

Fig. 11
figure 11

Contours of dimensionless temperature for the fluid phase for varying Soret number, \(Sr\), a Re \(= 50 , n = 1.0\), b Re = 50, \(n = 1.3\), c Re \(= 100 , n = 1.0\), d Re = 100, \(n = 1.3\), e Re \(= 150 , n = 1.0\)f Re = 160, \(n = 1.3\)

Full size image

Figure 12a shows the effect of variation in the wall heat flux on the Nusselt number. As can be seen by increasing the value of wall heat flux ratio, Q, performed by strengthening the thermal asymmetry of the problem, the Nusselt number increases. This increment in Nusselt number is a consequence of changes in the shape of temperature contours and resultant modification of temperature gradient on the surface of the wall [33,34,35,36]. The effects of Darcy number on the Nusselt number are demonstrated in Fig. 12b.

Fig. 12
figure 12

Nusselt number versus the lower wall thickness, Y1, a on the upper wall for different values of Q, b on the lower wall for different values of Darcy number, c on the upper wall for different values of thermal conductivity of the porous medium, ks (W m−1 K−1)

Full size image

As can be seen, the smaller the Darcy number, meaning the lower the permeability, the rate of heat transfer is increased. This is a well-known behavior of the Nusselt number [1, 5, 11, 15] and shows the consistency of the current Non-Newtonian simulations with those conducted earlier on Newtonian fluids. In Fig. 12c, the effect of variations in the conductivity coefficient of the solid part of the porous media (\(k_{{\rm s}}\)) is presented. This graph shows that with augmentation of \(k_{{\rm s}}\) the value of Nusselt number increases. This can be attributed to the increase in heat transfer between the fluid and the solid part of the porous medium, which is enhanced by boosting the conductivity of the porous solid [37, 38].

Figure 13 shows the influences of power-law index upon the values of Nusselt number and total entropy generation against the Reynolds number. As a general trend, both Nusselt number and total entropy generation increase monotonically with Reynolds number. It is to be expected that Nusselt number in forced convection is often strongly correlated with flow Reynolds number. However, the growth of total entropy generation with Reynolds number may sound counterintuitive. This is because Nusselt number rising relaxes the internal temperature gradients inside the microchannel, and this results in the thermal irreversibility reduction. These apparently contradicting observations can be justified by noting that the entropy generation in the current problem is dominated by flow friction and not heat transfer. Switching to non-Newtonian fluid intensifies the flow friction and thus magnifies the total generation of entropy [39]. Evidently, for all Reynolds numbers, the application of non-Newtonian fluid (n = 1.3) leads to a smaller value of Nusselt number (see Fig. 13a). The reduction in heat transfer and the resultant increase in the internal temperature gradient, as well as increases in the frictional losses of the flow due to non-Newtonian effects, are the reasons for augmentation of entropy generation in comparison with that of Newtonian fluid [40, 41].

Fig. 13
figure 13

a Nusselt number and b Total entropy generation versus the Reynolds number for different values of non-Newtonian fluid (n = 1.3) and Newtonian fluid (n = 0.5) indices

Full size image

Conclusions

Transport of heat and mass and thermodynamic irreversibilities in a parallel-plate microreactor filled by a homogenous porous medium and with a non-Newtonian working fluid were investigated. The considered configuration was assumed to be geometrically and thermally asymmetric. The power-law behavior was assumed for the fluid, and the porous medium was set under local thermal non-equilibrium. A set of governing equations were first derived theoretically. The resultant nonlinear system of partial differential equations was then solved numerically through using a finite volume solver. This led to the development of two-dimensional solutions for the temperature concentration and local entropy generation fields and evaluation of Nusselt number and total entropy generation. The numerical results were validated against the existing fully analytical solutions for the Newtonian fluids. It was shown that increases in the value of power-law index reduce the rate of heat transfer and thus drop the value of Nusselt number. Hence, the local and total generations of entropy are both strongly affected by the value of power-law index in which increases in this parameter highly enhance the local and total irreversibilities. The other qualitative characteristics of the investigated system were found to remain consistent with those reported for the Newtonian fluids.