Introduction

Environmental concerns and the advancement of the prevailing technologies are complementary to each other, which are to be comprehensively addressed in the present time. As the necessities of mankind increase with the population size of society, so is the scope of evaluating the new alternative resources. However, there are many areas where the transition period demands the optimisation and refinement of the conventional methodologies. One of such areas which drew the attention of the twenty-first century is the energy sector. The energy sector itself has several ancillary units to serve the miscellaneous activities of society. The role of the energy sector in the industrial revolution of the world is remarkable and unforgettable. But on the other hand, every success has some hidden aspects which have been vexing the whole world for a long time. In 1959, carbon dioxide (CO2) concentration in the atmosphere was 316 ppm of air that reached 400 ppm in 2013, which is equal to 27% increase in just over half a century and more than 50% higher than the global pre-industrial level. Owing to differences in isotopic composition of carbon in the biosphere and the fossil fuel, the increment in CO2 concentration has been observed and it may keep increasing by two–three times of the current levels if the overdependence on the fossil fuel is not discouraged. However, there is an advent of various coal types and other conventional fuel improvement technologies, but their installation cost is very high. The physical laws of thermodynamics and radiative exchanges provide a basic tenet that if the concentration of long-wave radiation trapping gases, such as CO2, is increased, the global temperature will also be affected. If this is not addressed, the food supply, biodiversity and the ecosystem will be under flak. As the CO2 neutraliser or the medium of balancing the carbon cycle, bioenergy derived from plants could be a promising scheme. Plants store the solar energy to absorb CO2 and trap chemical energy in the form of plant biomass. When the biomass or secondary fuel derived from the biomass undergoes oxidation, the same CO2 which the plant had absorbed in its whole life is returned to the atmosphere.

Apart from coal and oil, biomass is the third largest reservoir of energy in the world [1]. Until the middle of the nineteenth century, biomass dominated global energy consumption. Owing to industrialisation, biomass consumption is outshone by fossil usage, yet it provides about 1.25 billion tonnes of oil equivalence or about 14% of the world’s annual energy consumption [2,3,4]. The USA and Sweden obtain about 4% and 13% of their energy, respectively, from biomass [5]. Sweden has decided to decommission the nuclear power plants, reduce fossil-fuel utilisation and encourage the use of biomass energy [6]. Therefore, it is necessary to discuss the conversion technologies that can convert biomass into useful end products. But before that, it is inevitable to study the chemical composition and the kinetic behaviour of biomass during the thermal degradation in the absence of air, i.e. pyrolysis of biomass. Pyrolysis is very similar to cracking process. But it becomes difficult to evaluate mathematically, since the occurrence of simultaneous reactions make the pyrolysis more complex. Thus, it is indispensable to analyse a system at the microscopic level. Thermal history and the kinetics of parallel reactions affect chemical attributes of a bio-material. Hence, the mathematical model must be generalised for the complex thermal history so that the obtained solution can simulate the pyrolysis efficiently without any noisy data [7].

The objective of this study is to generalise the numerical solution for the complex thermal history so that the different possibilities can be explored from the industrial perspective. The multi-step reaction scheme is to be evaluated through the Laplace integral method. The non-monotonicity behaviour of activation energies due to the set of the competitive reactions is explored through the dynamic nature of a moving maximum with time. The overlapping of parallel independent reactions and the concurrent reactions brings inconsistency in the activation energies with conversion as a function of temperature; therefore, a robust methodology is developed through an advance calculus scheme for solving the chemical kinetics problems.

Materials and methods

Thermal analysis

Thermal analysis implies the detailed anatomy of alteration of the physical property of a biomass, which is subjected to an imposed thermal history. Variation in thermal history involves either a stepwise alteration of one constant temperature to another, a linear rate of change in temperature and modulation of a constant or linearly varying temperature with constant frequency and amplitude, or uncontrolled heating or cooling. Therefore, interpretation of physical properties is not only related to monitoring of property but also includes structural analysis of sample which is not merely function of property of biomass alone. Moreover, the ambience temperature of the substrate (combustion chamber) is of main concern than the actual sample temperature which is programmed [8]. The temperature may also be altered so that a constant rate of reaction can be retained during thermal degradation of material. This type of programmed history is called sample-controlled program. Thermodynamic aspect of thermal analysis and calorimetry is comprehensively explained by van Ekeren [9]. However, chemical kinetics and thermodynamic characteristic of reactions are intertwined, although the parametric influence is to be unveiled.

Reaction kinetic has a pivotal role in gathering information about the reaction mechanism, which in turn provides a passage to modify the pathway of the chemical reactions or assists in predicting the behaviour of the similar reactions, which do not yet occur with the course of time. The values of kinetic parameters for the reaction of interest can also be determined. The kinetic parameters, which may let the rates of reaction to be simulated under the different conditions, are calculated through interpolation or extrapolation of the numerical solution. However, obtaining of the detailed information and calculation of kinetic parameters are loosely related to each other, as the reaction mechanism is mostly mandated by the mathematical modelling of the kinetic reactions. Therefore, there is always some scope of incongruence remaining in the results. The most common way of carrying out thermal analysis is to study the heterogenous reactions which involve at least a solid reactant [10, 11]. The reaction temperature mainly exhibits monotonic attribute (either decreasing or increasing) with time. Unlikely, the homogenous kinetics involves simultaneous increasing of product or decreasing of reactants at the constant temperature. The rate equations of the heterogenous kinetics are often programmed for non-isothermal kinetics. However, a similar methodology is involved in the homogenous kinetics, but the limitation of the thermal analysis technique is confined to the study of the initial solid samples; therefore, the heterogenous system must be examined. Some of main reasons are that the heterogenous reactions offer incoherent environment, which can vary with the state variables. However, the pure form of fluid also undergoes the change in ambience conditions, yet the structural transformations (cracks, defects and trapped radicals) are essentially absent in liquid [12]. Real solid-state reaction follows the multi-step reaction, which is usually governed by the concurrent reactions in thermal degradation of biomass. Therefore, the inconsistency in evaluating kinetic parameters demands a robust functional form for parameterising the reaction rate.

When a solid substrate undergoes thermal treatment, it decomposes with time, thus providing sundry intermediate products which further react with unreacted substrate to form a set of competitive reactions. For a heterogenous class of reactions, the concentration of reactant (or product) does not play a pivotal role in determining the extent of reaction. Usually, the fraction of reactant partake in the chemical rearrangement is of main concern; that is, the initial mass and the residual mass of solid sample when reaction is completed, or the amount of gas evolved, or heat absorbed or evolved must be properly defined in the context of the reaction stoichiometry. The serious problem arises when the composition of products changes with the extent of reaction, or the gaseous products of a reversible reaction are not being scavenged from the chamber, where the sample is kept, or if the kinetic energy varies rapidly and reactant either gets melted or sublimated. Anomality of products and reactants in heterogenous reactions may lead to variation in geometry (structural defects) of crystal structure of a single pure solid; thus, it affects physical properties, mainly thermal stability [13]. Generally, it has been observed that the decomposition of solid reactant occurs at defective sites of the crystal, such as dislocation at surface. The nuclei of product, B, are formed in such a way that the escaped gas causes the structural deformation of the unreacted reactant, A, which results in progradation of the nuclei sites. Therefore, the process of nucleation and growth manifests rate of reaction that governs evolving of the product gas, C [11]. Instead of surface reactions, some other chemical reactions take place at the interface between reactant and product sides; such physical processes are diffusion and heat transfer. These processes influence the kinetic modelling of thermal degradation of biomass.

$$A\left( s \right) \to B\left( s \right) + C\left( g \right)$$

The solid-state reaction follows the multi-step reaction pathway which usually has varying Arrhenius parameters, e.g. formation and growth of nuclei. Detailed information about kinetic models of solid decomposition is reported in the literature [14,15,16]. When a solid sample undergoes thermal treatment, the amplitudes of the vibration of the lattice increase proportionally with temperature, which finally allows physical as well as chemical transformation of sample. Phase transition, melting, sublimation and thermal decomposition are some of processes, related to rearrangement of atoms and molecules [11, 12, 17], which are the function of thermal and kinetic energies availed through thermal stimuli. Thermal decomposition takes place whilst bonding force within constituent molecules or ions which are weaker than interatomic forces between the atoms of solid sample. Increasing temperature may lead to redistribution of bond and the formation of products which are chemically different from the reactant. Such phenomenon is referred as thermal decomposition (or crystolysis reactions) [18]. Much of kinetic information related to chemical transformation is furnished by thermal analysis of the sample [17]. Succinctly, the course of development of non-isothermal kinetic analysis and mathematical scheme associated with it is mentioned in the current literature [17, 19,20,21,22,23]. Whilst carrying out experiments in non-isothermal conditions, Garn and Hulber [24] reported the limitation of heat transfer from the furnace to the outer areas of the sample and then into the sample accompanied with self-cooling or self-heating of the sample during reaction. Therefore, it is difficult to precisely measure the sample temperature. Moreover, scavenging of evolved product gases from the neighbourhood of the sample and the intervention of gaseous products, for highly reversible reactions, in the rate of reaction are some initial complication arisen during non-isothermal approach [24]. On the other hand, Vyazovkin and Wright [19] expressed their concern related to the isothermal approach. A major problem of the isothermal experimentation is the time limitation, as a sample needs some time to reach the desired temperature. During this span of time, the sample experienced some initial transformation, which is likely to influence the kinetic analysis. This situation is compounded under isothermal condition and a typical solid-state process confined the application of higher temperature regime, as the maximum reaction rate is obtained at the onset of the transformation stage [19]. According to their unbiased perspective, the non-isothermal heating curtails this problem, and therefore it can rather be used in the field of solid-state kinetic than the classic isothermal experiments. However, the merit of non-isothermal approach is overshadowed by the associated computational difficulties with the kinetic analysis [19].

Analysis of kinetic behaviour is mainly inferred through experimental techniques. Thermally activated kinetics reactions are determined with help of thermogravimetry (TG), differential scanning calorimetry (DSC) and differential thermal analysis (DTA). These techniques are mainly used for knowing the change in the physical and thermal properties of the sample, but they are not suitable for analysing the chemical species evolved during the reaction. Therefore, sometimes the thermal analysis techniques are carried out along with chemically specific detection units. Fourier transform infrared (FTIR), mass spectrometry (MS) and gas chromatography are employed to analyse the gaseous product. To analyse the solid reaction products, X-ray diffractometry (XRD), FTIR and electron paramagnetic resonance (EPR) are also used as the complementary techniques, whereas thermogravimetric (TG), differential scanning calorimetry (DSC), derivative thermogravimetry (DTG) and differential thermal analysis (DTA) provide the information of the overall (global) kinetics of thermally stimulated reactions. For in-depth study of solid-state reactions, these techniques can be accompanied with commentary methods. The information imparted through chemically specific units is helpful to explore the overall kinetic scheme [25,26,27,28,29]. The TG technique mainly records measured mass loss from a sample due to gas formation as function of time or temperature for the predefined thermal history. The overall reaction rate determined by TG correlates with the rate of gas formation. However, many heterogenous reactions have partial conversion to the gas phases; thus, TG can widely be used. However, the DTG method correlates the sample temperature with the reference material (Tin or Indium) per unit mass of sample when both are subjected to the same heat flux. DSC measures the power \(\left( {\Phi _{\rm{S}} -\Phi _{\rm{R}} } \right)\) required to keep the sample and the reference material at the same temperature throughout the imposed temperature program. The nature (exergonic or endergonic) as well as enthalpy of reaction can be determined by DTA and DSC. In the following section, a polynomial profile of temperature is examined on the basis of nonlinear differential equation of heating rate.

Suppose thermal profile follows the polynomial form, and let \(T_{\rm{n}}\) be continuous and n times differential function of time (t) in the domain of \({\mathbb{R}}\); then, it can be expressed as

$$T_{\rm{n}} \left( K \right) = a_{0} t^{\rm{n}} + a_{1} t^{{\rm{n}} - 1} + a_{2} t^{{\rm{n}} - 2} + \cdots + T_{0}$$
(1)

where the coefficients of polynomial equation (Eq. (1) \(a_{0} , a_{1} , a_{2} , \ldots a_{{{\rm{n}} - 1}}\) are \(a_{0} = \frac{{\beta^{n - 1} }}{n!},\;a_{1} = \frac{{\beta^{n - 2} }}{{\left( {n - 1} \right)!}},\;a_{2} = \frac{{\beta^{n - 3} }}{{\left( {n - 2} \right)!}}, \ldots a_{{{\rm{n}} - 1}} = \beta\), respectively.

The relationship between difference in successive thermal histories and the recurrence form of heating rate is expressed by Eqs. (2), (3) and (4)

$$\mathop \sum \limits_{{{\rm{i}} = 1}}^{i = n - 1} \left( {T_{{{\rm{i}} + 1}} - T_{\rm{i}} } \right) = \frac{1}{n!}\frac{{{\rm{d}}^{{\rm{n}} - 1} \beta }}{{{\rm{d}}t^{{\rm{n}} - 1} }}\mathop \sum \limits_{{{\rm{i}} = 1}}^{i = n - 1} \left( {t^{{\rm{i}} + 1} } \right)$$
(2)

Differentiating Eq. (2) w.r.t. ‘t’, we have

$$\mathop \sum \limits_{{{\rm{i}} = 0}}^{i = n - 1} \left( {\beta_{{{\rm{i}} + 1}} - \beta_{\rm{i}} } \right) = \frac{1}{n!}\left( {\frac{{{\rm{d}}^{{\rm{n}} - 1} \beta }}{{{\rm{d}}t^{{\rm{n}} - 1} }}} \right)\mathop \sum \limits_{{{\rm{i}} = 1}}^{n - 1} \left( {i + 1} \right)t^{\rm{i}} + \frac{{{\rm{d}}^{\rm{n}} \beta }}{{{\rm{d}}t^{\rm{n}} }}\mathop \sum \limits_{{{\rm{i}} = 1}}^{i = n - 1} \left( {t^{{\rm{i}} + 1} } \right)$$

As \(\beta\) is continuous and (n − 1) times differentiable in interval \(I \in \left( { - \infty , \infty } \right)\), hence

$$\mathop \sum \limits_{{{\rm{i}} = 0}}^{i = n - 1} \left( {\beta_{{{\rm{i}} + 1}} - \beta_{\rm{i}} } \right) = \frac{1}{n!}\left( {\frac{{{\rm{d}}^{{\rm{n}} - 1} \beta }}{{{\rm{d}}t^{{\rm{n}} - 1} }}} \right)\left[ {\frac{{\left\{ {\left( {n + 1} \right)t^{\rm{n}} - nt^{{\rm{n}} + 1} - t^{2} + t - 1} \right\}}}{{\left( {t - 1} \right)^{2} }}} \right]$$
(3)
$$\frac{{2t\left( {\mathop \sum \nolimits_{{{\rm{i}} = 1}}^{i = n} \left( {\beta_{\rm{i}} - \beta_{{{\rm{i}} - 1}} } \right)} \right)}}{{n\left( {n + 3} \right)}} = \left( {\mathop \sum \limits_{{{\rm{i}} = 1}}^{i = n} \left( {T_{\rm{i}} - T_{{{\rm{i}} - 1}} } \right)} \right)$$
(4)

The non-homogenous linear differential equation in terms of heating rate (β) is given by Eq. (5)

$$\begin{aligned} & \beta^{{\rm{n}} - 1} + \left( {n - 1} \right)m_{0} \left( t \right)\beta^{{\rm{n}} - 2} + \left( {n - 1} \right)\left( {n - 2} \right)m_{1} \left( t \right)\beta^{{\rm{n}} - 3} \\ & \quad + \cdots + m_{{{\rm{n}} - 1}} \left( t \right)\beta^{\prime} = \left( {n - 1} \right)!\left( {\beta_{\rm{n}} - \beta_{0} } \right) \\ \end{aligned}$$
(5)

where \(\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = \beta\).

Let ‘\(\theta\)’ be the solution of (n − 1)-order differential Eq. (5), then by principle of superposition complete solution of Eq. (5) is given by

$$\theta \left( t \right) = \theta_{\rm{CF}} + \theta_{\rm{PI}}$$

Kinetic analysis

Variation in the thermal profile changes the course of kinetic analysis; however, distortion of kinetic analysis due to time lag or ‘warm-up’ span is prevented. But experiments conducted at different heating rates may lead to fallacious conclusion as undulation of temperature gradient in the sample affects the kinetics behaviour of the parallel reactions at different extents of reaction. The uniqueness of the experimentally derived values of the Arrhenius parameters or the functional forms, \(g\left( \alpha \right)\) and \(f\left( \alpha \right)\) used for evaluating the kinetic parametes from a single thermal history should be studied. It is clearly illustrated that the same TG pattern could be drawn using three different kinetic models with different Arrhenius parameters [30]. Thermoanalytical data alone are not sufficient enough to delineate reaction mechanism. However, the proposed scheme, whose prediction abilities rely upon robust nature of its functional form used for parameterisation, can be congruent with kinetic data.

$$\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = \frac{A}{\beta }{\rm{e}}^{{ - \frac{\rm{E}}{\rm{RT}}}} f\left( \alpha \right)$$
(6)
$$g\left( \alpha \right) = \mathop \smallint \limits_{0}^{\alpha } \frac{{{\rm{d}}\alpha }}{f\left( \alpha \right)}$$
(7)

The methodology involved to analyse the kinetic data is distinguished on the basis of differential \(f\left( \alpha \right)\) [Eq. (6)] and integral \(g\left( \alpha \right)\) [Eq. (7)] functional forms. But these functional forms create uncertainty whilst calculating kinetic parameters, as it refers to the type of experimental data used. Thus, a new classification based on the estimation of kinetic parameters imbibes the notion of ‘discriminatory and non-discriminatory’ schemes. Here, the discriminatory scheme is based on the phenomenological models, which can either be a method of ‘synthesis’ or method of ‘analysis’. Method of synthesis relies on a single model, where a single model is used for force-fitting. On the other hand, several other models are combined to provide a better illustration of data which is referred to as a method of ‘synthesis’. Further, the non-discriminatory methods center around the invariance of the extent of reaction with temperature. In other words, non-discriminatory methods are isoconversional models, which ascertain that the characteristics of reaction are not necessarily defined by the differential \(\left( { f\left( \alpha \right)} \right)\) and integral functional forms \(\left( { g\left( \alpha \right)} \right)\) [31]. The relative importance of derivative methods to integral forms is known by the fact that approximations to the temperature integral are not required. Moreover, the measurements are also intact of cumulative error arisen due to speculated boundary conditions for integral [Eq. (7)] [32]. Implementation of numerical tools to solve integral equation generates data which are to be filtered before performing further analysis. On the contrary, the derivative methods may be more sensitive to determining the kinetic model [33], but filtering may cause distortion [34]. Assessment of thermal conversion process pivots on the methodology adopted to analyse the kinetic data. Dhaundiyal et al. [22] used approximations to temperature integral through the bivariant nature of activation energies and concluded that kinetic parameters evaluated through methodology are very near to a solution obtained by derivative methods [14]. If the robust mathematical technique is applied to a given model, the obtained solution can converge to the differential schemes. Despite some mathematical schemes [35, 36] exhibit deviation in calculating kinetic parameters from the same set of experimental data. Several models which are considered to mandate a reaction pathway have been criticised [31]. A model can only be emerged as a true model if there is lack of alternatives. However, any model can also be consistent with the kinetic data only if fitting is the main concern. Error can be introduced by both differentiation and integration if the procedure is faulty. A minimum requirement of any method is that successive differentiation and integration of integral data must provide the original integral data [37].

Both the kinetic models (isoconversional and model fitting) for a condensed phase reaction suffer from the same problem, that is, inconsistent values of kinetic parameters. Isoconversional methods are also called model-free kinetics since they do not rely on fitting of data to phenomenological models. The tenet of this methodology is that at any given extent of reaction (α), the same reactions occur in the same ratio, which is independent of temperature. However, a set of parallel independent reactions show the change in relative reactivity as a function of temperature due to variation in activation energies [38], whereas the overall reaction pathway of the concurrent or competitive reactions have different activation energies which change with the temperature [39]. However, the isoconversional methods are mainly recommended to develop a robust kinetic model [40]. Another method for analysing the kinetic data was given by Coats–Redfern method [41], which relies upon fitting of data obtained at single heating rate to Eq. (8)

$$\ln \left[ {\frac{{\ln \left( {1 - \alpha } \right)}}{{T^{2} }}} \right] = \frac{ - E}{\rm{RT}} + \ln \left[ { - {\rm{AR}}\left( {1 - \frac{{2{\rm{RT}}}}{E}} \right)\beta E} \right]$$
(8)

This method is considered to be highly ambiguous; therefore, some researchers have reported their reservation about its validation for kinetic analysis [42, 43]. Among all these models, Kissinger’s method [44] is one the most reliable and robust methods to derive an activation energy and pre-exponential factor. It provides an excellent approximation for nth order [44], nucleation growth [45] and distributed reactivity reactions [46]; however, there are some cases where it does not work [42]. One of the most reliable and up-to-date schemes for kinetic modelling is distributed activation energy model [23, 47,48,49,50]. The foundation of this scheme is based on the remarkable work of Constable [51] and Vand [52]. Miura et al. [53, 54] adopted the work of Vand [52]. He reported that overlapping of parallel reactions built up the distribution pattern of reactivity; therefore, an effective fraction reacted should rather be involved in the isoconversional methods than the actual fraction reacted. The concept of distribution of independent parallel reaction was given by Constable [51], in which he figured out a compensatory effect between frequency factor (A) and activation energy (E) for surface-catalysed reactions and proposed that the surface had a variety of sites which resulted in the distribution of activation energies governing the complex reaction. Later, Vand [52] proposed a reactivity distribution model for irreversible electrical resistance changes upon appealing of evaporated metal films. But this approach is exposed by the work of Pitt [55] and Hanbaba [56] in the coal pyrolysis. Thereafter, Anthony and Howard [57] introduced the Gaussian energy distribution model for coal pyrolysis. Recently, Dhaundiyal et al. [58] introduced variability of activation energy through copula, which can be used to obtain better prediction than other methodologies. There is also a possibility that the continuous density function of activation energy can be replaced by the discrete energy distribution model [59]. Hypothesis and solution of distributed activation energy model (DAEM) can be found in the literature [23]. The non-isothermal DAEM equation is expressed by the following equation

$$1 - \alpha = \mathop \smallint \limits_{0}^{\infty } \exp \left\{ {\left( { - \mathop \smallint \limits_{0}^{t} {\rm{Ae}}^{{ - \frac{\rm{E}}{{RT_{\rm{n}} }}}} {\rm{d}}t} \right)} \right\}p \left( E \right){\rm{d}}E$$
(9)

Simplifying Eq. (9), we get

$$1 - \alpha = \mathop \smallint \limits_{0}^{\infty } \exp \left\{ {\left( { - \mathop \smallint \limits_{{T_{0} }}^{{T_{f} }} \frac{A}{{\left( {n - 1} \right)!}}{\rm{e}}^{{ - \frac{\rm{E}}{{RT_{\rm{n}} }}}} \left( {\frac{{{\rm{d}}T_{n} }}{{\beta_{n} }}} \right)} \right)} \right\}p \left( E \right){\rm{d}}E$$
(10)

where \(\beta_{\rm{n}}\) denotes the heating rate of polynomial thermal history and the function \(J\left( T \right) = \frac{E}{{{\rm{RT}}_{\rm{n}} }}\).

The temperature integral \(\left( { - \mathop \smallint \limits_{{T_{0} }}^{{T_{\rm{f}} }} \frac{A}{{\left( {n - 1} \right)!}}{\rm{e}}^{{ - \frac{\rm{E}}{{{\rm{RT}}_{\rm{n}} }}}} \left( {\frac{{{\rm{d}}T_{\rm{n}} }}{{\beta_{\rm{n}} }}} \right)} \right)\) can be evaluated through the Laplace integral approach.

Here, the parameter \(\frac{E}{{{\rm{RT}}_{\rm{n}} }} \to \infty\) is considered to be very large; therefore, the dominant contribution from the integral is when temperature is near its maximum. Thus, the well-known approximation to the function is expressed as

$$= - \mathop \smallint \limits_{{T_{0} }}^{{T_{f} }} \frac{A}{{\left( {n - 1} \right)!}}{\rm{e}}^{{ - \frac{\rm{E}}{\rm{RT}}}} \left( {\frac{{{\rm{d}}T_{\rm{n}} }}{{\beta_{\rm{n}} }}} \right)\sim - \frac{{{\rm{AR}}\left( {T_{\rm{f}} } \right)^{2} }}{{E\left( {n - 1} \right)!}}\left\{ {\frac{1}{{\beta_{\rm{n}} }}} \right\}{\rm{e}}^{{\left( {\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}} }}} \right)}} \left( {{\rm{e}}^{{\left( {{\rm{T}}_{\rm{f}} - {\rm{T}}_{0} } \right)}} - 1} \right)$$
(11)

Substituting the approximated form of temperature integral from Eq. (11) to Eq. (10), we have

$$1 - \alpha \sim\mathop \smallint \limits_{0}^{\infty } \exp \left\{ { - \frac{{{\rm{AR}}\left( {T_{\rm{f}} } \right)^{2} }}{{E\left( {n - 1} \right)!}}\left\{ {\frac{1}{{\beta_{\rm{n}} }}} \right\}{\rm{e}}^{{\left( {\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}} }}} \right)}} \left( {1 - {\rm{e}}^{{\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}}^{2} }}\left( {{\rm{T}}_{\rm{f}} - {\rm{T}}_{0} } \right)}} } \right)} \right\}p \left( E \right){\rm{d}}E$$
(12)

where \(\xi = \frac{{{\rm\rm{ART}}_{\rm{f}}^{2} }}{{E\left( {n - 1} \right)!}}\left\{ {\frac{1}{{\beta_{\rm{n}} }}} \right\}\).

Simplifying Eq. (12), we get

$$1 - \alpha \sim\mathop \smallint \limits_{0}^{\infty } \exp \left\{ { - \xi {\rm{e}}^{{\left( {\frac{ - E}{{{\rm{RT}}_{\rm{f}} }}} \right)}} \left( {1 - {\rm{e}}^{{\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}}^{2} }}\left( {{\rm{T}}_{\rm{f}} - {\rm{T}}_{0} } \right)}} } \right)} \right\}p \left( E \right){\rm{d}}E$$
(13)

The term \(\exp \left\{ { - \xi {\rm{e}}^{{\left( {\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}} }}} \right)}} \left( {1 - {\rm{e}}^{{\frac{ - {\rm{E}}}{{{\rm{RT}}_{\rm{f}}^{2} }}\left( {{\rm{T}}_{\rm{f}} - {\rm{T}}_{0} } \right)}} } \right)} \right\}\) in Eq. (13) can be rewritten as,

$$\sim\exp \left( { - \exp \left( { - \frac{{E - E_{\rm{s}} }}{{E_{\rm{w}} }}} \right)} \right)$$

Equation (14) varies rapidly from zero to one as E increases, over range of Ew, around Es. And this can be approximated in the following manner:

$${\rm{Let}},\;f\left( E \right) = - \left( {\frac{{E - E_{\rm{s}} }}{{E_{\rm{w}} }}} \right)$$
(14)

Comparing Eqs. (11) and (14), we have

$$f\left( E \right) \equiv \ln \left( \xi \right) - \frac{E}{{{\rm{RT}}_{\rm{f}} }}\left( {\frac{{T_{0} }}{{T_{\rm{f}} }}} \right)$$
(15)

Expanding Eq. (14) with the help of Taylor series expansion about \(z = z_{\rm{s}}\), we get

$$f\left( E \right) = f\left( {E_{\rm{s}} } \right) + \left( {E - E_{\rm{s}} } \right)f\left( {E_{\rm{s}} } \right)^{{\prime }} + \cdots$$
(16)

Boundary conditions: \(f\left( {E_{\rm{s}} } \right) = 0\) and \(f^{\prime}\left( {E_{\rm{s}} } \right) = \frac{ - 1}{{E_{\rm{w}} }}\).

Solving Eqs. (15) and (16), we have

$$E_{\rm{s}} = {\rm{RT}}_{\rm{f}}^{2} Y\left( \tau \right)$$
$$E_{\rm{w}} = \frac{{E_{\rm{s}} }}{{1 + \left( {T_{0} + \left( {\frac{{{\rm{d}}\beta_{\rm{n}} }}{{{\rm{d}}E_{\rm{s}} }}} \right)} \right)Y\left( \tau \right)}}$$

Suppose \(z\) is the energy correction factor, then

$$z_{\rm{s}} = \frac{{{\rm{RT}}_{\rm{f}}^{2} Y\left( \tau \right)}}{{\left( {\Gamma \,{\rm{or}}\,\phi } \right)}}$$
$$z_{\rm{w}} = \frac{{z_{\rm{s}} }}{{1 + \left( {T_{0} + \left( {\frac{{{\rm{d}}\beta_{\rm{n}} }}{{{\rm{d}}E_{\rm{s}} }}} \right)} \right)Y\left( \tau \right)}}$$

where \(\tau = \frac{1}{{\left( {n - 1} \right)!}}\left( {\frac{{{\rm{AT}}_{0} }}{{\beta_{\rm{n}} }}} \right)\) is the timescale factor.

Note: \(J^{\prime}\left( {T_{\rm{f}} } \right) > 0,\;\frac{E}{{{\rm{RT}}_{\rm{n}} }} \to \infty\).

Transmutation of density function

Logistical approach is not the only way to introduce distribution of activation energies among several parallel reactions [60]. There are numerous ways to solve complexity of distribution in reactivity. However, logistical information might be beneficial for pre-processing reaction profile to reduce noisy data, but it does not generate valuable information about nature of kinetic parameters, which can be rather useful for modelling the conditions than those fitted. Some researchers have looked for analytical equation to make use of continuous reactivity distribution favourable for specific situations, such as the Gaussian energy model for a constant heating rate [61]. However, there is also likelihood of breaking any continuous distribution of activation energy into a discrete distribution of evenly spaced energies [37]. The cogent argument behind philosophy of discrete distribution is to ease the computational effort required to evaluate complex exponential functions. However, there are numerous schemes to reduce time-consuming iterative steps [22, 23, 58, 62]. Furthermore, it is preferred to derive a solution for arbitrary thermal histories as experimental data and industrial application seldom follow the idealistic approach which is usually adopted. Linear mixing of density function of activation energy may also be significant to determine the domain of activation energy valid for a particular model.

$$p^{t} \left( E \right) = \left( {1 + \delta } \right)p\left( E \right) - \delta \left( {p\left( E \right)} \right)^{2} , \left| \delta \right| \le 1$$
(17)

where E is the activation energy.

Therefore, the concept of transmutation is proposed to analyse the thermal conversion process qualitatively. The density function of activation energy is said to be transmuted if it follows Eq. (17). However, the expression for linear mixing is also valid for cumulative distribution function of activation energy. Shaw and Buckley [7] did notable work to explore distributional flexibility through introducing a new parameter to an existing distribution. They have reported that involvement of an additional parameter does not make solution cumbersome but quantifies the reproducibility of the modelling of natural process. The output of transmuted form provides more dynamical characteristic to simulated solution for miscellaneous type of data than the conventional logistic approach. In the support of transmutation approach, metrological studies are carried out to analyse the snowfall data of a region. It is found that the transmuted Gumbel distribution tackled regional perturbance effectively [63]. The competitiveness of transmuted Frechet distribution over the conventional Frechet distribution is employed to solve the wind speed data to muster the statistical information about a wind energy conversion system. It is indicated that the obtained solution is relatively good to the parent model [64]. In another application of manufacturing industries [65], reliability data obtained by transmutation are very useful to predict the life expectancy of a component. Therefore, it is necessary to enlarge sphere of computation through introducing the new methodology to solve the complex problems of thermal science.

In the subsequent sections, a varying heating rate profile is adopted along with transmuted form to determine the effect of thermal history on the computation process of kinetic parameters. This not only influences kinetic analysis but also enlightens the industrial aspects of the proposed scheme.

Asymptotic approximations are given according to the limit imposed on density function and the varying activation energy, E [66].

Proposition 1

If \(p \left( E \right) \to 0\), the transmuted form of density function is given by

$$p^{t} \left( E \right) = \left( {1 + \delta } \right)p \left( E \right)$$

Proposition 2

When activation energy tends to very large value, i.e., \(E \to \infty\), then

$$p^{t} \left( E \right) = \left( {1 - \delta } \right)p \left( E \right)$$

Approach applied in the subsequent sections is aimed at the method of the moving maximum for Laplace problems [67]. The simultaneous variation of the initial distribution and the term DExp is considered in such a way that more robust and accurate approximation can be obtained for a wide range of operating parameters. The maximum of total integrand is considered to move in time-dependent manner.

Rayleigh Distribution (Three Parameters)

The density function of the Rayleigh distribution is expressed as

$$p\left( E \right) = 2\mu \omega \left( {E -\Gamma } \right) {\rm{e}}^{{ - \omega \left( {E -\Gamma } \right)^{2} }} \left( {1 - {\rm{e}}^{{ - \omega \left( {E -\Gamma } \right)^{2} }} } \right)^{\mu - 1}$$

Here, \(\mu > 0\) and \(\omega > 0\) are the shape parameters of the generalised form of Rayleigh distribution, and \(0 < E\) and \(0 <\Gamma\) denote the activation energy and location parameter of the Rayleigh distribution function, respectively.

The nondimensional ‘z’ form of the Rayleigh distribution (3-P) can be expressed as,

Introduce the energy correction factor ‘z’, which is represented by \(z = \frac{E}{\Gamma }\) and \(\Upsilon\) is a dimensionless number, \(\Upsilon = \frac{{\Gamma ^{2} }}{{\left( {\frac{1}{\omega }} \right)}}\). After simplification of Rayleigh distribution, we get

$$p \left( z \right) = 2\mu \Upsilon \left( {z - 1} \right) {\rm{e}}^{{ - \Upsilon \left( {z - 1} \right)^{2} }} \left( {1 - {\rm{e}}^{{ - \Upsilon \left( {z - 1} \right)^{2} }} } \right)^{\mu - 1}$$
(18)

Simplifying the DAEM equation for the first-order reaction, we get

$$1 - \alpha = \mathop \smallint \limits_{0}^{\infty }\Gamma \exp \left\{ { - \exp \left( { - \left( {{\rm{e}}^{{ - \left( {\frac{{z - z_{s} }}{{z_{w} }}} \right)}} } \right)} \right)} \right\}p \left( z \right){\rm{d}}z$$
(19)

Substituting the value of \(p \left( z \right)\) from Eq. (18) into Eq. (19), we have

$$1 - \alpha = \mathop \smallint \limits_{0}^{\infty } 2\mu \Upsilon \left( {z - 1} \right){\rm{e}}^{{\left\{ { - \left( {{\rm{e}}^{{ - \left( {\frac{{z - z_{\rm{s}} }}{{z_{\rm{w}} }}} \right)}} + \Upsilon \left( {z - 1} \right)^{2} } \right)} \right\}}} \left( {1 - {\rm{e}}^{{ - \Upsilon \left( {z - 1} \right)^{2} }} } \right)^{\mu - 1} {\rm{d}}z$$
(20)

Suppose

$$h\left( z \right) = \left( {z - 1} \right)\left( {1 - {\rm{e}}^{{ - \Upsilon \left( {z - 1} \right)^{2} }} } \right)^{\mu - 1}$$
(21)
$$M\left( z \right) = {\rm{e}}^{{ - \left( {\frac{{z - z_{\rm{s}} }}{{z_{\rm{w}} }}} \right)}} + \Upsilon \left( {z - 1} \right)^{2}$$
(22)

Differentiating Eq. (22), we have

$$M^{\prime}\left( z \right) = - \frac{{{\rm{e}}^{{ - \left( {\frac{{z - z_{\rm{s}} }}{{z_{\rm{w}} }}} \right)}} }}{{z_{\rm{w}} }} + 2\Upsilon \left( {z - 1} \right)$$
(23)

Equating \(M^{\prime}\left( {z_{\rm{e}} } \right) = 0\) to obtain the maximum point \(z_{\rm{e}}\) in terms of time (t), we get

$$2\Upsilon \left( {z_{\rm{e}} - 1} \right) = \frac{{{\rm{e}}^{{ - \left( {\frac{{{\rm{z}}_{\rm{e}} - {\rm{z}}_{\rm{s}} }}{{{\rm{z}}_{\rm{w}} }}} \right)}} }}{{z_{\rm{w}} }}$$
$$z_{\rm{e}} = \left\{ {1 + z_{\rm{w}} \Upsilon \left( {\frac{{{\rm{e}}^{{ - \left( {\frac{{{\rm{z}}_{\rm{s}} - 1}}{{{\rm{z}}_{\rm{w}} }}} \right)}} }}{{2\Upsilon z_{\rm{w}}^{2} }}} \right)} \right\}$$

Substituting the value of \(z_{\rm{e}}\) in Eq. (20), we get

$$\begin{aligned} & 1 - \alpha \sim2\mu \Upsilon \mathop \smallint \limits_{0}^{\infty } {\rm{e}}^{{\left[ { - \left( {{\rm{M}}\left( {{\rm{z}}_{\rm{e}} } \right) + \frac{{\left( {{\rm{z}} - {\rm{z}}_{\rm{e}} } \right)^{2} }}{2}{\rm{M}}^{\prime\prime}\left( {{\rm{z}}_{\rm{e}} } \right)} \right)} \right]}} \\ & \quad \left( {h\left( {z_{\rm{e}} } \right) + \left( {z - z_{\rm{e}} } \right)h^{\prime}\left( {z_{\rm{e}} } \right) + \frac{{\left( {z - z_{\rm{e}} } \right)^{2} }}{2}h^{\prime\prime}\left( {z_{\rm{e}} } \right)} \right){\rm{d}}z \\ \end{aligned}$$
(24)

Solving Eq. (24) by using Laplace method, we have

$$\begin{aligned} &1 - \alpha \sim 2\mu \Upsilon h\left( {z_{\rm{e}} } \right){\rm{e}}^{{ - {\rm{M}}\left( {{\rm{z}}_{\rm{e}} } \right)}} \mathop \smallint \limits_{0}^{\infty } {\rm{e}}^{{\left\{ { - \left( {\frac{{\left( {{\rm{z}} - {\rm{z}}_{\rm{e}} } \right)^{2} }}{2}{\rm{M}}^{\prime\prime}\left( {{\rm{z}}_{\rm{e}} } \right) + \frac{{{\rm{O}}\left( {\left( {{\rm{z}} - {\rm{z}}_{\rm{e}} } \right)^{3} } \right)}}{6}} \right)} \right\}}} {\rm{d}}z \\ & \quad + O\left( {\left( {z - z_{\rm{e}} } \right)} \right) \\ \end{aligned}$$

The value of the remaining mass fraction is obtained by

$$\left( {1 - \alpha } \right)\sim 0.5\mu \Upsilon h\left( {z_{\rm{e}} } \right){\rm{e}}^{{ - {\rm{M}}\left( {{\rm{z}}_{\rm{e}} } \right)}} \sqrt {\frac{2\pi }{{\left| {M^{\prime\prime}\left( {z_{\rm{e}} } \right)} \right|}}} \left( {{\rm{erf}}\left( {z_{\rm{e}} } \right) + 1} \right)$$
$$\begin{aligned} & \left( {1 - \alpha } \right)\sim0.5\mu \left[ {\left( {z_{\rm{e}} - 1} \right)\left( {1 - {\rm{e}}^{{ - \Upsilon \left( {{\rm{z}}_{\rm{e}} - 1} \right)^{2} }} } \right)^{\upmu - 1} {\rm{e}}^{{ - \left\{ {\Upsilon \left( {{\rm{z}}_{\rm{e}} - 1} \right)\left( {{\rm{z}}_{\rm{e}} + 2{\rm{z}}_{\rm{w}} - 1} \right)} \right\}}} \left( {{\rm{erf}}\left( {z_{\rm{e}} } \right) + 1} \right)} \right] \\ & \quad \left( {\sqrt {\frac{\pi \Upsilon }{{\left( {\frac{{z_{\rm{e}} - 1}}{{z_{\rm{w}} }} + 1} \right)}}} } \right) \\ \end{aligned}$$
(25)
$$\left( {1 - \alpha } \right)_{\rm{t}} = \mathop {\left( {1 + \delta } \right) \lim }\limits_{ p \left( E \right) \to 0} \left( {1 - \alpha } \right)$$
(26)
$$\left( {1 - \alpha } \right)_{\rm{t}} = \mathop {\left( {1 - \delta } \right) \lim }\limits_{{{\rm{E}} \to \infty }} \left( {1 - \alpha } \right)$$
(27)

 Eqs. (26) and (27) are the desired approximated form of DAEM for first-order reaction.

Differentiating Eq. (25), we get the expression for rate of change of remaining mass fraction with respect to time:

$$\frac{{{\rm{d}}\left( {1 - \alpha } \right)_{t} }}{{{\rm{d}}t}} \approx \left( {1 + \delta } \right)\frac{{\mu \sqrt {\pi \Upsilon } {\rm{e}}^{{ - \left\{ {\Upsilon \left( {{\rm{z}}_{\rm{e}} - 1} \right)\left( {{\rm{z}}_{\rm{e}} + 2{\rm{z}}_{\rm{w}} - 1} \right)} \right\}}} }}{{2z_{\rm{w}} }}\left\{ {\frac{{\left( { - 4\Upsilon \left( {z_{\rm{w}} + z_{\rm{e}} - 1} \right)^{2} - 1} \right)}}{{\sqrt[3]{{\left( {\frac{{z_{\rm{e}} - 1}}{{z_{\rm{w}} }} + 1} \right)}}}}} \right\}\frac{{{\rm{d}}z_{\rm{e}} }}{{{\rm{d}}t}}$$
(28)
$$\frac{{{\rm{d}}\left( {1 - \alpha } \right)_{t} }}{{{\rm{d}}t}} \approx \left( {1 - \delta } \right)\frac{{\mu \sqrt {\pi \Upsilon } {\rm{e}}^{{ - \left\{ {\Upsilon \left( {{\rm{z}}_{\rm{e}} - 1} \right)\left( {{\rm{z}}_{\rm{e}} + 2{\rm{z}}_{\rm{w}} - 1} \right)} \right\}}} }}{{2z_{\rm{w}} }}\left\{ {\frac{{\left( { - 4\Upsilon \left( {z_{\rm{w}} + z_{\rm{e}} - 1} \right)^{2} - 1} \right)}}{{\sqrt[3]{{\left( {\frac{{z_{\rm{e}} - 1}}{{z_{\rm{w}} }} + 1} \right)}}}}} \right\}\frac{{{\rm{d}}z_{\rm{e}} }}{{{\rm{d}}t}}$$
(29)

Computational algorithm

MATLAB 2017b is considered as an interface between chemical model and the numerical solution. Computational programming is based upon solution of differential equation of varying heating rate (β). The different degree of thermal profile is tested to assess the variation in Arrhenius parameters with time and temperature. Each assigned value is checked until it does not converge within defined range of error. Asymptotic solution is obtained by the Laplace integral of the dynamical system. The two different limits are imposed on the numerical solution of multi-reaction model, so that the precise and accurate picture can be delineated. Moreover, the nature of distribution pattern shed light on variation in amplitude of the whole integrand of multi-reaction model. An iterative loop is used to evaluate the Arrhenius parameters for the first-order chemical reaction. Each loop evaluates and compares tolerance with maximum permissible tolerance allowed for convergence of solution. Once the value is obtained, the program stops. In case the derived values do not qualify, the program searches for another value.

Unlike the constant or linear ramping of temperature with respect to time, varying form of heating rate is used to develop the versatile methodology to adopt any kind of thermo-analytical data. However, the numerical solution derived by assuming the polynomial equations deviates from the equilibria of the experimental heating rates of 5 °C min−1, 10 °C min−1 and 15 °C min−1. The miscellaneous form of heating rate implicates different solutions to differential equation of heating rate. The derived values of Arrhenius parameters for different heating profiles are compared with isothermal and non-isothermal degradation of material.

Application of bio-waste

For application perspective, the chemical and the thermogravimetric tests are carried out to demonstrate the mathematical scheme for thermal history of nth degree. The complex thermal history is solved for the general solution, and the obtained value is substituted in the derived numerical solution of the multi-reaction model. The pine sample is collected from pest county of Hungary.

The chemical characteristic of bio-waste is evaluated by CHNS-O analyser (vario MACRO). The elemental composition (C%, N%, S%, H% and O%) is calculated on the dry basis. Before performing chemical test, the furnace is heated up to 1473 K for 30 min. Once the apparatus is ready to operate, the capsule form of sample wrapped in a tin foil is placed inside the rotating disc. The flow of oxygen maintains the catalytic combustion, whereas helium gas is allowed to sweep away the product of combustion. The volatile gases carried away by helium gas are separated at different reduction columns, where the gas mixture is separated into its components through purge or trap chromatography. These tubes are in-between the combustion chamber and the signal-processing unit. They are connected to computer-based software via thermal conductivity detector (TCD). The TCD generates the electrical signal that is proportional to the concentration of elementary components of material. The standard reference material for correlating value is birch leaf powder. The calorific value is evaluated at constant volume by the bomb calorimeter. Thermal behaviour of pine waste is computed with the help of thermogravimetric/differential thermal analyser (Diamond TG/DTA, Perkin Elmer, USA). The sample has undergone thermal degradation for the temperature range of 303–923 K. To nullify the measurement error, the horizontal differential-type balance is used for experimentation. Thermocouple type ‘R’ (Platinum–Rhodium–13%/Platinum) is adopted to measure the temperature inside the furnace. The purge flow rate of non-interactive gas is calibrated as 200 mL min−1. Indium and tin are used as reference materials for differential curves. Table 1 lists the chemical composition of pine needles.

Table 1 Chemical composition of pine needles
Full size table

Results and discussion

Thermo-analytical data are examined through the proposed mathematical scheme for nonlinear thermal history. Unlike the linear ramping of temperature, a polynomial form of temperature is considered to determine the correlation between thermal and kinetic parameters. Different limits on activation energy are imposed to derive the numerical solution for first-order reactions.

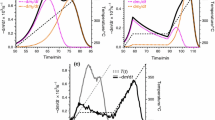
Comparative evaluation of the predicted solution for linear ramping rate is depicted in Fig. 1a, b. It is observed that the plateauing effect of predicted curves during the initial phase of pyrolysis is sufficiently longer than that of experimental curves obtained at different heating rates. However, the char formation is properly described through predicted curves at the end of pyrolysis, yet the second stage of decomposition is not clearly explained at 600 K. The main reason of anomaly is the dormant nature of timescale factor (τ) during the initial stage of decomposition of biomass. Inability to explain a sudden slowdown in the remaining mass proportion \(\left( {1 - \alpha } \right)\) after 600 K is related to the monotonicity of numerical solution as ‘zs’ energy correction factor increases with time. The similar trend has been observed for predicted solutions derived at different heating rates (5 °C min−1, 10 °C min−1, 15 °C min−1). On the contrary, the numerical solution determined at different transmutation limits \(\left( {E \to \infty } \right)\) causes the relative shifting of the remaining mass fractions curves to the experimental results. The integral limit activation energy dE (kJ mol−1) determined at different linear heating rates of 5 °C min−1, 10 °C min−1 and 15 °C min−1 varies from \(\left[ {4.8 \times 10^{ - 3} , 116.81} \right]\), \(\left[ {8.2 \times 10^{ - 3} , 104} \right]\) and \(\left[ {10.1 \times 10^{ - 3} , 95.91} \right]\), respectively. The frequency factors (A min−1) and the threshold parameters (or location parameters) (Г kJ mol−1) obtained at different asymptotic limits of the transmuted distribution function are given in Table 2.

Fig. 1
figure 1

Comparative illustration of the predicted solution for linear ramping temperature: a (\(p \left( E \right) \to 0\)) \(\left( {n = 1,\delta = 0.05 } \right)\), b \(\left( {E \to \infty } \right)\) \(\left( {n = 1,\delta = 0.01 } \right)\)

Full size image
Table 2 Kinetic and distribution parameters obtained at linear thermal history (n = 1)
Full size table

The effect of quadratic ramping of temperature is illustrated in Fig. 2a, b. Unlike the linear thermal history, the nonlinear programming of temperature reduces the time of a mathematical system to response as degree of freedom increases. Therefore, the limit of integral dE shrinks with increases in the polynomial degree (n). Devolatilisation of pine needles is precisely described by polynomial ramping of temperature at n = 2. However, in the context of relative fitting of data, the nonlinear thermal history provides better curve-fitting than linear thermal programming. The coefficient of regression (R2) (Tables 3 and 4) is estimated for polynomial ramping (n = 2,3) of temperature at different heating rates. Although the fitting of curves not only relies upon the higher value of R2 but also the residual plot, the residual values also are computed for different heating rates. The kinetic and distribution parameters obtained for nonlinear thermal profile at different heating rates are provided in Table 3. It can be observed that the frequency factor is relatively low and constant for the nonlinear profile to the linear thermal profile. Moreover, the threshold energies required to initiate the pyrolysis reaction decreased with increase in the polynomial degree. However, there is a nominal variation in kinetic and distribution parameters with asymptotic limits of transmutation.

Fig. 2
figure 2

Demonstration of the predicted solution for the nonlinear thermal history (with respect to experimental results for linear ramping): a (\(p \left( E \right) \to 0\)) \(\left( {n = 2,\delta = 0.05 } \right)\), b (\(E \to \infty\)) \(\left( {n = 2,\delta = 0.05 } \right)\)

Full size image
Table 3 Kinetic and distribution parameters derived for polynomial equation (n = 2)
Full size table
Table 4 Kinetic and distribution parameters obtained for polynomial equation (n = 3)
Full size table

The experimental data can be explained in far better way by polynomial ramping than by the linear thermal history. To prove the dependence of thermoanalytical data on a thermal profiling, the generalisation of a numerical solution for another higher polynomial degree (cubic thermal profile) is carried out, which is illustrated by Fig. 3a, b. It is observed that the predicted solution tends to be steadier and more stable than linear programming, as degree of freedom of a system increases. The plateauing behaviour of predicted \(\left( {1 - \alpha } \right)\) curves is subdued, and the average activation energy tends to decrease with n for polynomial thermal history. Furthermore, in another observation, for asymptotic limit \(E \to \infty\), the behaviour of remaining mass fraction curves of polynomial thermal profile (Figs. 2b,3b) is different from the linear thermal history (Fig. 1b). The limit \(E \to \infty\) affects the attribute of \(\left( {1 - \alpha } \right)\) when \(y < y_{\rm{s}}\). There is a negligible shifting of \(\left( {1 - \alpha } \right)\) curves to the right for \(y > y_{\rm{s}}\). However, the shifting of \(\left( {1 - \alpha } \right)\) curves at initial stage of pyrolysis is similar. Thus, the dynamic nature of temperature integral (\(- \mathop \smallint \limits_{0}^{t} A{\rm{e}}^{{ - \frac{\rm{E}}{{{\rm{RT}}_{\rm{n}} }}}} {\rm{d}}t\)) is controlled by using polynomial thermal profile, whereas other methodologies [22, 58] are not able to maintain the rapid variation in double exponential term about mean value, \(y_{\rm{s}}\). The key factor of computation is moving maxima of the whole integrand with time. During the initial stage of pyrolysis, ye remains dormant during temperature interval of 300–550 K for the linear thermal profile and thereafter it varies linearly, whereas function ye varies linearly throughout the temperature range of 300–900 K. It shows that the subtle variation in time and temperature is detected by the proposed mathematical model for nonlinear thermal history. Thus, the proposed system attempts to simulate each decomposition step precisely and effectively. Moreover, computational time required for solving the same algorithm is significantly decreased for the similar number of computational loops.

Fig. 3
figure 3

Comparative illustration of the predicted solution for the nonlinear thermal history: a (\(p \left( E \right) \to 0\)) \(\left( {n = 2,\delta = 0.05 } \right)\), b (\(E \to \infty\)) \(\left( {n = 3,\delta = 0.05 } \right)\)

Full size image

The scale of the remaining mass fraction is increased by 6.3% as activation energy tends to \(E \to \infty\). Similar behaviour is obtained for polynomial ramping of temperature performed at n = 3. Parametric values estimated for n = 3 are depicted in Table 4. It can be concluded through predicted thermogravimetric curves that if the linear thermal history is replaced by polynomial form, the predicted model delineates the experimental data more precisely than the ideal thermal history. Peculiarity found during the prediction of the first-order reaction is overshadowed by nonlinear thermal profile.

Variation of variance (σ2 kJ mol−1) with heating rate is illustrated in Fig. 4a–f. It is observed that the scale of variation in activation energy of parallel reactions is reduced drastically. Activation energy spectrum tends to shrink as thermal profile changes from linearity to nonlinearity. Therefore, similar nature of the numerical solutions are observed when the quadratic and the cubic temperature profiles are considered for energy modelling. The estimated values of σ2 obtained at different heating rates exhibit similar trends for both the asymptotic cases. However, the magnitude of σ2 varies as heating rate changes.

Fig. 4
figure 4

Effect of heating rate on the energy variance \(\left( {\sigma^{2} } \right)\) (kJ mol−1) (a, c and e- (\(p \left( E \right) \to 0\)), b, d and f (\(E \to \infty\)))

Full size image

The effect of heating rate on the average activation energies is depicted in Fig. 5a–f. It is observed that the mean value of activation energy decreases drastically as polynomial ramping of temperature is employed in the mathematical model. However, the average value of activation energy decreases linearly in the domain of the heating rate of \(5 \le \beta \left( {^\circ {\rm{C}}\,\min^{ - 1} } \right) \le 15\) for the linear thermal profile (Fig. 5a). On the other hand, the activation energy linearly increases which is limited to \(10 \le \beta \left( {^\circ {\rm{C}}\,\min^{ - 1} } \right) \le 15\) for other cases (Fig. 5b–f). The main reason for this singularity is relative dilation of activation energy spectrum (or domain). Therefore, the average value of activation energy is slightly increased during heating rate interval of (10, 15). The variation in \(\bar{E}\) exhibits parabolic variation with a linear heating rate \(\beta\). The equation obtained for asymptotic limits \(p\left( E \right) \to 0\) and \(E \to \infty\) on the transmuted functions is \(\left( {0.044\beta^{2} - 1.9\beta + 66} \right)\) and \(\left( {0.16\beta^{2} - 3.6\beta + 66} \right)\), respectively.

Fig. 5
figure 5

Variation in average activation energy \(\bar{E}\) (kJ mol−1) with heating rate β (°C min−1) (a, c and e- (\(p \left( E \right) \to 0\)), b, d and f (\(E \to \infty\)))

Full size image

Influence of heating rate on the threshold parameter of the generalised Rayleigh distribution is shown in Fig. 6a–f. The threshold parameter (Г kJ mol−1) increases linearly with heating rate for nonlinear thermal history, whereas it decreases linearly with the linear thermal profile. However, it is almost constant during the interval of \(5 \le \beta \left( {^\circ {\rm{C}}\,\min^{ - 1} } \right) \le 10\) for the limit \(E \to \infty\).

Fig. 6
figure 6

Influence of heating rate on threshold parameter (Г kJ mol−1) of the generalised form of the Rayleigh Distribution (a, c and e- (\(p \left( E \right) \to 0\)), b, d and f (\(E \to \infty\)))

Full size image

It is observed from the comprehensive analysis of thermal profile that the mathematical solution is more responsive as imposed thermal programmed deviates from linearity. The solution obtained at nonlinear thermal history is much promising than that of the linear thermal profile. The range of activation energy decreases as a temperature program varies from linear to quadratic. Thus, it can be concluded that the predicted solution converges if the mathematical model involves the nonlinear thermal profile. The results obtained for pine needles are compared with similar kind of coniferous species, and it has been found that activation energy is within the range of activation energy derived from other statistical models [14, 68,69,70,71,72,73].

Conclusions

Thermoanalytical data are obtained at different heating rates through TG/DTA analysis. A nonlinear attribute of the thermal profile is tested upon the proposed mathematical model. Unlike the conventional modelling of the multi-reaction model (MRM), the transmuted form of the distribution function is used to impart the additional flexibility to the predicted solution via linear mixing of the density function. The results are derived at different asymptotic limits of transmuted function. It is observed that the dynamic nature of temperature integral can be controlled through slowing down the variation in timescale factor, which in turn allows the function to vary much sophisticatedly than linear ramping profile. The interdependence of activation energy with temperature and time is introduced through the concept of moving maxima. It is found that the response period of the mathematical model with time increases as alteration of the imposed temperature profile is performed. The activation energy derived through polynomial ramping of temperature varies from 69 to 73 kJ mol−1. In a similar study, the activation energy obtained at linear programming is in the interval of 92–117 kJ mol−1. Pre-exponential or frequency factor is found to vary from \(2 \times 10^{7} \le A\left( {\hbox{min} ^{ - 1} } \right) \le 2 \times 10^{9}\) for the linear thermal profile, whilst the frequency factor obtained at the nonlinear thermal profile is \(A\left( {{ \hbox{min} }^{ - 1} } \right) = 2 \times 10^{4}\). The results showed that the variation in averaged activation energy (\(\bar{E}\)) for constant heating rate followed the general parabolas equations \(\left( {0.044\beta^{2} - 1.9\beta + 66} \right)\) and \(\left( {0.16\beta^{2} - 3.6\beta + 66} \right)\) for different transmutation limits on the numerical solution.

However, the computation time required is relatively high for the linear thermal profile. But it is significantly reduced as the linear thermal history is replaced by the polynomial equation.