Abstract
It is well known that clothes used in sporting activity are a barrier for heat exchange between the environment and athlete, which should help in thermoregulation improvement. However, it is difficult to evaluate which top is best for each athlete according to the characteristics of the sport. Researchers have tried to measure the athlete’s temperature distribution during exercise at the base layers of tops with different approaches. The aim of this case study was to investigate the use of thermography for thermo-active base layer evaluation. Six new base layers were measured on one cyclist volunteer during a progressive training on a cycloergometer. As a control condition, the skin temperature of the same volunteer was registered without any layer with the same training. A training protocol was selected approximate to cycling race, which started from the warm-up stage, next the progressive effort until the race finished and at the end “cool-down” stage was over. In order to show which layer provided the strongest and weakest barrier for heat exchange in comparison with environment, the temperature parameters were taken into consideration. The most important parameter in the studies was the temperature difference between the body and the layers, which was changing during the test time. The studies showed a correlation between the ergometer power parameter and the body temperature changes, which has a strong and significant value. Moreover, the mass of every layer was checked before and after the training to evaluate the mass of the sweat exuded during the test. From this data, the layer mass difference parameter was calculated and taken into consideration as a parameter, which may correspond with the mean heart rate value from each training. A high and positive correlation coefficient was obtained between the average heart rate and the mass difference for the base layers. Thermal analysis seems to have a new potential application in the objective assessment of sports clothing and may help in choosing the proper clothes, which could support heat transfer during exercising and protect the body from overheating.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Thermal imaging is often used in clinical medicine applications (e.g., stomatology, dermatology, orthopedics, oncology or rehabilitation) [1,2,3,4]. There are increasing numbers of its applications in sports medicine [5,6,7]. Infrared thermography (IRT) may be used to measure the superficial temperature of any body characterized by higher than zero absolute (0 K).
It is generally known that the human body core temperature is kept on some basic level due to the thermoregulation mechanisms, which is supporting our thermal homeostasis and all living processes. So far in the literature one can see that the basic level of body temperature is 37.0 ± 1.0 °C [8]. However, some publications provide the basic value of body core temperature as 36.8 0 ± 0.5 °C or as a temperature range 36.5–37.5 °C with normal day changes by 0.5 °C [9, 10]. In fact, body core temperature is not easy to define. The variety of human physiology changes of body temperature due to gender and many environmental disorders may have a significant influence on results.
The body thermoregulation system may be described as a feedback system due to its wide range response to the environmental impact. The external temperature sources and many physical factors can induce temperature changes, which are detected by thermoreceptors. In consequence the temperature noise descended from environment can be classified as an error signal, which induces the thermogenesis or thermolysis reactions. However, the thermoregulation system of the human body is very complicated and it is related to systems of receptors, neurological structures and the cardiovascular system [11]. The main point of the thermoregulation system is the hypothalamus, which is a part of the brain. All information about temperature changes are transferred to the hypothalamus where the temperature regulation impulse is created [12, 13]. The body core and skin sensors are connected with the metabolic skin blood flow and sweating effectors [14]. The thermoreceptors have the main influence for all thermoregulation processes. Specific nerve fibers can be divided into intero- and exteroreceptors. As mentioned above, the thermo-interoreceptors are responsible for receiving stimuli from the body core, i.e., from organs, muscles. The thermo-exteroreceptors are sensitive to external impulses [11, 14].
All organisms need energy for living. They deliver it with nutrition and release it as metabolites and heat. Nearly 60% of the energy produced by the human body is released as infrared radiation (IR) [1, 9, 15, 16], which allows for measuring the temperature distribution on the human skin. The thermal energy emitted from the body core is provided mainly by the blood flow. In fact, the blood vessels are closely related to the skin and microcirculation plays the main role in skin surface temperature. The continuous venous plexus is supplied in blood from skin capillaries [8, 9]. The heat energy exuding from the body occurs in different ways—conduction, convection, radiation and the sweat evaporation. All processes, which are done to keep thermal homeostasis, are controlled by the hypothalamus; it is responsible for controlling blood flow and monitoring thermoregulation mechanisms [9, 16].
In normal conditions, the thermoregulation processes result from a specific scheme. Heat transfer is strictly dependent on the temperature gradient between the body surface and the environment. In rest, the heat energy is transported to the skeletal muscles from the body core. However, during exercising, the work is done by muscles and its temperature rises. In addition, the metabolism and body energy increase due to physical effort [14, 17]. One can say that during physical effort a lot of disorders appear not only in thermoregulation processes but also in all living processes.
Athlete’s bodies are exposed to different endogenous and exogenous thermal loads during training. Energy produced by the metabolic processes during exercise is transformed into heat, which causes the increase in body core temperature and is classified as endogenous thermal impact [5, 9, 16]. Temperature and humidity can be considered as exogenous thermal load.
The correct heat exchange between the body and environment is very important for all living organisms. For sure, sportsmen are more exposed to thermoregulation disorders, due to increasing metabolism during exercising. Normal functioning humans maintain a body core temperature on a basic level of about 37 °C [14, 16]. Thermal homeostasis is kept at constant level as a result of hypothalamus functioning. During physical activities, when body temperature is increasing, the hypothalamus sends information to the cardiovascular system and controls the vessels blood flow, which is one of the most important parts of body heat regulation [9, 18]. It is known that during sport activities the mechanisms of thermoregulation are more complicated than in rest. The process of hypothalamus excitation during exercise starts when skeletal muscle temperature rises because of work [17]. The temperature gradient has been reversed, and in consequence, heat energy is transferred from muscles to blood in vessels and finally the body core. When body core temperature is rising, the hypothalamus triggers the protection mechanisms, e.g., increase the blood flow and heart rate [14, 16, 17].
The heat transfer is also done by skin surface due to sweating and evaporation, convection and radiation. It was calculated that humans lose 2.43 kJ of heat energy per 1 mL of sweat evaporation [16].
That is why the type of clothing may have strong impact on heat dissipation for sportsmen. Generally, clothing is a barrier for heat transfer from the body [17]. Nowadays the thermo-active layers support the body from overheating and allow for the regulation of heat exchange [19, 20]. Thermo-active clothes are most often used as a bottom layer of appropriate clothes, or used instead of normal clothes in heat. That is why these layers are called base layers, as a basic layer of sporting clothes.
To characterize textile products, also thermo-active base layers, the base biophysical parameters are used: thermal resistance and conductivity, diffusion and absorption. These parameters characterize clothing materials and allow the creation of products able to assure thermal comfort [21, 22].
Currently, most measurements of sports textiles are done without participation of the human body. These tests only examine parameters using specialized equipment. In fact, all factors related to the actual human body are neglected, including negative ones like sweating.
That is why one of the aims of this study was to find if measuring and rating sports clothing during real training of real athletes is possible with all noises emitted during sports activity. To study this problem, the thermoregulation parameters of the body were checked with and without sport layers by using thermal imaging. The researchers performed thermal imaging of the cyclists during progressive training protocol on the cyclo-ergometer with different base layers and without any t-shirts.
Methods
In order to carry out the study, six different types of thermo-active layers from different manufacturers (Brubeck, Raso, Craft and Swix) were used to produce identical cycling tops. All tops used were standard layers produced for athletes. The layers were different in case of fabric type and base mass. However, each of the layers were chosen and measured specifically for cyclist in order to provide the best surface between layer and body.
The characteristics of the thermo-active layers of the tops are presented in Table 1.
Every base layer model was measured as a new product. Moreover, as a standard level, the measurement of sportsmen without any base layer was done during the specified training.
The assumption of the study was to measure the layer surface temperature distribution and compare it to a chosen region with the body temperature without the shirt. As described in the previous chapter, clothes are a kind of barrier for thermoregulation mechanisms of the body, especially when it comes to effort. Yet, the manufacturers say that thermal shirts are designed to support the thermoregulation processes, so it should not limit the thermal energy from the body. Researchers expected that for a sport t-shirt the surface temperature at the peak of training (Fig. 1) should not differ significantly from the model measure (without the layer). They expected that shirt would help the body to release the heat simultaneously, keeping the sweat away from the body so it should improve the comfort of the sportsman during activity. However, as mentioned in the last paragraph of previous chapter, it is important to remember interfering factors such as sweating. The absorption of water through the fabric will change the temperature distribution on the surface. Therefore, an additional parameter that was examined was the mass of the dry jersey, and after the training filled with sweat, to take into account the effect of the absorbed liquid.
The features of the thermo-active tops are shown in Table 1.
In this case study, a single semiprofessional cyclist (mass: 71.9 ± 2.0 kg, height: 1.80 m, body fat: 13.9 ± 0.9%; BMI: 22.2 ± 0.8 kg/m2) was evaluated with the six different tops, and without any top, performing the same training during the same regeneration period of the cyclist. The measurements were taken over 3 months in order to find the repeating conditions in cyclist training plan. Researchers carried out each test in the middle of a regeneration micro-period (1 week), which means that subject was studied 2–3 days after a one-day competition and was completely healthy with good physical conditions. The measurement recurrence was intended to keep similar conditions for athlete in every measure. All measurements were taken at the morning, and prior to training cyclist had a standard hydration protocol, and the amount of intake fluids was no higher than 0.5 L from the time of waking up. The breakfast was standardized and it was always pasta and fruit. And, in order not to upset the stomach, the previous evening dinner was also light. In order to keep the cyclists thermoregulation mechanisms at the same conditions, every measurement started with a 20-min acclimation to the test room (temperature: 20.0 ± 1.0 °C; humidity: 42.0 ± 5.0% [22].
In the test room, any temperature noise (i.e., heaters or air conditioners) was eliminated. As an emissivity parameter of measured tops, the value of 0.85 (polyester emissivity) was chosen and it was constant during test time [23]. The calibration of infrared camera was done once a week with black body used in a laboratory at The University of Silesia, Medical Physics Department in Chorzów. Calibrations were done by using the temperature stabilization test with a 28 °C temperature setting and taking thermal images with a 1-min interval during 30 min. All results had a margin of error of ± 2%.
To carry out the tests, the bicycle power method was selected for training protocol. The bicycle power parameter [W] is a reflection of the load size on the ergometer. Training with power settings are one of the most popular protocols to keep the training recurrence, due to the load setting on the ergometer. The training protocol of the cyclist for every base layer is outlined in Fig. 1.
Each training was done by using the Italian training simulator company Elite, the Real Turbo Muin B+ model (Fig. 2a) with a power measurement, Bluetooth system and ANT+ sensors system. Using the ANT+ system, the GARMIN (USA) model Edge 1000 device was connected to the simulator to get data about power, heart rate and speed. All devices were connected to the Elite Real Software installed on MacBook Pro OSX Yosemite to control training parameters. The use of the Elite Real Software (Italy) allowed for precision in repeatability of measurements [24,25,26]. The training protocol was strictly controlled and checked to make the deviations from the training plan as small as possible.
Thermal imaging was done before, during (each 5 min during the 50-min training) and immediately after the training (Fig. 1).
For the thermal data collection, an infrared camera (Flir Systems (USA) model E60 with sensitivity 0.05ºK) was placed at 2.0 ± 0.1 m from the cyclist. And, the body core temperature was measured from inside the ear by using a thermometer (TECH-MED model TM-350, Poland).
Temperature and standard parameters obtained from cycloergometer (i.e., power level, heat rate, cadence) were measured. Also the mass of the t-shirts was measured before and after the training using a jewelry mass scale PRO-TECH (Poland) with a precision of 0.01 g.
Other than the size of all base layers being the same, in fact, each of the base layers had a little different level of coface to the skin which the volunteer has reported. The term “coface” in terms of our research means the assessment of the layer fitting to the skin. Due to this fact, for every thermo-active shirt, cyclist did subjective assessments of their cofaces. Moreover, the cyclist also tried to assess the training comfort in every base layer model using a scale from 1 to 5, with 5 as the perfect comfort (Table 2).
All measurements were performed as close as possible to following the Glamorgan protocol, which includes thermal imaging in medicine standards and rules [27,28,29].
The method to calculate the average temperature of the layer surface on all thermal images was a computerized analysis using the ThermaCAM TM Researcher Pro 2.8 SR-3 program. All calculations took into account the selected region of interest (ROI), which is presented in Fig. 3. The ROI’s were chosen according to areas of the body, which were covered by each layer and was repeatable for every measurement.
The average surface temperature was calculated from the front side of the chest and abdomen (AR01) and the back (AR02—the area of pulsometer band was excluded from calculation). All pixels from both ROI’s were exported and used to calculate the mean value of the surface temperature.
As was mentioned in methodology, the thermal images were taken in 5-min intervals, except the last one measured when the interval was 10 min due to the body cool-down process. As a result, the researchers attained the average surface temperature for each layer and model in appointed intervals (Fig. 1) during all training protocol. In further analysis, the difference between the mean temperature of the model and mean temperature of each layer was calculated and called DTsurface(model layer) parameter. The DTsurface parameter was calculated for each interval in training protocol.
Statistical analyses were completed with the Statistica 12 program, and graphs were made in MS Office Excel 2010. The relationship between the power parameter (taken from the simulator Elite Real Turbo Muin B+) and the DTsurface parameter for each layer (calculated from analyzed thermal images) was performed with the use of the Pearson statistical correlation.
Differences with a p factor less than 0.05 were recognized as significant.
Results
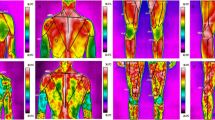
Representative thermal images in different moments of training for the chosen base layer and models are shown in Fig. 3. The average surface temperature of each layer and the model was calculated from all completed measurements during the test.
The difference in the mean temperature of the body surface (model) and top (layer) was calculated for every moment of the test and defined as DTsurface(model layer) and is presented in Fig. 5.
For each layer and for the model, the average surface temperature was calculated from all measurements completed during the test. The results are shown in Fig. 6, where one can see the average surface temperature value for the body (model) and every layer.
Additionally, the mass difference before and after the test was measured for each shirt. On the other hand, the heart rate is the most important parameter, which is used in training. That is why the mass difference was correlated with the average heart rate from each test. This correlation was intended to check whether it is possible to connect training comfort with the heart rate.
It is generally known that all disorders, which appear during training, for example, high temperature or exceeding mass, can increase heart rate. In this case, the heart-beat parameter is an indicator of all disorders, in addition to the temperature overload. Temperature overload seems to be correlated with the effect of heat transfer between the body and the environment, which takes place through the shirt (layer).
The relations are presented in Fig. 7, which shows that the smallest layer mass gain corresponds with the smallest value of the average heart rate.
Moreover, the correlations between the bicycle power and the surface temperature difference DTsurface(model layer) defined as a difference between model (skin temperature without shirt) and each of layers (data from Fig. 5) were done. As a bicycle power parameter, the value of cycling load was set in Elite ergometer according to Fig. 1, where training protocol is showed.
All Pearson’s coefficients from mentioned correlations are collected in Table 3.
It can be also seen that for layer E the Pearson coefficient is the lowest, and obtained negative correlation is the strongest correlation. It is also clearly seen in Table 3. Results for this layer are shown in Fig. 7.
Discussion
It is easy to see from Fig. 4 the differences in the body thermal map between the models with and without base layers on the body. However, the trends of temperature distribution changes seem to be similar for each layer. It also seems that the differences in temperature distribution between layers observed in the case of the 250 W level are very similar; it is the time in training when the body is sweating the most and the body surface cooling effect is seen very clearly.
Thermal images for model and chosen base layers before, in the 30th minute and after the test. The ROI’s used to compare base layers are defined in Fig. 3 and visible in thermal images of the model before the test (white mark)
Moreover, it is after the adaptation process, when sportsmen wear base layers for about 15 min before the first thermal imaging, that the surface temperature for layer E seemed to be lower, and for layers C and E is not as big as for layer E. Yet these considerations are related only to the visual evaluation from thermal images.
That is why the DTsurface(model layer) parameter was calculated and its changes as a function of training time are presented in Fig. 5. From this figure, the difference of surface temperature between the model and every layer DTsurface(model layer) can be clearly seen.
It is also noticeable that for layers F, B and A the DTsurface(model layer) value is higher than for other layers, but the mean temperature results were especially high in the case of layer F. On the other hand, the lowest values of DTsurface(model layer) were obtained for layer E. In the case of layers D and E, the temperature differences are similar to the model temperature.
For deeper insight into the problem, the mean value of surface temperature from all measurements for each layer was calculated and is presented in Fig. 6. The mean value of surface temperature was calculated by averaging all surface temperatures obtained for every imaging moment for each layer. The differences between mean surface values for each training are shown as a box graph in Fig. 6 with the standard error (SE) and standard deviation (SD) values.
The mean surface temperatures obtained for layers E, D and C are the most similar to the model surface temperature. One can see that the most similar to the model in the case of body surface temperature is layer E. It can be caused by heat transmission in fabric, which was used for these layers. The highest difference between model surface temperature and layer temperature was obtained for layer F, where it may be supposed that the fabric does not support the heat transfer. In consequence, the sweat may lock the fabric pores and the heat produced in the body cannot be effectively transferred outward into the environment. Additionally the mass gain for layer F is the smallest—the difference in mass value before and after is only about 19.6 g and for other layers this value is 36.0 g, as in layer C and more than 60.2 g for other layers.
This may point out that during training in layers with high sweat accumulation (Fig. 7) possibilities, athletes bodies show a greater demand for energy, which is needed for sweat evaporation. It can correspond with a higher-than-optimal value of heart rate due to high body energy expenditure, which is indicated by a high Pearson’s coefficient (r = 0.88) and the statistical significance (p < 0.05, p = 0.02). For tests in layers C, F and E, where the heart rate value is less than 120 bpm, the differences are smaller, about ± 2 bpm [30, 31].
On the other hand, it is observable for layer E, though the mass gain was higher than for layers F and C, the heart rate increase is not observed as much as in layer B. Such results suggest that the most important factor in base layers is a proper inner structure that allows the heat to flow out quickly and evaporate simultaneously without keeping the moisture inside the shirt.
In Table 3, one can see the Pearson coefficient values for correlations between the cycloergometer power [W] and DTsurface [°C]. All results are statistically significant with p < 0.05. It may indicate that the proposed training protocol may be appropriate for base layer testing. On the other hand, the correlations between DTsurface(model layer) value and power (Table 3) may show that in most cases, when the layer surface temperature is closer to the model (body), then a higher Pearson’s coefficient is obtained (all results are statistically significant).
The strongest correlation was gathered for layer E (r = − 0.87). For this layer, the temperature difference parameter DTsurface(model layer) resulted in the smallest value (Fig. 6). Such a comparison may suggest that the surface temperature of the model was similar to the layer E surface temperature. The smallest results for Pearson’s coefficient were obtained for layer F (Table 3), which corresponds with the Pearson’s coefficient value r = − 0.81 and the high difference between the mean surface temperature of the model and layer F (Fig. 6).
Data presented in Table 3 and Fig. 8 may show that an increase in bicycle power is strongly connected with a decreasing DTsurface(model layer) value. The load increase on the cycloergometer is connected with an increase in the athlete’s efficiency. It is known that for a higher load, stronger work must be done. For higher efficiency, it can be said that some threshold for sportsmen is reached. However, the body, aside from overheating is sweating at most due to some efficiency cutoff point.
The results indicate the smallest difference between the surface temperature of the model and layer E and also the highest correlation of DTsurface(model layer E) with power increase. It may be connected with the high efficiency of outward heat transfer for this layer than others.
Conclusions
The studies showed significant correlations between ergometer power and the temperature difference parameter DTsurface(model layer). The highest Pearson’s coefficient was found for the base layer in which the temperature difference parameter was the smallest. Furthermore, a high and positive correlation was obtained for the difference of the layer mass before and after the training compared with the mean heart rate from training.
Such results indicate that thermal imaging may give new potential applications in sport clothing assessment. Additionally, all measurements should be performed according to the guidelines. The measurements standardization process must be worked through in all situations, including temperature, humidity and importantly the training period of the athlete. Also, the emissivity of the material needs to be determined, as well as the accumulated moisture.
Our proposed analysis may support selecting clothing that will help the transfer of heat during exercise and protects athletes from overheating. Consequently it may indicate that the proposed training protocol may be appropriate for base layer testing.
Conclusions must be drawn carefully due to the low amount of base layers.
References
Więcek B, De Mey G. Termowizja w podczerwieni, podstawy i zastosowania. Warszawa: PAK; 2011.
Cholewka A, Stanek A, Sieroń A, et al. Thermography study of skin response due to whole-body cryotherapy. Skin Res Technol. 2011;18:180–7. https://doi.org/10.1111/j.1600-0846.2011.00550.x.
Cholewka A, Drzazga Z, Sieroń A, et al. Thermovision diagnostics in chosen spine diseases treated by whole body cryotherapy. J Therm Anal Calorim. 2010;102:113–9.
Madura H. Pomiary termowizyjne w praktyce. Warszawa: Agenda Wydawnicza PAKu; 2004.
Cholewka A, Kasprzyk T, Stanek A, et al. May thermal imaging be useful in cyclist endurance tests? J Therm Anal Calorim. 2016;123:1973–9. https://doi.org/10.1007/s10973-015-4662-5.
Kasprzyk T. The thermal imaging of sportsmen body surface. The influence of training cycle at organism metabolism, A. Chełkowski Institute of Physics, University of Silesia Katowice Poland, Master thesis; 2014.
Goraj M. Applications of thermal imaging in energy cost rating during training, A. Chełkowski Institute of Physics, University of Silesia Katowice Poland, Master thesis; 2015.
Guyton AC, Hall JE. Textbook of medical physiology. 11th ed. Philadelphia: Elsevier Inc; 2006.
Herman IP. Physics of the human body. New York: Springer; 2016.
Mackowiak PA, Wasserman SS, Levine MM. A, critical appraisal of 98.6°F, the upper limit of the normal body temperature, and other legacies of Carl Reinhold August Wunderlich. JAMA. 1992;268:1578–80.
Downey JA, Myers SJ, Gonzales EG. The physiological basis of rehabilitation medicine. 2nd ed. Amsterdam: Elsevier; 1994.
Lim CL, Byrne C, Lee JKW. Human thermoregulation and measurement of body temperature in exercise and clinical settings. Ann Acad Med Singap. 2008;37:347–53.
Bauer J, Hurnik P, Zdziarski J, et al. Zastosowanie termowizji w ocenie skutków krioterapii. Acta Bio-Optica et Inf Med. 1997;3:133–40.
Górski J. Human physiology. Warszawa: PZWL; 2010.
Wiśniewski S, Wiśniewski ST. Heat transfer. 6th ed. Warszawa: WNT; 2009. ISBN 978-83-204-3671-6.
Pilawski A. Biophysics basics. Warszawa: PZWL; 1983.
Wendt D, van Loon LJC, van Marken Lichtenbelt WD. Thermoregulation during exercise in the heat. Sports Med. 2007;37:669–82.
Skalik R, Borodulin-Nadzieja L, Wozniak W, et al. The significance of thermoregulation to physical capacity in humans—can dysregulation of core body temperature and its cortical perception have impact on the course of chronic heart failure? Kardiol Pol. 2009;67:449–54.
The thermo-active layers properties. Brubeck Company. http://www.brubeck.pl/pl/page/właściwości-odzieży-termoaktywnej. Accessed 8 Jan 2018.
Responsibility. Products developed with care. Craft Company. http://global.craftsportswear.com/craft-e-commerce/baselayer-1/stay-cool/1901381-1900/. Accessed 8 Jan 2018.
Frydrych I, Porada A, Bilska J, et al. Thermoinsulation fabrics parameters – part 1. Rewiev of measurements methods and devices. Przegląd Włókienniczy 2003;10.
Buther E, Masłowski E. Textiles for sport – part 1. Prz. Włókienniczy. 2002;2.
Emissivity table. Optotherm thermal imaging. https://www.optotherm.com/emiss-table.htm (accessed 20 August 2018).
Product overview. Garmin company. http://www.garmin.com/pl-PL/. Accessed 2 Jan 2018.
Product overview. Elite Company. http://www.elite-real.com. Accessed 2 Jan 2018.
Product overview. Elite Company. http://www.elite-it.com/en. Accessed 2 Jan 2018.
Gomes Moreira D, Costello JT, Brito C, et al. Thermographic imaging in sports and exercise medicine: a Delphi study and consensus statement on the measurement of human skin temperature. J Therm Biol. 2017;69:155–62. https://doi.org/10.1016/j.jtherbio.2017.07.006.
Ammer K. The Glamorgan protocol for recording and evaluation of thermal images of the human body. Thermol Int. 2008;18:125–44.
Ring EFJ, Ammer K. The technique of infrared imaging in medicine. Thermol Int. 2000;10:7–14.
Casa DJ, Armstrong LE, Hillman SK, et al. National athletic trainers’ association position statement: fluid replacement for athletes. J Athl Train. 2000;35:212–24.
Saltin B. Circulatory response to submaximal and maximal exercise after thermal dehydration. J Appl Physiol. 1964;19:1125–32.
Acknowledgements
The authors would like to submit acknowledgments for the thermo-active clothes companies for supporting science by freely sharing their products for research. In addition, the test equipment support was completed with a shared training simulator and a training parameters measurement device. We would like to offer sincere thanks for Brubeck brand, Swix Company, CRAFT brand, RASO Sport Wear, Elite Company and GARMIN Polska Company.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kasprzyk, T., Cholewka, A., Kucewicz, M. et al. A quantitative thermal analysis of cyclists’ thermo-active base layers. J Therm Anal Calorim 136, 1689–1699 (2019). https://doi.org/10.1007/s10973-018-7775-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10973-018-7775-9