Introduction

Cellulose fiber-based thermal insulating materials could be promising alternatives to the petroleum-based materials to meet the increase in demand for eco-friendly and sustainable building materials [1]. To improve the fire safety of cellulose fiber-based thermal insulating materials used in buildings, different types of fire retardants have been used, such as expandable graphite and a synergetic fire retardant that have low toxicity and low smoke production during combustion. Our previous study has shown that cellulose fiber-based thermal insulation developed from formulations containing cellulose fibers and 10–30% of two types of fire retardants were subjected to the reaction-to-fire tests, when 20% expandable graphite or 25% synergetic fire retardant was added to the formula, the thermal insulation materials can meet the requirements of fire class E according to the European standard [2, 3], and show an enhanced fire retardancy [4]. However, the effects of these fire retardants on the thermal degradation kinetics and pyrolysis products of cellulosic thermal insulating materials have yet to be investigated. And few publications focused on kinetics and mechanism of thermal degradation of cellulosic insulating materials developed from mechanical pulp fiber and fire retardants. Therefore, it is important to obtain a detailed information about the pyrolysis of cellulosic insulating materials with or without fire retardants to get a more in-depth understanding of the combustion process.

To elucidate the flame-retarding process, the thermal decomposition of the flame-retardant material can be quantitatively described by the thermal degradation kinetics. The kinetic parameters such as apparent activation energy (Ea) and pre-exponential factor (A) can be calculated using the model-free or isoconversional methods such as Kissinger–Akahira–Sunose (KAS) [5,6,7], the Friedman [8], the Flynn–Wall–Ozawa (FWO) [9, 10], and the model-fitting method such as Coats–Redfern method [11]. Among the different methods used to evaluate the kinetic parameters, the Coats–Redfern method could be less suitable for determination of kinetic parameters due to the uncertain reaction models [12].

It is difficult to model the material behavior when the material is exposed to a fire due to the complex combination of fluid dynamics, combustion, heat and mass transfer, and kinetics [13]. Many studies on the contributions of fire retardant have concluded that a fire retardant can catalyze the cellulose degradation and improve the generation of char that reduces the heat and mass transfer [14,15,16]. The thermal stability, decomposition rate, char-forming rate, and char yield of the thermal insulating materials also affect the fire retardancy [17, 18]. To understand the mechanism of fire retardancy, the master-plots method such as Criado method [19] can be used to predict the reaction mechanism [f(α)] or the possible kinetic models, e.g., experimental data are transformed into master plots, then the master plots are compared with the theoretical models to identify the potential reaction mechanism during the pyrolysis process [20]. Besides, pyrolysis–gas chromatography/mass spectrometry (Py–GC/MS) is an effective method to study the degradation products of cellulose fiber-based thermal insulating materials and is helpful to explain and confirm the fire retardancy mechanism.

The objectives of the present study were to determine the kinetic parameters and examine if the Eα is constant with the degree of conversion and the suitability of the proposed methods. In addition, thermal degradation, fire retardancy mechanisms and gaseous products emitted during the degradation of thermally insulating materials produced from mechanical pulp fiber, expandable graphite or a synergetic intumescent fire retardant need to be determined using the Thermogravimetry (TG) and Py–GC/MS to further understand the fire retardancy reactions.

In the present study, model-free methods such as the KAS, Friedman, and FWO methods were used to compare the difference of the activation energy of cellulosic thermal insulating materials with or without fire retardants. Expandable graphite and a synergetic intumescent fire retardant were selected to study their effects on the mechanical pulp fiber due to their wide use in the market. Master-plots method such as the Criado method was applied to identify the possible reaction models of cellulosic thermal insulating materials with and without fire retardant. The quantity and composition of volatile products from the decomposition and pyrolysis of the flame-retardant cellulose fiber-based thermal insulating materials were determined by Py–GC/MS to get a better understanding of fire retardancy mechanism.

Materials and methods

Materials

Bleached chemi-thermomechanical pulp (CTMP) was provided by Rottneros (Söderhamn, Sweden). The chemical composition of the CTMP is listed in Table 1. Sodium dodecyl sulfate (≥ 99.0%) was purchased from Sigma-Aldrich (Stockholm, Sweden). Commercial expandable graphite was provided by GrafTech (USA). A synergetic intumescent fire retardant (50% ammonium sulfate, 10% ammonium polyphosphate, and 40% aluminum hydroxide) was obtained from a local supplier.

Table 1 Chemical composition of CTMP
Full size table

Sample preparation

A suspension of CTMP (45 g of pulp fibers were suspended in 1 L of water) was mixed with 0.3 g of sodium dodecyl sulfate foaming agent and either 20% of expandable graphite or 25% of a synergetic intumescent fire retardant according to our previous study. It has been shown that the thermal insulation materials containing 20% expandable graphite or 25% synergetic fire retardant can meet the requirements of fire class E according to the European standard (CEN [3]; ISO [2]), and show an enhanced fire retardancy (Zheng et al. [1]). The mixtures were mechanically stirred (3000 rpm, 15 min) in an L&W Pulp Disintegrator (ABB, Zürich, Switzerland) to form foams, and then the foams that were drained by gravity for 30 min, followed by drying (90 °C, 8 h) in a TS8000 oven (TERMAKS, Bergen, Norway). The insulating materials containing the expandable graphite or synergetic fire retardants were denoted EGIM or SYIM (Fig. 1). A reference material was prepared from a suspension of CTMP without any addition of fire retardant.

Fig. 1
figure 1

Photographs of the samples containing expandable graphite or synergetic intumescent fire retardant

Full size image

Thermal analysis

The thermal degradation behavior of the samples was determined by TG, using a TGA/SDTA 851e (Mettler Toledo, Greifensee, Zürich, Switzerland). The samples (about 2 mg) were heated from 25 to 800 °C at heating rates of 5, 10, 15, or 20 °C min−1 in an inert atmosphere (a 50-mL min−1 flow of nitrogen). The onset temperature (temperature in 10% dry mass loss), the maximum decomposition temperature at the maximum mass loss, the production of volatiles in various temperature zones (25–150, 200–375, and 375–800 °C), and the residue at 800 °C were measured.

Thermal degradation kinetics

The thermal degradation kinetics parameters (Ea, f(a), A) can be accessed by two main approaches: isothermally where the temperature keeps constant over time, or non-isothermally where the temperature varies with temperature and time and is dependent on the heating rate (β). Compared with the method based on a single heating rate, the methods based on multiple-heating rates (model-free or isoconventional methods) make it easier to determine the Ea [21].

Therefore, model-free (isoconventional) methods: the KAS [5,6,7], the Friedman [8], and the FWO methods [9, 10] were used to determine the Ea and confirm the reliability of the values of Ea, and master-plots method such as the Criado method [19] was used to identify the possible degradation mechanism.

The thermal decomposition of a solid polymer can usually be described as \(A_{\text{solid}} \to B_{\text{solid}} + C_{\text{gas}}\). The degree of conversion a can be calculated using the equation:

$$\alpha = \frac{{W_{0}^{{}} - W_{\text t}^{{}} }}{{W_{0}^{{}} - W_{\infty }^{{}} }}$$
(1)

where W0, Wt, and W∞ are the initial, actual, and final mass of the sample in the TG, respectively. The initial mass of the sample W0 is the mass of the sample at 373.15 K to minimize the effect of moisture content on the results of activation energy.

A fundamental reaction rate of the kinetic degradation process can be expressed by the Arrhenius equation:

$$\frac{{\text{d}\alpha }}{{\text{d}t}} = kf(\alpha )$$
(2)

The rate constant associated with the temperature k is usually defined by the equation:

$$k = A{\text{e}}^{{ - \frac{{\text E_{\alpha } }}{\text {RT}}}}$$
(3)

By combining Eqs. (2) and (3), the reaction rate can be written as:

$$\frac{{\text{d}\alpha }}{{\text{d}t}} = A{\text{e}}^{{ - \frac{{\text E_{\alpha } }}{\text {RT}}}} f(\alpha )$$
(4)

The constant heating rate in TG is defined as β = dT/dt, and the reaction rate can be expressed as:

$$\frac{{\text{d}\alpha }}{{\text{d}t}} = \frac{{{\text d}T}}{{\text{d}t}}\frac{{\text{d}\alpha }}{{\text{d}T}} = \beta \frac{{\text{d}\alpha }}{{\text{d}T}}$$
(5)

By combining Eqs. (4) and (5), the reaction rate can be described as:

$$\frac{{\text{d}\alpha }}{{\text{d}T}} = \frac{A}{\beta }{\text{e}}^{{ - \frac{{\text E_{\alpha } }}{\text {RT}}}} f(\alpha )$$
(6)

Integration of Eq. (6) with the initial conversion degree a = 0 at T = T0 leads to:

$$g(\alpha ) = \int_{0}^{\alpha } {\frac{{{\text{d}}\alpha }}{f(\alpha )} = } \frac{A}{\beta }\int_{{T_{0} }}^{T} {{\text{e}}^{{ - \frac{{E_{\alpha } }}{RT}}} \text{d}T \equiv } \frac{{AE_{\alpha } }}{\beta R}{\text{p}}\left( {\frac{{E_{\alpha } }}{RT}} \right)$$
(7)

g(a) has different expressions (Table S1) that can be used to predict the solid reaction mechanism in the dynamic TG.

Model-free methods

The KAS method [5,6,7]

Equation (7) can be integrated into a logarithmic form as the equation:

$$\ln g(\alpha ) = \ln \left( {\frac{{AE_{\alpha } }}{R}} \right) - \ln \beta + \ln \left[ {p\left( {\frac{{E_{\alpha } }}{RT}} \right)} \right]^{{}}$$
(8)

Introducing the approximation

$$p\left( {\frac{{E_{\alpha } }}{RT}} \right) \cong \frac{{{\text{e}}^{{ - \frac{{\text E_{\alpha } }}{\text {RT}}}} }}{{\left( {\frac{{E_{\alpha } }}{RT}} \right)^{2} }}$$
(9)

Equation (8) can be rewritten as the KAS equation:

$$\ln \frac{\beta }{{T^{2} }} = \ln \frac{AR}{{E_{\alpha } g(\alpha )}} - \frac{{E_{\alpha } }}{RT}$$
(10)

Activation energies Ea can be calculated from the slope of ln(β/T2) versus 1000/T for different heating rates β. The slope is equal to − Eα/R.

The Friedman method [8]

Based on the logarithms of Eqs. (5) and (6), the Friedman method can be described by the equation:

$$\ln \frac{{\text{d}\alpha }}{{\text{d}t}} = \ln \left( {\beta \frac{{\text{d}\alpha }}{{\text{d}T}}} \right) = \ln \left[ {Af(\alpha )} \right] - \frac{{E_{\alpha } }}{RT}$$
(11)

Activation energies Ea can be obtained from the slope of the plots of ln(dα/dt) versus 1000/T, and the slope is equal to − Eα/R.

The FWO method [9, 10]

Using Doyle´s approximation \(\ln p\left( {\frac{{E_{\alpha } }}{RT}} \right) \cong - 5.3305 - 1.052\frac{{E_{\alpha } }}{RT}\) [22, 23], Eq. (8) can be simplified to:

$$\ln \beta = \ln \frac{{AE_{\alpha } }}{Rg(\alpha )} - 5.3305 - 1.052\frac{{E_{\alpha } }}{RT}$$
(12)

Master-plots method

The Criado method [19]

By combining Eqs. (5) and (6), the Criado method can be described by the expression:

$$\frac{Z(\alpha )}{Z(0.5)} = \frac{f(\alpha )g(\alpha )}{f(0.5)g(0.5)} = \left( {\frac{{T_{\alpha } }}{{T_{0.5} }}} \right)^{2} \frac{{({{\text{d}\alpha } \mathord{\left/ {\vphantom {{\text{d}\alpha } {\text{d}t)_{\alpha } }}} \right. \kern-0pt} {{\text d}t)_{\alpha } }}}}{{({{\text{d}\alpha } \mathord{\left/ {\vphantom {{\text{d}\alpha } {\text{d}t)_{0.5} }}} \right. \kern-0pt} {\text{d}t)_{0.5} }}}}$$
(13)

where 0.5 indicates the degree of conversion a.

\(\frac{f(\alpha )g(\alpha )}{f(0.5)g(0.5)}\) is used to plot the theoretical model curves by introducing the different f(a) and g(a) expressions, while the \(\left( {\frac{{T_{\alpha } }}{{T_{0.5} }}} \right)^{2} \frac{{({{\text{d}\alpha } \mathord{\left/ {\vphantom {{\text{d}\alpha } {{{\text d}}t)_{\alpha } }}} \right. \kern-0pt} {\text{d}t)_{\alpha } }}}}{{({{\text{d}\alpha } \mathord{\left/ {\vphantom {{\text{d}\alpha } {{\text d}t)_{0.5} }}} \right. \kern-0pt} {\text{d}t)_{0.5} }}}}\) is obtained from the experimental data.

Table 2 summarizes the different thermal degradation kinetic methods. The different algebraic expressions for f(a) and g(a) for the kinetic models are listed in Table S1 [24].

Table 2 Methods used in the evaluation of kinetic parameters and mechanisms
Full size table

Py–GC–MS

The volatile gases released during the thermal degradation of the materials were determined by Py–GC/MS consisting of a TGA/DSC 3+ (Mettler Toledo, Greifensee, Zürich, Switzerland), a sample storage unit IST16 (SRA Instrument Chromatographic Solutions, Marcy-l’Étoile, Lyon, France), 7820A GC, and a 5977B MSD System (Agilent Technologies, Santa Clara, California, United States). The samples were heated from 25 to 800 °C at a rate of 10 °C min−1 in an inert atmosphere (30 mL min−1 flow of nitrogen). The volatile gases at 250, 350, and 450 °C were identified according to their mass spectra using a NIST MS library.

Results and discussion

Thermal degradation analysis

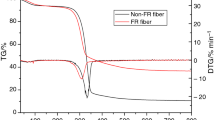
Figure 2 shows the TG curves and derivative (DTG) curves of the SYIM and EGIM fire-retardant cellulosic thermal insulating materials at a heating rate of 10 °C min−1, and the results are summarized in Table S2. The onset decomposition temperatures (temperature for 10% mass loss − Tonset10%) for EGIM and SYIM were lower than that of the reference. A decrease in thermal stability could promote an earlier dehydration of the materials and generate a protective char layer on the surface of the materials at a lower temperature [25]. An increase in the final char residue (about 12%) of the fire-retardant insulating materials was also observed in the TG curves.

Fig. 2
figure 2

a TG and b DTG curves for the reference and fire retardant-containing insulating materials

Full size image

As shown in the DTG curves (Fig. 2b), Tmax for the reference sample likely related to the dehydration of cellulose and hemicellulose which were predominant at temperatures lower than 300 °C, while lignin decomposition was less significant due to its lower content of free hydroxyls in this temperature region [26]. Tmax1 for EGIM was much lower than that for SYIM (209 vs. 254 °C). On the other hand, Tmax3 for EGIM was obviously higher than Tmax2 for SYIM (362 vs. 288 °C). The higher Tmax was here attributed to the generation of a more thermally stable char, as a result of the degradation of expandable graphite [27] and the dehydration of pulp fibers. Tonset10% for EGIM was 197 °C, which was related to the expansion of the expandable graphite pulp fibers into a “worm”-like char layer at a low temperature 160 °C due to the redox reaction between the inserted H2SO4 and the layered graphite [14]. For the SYIM sample, the Tmax1 (254 °C) could be due to the decomposition of aluminum hydroxide (ATH) at a temperature of 180 °C [15]; and the catalytic dehydration of pulp fibers by the polyphosphates produced in the decomposition of ammonium polyphosphate (APP) [16]. As a result, the thermally stable char generated and that resulted in a higher Tmax2 for SYIM. However, the rate of decomposition of the SYIM was faster than that of the EGIM according to the DTG curves, which could be due to synergetic effects of APP and ATH in SYIM. The water-soluble ammonium sulfate was not considered in the discussion, since it may have been lost during the wet production process as indicated by the retention calculation in the previous work [4].

Fig. 3
figure 3

TG and DTG curves of the samples at different heating rates: a TG–reference; b DTG–reference; c TG–SYIM; d DTG–SYIM; e TG–EGIM; f DTG–EGIM

Full size image

The dynamic TG and DTG curves at different heating rates (Fig. 3) show that the decomposition temperature increased when the heating rate rose from 5 to 20 °C min−1. There was a slight shift to a higher onset temperature and to a higher maximum temperature with increasing heating rate (Table S2) even though the TG and DTG profiles were similar, which could result from the higher thermal gradient in the sample crucible with increasing heating rate [28], i.e., the heat transfer was not uniform between the furnace and samples when the heating rate was faster [29], and there was a thermal lag between the thermosensor and the sample [12, 30].

These TG curves (Fig. 3a, c, and e) show different mass loss stages. Stage I, between 25 and 150 °C, Stage II, between 200 and 375 °C, and Stage III, between 375 and 800 °C. The quantities of volatiles released during these thermal degradation stages are presented in Table S2. The quantity of volatiles produced from a given material is more or less the same regardless of the increasing heating rate, e.g., the total volatile of the reference sample kept at about 77% when the heating rate increased from 5 to 20 °C min−1. In stage I, 3–7% moisture mainly volatilized between 25 and 150 °C. In stage II, a complicated thermal degradation process with several overlapping peaks in the DTG curves was observed between 200 and 375 °C, and the volatilization was 60, 45, and 35%, respectively, for the reference, SYIM, and EGIM. The lower volatile production implies that the dehydration of the pulp fiber is promoted and that the char formation is increased. In stage III, fire-retardant samples SYIM and EGIM showed a higher volatilization than the reference in the range of 375–800 °C, as could be concluded by further reactions of char formation.

Calculation of the activation energy according to the model-free methods

The activation energy Eα values were calculated according to the KAS, Friedman, and FWO methods (Fig. 4a, b, and c; Table S3), and the linear plots ln(β/T2) versus 1/T, ln(dα/dt) versus 1/T, and lnβ versus 1/T are shown in Fig. S1. For the reference sample without fire retardant, it has been seen that the plots (Fig. S1 a, b, and c) showed a good linear when the degree of conversion in the range of 0.15–0.6 at corresponding temperature of 280–330 °C (Fig. 4d), which could imply constant activation energies at different conversions and the possibility of single reaction mechanism (or the unification of multiple-step reaction mechanisms). For the fire-retardant insulating samples SYIM and EGIM (Fig. S1 d–i), the linear relationship was not significant when α < 0.3 and α > 0.6, which might be due to the complex reactions in the decomposition process of the fire retardant and the dehydration of cellulosic fibers.

Fig. 4
figure 4

Activation energy as a function of conversion calculated by different methods: a reference; b SYIM; c EGIM; d temperature as a function of the degree of conversion at a heating rate of 10 °C min−1

Full size image

The activation energy for each degree of conversion shown in Table S3 was calculated from the slope of the fitted linear line obtained by different kinetic methods. Figure 4 shows the plots of activation energy as a function of conversion in the range of 0.1–0.8 for all the samples. For the reference sample, the data obtained by the KAS, Friedman and FWO methods were very close and in good agreement when α < 0.6, which indicated the reliability of the Eα values obtained. An increased Eα indicates a greater thermal stability due to the formation of a thermally stable char when α > 0.6. But for the fire-retardant insulating samples SYIM and EGIM, the thermal decomposition may be a multiple-step mechanism because the relationship between Eα and α was not linear. The Friedman method produced higher Eα values than the KAS and FWO methods (Table S3). The numerical difference between the methods for SYIM and EGIM was 10–25%. According to the previous study, the Friedman method is usually the most accurate compared with the KAS and FWO methods when the actual Eα value varies with the degree of conversion α [31]. Because the KAS and FWO methods assume that the value of Eα is constant in the whole interval of integration (0–α). A 20–30% of systematic error could be introduced when the Eα value has significant variations. However, the differential method of Friedman can eliminate this error. Thus, the Friedman method can be regarded as the best method to evaluate the kinetic parameters compared with other model-free methods such as KAS and FWO [31,32,33,34]. For SYIM and EGIM, the activation energy varied significantly at the higher degree of conversions, indicating the existence of a complex multi-step mechanism including parallel, competitive, and consecutive reactions and activation energies [35].

The Eα can be divided into several regions with regards to α. For the reference, Eα remained constant at about 160 kJ mol−1 in the main region (0.15 ≤ α ≤ 0.6). For SYIM, Eα remained constant in the region 0.35 ≤ α ≤ 0.45, and increased significantly in the region (0.5 ≤ α ≤ 0.6), before decreasing gradually (0.65 ≤ α ≤ 0.8). For EGIM, an increase in Eα was evident in the region (0.1 ≤ α ≤ 0.4) and a decrease in the region (0.4 ≤ α ≤ 0.7).

As shown in Fig. 4a, b, and c, the Eα value of SYIM increased gradually when the degree of conversion was increased from 0.1 to 0.65, and the Eα value of EGIM showed an increasing trend when the α was below 0.4, in contrast that of the reference that remained constant at about 160 kJ mol−1. This indicated that the fire retardants improved the formation of a thermally stable char. In general, the activation energy is defined as the minimum energy needed to start a chemical reaction, and a higher Eα value means a slower reaction [12]. Here, a higher Eα indicates a greater thermal stability because of the generation of a thermally stable char. The trend is similar to that of fire-retardant materials previously reported [12, 17, 36]. A lower Eα after the increasing region can be related to the catalytic reaction of phosphoric acid produced from the decomposition of APP or of H2SO4 between the carbon layers in EG. The reaction catalyzed the dehydration of the main components (cellulose, hemicellulose, and lignin) of the pulp fibers and led to a lower Eα.

Figure 4d shows the temperature as a function of the degree of conversion for the reference, SYIM, and EGIM at a heating rate of 10 °C min–1. In the early thermal degradation stage (α = 0.1), the Eα value of the fire-retardant cellulosic thermal insulating materials SYIM was lower than that of the reference without any fire retardant, and the temperatures at α = 0.1 showed the same tendency. This means the decomposition of  synergetic fire retardant and the dehydration of pulp fibers at a lower temperature, which is similar to the results for the fire-retardant wood plastic composite [36]. In contrast, the Eα of EGIM (α = 0.1) was higher than that of the reference and SYIM, indicating a slower decomposition of pulp fibers due to the earlier generation of protective char during the redox reaction between H2SO4 and the graphite.

Determination of the degradation mechanism by the master-plots method

The Z(α)/Z(0.5) versus \(\alpha\) curves based on the different mechanisms f(α) are shown in Fig. 5. For the reference, the experimental curve almost overlapped the D3 curve in the range (0.1 < α < 0.6) (Fig. 5a), indicating that the reference without any fire retardant could possibly be governed by a D3 mechanism, where degradation occurs by diffusion in three dimensions (diffusion of heat from heating source and hot gases produced throughout the sample). This is in accordance with the results previously reported [37,38,39,40]. When the conversion values are higher than 0.6, the suitable mechanism model was difficult to identify, which could be due to the complex degradation of char.

Fig. 5
figure 5

Master curves and experimental curves at 10 °C min−1 obtained using the Criado method: a reference; b SYIM; c EGIM

Full size image

For SYIM and EGIM, in the beginning, the experimental curves (0.1 ≤ α ≤ 0.15) could overlap F3 and F2 theoretical models, respectively. But with the increasing of α, these fire-retardant samples showed very complicated reaction mechanisms or may have deviated from the basic theoretical models, e.g., the experimental curve of SYIM may fit the A3 model when the α value was between 0.35 and 0.5. It did not fit the proposed models when the α increased from 0.5 to 0.8. For EGIM, the experimental curve could overlap the F2, F3, and P2 models alternately when the α was lower than 0.5, i.e., it probably fit F2 (0.1 ≤ α ≤ 0.15, 0.25 ≤ α ≤ 0.3), F3 (0.35 ≤ α ≤ 0.4), and P2 (0.45 ≤ α ≤ 0.5). Similarly, no proposed models overlapped the experimental curve when the α was higher than 0.5.

Analysis of volatile products of thermal degradation using Py–GC–MS

Gas chromatograms of the volatile products during the thermal degradation of insulating materials are shown in Fig. 6, i.e., the volatile products produced from the thermal degradation of the major components of CTMP fibers (such as cellulose, hemicellulose, and lignin). As summarized in Table 1, the CTMP raw material consisted mainly of 42% of glucose, 26% of lignin, and 20% of monosaccharide-containing hemicellulose. Cellulose is a long-chain polymer with alternating repeating units of glucose linked by β-1,4-glycosidic bonds [41]. Hemicellulose consists of a variety of monomers such as xylose, mannose, glucose, galactose, and arabinose. Hemicellulose has a more complex structure than cellulose due to its higher content of branched chains attached to the backbone through glycosidic linkages [42]. Lignin is composed of three basic monomeric units, syringyl, guaiacyl, and p-hydroxyphenyl alcohol [43].

Fig. 6
figure 6

Gas chromatogram of the volatile products formed during thermal degradation (in N2) of cellulosic thermal insulating materials at a 250 °C; b 350 °C; c 450 °C

Full size image

As shown in Fig. 6a, fire-retardant materials released a large quantity of furfural that could be derived from the loss of formaldehyde of the cyclic or chain conformations of β-d-glucose in cellulose [44]. Similarly, the improved formation of levoglucosenone could result from the accelerated degradation of β-d-glucose. The dehydration of cellulose and hemicellulose generated C=C bonds through cleavage of the glycosidic links [45]. In addition, the generation of phenols was suppressed when the fire retardants were present so that less volatile phenol compounds were formed from lignin and more solid char generation arose from the catalysis of the fire retardants [46]. Also, rearrangement of the aromatic rings occurred, resulting in a reduction in the amount of volatile aromatic compounds [47].

The SYIM produced more furfural and levoglucosenone than EGIM, which may be attributed to the formation of polyphosphates during the degradation of APP. This reaction can enhance the catalysis of the char generation and promote the formation of anhydrosugars. Acidic metal oxides such as aluminum oxide produced from ATH also increased the total yield of anhydrosugars (levoglucosenone) as a result of the promotion of the dehydration, decarbonylation and cracking of organic molecules [48]. Besides, the significant increase in furfural yield may be attributed to the improved catalytic dehydration of the pentosyl and glucosyl residues and anhydrosugars [49]. Furfural was the most abundant product created during the degradation of hemicellulose when monosaccharide units in hemicellulose were ring-opened and cracked [50].

The release of furfural and levoglucosenone increased, which is linked to the onset temperature shift in TG (Fig. 2a) and the destabilization in the DTG curve (Fig. 2b). Intensive dehydration of glycoside units of cellulose leads to an increase in the production of levoglucosenone from a potential catalyzed degradation [51]. This result agrees with what has been reported by Czégény et al. [52] and by Pappa et al. [53]. A possible reaction pathway [45] for the formation of levoglucosenone from cellulose is shown in Fig. S2. As shown in Fig. 6, the yield of furfural and levoglucosenone dramatically decreased with increasing temperature from 250 to 450 °C, because of the char formation.

Most of the identified pyrolysis products and the percentages of the individual products are presented in Table 3. In the volatiles from SY, the phosphoric acid, dimethyl 1-propenyl ester (C5H11O4P) and phosphonic acid, phenyl-, bis[5-methyl-2-(1-methyl ethyl)cyclohexyl] ester (C26H43O3P) were found, which further supports the discussion about the fire retardancy mechanism of SYIM.

Table 3 Volatile pyrolysis products of cellulosic thermal insulating materials heated at 250 °C
Full size table

Conclusions

Fire-retarded cellulose thermal insulation was produced from mechanical pulp and synergetic fire retardant or expandable graphite by a foam-forming technique, and the final materials can fulfill the requirements of fire safety in energy-efficient buildings. To understand the fire retardancy mechanism and predict the thermal behavior of fire-retardant thermal insulating materials, the thermal degradation kinetics of cellulose fiber-based thermal insulating materials have been systematically investigated. Fire-retardant thermal insulating materials consisting of cellulose fiber and synergetic fire retardant or expandable graphite had a gradual increase in the apparent activation energies in the early decomposition process. The reaction mechanism of the reference material followed a diffusion model (D3) when the conversion values were below 0.6, but the fire-retardant samples containing synergetic fire retardant or expandable graphite exhibited complex reaction mechanisms that involved in several proposed theoretical models in different conversion ranges. The Friedman method can be expected as the most accurate method to determinate the kinetic parameters compared with Kissinger–Akahira–Sunose and Flynn–Wall–Ozawa methods.

Analysis of thermal degradation gases showed that the fire retardants could catalyze the degradation of cellulosic fibers as well as increase the total yields of anhydrosugars (levoglucosenone) and furfural resulting from the dehydration of carbohydrates. A decrease in the yield of volatile phenols and an increased formation of solid char were in agreement with the proposed mechanism of fire retardancy.