Abstract
The microstructure that is attributable from the distinct casting method dictates new engineering and physical attributes of the material. To understand how to manage the microstructure of the casts, it is necessary to comprehend the differences in microstructure through crystallisation. The effects of cooling rate (0.5, 0.9 and 2.1 °C s−1) on the characteristic parameters of the evaluation of aluminium dendrites in Al–Mg alloy during solidification at different cooling rates were investigated by thermal derivative analysis. Because of the facts that castability is influenced significantly by the dendrite coherency point, which represents the time, temperature, and solid fraction at which interlocking solid network forms through solidification, an increment in the solid fraction at coherency can improve the casting attributes of the material and diminish casting defects. Castability of aluminium is defined with a new approach based on one thermocouple thermal analysis technique of fraction solid at a dendrite coherency point. Changes of sample linear dimensions and the coefficient of linear thermal expansion and diagrams of this coefficient as a temperature function during heating and cooling cycle of investigated materials were registered and presented. The analysis shows that the thermal interpretation is carried out on Universal Metallurgical Simulator and Analyzer device which is a useful instrument for the accumulation and calculation of thermal parameters. The manuscript provides to the better understanding non-equilibrium metallurgical characterisation of aluminium alloys.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The increasing demands to decrease the fuel usage in automotive industry triggered by concerns about global warming and energy usage has a significant effect on the selection of materials. Mass reduction through the use of non-ferrous metals is a very successful and efficient way of improving fuel economy and reducing CO2 emission into the atmosphere [1]. The growing interest in aluminium alloys for automotive applications provide significant opportunities for mass reduction and therefore simplifies the scope to achieve environmental goals [2]. The automotive industry at present uses a wide range of aluminium alloys, from which are made components used in power trains and chassis including transmission housings, cylinder heads, inlet manifolds, engines, wheels, as well as decorative trim items. An increasing trend in replacing steel parts with lighter aluminium ones has seen aluminium alloys being used extensively also in other automotive areas [3, 4].
The quality and final properties of the cast products are affected by microstructural changes during the crystallisation process of the melted alloy. Understanding the phase formation during the casting process is very important and beneficial to obtain desired material properties. Due to its ease of use and low cost, the thermal derivative analysis is much more suitable for industrial applications compared to other techniques, and TDA method has been successfully applied in investigations of solidification sequences of Al and Mg alloys in recent years [5, 6]. In this technique, the temperature variances in the analysed metallic material are registered from entirely liquid to fully solidified phases generating a curve plot of temperature as a function of time. A cooling curve reveals the release of latent heat of crystallisation. This release of latent heat in multi-component alloys shifts the slope of the cooling curve which is then used to identify the characteristics of transitions and phase reactions during crystallisation.
The casting aluminium–magnesium alloys are mainly used to produce the automotive security parts due to low density, from which follows the cast part reduction, but the severe oxidation of magnesium and poor formability limited its application. For this reason, casting alloys with higher strength and outlook are urgent to be developed to produce the high-integrity-shape automotive parts that can be subjected to cyclic stress, such as sub-frame and door frame. Excellent mechanical properties of Al–Mg alloys with Si addition and low production costs have earmarked this alloy for selection as a structural material in the production of most industrial products mainly to produce structural components in automotive industry [7,8,9,10,11,12].
In the aluminium–magnesium–silicon system solidification path can be characterised as quite simple. In most alloys, the formation of the eutectic Mg2Si phase having a “Chinese-Script” morphology can be observed, and due to the presence of iron as the impurity, a variety of Fe-rich intermetallic phases can be identified. In the alloys containing Fe, Mn and Mg, three Fe-rich phases of α-Al15(FeMn)3Si2, β-Al5FeSi and π-Al8FeMg3Si6 phases have been identified. In the commonly used Al–Si–Mg cast alloys, with an Mn/Fe ratio of 0.5, the structure of Fe-rich intermetallics has a body-centred cubic crystal structure α-Al15(FeMn)3Si2, which also may be present as hexagonal, star-like, or dendritic crystals at different Mn/Fe ratios. Some research on Al–Si–Fe–Mn system indicated that the Fe-rich precipitates mostly form polyhedral morphology at high Mn contents [13], i.e. in the form of Chinese-script phase Al8Fe2Si at low Mn content and high cooling rate and in the form of Al15(Fe, Mn)3Si2 phase at high Mn content and low cooling rate [14]. During the solidification process, usually, the first phase to form is Al(MnFe)Si which may or may not contain Mn or Fe depending on the chemistry, which the crystal structure and morphology was subject of many studies [13,14,15]. Then the Mg2Si precipitates start to form and the last phase to solidify is in accordance with the binary diagram the equilibrium β-Al8Mg5 phase [15,16,17,18,19,20].
The manuscript presents the results of the microstructural evolution of the AlMg9 aluminium alloy that was subjected to different cooling rate. Based on the metallographic examination connected with quantitative image processing using Fiji/ImageJ software, a quantitative phase analysis was performed. The next step of the investigation was to determine, based on the image processing, precipitates size and their distribution and average grain/dendrite size that can be influenced by the cooling rate. The quantitative image analysis was compared by analysing the data obtained using X-ray diffraction, scanning electron microscopy and energy-dispersive X-ray spectroscopy.
Experimental
The material for the experiment was AlMg9 alloy with chemical composition listed in Table 1.
The TDA through melting and solidification sequences were carried out using the Universal Metallurgical Simulator and Analyzer (UMSA). The cooling curves and analogous derivative curves were drafted to define individual thermal effects, based on the first and second derivative of cooling curve. The examined material was heated up to 700±2°C and isothermally held at this temperature for period 90 s. In the next step, the test sample was solidified at a cooling rate of approximately 0.5, 0.9 and 2.1 °C s−1, where 0.5 °C s−1 is equivalent to the solidification process under natural condition. The individual thermal events were detected as presented in Table 2.
For the determination of solid fraction at dendrite coherency point DCP, the Newtonian baseline has been determined by sixth polynomial fitting (dT/dt)BL= a0 + a1T + a2T2 + a3T3 + a4T4 + a5T5 + a6T6 within the beginning and the end of solidification in the 1st derivative curve. The sixth-order polynomial yields a correlation coefficient higher than 0.99. The solid fraction at DCP was estimated from the accumulative area between the first derivative and the baseline at tDCP as a fraction of the area between these curves.
The linear expansion coefficient of Al–Mg alloy has been carried out using dilatometer DIL 805A/D. Moreover, information about changes in linear dimensions can explain changes in solid state according to the solvus line of Al–Mg system (Fig. 1).
Al–Mg binary system [24]
To determine the linear expansion coefficient, the samples were subjected to heating and cooling cycle under a protective atmosphere of argon. The cylindrical samples with a length of 10 mm and a diameter of 4 mm were heated from ambient temperature up to 370 °C with heating rate 2 °C s−1 and then cooled down to ambient temperature with the cooling rate 10 °C s−1. The dilatometric curve was used to determine the changes in the dimensions of the samples after heating and cooling cycle and the value of the linear expansion coefficient.
The metallographic examinations of the AlMg9 aluminium alloy were made on the as-cast samples taken from an ingot. The change of the microstructure of samples subjected to the different cooling rates has been investigated. Samples were cold-mounted and then round on 240#, 320#, 400#, 600# and 1200# SiC abrasive papers and then finished with 6- and 3-μm diamond pastes followed by Struers Op-S. The next step of the investigation was the selection of a suitable etchant and etching time (Table 3). The microstructure of the alloy was characterised using light optical microscope Axio Observer Image Analyser A1 and observed under the bright field, Nomarsky contrast and using polarised light. To perform the grain size calculation, the observation was made under polarised light.
To analyse the effect of cooling rate on primary dendrite size, the samples were over-etched using Weck’s reagent. Chemical composition microanalysis was prepared on the scanning electron microscope equipped with an EDS—energy-dispersive X-ray spectroscopy detector. The X-ray examinations of the investigated AlMg9 alloy were made using an X’Pert Pro diffractometer with a Co anode. Diffraction analyses were performed within the range of angles from 20° to 120°. The measurement step was 0.05° in length, and the pulse counting time was 5 s. The quantitative phase analysis was performed using the Rietveld method. A Rietveld refinement involves the fitting of the full experimental diffraction pattern with calculated profiles and background. The knowledge of the crystallographic structure corresponding to the present phases leads to the simulation of the theoretical X-ray spectrum for each precipitate and allows to determine the angular position and the relative intensity associated with each reflection and based on these calculations to quantify mass fraction of precipitates. Details of the complete refinement method are shown in Ref. [21]. The quantitative image analysis—grain size and dendrite arm spacing—was performed using the ImageJ software.
Results and discussion
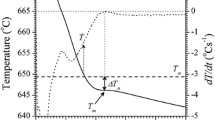
The thermal derivative analysis results of the examined aluminium alloy are shown in Fig. 2. More detailed information related to the alloy’s thermal characteristics was obtained using first derivative curves. The temperatures of the metallurgical reactions are summarised in Table 4. Using the first derivation of the cooling curve, the liquidus and solidus temperatures can be determined, as well as the eutectic temperatures of the tested sample.
The crystallisation order is controlled to a considerable extent by the presence of magnesium. This element, concurrently with Al and Si, begins to precipitate just after the formation of the dendritic network. Solidification starts with the establishment of a dendritic network of aluminium, and this is immediately followed by precipitation of Mg2Si. According to binary alloy system Al–Mg, the last final result with thermal effect belongs to the precipitation of the Al8Mg5 phase. By the Al–Mg–Si phase diagram, investigated alloy should contain (α-Al + Al15(FeMn)3Si2 + Mg2Si + Al8Mg5) phases, where the morphology of Al8Mg5 is appropriate for the mechanical characteristics of the alloy.
Using the first derivation cooling curve of alloy solidified under natural cooling, i.e. 0.5 °C s−1, the liquidus temperature T αDEN NUC = 593.7 °C, the Al15(FeMn)3Si2 phase participation TAl15(FeMn)3Si2= 591.5 °C, the temperatures of the first and the second eutectics TE(Al+Mg2Si)= 577.9 °C and TE(Al+Al8Mg5)= 441.4 °C, as well as the solidus temperature Tsol= 434.8 °C, were determined. The solidification time for the cooling rate 0.5 °C s−1, as the difference of the times, at which the liquidus and solidus temperatures occur, amounts to Δt= 336 s. The cooling curve on Fig. 2b indicates the cooling rate of 0.9 °C s−1, and here the following temperatures of the phase transitions were obtained: T αDEN NUC = 591 °C, TAl15(FeMn)3Si2= 585.6 °C, TE(Al+Mg2Si)= 576.3 °C, TE(Al+Al8Mg5)= 441.8 °C and Tsol= 429.2 °C. In this case, the solidification is completed in Δt= 184 s.
From the TDA of a sample cooled down with 2.1 °C s−1 cooling rate (Fig. 2c), it could be noted that the solidification starts at the temperature of T αDEN NUC = 608.6 °C. The Al15(FeMn)3Si2 phase participation was 584.6 °C, and eutectic solidification of the melt into eutectic TE(Al+Mg2Si) occurs at the temperature of 577.7 °C. At TE(Al+Al8Mg5)= 445.3 °C, the second eutectic occurs. The solidification ceases at the temperature solidus of Tsol= 412.7 °C, so that the obtained time of the solidification amounts to Δt= 87 s. It was found that increasing cooling rate cause rising in T αDENNUC and decrease in Tsol. With increasing cooling rate, the temperature of a TAl15(FeMn)3Si2 reaction decreases, while the temperature of the eutectic reaction remains almost constant.
The second derivative of the cooling curves was applied to define the DCP (Fig. 3). The first smallest value of the second derivative of the cooling curve is described as the DCP, by Djurdjevic et al. [22]. In this work, applied a thermal derivative analysis based on the one thermocouple measurements placed in the centre of a sample for the determination the DCP.
The dendrite coherency point characteristics are critical features for knowing and consequent control of the alloy solidification process. This point indicates the transformation from mass feeding to interdendritic feeding in the solidification process [5, 22]. Following this point, dendrites extended to grow and become thicker with further cooling of the melt.
The variations of the temperature at DCP and the solid fraction matching to the dendrite coherency (fDCP) are presented in Table 5. It can be seen that fraction solid of primary Al dendrite coherency point increased from 3.29 to 9.3% with progressing cooling rate. For analysed aluminium alloy, it can be mentioned that the rising cooling rate caused reductions in the temperature at DCP from 592.12 to 586.35 °C. In other words, the coherency parameters display that grain refinement decreases the dendrite coherency temperature and can delay dendrite coherency. The DCP has a direct relationship with fluidity; if DCP is delayed, larger fluidity will be achieved. In summary, the research of DCP development by way of TDA confirms that the dendrite becomes coherent later with a higher cooling rate.
Based on the dilatometric tests (Fig. 4), coefficient of thermal expansion α (CTE) was determined. Analysis of the heating and cooling curves has been found that an AlMg9 alloy is characterised by a linear increase in expansion coefficient as a function of temperature. The CTE slightly increases with an increase in temperature from 20.4 to 26.6 × 10−6 K−1. Moreover, based on changes in elongation during heating and cooling cycle, it was found that shape of a graph has a linear relationship, that means no transitions in solid state occurs.
The initial microstructure in the as-cast condition of the AlMg9 alloy is shown in Fig. 5a–b. Based on the structure observation and Al–Mg–Si ternary diagram [23], it can be concluded that microstructure consists of three phases. The primary aluminium phase α-Al that is a matrix of the alloy (Al + Mg2Si) eutectic phase in the form of “Chinese Script” that can be identified by its darker colour and the β-Al8Mg5 (bright precipitates). The development of the Al8Mg5 phase was observed on the boundaries of eutectic cells—between the primary aluminium dendrites. There are two aspects of the formation of Mg2Si compound. One is the binary eutectic reaction L → α-Al + Mg2Si. When the eutectic composition was reached on the interface front, the eutectic reaction occurred and second phase Mg2Si appeared as the lamellar or Chinese-script structure such as in this investigation. The stoichiometric composition of the Mg2Si phase is 66.6 at.% Mg, 33.4 at.% Si. Liu et al. [15] found that beyond the phases mentioned above, irregularly shaped precipitates that contain Mn might also be identified in the microstructure of Al–Mg–Si–Mn–Fe alloy. To confirm the chemical composition of the remaining phases, an EDS quantitative analysis was used. Table 6 presents the results of the pointwise chemical composition analysis, whereas Fig. 6 shows the microstructure of AlMg9 alloy with indicated measurement points and line scan.
A typical concentration profile of the elements aluminium, manganese, magnesium silicon, and iron across the interface is shown in Fig. 7a–b. This line scan refers to the microstructure shown in Fig. 6. The striking rise of the magnesium concentration in this region can be related to the Al8Mg5 phase. (The stoichiometric composition of Al8Mg5 phase is 60 at.% Al, 40 at.% Mg.) The presence of Al8Mg5 phase in Al–Mg–Si alloys was also confirmed by [24]. It can be seen that the besides the phase mentioned above, the presence of Mn-containing phase can be confirmed. The stoichiometric composition (Table 5) is close to the Al15(FeMn)3Si2 phase (72.7–74.7 at.% Al, 9.1–13.7 at.% Fe, 2.8–5.7 at.% Mn and 9.5–11.5 at.% Si) [25], but deviates from the nominal composition of Al15(Fe, Mn)3Si2 which is the result of the non-equilibrium eutectic reaction. An addition of manganese to Al–Mg–Si alloy had a significant influence on the morphologies of iron-rich precipitates. In the Mn-free alloys, the Fe intermetallics forms Al5FeSi phase with plate structure, while in Mn-containing alloys the morphology of the iron precipitates changes remarkably and its constituent became Al15(Fe, Mn)3Si2 phase [26]. The formation of Fe-rich intermetallics is usually affected by solidification conditions. The cooling rate has been reported to influence the nucleation and growth of the Fe-rich phases and thus to be able to modify the morphology and size of the intermetallics in aluminium alloys [25].
To quantify the volume fraction, of the phases identified above, the XRD analysis was used. Figure 8 presents the XRD diffraction pattern of the examined alloy in as-cast condition with the results of the quantitative study that was performed using Rietveld method. It can be seen that the Mg2Si (which amount was quantified for 4.3%) phase peaks are visible, but for the Al8Mg5 phase, identification was not possible because peaks of the α-Al phase overlap with Al8Mg5 (the lattice parameter is similar to Al), and for this phase the quantitative analysis was not possible. The calculation of the quantitative share of the Mn-rich phase was not possible because of the detection limit of the XRD method.
Figure 9a–c presents the microstructures of AlMg9 alloy cooled with different rates. Based on the microstructure observation, it can be concluded that in this study, the cooling rate has a significant effect on the grain size of the investigated AlMg9 alloy. As it was predicted, an increase in the cooling rate decreases the average grain size to ~ 371 µm. The grain size and characteristics of developed phases related to the quenching temperature are compared in Table 7. The data analysis allows a conclusion that faster cooling produces also fine and highly oriented dendrites, while slow cooling produces large and coarse dendrites. Figure 10a–c presents the microstructure of the AlMg9 alloy etched using Weck’s reagent. It is visible that with an increase in cooling rate, the average size of primary dendrites decreases from 605 to 232 µm2. This finding is in good agreement with solidification theory which shows that rapid solidification reduces the time necessary for diffusion, resulting in a finer dendrite microstructure. A small dendrite size implies that the structure is fine, with all of the associated benefits such as finer intermetallic, better micro-homogeneity and less as well as better-distributed porosity. All of these desirable features of the cast structure are responsible for the excellent mechanical properties.
Cooling rate played a critical role in the control of the solidification structures. To examine the effect of this variable on the Mg2Si precipitates size, the particle size analysis was preformed (Fig. 11a–b). It can be seen that the coarse intermetallic are refined to a significant extent and are more homogeneously distributed in the microstructure by increasing the cooling rate. It is due to the fact that high cooling rate promotes the formation of fine eutectic cells that are distributed randomly in the matrix. In contrast, the lower cooling rate results in the formation of coarser eutectic Mg2Si phases. A similar conclusion can be stated by analysing the diagram presented in Fig. 12. It is visible that increased cooling rate (2.1 °C s−1) promotes the formation of finer Mg2Si particles—the percentage fraction of precipitates having a size < 100 µm is almost ~ 0.97. In contrast, when the sample is cooled with slower rates (0.5 °C s−1), the percentage amount of fine precipitates decreases to ~ 0.92. To compare the results of the XRD and image quantitative analysis, the percentage share of the Mg2Si phase was also determined. It can also be concluded that the results of image analysis are in good agreement with those derived from the X-ray quantitative analysis.
The solidification pathway of investigated AlMg9 alloy based on thermal derivative analysis and microstructure investigation may be proposed as:
-
1.
L → αAl
-
2.
L → αAl + Al15(FeMn)3Si2
-
3.
L → αAl + Mg2Si
-
4.
L → αAl + Al8Mg5
Conclusions
The influence of different cooling rates on the temperatures of the phase transitions during the solidification of the AlMg9 alloy was examined. The following conclusions can be made:
-
By using an UMSA device, a thermal derivative analysis at different cooling rates the cooling rates of (0.5, 0.9 and 2.1) °C s−1 were obtained. The following reference temperatures from the crystallization were determined: T αDENNUC , TAl15(FeMn)3Si2, TE(Al+Mg2Si), TE(Al+Al8Mg5), Tsol and Δt. Generally speaking, liquidus temperature T αDENNUC increase with an increase in cooling rate, while temperatures TE(Al+Mg2Si) and TE(Al+Al8Mg5) remains almost unchanged and Tsol decrease with an increase in the cooling rate.
-
A solid fraction at the DCP given from the second derivative of the cooling curve grows with rising cooling rate. Moreover, in analysed AlMg9 alloy, as the cooling rate increases from 0.5 to 2.1 °C s−1, the dendrite coherency temperature decreases from 592.1 to 586.3 °C.
-
The metallographic analysis performed using light and scanning microscopy revealed the presence of an α-Al solid solution matrix with Chinese-script—like morphology Mg2Si precipitates as the primary dendrites and β-Al8Mg5 phase that was located on grain boundaries in the interdendritic regions. Additionally, it was found that the microstructure also contained hard precipitates of Al15(FeMn)3Si2 having an irregular shape. Those particles solidify with the primary aluminium dendrites.
-
Increasing the cooling rate of the AlMg9 aluminium alloy from 0.5 to 2.1 °C s−1 changed the primary dendrite size from 605 to 232 μm2, simultaneously a refinement of the Mg2Si precipitates was observed. Moreover, a significant grain refinement with an increase in cooling rate was observed.
-
The obtained quantitative image analysis results are in good agreement with those measured using an X-ray phase analysis—Rietveld method. The measured volume fraction of Mg2Si phase was with good agreement with this obtained using quantitative image analysis.
-
The performed investigations of AlMg9 alloy resulted in the description of the solidification sequence at a corresponding cooling rate, temperature and time intervals. The understanding of solidification sequence enables stability prediction of required or suitable phases, and therefore provided the parameters for the solidification process to obtain required microstructural characteristics and thus needed strength of the material.
References
Miller W, Zhuang L, Bottema J, Wittebrood A, De Smet P, Haszler A, et al. Recent development in aluminium alloys for the automotive industry. Mater Sci Eng A. 2000;280:37–49.
Tharumarajah A. Benchmarking aluminium die casting operations. Resour Conserv Recycl. 2008;52:1185–9.
Snopiński P, Tański T, Labisz K, Rusz S, Jonsta P, Król M. Wrought aluminium–magnesium alloys subjected to SPD processing. Int J Mater Res. 2016;107:637–45.
Kumar S, Grant PS, O’Reilly KAQ. Evolution of Fe bearing intermetallics during DC casting and homogenization of an Al–Mg–Si Al alloy. Metall Mater Trans A Phys Metall Mater Sci. 2016;47:3000–14.
Król M, Tañski T, Matula G, Snopiñski P, Tomiczek AE. Analysis of crystallisation process of cast magnesium alloys based on thermal derivative analysis. Arch Metall Mater. 2015;60:2993–9.
Król M, Tański T, Snopiński P, Tomiczek B. Structure and properties of aluminium–magnesium casting alloys after heat treatment. J Therm Anal Calorim. 2017;127:299–308.
Brito C, Reinhart G, Nguyen-Thi H, Mangelinck-Noël N, Cheung N, Spinelli JE, et al. High cooling rate cells, dendrites, microstructural spacings and microhardness in a directionally solidified Al–Mg–Si alloy. J Alloys Compd. 2015;636:145–9.
Król M. Effect of grain refinements on the microstructure and thermal behaviour of Mg–Li–Al alloy. J Therm Anal Calorim. 2018. https://doi.org/10.1007/s10973-018-7223-x.
Dedavid BA, Costa EM, Ferreira CRF. A study of precipitates formation in aluminium alloys modified by the addition of magnesium. J Therm Anal Calorim. 2002;67:473–80. https://doi.org/10.1023/a:1013949215921.
Timelli G, Capuzzi S, Fabrizi A. Precipitation of primary fe-rich compounds in secondary AlSi9Cu3(fe) alloys. J Therm Anal Calorim. 2016;123:249–62. https://doi.org/10.1007/s10973-015-4952-y.
Król M, Mikuszewski T, Kuc D, Tański T, Hadasik E. Thermal assessment of modified ultra-light magnesium–lithium alloys. Arch Metall Mater. 2017;62:2433–40.
Zieliński A, Golański G, Sroka M. Comparing the methods in determining residual life on the basis of creep tests of low-alloy Cr–Mo–V cast steels operated beyond the design service life. Int J Press Vessel Pip. 2017;152:1–6.
Hwang JY, Doty HW, Kaufman MJ. The effects of Mn additions on the microstructure and mechanical properties of Al–Si–Cu casting alloys. Mater Sci Eng A. 2008;488:496–504.
Liu Y, Luo L, Han C, Ou L, Wang J, Liu C. Effect of Fe, Si and cooling rate on the formation of Fe- and Mn-rich intermetallics in Al–5Mg–0.8Mn alloy. J Mater Sci Technol. 2016;32:305–12.
Liu CL, Azizi-Alizamini H, Parson NC, Poole WJ, Du Q. Microstructure evolution during homogenization of Al–Mg–Si–Mn–Fe alloys: modelling and experimental results. Trans Nonferrous Met Soc China. 2017;27:747–53.
Krupiński M, Krupińska B, Rdzawski Z, Labisz K, Tański T. Additives and thermal treatment influence on microstructure of nonferrous alloys. J Therm Anal Calorim. 2015;120:1573–83.
Marthinsen K, Holmedal B, Li Y. The effect of mn on microstructure evolution during homogenization of Al–Mg–Si–Mn alloys. Mater Sci Forum. 2014;794–796:1199–204.
Kuijpers NCW, Vermolen FJ, Vuik C, Koenis PTG, Nilsen KE, van der Zwaag S. The dependence of the β-AlFeSi to α-Al(FeMn)Si transformation kinetics in Al–Mg–Si alloys on the alloying elements. Mater Sci Eng A. 2005;394:9–19.
Hsu C, O’Reilly KAQ, Cantor B, Hamerton R. Non-equilibrium reactions in 6xxx series Al alloys. Mater Sci Eng A. 2001;304–306:119–24.
Sha G, O’Reilly K, Cantor B, Worth J, Hamerton R. Growth related metastable phase selection in a 6xxx series wrought Al alloy. Mater Sci Eng A. 2001;304–306:612–6.
Pérez-Landazábal JI, Nó ML, Madariaga G, San JJ. Quantitative δ′ phase analysis in Al–Li alloys using the Rietveld method. J Appl Crystallogr. 1997;30:107–13.
Djurdjevic MB, Sokolowski JH, Odanovic Z. Determination of dendrite coherency point characteristics using first derivative curve versus temperature. J Therm Anal Calorim. 2012;109:875–82.
Feufel H, Gödecke T, Lukas HL, Sommer F. Investigation of the Al–Mg–Si system by experiments and thermodynamic calculations. J Alloys Compd. 1997;247:31–42.
Okamoto H, Schlesinger ME, Mueller EM, editors. ASM handbook volume 3: alloy phase diagrams. Materials Park: ASM International; 1992.
Ji S, Yang W, Gao F, Watson D, Fan Z. Effect of iron on the microstructure and mechanical property of Al–Mg–Si–Mn and Al–Mg–Si diecast alloys. Mater Sci Eng A. 2013;564:130–9.
Liu YL. The solidification process of Al–Mg–Si alloys. J Mater Sci. 1997;32:1443–7.
Acknowledgements
This publication was financed by the Ministry of Science and Higher Education of Poland as the statutory financial grant of the Faculty of Mechanical Engineering SUT in 2017.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Snopiński, P., Król, M., Tański, T. et al. Effect of cooling rate on microstructural development in alloy ALMG9. J Therm Anal Calorim 133, 379–390 (2018). https://doi.org/10.1007/s10973-018-7313-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10973-018-7313-9