Introduction

Convection of nanofluids in porous media is as an attractive area for heat transfer and thermodynamic research communities [1, 2]. Free convection of nanofluids in porous media has already received significant attention [3, 4]. However, the equivalent problem under forced and mixed convection is relatively much less investigated. In particular, evaluation of thermodynamic irreversibilities encountered during forced convection of nanofluids in porous media has been identified as an underdeveloped area demanding more research [2].

The general problem of forced convection of nanofluids through porous media has been, so far, visited by few researchers [5]. The existing studies can be generally categorised into two classes of nanofluid flows in porous conduits [6, 7] and those over rotating porous discs [8, 9]. Only the latter can involve boundary layer flows and thus is further discussed here. In a numerical investigation, Bachok et al. [10] analysed fluid dynamics and heat transfer of nanofluids in a configuration including rotating porous discs. These authors used two different models of the effective thermal conductivity and examined the fluid dynamics and heat transfer behaviours of the system [10]. Hatami et al. [11] studied the nanofluid flow between two counter-rotating discs with porous faces. They considered water-based nanofluids with a number of different metal and metal oxide as nanoparticles [11]. Their investigation included an elaborated study of the effects of nanoparticle size and type on the heat transfer characteristics of the system [11]. The problem of convective heat transfer by nanofluid flows between rotating porous discs was also examined by Hosseini et al. [12]. These authors employed homotopy perturbation method and showed that increasing the concentration of nanoparticles enhances the convection coefficient. This finding was later confirmed by another group of authors in other configurations [6, 7]. According to Hooseini et al. [12], there is a monotonic and nearly linear relationship between the volumetric fraction of nanoparticles and the increase in Nusselt number. A three-dimensional investigation was conducted by Saidi and Tamim [8] to predict the heat and mass transfer behaviours of a system involving two rotating porous discs. The Brownian motion of nanoparticles was considered in this study, and the magnetohydrodynamic effects were also investigated [8]. Amongst other findings, it was reported that augmenting the permeability of the porous discs enhances the heat and mass transfer coefficients on the surfaces of the discs [8]. Through considering a moving permeable surface, Khazayinejad et al. [13] solved the governing equations of the transport of momentum in a nanofluid boundary layer. They put forward a similarity solution for the problem and included the influences of nanofluid suction and injection in their analysis [13].

A particular type of boundary layer flows in porous media includes stagnation points [14,15,16]. This class of flow finds wide applications in cooling technologies and, therefore, has been investigated by different authors. These have been mostly focused on the stagnation flows of ordinary fluids over flat porous inserts. Here, a concise summary of the literature in this area is presented. A pioneering work on the hydrodynamics of stagnation-point, isothermal flows on a flat porous insert was conducted by Wu et al. [17]. They assumed a Darcy–Brinkman flow and developed an asymptotic solution for the velocity field in a horizontal porous plate under an impinging jet configuration [17]. In their numerical investigation, Jeng and Tzeng [18] investigated the transport of heat when a slot jet impinges upon the surface of a metallic foam heat sink. These authors reported that the location of the maximum convection coefficient varies with the jet Reynolds number [18]. Jeng and Tzeng, later, set an experimental study of the same problem [19] and demonstrated that by increasing the jet Reynolds number the convection coefficient grows in magnitude. Nevertheless, the flow pressure drop is also intensified [19]. Subsequently, Wong and Saeid [20, 21] conducted a heat transfer optimisation on the problem of jet flow blowing on the surface of a horizontal porous insert heated from below.

Harris et al. [22] built a similarity solution for the boundary layer developed near the stagnation point on a porous plate positioned vertically. A numerical work on mixed convection in jet impingement on a flat porous plate revealed that increasing the jet width and the Reynolds number lead to the magnification of the average Nusselt number [23]. It was also shown that decreasing the distance between the jet and the heated section increases the Nusselt number [23]. Kokubun and Fichini [24] presented an analytical solution for the stagnation-point flow in an infinitely long, horizontal porous insert subject to different thermal boundary conditions. This work showed that a dimensionless parameter, including information on the transport properties of the fluid and solid, dominates the heat transfer process. In an experimental and numerical study, Feng et al. [25] investigated the problem of tube flow impingement on a heated porous insert. They examined metal foam and finned metal foam and demonstrated that by magnifying the thickness of the metal foam heat transfer coefficient decreases. Yet, this was not the true for the metal finned foam [25]. More recently, Buonomo et al. [26] investigated the interactions between a downward vertical, laminar jet and a confined, horizontal porous insert in an axisymmetric configuration. Buonomo et al. illustrated that Peclet number determines the opposing or supporting arrangements of natural and forced convection [26]. Mixed convection of stagnation-point flows over a vertical plate covered by a porous layer was investigated by Makinde [27] and also by Rosca and Pop [28]. Thermal radiation and magnetic effects have been further considered in the problem of mixed convection on vertical flat, porous walls [29].

All cited literatures, so far, have been entirely focussed on flow configurations over flat porous inserts. A review of literature reveals that the problem of stagnation-point flow formed upon curved surfaces in porous media has been rarely studied. An exception to this is the most recent work of the authors, in which they developed a semi-similar solution for the stagnation flow upon the surface of cylinder embedded in a homogenous porous medium [5]. This investigation was concerned with the hydrodynamics and heat convection only [5]. Importantly, it was limited to ordinary fluids and did not consider magnetic and gravitational effects nor it involved analysis of entropy generation. Another highly unexplored area includes nanofluid stagnation-point flow in porous media. The shortage of research in this area extends to both flat and curved configurations. An early investigation of flow over a cylinder embedded in porous media was reported by Abu-Hijleh [30]. A laminar flow of ordinary fluid through the porous media and over a cylinder was investigated in this work and the rate of entropy generation was calculated numerically [30]. It was demonstrated that increasing the thickness of the porous layer covering an isothermal cylinder reduces the total generation of entropy [30]. Entropy generation in magnetohydrodynamic (MHD) flow of nanofluids in porous media has been analysed in a few recent works. Rashidi and Freidoonmehr [31] considered the MHD and nanofluid equivalent of the classical configuration of Heimenz [32] when the solid plate was replaced by a flat porous insert. Their work was exclusively concerned with the generation of entropy and made the conclusion that the effects of increasing the values of Hartmann, Brinkman and magnetic interaction numbers and reducing Prandtl and Reynolds numbers are similar and lead to an augmentation of the entropy generation. This study was later extended to the configurations including rotating porous discs with ordinary fluids [33] and nanofluid [34]. In addition to these studies, there exists a series of studies on entropy generation by nanofluid flow over permeable surfaces [35,36,37]. Although mathematical models similar to those of porous media are used in these works, the physical differences between them and stagnation flows inside porous media are rather significant. Thus, these investigations are not further discussed here.

The preceding review of literature reveals that the general problem of forced and mixed convection of nanofluids in porous media and the particular problem of entropy generation by such flows have been highlighted as largely unexplored fields. Further, there have been already a number of studies on the impingement of external flows in flat porous plates under. However, stagnation-point flows in curved porous media have so far received very little attention. The existing studies on boundary layer nanofluid flows in porous media are entirely concerned with flat porous inserts or preamble surfaces. Thus, there is currently no study of nanofluid stagnation-point flow in curved porous inserts. In practice, many curved objects are covered with porous layers and nanofluids are increasingly used as the cooling agents in such configurations [38]. However, there is currently no systematic evaluation of the heat transfer and second law performance of such systems.

The present work, therefore, aims to fill this gap through a study of a cylindrical object embedded in porous media and subject to non-axisymmetric, nanofluid stagnation-point flow. The current study builds upon the earlier work of the authors [5] and advances that on four main fronts. These include consideration of a nanofluid flow, addition of gravitational and magnetohydrodynamic effects upon the convection problem and also evaluation of the encountered thermodynamic irreversibilities.

Theoretical and numerical methods

Problem configuration, assumptions and governing equations

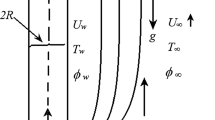
Figure 1 shows schematically the problem under investigation. This includes a cylinder with radius a centred at r = 0 covered with a porous medium. The surface of the cylinder can include uniform or non-uniform transpiration with prescribed circumferential distributions, while the temperature of the external surface of the cylinder is maintained constant. It should be noted that the mathematical model developed in the following section can accommodate transpiration in either of suction or injection of the fluid. An external axisymmetric radial stagnation-point flow of strain rate of \(\bar{k}\) impinges on the cylinder. Because of the non-uniformity of transpiration, the flow configuration around the cylinder can be un-axisymmetric. Although the investigated configuration is rather generic, it finds specific applications in magnetic chemical separation [5]. The following assumptions are made through this work.

Fig. 1
figure 1

Schematic view of a stationary cylinder under radial stagnation flow of nanofluid in porous media

Full size image

  • The flow is steady, incompressible and laminar.

  • The nanofluid is assumed to be Newtonian, electrically conductive and single phase.

  • The cylinder is assumed to be infinitely long and its axis is parallel to the direction of gravity. Also, the cylinder is subject to a uniform magnetic field.

  • The porous medium is homogenous, isotropic and under local thermal equilibrium.

  • The radiation heat transfer and viscous dissipation of kinetic energy of the flow are ignored.

  • Physical properties such as porosity, specific heat, density and thermal conductivity are assumed to be constant and hence the thermal dispersion effects are negligible.

  • A moderate range of pore-scale Reynolds number is considered in the porous medium and hence nonlinear effects in momentum transfer are negligibly small.

  • The physical mechanisms causing significant deviations from the local thermal equilibrium, such as internal heat generations, are ignored [39, 40].

A three-dimensional Darcy–Brinkman model of transport of momentum together with the one-equation model of transport of thermal energy in cylindrical coordinate is used in this work [41,42,43]. The governing equations and boundary conditions, in the cylindrical coordinate system shown in Fig. 1, can be summarised as follows.

The continuity of mass reads,

$$\frac{{\partial \left( {ru} \right)}}{\partial r} + \frac{\partial v}{\partial \varphi } + r\frac{\partial w}{\partial z} = 0$$
(1)

The transport of momentum in the radial direction is

$$\frac{{\rho_{\rm nf} }}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{\partial r} + \frac{v}{r}\frac{\partial u}{\partial \varphi } - \frac{{v^{2} }}{r} + w\frac{\partial u}{\partial z}} \right) = - \frac{\partial p}{\partial r} + \frac{{\mu_{\rm nf} }}{\varepsilon }\left[ {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] - \frac{{\mu_{\rm nf} }}{{k_{1} }}u,$$
(2)

and that in the angular direction is given by

$$\frac{{\rho_{\rm nf} }}{{\varepsilon^{2} }}\left( {u\frac{\partial v}{\partial r} + \frac{v}{r}\frac{\partial v}{\partial \varphi } + \frac{uv}{r} + w\frac{\partial v}{\partial z}} \right) = - \frac{1}{r}\frac{\partial p}{\partial \varphi } + \frac{{\mu_{\rm nf} }}{\varepsilon }\left[ {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{\partial r} - \frac{v}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} v}}{{\partial \varphi^{2} }} + \frac{2}{{r^{2} }}\frac{\partial u}{\partial \varphi } + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right] - \frac{{\mu_{\rm nf} }}{{k_{1} }}v - \bar{\sigma }B_{0}^{2} v.$$
(3)

The transport of momentum in the axial direction takes the form of

$$\begin{aligned} \frac{{\rho_{\rm nf} }}{{\varepsilon^{2} }}\left( {u\frac{\partial w}{\partial r} + \frac{v}{r}\frac{\partial w}{\partial \varphi } + w\frac{\partial w}{\partial z}} \right) = & - \frac{\partial p}{\partial z} + \frac{{\mu_{\rm nf} }}{\varepsilon }\left[ {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right] \\ & \pm \left( {\rho \beta } \right)_{\rm nf} g\left( {T - T_{\infty } } \right) - \frac{{\mu_{\rm nf} }}{{k_{1} }}w - \bar{\sigma }B_{0}^{2} w \\ \end{aligned}$$
(4)

The transport of thermal energy is expressed by

$$u\frac{\partial T}{\partial r} + \frac{v}{r}\frac{\partial T}{\partial \varphi } + w\frac{\partial T}{\partial z} = \frac{{k_{\rm nf} }}{{\left( {\rho \cdot C_{\text{p}} } \right)_{\rm nf} }}\left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right].$$
(5)

As also defined in the nomenclature, in Eqs. (1–5) \(p\), \(\rho_{\text{nf}}\), \(\mu_{\text{nf}}\), \(T\), \(\left( {\rho \cdot C_{\text{p}} } \right)_{\text{nf}}\), \(k_{\text{nf}}\) and \(\beta\) are the pressure, density, kinematic viscosity of the nanofluid, temperature, the heat capacitance of the nanofluid, effective thermal conductivity of the nanofluid and thermal expansion coefficient of the fluid, respectively. It is noted that in general the effective viscosity should be used in the governing equations. However, it has been shown previously [7, 39, 40] that ignoring the effective viscosity does not result in any noticeable error. Further,\(g\), \(T_{\infty }\), \(\varepsilon\), \(\bar{\sigma }_{\text{nf}}\), \(B_{0}\) and \(k_{1}\) denote gravitational acceleration, given temperature at the wall, porosity, nanofluid electrical conductivity, uniform magnetic field and permeability of the porous medium, respectively. The flow characteristics are evaluated inside the boundary layer and in the vicinity of the flow impingement point. These nanofluid properties are defined by [6, 7, 44],

$$\begin{aligned} \rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{s}} ,\quad \left( {\rho \cdot C_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho \cdot C_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho \cdot C_{\text{p}} } \right)_{\text{s}} \hfill \\ \mu_{\text{nf}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \phi } \right)^{2.5} }},\quad \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{k_{\text{s}} + 2k_{\text{f}} - 2\phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}{{k_{\text{s}} + 2k_{\text{f}} + 2\phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}} \hfill \\ \end{aligned}$$
(6)

where \(\phi\) denote the nanoparticles volume fraction. In Eq. (6), the subscripts, “f” and “s”, refer to fluid and solid fraction properties, respectively. The thermo-physical properties of the base fluid (water) and the investigated nanoparticle (CuO) are given in Table 1.

Table 1 Thermo-physical properties of the base fluid and different nanoparticles [36]
Full size table

The velocity conditions for the momentum equations are as follows.

$$r = a:w = 0,\quad v = 0,\quad u = - {\kern 1pt} U_{0} \left( \varphi \right),$$
(7)
$$r \to \infty :w = 2\bar{k}z,\quad \mathop {\lim }\limits_{r \to \infty } rv = 0,.\quad u = - \bar{k}\left( {r - \frac{{a^{2} }}{r}} \right)$$
(8)

Further, the two boundary conditions with respect to \(\varphi\)(angular coordinate) are given by

$$\begin{aligned} u\left( {r,0} \right) = u\left( {r,2\pi } \right),\quad v\left( {r,0} \right) = v\left( {r,2\pi } \right), \hfill \\ \frac{{\partial u\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial u\left( {r,2\pi } \right)}}{\partial \varphi },\quad \frac{{\partial v\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial v\left( {r,2\pi } \right)}}{\partial \varphi }. \hfill \\ \end{aligned}$$
(9)

Equation (7) represents no-slip conditions on the external surface of the cylinder. Further, Eq. (8) indicates that the viscous flow solution approaches, in a manner analogous to the Hiemenz flow, the potential flow solution as \(r \to \infty\) [41, 42, 45]. This can be verified by starting from the continuity equation in the following. \(- \frac{1}{r}\frac{\partial }{\partial r}\left( {ru} \right) - \frac{\partial v}{\partial \varphi } = \frac{\partial w}{\partial z} =\) Constant \(= 2\bar{k}z\) and integrating in \(r\) and \(z\) directions with boundary conditions,\(w = 0\) when \(z = 0\) and \(u = - U_{0} \left( \varphi \right)\) when \(r = a\).

The boundary condition for the transport of thermal energy is given by

$$\begin{aligned} r = a:T = T_{\rm w} = {\text{Constant,}} \hfill \\ r \to \infty :T \to T_{\infty } \hfill \\ \end{aligned}$$
(10)

and the two boundary conditions with respect to angular coordinate \(\varphi\) are

$$\begin{aligned} T\left( {r,0} \right) = T\left( {r,2\pi } \right), \hfill \\ \frac{{\partial T\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial T\left( {r,2\pi } \right)}}{\partial \varphi }, \hfill \\ \end{aligned}$$
(11)

in which \(T_{\text{w}}\) is the cylinder surface temperature and \(T_{\infty }\) is the freestream temperature.

Self-similar solutions

A reduction in the governing Eqs. (1–5) is obtained through applying the following similarity transformations.

$$u = - \frac{{\bar{k}a}}{\sqrt \eta }f\left( {\eta ,\varphi } \right),\quad v = \frac{{\bar{k}a}}{\sqrt \eta }G\left( {\eta ,\varphi } \right),\quad w = \left[ {2\bar{k}f^{{\prime }} \left( {\eta ,\varphi } \right) - \frac{{\bar{k}}}{\eta }\frac{\partial G}{\partial \varphi }} \right]z,\quad p = \rho_{\rm f} \bar{k}^{2} a^{2} P.$$
(12)

where \(\eta = \left( {\frac{r}{a}} \right)^{2}\) is the dimensionless radial variable. Transformations (12) satisfy Eq. (1) automatically and their substitution into Eqs. (2), (3) and (4) leads to the following system of coupled differential equations.

$$\begin{aligned} & \varepsilon \cdot \left( {\eta f^{{{\prime \prime \prime }}} + f^{{\prime \prime }} - \frac{1}{{8\eta^{2} }}\frac{{\partial^{3} G}}{{\partial \varphi^{3} }} - \frac{1}{2}\frac{{\partial G^{{\prime \prime }} }}{\partial \varphi } + \frac{1}{2\eta }\frac{{\partial G^{{\prime }} }}{\partial \varphi } - \frac{1}{{2\eta^{2} }}\frac{\partial G}{\partial \varphi } + \frac{1}{4\eta }\frac{{\partial^{2} f^{{\prime }} }}{{\partial \varphi^{2} }}} \right) \\ & + \text{Re} \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {1 + ff^{{\prime \prime }} - (f^{{\prime }} )^{2} - \frac{f}{2\eta }\frac{{\partial G^{{\prime }} }}{\partial \varphi } + \frac{f}{{2\eta^{2} }}\frac{\partial G}{\partial \varphi } - \frac{G}{2\eta }\frac{{\partial f^{{\prime }} }}{\partial \varphi } + \frac{G}{{4\eta^{2} }}\frac{{\partial^{2} G}}{{\partial \varphi^{2} }} + \frac{{f^{{\prime }} }}{\eta }\frac{\partial G}{\partial \varphi } - \frac{1}{{4\eta^{2} }}\left( {\frac{\partial G}{\partial \varphi }} \right)^{2} } \right] \\ & + \varepsilon^{2} .\lambda \left[ {1 - f^{{\prime }} } \right] \pm \varepsilon^{2} \cdot A_{4} \cdot \lambda_{1} \cdot \theta + \varepsilon^{2} \cdot \text{Re} \cdot M\left[ {1 + \frac{1}{2\eta }\frac{\partial G}{\partial \varphi } - f^{{\prime }} } \right] = 0, \\ \end{aligned}$$
(13)
$$\begin{aligned} P - P_{0} = & \frac{1}{{\varepsilon^{2} }}\frac{1}{{2\bar{k}^{2} }}\int_{1}^{\eta } {\frac{1}{{\eta^{2} }}\left[ {G^{2} + G\frac{\partial f}{\partial \varphi }} \right]{\kern 1pt} {\kern 1pt} } {\text{d}}\eta - \frac{1}{{\varepsilon \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\left[ {\left( {\frac{{f^{{\prime }} }}{\text{Re}} - \frac{1}{{4\text{Re} }}\int_{1}^{\eta } {\frac{1}{{\eta^{2} }}\frac{{\partial^{2} f}}{{\partial \varphi^{2} }}{\kern 1pt} {\kern 1pt} } {\text{d}}\eta + \frac{1}{{2\text{Re} }}\int_{1}^{\eta } {\frac{1}{{\eta^{2} }}\frac{\partial G}{\partial \varphi }{\kern 1pt} {\kern 1pt} } {\text{d}}\eta } \right) + \frac{\lambda }{\text{Re}}\int_{1}^{\eta } {\frac{f}{\eta }{\kern 1pt} } {\text{d}}\eta } \right] \\ & - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{1}{{A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\frac{\lambda }{\text{Re}} + M} \right]\left( {\frac{z}{a}} \right)^{2} - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) \\ \end{aligned}$$
(14)

in which \(\text{Re} = \frac{{\bar{k}a^{2} }}{{2\upsilon_{\text{f}} }}\) is the freestream Reynolds number, \(\lambda = \frac{{a^{2} }}{{4k_{1} }}\) is referred to as permeability parameter, \(M = \frac{{\bar{\sigma } \cdot B_{0}^{2} }}{{2\rho_{\text{f}} \bar{k}}}\) is the magnetic parameter, \(G{\text{r}} = \frac{{g \cdot \beta_{\text{f}} \cdot a^{3} \cdot \left( {T_{\text{w}} - T_{\infty } } \right)}}{{16\upsilon_{\text{f}}^{2} }}\) is the Grashof number,\(\lambda_{1} = \frac{Gr}{{\text{Re}^{2} }} = \frac{{g.\beta_{f} .\left( {T_{w} - T_{\infty } } \right)}}{{4a.\bar{k}^{2} }}\) is the dimensionless mixed convection parameter and prime indicates differentiation with respect to \(\eta\). Considering Eqs. (6), (7) and (8), the boundary conditions for Eqs. (13) and (14) reduce to:

$$\eta = 1:f^{{\prime }} (1,\varphi ) = 0,\quad f(1,\varphi ) = S\left( \varphi \right)$$
(15)
$$\eta \to \infty :f^{{\prime }} (\infty ,\varphi ) = 1$$
(16)
$$f\left( {\eta ,0} \right) = f\left( {\eta ,2\pi } \right),\quad \frac{{\partial f\left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial f\left( {\eta ,2\pi } \right)}}{\partial \varphi },$$
(17)

in which \(S\left( \varphi \right) = \frac{{U_{0} \left( \varphi \right)}}{{\bar{k}a}}\) is the transpiration rate function. Note that Eqs. (13) and (14) are the complete form of Eqs. (9) and (11) in Ref. [46]. Substitution of Eq. (12) into Eqs. (3) and (4) results in a differential equation in terms of \(G\left( {\eta ,\varphi } \right)\) as well as an expression for the pressure. This reads

$$\varepsilon \cdot \left( {\eta G{\prime \prime } + \frac{1}{4\eta }\frac{{\partial^{2} G}}{{\partial \varphi^{2} }} - \frac{1}{2\eta }\frac{\partial f}{\partial \varphi }} \right) + \text{Re} \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {f \cdot G^{\prime} - \frac{G}{2\eta }\frac{\partial G}{\partial \varphi }} \right] - \varepsilon^{2} \cdot G\left[ {\lambda + M} \right] = 0 ,$$
(18)

Considering conditions (7)–(9), the boundary and initial conditions for Eq. (18) can be written as

$$\eta = 1:G(1,\varphi ) = 0,\quad \frac{\partial G(1,\varphi )}{\partial \varphi } = 0,$$
(19a)
$$\eta \to \infty :G(\infty ,\varphi ) = 0$$
(19b)
$$G\left( {\eta ,0} \right) = G\left( {\eta ,2\pi } \right),\quad \frac{{\partial G\left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial G\left( {\eta ,2\pi } \right)}}{\partial \varphi }.$$
(20)

To transform the energy Eq. (5) into a dimensionless form, the following transformation is introduced,

$$\theta \left( {\eta ,\varphi } \right) = \frac{{T\left( {\eta ,\varphi } \right) - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}$$
(21)

Substitution of Eqs. (12) and (20) into Eq. (5) and ignoring the small dissipation terms yields

$$\eta \theta^{{\prime \prime }} + \theta^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \theta }}{{\partial \varphi^{2} }} + \text{Re} \cdot \Pr \cdot \frac{{A_{2} }}{{A_{3} }} \cdot \left( {f\theta^{{\prime }} - \frac{G}{2\eta }\frac{\partial \theta }{\partial \varphi }} \right) = 0,$$
(22)

while the boundary conditions reduce to

$$\eta = 1:\theta (1,\varphi ) = 1,$$
(23a)
$$\eta \to \infty :\theta (\infty ,\varphi ) = 0,$$
(23b)
$$\theta \left( {r,0} \right) = \theta \left( {r,2\pi } \right),\quad \frac{{\partial \theta \left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial \theta \left( {r,2\pi } \right)}}{\partial \varphi }.$$
(24a,b)

In Eqs. (18) and (22), A1, A2, A3 and A4 are constants in the following forms.

$$\begin{aligned} A_{1} = \left( {1 - \phi } \right) + \frac{{\rho_{\text{s}} }}{{\rho_{\text{f}} }}\phi ,\quad A_{2} = \left( {1 - \phi } \right) + \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{s}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}\phi , \hfill \\ A_{3} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{k_{\text{s}} + 2k_{\text{f}} - 2\phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}{{k_{\text{s}} + 2k_{\text{f}} + 2\phi \left( {k_{\text{f}} - k_{\text{s}} } \right)}},\quad A_{4} = \left( {1 - \phi } \right) + \frac{{\left( {\rho \beta } \right)_{\text{s}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\phi , \hfill \\ \end{aligned}$$
(25)

It is recalled here that Eq. (22) is the complete form of Eq. (14) in Ref. [46]. Equations (12), (18) and (22), together with the boundary conditions (15–17), (19–20), (23) and (24), are solved numerically using an implicit, iterative tri-diagonal finite difference method similar to that discussed in Refs. [47, 48]. Although not shown here, the full solution of the momentum equations in three dimensions reveals that the component G is rather negligible (see Ref. [5] for the details). It is therefore assumed in the reset of the analysis that \(G(\eta ,\varphi ) = 0\).

$$\varepsilon \cdot \left( {\eta f^{\prime \prime \prime } + f^{\prime \prime } + \frac{1}{4\eta }\frac{{\partial^{2} f^{\prime } }}{{\partial \varphi^{2} }}} \right) + \text{Re} \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {1 + ff^{\prime \prime } - (f^{\prime})^{2} } \right] + \varepsilon^{2} \cdot \lambda \left[ {1 - f^{\prime } } \right] \pm \varepsilon^{2} \cdot A_{4} \cdot \lambda_{1} \cdot \theta + \varepsilon^{2} \cdot \text{Re} \cdot M\left[ {1 - f^{\prime } } \right] = 0, ,$$
(26)
$$\begin{aligned} P - P_{0} = & - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) - \frac{1}{{\varepsilon \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\left[ {\left( {\frac{{f^{{\prime }} }}{\text{Re}} - \frac{1}{{4\text{Re} }}\int_{1}^{\eta } {\frac{1}{{\eta^{2} }}\frac{{\partial^{2} f}}{{\partial \varphi^{2} }}{\kern 1pt} {\kern 1pt} } {\text{d}}\eta } \right) + \frac{\lambda }{\text{Re}}\int_{1}^{\eta } {\frac{f}{\eta }{\kern 1pt} } {\text{d}}\eta } \right] \\ & - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{1}{{A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\frac{\lambda }{\text{Re}} + M} \right]\left( {\frac{z}{a}} \right)^{2} , \\ \end{aligned}$$
(27)
$$\eta \theta^{{\prime \prime }} + \theta^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \theta }}{{\partial \varphi^{2} }} + \text{Re} \cdot \Pr \cdot \frac{{A_{2} }}{{A_{3} }} \cdot \left( {f\theta^{{\prime }} } \right) = 0$$
(28)

Shear stress and Nusselt number

The shear stress induced by the nanofluid flow on the external surface of the cylinder is given by [5, 43]

$$\sigma = \mu_{\text{nf}} \left[ {\frac{\partial w}{\partial r}} \right]_{r = a} ,$$
(29)

where \(\mu_{\text{nf}}\) is the nanofluid viscosity. Employing Eq. (12), a semi-similar solution for the shear stress on the surface of the cylinder can be developed. This reads

$$\sigma = \mu_{\text{nf}} \frac{2}{a}\left[ {2\bar{k}zf^{{\prime \prime }} (1,\varphi )} \right] \Rightarrow \frac{\sigma a}{{4\mu_{f} \bar{k}z}} = \left( {1 - \phi } \right)^{ - 2.5} f^{{\prime \prime }} (1,\varphi ).$$
(30)

For the current problem with isothermal boundaries, the local heat transfer coefficient and rate of heat transfer are defined as

$$h = \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\infty } }} = \frac{{ - k_{\text{nf}} \left( {\frac{\partial T}{\partial r}} \right)_{r = a} }}{{T_{\text{w}} - T_{\infty } }} = - \frac{{2k_{\text{nf}} }}{a}\frac{{\partial \theta \left( {1,\varphi } \right)}}{\partial \eta },$$
(31)

and

$$q_{\text{w}} = - \frac{{2k_{\text{nf}} }}{a}\frac{{\partial \theta \left( {1,\varphi } \right)}}{\partial \eta }\left( {T_{\text{w}} - T_{\infty } } \right).$$
(32)

Hence, Nusselt number can be written as

$$N{\text{u}} = \frac{h \cdot a}{{2k_{\text{f}} }} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\theta^{{\prime }} \left( {1,\varphi } \right) = - A_{3} \cdot \theta^{{\prime }} \left( {1,\varphi } \right).$$
(33)

Entropy generation

Considering the assumption stated in Sect. 3.1, the volumetric rate of local entropy generation in the problem is given by [49, 50]:

$$\begin{aligned} \dot{S}_{\text{gen}}^{\prime \prime \prime } = & \frac{{k_{\text{nf}} }}{{T_{\text{w}}^{2} }}\left[ {\left( {\frac{\partial T}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial T}{\partial \varphi }} \right)^{2} } \right] + \frac{{2\mu_{\text{nf}} }}{{T_{\text{w}} }}\left[ {\left( {\frac{\partial u}{\partial r}} \right)^{2} + \left( {\frac{u}{r}} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right] \\ & + \frac{{\mu_{\text{nf}} }}{{T_{\text{w}} }}\left[ {\left( {\frac{1}{r}\frac{\partial w}{\partial \varphi }} \right)^{2} + \left( {\frac{\partial w}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial u}{\partial \varphi }} \right)^{2} } \right] + \frac{{\mu_{\text{nf}} }}{{k_{1} \cdot T_{\text{w}} }}\left[ {u^{2} + w^{2} } \right] + \frac{{\bar{\sigma } \cdot B_{0}^{2} }}{{T_{\text{w}} }}w^{2} . \\ \end{aligned}$$
(34)

Using the similarly variables given in Eqs. (12) and (34), the local entropy generation becomes:

$$\begin{aligned} \dot{S}_{\text{gen}}^{\prime \prime \prime } = & \frac{{4k_{\text{nf}} \left( {T_{\text{w}} - T_{\infty } } \right)^{2} }}{{a^{2} T_{\text{w}}^{2} }}\left[ {\eta \theta^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \theta }{\partial \varphi }} \right)^{2} } \right] \\ & + \frac{{4\bar{k}^{2} \mu_{\text{nf}} }}{{T_{\text{w}} }}\left[ {\eta f^{\prime \prime 2} + 4f^{\prime 2} + \frac{{f^{2} }}{{\eta^{2} }} - \frac{{2ff^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{{\partial f^{\prime } }}{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \frac{{\bar{k}^{2} \mu_{nf} a^{2} }}{{k_{1} T_{w} }}\left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f^{\prime 2} } \right] + \frac{{\bar{\sigma } \cdot B_{0}^{2} }}{{T_{w} }}4\bar{k}^{2} f^{\prime 2} \\ \end{aligned}$$
(35)

in which \(N_{G} = \frac{{\dot{S}_{\text{gen}}^{\prime \prime \prime } }}{{S_{0}^{\prime \prime \prime } }}\) and \(S_{0}^{\prime \prime \prime } = \frac{{8k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)^{2} \upsilon_{\text{f}} }}{{\bar{k} \cdot a^{4} T_{\text{w}}^{2} }}\) is the characteristic entropy generation rate.

The dimensionless form of volumetric rate of local entropy generation (NG) can be presented as follows.

$$\begin{aligned} N_{\text{G}} = & \text{Re} \cdot A_{3} \left[ {\eta \theta^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \theta }{\partial \varphi }} \right)^{2} } \right] \\ & + \frac{{\text{Re} \cdot Br}}{\varLambda } \cdot \left( {1 - \phi } \right)^{ - 2.5} \left\{ {\left[ {\eta f^{\prime \prime 2} + 4f^{\prime 2} + \frac{{f^{2} }}{{\eta^{2} }} - \frac{{2ff^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{{\partial f^{\prime } }}{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \lambda \left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f^{\prime 2} } \right] + 2Mf^{\prime 2} } \right\} \\ \end{aligned}$$
(36)

where \(\varLambda = \frac{{\left( {T_{\text{w}} - T_{\infty } } \right)}}{{T_{\text{w}} }}\) is the dimensionless temperature difference, and \(B{\text{r}} = \frac{{\mu_{\text{f}} \left( {\bar{k} \cdot a} \right)^{2} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)}}\) is the Brinkman number. The Bejan number, defined as the ratio of entropy generation due to heat transfer to the total entropy generation, is used to facilitate understanding of the mechanisms of entropy generation. Bejan number for the current problem can be expressed as

$$B{\text{e}} = \frac{{\text{Re}} \cdot A_{3} \left[ {\eta \theta^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \theta }{\partial \varphi }} \right)^{2} } \right]}{{\frac{{\text{Re}} \cdot B{\text{r}} }{\varLambda } \cdot \left( {1 - \phi } \right)^{ - 2.5} \left\{ {\left[ {\eta f^{\prime \prime 2} + 4f^{\prime 2} + \frac{{f^{2} }}{{\eta^{2} }} - \frac{{2ff^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{\partial f\prime }{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \lambda \left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4^{\prime 2} } \right] + 2Mf^{\prime 2} } \right\}}}$$
(37)

Grid independency and validation

To establish grid independency of the developed numerical solution, Fig. 2 plots \(f(\eta ,\varphi\)) as a function of \(\eta\) with varying mesh sizes of 51 × 18, 102 × 36, 204 × 72, 408 × 144 and 816 × 288. It is clear from Fig. 2a that there are no considerable changes of \(f(\eta ,\varphi\)) for (\(\eta ,\varphi\)) mesh sizes of (204 × 72), (408 × 144) and (816 × 288). Hence, a (408 × 144) grid in \(\eta - \varphi\) directions was used for the computational domain reported in this work. A non-uniform grid was applied in \(\eta\)-direction to capture the sharp gradients around the external surface of the cylinder, and a uniform mesh was implemented in \(\varphi\) direction. The computational domain extends over \(\varphi_{ \hbox{max} } = 360^\circ\) and \(\eta_{ \hbox{max} } = 15\). In this expression, \(\eta_{ \hbox{max} }\) corresponds to \(\eta \mathop \to \limits_{{}} \infty\), which for all investigated cases, is located outside the momentum and thermal boundary layers. Figure 2b shows the computational mesh utilised in the current study. A convergence criterion was employed in the numerical simulations. This was such that when the difference between the two consecutive iterations became less than 10−7, the solution was assumed to have converged and hence the iterative process was terminated. On the basis of the implemented numerical scheme, the numerical error is of \(O\left( {\Delta \eta } \right)^{2}\) [46, 47]. The solutions developed in Sects. 2.2 and 2.3 were validated by comparing the Nusselt number calculated by Eq. (33) with those from the literature for flows over cylinders with no transpiration and large permeability (no porous layer). Table 2 shows the outcomes of this comparison. The close agreement between the two sets of Nusselt number ensures the validity of the numerical simulations. Further, at \(\phi = 0\) the temperature and Nusselt numbers reported in this work reduce to those in Ref. [5] for an ordinary fluid flow on a cylinder embedded in porous media.

Fig. 2
figure 2

a Profiles of \(f(\eta ,\varphi )\) distributions on the cylinder for various mesh sizes. b Sample of grid system

Full size image
Table 2 Comparison between the current results and those of Alizadeh et al. [9] when \(S\left( \varphi \right) = 0\), \(\text{Re} = 1.0\)
Full size table

Results and discussion

Table 3 summarises the default values of parameters that the results presented in this section are based on. Any changes to these default values have been explicitly stated in the figures and tables. Further, three types of transpiration functions including \(S = 0, \quad S = {\text{const}}., \quad S = Ln(\varphi )\) (see Fig. 1) have been used in this section.

Table 3 Default values of the simulation parameters
Full size table

Flow velocity, temperature fields and heat convection coefficient

Figures 3 and 4 show variations of the hydrodynamic parameters \(f^{{\prime }}\) and \(f\) in the radial and angular directions as the mixed convection parameter, \(\lambda_{1}\), varies over several orders of magnitude. Figure 3 clearly shows that the radial distribution of \(f^{{\prime }}\) is significantly affected by variations in \(\lambda_{1}\). For high values of \(\lambda_{1} ,\) where free convection is approached, the values of \(f^{{\prime }}\) are considerably higher at radii close to the surface of the cylinder. However, as the numerical value of \(\lambda_{1}\) decreases and mixed convection and subsequently forced convection are realised, values of \(f^{{\prime }}\) remain almost indifferent to \(\lambda_{1}\). This trend is clear in Fig. 3b in which for a given transpiration function little changes to angular distribution of \(f^{{\prime }}\) is observed for all investigated values of \(\lambda_{1}\). Figures 3a and 3b both indicate that the functional form of the transpiration function is influential upon the radial and angular distribution of \(f^{{\prime }}\). Very similar behaviours are observed in Fig. 4, which depicts the radial and angular distribution of \(f\) for different values of mixed convection parameter and two different transpiration functions.

Fig. 3
figure 3

Variation of \(f^{{\prime }} (\eta ,\varphi )\) in terms of a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\), \(\phi = 0.05\) and for different values of dimensionless mixed convection

Full size image
Fig. 4
figure 4

Variation of \(f^{{\prime }} (\eta ,\varphi )\) in terms of a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\), \(\phi = 0.05\) and for different values of dimensionless mixed convection

Full size image

Figure 5 illustrates the distribution of the dimensionless flow temperature as the volumetric concentration of nanoparticles vary in the nanofluid. It is clear from this figure that increasing the concentration of nanoparticles has almost negligible effects upon the radial distribution of the dimensionless temperature. However, considering the angular direction, some slight increases are observed in the dimensionless temperature for higher values of nanoparticles’ concentration. This is to be expected, as higher concentration of nanoparticles renders higher thermal conductivity of the nanofluid, which enhances the heat convection from the surface of the cylinder and hence increases the nanofluid temperature. Influences of the magnetic field upon the non-dimensional temperature field have been shown in Fig. 6. This figure clearly shows that by magnifying the strength of the magnetic field, the flow temperature drops significantly in both radial and angular directions. Magnetic field tends to decelerate the nanofluid flow through application of Lorentz force. This hinders the flow and therefore suppresses the heat convection process and results in lowering the temperature of the nanofluid.

Fig. 5
figure 5

Variation of \(\theta (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\) and for different values of nanoparticle volume fraction

Full size image
Fig. 6
figure 6

Variation of \(\theta (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 100\), \(\lambda = 10\) and for different values of magnetic parameter

Full size image

Figure 7 illustrates the influences of variations in mixed convection parameter upon the dimensionless temperature field. This figure indicates that substantial variations in the mixed convection parameter, from free convection dominated to forced convection dominated, imparts relatively small changes on the dimensionless temperature. This is such that for high values of \(\lambda_{1}\), reflecting free convection, dimensionless temperature is slightly smaller than those values of \(\lambda_{1}\) that indicate mixed and forced convection. The observed behaviour implies that the heat transfer process is slightly weaker for high values of \(\lambda_{1}\) and under free convection in comparison with that for lower values of \(\lambda_{1} ,\) representing mixed and forced convection. This is physically conceivable as free convection is often the weakest mode of heat convection. Nonetheless, the existence of laminar flow in the current problem has minimised the differences between the forced and free convection. Figure 7 further illustrates the strong effects of transpiration upon the dimensionless temperature distribution. This figure shows that for a case with no transpiration (\(S = 0\)) radial dimensionless temperature is always smaller than those corresponding to a non-uniform transpiration. However, the situation is more involved in the angular direction and the relative magnitudes of dimensionless temperature in the transpirating and non-transpirating cases that depend upon the specific location on the cylinder circumference.

Fig. 7
figure 7

Variation of \(\theta (\eta ,\varphi )\) in terms of a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 10\), \(\lambda = 10\), \(\phi = 0.05\) and for different values of dimensionless mixed convection

Full size image

The angular distribution of Nusselt number and dimensionless shear stress has been shown in Figs. 8 and 9. Figure 8a shows the response of Nusselt number to variations in the volumetric concentration of nanoparticles. This figure indicates that at \(\varphi = 0\) the value of Nusselt number is rather high, while it drops sharply for small values of \(\varphi .\) This represents a characteristic feature of stagnation-point flows upon curved objects and has been already reported in other configurations [5, 42, 43]. Further, Fig. 8 shows that by increasing the concentration of nanoparticles the value of Nusselt number increases considerably. This finding is in agreement with the that observed in other flow conduits involving convection of nanofluids in porous media [6, 7] and it is also consistent with the temperature distribution shown in Fig. 5. Part b of Fig. 8 clearly shows that the viscous friction increases quite considerably through increases in the concentration of nanoparticles. Once again, this is a plausible behaviour and stems from the fact that increasing the concentration of nanoparticles boosts the viscosity of the nanofluid and hence strengthens the imposed shear stress.

Fig. 8
figure 8

Effect of different values of nanoparticle volume fraction on a Nusselt number against \(\varphi\), b dimensionless shear stress against \(\varphi\), at \(\text{Re} = 10\) and \(\lambda = 10\)

Full size image
Fig. 9
figure 9

Effect of different values of reciprocal of Darcy number on a Nusselt number against \(\varphi\), b dimensionless shear stress against \(\varphi\), at \(\text{Re} = 10\), \(\lambda_{1} = 1\), and \(\phi = 0.1\)

Full size image

Figure 9 shows the angular variation of Nusselt number with respect to permeability parameter indicating that by increasing the permeability parameter Nusselt number grows to a small extent. Increase in Nusselt number with decreasing the permeability (or increasing the permeability parameter) has been already reported in studies of convection of nanofluid in straight porous flow conduits [6, 7]. The present study extends this to curved surfaces embedded in porous media. Figure 9b shows that, as expected, by increasing the permeability parameter the dimensionless stress increases. The amount of this increase is particularly large at small values of \(\varphi\) and appears to feature a jump at \(\lambda = 100.\)

To provide further quantitative data, Tables 4, 5 and 6 present the numerical values of circumferentially averaged Nusselt number and dimensionless shear stress as a function of different pertinent quantities. In these tables, two types of transpiration functions including non-uniform and uniform mass transpiration have been incorporated. The increase in average Nusselt number and shear stress with increases in the concentration of nanoparticles is evident from Table 4. This table also shows that the average value of Nusselt number is generally higher when there is no mass transpiration. Table 5 indicates that large increases in the value of \(\lambda_{1}\) (or approaching free convection) are associated with small decreases in the average number. However, as that observed in Table 4, suppressing transpiration enhances the average Nusselt number noticeably. Similarly, Table 6 shows that increasing the magnetic parameter by a few orders of magnitude reduces the average Nusselt number to a very minor extent. Yet, setting S = 0 has much larger enhancing effects upon the average Nusselt number. It is noted that increasing the magnetic parameter causes substantial gains in the averaged shear stress in both mass transpirating and non-transpirating cases.

Table 4 Effects of the nanoparticle volume fraction on average Nusselt number and average shear stress (\({\raise0.7ex\hbox{${\sigma_{\rm m} .a}$} \!\mathord{\left/ {\vphantom {{\sigma_{\rm m} .a} {4\mu \bar{k}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${4\mu \bar{k}z}$}}\)) for \(\text{Re} = 1\), \(\phi = 0.1\), \(\lambda_{1} = 1\), \(\lambda = 100\)
Full size table
Table 5 Effects of the dimensionless mixed convection in nanofluid water-Cuo on average Nusselt number and average shear stress (\({\raise0.7ex\hbox{${\sigma_{\text{m}} \cdot a}$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{m}} \cdot a} {4\mu \bar{k}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${4\mu \bar{k}z}$}}\)) when \(\phi = 0.1\), \(\lambda = 100\), \(\text{Re} = 1\)
Full size table
Table 6 Effects of the magnetic parameter in nanofluid water-Cuo on average Nusselt number and average shear stress (\({\raise0.7ex\hbox{${\sigma_{\text{m}} \cdot a}$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{m}} \cdot a} {4\mu \bar{k}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${4\mu \bar{k}z}$}}\)) when \(\phi = 0.1\), \(\text{Re} = 1\), \(\lambda = 10\), \(\lambda_{1} = 10\)
Full size table

Thermodynamic irreversibilities

The dimensionless form of local entropy generation has been shown in Figs. 10 and 11. These figures illustrate the variation of local entropy generation in the radial angular directions shown for discreet values of mixed convection parameter and concentration of nanoparticles. Figure 10 indicates that for small and moderate values of \(\lambda_{1}\) (\(\lambda_{1} = 0.1,1\) representing forced and mixed convection modes) the radial and angular distributions of entropy generation are quite similar and almost indifferent to the value of \(\lambda_{1} .\) However, for higher values of \(\lambda_{1}\) (\(\lambda_{1} = 10,100)\) the numerical value of entropy generation increases in both radial and angular directions. The extent of this increase is particularly significant at \(\lambda_{1} = 100\) in which heat transfer process is dominated by free convection. This is an important result and indicates that the mode of heat transfer can substantially affect the irreversibility of the heat transfer process. It should be emphasised that the results presented in Sect. 3.1 already showed that changes in the mixed convection parameter have relatively minor influences upon the temperature field and Nusselt number. However, these influences are highly magnified in entropy generation analysis due to strong dependency of irreversibilities on temperature gradients. As shown in Fig. 10, increases in the concentration of nanoparticles lead to an increase in the entropy generation in radial and angular directions. Similar to that shown in Fig. 10, it is clear from Fig. 11 that for a fixed concentration of nanoparticles increasing the value of \(\lambda_{1}\) from 0.01 to 10 results in major increases in entropy generation.

Fig. 10
figure 10

Variation of \(N_{\text{G}} (\eta ,\varphi )\) in terms of a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\), \(\phi = 0.05\) and for different values of dimensionless mixed convection

Full size image
Fig. 11
figure 11

Variation of \(N_{\text{G}} (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\) and for different values of nanoparticle volume fraction

Full size image

Figures 12 and 13 depict the spatial distribution of Bejan number for the cases investigated in Figs. 10 and 11. This reveals some interesting facts about the shares of viscous and thermal entropy in the total entropy generation. For instance, Fig. 12 shows that the magnitude of Bejan number decreases as the numerical value of \(\lambda_{1}\) increases. This indicates that the relative share of thermal entropy in the irreversibility of the process decreases at higher values of mixed convection parameter. Given that Fig. 10 has already shown a significant intensification of entropy generation at higher values of \(\lambda_{1} ,\) the observed behaviour of Bejan number reflects a major growth in the significance of viscous entropy generation at high values of \(\lambda_{1}\). Figure 13 shows that by increasing the concentration of nanoparticles, the value of Bejan number increases in the radial direction. The extent of this increase is more noticeable at \(\eta \cong 1.\) In the angular direction, however, the value of Bejan number depends upon the circumferential location. For values of \(\varphi < 80^\circ ,\) increases in the concentration of nanoparticles result in increasing the value of Bejan number. Nevertheless, this trend is reversed in the larger values of \(\varphi .\)

Fig. 12
figure 12

Variation of \(B{\text{e}} (\eta ,\varphi )\) in terms of a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\), \(\phi = 0.05\) and for different values of dimensionless mixed convection

Full size image
Fig. 13
figure 13

Variation of \(B{\text{e}} (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 1.0\), \(\lambda = 10\) and for different values of nanoparticle volume fraction

Full size image

The influences of the magnetic field upon the entropy generation distribution is depicted in Fig. 14. This figure shows that for small and moderate value of M the entropy generation distribution remains almost unaltered. Yet, further magnification of M (M = 10,100) results in large increases in the value of NG in both radial and circumferential direction. Figure 15 shows that Bejan number is highly suppressed at large value of M. This is an indication of the fact that as the magnetic field goes up in strength the motion of nanofluid becomes progressively more difficult and hence the viscous irreversibility plays a stronger role in the entropy generation. Figures 14, 15 show, once again, that the parameters that only marginally contribute with the thermal aspects of the problem can affect the thermodynamics of the system quite significantly.

Fig. 14
figure 14

Variation of \(N_{\text{G}} (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 100\), \(\lambda = 10\) and for different values of magnetic parameter

Full size image
Fig. 15
figure 15

Variation of \(B{\text{e}} (\eta ,\varphi )\) with a\(\eta\) (radial), b\(\varphi\)(angular), \(\text{Re} = 100\), \(\lambda = 10\) and for different values of magnetic parameter

Full size image

Conclusions

This work presented an analysis of heat transferring stagnation-point nanofluid flow over a cylinder embedded in porous media in the presence of gravitational and magnetic effects. By surveying the literature, it was shown that this was the first analysis of mixed convection of nanofluids through curved porous conduits. In the analysis, three-dimensional equations of transport of momentum together with one-equation model of transport of heat in porous media were employed and a temperature-independent model of nanofluid was considered. Through assuming certain self-similar solutions, these equations were reduced to simpler versions solvable with a finite difference technique. Hydrodynamic, thermal and entropy generation fields were analysed in details. The followings summarise the main findings of this study.

  • In keeping with that reported for other porous configurations, the Nusselt number was observed to increase in magnitude by increasing the concentration of nanoparticles.

  • Intensifying the magnetic field was shown to result in reducing the flow temperature slightly and also causing a small decrease in the averaged Nusselt number.

  • The functional form of mass transpiration was shown to have important effects upon the average Nusselt number.

  • By increasing the numerical value of mixed convection parameter, \(\lambda_{1} ,\) the numerical value of the dimensionless temperature and that of the average Nusselt number decreases. That indicates that, as expected, under free convection the flow is colder and the rate of heat transfer is smaller than that under mixed and forced convection.

  • The entropy generation was found to substantially increase at high values of mixed convection parameter, which means free convection in the investigated configuration involves much more irreversibility compared to mixed and forced convection.

  • It was argued that the share of viscous irreversibility in entropy generation under free convection is significantly higher than that of thermal irreversibility.

  • Strong magnetic effects were shown to generate large irreversibilities, while they reduce Bejan number and magnify the relative importance of viscous irreversibilities.