Introduction

Reliable knowledge of thermophysical properties is essential for the interpretation and the modelling of solidification behaviour of materials. Although steels are commonly used materials, there still exists a lack of thermophysical data for concrete steel grades. Most of the steels are produced in continuous casting process; however, some steel grades still cause technological problems. One of the most difficult materials for casting are steels, in which the peritectic transition during solidification occurs—steels have significant practical implications with respect to issues such as cast surface quality, cracks, and breakouts. The surface quality of continuously cast slabs is a dominant function of events appearing in the early stages of solidification in the mould. Thus, the study of high-temperature phase transition is of great importance to the control of the casting process.

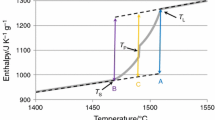
Peritectic phase transition L+δ → γ in Fe–C system appears from point H to B which corresponds to 0.09 and 0.53 C mass%, respectively, as shown in Fig. 1.

Fig. 1
figure 1

Fe–C equilibrium phase diagram in the range of peritectic phase transition calculated making use of FactSage 6.3 software with SGTE 2011 database. The dashed line represents the carbon content of investigated steels

Full size image

However, the most critical materials for casting are the steels with carbon content in the range of 0.09–0.17 mass%, due to the fact that transformation of δ-Fe to γ-Fe coincides with the final solidification and ends in the solid. During non-equilibrium solidification, alloying elements segregate to the liquid phase, and hence, the compositional range in which the peritectic reaction and subsequent peritectic transformation take place is extended. The presence of alloying elements in the steel such as Cr, Ni, Mn, Cu, Si, S, and P may shift characteristic points H, J and B as shown in Fig. 1. The effect of alloying elements on the position of the peritectic transformation in steels is more precisely described in the literature [1].

The mechanism and the rate of peritectic transition in steels were first explained by Shibata et al. [2]. In-situ observations using high-temperature laser-scanning confocal microscope revealed that peritectic transition in carbon steels consists of two stages. The first stage is the so-called peritectic reaction that indicates and propagates at high speed by the growth of thin austenitic layer along the liquid/δ-ferrite interface. Once all the interfaces are covered with the austenite, the peritectic transformation starts. The δ-ferrite to austenite transformation takes place by solid-state diffusion of carbon through the austenitic layer, while the austenite grows by direct solidification into the liquid phase. It is believed that the occurrence of peritectic transition during cooling is responsible for defects of continuously cast slabs, such as hot tears, surface defects, depressions, or even breakouts [3].

The most widely used method to characterize steel grades regarding peritectic transition is the calculation of carbon equivalent in which carbon content (C) and other alloying elements (X i) in mass% are added up together with dimensionless coefficients (f i). The coefficients were published by several authors [4, 5], and they can be used in general expression for carbon equivalent:

$$ {\text{CE}} = {\text{C}} + \sum\limits_{i = 1}^{i = 1} {f_{\text{i}} X_{\text{i}} } . $$
(1)

If the calculated value of CE falls between 0.09 and 0.17, then the steel is considered as peritectic and prone to cracks during casting.

Many researchers of late deal with the counteraction of defects formation by changing casting speed or mould flux properties and modelling of peritectic transition [6–8]. Modelling of continuous steel casting process usually requires solving temperature field. This is often realized by solving Fourier–Kirchhoff equation. However, to solve this equation, thermal conductivity, density, and specific heat or enthalpy must be known [9]. Additional thermophysical data necessary for modelling of continuous casting process are solidus and liquidus temperatures, latent heat of solidification and other phase transformations, viscosity, and solid or liquid fraction [10]. For some materials such as steels, these properties can be calculated using thermodynamical software such as FactSage, ThermoCalc, JmatPro, IDS, etc.; however, the influence of alloying elements on the solidus and liquidus temperatures must be verified experimentally since the results of the calculations are only as accurate as the content of the databases allows. In the current study FactSage software [11] was used for running thermophysical calculations under equilibrium conditions. The software is based on the principle of Gibbs free energy minimization. FactSage calculations were run for both complex chemical composition of steels and Fe–C system with constant carbon content corresponding to its content in steels.

Two thermal analysis techniques, differential thermal analysis (DTA) and differential scanning calorimetry (DSC), are usually used for metallic systems’ measurements. Both these techniques enable determination of temperature of phase transitions, latent heats and (in case of DSC) specific heat [1, 12–14]. However, peritectic steels are highly reactive materials at elevated temperatures [1]; thus, a great care must be taken during measurements to avoid the decarburization and oxidation of steel samples [15, 16].

In this study, the DSC method [17, 18] was used to examine real steel grades with hypo-peritectic composition. The main aim of the study was to determine the temperatures of phase transitions in two peritectic steel grades. As a result of the research, characteristic temperatures such as solidus, liquidus, peritectic transition temperature and temperature of γ↔δ transformation were determined.

Experimental

Samples characterization

Two steel grades falling into hypo-peritectic composition range, which is most critical for casting, were chosen as the materials for investigations. Chemical compositions of the investigated steel grades measured with WAS Foundry-Master spark spectrometer are summarized in Table 1.

Table 1 Chemical compositions of investigated steel grades
Full size table

Carbon equivalent was calculated according to Eq. (1) with coefficients taken from Ref. [4]. The value of CE indicates the both steel grades are hypo-peritectic and prone to cracking during casting. The samples were taken from the mould of continuous casting machine to the vacuum samplers, solidified slowly in the air and machined into small samples with the diameter of approx. 5 mm and height of approx. 1.5 mm. Masses of samples for steel 1 were 151.5 mg and 43.3 mg at the heating rates of 5 and 20 °C min−1, respectively. In case of steel 2, the corresponding sample masses were 177.6 mg and 176.2 mg, respectively. Such prepared samples were degreased in alcohol, rinsed in distilled water and dried.

Experimental conditions

Heat-flux calorimeter, STA 449 F3 Jupiter made by Netzsch, was used for measurements (Fig. 2). The samples were analysed in corundum crucibles (Al2O3) with lids. The reference sample in case of all measurements was empty crucible. The measurements were conducted in the inert atmosphere of pure argon (>99.9999 %). The furnace chamber was evacuated and filled for the three times prior to each measurement to avoid decarburization and oxidation of steel samples, which occur at high temperatures in the presence of residual oxygen [19]. Pure titanium chips were put into the furnace chamber for additional purification of the atmosphere. In order to shorten the duration of measurement, the samples were heated at the heating rate of 50 °C min−1 to 1,350 °C. Further heating was continued after short isothermal time with heating rates of 5 and 20 °C min−1 up to 1,570 °C. Samples were remelted during experiments. Cooling from liquid state was run with the same mode of rates as heating. During all the trials, the thermogravimetric (TG) function was registered to control the mass of the sample. This is very important, as peritectic steels are highly reactive alloys, and any increase in the sample mass indicates the oxidation, thus resulting in invalid measurement data. During all the tests, TG signal did not indicate any changes in the mass of the samples. This has been achieved thanks to the use of titanium, which acts as an oxygen trap. Preliminary tests, in which no titanium was used, showed that the peritectic transformation was very difficult to identify in investigated steel grades, probably because of the decarburization of the sample, especially at low heating rates [15].

Fig. 2
figure 2

Netzsch STA 449 F3 Jupiter experimental equipment scheme: 1 furnace thermocouple, 2 heating element, 3 sample carrier, 4 protective tube, 5 radiation shield, 6 evacuation system inlet, 7 balance system, 8 gas outlet valve, 9 hoisting device, 10 purge 1 gas inlet, 11 purge 2 gas inlet, 12 protective gas inlet

Full size image

Prior to the measurements, the calibration of temperature was made making use of melting temperatures of standard metals in the whole temperature range of the instrument. For calibration, standard metals were used. Purity standards for In, Bi, Al, and Au were 99.999 %, and for Ni 99.99 %. All the results presented in this paper were temperature corrected.

Results and discussion

Figures 3 and 4 show the DSC curves obtained during heating (Figs. 3a, 4a) and cooling (Figs. 3b, 4b) of steels 1 and 2, respectively, with the heating/cooling rates of 5 and 20 °C min−1 together with markings of the characteristic temperatures. As the chemical compositions of both investigated steel grades are congenial, DSC curves thus represent similar characteristics. Melting of steels entails endothermic phase change, while solidification is accompanied by heat release.

Fig. 3
figure 3

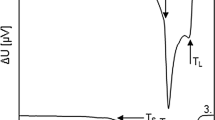
DSC curves of steel 1 obtained during heating (a) and cooling (b) with the heating/cooling rates of 5 and 20 °C min−1; characteristic temperatures: T γ→δ temperature of δ-ferrite formation, T PER temperature of peritectic reaction, T L+δ temperature of the “end of peritectic transformation”, T SOL solidus temperature, T LIQ liquidus temperature

Full size image
Fig. 4
figure 4

DSC curves of steel 2 obtained during heating (a) and cooling (b) with the heating/cooling rates of 5 and 20 °C min−1; characteristic temperatures: T γ→δ temperature of δ-ferrite formation, T PER temperature of peritectic reaction, T L+δ temperature of the “end of peritectic transformation”, T SOL solidus temperature, T LIQ liquidus temperature

Full size image

During heating, the first deviation from DSC baseline is observed at the starting temperature of γ to δ transformation, T γ→δ. The temperature of this transition was determined as extrapolated onset of the disorder on DSC curve. However, only very small increase in heat flow can be observed with small change in heat capacity. This small change is typical for transformation of austenite to δ-ferrite in hypo-peritectic steel grades. Considering that the two-phase region (γ+δ) is wide, the heat flow per unit time is small. This causes the austenite to δ-ferrite to be hardly measurable with DSC, especially at small heating rates.

The temperature of peritectic transition T PER is associated with the temperature of the extrapolated onset of first peak appearing in DSC signal during heating. With the start of peritectic reaction, the first liquid appears in the steel structure; thus, the temperature T PER is also interpreted as solidus temperature of steel (T PER = T SOL). Peritectic transformation of the steel takes place at a constant temperature. Due to the presence of temperature gradient in the analysed samples, peritectic transformation does not occur simultaneously over the entire volume of the sample. In this manner, T L+δ could be interpreted as the temperature of “the end of peritectic transformation” but only based on the fact that peritectic transition takes place in different parts of the sample; thus, it is dependent on sample mass. In the structure after reaction between austenite and δ-ferrite, only δ-ferrite and liquid are stable. During further heating, the residual δ-ferrite melts, and the amount of liquid phase consequently increases until reaching the temperature of liquidus T LIQ. Determination of this temperature depends also on the sample mass.

In case of steel 2, between the T L+δ and T LIQ, another peak appears registered during heating at the heating rate of 20 °C min−1. The disorder is probably associated with the movement of the sample during melting. This disturbing effect might have occurred in this case as the sample mass was small.

The measured temperatures of phase transformations are summarized in Table 2 for heating rates of 5 and 20 °C min−1. Experimental conditions influence the temperatures measured with DSC. The higher the heating rate used is the greater is the shift of phase transformation temperatures to higher values. The most sensitive temperature on the impact of heating rate is T LIQ in case of both the examined steel grades. The smallest impact of the heating rate was observed on the solidus temperature marked as the temperature of the beginning of peritectic transformation T PER.

Table 2 Characteristic temperatures of phase transitions of investigated steel grades obtained during heating and calculated making use of FactSage software
Full size table

In order to compare the obtained temperatures of phase transitions to theoretical values, it is necessary to eliminate the influence of heating rate on temperature shifts. One of the methods is the extrapolation of temperature to the so-called zero heating rate [20]. The temperatures for the zero heating rates approach the temperatures of phase transformations at equilibrium. FactSage 6.3 software is used to carry out thermodynamic calculations under equilibrium conditions. Thus, temperatures calculated for the zero heating rates were compared to the calculated temperatures using FactSage software with SGTE database for both steel compositions and the Fe–C system. SGTE database includes thermodynamic data for over 538 completely assessed binary alloy systems and 136 ternary and higher-order systems that include the 78 elements. Very good agreement was obtained between the calculated temperatures and the values measured during heating. Comparison of extrapolated T PER = T SOL values (1483.6 °C—steel 1, 1489.2 °C—steel 2) to the temperatures obtained making use of FactSage (1487.1, 1487.7 °C) reveals that they are in good agreement. The greatest differences between the extrapolated (1446.1, 1459.3 °C) and the calculated (1471.8, 1483.2 °C) temperatures were found for T γ→δ since it is hardly measurable with DSC, as mentioned before. The accuracy of the temperature of extrapolation can be improved by performing experiments at several heating rates, especially in case of T γ→δ.

The fact that experimentally obtained temperatures of phase transformations are lower in comparison with Fe–C diagram is probably caused by the contents of other elements present in the samples. The biggest impacts on the decreasing of peritectic temperature, according to Ref. [21], are caused by the presence of P, S and Si. The influences of Mn, Ni and Cu are just the opposite, but the rise in peritectic temperature caused by these elements is much smaller than the decrease, as a consequence of phosphorus and sulphur contents. This may be an explanation for the lower peritectic temperature in steel 1 than that in steel 2, as it has much higher sulphur content.

Additional studies were conducted during heating for both the investigated steel grades to verify the reproducibility of the results. The results of this study showed that the difference in determining the peritectic temperature was approximately 0.3 °C with respect to the values presented in Table 2. In case of other phase transitions, it does not exceed 3 °C.

During continuous casting of steels, the mass of liquid is cooled and solidified in the mould of the casting machine. For this reason, to determine the phase-transition temperatures, the experiments at cooling rates of 5 and 20 °C min−1 were performed. The phase-transition temperatures obtained during cooling for the investigated steel grades are summarized in Table 3.

Table 3 Characteristic temperatures of phase transitions of investigated steel grades obtained during cooling
Full size table

Solidification of the samples starts at T LIQ with the origination of first δ-ferrite crystals in liquid steel. Some degree of supercooling was observed (max. 52 °C compared with FactSage). The solidification process of investigated steels is dependent on first critical nuclei formation and its existence. The nucleation of small samples is difficult, and therefore alloys start often to solidify at lower temperatures. Degree of supercooling in case of solidification of the sample is not always correlated to the cooling rate [22].

Two-phase structure L+δ is undercooled until the start of peritectic transition, which occurs at the temperature T PER. In case of steel 1, the temperature obtained with different cooling rates are the same. In case of steel 2, the higher cooling rate shifted the temperature to the lower values. This is in line with the generally known trend for cooling of steel samples [22].

In case of cooling measurements, the solidus temperature TSOL was identified as the temperature of the peak minimum (see Figs. 3b, 4b). T SOL is also shifted to the lower values when compared with the equilibrium calculations. Higher cooling rate caused bigger decrease in phase-transition temperatures compared to the results obtained at lower cooling rate and FactSage calculations.

The temperature of the end of δ-ferrite to austenite transformation was not possible to measure reliably during cooling; hence, it is not included in Table 3. More preferable methods for the measurement of the temperature of δ↔γ transformation are, for instance, dilatometric and X-ray diffraction measurements.

Additional verification studies were conducted during cooling experiments. The results of this study showed a similar nature, but the characteristic temperatures have been shifted in different ways. Due to the different values of the samples’ undercooling, the mean values of temperatures have not been determined. Undercooling, which is much higher for steels than overheating, has a greater dispersion of temperature values measured for samples tested under desired conditions. For this reason, temperatures registered during heating are considered to be more representative for the usage in modelling of steel continuous casting process.

Conclusions

The current study illustrates and discusses a high-temperature phase transformations of steel with the hypo-peritectic composition. Differential scanning calorimetry was used as this is powerful method for determination of phase-transition temperatures in steels. The temperatures of solidus, peritectic transition, and liquidus were investigated. Two real steel grades with different chemical compositions falling into hypo-peritectic region were investigated using Netzsch STA 449 F3 Jupiter thermal analyser. Following conclusions are drawn from investigations:

  • Temperatures of peritectic transition (solidus temperatures) were found during heating experiments. It was observed that the heating rate slightly affects this temperature. In case of steel 1, for both heating rates, T PER = 1,485 ± 1 °C, and for steel 2, it was approx. T PER = 1,489 °C.

  • The strongest dependency on heating rate was observed for liquidus temperature. For the heating rate of 5 °C min−1, the obtained results are more reliable because of the smallest overheating of the samples. Liquidus temperature in case of steel 1 was T LIQ = 1,537 ± 3 °C, and in case of steel 2 T LIQ = 1,524 ± 3 °C.

  • During cooling experiments, the peritectic transition temperature was shifted to lower values due to the supercooling of the sample. In case of steel samples, overheating is much smaller than overcooling. Thus, more reliable results are obtained during heating experiments.

  • Owing to small enthalpy changes during austenite transformation into δ-ferrite, the DSC method has limitations, and the temperature of the transformation is hardly measurable. More reliable methods for the identification of γ to δ transformation would be dilatometric measurements or X-ray diffraction.

  • The obtained values of temperatures of phase transitions are in good agreement with those calculations conducted for equilibrium state using FactSage software.

The obtained data are essential information both for the casting process practice and modelling.