Displacement chromatography of gadolinium isotopes with strong cation exchange resin using 1,2-cyclohexanedinitrilotetraacetic acid (CDTA)

Abstract

Adsorptive separation of Gd³⁺ ions was evaluated using DOWEX-50×8 ion exchange resin. It has shown a maximum adsorption capacity of 228.50 mg/g at optimum pH 5 and room temperature. Separation of Gd isotopes was investigated using packed bed columns of the resin in displacement chromatographic techniques where 1,2-cyclohexanedinitrilotetraacetic acid was used as displacer in the mobile phase. Isotopic analysis data by using MC‒ICP‒MS confirmed that the front end of the Gd adsorption band exhibited enrichment of the heavier isotope (¹⁶⁰Gd), while the lighter isotopes (¹⁵⁷Gd and ¹⁵⁵Gd) were concentrated at the rear end of the stationary phase.

Introduction

Natural Gd consists of seven stable isotopes: 152, 154, 155, 157, 158, and 160. The abundance ratios of the seven isotopes are 0.20, 2.18, 14.80, 20.47, 15.65, 24.84 and 21.86%, respectively [1]. Its exceptional ability to absorb thermal neutrons makes it a preferred choice as a burnable poison in nuclear reactors. This is due to the high neutron absorption cross sections of the ¹⁵⁷Gd (2.54 × 10⁶ barn) and ¹⁵⁵Gd (0.609 × 10⁶ barn) isotopes. Although natural Gd is presently used as a burnable poison in nuclear reactors, enriched ¹⁵⁵Gd or ¹⁵⁷Gd will be increasingly used as a viable neutron poison [2]. In addition, the ¹⁵²Gd isotope is used in producing radioactive ¹⁵³Gd isotopes. ¹⁵³Gd is used for research on osteoporosis and bone thickness estimations. Therefore, a process is needed for the enrichment of Gd isotopes. The standard methods for producing isotopes are electromagnetic enrichment [3,4,5,6,7] (calutron), distillation [8,9,10], and centrifuge enrichment [11, 12]. There are also many other methods, such as plasma separation, laser enrichment, and photochemical enrichment. However, every method has its own limitations in terms of cost and scale of production.

On the other hand, chemical exchange methods can be used for isotope separations. These processes are usually associated with smaller separation coefficient values and thus require more time to obtain enriched products than other physical processes; however, these chemical exchange reactions are naturally feasible equilibrium routes. Therefore, these methods are regarded as energy-efficient processes. Displacement chromatography employing ion exchange, which relies on the establishment of equilibrium between isotopic species across mobile and stationary phases, is a highly effective technique for isotopic separation. These methods have been successfully applied for the isotopic separation of different elements, such as Li [13], N [14], Ca [15], Zn [16,17,18,19], Ce [20], Cu [21, 22], Eu [23, 24], V [25], Nd [26, 27] and Gd [28,29,30]. We previously carried out isotope separation of Zn and Gd using chemical exchange methods along with computational methods [31,32,33,34,35,36,37]. However, to date, CDTA has not been utilized for displacement chromatography of gadolinium isotopes with strong cation exchange (DOWEX-50×8) resin. In the current study, we aimed to explore the use of CDTA as a displacement agent to separate Gd isotopes via DOWEX-50×8 resin. The following details are reported in the present paper.

• In batch-mode equilibrium studies, the effects of the initial concentration of Gd³⁺ ions and solution by DOWEX-50×8 resin pH by were reported. The adsorption data were fitted with different adsorption isotherm models.

• In kinetic studies, the effect of shaking time on the adsorption of Gd³⁺ ions from aqueous solution by resin at optimized pH and room temperaturewas reported. The data were fitted with kinetic models.

• In thermodynamics studies, the dependence of adsorption of Gd³⁺ ions from aqueous solution by the adsorbent resin on the temperature at optimized pH was reported. Thermodynamic parameters were calculated from the van’t Hoff plot and Gibbs- Helmholtz equation.

• Furthermore, in the chromatographic experiments, the adsorption band of Gd was displaced using CDTA in the column loaded with DOWEX-50×8 resin to study the isotope separation of gadolinium.

Experimental

Chemicals

In this study, cation-exchange resin, DOWEX-50×8 mesh size 20–50 was utilized. Gd(NO₃)₃ solutions were prepared using Gd₂O₃ (99.999%), sourced from Otto Chemical Industries. The other reagents were of analytical grade and used without additional purification in the present study.

Elemental analysis

For Gd concentration and isotopic analysis, samples were prepared using AR grade ~ 15.0 M HNO₃, > 18 MΩ-cm H₂O and ~ 30% hydrogen peroxide. The sample preparation was carried out in a manner similar to our earlier work [38]. Sample aliquots were diluted with 2% HNO₃ for Gd elemental analysis. The Gdcontent was measured using an inductively coupled plasma optical emission spectrometer (ICP‒OES) model HORIBA ULTIMA.

Isotopic analysis

For Gd isotope analysis, the sample aliquots were diluted with 2% HNO3 to achieve concentrations ranging from 50 to 100 μg/L. Gd isotope measurements were conducted using a Thermo Fisher Scientific Neptune Plus multicollector inductively coupled plasma mass spectrometer (MC‒ICP‒MS) employing the standard sample introduction system at the Radiogenic Isotope Facility, Department of Geology and Geophysics, Indian Institute of Technology Kharagpur, India. Simultaneous detection of masses ¹⁵⁴Gd, ¹⁵⁵Gd, ¹⁵⁶Gd, ¹⁵⁷Gd, ¹⁵⁸Gd, and ¹⁶⁰Gd was achieved using Faraday cups. Instrumental mass bias and drift were corrected using the standard-sample-standard bracketing (SSB) technique. [38]. The mass bias factors were calculated assuming ¹⁵⁶Gd/¹⁶⁰Gd = 0.9400 and using the exponential law. The reproducibility of replicate measurements of the Fluka ICPMS solutions changed in the range of 0.11⁰/_00, 0.070/₀₀, 0.02⁰/₀₀, and 0.07⁰/₀₀ for the ¹⁵⁵Gd/¹⁵⁸Gd, ¹⁵⁶Gd/¹⁵⁸Gd, ¹⁵⁷Gd/¹⁵⁸Gd and ¹⁶⁰Gd/¹⁵⁸Gd ratios, respectively.

Batch adsorption studies of Gd³⁺ by DOWEX-50×8

Batch adsorption experiments were conducted using DOWEX-50×8 to study Gd ion adsorption. Parameters like pH, contact time, Gd³⁺ ion concentration, and temperature were varied systematically. A 10000 ppm Gd³⁺ stock solution was prepared from Gd(NO₃)₃ in deionized water. A 200 mg of DOWEX-50×8 resin was mixed with Gd ion solution of desired concentration in a screw capped glass bottle at room temperature and the mixture was shaken for 60 min in an orbital incubator shaker (make: IKA, model: KS 4000). After settling down the resin phase on the bottom of the bottle, supernatant aliquot analyzed for Gd concentration using Inductively CoupledPlasma Optical Emission Spectroscopy ICP-OES (make: Horiba Scientific, model: JobinYvonUltima 2). pH studies were done with 5000 ppm Gd concentration, adjusting pH with HNO₃ and NaOH solutions. Equilibrium studies covered Gd ion concentrations from 200 to 10,000 ppm. Kinetic studies were conducted at optimum pH and room temperature. Adsorption was tested at temperatures from 30 to 60 °C with constant adsorbent dosage. Adsorption equilibrium data were used for isotherm modeling, and kinetics were analyzed for the relationship between contact time and adsorption data. Thermodynamic properties were determined from temperature-dependent separation results. Adsorption capacity (Qe, mg/g) was calculated using Eq. 1.

$$ Q_{{\text{e}}} = \left( {C_{{\text{o}}} {-} \, C_{{\text{f}}} } \right) \times \left( {V/m} \right) $$

(1)

Here, C_o and C_f denote the initial and final equilibrium concentrations (mg/L) of Gd ions, respectively. V represents the volume of the solution (mL), and m indicates the weight of the adsorbent. Experiments were performed by duplicate and average values were considered for the calculation. The relative standard deviation of the repeat analysis was within 5%.

Chromatographic separation studies of Gd³⁺ ions by DOWEX-50×8 resin

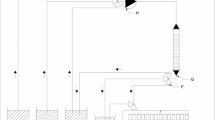
Gadolinium isotope separation by displacement chromatography was carried out in a system for which a schematic of the experimental setup is displayed in Fig. 1. Three glass columns with 10 mm internal diameters (i.d.) and 1000 mm long were connected in series with PTFE tubes (1 mm i.d.). Columns were used repeatedly in a rotational manner (merry-go-round) to achieve the desired migration lengths.

Fig. 1

Schematic of the experimental setup for the isotope separation of gadolinium

Theoretical models

Isotherm models

Adsorption isotherms can provide useful information such as the adsorption ability of the adsorbent and the type of adsorption [37, 39]. The adsorption equilibrium data were fitted with established two- and three-parameterisotherm models, including the Langmuir [40] (Eq. 2), Freundlich [41] (Eq. 3), Temkin [42] (Eq. 4), Dubinin‒Radushkevich [43, 44] (Eq. 5) and Toth [45] (Eq. 6) models.

$$ Q_{{\text{e}}} = \frac{{q_{{\text{m}}} bC_{{\text{e}}} }}{{1 + bC_{{\text{e}}} }} $$

(2)

$$ Q_{{\text{e}}} = K_{{\text{f}}} C_{{\text{e}}}^{1/n} $$

(3)

$$ Q_{{\text{e}}} = \frac{{{\text{RT}}}}{b}\ln \left( {K_{{{\text{T}}_{{\text{e}}} }} C_{{\text{e}}} } \right) $$

(4)

$$ Q_{{\text{e}}} = q_{{\text{m}}} \exp \left( {\frac{{\left( {{\text{RT}}\ln \left( {1 + \frac{1}{Ce}} \right)} \right)^{2} }}{{ - 2E^{2} }}} \right) $$

(5)

$$ Q_{{\text{e}}} = \,\frac{{q_{{\text{m}}} K_{{{\text{To}}}} C_{{\text{e}}} }}{{\left[ {1 + \left( {K_{{{\text{To}}}} C_{{\text{e}}} } \right)^{n} } \right]^{\frac{1}{n}} }} $$

(6)

In the Langmuir model, q_m (mg/g) shows adsorption capacity, and b (L/mg) denotes binding site affinity. The Freundlich model uses K_f and n to determine adsorption capacity and intensity. In the Temkin model, K_Te (L/g) and b relate to the constant and heat of adsorption. R is the gas constant, and T is temperature. The Dubinin‒Radushkevich model uses E for adsorption energy. The Toth model uses K_To and n, where n = 1 simplifies to the Langmuir model, otherwise indicating heterogeneous adsorption.

Kinetics models

The adsorption kinetics are investigated, including pseudo-first-order and pseudo-second-order models. The pseudo-first and second-order equations can be expressed as follows:

$$ q_{{\text{t}}} = q_{{\text{e}}} \left( {1 - \exp \left( { - k_{1} t} \right)} \right) $$

(7)

$$ q_{{\text{t}}} = \frac{{q_{{\text{e}}}^{2} k_{2} t}}{{1 + q_{{\text{e}}} k_{2} t}} $$

(8)

where q_t and q_e are the quantity of Gd³⁺ions adsorbed at time t and equilibrium, k₁ (L/min) and k₂ (g/mg min) are the first and second order rate constants of adsorption.

Results and discussion

Experimental results

Effect of pH

The pH of the initial solution containing metal ions significantly influences the adsorption process. Figure 2 illustrates the impact of pH on the adsorption of Gd³⁺ ions (5000 ppm). The adsorption of Gd³⁺ ion increases notably from pH 1.0 (22.94 mg/g) to 3.0 (190.94 mg/g) and remains constant up to pH 7.0. At lower pH values, thedecrease inadsorption is due to competition between H + and Gd³⁺ ions. With increase in the pH, the concentration of H+ ions decreases, increasing the availability of Gd³⁺ ions and subsequently increasing the adsorption capacity. A pH of 5 was identified as optimal for subsequent adsorption investigations.

Fig. 2

pH versus the amount of Gd³⁺ ions adsorbed by the DOWEX-50×8 resin at 5000 ppm

Effect of initial Gd³⁺ ion concentration and modeling of the adsorption isotherm

Figure 3 illustrates the calculated adsorption behavior of DOWEX-50×8 relative to the equilibrium concentration of Gd³⁺ ions. The plot indicates a proportional increase in sorption with the initial concentration of the adsorbate. These findings directly indicate that the uptake capacity of the DOWEX-50×8 resin increases with increasing C_e, leading to more Gd³⁺ ions being accessible for binding to the adsorbent surface.

Fig. 3

Experimental equilibrium Gd³⁺ ion adsorption data fitted with different isotherm models

Adsorption isotherm models offer valuable insights into the interactions between adsorbates and adsorbents, aiding in the design of effective adsorption systems. The computed parameters for each model, along with the correlation coefficient (R²), are presented. Table 1 presents the fitted models. As per the Langmuir model, the maximum adsorption capacity (qm) of the DOWEX-50×8 resin was determined to be 385.48 mg/g, considerably surpassing the experimental capacity (qm, exp.) of 229.39 mg/g. The Toth isotherm model exhibited the closest fit to the experimental data, as evidenced by its highest R² value of 0.9914. The maximum adsorption capacity (q_m) of DOWEX-50×8 determined by the Toth model was 228.50 mg/g, which closely resembled the experimentally observed value. Notably, Gd³⁺ adsorption on DOWEX-50×8 manifests as a heterogeneous adsorption process, with an n value deviating from unity.

Table 1 Isotherm model parameters of the DOWEX-50×8 resin

Kinetic studies

Figure 4 displays the variation in adsorption capacity over time during the adsorption of Gd ions by DOWEX-50×8. The removal of Gd³⁺ ions by the resin increased with time, peaking at approximately 15 min before stabilizing. Initial adsorption proceeded rapidly until 15 min, with equilibrium achieved by 60 min. Consequently, a shaking duration of 60 min was adopted for all experiments to ensure equilibrium attainment. These data were fitted using kinetic models. The fitted graphs are displayed in Fig. 4, with the calculated parameters presented in Table 2. Both the pseudo-first and second-order models are suitable for describing Gd adsorption on DOWEX-50×8 resin, as indicated by the highest R² value (0.9267) and maximum adsorption capacity. Moreover, the best fit to pseudo-second-order kinetics indicates that the sorption process is likely chemisorption. This indicates that the rate-limiting step is ion exchange through chemical sorption, involving which the surface-site density of the DOWEX-50×8 resin can be instrumental to the sorption affinity of Gd³⁺ ions [46].

Fig. 4

Adsorption of Gd³⁺ ions by DOWEX-50×8 with respect to contact time

Table 2 Kinetic parameters of the DOWEX-50×8 resin for Gd³⁺ ion adsorption

Adsorption thermodynamics

The significant role of temperature in the adsorption process is well acknowledged. The present observations revealed that the Gd ion adsorption in the resin increased with increasing temperature from 300 to 800 °C. Subsequently, thermodynamic parameters for the adsorption of Gd³⁺ ions onto the resin were derived from these findings. The enthalpy (ΔH⁰) and entropy (ΔS⁰) of adsorption were determined from the van’t Hoff plot (lnKd vs. 1/T), as illustrated in Fig. 5, following Eq. 9.

$$ \ln (K_{{\text{d}}} ) = \left( {\Delta S^{0} /R} \right){-} \, \left( {\Delta H^{0} /\left( {RT} \right)} \right) $$

(9)

where K_d is the distribution coefficient of Gd³⁺ ions by the DOWEX-50×8 resin. The Gibbs free energy (ΔG⁰) of the adsorption process is given by

$$ \Delta G^{0} = \Delta H^{0} - T \, \Delta S^{0} $$

(10)

Fig. 5

ln(K) versus 1/T plot for Gd³⁺ adsorption by DOWEX-50×8

The derived values of the thermodynamic parameters are presented in Table 3. These findings demonstrate that the adsorption of Gd³⁺ ions by the DOWEX-50×8 resin is exothermic, as evidenced by the negative enthalpy of − 5.887 kJ/mol. The observed gibbs free energy values indicates the nature of the adsorption process as spontaneous. Furthermore, a more negative free energy of adsorption suggested the preferred binding of Gd³⁺ ions by DOWEX-50×8 at temperatures up to 80 °C. The positive entropy change (0.0122 kJ/mol K) coupled with the negative enthalpy change can be attributed to the chemisorption process.

Table 3 Thermodynamic parameters of the DOWEX-50×8 resin

Chromatographic system

The DOWEX-50×8 resin was uniformly packed into the three columns. Prior to usage, the resin underwent pretreatment with 2 M HNO₃ solutions, converting it into H + form. Subsequently, a solution containing 0.3 M CuCl₂ at pH = 1 was circulated through the columns to transform the resin into Cu2 + form. The equations describing these ion exchange processes can be expressed as follows:

$$ \left[ {{\text{RSO}}_{{3}}^{ - } } \right]\left[ {{\text{Na}}^{ + } } \right] + {\text{ H}}^{ + } \rightleftharpoons \left[ {{\text{RSO}}_{{3}}^{ - } } \right] \, \left[ {{\text{H}}^{ + } } \right] + {\text{ Na}}^{ + } $$

(11)

$$ \left[ {{\text{RSO}}_{{3}}^{ - } } \right] \, \left[ {{\text{H}}^{ + } } \right] + {\text{ Cu}}^{{{2} + }} \rightleftharpoons \left[ {{\text{RSO}}_{{3}}^{ - } } \right]_{{2}} \left[ {{\text{Cu}}^{{ + {2}}} } \right] + {\text{ 2H}}^{ + } $$

(12)

where the underlining represents the resin phase.

A solution of 0.05 M Gd(NO₃)₃ was passed through the first column on top of the Cu²⁺ ion band to form a Gd³⁺ ion adsorption band. Gd³⁺ ion exchange process can be represented by the equations

$$ {3}\left[ {{\text{RSO}}_{{3}}^{ - } } \right] \, \left[ {{\text{H}}^{ + } } \right] + {\text{ Gd}}^{{{3} + }} \rightleftharpoons \left[ {{\text{RSO}}_{{3}}^{ - } } \right]_{{3}} \left[ {{\text{Gd}}^{{ + {3}}} } \right] + {\text{ 3H}}^{ + } $$

(13)

$$ {3}\left[ {{\text{RSO}}_{{3}}^{ - } } \right]_{{2}} \left[ {{\text{Cu}}^{{ + {2}}} } \right] + {\text{ 2 Gd}}^{{{3} + }} \rightleftharpoons {2}\left[ {{\text{RSO}}_{{3}}^{ - } } \right]_{{3}} \left[ {{\text{Gd}}^{{ + {3}}} } \right] + {\text{ 3Cu}}^{{ + {2}}} $$

(14)

After the Gd- band reached a width of 30.0 cm, the passage of the Gd³⁺ ion solution was closed. Both the Gd³⁺ ion and Cu²⁺ ion bands were displaced using 0.05 M (NH₄)₄CDTA + 0.1 M NH₄Cl adjusted to pH 8. The symbol “Z” indicates CDTA. The complexation process of Gd³⁺ ions with CDTA can be represented as:

$$ \left[ {{\text{Gd}}^{{ + {3}}} } \right] + {\text{ NH}}_{{4}}^{ + } + {\text{ Z}}^{{{4} - }} \rightleftharpoons {\text{Gd}} - {\text{Z}}^{ - } + \left[ {{\text{NH}}_{{4}}^{ + } } \right] $$

(15)

$$ {\text{Gd}} - {\text{Z}}^{ - } + \left[ {{\text{H}}^{ + } } \right] \rightleftharpoons {\text{H}} - {\text{Gd}} - {\text{Z}} $$

(16)

The absorption band attributed to Gd³⁺ ions was distinctly visible and characterized by a pale brown color, which contrasts with the earlier observed blue band indicative of Cu²⁺ ions. Upon reaching a migration length of 10 m, the Gd³⁺ ion band was eluted from the final column. The resulting effluent was collected in small fractions and subsequently analyzed for concentration and isotopic ratio.

Changes in the concentration profile and pH of the Gd³⁺ ion band

As (NH₄)₄CDTA reaches the leading edge of the Gd³⁺ ion band, the CDTA ligands undergo transfer to the Gd³⁺ ion due to the considerably higher stability constant of the Gd³⁺-CDTA complex in comparison to NH⁴⁺. As the Gd-CDTA complex species progress downward through the Gd³⁺ band within the column, isotopic exchange occurs between the Gd-CDTA complex species and Gd³⁺ ions present in the resin phase.

$$ {\text{H}} -^{{\text{X}}} {\text{Gd}} - {\text{Z}} + \left[ {^{{\text{Y}}} {\text{Gd}}} \right] \rightleftharpoons {\text{H}} -^{{\text{Y}}} {\text{Gd}} - {\text{Z}} + \left[ {^{{\text{X}}} {\text{Gd}}} \right] $$

(17)

Here, X and Y represent lighter and heavier isotopes of gadolinium, respectively.

Subsequently, the Gd-ligand complex advances to the Cu²⁺ ion band, where CDTA is transferred to Cu²⁺ ions, facilitating the adsorption of Gd³⁺ ions onto the resin phase through exchange reactions.

$$ \left[ {{\text{Cu}}^{{ + {2}}} } \right] + {\text{ H}} - {\text{Gd}} - {\text{Z}} \rightleftharpoons {\text{H}} - {\text{Cu}} - {\text{Z}}^{ - } + \left[ {{\text{Gd}}^{{ + {3}}} } \right] $$

(18)

$$ {\text{H}} - {\text{Cu}} - {\text{Z}}^{ - } + \left[ {{\text{H}}^{ + } } \right] \rightleftharpoons {\text{H}}_{{2}} - {\text{Cu}} - {\text{Z}} $$

(19)

The separation factor, α = 1 + ε, for the Gd isotope pair (for Eq. 17) can be represented as:

$$ \alpha = \frac{{\left[ {\frac{{{}^{X}{\text{Gd}}}}{{{}^{Y}{\text{Gd}}}}} \right]_{{{\text{resin}}}} }}{{\left[ {\frac{{{}^{X}{\text{Gd}}}}{{{}^{Y}{\text{Gd}}}}} \right]_{{{\text{sol}}}} }} $$

(20)

The separation coefficients, denoted as ε, were determined utilizing the equation formulated by Spedding et al. [47] and Kakihana and Kanzaki [48]:

$$ \varepsilon = \sum {\left( {\frac{{q_{{\text{j}}} }}{{Qr_{0} }}} \right)} \left[ {\frac{{r_{{\text{j}}} - r_{0} }}{{1 - r_{0} }}} \right] $$

(21)

where q represents the amount of Gd in the sample volume, Q represents the total capacity of sorbed Gd in the packed column, and r_j and r_o represent the isotopic ratios of the ^LGd/^HGd jth fraction and the feed, respectively.

The concentration profile of Gd within the effluent fractions following a migration length of 10 m is depicted in Fig. 6, accompanied by the corresponding pH values of the effluent, as illustrated in Fig. 7. The clear demarcations of the band observed in Fig. 6 are complemented by the pH alterations, indicating similar displacements at both the leading and trailing boundaries.

Fig. 6

The chromatographic profile of Gd³⁺ ions in the 30.0 cm displacement band

Fig. 7

The pH profile of Gd³⁺ ions in the 30 cm displacement band

The Gd isotopic fractionation values in the Gd band are given in Fig. 8. The calculated separation coefficient values are presented in Table 4.

Fig. 8

The estimated isotopic ratios of Gd (a) Gd_155/158 (b) Gd_157/158 (c) Gd_156/158 (d) Gd_160/158 (e) Gd_155/160 and (f) Gd_157/160 for the 30 cm displacement band

Table 4 Experimentally observed separation coefficients of Gd isotopes with the DOWEX-50×8 resin via displacement chromatography

From Table 4, it is observed that the lighter isotopes, i.e., ¹⁵⁵Gd or ¹⁵⁷Gd, are depleted in the front end of the sample fractions, which verifies that the rear end of the Gd³⁺-band is enriched with lighter isotopes compared to that of natural gadolinium. The separation coefficients, ε × 10⁴, were 0.935, 1.470, 0.382, 2.420, 2.07 and 1.54 for the Gd_155/158, Gd_156/158, Gd_157/158, Gd_160/158 Gd_155/160, and Gd_157/160 Isotope Pairs, respectively. The present calculated ' ε ' values are compared with the earier reported experimental values. The present experimental values are found to be higher compared to the earlier reported values [28, 29, 36] for Gd_157/160 isotopic pair with cation-exchange resins (Table 4).

Conclusion

Batch adsorption studies for gadolinium adsorption were carried out by varying the pH, concentration and temperature of the strong cation exchange resin. The optimum pH for the efficient adsorption of Gd³⁺ ions was found to be 5. The equilibrium time for the maximum adsorption of Gd³⁺ ions was determined to be 60 min. The adsorption of Gd³⁺ ions with the DOWEX-50×8 resin is an exothermic process, as revealed by the negative enthalpy of adsorption. A negative Gibbs free energy indicates the spontaneous nature of the adsorption process. From the thermodynamic study, it is concluded that the adsorption efficiency of Gd³⁺ ions increases with increasing temperature from 30⁰ to 80⁰ °C. The best fit to pseudo-second-order kinetics indicates that the nature of the sorption process is chemisorption. The adsorption of Gd³⁺ on DOWEX-50×8 occurred heterogeneously. Furthermore, from the displacement chromatography experiment conducted for Gd isotope separation using DOWEX-50×8 resin with the CDTA ligand as a complex-forming agent, the displacement band is enriched with lighter and heavier isotopes in the rear and front ends, respectively. The separation coefficients, ε × 10⁴, were 0.935, 1.470, 0.382, 2.420, 2.07 and 1.54 for the Gd_155/158, Gd_156/158, Gd_157/158, Gd_160/158 Gd_155/160, and Gd_157/160 Isotope Pairs, respectively.