Introduction

\(\mathrm{Radon}\) Is well recognized as a major \(\mathrm{source}\) for the cancer of lungs [1,2,3,4,5,6]. Being a gas, the \(\mathrm{radon}\) atoms could \(\mathrm{escape}\) from any surface out to the \(\mathrm{air}\) where they decay to their progeny that may attach to dust particles to create \(\mathrm{radioactive dust}\), which we inhale. Early researches on \(\mathrm{radon}\) were mainly \(\mathrm{concerned}\) about \(\mathrm{mines}\) of uranium, but it was realized later that \(\mathrm{radon}\) levels have to be monitored at all work places and residences, because \(\mathrm{radon}\) is emitted from everything surrounding us; from \(\mathrm{ground}\), \(\mathrm{walls}\), water, etc. With these investigations carried on over the years, many articles have been written that report \(\mathrm{radon}\) \(\mathrm{concentrations}\) at various places of work, homes and schools, at different cities from different countries. It is, however, worthy of mention that the risk of \(\mathrm{radon}\) promoting a lung cancer is not only related to its \(\mathrm{concentration}\) inside the place of concern, but it is also related to how many hours the person stays in that place, and whether they are smokers. Some surveys indicate that smokers could be ten \(\mathrm{times}\) more susceptible to lung cancer than \(\mathrm{non}-\mathrm{smokers}\) [7,8,9,10,11,12,13]. Therefore, in addition to having reports about the \(\mathrm{concentrations}\) of the \(\mathrm{indoor}\) \(\mathrm{radon}\), it is necessary to have deliberate studies on its behavior. This comes only by carrying both theoretical and \(\mathrm{experimental}\) researches on all the relevant elements, e.g. the \(\mathrm{concentration}\) of \(\mathrm{radon}\) in the constructing \(\mathrm{walls}\) of the \(\mathrm{buildings}\) and in the \(\mathrm{soil}\) underneath. Other \(\mathrm{important}\) influencing factors are also the levels of \(\mathrm{radon}\) in the surrounding \(\mathrm{outside}\) \(\mathrm{air}\), the \(\mathrm{radon}\) \(\mathrm{diffusive}\) and \(\mathrm{advective}\) characteristics, different contributors to the \(\mathrm{radon}\) \(\mathrm{indoors}\), and \(\mathrm{temporal}\) changes. These studies can help in finding and developing methods to minimize the exposure of the individuals to \(\mathrm{radon}\).

In this paper, one of the \(\mathrm{important}\) factors that will be studied is the \(\mathrm{time}\) \(\mathrm{variation}\) of the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\). In previous researches, \(\mathrm{measurements}\) on \(\mathrm{indoor}\) \(\mathrm{radon}\) usually focused on \(\mathrm{long}-\mathrm{term}\) \(\mathrm{temporal}\) \(\mathrm{variations}\) [14,15,16,17], while calculations usually assumed a steady state condition [18,19,20]. In this research, however, a theoretical investigation is performed on the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) \(\mathrm{short}-\mathrm{term}\) \(\mathrm{temporal}\) \(\mathrm{variations}\); at top, for one or two days, on an hourly basis. This is \(\mathrm{important}\) for places that have very high \(\mathrm{radon}\) \(\mathrm{concentrations}\), in particular when the residents remain for long \(\mathrm{time}\) periods \(\mathrm{indoors}\), especially in winter with poor \(\mathrm{ventilation}\), or for workers at unventilated \(\mathrm{mines}\) for example. Another remarkable side of the \(\mathrm{model}\) is that, unlike most of the previous theoretical studies, where only some \(\mathrm{sources}\) are considered, this \(\mathrm{model}\) considers all known \(\mathrm{sources}\) of \(\mathrm{indoor}\) \(\mathrm{radon}\) [18,19,20,21]. It additionally provides a prediction of possible existence of \(\mathrm{unknown}\) \(\mathrm{sources}\). Furthermore, as different from previous schemes, this \(\mathrm{model}\) gives the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) in an analytical form, not by numerical calculations [18,19,20,21]. Moreover, the \(\mathrm{model}\), with its \(\mathrm{semi}\) \(\mathrm{empirical}\) feature, is expected to give better description to the \(\mathrm{experimental}\) \(\mathrm{measurements}\).

\(\mathbf{S}\mathbf{o}\mathbf{u}\mathbf{r}\mathbf{c}\mathbf{e}\mathbf{s}\) and \(\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{c}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{s}\) of \(\mathbf{r}\mathbf{a}\mathbf{d}\mathbf{o}\mathbf{n}\)

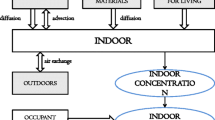
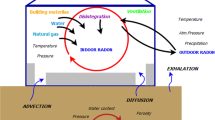
\(\mathrm{Soil}\) Is the most \(\mathrm{important}\) \(\mathrm{radon}\) \(\mathrm{source}\). Annual estimation of the \(\mathrm{radon}\) flow from the \(\mathrm{ground}\) worldwide is nearly \(90\times {10}^{18}\mathrm{Bq}\) [22]. Almost 50% of the \(\mathrm{radon}\) \(\mathrm{indoors}\) is from the \(\mathrm{soil}\) (supposing the \(\mathrm{room}\) is in the \(\mathrm{ground}\) \(\mathrm{floor}\)) [23]. Beside \(\mathrm{soil}\), there are other different \(\mathrm{sources}\) of the \(\mathrm{indoor}\) \(\mathrm{radon}\). These are outlined in Fig. 1. Considerable \(\mathrm{radon}\) levels can be detected in water streams [24]. The higher layers of these waters constantly release \(\mathrm{radon}\) to the surrounding atmosphere by \(\mathrm{volatilization}\) [25]. This indicates that the water lower layers have more \(\mathrm{concentrations}\) of \(\mathrm{radon}\) than the higher ones. Similarly, because of \(\mathrm{radon}\) release to the \(\mathrm{outside}\) \(\mathrm{air}\) by \(\mathrm{advection}\) and \(\mathrm{diffusion}\), bottom parts of the \(\mathrm{soil}\) have higher \(\mathrm{concentrations}\) of \(\mathrm{radon}\) than the top parts [25]. From this argument, it is clear that \(\mathrm{radon}\) \(\mathrm{concentration}\) can differ widely from one place to another. For instance, in \(\mathrm{outside}\) \(\mathrm{air}\) it covers a range of \(1\mathrm{ Bq}.{\mathrm{m}}^{-3}- 100\mathrm{ Bq}.{\mathrm{m}}^{-3}\) [26]. In poorly ventilated residences, it covers a range of \(20\mathrm{ Bq}.{\mathrm{m}}^{-3}- 2000\mathrm{ Bq}.{\mathrm{m}}^{-3}\), with a close range for \(\mathrm{mines}\) with good \(\mathrm{ventilation}\) [26]. \(\mathrm{Mines}\) without good \(\mathrm{ventilation}\) can have a much larger range [26]. Furthermore, \(\mathrm{radon}\) \(\mathrm{concentration}\) can broadly vary with \(\mathrm{different seasons}\) and atmospheric conditions [16, 17].

Fig. 1
figure 1

Outline of the indoor sources

Full size image

\(\mathbf{T}\mathbf{i}\mathbf{m}\mathbf{e}\)rate of \(\mathbf{v}\mathbf{a}\mathbf{r}\mathbf{i}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\) of the \(\mathbf{r}\mathbf{a}\mathbf{d}\mathbf{o}\mathbf{n}\) \(\mathbf{i}\mathbf{n}\mathbf{d}\mathbf{o}\mathbf{o}\mathbf{r}\) \(\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{c}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\)

To have an appropriate evaluation of the inhaled dose of the \(\mathrm{radon}\) \(\mathrm{indoors}\), it is sometimes necessary to observe the exposures closely, which in turn means having convenient methods to estimate the changes of the \(\mathrm{concentrations}\) of the \(\mathrm{radon}\) \(\mathrm{indoors}\) in short terms. Due to several factors, the \(\mathrm{radon}\) \(\mathrm{concentration}\) is a function of \(\mathrm{time}\) and position, and therefore to estimate the indoor exposure, an integration must be performed over the dimensions of the \(\mathrm{room}\) and over the \(\mathrm{time}\) interval of interest. However, this study concerns about the \(\mathrm{temporal}\) \(\mathrm{variation}\), and so, for simplicity, the \(\mathrm{radon}\) \(\mathrm{concentration}\) at a given \(\mathrm{time}\) is assumed to be the same at all positions in the \(\mathrm{room}\), i.e. position independent, and hence the integration over the dimensions will just yield the \(\mathrm{room}\)’s volume. Thus, the exposure to an individual in a \(\mathrm{time}\) interval \(\Delta t={{t}_{2}-t}_{1}\) is taken as \(V\int_{{t_{1} }}^{{t_{2} }} {C_{i} (t)dt}\), where \(V ({\mathrm{m}}^{3})\) is the \(\mathrm{room}\)’s volume and \(C_{i} \left( t \right) \left( {\frac{{{\text{Bq}}}}{{{\text{m}}^{3} }}} \right)\) is the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) at a given \(\mathrm{time}\) \(t (\mathrm{h})\). To have a theoretical evaluation of \({C}_{i}\left(t\right)\), we begin by the \(\mathrm{radon}\) \(\mathrm{mass}\) \(\mathrm{balance}\) form that describes the different \(\mathrm{sources}\) of \(\mathrm{indoor}\) \(\mathrm{radon}\) and its sinks

$${\text{Radon in a room}} = {\text{radon sources}} + {\text{radon sinks}} ,$$
(1)

or

$$\frac{{dC_{i} \left( t \right)}}{dt} = \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{{\text{bm}}}} + \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{S}}} + \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{O}}} + \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{u} + \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{D}}}$$
(2)

where \({\left.\frac{d{C}_{i}(t)}{dt}\right]}_{\mathrm{bm}}\) is from \(\mathrm{building}\) \(\mathrm{materials}\), \({\left.\frac{d{C}_{i}(t)}{dt}\right]}_{\mathrm{S}}\) is from \(\mathrm{soil}\), \({\left.\frac{d{C}_{i}(t)}{dt}\right]}_{\mathrm{O}}\) is due to exchange with the \(\mathrm{outside}\) \(\mathrm{air}\), \({\left.\frac{d{C}_{i}(t)}{dt}\right]}_{u}\) is from \(\mathrm{sources}\) that might be unknown, and \({\left.\frac{d{C}_{i}(t)}{dt}\right]}_{\mathrm{D}}\) is due to \(\mathrm{radon}\) disintegration.

\(\mathrm{Radon}\) release from \(\mathrm{walls}\) adds up to the \(\mathrm{concentration}\) of \(\mathrm{radon}\) inside the \(\mathrm{room}\). In a very short \(\mathrm{time}\) interval, the rate of that addition can be put in the form \(\frac{{S}_{\mathrm{bm}}}{V} {D}_{\mathrm{bm}} \left({C}_{\mathrm{bm}}-{C}_{i}\right)\), where \({S}_{\mathrm{bm}} ({\mathrm{m}}^{2})\) is the \(\mathrm{room}\)’s internal area with \(\mathrm{building}\) \(\mathrm{materials}\), \(D_{{{\text{bm}}}} \left( {\frac{{\text{m}}}{{\text{h}}}} \right)\) is the \(\mathrm{diffusive}\) transfer coefficient through the \(\mathrm{walls}\), and \(C_{{{\text{bm}}}} \left( {\frac{{{\text{Bq}}}}{{{\text{m}}^{3} }}} \right)\) is the \(\mathrm{concentration}\) of \(\mathrm{radon}\) in the \(\mathrm{walls}\) including both the emanated \(\mathrm{radon}\) atoms and the non-emanated ones. On the other hand, in a very short \(\mathrm{time}\) interval, the addition rate to the \(\mathrm{concentration}\) of \(\mathrm{radon}\) inside the \(\mathrm{room}\), by \(\mathrm{radon}\) release from the \(\mathrm{soil}\), can be put in the form \(\frac{{S}_{f}}{V}. {\varphi }_{s}\), where \({S}_{\mathrm{f}} ({\mathrm{m}}^{2})\) is the \(\mathrm{floor}\)’s area, and \(\varphi_{s} \left( {\frac{{{\text{Bq}}}}{{{\text{m}}^{2} {\text{h}}}}} \right)\) is the \(\mathrm{soil}\) \(\mathrm{radon}\) flux to the inside of the \(\mathrm{room}\). This flux, taking place by \(\mathrm{advection}\) and \(\mathrm{diffusion}\), is given by \({\varphi }_{s}={C}_{s} \Delta {P}_{si} A+{D}_{\mathrm{s}}\left({C}_{s}-{C}_{i}\right)\), where \({C}_{\mathrm{s}} \left(\frac{\mathrm{Bq}}{{\mathrm{m}}^{3}}\right)\) is the \(\mathrm{soil}\) \(\mathrm{radon}\) \(\mathrm{concentration}\), \(\Delta {P}_{si} (\mathrm{Pa})\) is the difference in pressure between the inner of the \(\mathrm{room}\) and the \(\mathrm{soil}\), \(A \left(\frac{\mathrm{m}}{\mathrm{h}.\mathrm{Pa}}\right)\) and \({D}_{\mathrm{s}} \left(\frac{\mathrm{m}}{\mathrm{h}}\right)\) are the \(\mathrm{advective}\) and \(\mathrm{diffusive}\) transfer coefficients through the \(\mathrm{soil}\), respectively. Thus [18,19,20,21]

$$\left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{{\text{bm}}}} = \frac{{S_{{{\text{bm}}}} }}{V} D_{{{\text{bm}}}} \left( {C_{{{\text{bm}}}} - C_{i} } \right) ,$$
(3)
$$\left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{S}}} = \frac{{S_{f} }}{V}\left( {C_{s} \Delta P_{si} A + D_{{\text{s}}} \left( {C_{s} - C_{i} } \right)} \right) ,$$
(4)

and hence Eq. (2) becomes

$$\frac{{dC_{i} \left( t \right)}}{dt} = \frac{{S_{{{\text{bm}}}} }}{V}D_{{{\text{bm}}}} \left( {C_{{{\text{bm}}}} - C_{i} } \right) + \frac{{S_{f} }}{V}\left( {C_{s} \Delta P_{si} A + D_{{\text{s}}} \left( {C_{s} - C_{i} } \right)} \right) - \lambda_{{\text{v}}} \left( {C_{i} - C_{o} } \right) + \left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{u} - \lambda C_{i} \left( t \right) ,$$
(5)

where

$$\left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{O}}} = - \lambda_{{\text{v}}} \left( {C_{i} - C_{o} } \right) ,$$
(6)
$$\left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{{\text{D}}} = - \lambda C_{i} \left( t \right) ,$$
(7)

where \({\lambda }_{\mathrm{v}} ({\mathrm{h}}^{-1})\) is the \(\mathrm{ventilation}\) rate, \({C}_{o} \left(\frac{\mathrm{Bq}}{{\mathrm{m}}^{3}}\right)\) is the \(\mathrm{concentration}\) of \(\mathrm{radon}\) in the surrounding outdoor, and \(\lambda ({\mathrm{h}}^{-1})\) is the constant of \(\mathrm{radon}\) decay. In Eq. (6), the exchange with the \(\mathrm{outside}\) \(\mathrm{air}\) is assumed to be due to \(\mathrm{ventilation}\) only, without taking into account the negligible contribution from the leakage processes.

Solution of the \(\mathbf{m}\mathbf{a}\mathbf{s}\mathbf{s}\) \(\mathbf{b}\mathbf{a}\mathbf{l}\mathbf{a}\mathbf{n}\mathbf{c}\mathbf{e}\) equation

The \(\mathrm{mass}\) \(\mathrm{balance}\) equation in its form as given by Eq. (5) has a number of unspecified functions. This makes it hard to attain its solution. To make it less complicated, and put it in a more convenient form, we approximate the involved functions by making use of some of the data from relevant \(\mathrm{measurements}\) [14,15,16,17, 27,28,29]. We may develop the formulas

$$C_{{{\text{bm}}}} = a_{{{\text{bm}}}} C_{i} ,$$
(8)
$$C_{s} = a_{s} C_{i} ,$$
(9)
$$C_{o} = a_{o} C_{i} ,$$
(10)

where \({a}_{\mathrm{bm}}\) is a \(\mathrm{parameter}\) that can relate the \(\mathrm{concentration}\) of \(\mathrm{radon}\) inside the \(\mathrm{building}\) \(\mathrm{material}\) to that of the \(\mathrm{indoor}\) \(\mathrm{air}\), \({a}_{s}\) is a \(\mathrm{parameter}\) that can relate the \(\mathrm{concentration}\) of \(\mathrm{radon}\) in the \(\mathrm{soil}\) to that of the \(\mathrm{indoor}\) \(\mathrm{air}\), and \({a}_{o}\) is a \(\mathrm{parameter}\) that can relate the \(\mathrm{concentration}\) of \(\mathrm{radon}\) in the outdoor \(\mathrm{air}\) to that of the \(\mathrm{indoor}\) \(\mathrm{air}\). All these \(\mathrm{parameters}\) are dimensionless and they are to be evaluated from the \(\mathrm{experimental}\) observations.

For not long durations, the term \({\left.\frac{d{C}_{i}\left(t\right)}{dt}\right]}_{u}\) can be assumed to be almost constant

$$\left. {\frac{{dC_{i} \left( t \right)}}{dt}} \right]_{u} \cong {\text{U }}.{ }$$
(11)

Substituting Eqs. (8–11) in Eq. (5)

$$\frac{{dC_{i} }}{dt} = \frac{{S_{{{\text{bm}}}} }}{V}D_{{{\text{bm}}}} \left( {a_{{{\text{bm}}}} - 1} \right)C_{i} + \frac{{S_{f} }}{V}\left( {a_{s} \Delta P_{si} A + D_{{\text{s}}} \left( {a_{s} - 1} \right)} \right)C_{i} - \lambda_{{\text{v}}} \left( {1 - a_{o} } \right)C_{i} + {\text{U}} - \lambda C_{i} ,$$
(12)

or

$$\frac{{dC_{i} }}{dt} = \left( {{\text{b}}_{{{\text{bm}}}} + {\text{b}}_{s} - {\text{b}}_{{\text{o}}} - \lambda } \right)C_{i} + {\text{U}} ,$$
(13)

where

$${\text{b}}_{{{\text{bm}}}} = \frac{{S_{{{\text{bm}}}} }}{V}D_{{{\text{bm}}}} \left( {a_{{{\text{bm}}}} - 1} \right) ,$$
(14)
$${\text{b}}_{{\text{s}}} = \frac{{S_{f} }}{V}\left( {a_{s} \Delta P_{si} A + D_{{\text{s}}} \left( {a_{s} - 1} \right)} \right) ,$$
(15)
$${\text{b}}_{{\text{o}}} = \lambda_{{\text{v}}} \left( {1 - a_{o} } \right) .$$
(16)

Putting

$$q = {\text{b}}_{{{\text{bm}}}} + {\text{b}}_{s} - {\text{b}}_{{\text{o}}} - \lambda ,$$
(17)

Equation (13) becomes

$$\frac{{dC_{i} }}{dt} = qC_{i} + {\text{U}} ,$$
(18)

which has the solution

$$C_{i} \left( t \right) = - \frac{{\text{U}}}{q} + we^{qt} .$$
(19)

If \({C}_{i}\left(t\right)\) has an initial value \({C}_{i}\left(0\right)\) at \(t=0\), then

$$w = C_{i} \left( 0 \right) + \frac{{\text{U}}}{q} ,$$
(20)

and therefore

$$C_{i} \left( t \right) = \frac{{\text{U}}}{q}\left( {e^{qt} - 1} \right) + C_{i} \left( 0 \right)e^{qt} .$$
(21)

Applying the \(\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}\) and discussing the \(\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{s}\)

We start by estimating the \(\mathrm{parameters}\) \({a}_{\mathrm{bm}}\), \({a}_{s}\) and \({a}_{o}\) of Eqs. (8–10). They are dimensionless, with the evaluations

$$a_{{{\text{bm}}}} = 229 ,$$
(22)
$$a_{s} = 100 ,$$
(23)
$$a_{o} = 0.7$$
(24)

Eqs. (22) and (8) develop from using the formula [27]

$$C_{i}^{{{\text{bm}}}} = \frac{{E_{s} .S_{{{\text{bm}}}} }}{{\lambda_{{\text{v}}} .V}} ,$$
(25)

together with Fig. 2. \({C}_{i}^{\mathrm{bm}}\) is the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) occurring by \(\mathrm{radon}\) release from the constructing \(\mathrm{material}\) that has an observed areal release rate \({E}_{s}\) (\(\frac{\mathrm{Bq}}{{\mathrm{m}}^{2}\mathrm{ h}}\)). The plot of Fig. 2 is a relation between \({E}_{s}\) and \(\mathrm{concentration}\) of \(\mathrm{radon}\) in a \(\mathrm{material}\) [28]. 34 samples were analyzed, where \({E}_{s}\) \(\mathrm{and}\) \(\mathrm{concentration}\) \(\mathrm{of}\) \(\mathrm{radon}\) \(\mathrm{were}\) \(\mathrm{measured}\) \(\mathrm{by}\) \(\mathrm{applying}\) \(\mathrm{the}\) \(\mathrm{sealed}\) \(\mathrm{can}\) \(\mathrm{technique}\) [28]. A linear correlation between \({E}_{s}\) and \(\mathrm{concentration}\) of \(\mathrm{radon}\) was developed, with correlation coefficient 0.95. The \(\mathrm{straight}\)-\(\mathrm{line}\) used to describe the data is

$$E_{s} = 0.433C_{{{\text{bm}}}} .$$
(26)
Fig. 2
figure 2

Radon areal release rate from a material in relation to its radon concentration, according to the measurements in ref [28]

Full size image

In accordance with ref [23], constructing \(\mathrm{materials}\) shares by \(\sim 20\%\) of the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentr}\), i.e. \(C_{i}^{{{\text{bm}}}} \approx 0.2C_{i}\). Therefore, using Eqs. (25) and (26)

$$C_{i}^{{{\text{bm}}}} \approx 0.2C_{i} = \frac{{0.433 \times 10^{ - 3} C_{{{\text{bm}}}} S_{{{\text{bm}}}} }}{{\lambda_{{\text{v}}} V}} ,$$
(27)

or

$$C_{{{\text{bm}}}} = \frac{{0.2 \lambda_{{\text{v}}} V}}{{0.433 \times 10^{ - 3} S_{{{\text{bm}}}} }}C_{i} ,$$
(28)

which gives Eqs. (8) and (22), where

$$a_{{{\text{bm}}}} = \frac{{0.2 \lambda_{{\text{v}}} V}}{{0.433 \times 10^{ - 3} S_{{{\text{bm}}}} }} .$$
(29)

Eqs. (23) and (9) develop from Fig. 3 that relates the \(\mathrm{concentration}\) of \(\mathrm{radon}\) \(\mathrm{indoors}\) to that in \(\mathrm{soil}\), for \(\mathrm{ground}\)-\(\mathrm{floor}\) \(\mathrm{rooms}\) [29]. The \(\mathrm{radon}\) \(\mathrm{concentration}\) \(\mathrm{indoor}\) \(\mathrm{measurements}\) were made by the \(\mathrm{alpha}\) \(\mathrm{scintillation}\) \(\mathrm{cells}\) \(\mathrm{ASC}\) \(\mathrm{and}\) \(\mathrm{the}\) \(\mathrm{portable}\) \(\mathrm{AlphaGuard}\) \(\mathrm{radon}\) \(\mathrm{monitor}\). The \(\mathrm{concentrations}\) of \(\mathrm{radon}\) in \(\mathrm{soil}\) were made by the \(\mathrm{EDA}-\mathrm{ASC}\) and the \(\mathrm{portable}\) \(\mathrm{RDA}-200\) detector [29]. 53 samples were analyzed. From Fig. 3, one can see that most of the data are gathered at small \(\mathrm{concentrations}\) of the \(\mathrm{indoor}\) \(\mathrm{radon}\). Therefore, in our \(\mathrm{model}\), the dots are described by the following \(\mathrm{straight}\)-\(\mathrm{line}\) relation

$$C_{i} = 0.01 C_{s} ,$$
(30)

or

$$C_{s} = 100 C_{i} ,$$
(31)

which means that \({a}_{s}\) has the value 100. Eqs. (24) and (10) develop from taking the average of \(\mathrm{concentrations}\) of \(\mathrm{radon}\) outdoors recorded at various seasons in relation to that of \(\mathrm{indoors}\) [15,16,17]. Better evaluation of \({a}_{o}\) could be obtained by taking into account only the season relevant to the \(\mathrm{radon}\) \(\mathrm{indoors}\) in study.

Fig. 3
figure 3

Relating the concentration of radon indoors to that in soil, for ground-floor rooms, according to the measurements in ref [29]

Full size image

Beside \({a}_{\mathrm{bm}}\), \({a}_{s}\) and \({a}_{o}\), there are some \(\mathrm{parameters}\) that describe the studied \(\mathrm{room}\). Because the values of these \(\mathrm{parameters}\) are not provided with the data of the \(\mathrm{measured}\) \(\mathrm{indoor}\) \(\mathrm{concentrations}\) [30], they are given typical numbers. The length, width and height of the \(\mathrm{room}\) are taken as \(5 \mathrm{m}, 4 \mathrm{m} \mathrm{and} 2.8 \mathrm{m}\), respectively. The volume of the \(\mathrm{room}\) is therefore \(56 {\mathrm{m}}^{3}\), with \(\frac{{S}_{\mathrm{bm}}}{V}\approx 1.6 {\mathrm{m}}^{-1}\). The rate of \(\mathrm{ventilation}\) and the \(\mathrm{soil}\)-\(\mathrm{indoor}\) difference in pressure are assumed to be \({\lambda }_{\mathrm{v}}=0.8 {\mathrm{h}}^{-1}\) and \(\Delta {P}_{si}=4 \mathrm{Pa}\).

All the needed \(\mathrm{parameters}\) to calculate \({C}_{i}\left(t\right)\) are now set. Only left, to be evaluated from fitting Eq. (21) to the \(\mathrm{measured}\) \(\mathrm{concentrations}\), are the \(\mathrm{diffusive}\) transfer coefficient through the \(\mathrm{walls}\) \({D}_{\mathrm{bm}}\), the share from unknown-\(\mathrm{sources}\) \(U\), the \(\mathrm{advective}\) and \(\mathrm{diffusive}\) transfer coefficients through the \(\mathrm{soil}\), \(A\) and \({D}_{\mathrm{s}}\), respectively.

Figure 4 shows a set of \(\mathrm{experimental}\) data [30] for the \(\mathrm{variation}\) of the \(\mathrm{indoor}\) \(\mathrm{radon}\) \(\mathrm{concentration}\) over a couple of days. The \(\mathrm{measurements}\) were performed by the \(\mathrm{PQ}2000\mathrm{PRO}\) \(\mathrm{AlphaGuard}\). 33 samples were analyzed. To fit Eq. (21) to the \(\mathrm{measurements}\) of ref [30], the \({D}_{\mathrm{bm}}\), \(A\), \({D}_{\mathrm{s}}\), and \(\mathrm{U}\) \(\mathrm{parameters}\) are found to be

$$D_{{{\text{bm}}}} \approx 2.06 \times 10^{ - 6} \frac{{\text{m}}}{{\text{h}}} ,$$
(32)
$$A \approx 1.04 \times 10^{ - 3} \frac{{\text{m}}}{{{\text{h}}.{\text{Pa}}}} ,$$
(33)
$$D_{{\text{s}}} \approx 0.91 \times 10^{ - 4} \frac{{\text{m}}}{{\text{h}}} ,$$
(34)
$${\text{U }} \approx { }30.61{ }\frac{{{\text{Bq}}}}{{{\text{m}}^{3} .{\text{h}}}} .$$
(35)
Fig. 4
figure 4

Results of the model for estimating the radon indoor concentration as compared to the data of ref [30]

Full size image

These are significant \(\mathrm{parameters}\) for describing the \(\mathrm{indoor}\) \(\mathrm{radon}\)-entry. The good fit demonstrated in Fig. 4 implies the \(\mathrm{model}\)’s efficacy in giving a description of the \(\mathrm{temporal}\) change of \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\). However, the \(\mathrm{time}\) span during which the \(\mathrm{model}\) is applicable is not clearly known. Trying to fit Eq. (21) to less data, or more, than those in Fig. 4, causes a slight change in the resulting \(\mathrm{parameters}\). Therefore, in order to have a better argument, several sets of data should be involved to test the range of applicability of the adopted approximations that constrain the \(\mathrm{time}\) validity of the \(\mathrm{model}\) (Eqs. 10 and 11). For the \(\mathrm{time}\) being, however, this cannot be carried on as the available \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) data are usually from long term observations (not on an hourly basis).

It is \(\mathrm{important}\) to remark two points; first, the values of the \(\mathrm{parameters}\) in Eqs. (22–24) are not exactly unique, but can have some ranges. However, it has been tested that, within these ranges, the \(\mathrm{results}\) of Eqs. (32–35) and Fig. 4 are not so sensitive, given the uncertainties in the \(\mathrm{experimental}\) data. Second, the \(\mathrm{results}\) of Fig. 4 and Eqs. (32–35) are not just about a transition from an initial \(\mathrm{radon}\) \(\mathrm{concentration}\) to a steady state final one, but it is about how the transition takes place.

The \(\mathrm{semi}\) \(\mathrm{empirical}\) side of the presented \(\mathrm{model}\) gives it the advantage of being able to be refined and updated when further data are provided. This allows the improvement of the underlying approximations and assumptions, and hence the \(\mathrm{model}\) \(\mathrm{results}\). Moreover, it is \(\mathrm{important}\) to know the exact conditions and descriptions of the \(\mathrm{room}\) under study, in order to have outcomes that are more precise. Additionally, as suggested by ref [31], the \(\mathrm{model}\) can be polished further by putting in the scheme the \(\mathrm{radon}\) areal release rate \({E}_{s}\) as observed from the constructed \(\mathrm{walls}\) in the \(\mathrm{room}\) instead of using the one \(\mathrm{measured}\) from a sample of the constructing \(\mathrm{material}\).

Conclusion

Time \(\mathrm{variation}\) of the \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\) has been studied by the application of the \(\mathrm{mass}\) \(\mathrm{balance}\) equation on the \(\mathrm{radon}\) \(\mathrm{indoors}\). Each \(\mathrm{source}\) and sink of \(\mathrm{radon}\) was considered. The resultant equation was solved after simplifying its form by involving some approximate relations that were developed from \(\mathrm{empirical}\) observations. An analytical formula was reached that well described the data of \(\mathrm{radon}\) \(\mathrm{indoor}\) \(\mathrm{concentration}\). As a result, some significant \(\mathrm{parameters}\) that describe the entrance of \(\mathrm{radon}\) into \(\mathrm{buildings}\) were predicted. It is one of the merits of this \(\mathrm{model}\) that it can predict \(\mathrm{radon}\) \(\mathrm{diffusion}\) coefficients without going through their dependence on the structural specifications of the \(\mathrm{soil}\) and the \(\mathrm{building}\) \(\mathrm{material}\), like porosity, water saturation fraction, etc. The scheme is designed for describing not long \(\mathrm{time}\)-span, which is mostly around two days. The \(\mathrm{model}\) has the \(\mathrm{important}\) advantage that it can easily be upgraded any \(\mathrm{time}\), once new \(\mathrm{empirical}\) data are available.

In spite of the encouraging \(\mathrm{results}\), the \(\mathrm{model}\)’s outcomes still require a comparison to be made to some \(\mathrm{measurements}\). In a prospective future work, the \(\mathrm{model}\) applicability will be tried to be extended by applying it successively on consecutive short periods to describe a long period overall. Meanwhile, if suitable \(\mathrm{measurements}\) are to be available, a comparison will be made against the \(\mathrm{results}\) expected by the \(\mathrm{model}\).