A new measurement of the ¹²²Sb half-life

Abstract

Following significant discrepancies observed when decay-correcting ¹²²Sb γ-peak count rates to a reference time, we looked at the literature supporting the presently recommended 2.7238(2) d (1σ) ¹²²Sb half-life value as the source of these discrepancies. Investigation revealed that the value was derived from an inconsistent dataset and was published without reporting details of the experiment nor the uncertainty budget. In this work we performed a new measurement of the ¹²²Sb half-life by measuring the ¹²²Sb decay of neutron-activated antimony samples using state-of-the-art γ-detection systems characterized in terms of efficiency drift and random pulse pile-up. The measurement was carried out in two different laboratories with the same method. The resulting 2.69454(39) d  and 2.69388(30) d (1σ) ¹²²Sb half-life values are in agreement at the evaluated 10^–4 relative combined standard uncertainty level but are significantly lower (1.07% and 1.10% lower, respectively) than the preexisting recommended value.

Introduction

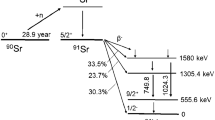
Antimony has two stable isotopes (¹²¹Sb and ¹²³Sb) that can be detected by neutron activation via nuclear reactions ¹²¹Sb(n,γ)¹²²Sb and ¹²³Sb(n,γ)¹²⁴Sb and quantified by counting γ-photons emitted by ¹²²Sb and ¹²⁴Sb at the interference-free energies 564.2 keV and 602.7 keV, respectively. Preliminary measurements carried out to test the possibility of determining the ¹²¹Sb/¹²³Sb ratio at 0.1% relative uncertainty level unexpectedly showed a linear negative drift of 2% over about 200 h for the ¹²²Sb 564.2 keV γ-peak count rate after correction for decay. Notably, the stability of the decay corrected ¹²⁴Sb 602.7 keV γ-peak count rate obtained with the same data did not show the same drift of the detection system. This experimental evidence suggested a potential bias affecting the presently recommended 2.7238(2) d ¹²²Sb half-life, t_1/2 [1], adopted for the decay correction. Here and hereafter uncertainties in parentheses are standard uncertainties (k = 1). A literature review revealed that the recommended t_1/2(¹²²Sb) value is based on the most recent result of an inconsistent dataset published in 1990 [2] without reporting details on the experiment nor the uncertainty budget which are compulsory to support the claimed 10^–4 relative standard uncertainty level [3].

In this work we aimed to refine the knowledge of the t_1/2(¹²²Sb). We repeated the measurement of the ¹²²Sb half-life by taking advantage of state-of-the-art digital signal processing γ-spectrometers coupled to high-purity germanium detectors characterized in terms of efficiency drift and random pulse pile-up. This paper reports the adopted measurement method and the experiments carried out to measure the t_1/2(¹²²Sb). The uncertainty budget is included and the result is compared with the published values.

Measurement method

The approach used to measure the t_1/2(¹²²Sb) is based on a method previously applied for the determination of the t_1/2(³¹Si) [4] and consists of repeated observations of the exponential decay of the activity performed via γ-spectrometry measurements. A single observation is a sequence of repeated count rate measurements performed by recording consecutive γ-spectra of neutron-activated samples. The (full-peak) ¹²²Sb γ-photon count rate at the beginning of the ith count of the jth sequence,$C_{ij}$, starting at t_dij is computed using the formula (1) found in [4] adjusted to include the effect of a linear drift of the γ-photon detection efficiency:

$$C_{ij} \left( {t_{dij} } \right) = \frac{{\lambda n_{ij} }}{{\left( {1 - e^{{ - \lambda t_{c ij} }} } \right) + \alpha \lambda^{ - 1} \left[ {1 - e^{{ - \lambda t_{c ij} }} \left( {1 + \lambda t_{c ij} } \right)} \right]}}\delta_{ij} f_{ij} ,$$

(1)

where $\lambda = \ln \left( 2 \right)/t_{1/2}$ is the ¹²²Sb decay constant, $n_{ij}$ is the full-peak net count, t_dij is the decay time, t_cij is the (real) counting time, $\alpha$ is the (constant) relative variation of efficiency per unit time, $\delta_{ij}$ and $f_{ij}$ are the dead time and pile-up correction factors, respectively. Specifically, $\delta_{ij} = t_{{{\text{c}}ij}} /\left( {t_{{{\text{c}}ij}} - t_{{{\text{dead }}ij}} } \right)$ and $f_{ij} = e^{{\mu \left( {t_{{{\text{dead }}ij}} /t_{{{\text{c}}ij}} } \right)}}$, where $t_{{{\text{dead }}ij}}$ is the dead time and $\mu$ is the pile-up constant.

If the activated sample is fixed at steady distance from the detector end-cap during the recording of a sequence, the γ-photon count rate is proportional to the activity via the γ-emission yield multiplied by the γ-photon efficiency of the detection system. Accordingly, the nonlinear equation modeling $C_{ij}$ versus t_dij is

$$C_{ij} \left( {t_{dij} } \right) = \left[ {1 + \alpha \left( { t_{dij} - t_{d1j} } \right)} \right] C_{j} \left( {t_{d1j} } \right) e^{{ - \lambda \left( { t_{dij} - t_{d1j} } \right)}} + \varepsilon_{ij} ,$$

(2)

where $C_{j} \left( {t_{d1j} } \right)$ is the expected value of the count rate at the starting time of the first count of the jth sequence, $t_{d1j}$, and $\varepsilon_{ij}$ is the error term.

If the detector is in normal working conditions $\alpha \ll 1$, and the experiments are carried out to assure $t_{{{\text{c}} ij}} < t_{1/2}$ and $\varepsilon_{r ij} = {{\varepsilon_{ij} } \mathord{\left/ {\vphantom {{\varepsilon_{ij} } {C_{ij} \left( {t_{dij} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{ij} \left( {t_{dij} } \right)}} \ll 1$, i.e. the error term normalized to $C_{ij} \left( {t_{dij} } \right)$, Eq. (1) simplifies to

$$C_{ij} \left( {t_{dij} } \right) = \frac{{\lambda n_{ij} }}{{\left( {1 - e^{{ - \lambda t_{c ij} }} } \right)}}\delta_{ij} f_{ij}$$

(3)

and Eq. (2) can be adjusted to get the linear equation

$$Y_{ij}^{\lambda } = m_{j}^{\lambda } - \lambda \left( { t_{dij} - t_{d1j} } \right) + \varepsilon_{r ij} ,$$

(4)

where $Y_{ij}^{\lambda } = \ln \left( {{{C_{ij} \left( {t_{dij} } \right)} \mathord{\left/ {\vphantom {{C_{ij} \left( {t_{dij} } \right)} {C_{1j} \left( {t_{d1j} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{1j} \left( {t_{d1j} } \right)}}{1 \mathord{\left/ {\vphantom {1 {\left[ {1 + \alpha \left( { t_{dij} - t_{d1j} } \right)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {1 + \alpha \left( { t_{dij} - t_{d1j} } \right)} \right]}}} \right)$ is the natural logarithm of the count rate $C_{ij} \left( {t_{dij} } \right)$ normalized to $C_{1j} \left( {t_{d1j} } \right)$ and corrected for efficiency drift, and $m_{j}^{\lambda } = \ln \left( {{{C_{j} \left( {t_{d1j} } \right)} \mathord{\left/ {\vphantom {{C_{j} \left( {t_{d1j} } \right)} {C_{1j} \left( {t_{d1j} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{1j} \left( {t_{d1j} } \right)}}} \right)$ is the natural logarithm of the count rate $C_{j} \left( {t_{d1j} } \right)$ normalized to $C_{1j} \left( {t_{d1j} } \right)$.

The t_1/2(¹²²Sb) and $C_{j} \left( {t_{d1j} } \right)$ values are obtained from the (common) slope, $\lambda$, and intercepts, $m_{j}^{\lambda }$, respectively, of the j straight lines fitted to $Y_{ij}^{\lambda }$ versus $t_{dij} - t_{d1j}$ data. Since $C_{ij} \left( {t_{dij} } \right)$ and $C_{1j} \left( {t_{d1j} } \right)$ depends on $\lambda$ via (3), the final $\lambda$ value is obtained iteratively until convergence. It is worth noting that $\varepsilon_{{{\text{r}} ij}}$ corresponds to the relative error of $n_{ij}$, which in turn depends on counting statistics. As a result, the standard deviation of $\varepsilon_{{{\text{r}} ij}}$ can be kept constant (and small) by properly increasing t_cij during the activity decay. This removes the need to assign varying weights to the fitted $Y_{ij}^{\lambda }$ data when γ-spectra are recorded at constant t_cij [5] and allows performing an unweighted fit.

While $n_{ij}$, $t_{{{\text{c}} ij}}$, $t_{{{\text{dead }}ij}}$, $t_{dij}$ and $t_{d1j}$ values adopted in Eqs. (3) and (4) are determined during the observation of the ¹²²Sb decay, $\alpha$ and $\mu$ are parameters previously measured during the characterization of the detection system carried out by repeated count rate measurements of a long-lived γ-photon source.

Experimental

We carried out two separated experiments, the first at the Istituto Nazionale di Ricerca Metrologica (INRIM) and the latter at the National Institute of Standards and Technology (NIST), using detection systems consisting of a coaxial germanium detector connected to a digital multichannel analyzer.

The ORTEC GEM 50P4-83¹ (relative efficiency 50%, resolution 1.90 keV FWHM at 1332 keV) detector was used at INRIM and the ORTEC GEM 40P4-S (relative efficiency 51%, resolution 1.72 keV FWHM at 1332 keV) detector was used at NIST. In both cases, the ORTEC DSPEC 502 was adopted as the digital multichannel analyzer.

The end-cap of the GEM 50P4-83 was placed inside a low-background graded lead shield located in a room of an underground laboratory with temperature controlled at 23 °C whereas the GEM 40P4-S was placed inside a low-background graded lead shield located in a room of a shielded laboratory with temperature controlled at 20 °C. In these shielding conditions, the (total) input pulse rate due to background was limited to below 15 pulses per second for both detectors. The rise time and flat top digital filter shaping-time constants of the multichannel analyzers were set to 12 μs and 1 μs, respectively, at both INRIM and NIST. The acquisitions were performed in extended live-time correction mode according to the Gedcke-Hale method to compensate for the loss of counts due processing (dead) time, with pulse pile-up rejection in automatic set threshold.

Prior to performing the experiments, we tested the long-term temporal stability of the γ-photon efficiency of the detection systems by recording a single (uninterrupted) sequence of successive counts of the 661.8 keV γ-photons emitted by a ¹³⁷Cs source kept at a fixed position from the detector end-cap. Additionally, the pile-up constant was measured using the moving source method [6] by recording a number of sequences of successive counts of the γ-photons emitted by the ¹³⁷Cs source always kept at a fixed position. A supplementary moving ¹⁵²Eu source was located at different distances from the detector end-cap to change the rate of input pulses at the gate of the detection systems. Along with the sequence collected with the ¹³⁷Cs source alone, we collected 6 and 3 sequences with the ¹⁵²Eu source located in 6 and 3 different positions for the GEM 50P4-83 and GEM 40P4-S, respectively.

It is worth noting that the 661.8 keV ¹³⁷Cs γ-emission used to measure the pile-up constant is close to the 564.2 keV ¹²²Sb γ-emission adopted to measure the t_1/2(¹²²Sb). This makes the second order effects due to the γ-energy dependence of the pile-up constant negligible [7]. In addition, the use of ¹⁵²Eu as a moving source is a common choice because the shape of its spectrum looks like the neutron-activated materials used in this study. Specifically, the ¹⁵²Eu spectrum shows eight main and fifteen minor γ-emissions within the range 122–1458 keV, which is to some extent similar to the seven main and ten minor γ-emissions within the range 564–2090 keV of a neutron-activated antimony sample.

The measurement of the t_1/2(¹²²Sb) was carried out by recording counts of the ¹²²Sb 564.2 keV γ-photons emitted from two different high-purity antimony samples after neutron activation. At INRIM, two 1 mg samples were prepared by pipetting and drying in five subsequent steps 1 mL of a 1000 µg mL⁻¹ Sb solution (99.9999% purity) on filter papers placed into polyethylene vials. The two samples were irradiated and the activity decay measured. Each neutron irradiation lasted 1 h and was carried out at a thermal neutron flux of about 6 × 10¹² cm⁻² s⁻¹ in the central thimble of the 250 kW TRIGA Mark II reactor operated by the University of Pavia. After activation, each sample was fixed and counted at about 20 cm from the end cap of the detector.

At NIST, two 50 mg samples of high-purity (99.999%) Sb in metal shot form deposited as-is into polyethylene vials were used. Each neutron irradiation lasted 2 min and was carried out at a thermal neutron flux of about 2 × 10¹³ cm⁻² s⁻¹ in the RT-2 irradiation position at the NIST Center for Neutron Research (NCNR). After activation, each sample was fixed and counted at approximately 20 cm from the end cap of the detector.

Both at INRIM and NIST, the counting time window was adjusted on line by the acquisition software to achieve a 0.1% relative standard uncertainty due to counting statistics of the ¹³⁷Cs 661.8 keV γ-peak net count in the stability and pile-up measurements and of the ¹²²Sb 564.2 keV γ-peak net count in the t_1/2(¹²²Sb) measurements. In details, the software performs repeated fits of the γ-peak to evaluate the uncertainty of the net count and stops the acquisition when the target 0.1% relative uncertainty is reached.

Results and discussion

The Hyperlab software [8] was used to process the collected spectra and obtain the full-peak net count of the ¹³⁷Cs 661.8 keV and ¹²²Sb 564.2 keV γ-emission. The fitting algorithm evaluates also the net count uncertainty based on Poisson statistics, $\sigma_{{\text{P}}} \left( {n_{ij} } \right)$.

Stability and pile-up of the detection systems

The stability and pile-up constant of the detection systems was checked and measured, respectively, by analysing the γ-spectra collected during the sequences of counts of the ¹³⁷Cs source. The sequences performed to check the stability of the GEM 50P4-83 and GEM 40P4-S consisted of 74 and 93 counts per sequence, N_c, respectively, collected in an observation time of 480 h and 470 h. Both the detection systems worked with a 1.4% relative dead time.

The equation adopted to determine the (constant) relative variation of efficiency per unit time, $\alpha$, is obtained by adjusting Eq. (2) to

$$Y_{i1}^{\alpha } = m_{1}^{\alpha } + \tilde{\alpha }\left( { t_{di1} - t_{d11} } \right) + \varepsilon_{r i1} ,$$

(5)

where $Y_{i1}^{\alpha } = {{C_{i1} \left( {t_{di1} } \right)} \mathord{\left/ {\vphantom {{C_{i1} \left( {t_{di1} } \right)} {C_{11} \left( {t_{d11} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{11} \left( {t_{d11} } \right)}}{1 \mathord{\left/ {\vphantom {1 {e^{{ - \lambda \left( { t_{di1} - t_{d11} } \right)}} }}} \right. \kern-\nulldelimiterspace} {e^{{ - \lambda \left( { t_{di1} - t_{d11} } \right)}} }}$ is the count rate $C_{i1} \left( {t_{di1} } \right)$ normalized to $C_{11} \left( {t_{d11} } \right)$ and corrected for decay, $m_{1}^{\alpha } = {{C_{1} \left( {t_{d11} } \right)} \mathord{\left/ {\vphantom {{C_{1} \left( {t_{d11} } \right)} {C_{11} \left( {t_{d11} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{11} \left( {t_{d11} } \right)}}$ is the count rate $C_{1} \left( {t_{d11} } \right)$ normalized to $C_{11} \left( {t_{d11} } \right)$, $\tilde{\alpha } = \alpha m_{1}^{\alpha }$ and $\varepsilon_{r i1} = {{\varepsilon_{i1} } \mathord{\left/ {\vphantom {{\varepsilon_{i1} } {C_{i1} \left( {t_{di1} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{i1} \left( {t_{di1} } \right)}}$ is the error term normalized to $C_{i1} \left( {t_{di1} } \right)$. In this case, $\lambda$ is the ¹³⁷Cs decay constant, j = 1 and i = 1, 2,…, N_c (number of counts per sequence). The $C_{i1} \left( {t_{di1} } \right)$ and $C_{11} \left( {t_{d11} } \right)$ values are calculated using Eq. (3) by substituting for convenience $f_{i1}$ = $f_{11}$ = 1, i.e.$\mu$ = 0.

The $Y_{i1}^{\alpha }$ versus $t_{{{\text{d}}i1}} - t_{{{\text{d}}11}}$ values for the GEM 50P4-83 and GEM 40P4-S are plotted in Fig. 1a and b, respectively. The expected 0.1% relative standard deviation of $Y_{i1}^{\alpha }$, due to counting statistics, is evaluated by $\sigma_{{\text{P}}} \left( {n_{i1} } \right)/n_{i1}$.

Fig. 1

The $Y_{i1}^{\alpha }$ versus $t_{di1} - t_{d11}$ values and the fitted straight line obtained during the stability test of the GEM50P4-83 (a) and GEM 40P4-S (b). Error bars indicate a 95% confidence interval due to counting statistics

The $\alpha$ value is calculated from the slope, $\tilde{\alpha }$, and intercept, $m_{1}^{\alpha }$, of the straight line fitted to $Y_{i1}^{\alpha }$ versus $t_{di1} - t_{d11}$ data. Since the rate of input pulses at the gate of the detection systems is constant during the stability measurement, outcomes are independent of the $\mu$ value.

The resulting $\alpha$ values for the GEM 50P4-83 and GEM 40P4-S were 88(80) × 10^–8 h⁻¹ and 91(66) × 10^–8 h⁻¹, respectively. The quoted uncertainties are due to fitting. In addition, experimental standard deviations of $Y_{i1}^{\alpha }$ are 1.0 × 10^–3 and 0.9 × 10^–3, in agreement with the expected 0.1% relative standard deviations of the ¹³⁷Cs 661.8 keV γ-peak net count due to counting statistics. Accordingly, both the detection systems are considered stable, i.e. $\alpha$ = 0 h⁻¹ within the quoted 10^–7 h⁻¹ level uncertainties, and in perfect working conditions.

The pile-up constant was determined using a sequence of 7 measurements on the GEM 50P4-83 and 4 measurements on the GEM 40P4-S. The GEM 50P4-83 operated at relative dead times of 8%, 12%, 15%, 19%, 22%, 25% and 29%, and the GEM 40P4-S operated at relative dead times of 1%, 11%, 20% and 30%. For the GEM 50P4-83 measurements, the number of counts per sequence was 67 for the 1st, 3rd and 4th sequence, 64 for the 2nd and 5th sequence, 60 for the 6th sequence and 61 for the 7th sequence. For the GEM 40P4-S, the number of counts per sequence was 25 for the 1st sequence, 15 for the 2nd sequence and 10 each for the 3rd and 4th sequence.

The following equation is adopted to measure the pile-up constant and is obtained by adjusting Eq. (2) after replacing $C_{ij} \left( {t_{dij} } \right) = C_{ij}^{\mu } \left( {t_{dij} } \right) e^{{\mu \left( {t_{{{\text{dead}} ij}} /t_{cij} } \right)}}$:

$$Y_{j}^{\mu } = m_{j}^{\mu } - \mu t_{{r {\text{dead }}j}} + \varepsilon_{rj} ,$$

(6)

where $Y_{j}^{\mu } { = }\left. {{\text{ln}}\left( {{{C_{ij}^{\mu } \left( {t_{dij} } \right)} \mathord{\left/ {\vphantom {{C_{ij}^{\mu } \left( {t_{dij} } \right)} {C_{11}^{\mu } \left( {t_{d11} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{11}^{\mu } \left( {t_{d11} } \right)}}{1 \mathord{\left/ {\vphantom {1 {\left[ {1 + \alpha \left( { t_{dij} - t_{d11} } \right)} \right] e^{{ - \lambda \left( { t_{dij} - t_{d11} } \right)}} }}} \right. \kern-\nulldelimiterspace} {\left[ {1 + \alpha \left( { t_{dij} - t_{d11} } \right)} \right] e^{{ - \lambda \left( { t_{dij} - t_{d11} } \right)}} }}} \right)} \right|_{{{\text{ave }}i}}$ is the natural logarithm of the count rate $C_{ij}^{\mu } \left( {t_{dij} } \right)$ normalized to $C_{11}^{\mu } \left( {t_{d11} } \right)$ and corrected for drift and decay, $m_{j}^{\mu } = \left. {{\text{ln}}\left( {{{C_{ij} \left( {t_{d11} } \right)} \mathord{\left/ {\vphantom {{C_{ij} \left( {t_{d11} } \right)} {C_{11}^{\mu } \left( {t_{d11} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{11}^{\mu } \left( {t_{d11} } \right)}}} \right)} \right|_{{{\text{ave }}i}}$ is the natural logarithm of the count rate $C_{ij} \left( {t_{d11} } \right)$ normalized to $C_{11}^{\mu } \left( {t_{d11} } \right)$, $t_{{{\text{r dead }}j}} = \left. {t_{{{\text{dead }}ij}} /t_{{{\text{c}}ij}} } \right|_{{{\text{ave }}i}}$ is the average relative dead time and $\varepsilon_{{{\text{r}} j}} = \left. {{{\varepsilon_{ij} } \mathord{\left/ {\vphantom {{\varepsilon_{ij} } {C_{11}^{\mu } \left( {t_{d11} } \right)}}} \right. \kern-\nulldelimiterspace} {C_{11}^{\mu } \left( {t_{d11} } \right)}}} \right|_{{{\text{ave }}i}}$ is the average error term normalized to $C_{11}^{\mu } \left( {t_{d11} } \right)$. In this case, $\lambda$ is the ¹³⁷Cs decay constant, j = 1, 2, …, 7 for the GEM 50P4-83 and j = 1, 2, …, 4 for the GEM 40P4-S and i = 1, 2, …, N_c. The $C_{ij}^{\mu } \left( {t_{dij} } \right)$ and $C_{11}^{\mu } \left( {t_{d11} } \right)$ values are calculated using Eq. (3) by substituting $f_{i1}$ = $f_{11}$ = 1, i.e.$\mu$ = 0.

The $Y_{j}^{\mu }$ versus $t_{{r {\text{dead }}j}}$ values obtained in case of zero efficiency drift, i.e. $\alpha$ = 0 h⁻¹, for the GEM 50P4-83 and GEM 40P4-S are plotted in the upper graph of Fig. 2a and b, respectively. The expected standard deviation of $Y_{j}^{\mu }$, due to counting statistics, is evaluated by ${{\left. {\sigma_{{\text{P}}} \left( {n_{ij} } \right)/n_{ij} } \right|_{{{\text{ave }}i}} } \mathord{\left/ {\vphantom {{\left. {\sigma_{{\text{P}}} \left( {n_{ij} } \right)/n_{ij} } \right|_{{{\text{ave }}i}} } {\sqrt {N_{{\text{c}}} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {N_{{\text{c}}} } }}$. The $\mu$ is the absolute value of the slope of the straight line fitted to $Y_{j}^{\mu }$ versus $t_{{{\text{r dead }}j}}$ data. The fitting residuals are plotted in the lower graph of Fig. 2a and b, respectively.

Fig. 2

The straight line fitted to the $Y_{j}^{\mu }$ versus $t_{{r{\text{ dead }}j}}$ and the corresponding residuals obtained during the pile-up constant measurement of the GEM 50P4-83 (a) and GEM 40P4-S (b). Error bars indicate a 95% confidence interval due to counting statistics

The resulting values of $\mu$ for the GEM 50P4-83 and GEM 40P4-S are 2.51(13) × 10^–2 and 3.42(12) × 10^–2, respectively. The uncertainty budget of the quoted uncertainties includes a contribution of approximately 70% and 95%, respectively, from counting statistics; the remaining part, 30% and 5%, are due to a possible efficiency drift within the quoted 10^–7 h⁻¹ level uncertainties of $\alpha$ obtained during the stability test. Specifically, the uncertainty of $\mu$ due to an efficiency drift is computed as the average of the absolute error of $\mu$ obtained by substituting in (6) $\alpha$ =  ± 80 × 10^–8 h⁻¹ and $\alpha$ =  ± 66 × 10^–8. It is worth noting that the residuals are in agreement with the expected ${{0.1 \% } \mathord{\left/ {\vphantom {{0.1 \% } {\sqrt {N_{{\text{C}}} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {N_{{\text{C}}} } }}$ relative standard deviation of $Y_{j}^{\mu }$ and validate the application of the pile-up correction at least up to a 30% relative dead time on the detection system.

The half-life time of ¹²² Sb

The ¹²²Sb half-life time was measured by processing the γ-spectra collected during the decay of the activated antimony samples. At INRIM, the 2 sequences performed with the GEM 50P4-83 lasted 251 h and 236 h, i.e. periods corresponding to 3.9 and 3.6 times the t_1/2(¹²²Sb), and consisted of 172 and 166 successive counts, respectively. The relative dead time varied from 20 to 4.6% and from 24 to 4.9%, respectively. At NIST the 2 sequences performed with the GEM 40P4-S lasted 274 h and 400 h, i.e. periods corresponding to 4.2 and 6.2 times the t_1/2(¹²²Sb), and consisted of 148 and 267 successive counts, respectively. The relative dead time varied from 13 to 4.9% and from 19 to 3.4%, respectively.

Equation (4) is used to measure $\lambda$, i.e. $t_{1/2} = \ln \left( 2 \right)/\lambda$. In this case j = 1, 2 and i = 1, 2, …, N_c. The $C_{ij} \left( {t_{{{\text{d}}ij}} } \right)$ and $C_{1j} \left( {t_{d1j} } \right)$ values are calculated using Eq. (3) and adopting the measured $\mu$ value. The $t_{c ij}$, $t_{{{\text{dead }}ij}}$ and $t_{{{\text{d}}ij}}$ values used to calculate the dead time and pile up corrections, $\delta_{ij}$ and $f_{ij}$, respectively, and the fitted $Y_{ij}^{\lambda }$ values via Eq. (4) have negligible uncertainties. Accordingly, uncertainty of $\delta_{ij}$ is negligible and the uncertainty of $f_{ij}$ depends on the uncertainty of $\mu$. In addition, the uncertainty of the relative variation of efficiency per unit of time, $\alpha$, affects the $Y_{ij}^{\lambda }$ values via Eq. (4) and counting statistics affect the ¹²²Sb γ-photon count rate $C_{ij} \left( {t_{dij} } \right)$ via Eq. (3).

The $Y_{ij}^{\lambda }$ versus $t_{dij} - t_{d1j}$ values obtained in case of zero efficiency drift, i.e. $\alpha$ = 0 h⁻¹, for the GEM 50P4-83 and GEM 40P4-S are plotted in the upper graph of Fig. 3a and b, respectively. The relative standard deviation of $Y_{ij}^{\lambda }$, due to counting statistics, is evaluated by $\sigma_{P} \left( {n_{ij} } \right)/n_{ij}$.

Fig. 3

The two straight lines fitted to the $Y_{ij}^{\lambda }$ versus $t_{{{\text{d}}ij}} - t_{{{\text{d}}1j}}$ values and the correspondent residuals obtained during the t_1/2(¹²²Sb) measurement with the GEM 50P4-83 (a) and GEM 40P4-S (b). Error bars indicate a 95% confidence interval due to counting statistics

The $\lambda$(¹²²Sb) value is the (shared) slope of the two straight lines fitted to $Y_{j}^{\lambda }$ versus $t_{dij} - t_{d1j}$ data. The fitting residuals, plotted in the lower graph of Fig. 3a and b, are in agreement with the constant 0.1% relative standard deviation of $Y_{j}^{\lambda }$ expressed in terms of error bars at 95% confidence interval.

The resulting values of t_1/2(¹²²Sb) obtained with the GEM 50P4-83 and GEM 40P4-S are 2.69457(22) d  and 2.69368(17) d , respectively; the quoted uncertainties are only due to counting statistics.

Uncertainty evaluation and net count correction due to systematic errors in γ-peak fitting

The absence of a measurement equation directly linking input parameters to the $\lambda$(¹²²Sb) value prevents the propagation of the uncertainties of the input quantities through a functional relationship. A propagation formula is suggested in [3] to evaluate the uncertainty. However, the proposed formula cannot be applied in practice because it assumes that count rates are measured with the same relative uncertainty at regular time intervals during the decay. As an alternative, we consider the fitting uncertainty of $\lambda$ as the contribution due to counting statistics affecting the $Y_{j}^{\lambda }$ values and we evaluate the effect of efficiency drift and pile-up correction by fitting the $Y_{j}^{\lambda }$ values obtained by separately substituting in Eq. (4) $\alpha$ and $\mu$ values calculated at their standard uncertainty values. Specifically, the uncertainty of $\lambda$ due to an efficiency drift is computed as the average of the absolute error of $\lambda$ obtained by substituting in Eq. (4) $\alpha$ =  ± 80 × 10^–8 h⁻¹ and $\alpha$ =  ± 66 × 10^–8 for the GEM 50P4-83 and GEM 40P4-S, respectively. Similarly, the uncertainty of $\lambda$ due to the pile-up correction is computed as the average of the absolute error of $\lambda$ obtained by substituting in (4) $\mu$ = (2.51 ± 0.13) × 10^–2 and $\mu$ = (3.42 ± 0.12) × 10^–2 for the GEM 50P4-83 and GEM 40P4-S, respectively.

Systematic errors affecting γ-peak net counts values, $n_{ij}$, and due to a non-perfect separation of the γ-peak from the underlying background are estimated by observing the peak fitting residuals obtained with the Hyperlab software. To increase the sensitivity we overlapped the residuals of the first 20 and the last 10 γ-peaks recorded at the beginning and the end of a decay observation, respectively; data of the second sequence collected with the GEM 50P4-83 and GEM 40P4-S are considered.

Residuals of the γ-peaks at the end of the sequence, and the first and last γ-peak with the underlying backgrounds are plotted in Fig. 4; the γ-peak net count to background ratio is about 3.3% and 4.0% for GEM 50P4-83 and GEM 40P4-S, respectively. The scattering of the residuals is (largely) within ± 3σ(n), where n is the channel count, and does not reveal significant systematic trends. Therefore, we consider the net count values at the end of the sequence unbiased.

Fig. 4

Fitting residuals of the last 10 γ-peaks of the second decay sequence collected with the GEM 50P4-83 (a1, a2) and GEM 40P4-S (b1, b2). The first and last γ-peak of the 10 γ-spectra, and their underlying background are also displayed

Residuals of the γ-peaks at the beginning of the sequence, and the first and last γ-peak with the underlying backgrounds are plotted in Fig. 5; the γ-peak net count to background ratio is about 1.4% and 0.8% for GEM 50P4-83 and GEM 40P4-S, respectively. The scattering of the residuals is (largely) within ± 3σ (n) and ± 4σ (n) for GEM 50P4-83 and GEM 40P4-S, respectively; in both cases systematic trends affecting the accuracy of the γ-peak net count are revealed, most significantly for the GEM 40P4-S.

Fig. 5

Fitting residuals of the first 20 γ-peaks of the second decay sequence collected with the GEM 50P4-83 (a1, a2) and GEM 40P4-S (b1, b2). The first and last γ-peak of the 20 γ-spectra, and their underlying background are also displayed

To improve the accuracy we repeated the fit by adding one interfering γ-peak at about 561 keV for the GEM 50P4-83, and two interfering γ-peaks at about 560 keV and 568 keV for the GEM 40P4-S. The new residuals are plotted in Fig. 6 together with a representative γ-peak, the interfering γ-peaks and the underlying background. The systematic trends affecting the residuals were removed for the GEM 50P4-83 and significantly decreased for the GEM 40P4-S.

Fig. 6

Fitting residuals of the first 20 γ-peaks of the second decay sequence collected with the GEM 50P4-83 (a1, a2) and GEM 40P4-S (b1, b2), and obtained with additional interfering γ-peaks. A representative γ-peak with the interfering γ-peaks is also displayed

The averaged uncorrected to corrected net count ratio at the beginning of the sequence is 0.99997 and 1.00032 for the GEM 50P4-83 and GEM 40P4-S, respectively; the corresponding relative correction of the measured t_1/2(¹²²Sb) value is − 1.2 × 10^–5 and 7.4 × 10^–5, respectively. We conservatively assign a relative uncertainty of the t_1/2(¹²²Sb) of 0.7 × 10^–5 and 4.3 × 10^–5 for the GEM 50P4-83 and GEM 40P4-S, respectively, corresponding to a uniform probability distribution having a half-width equal to the total γ-peak net count correction.

Uncertainties of t_1/2(¹²²Sb) due to (1) counting statistics, (2) possible efficiency drifts, (3) pile-up and (4) γ-peak fitting are listed in Table 1 together with the combined standard uncertainty, u_c(t_1/2), obtained as the positive square root of the sum of variances.

Table 1 Uncertainties of t_1/2(¹²²Sb) due to the influence factors

Comparison with the recommended and literature values

The presently recommended t_1/2(¹²²Sb) value, 2.7238(2) d [1], was published in 1990 [2] and selected by the evaluators after discarding nine additional values published as just half-life values between 1951 and 1973: 2.80(2) d  [9], 2.75(2) d  [10], 2.73(3) d  [11], 2.75(1) d  [12], 2.681(3) d [13], 2.82(5) d [14], 2.68(4) d [15], 2.714(6) d [16] and 2.84(12) d [17]. The values are plotted in Fig. 7 and compared with the values obtained in this study by INRIM and NIST, i.e. 2.69454(39) d and 2.69388(30) d, respectively.

Fig. 7

The t_1/2(¹²²Sb) values measured in this study by INRIM and NIST compared to the published values (a) and a zoom of the INRIM and NIST values (b). The publication year and reference are reported. The horizontal dashed line shows the presently recommended t_1/2(¹²²Sb) value. The error bars, where they are not obscured by the data point, indicate a 95% confidence interval

Conclusions

We carried out two independent measurements of the ¹²²Sb half-life. The uncertainties due to counting statistics, efficiency drift, pile-up and γ-peak fitting were evaluated and propagated to obtain a 10^–4 relative standard uncertainty. Although the resulting ¹²²Sb half-life values were in agreement, there is a 1.1% relative difference with respect to the recommended value.

The importance of adopting an accurate half-life value is fundamental in analytical chemistry measurements carried out by Neutron Activation Analysis (NAA). As an example, we reprocessed data collected during an experiment carried out to test the application of the k₀ standardisation method [18] using the new instead of the recommended ¹²²Sb half-life value. Specifically, the quantification of Sb in a soil reference material via the nuclear reaction ¹²¹Sb(n,γ)¹²²Sb is affected by a 2.8% relative difference when the sample is counted for 6 d after a decay of 11.7 d. In addition, attempting to calculate isotopic compositions of Sb at 0.1% uncertainty level using NAA, an incorrect ¹²²Sb half-life would potentially affect the results.

The paper published in 1990 [2] report the presently recommended ¹²²Sb half-life value together with the half-life of ⁴¹Ar, ^80mBr, ^94mNb, ¹⁰¹Mo, ¹⁰¹Tc, ¹⁰⁹Pd, ^109mPd, ^122mSb, ^123mSn, ^152mEu and ²³⁹Np. The authors did not describe the experiments nor the elaboration of the collected data. Decay curves were plotted only in the case of ⁴¹Ar, ^122mSb, ^152mEu and ²³⁹Np, and without the fitting residuals, which might reveal possible uncertainty sources. In addition, uncertainties of the half-life values are given without any discussion. Similarly, ¹²²Sb half-life values published over the previous years were reported just as results, without experimental and data elaboration details. These shortcomings make the presently recommended value and the other reported values less reliable than the values reported in this study, which we suggest to consider for the next recommended ¹²²Sb half-life value.