Introduction

Plutonium in transuranic elements is a special nuclear material used in the nuclear energy and an important raw material for MOX fuel. Due to the active nature, highly radioactive and radiotoxic of plutonium, its manipulation is generally carried out in a glovebox with inert atmosphere, such as the argon [1]. However, the high oxophilicity property can still lead to the oxidation of plutonium. And its volume can be expanded by up to 70% during the process of oxidation [2], which may result in radioactive aerosol release to the atmosphere in a glovebox gas exchange. The U.S. Department of Energy estimates that the lifetime cancer risk from inhaling 5000 plutonium particles, each about 3 μm wide, to 1% over the background U.S. average [3]. Considering the severe consequence, the generation rate of the aerosol of plutonium in argon atmosphere needs to be estimated for the health of staff onsite.

In the oxygen environment, there are mainly two compounds generated, Pu2O3 and PuO2. The free energies of Pu2O3 and PuO2 are − 378 kcal/mol and − 238.5 kcal/mol [4], respectively. When the oxygen is enough, the reaction is

$$ Pu + O_{2} = PuO_{2} $$
(1)

When oxygen is scarce, the reaction below happens

$$ Pu + 3PuO_{2} = 2Pu_{2} O_{3} $$
(2)

The above reaction can be backward again with more oxygen

$$ 2Pu_{2} O_{3} + 1 /2O_{2} \to 2PuO_{2} $$
(3)

Hydrogen would be generated with moisture appearance

$$ Pu + 2H_{2} O = PuO_{2} + 2H_{2} $$
(4)
$$ PuO_{2} + xH_{2} O = PuO_{2 + x} + xH_{2} $$
(5)

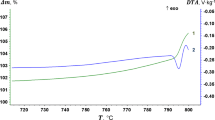
Studies have shown that the oxidation of plutonium is a two-stage process [1]. The first stage is a diffusion control process. With a thicker oxide layer accumulated on the surface, oxygen and metal ions have a higher barrier to diffuse to the interface to react, leading to a slower oxidation rate. The oxide layer thickness for the first stage can be depicted by a parabolic curve, as shown in Figs. 1 and 2. Then the oxidation enters the second stage, and the thickness of the oxide layer reaches a critical value, which is determined by the stress accumulation induced by the formation of low-density oxide (23.67 cm3/mol) on the high-density plutonium (12.20 cm3/mol). The accumulated stress causes the oxide crack and spallation. The decrease of oxide layer thickness due to the spallation promotes the formation of the oxide layer inversely. Eventually, the average thickness of the oxide layer remains constant, as shown in Figs. 1 and 2.

Fig. 1
figure 1

Oxide thickness of plutonium metal in dry atmosphere [1]

Full size image
Fig. 2
figure 2

Oxidation and spallation of plutonium in a dry environment [1]

Full size image

A number of studies by the United States Department of Energy [5] Sandia National Laboratory [6] and Los Alamos National Laboratory [1, 4] have shown that oxide crack and spallation may be the primary pathway for aerosol generation of the plutonium. However, the aerosol generation rate is still unknown to us now.

In the present paper, based on the point defect model (PDM), the oxidation process was studied to figure out the aerosol generation rate of plutonium in different conditions. The PDM is a popular model examining the growth and breakdown of passive films on the surfaces of reactive metals in contact with corrosive environments [7].

Model construction

Figure 3 is the phase diagram of Pu–O system, which shows that PuO2 only forms when the mole fraction of oxygen is more that 60% [8]. Considering the oxygen level in the argon glovebox is generally kept at several or tens ppm, only the Pu2O3 is considered in model construction. The procedure to estimate the aerosol generation rate is first to find the oxide layer thickness in steady state condition, and then to calculate the oxidation rate based on the PDM. The main assumptions in the model construction include:

Fig. 3
figure 3

Phase diagram of Pu–O system [8]

Full size image
  1. (1)

    After arriving at the critical thickness, the oxide thickness keeps constant.

  2. (2)

    After arriving at the critical thickness, the oxidation rate equals the aerosol generation rate, which means all the oxide generated after that cracks and becomes aerosol.

  3. (3)

    No thermal stress is taken into account.

  4. (4)

    Only one dimensional model is considered.

It should be noted that in our case of plutonium operation, the temperature almost keeps constant, so that the thermal stress is neglected. The expansion coefficient of PuO2 is 11.16 × 10−6/K at room temperature [9], however the value is 60–70 × 10−6/K for the Pu metal [10]. The expansion coefficient of Pu2O3 is expected to be significantly different from that of Pu. Thus, if the temperature is changed during Pu operation, the thermal stress should be taken into account to reduce the calculation error. For the process of model development, one dimentional model can be a very good start. Even though it is may not enough for very weird shapes of Pu, it can depict main characteristics of the process. Also, once the one dimentional model is developed, it is easy to extrapolate it to a two or three dimentional ones.

The cracks of the oxide are mainly due to the tensile stress during the oxide development, resulting in different expansion in multiple layers. The growth stress can be expressed by [11]

$$ \sigma_{gs} = \frac{{DHE_{m} \left( {e^{{ - \frac{{E_{m} \left( {1 - v_{B} } \right)\sqrt {H_{O} } }}{{E_{m} \left( {1 - v_{B} } \right)H_{M} }}}} - 1} \right)}}{{1 - v_{m} }} $$
(6)

where D is a coefficient related with the oxide, H is the thickness of metal, E is the Young’s modulus, v is the Poisson constant, h is the oxide thickness, the subscript m stands for the plutonium, O stands for oxide. The strain is thus

$$ \varepsilon_{gs} = \frac{{\sigma_{gs} }}{{E_{O} }} = \frac{{DHE_{m} \left( {e^{{ - \frac{{E_{m} \left( {1 - v_{B} } \right)\sqrt {H_{O} } }}{{E_{m} \left( {1 - v_{B} } \right)H_{M} }}}} - 1} \right)}}{{1 - v_{B} }} $$
(7)

The critical strain when the oxide crack is

$$ \varepsilon_{gs} = \sqrt {\frac{{2\gamma_{O} }}{{H_{O} E_{O} (1 - v_{O} )}}} $$
(8)

when γ is the surface energy of oxide. Combining all the equations above, the critical oxide thickness corresponding to oxide crack can be calculated, which is used as the domain for the diffusion of oxygen and metal vacancies. The model development is based on the point defect model (PDM), where the growth of the oxide film can be modeled by tracking the diffusion of metal cationic vacancies (CM) and oxygen anionic vacancies (CO) [12]. First, the oxygen vacancies are produced at the metal-oxide interface via the reaction:

$$ m\mathop{\rightarrow}\limits^{{k_{1} }} M_{M} + \frac{n}{2}V_{{\ddot{O}}} + ne^{\prime}(m) $$
(9)

where m represents the metal, MM is the metal cation in cation site, Vo is the oxygen vacancy, the 2 points mean the oxygen vacancy is with the charge of + 2, e′(m) is the electron located in the metal. Due to the concentration gradient, the oxygen vacancies diffuse to the oxide-atmosphere interface, and consumed by reacting with water

$$ V_{{\ddot{O}}} + H_{2} O\mathop \rightarrow \limits^{{k_{2} }} O_{O} + 2H^{ + } $$
(10)

The OO is the oxygen atom. This process is equivalent to the diffusion of oxygen atoms from oxide-atmosphere interface to the oxide-metal interface. Analogously, the metal vacancies are produced at the oxide-atmosphere interface by the reaction

$$ M_{M} \mathop \rightarrow \limits^{{k_{3} }} M^{n + } + V_{M}^{{n^{\prime}}} $$
(11)

where \( V_{M}^{{n^{\prime}}} \) means the metal vacancy with the charge of − n. Like the oxygen vacancies, these metal vacancies diffuse to the oxide-metal interface driven by the concentration gradient, and are consumed by combining with the metal atoms to produce the vacancies in the atom positions.

$$ m + V_{M}^{{n^{\prime}}} \mathop \rightarrow \limits^{{k_{4} }} M_{M} + v_{m} + ne^{\prime}(m) $$
(12)

where the Vm is the vacancy in an atom position with no charge. All the k in the equations above stands for the reaction rate. The illustration of the model is shown in Fig. 4.

Fig. 4
figure 4

An illustration of the model

Full size image

When the vacancies transport in the oxide, they are driven by two forces, the electric force and the concentration gradient driving force. The electric potential in the oxide can be determined by the Poisson equation as

$$ \frac{{\partial^{ 2} \phi }}{{\partial x^{2} }} = - \frac{F}{{\varepsilon_{r} \varepsilon_{o} }}\left[ {z_{M} C_{M} + z_{O} C_{O} } \right] $$
(13)

where F is the Faraday constant, ε0 is the permittivity of vacuum, εr is the relative permittivity of the oxide. ZM and ZO are the charges of the metal and oxygen vacancies, respectively. The governing equations of the oxygen and metal vacancies are

$$ \frac{{\partial C_{M} }}{\partial t} = \frac{\partial }{\partial x}\left[ {D_{M} \frac{{\partial C_{M} }}{\partial x} + \frac{{z_{M} FD_{M} }}{{R_{u} T}}\left( {C_{M} \frac{\partial \phi }{\partial x}} \right)} \right] $$
(14)
$$ \frac{{\partial C_{O} }}{\partial t} = \frac{\partial }{\partial x}\left[ {D_{O} \frac{{\partial C_{O} }}{\partial x} + \frac{{z_{O} FD_{O} }}{{R_{u} T}}\left( {C_{O} \frac{\partial \phi }{\partial x}} \right)} \right] $$
(15)

where Ru is the universal gas constant, T is the temperature in kelvin, DM and DO are the diffusion coefficients of the metal and oxygen vacancies, respectively. Taking the oxide-metal interface as the origin, direction to the oxide-atmosphere as the x-axis, the boundary conditions x = 0 are

$$ \left[ { - D_{O} \frac{{\partial C_{M} }}{\partial x} - \frac{{z_{O} FD_{O} }}{{R_{u} T}}\left( {C_{O} \frac{\partial \phi }{\partial x}} \right)} \right]_{x = 0} = k_{1} \exp \left[ {\frac{{\alpha_{1} \cdot n_{1} F}}{{R_{u} T}}\left( {E_{m} - \phi } \right)} \right] $$
(16)
$$ \left[ { - D_{M} \frac{{\partial C_{M} }}{\partial x} - \frac{{z_{M} FD_{M} }}{{R_{u} T}}\left( {C_{M} \frac{\partial \phi }{\partial x}} \right)} \right]_{x = 0} = - \;C_{M} k_{4} \exp \left[ {\frac{{\alpha_{2} \cdot n_{2} F}}{{R_{u} T}}\left( {E_{m} - \phi } \right)} \right] $$
(17)

The boundary conditions at x = hc are

$$ \left[ { - D_{O} \frac{{\partial C_{M} }}{\partial x} - \frac{{z_{O} FD_{O} }}{{R_{u} T}}\left( {C_{O} \frac{\partial \phi }{\partial x}} \right)} \right]_{{x = h_{c} }} = C_{O} k_{2} \exp \left[ {\frac{{\alpha_{3} \cdot n_{1} F}}{{R_{u} T}}\left( {\phi - E_{a} } \right)} \right] $$
(18)
$$ \left[ { - D_{M} \frac{{\partial C_{M} }}{\partial x} - \frac{{z_{M} FD_{M} }}{{R_{u} T}}\left( {C_{M} \frac{\partial \phi }{\partial x}} \right)} \right]_{{x = h_{c} }} = - k_{3} \exp \left[ {\frac{{\alpha_{4} \cdot n_{2} F}}{{R_{u} T}}\left( {\phi - E_{a} } \right)} \right] $$
(19)

where α is the cathodic electron transfer coefficient, n is the number of electron involved in each reaction, Em is the potential in metal and Ea is the potential in atmosphere.

Results and discussion

The oxidation rate at the room temperature of 298 K was calculated. The input parameters of the model is shown in Table 1. Each simulation was run in 10 million steps with step size of 0.01 s to reach the equilibrium.

Table 1 Input parameters for the simulation
Full size table

The Figs. 5 and 6 show the potential profile and oxygen and metal vacancies, respectively. The results show shat the potential is symmetric and its value decreases with the thickness. Since when the Pu2O3 forms, more oxygen is consumed than plutonium, the concentration of the oxygen is less than that of plutonium. When the reaction reaches equilibrium, oxygen and metal vacancies both show a plateau phase in majority of oxide film. Figure 7 shows the derivative of the oxygen and metal vacancies at the two sides of the oxide film, from which the aerosol generation rate is calculated

$$ Ag = D_{O} \frac{{\partial C_{O} }}{\partial x}|_{x = 0} \times \frac{2}{3} + D_{M} \frac{{\partial C_{M} }}{\partial x}|_{{x = h_{c} }} $$
(20)

\( \frac{{\partial C_{O} }}{\partial x}|_{x = 0} \) (referring as the ΔCO) is 6.11 × 106 mol/m4 and \( \frac{{\partial C_{M} }}{\partial x}|_{{x = h_{c} }} \) (referring as the ΔCM) is 3.89 × 106 mol/m4, corresponding an aerosol generation rate of 8.189 × 106 particles/cm2/s.

Fig. 5
figure 5

The potential profile in the oxide film

Full size image
Fig. 6
figure 6

Concentration profile of the oxygen and metal vacancies

Full size image
Fig. 7
figure 7

The derivative of the oxygen and metal vacancies at the two sides of the oxide film

Full size image

Effect of diffusivity

Diffusivity of vacancy in the oxide determines how fast the transport is. It is determined by the temperature, however, only diffusivity itself currently is considered to examine how it affects the aerosol generation rate. Both the diffusivities of the oxygen and metal vacancies are multiplied by 2 and 4.

Figures 8 and 9 show the effects of diffusivity on the potential and concentration profile, respectively. It can be observed that with a larger diffusivity, the electric field in the oxide film becomes stronger. Both concentrations of oxygen and metal vacancies decrease with the larger diffusivity. However, the metal vacancy has a larger decreasing value compared with the oxygen vacancy. Besides the reason of the stoichiometry of the Pu2O3, it could be because the metal vacancy has a charge of 3, which is more affected by the increase of electric field. The ΔCO and ΔCM are listed in Table 2. It can be seen that with the increase of diffusivity, both the values of ΔCO and ΔCM increase, which means a larger rate of aerosol generation. It makes sense because a larger diffusivity indicates a larger reaction rate at equilibrium.

Fig. 8
figure 8

Effect of the diffusivity on the potential profile

Full size image
Fig. 9
figure 9

Effect of the diffusivity on the concentration profile

Full size image
Table 2 The effects of diffusivity on the ΔCO and ΔCO
Full size table

Effect of the rate constant

In this study, four rate constants are involved, namely the oxygen vacancy generation rate constant k1, the oxygen vacancy consumption rate constant k2, the metal vacancy generation rate constant k3, and the metal consumption rate constant k4. Here all the rate constants are multiplied by 2 and 4 to figure out their effects on the aerosol generation. Figures 10 and 11 show the effect of the rate constant on the potential and vacancy concentration profiles. It can be seen that the increase of rate constant actually has little effect on the potential or vacancy concentration. It makes sense since both the generation and consumption rates are increased, which offsets the individual effect at equilibrium. Table 3 shows that effect of rate constant on the ΔCO and ΔCM. Even thought the little effect on the potential or vacancy concentration distribution, the rate constant does affect the ΔCO and ΔCM significantly. Both ΔCO and ΔCM show a proportional relationship with the rate constant, because a larger rate constant indicates a larger reaction rate at equilibrium.

Fig. 10
figure 10

Effect of the rate constant on the potential profile

Full size image
Fig. 11
figure 11

Effect of the rate constant on the concentration profile

Full size image
Table 3 The effects of rate constant on the ΔCO and ΔCM
Full size table

Effect of oxide film layer

If the temperature or the oxygen or the moisture increases in the atmosphere, the oxide film layer increases due to a more intense oxidation reaction. Here three oxide thicknesses of 200 Å, 300 Å, and 400 Å were studied to see their effects on the aerosol generation rate. Figures 12 and 13 show the effect of oxide thickness on the potential and vacancy concentration. Table 4 shows the effect on the ΔCO and ΔCM. It shows that the effect on the concentration or ΔCO or ΔCM is not significant because what is cared about is actually the equilibrium state. A thicker oxide layer only requires more time to reach equilibrium. However, the oxide thickness has pretty much effect on the potential profile. It can be explained because the vacancy concentration is almost the same everywhere, which results in a larger stack effect on the potential distribution.

Fig. 12
figure 12

Effect of the oxide thickness on the potential profile

Full size image
Fig. 13
figure 13

Effect of the rate constant on the concentration profile

Full size image
Table 4 The effects of oxide thickness on the ΔCO and ΔCM
Full size table

Effect of the temperature

Temperature actually affects the diffusivity, rate constant, oxide thickness. However, there merely the temperature is examined to figure out its effect on the aerosol generation. Three temperatures of 298 K, 500 K, 700 K were applied. Figures 14 and 15 show the temperature effect on the potential and vacancy concentration. Since other parameters are not changed with the temperature, the temperature itself has little effect on the concentration profile. However, the temperature has significant effect on the potential, which can be obtained by Eqs. (14) and (15). The potential needs to be changed to offset the effect of temperature. With the temperature increases, the electric field in the oxide increases dramatically. If the dependence of other parameters on the temperature is considered, a more significant effect can be expected. No much effect on the ΔCO and ΔCO are found (Table 5).

Fig. 14
figure 14

Effect of the temperature on the potential profile

Full size image
Fig. 15
figure 15

Effect of the temperature on the concentration profile

Full size image
Table 5 The effects of temperature on the ΔCO and ΔCO
Full size table

Conclusion

Based on the PDM model, the transport of the oxygen and metal vacancies are simulated considering their diffusion and electromigration. The potential is distributed symmetric in the oxide film and can be approximated in a linear relationship. With the assumption that at equilibrium, the oxidation rate is equal to the aerosol generation rate, the aerosol generation rate at 298 K is calculated, which is about 8.19 × 106 particles/cm2/s. Also, the dependence of the results on the diffusivity, rate constant, oxide thickness, temperature was investigated. The results show that the diffusivity has the most significant effect on both the potential and the vacancy concentration. If all the rate constant changes together, it has little effect on the potential and vacancy concentration profile but affects the aerosol generation rate significantly. The oxide thickness and temperature have no much effect on the potential or vacancy concentration but increases the electric field in the oxide film. This study contributes to the aerosol generation mechanism when the plutonium is manipulated in a glove box under different conditions. Currently, all the research is about the model development and parameter studies. For a more accurate result, the experiments are merited in the future to verify the model and optimize the input parameters.