Recommended nuclear data for medical radioisotope production: diagnostic positron emitters

Abstract

An IAEA coordinated research project that began in 2012 and ended in 2016 was primarily dedicated to the compilation, evaluation and recommendation of cross-section data for the production of medical radionuclides. One significant part of this work focused on diagnostic positron emitters. These particular studies consist of 69 reactions for direct and indirect or generator production of ⁴⁴Sc(⁴⁴Ti), ^52mMn(⁵²Fe), ^52gMn, ⁵⁵Co, ⁶¹Cu, ⁶²Cu(⁶²Zn), ⁶⁶Ga, ⁶⁸Ga(⁶⁸Ge), ⁷²As(⁷²Se), ⁷³Se, ⁷⁶Br, ⁸²Rb(⁸²Sr), ^82mRb, ⁸⁶Y, ⁸⁹Zr, ⁹⁰Nb, ^94mTc, ^110mIn(¹¹⁰Sn), ¹¹⁸Sb(¹¹⁸Te), ¹²⁰I, ¹²²I(¹²²Xe), ¹²⁸Cs(¹²⁸Ba), and ¹⁴⁰Pr(¹⁴⁰Nd) medical radionuclides. The resulting reference cross-section data were obtained from Padé fits to selected and corrected experimental data, and integral thick target yields were subsequently deduced. Uncertainties in the fitted results were estimated via a Padé least-squares method with the addition of a 4% assessed systematic uncertainty. Experimental data were also compared with theoretical predictions available from the TENDL-2015 and TENDL-2017 libraries. All of the numerical reference cross-section data with their corresponding uncertainties and deduced integral thick target yields are available on-line at the IAEA-NDS medical portal www-nds.iaea.org/medicalportal and also at the IAEA-NDS web page www-nds.iaea.org/medical/positron_emitters.html.

Introduction

The importance of positron-emitting radionuclides in molecular imaging (Positron Emission Tomography, PET) has constantly increased over the years, especially to follow metabolic processes and to quantify radiation dose in internal radiotherapy. Nuclear data identified with these radionuclides are important for the optimisation of their production routes and medical applications. Judicious selection of the projectile energy range will maximise the yield of the product and minimise that of any radioactive impurities. Several charged-particle and neutron production routes exist for the production of such radionuclides. The International Atomic Energy Agency (IAEA) initiated and supported a Coordinated Research Project (CRP) from 1997 to 2001 with the primary aim of establishing a reference nuclear reaction database for the most important gamma-ray and positron emitters and associated monitor reactions in order to optimise their production [1]. No uncertainties in the recommended data were produced at that time. The list of positron emitters that was included in this earlier effort is shown in Table 1. The reference cross-section data and integral thick target yields were made available in a hard-copy technical document, and later became accessible on the medical portal of the IAEA Nuclear Data Section (IAEA-NDS) with further updates from 2001 to 2007 [2].

Table 1 Earlier evaluated nuclear reactions for the production of diagnostic PET isotopes (1995–1999), and also made available as an IAEA nuclear database [1, 2]

Over the previous two decades new experimental data have been measured for the earlier evaluated reactions, and numerous new and potentially suitable candidate PET-isotopes have appeared in the literature along with pre-clinical studies. Therefore, a new CRP was initiated at the end of 2012 in order to redefine the production routes and upgrade the production data for the previously studied radionuclides, and to complement the database with the equivalent results for emerging prospective radionuclides. An additional goal of the working programme was to provide uncertainties for the recommended cross sections of all the reactions studied [3]. The results of this evaluation work are summarised for production routes applicable to diagnostic positron emitters, including generator systems for short-lived radionuclides.

Evaluation method

The evaluation process was performed in a similar manner to previous studies [1, 6], and includes the following steps that will be discussed in more detail below:

• thorough compilation of experimental data (Section "Thorough compilation of experimental data");

• undertake new measurements if required (Section "New CRP measurements");

• correct and normalise earlier experimental data (decay data, enriched target abundances, monitor data, recognised systematic errors) (Sections "Status of earlier experimental data" and "Correction of earlier experimental data");

• compare with theoretical predictions (Section "Comparisons with theoretical predictions");

• critical comparison of all experimental datasets, and rejection of unreliable and erroneous sets (Section "Critical comparisons and selection of the most reliable experimental data");

• least-square fit of selected experimental datasets to derive mean values and corresponding uncertainties of the resulting recommended reference data (Section "Data fitting and resulting uncertainties- Padé fit of selected experimental data");

• calculate integral yield as a function of the incident particle energy (Section "Integral yields for thick targets as a function of particle energy").

Thorough compilation of experimental data

Detailed searches for published experimental cross sections were made, including the following sources: primary publications in journals, EXFOR database of IAEA-NDS [7], IAEA INIS database [8], evaluated libraries (ENDF) [9], bibliographies of Brookhaven National Laboratory (Burrows and Dempsey [10], Holden et al. [11], Karlstrom and Christman [12]), reports of the International Atomic Energy Agency (Dmitriev [13], Gandarias-Cruz and Okamoto [14]), Landolt Börnstein Series [15], Landolt Börnstein New Series [16], Tobailem et al. [17], Albert et al. [18], Münzel et al. [19], PhD theses, other relevant evaluations, private communications, etc. All experimental references are cited in each of the subsections that describe specific reaction paths.

The cut-off for inclusion of new data was set at June 2016, and therefore some results published in the final year of this compilation exercise were not added into the already completed fits but are still shown among the datasets retrieved. Duplications of original data published in the numerous review papers on production and/or use of medical radionuclides are explicitly mentioned in this study.

New CRP measurements

Additional experiments were performed by various CRP participants as crucial support in defining the excitation functions of the ⁴⁵Sc(d,3n)⁴⁴Ti, ^natNi(p,x)⁵²Fe, ⁵⁵Mn(p,4n)⁵²Fe, ⁵⁰Cr(α,2n)⁵²Fe, ⁵⁸Ni(p,α)⁵⁵Co, ⁶¹Ni(p,n)⁶¹Cu, ⁶⁰Ni(d,n)⁶¹Cu, ^natGa(p,x)⁶⁸Ge, ^natGe(p,xn)⁷²As, ^natGe(d,xn)⁷²As, ⁸⁹Y(d,2n)⁸⁹Zr, ⁹³Nb(p,x)⁹⁰Nb, ⁹²Mo(α,x)^94mTc, ¹¹⁰Cd(p,n)^110mIn, ¹⁰⁷Ag(α,n)^110mIn, ^natSb(p,xn)¹¹⁸Te and ¹⁴¹Pr(d,3n)¹⁴⁰Nd reactions. Details of these studies have been reported individually and separately in other dedicated publications (see references for specific reactions given below).

Status of earlier experimental data

Large sets of experimental data are available for some reactions, but only one or two relevant measurements exist for other reactions. Investigation of the published data permits some general remarks and conclusions to be made:

• Early investigations from 1945 to 1970 were mostly dedicated to the study of nuclear reaction mechanisms, and were performed on accelerators possessing somewhat limited technology of that time. The information on decay data and estimated uncertainties adopted for these experiments are poor in most cases.

• Production of medical radionuclides used in clinical practice would normally involve monoisotopic or at least enriched targets. However, production cross sections are sometimes determined by evaluators from data obtained with natural targets over limited energy ranges (up to the threshold of the next contributing reaction) in order to derive suitable data for subsequent evaluation. These data are in many cases more reliable due to the higher quality of the targets employed (with respect to thickness and uniformity).

• Nowadays, excitation functions are commonly measured over a broader energy range by means of the stacked-foil technique. This method possesses significant advantages in irradiation time and the determination of good relative values because of the fixed number of bombarding particles in each sample. However, long stacks suffer from an accumulation of effects caused by uncertainties in foil thicknesses that result in a possible increasing energy shift throughout the stack. The precise energy in each foil can be controlled by simultaneous measurements of the excitation function of reference monitor reactions over the whole energy range, but this is very rarely undertaken.

• Another possibility is to irradiate a large number of targets simultaneously in conjunction with rotating wheels in which different energy absorbers with well-measured thicknesses are inserted before each target. The number of bombarding particles incident on each target is the same and well controlled, although one disadvantage is the much longer irradiation time needed when compared with stacked-foil irradiations.

• Overwhelming parts of the datasets exhibit consistent and realistic behaviour, but in some cases points in a given set may disagree significantly from the observed trend and with other data without any obvious reason (although a most probable cause is an incorrect estimation of the real target thickness). These clearly discrepant data points were not considered as valid data during the fitting process.

Knowledge of the energy and energy distribution of the incident particle beam is important in reducing the uncertainty of the energy values of the data points. This information is preferably obtained by prior measurement, However, these incident beam parameters are rarely known for production machines in which the use of high-intensity beams causes changes in target quality (i.e., surface density and uniformity of target atoms). Gas targets are especially sensitive to density reduction caused by the heat generated from high-current beams.

Essentially two methods were used in these experiments to determine the number of incident particles: direct collection of the total charge in a Faraday cup, or indirectly by means of the reference data from a series of monitor reactions. Some experiments involve only the activity of a single monitor foil inserted in front of the target stack compared with the activity of the same foil target measured in a Faraday cup at the same energy. An additional factor of uncertainty is the constancy over time of the number of incident particles, especially when the half-life of the radionuclide investigated is comparable to or shorter than the irradiation time. Not all laboratories have the instrumentation needed to monitor and quantify the beam intensity on the target during the irradiation.

Other factors are the method of detection of the different types of radiation emitted in order to quantify the product nuclei: X-rays, gamma rays, alpha and beta particles, and neutron emissions involve the use of detectors that possess very different energy resolution and efficiency. Nevertheless, recent developments in detector technology have resulted in greater reliability and commensurate reductions in the uncertainties. Compilations and evaluations of the measured results and assessment of the quality of the reported work from different laboratories require all these factors be taken into account, which requires detailed investigations of all of the original publications.

Correction of earlier experimental data

Where possible, published cross sections that rely on outdated decay data were corrected by taking new decay data into account by means of NuDat [4] (with the Evaluated Nuclear Structure Data File (ENSDF) [5] as the data source). This form of correction was also carried out with respect to the decay data associated with the adopted monitor reactions. As any correction with respect to updated half lives has a non-linear impact on the well-known activation equation used to determine the cross section (primarily factors related to time), caution has to be taken when applying such adjustments. They are only possible if timing information is available in the original publication. The correction for other linear factors can be more easily performed, but also requires knowledge of the decay data used by the original authors.

Excitation functions measured over a broad energy range that show often relatively small uncertainties are sometimes significantly different from more reliable data determined over a shorter energy range. These higher energy data were normalised in such cases to the well measured data to produce reference data in a broad energy range. The same method was also adopted in the case of systematic energy shifts observed in the stacked-foil technique, which can be linearly corrected with respect to data measured on accelerators with high-energy definition.

Fitting procedures require reliable uncertainties in the experimental data selected for such statistical analyses. Unfortunately, the uncertainties in the cross-section values and the beam energy are not always appropriately provided as a significant part of the published experimental data. Therefore, missing cross-section uncertainties were estimated on the basis of the measurement methodology and the experience of the compilers/evaluators.

The experimental data for a given reaction measured with similar methods and comparable technology in different laboratories often have significantly different quoted uncertainties. Some studies report uncertainties that are unrealistically low because all contributing statistical or systematic effects have not been taken into account, or are incorrectly estimated. Therefore, such values were corrected to more realistic average uncertainties to avoid incorrect weighting in the fitting procedure.

Comparisons with theoretical predictions

Experimental data were compared with theoretical predictions of activation by charged-particle reactions, as assembled and made available in the online TENDL-2015 and TENDL-2017 libraries [20]. Both of these libraries are based on the reaction modelling adopted in the TALYS code [21]. The TENDL libraries are derived from both default and adjusted TALYS calculations, and occasionally from other sources.

The aim of the comparisons was to obtain a general impression of the shape of each excitation function over a broad energy range, including the magnitude of the maximum cross-section value and the effective threshold of reaction in cases where there were contradicting data. These predictions also permitted extrapolation of the excitation function in cases where experimental data were only available over a short and limited energy range as input for the Bayesian least-square fit (e.g., for the Padé fit). All TENDL predictions are shown along with the experimental data in the various figures of the excitation functions. Recently published results of evaluations for different activation products obtained from fitting by adjustment of theoretical codes to a compilation of existing experimental results (including some from this coordinated research project) have not been considered here, as the Bayesian non-model evaluation is the preferred evaluation method.

Critical comparisons and selection of the most reliable experimental data

Corrected and analysed experimental data were visually compared in figures that also included the theoretical predictions.

Measurement of radioactivity

The main sources of error when determining absolute activity are faulty estimates of the detector efficiency (especially in the low-energy region), self-absorption of low-energy gamma rays, geometry deviations between point source calibrations and the activated spot size on targets, dead-time and pile-up corrections, and the adoption of incorrect decay data.

Determination of the energy scale

Errors in the energy scale are introduced by improper estimation of the energy of the primary beam, uncertainties in the effective thickness of the individual targets, the cumulative effect of the stacked-foil technique, and the ill-defined impact of absorbers introduced to vary the energy of the incoming beam. Accelerators used for data measurements in nuclear physics usually have the necessary facilities to measure the energy of the beams precisely.

Estimation of uncertainties of the cross sections and energy scale

Despite the existence of the JCGM guide for the expression of uncertainty in measurements that experimentalists are strongly advised to follow [22], we have found that no such recommended systematic procedures have been undertaken to estimate properly the uncertainty of the measured cross sections and their energy scale. Various factors contribute to the assessment of the uncertainty associated with cross-section measurements. Unfortunately, authors in many original publications present only the total uncertainty in their tables of cross sections, without discussing or defining the estimated uncertainties of the contributing processes (i.e., no sufficiently detailed uncertainty budget is given).

A number of noteworhy observations were made during the course of the evaluation process:

• data from different authors often show striking systematic disagreements over the whole energy range;

• data below the reaction threshold were frequently reported;

• sometimes the data were extensively scattered, without any explanation;

• specific laboratories carried out systematic investigations, and as a consequence generated good results for many reactions.

Due to a general lack of information reported in the original publications and earlier compilations, the quality of the data could not be assessed in most cases, nor reasons identified for disagreements with other publications apart from a few exceptions. The most likely sources of disagreement or reasons for discrepancies among the experimental data were as follows:

Beam current. While relying on monitor reactions, the main problem originates from the use of outdated monitor cross sections. Another source of error was improper use of monitors, especially an incorrect estimation of the energy of the bombarding particle in a region where the excitation function curve has a steep slope (which will lead to an under- or overestimation of the beam flux).

Determination of the number of target nuclei. Although difficult to determine the number of target nuclei with high precision, an uncertainty below five percent can be easily achieved. The main challenges in the case of thin solid targets are uncertainties associated with the chemical state caused by surface oxidation, non-uniformity in the thickness of the foil, and improper estimation of the shape or dimensions influencing the thickness derived from weighing. Furthermore, well-known density reductions along the beam due to the heat effect play a very important role in the case of gas targets.

On the basis of emerging inconsistencies and trends, contradictory and scattered data were rejected from the analyses. Such an extensive selection process takes into account many factors, of which a few cannot be formulated in a mathematical manner, but rather are based on invaluable experienced, yet subjective, judgements by the evaluators.

Data fitting and resulting uncertainties- Padé fit of selected experimental data

Previous evaluations of the experimental cross-section data for diagnostic radionuclides were usually fitted by the spline method. Such a procedure is based on a piecemeal approximation of the data between specified points (knots of the spline) based on individual interpolating polynomials. These polynomials match in such a way that the zeroeth, first and second derivatives are continuous at the knots, and are usually selected by the second (quadratic interpolation) or third order (cubic interpolation). A continuous and smooth fit is obtained with minimum twisting (oscillating behaviour) of the fitting curve, which arises from the conditions for continuity. A particular feature of the spline method is that the fit in a selected interval is independent from the data in other intervals.

The spline method is well known (e.g., see Ref. [23] and references therein), and has been applied in nuclear data evaluations. Some known shortcomings relate to the following requirements and inadequacies:

• knots have to be selected by a user, which makes the fit time consuming with partially arbitrary results;

• cubic splines are not always adequate for complex-shaped curves.

A more general class of analytical function is the rational function defined as the ratio of two polynomials. Such an approximation was proposed by Padé over one hundred and twenty years ago [24], and has become one of the most important interpolation techniques of statistical mathematics [25, 26]. As a rational function, the Padé approximant can be expressed by a set of real polynomial coefficients, or by a set of real coefficients of the pole expansion

$$ p_{L} (z) = c + \sum\limits_{l} {\tfrac{{a_{l} }}{{z - \eta_{l} }} + \sum\limits_{k} {\frac{{\alpha_{k} (z - \varepsilon_{k} ) + \beta_{k} }}{{(z - \varepsilon_{k} )^{2} + \gamma_{{_{k} }}^{2} }}} } , $$

(1)

where z = x + iy are complex variables, and L is the order of the polynomial representation of the Padé approximant (therefore all coefficients depend implicitly on L) [25, 26]. This equation is also called the resonance expansion, in which ε_k and γ_k are the energy and the total half-width of the kth resonance, respectively, while α_k and β_k are the partial widths and interference parameters. The first sum corresponds to the real poles, while the second sum relates to the complex poles.

Effective codes for practical applications of the Padé approximation were developed by the IPPE, Obninsk group [27]. The simplest version of these codes permits analyses of up to 500 experimental points, with the number of parameters L ≤ 40 and the ratio limit of analysed functions up to f^max/f^min≤ 10⁶. A more detailed description of the method can be found in Ref. [27], and some important questions of application are presented in Refs. [28, 29].

Padé approximations are also very convenient for calculations of the data uncertainties and the corresponding covariance matrices. The fitting procedure is always based on a minimisation of the deviation functional

$$ \chi^{2} = (N - L)^{ - 1} \sum\limits_{j = 1}^{N} {(p_{L} (x_{j} ) - f_{j} )^{2} /\sigma_{j}^{2} } , $$

(2)

where f_j are the available experimental data, σ_j are their total uncertainties (including both systematic and statistical components) and N is the number of analysed points. Such minimisation is carried out iteratively by means of the discrete optimization approach. Minimal deviation for a given L is computed by assessing and selecting L points from the available N points (L < N), and then determining the corresponding approximants from Eq. (2). Once this process has been completed, L is changed and the iteration is repeated until an overall minimum is found from all discrete possibilities available. Some additional details of the method are considered in our earlier paper that focused on the evaluation of charged-particle monitor reactions [30].

Along with a consistent consideration of the statistical uncertainties of experimental data, the Padé method allows the determination of some systematic uncertainties that are usually underestimated by their authors, and also establishes some implicit correlations of the data. The averaged deviation of the full experimental dataset from the approximating function is regarded as the systematic uncertainty, while the variances of deviations around the averaged values are regarded as the statistical uncertainties. An optimal description of all data is achieved by the traditional iteration procedure of minimizing the mean squares deviations with the statistical and systematic uncertainties.

Only total uncertainties are determined in the majority of the experimental studies, and reasonable reconstructions of the corresponding systematic uncertainties are judged to be impossible to achieve in many of these cases. The method described above provides estimates of the systematic uncertainties on the basis of general statistical criteria which are valid for a reasonable number of studies. However, for a small number of the experimental measurements, underestimation of the systematic uncertainties is highly probable. Such underestimations also occur in those cases whereby the same, very similar, or other components of the same experimental equipment are used in a range of different studies, since any related correlations have been neglected.

After analysing the complete set of available data, we have come to the conclusion that realistic total uncertainties cannot be defined as less than 4% for each of the reactions considered. Therefore, an additional systematic uncertainty of 4% has been introduced as part of each systematic uncertainty derived from statistical analyses of all the recommended cross sections.

Integral yields for thick targets as a function of particle energy

Integral thick target yields as a function of energy were calculated from the recommended cross section data. We have quantified the production rates for radionuclides whose half-lives are short relative to the length of irradiation. This rate is also known as the “physical yield”, or “instantaneous production rate”, since the effect of decay of the radionuclide is small compared with the activity being created. Two other yields are also defined on the IAEA medical portal [2], namely the activity of a fixed 1 h and 1 µA irradiation, and the saturation activity at EOB for a 1 µA irradiation.

The activity of a fixed 1 h/1 μA irradiation is meaningful and can be used in practice for longer-lived radionuclides where the activity is increasing linearly with irradiation time. Saturation activity is used in the case of short half-life radionuclides, when a constant activity is obtained for even relatively short irradiations. The definition of these parameters can be found in Bonardi [31], and Otuka and Takács [32]. Thick target yields for the different production routes leading to a given radionuclide are summarised within a figure at the end of every subsection.

Medically relevant radionuclides can be obtained in many cases from the decay of a parent with a different half-life (indirect production, or generator couple). Two separate figures are shown in such cases, corresponding to the yields at EOB for the shorter-lived daughter and the longer-lived parent (often orders of magnitude lower). Depending on the relative half-lives, either time-dependent partial equilibrium (indirect production in which mother and daughter have comparable half-lives), or total equilibrium (long-lived parent/short-lived daughter generators) is obtained.

Results for charged-particle reactions

The list of reactions evaluated in the present studies consists altogether of 69 charged-particle reactions for the production of 23 radionuclides of interest for PET imaging, including 11 generator systems for short-lived medically interesting radioisotopes (Table 2). There are 39 proton reactions, 16 deuteron reactions, one reaction for ³He, and 13 reactions for α particles. Energies of incident particles cover the range from a few MeV up to 100 MeV. Every subsequent subsection contains a summary of the most frequent use of each of the 23 medically relevant radionuclides, and the literature references found for each production route (given in both the text and figures), selected data (text and figures) and the characteristics of the Padé fit (text and figures). As mentioned previously, the physical yields are included in one or two additional figures at the end of each subsection if indirect and/or generator production is being considered.

Table 2 Evaluated nuclear reactions and decay data adopted for production of diagnostic PET radionuclides (2012–2016) [2]. Reaction thresholds for natural targets estimated approximately from the plots, and are given in bold

Half-lives and limited decay-scheme data for the different radionuclides discussed in the following subsections can be found in Table 2. The γ-ray energies in keV and the corresponding absolute emission probabilities (absolute intensities, P_γ(%)) used to identify and quantify the activity of a given radionuclide in the experimental studies (and β⁺ decay fraction instead of the intensity of the 511 keV annihilation radiation) are listed, and have also been included within each of the primary subsections of this Section.

Reactions for radionuclides present in Table 1 but not considered during the course of this CRP will be evaluated in a similar manner as part of a future series of IAEA-sponsored studies and will be published elsewhere.

Production of ^44gSc (T _1/2 = 3.97 h) and long-lived ⁴⁴Ti parent (T _1/2 = 59.1 y)

Applications: ⁴⁴Sc (av. E_β+ = 632.0 keV, 94.27% intensity) has emerged as an attractive radiometal candidate for PET imaging by means of e.g., DOTA-functionalised biomolecules. ⁴⁴Sc-labelled PET radiopharmaceuticals appear of interest for molecular imaging of medium-lasting physiological processes. Also forms a theranostic pair with therapeutic ⁴⁷Sc.

⁴⁴Sc (3.97 h): β⁺ (94.27%), and E_γ (keV) (P_γ(%)): 1157.020 (99.9).

⁴⁴Ti (59.1 y): detected by means of radiation emitted by daughter ⁴⁴Sc.

⁴⁴Ca(p,n)⁴⁴Sc, ⁴⁴Ca(d,2n)⁴⁴Sc and ⁴³Ca(d,n)⁴⁴Sc direct reactions and ⁴⁵Sc(p,2n)⁴⁴Ti-⁴⁴Sc, ⁴⁵Sc(d,3n)⁴⁴Ti-⁴⁴Sc generator production routes were evaluated.

⁴⁴Ca(p,n)^44gSc

The six experimental datasets available in the literature are shown in Fig. 1 [33,34,35,36,37,38], together with the TENDL calculations. Three sets were rejected Cheng et al. [34] and Mitchell [35] (too high values near the threshold), and Krajewski et al. [37] (strange overall shape)), while the remaining four datasets were used in the statistical fitting procedure. Both the selected data and their experimental uncertainties are shown in Fig. 2 together with the Padé fit (L = 14, N = 49, Χ² = 1.63) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 1

Six experimental datasets for the ⁴⁴Ca(p,n)⁴⁴Sc reaction available in the literature [33,34,35,36,37,38], and TENDL calculations

Fig. 2

Three selected experimental datasets for the ⁴⁴Ca(p,n)⁴⁴Sc reaction [33, 36, 38] with the Padé fit (L = 19, N = 56, χ² = 1.86, solid line), and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁴⁴Ca(d,2n) ^44gSc

Only one experimental dataset is available in the literature, and is shown in Fig. 3 [39] together with the TENDL calculations. These data and their experimental uncertainties are shown in Fig. 4 together with the Padé fit (L = 9, N = 9, χ² = 0.53) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 3

One experimental dataset for the ⁴⁴Ca(d,2n)^44gSc reaction available in the literature [39], and TENDL calculations

Fig. 4

Experimental dataset for the ⁴⁴Ca(d,2n)^44gSc reaction [39] with the Padé fit (L = 9, N = 9, χ² = 0.53, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁴³Ca(d,n)^44gSc

Only one experimental dataset is available in the literature, and is shown in Fig. 5 [40] together with the TENDL calculations. These data and their experimental uncertainties are shown in Fig. 6 together with the Padé fit (L = 5, N = 16, χ² = 1.49) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 5

One experimental dataset for the ⁴³Ca(d,n)^44gSc reaction available in the literature [40], and TENDL calculations

Fig. 6

Experimental dataset for the ⁴³Ca(d,n)^44gSc reaction [40] with the Padé fit (L = 5, N = 16, χ² = 1.49, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁴⁵Sc(p,2n)⁴⁴Ti

The five experimental datasets available in the literature are shown in Fig. 7 [36, 41,42,43] together with the TENDL calculations—Ref. [42] contains two sets labelled (a) and (b). Three datasets were rejected (both datasets of Ejnisman et al. [42], and McGee et al. [41] exhibit significant disagreement), while the remaining two datasets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 8 together with the Padé fit (L = 7, N = 26, χ² = 1.58) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 7

Five experimental datasets for the ⁴⁵Sc(p,2n)⁴⁴Ti reaction available in the literature [36, 41,42,43], and TENDL calculations

Fig. 8

Two selected experimental datasets for the ⁴⁵Sc(p,2n)⁴⁴Ti reaction [36, 43] with the Padé fit (L = 7, N = 26, χ² = 1.58, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁴⁵Sc(d,3n)⁴⁴Ti

Only one experimental dataset is available in the literature, and is shown in Fig. 9 [44] together with the TENDL calculations. These data and their experimental uncertainties are shown in Fig. 10 together with the Padé fit (L = 6, N = 18, χ² = 0.406) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 9

One experimental dataset for the ⁴⁵Sc(d,3n)⁴⁴Ti reaction available in the literature [44], and TENDL calculations

Fig. 10

One experimental dataset for the ⁴⁵Sc(d,3n)⁴⁴Ti reaction [44] with the Padé fit (L = 6, N = 18, χ² = 0.406, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ^44gSc, and long-lived ⁴⁴Ti parent

See Figs. 11 and 12.

Fig. 11

Thick target yields calculated from the recommended cross sections for the ⁴⁴Ca(p,n)^44gSc, ⁴⁴Ca(d,2n)^44gSc and ⁴³Ca(d,n)^44gSc reactions

Fig. 12

Thick target yields calculated from the recommended cross sections for the ⁴⁵Sc(p,2n)⁴⁴Ti and ⁴⁵Sc(d,3n)⁴⁴Ti reactions to produce long-lived parent for ⁴⁴Sc generator

Production of ^52mMn (T _1/2 = 21.1 min) and longer-lived ⁵²Fe parent (T _1/2 = 8.275 h)

Applications: ^52mMn has been suggested for myocardial and cerebral perfusion imaging, more recently for studies similar to Mn-enhanced neuronal MRI, and for diagnosis in other organ systems—bones, spinal cord and the digestive tract.

^52mMn (21.1 min): β⁺ (96.6%), and E_γ (keV) (P_γ(%)): 1434.092 (98.2).

⁵²Fe (8.275 h): detected by means of radiation emitted from daughter ^52mMn.

Evaluations have been made of the ⁵²Cr(p,n)^52mMn and ⁵²Cr(d,2n)^52mMn direct production routes and ^natNi(p,x)⁵²Fe, ⁵⁵Mn(p,4n)⁵²Fe and ⁵⁰Cr(α,2n)⁵²Fe reactions for indirect production through decay of the longer-lived parent.

^natNi(p,x)⁵²Fe

The four experimental datasets available in the literature are shown in Fig. 13 [45,46,47,48] together with he TENDL calculations. One set was rejected (Titarenko et al. [47], values too high), and the remaining three datasets were used in the statistical fitting procedure. These selected data and their experimental uncertainties are shown in Fig. 14 together with the Padé fit (L = 11, N = 41, χ² = 0.57) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 13

Four experimental datasets for the ^natNi(p,x)⁵²Fe reaction available in the literature [45,46,47,48], and TENDL calculations

Fig. 14

Three selected experimental datasets for the ^natNi(p,x)⁵²Fe reaction [45, 46, 48] with the Padé fit (L = 11, N = 41, χ² = 0.57, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵⁵Mn(p,4n)⁵²Fe

The four experimental datasets available in the literature are shown in Fig. 15 [46, 49,50,51] together with the TENDL calculations. All sets were used for the statistical fitting procedure. These data and their experimental uncertainties are shown in Fig. 16 together with the Padé fit (L = 17, N = 157, χ² = 1.01) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 15

Four experimental datasets for the ⁵⁵Mn(p,4n)⁵²Fe reaction available in the literature [46, 49,50,51], and TENDL calculations

Fig. 16

Four experimental datasets for the ⁵⁵Mn(p,4n)⁵²Fe reaction [46, 49,50,51] with the Padé fit (L = 17, N = 157, χ² = 1.01, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵⁰Cr(α,2n)⁵²Fe

The four experimental datasets available in the literature are shown in Fig. 17 [36, 52,53,54] together with the TENDL calculations. Two datasets were rejected (Akiha et al. [52], energy shift; Chowdhury et al. [53], unusual shape,with one outlying data point at 27.3 MeV not represented in Fig. 17), while the remaining two datasets were used in the statistical fitting procedure. Both the selected data and their experimental uncertainties are shown in Fig. 18 together with the Padé fit (L = 9, N = 52, χ² = 0.616, solid line) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 17

Four experimental datasets for the ⁵⁰Cr(α,2n)⁵²Fe reaction available in the literature [36, 52,53,54], and TENDL calculations

Fig. 18

Two selected experimental datasets for the ⁵⁰Cr(α,2n)⁵²Fe reaction [36, 54] with the Padé fit (L = 9, N = 52, χ² = 0.616, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵²Cr(p,n)^52mMn

The nine experimental datasets available in the literature are shown in Fig. 19 [36, 55,56,57,58,59,60,61,62] together with the TENDL calculations. Three datasets were rejected (Blosser and Handley [56], Wing and Huizenga [58], and West et al. [62], all values too high), while the remaining six datasets were used in the statistical fitting procedure. Both the selected data and their experimental uncertainties are shown in Fig. 20 together with the Padé fit (L = 14, N = 68, χ² = 1.15) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 19

Nine experimental datasets for the ⁵²Cr(p,n)^52mMn reaction available in the literature [36, 55,56,57,58,59,60,61,62], and TENDL calculations

Fig. 20

Six selected experimental datasets for the ⁵²Cr(p,n)^52mMn reaction [36, 55, 57, 59,60,61] with the Padé fit (L = 14, N = 68, χ² = 1.15, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵²Cr(d,2n)^52mMn

The two experimental datasets available in the literature are shown in Fig. 21 [62, 63] together with the TENDL calculations. Both datasets were used for the statistical fitting procedure. These data and their experimental uncertainties are shown in Fig. 22 together with the Padé fit (L = 8, N = 16, χ² = 0.71) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 21

Two experimental datasets for the ⁵²Cr(d,2n)^52mMn reaction available in the literature [62, 63], and TENDL calculations

Fig. 22

Two experimental datasets for the ⁵²Cr(d,2n)^52mMn reaction [62, 63] with the Padé fit (L = 8, N = 16, χ² = 0.71, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ^52mMn, and long-lived ⁵²Fe parent

See Figs. 23 and 24.

Fig. 23

Thick target yields calculated from the recommended cross sections for the ⁵²Cr(p,n)^52mMn and ⁵²Cr(d,2n)^52mMn reactions

Fig. 24

Thick target yields calculated from the recommended cross sections for the ^natNi(p,x)⁵²Fe, ⁵⁵Mn(p,4n)⁵²Fe and ⁵⁰Cr(α,2n)⁵²Fe parent reactions

Production of ^52gMn (T _½ = 5.591 d)

Applications: The longer-lived ⁵²Mn ground state has potential as a PET tracer for preclinical in vivo neuroimaging and other applications such as cell tracking, immuno-PET and functional β-cell mass quantification. Unfortunately, a half-life of 5.591 d coupled with an extremely high radiation burden that arises from the resulting gamma-ray emissions has limited ^52gMn clinical applications.

^52gMn (5.591 d): β⁺ (29.4%), and E_γ (keV) (P_γ(%)): 744.233 (90.0), 935.544 (94.5), 1434.092 (100).

Evaluations have been made of the direct ⁵²Cr(p,n)^52gMn(m+) and ⁵²Cr(d,2n)^52gMn(m+) production routes, including the partial decay of the simultaneously produced short-lived ^52mMn metastable state (IT = 1.78%, noted as (m+)) which has already been assessed and discussed in section “Production of ^52mMn (T_1/2 = 21.1 min) and longer-lived ⁵²Fe parent (T_1/2 = 8.275 h)”.

⁵²Cr(p,n)^52gMn (m+)

The thirteen experimental datasets available in the literature are shown in Fig. 25 [36, 55, 56, 58, 59, 61, 62, 64,65,66,67,68,69] together with the TENDL calculations. Six sets of data were rejected (Blosser and Handley [56], Tanaka and Furukawa [64], Lindner and James [65], Antropov et al. [66], Buchholz et al. [67], and Zherebchevsky et al. [69], all disagree significantly with the other datasets), while the remaining seven datasets were used in the statistical fitting procedure. These selected data and their experimental uncertainties are shown in Fig. 26 together with the Padé fit (L = 9, N = 103, χ² = 1.84) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 25

Thirteen experimental datasets for the ⁵²Cr(p,n)^52gMn(m+) reaction available in the literature [36, 55, 56, 58, 59, 61, 62, 64,65,66,67,68,69], and TENDL calculations

Fig. 26

Seven selected experimental datasets for the ⁵²Cr(p,n)^52gMn(m+) reaction [36, 55, 58, 59, 61, 62, 68] with the Padé fit (L = 9, N = 103, χ² = 1.84, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵²Cr(d,2n)^52gMn(m+)

The six experimental datasets available in the literature are shown in Fig. 27 [62, 63, 70,71,72,73] together with the TENDL calculations. Two sets were rejected (Cheng Xiaowu et al. [71], values too low and no contribution from decay of metastable state marked as “g” in Fig. 27, and Nassiff and Münzel [72], values too high), and the remaining four datasets were used in the statistical fitting procedure. These selected data and their experimental uncertainties are shown in Fig. 28 together with the Padé fit (L = 8, N = 36, χ² = 0.54) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 27

Six experimental datasets for the ⁵²Cr(d,2n)^52gMn(m+) reaction available in the literature [62, 63, 70,71,72,73], and TENDL calculations

Fig. 28

Four selected experimental datasets for the ⁵²Cr(d,2n)^52gMn(m+) reaction [62, 63, 70, 73] with the Padé fit (L = 8, N = 36, χ² = 0.54, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ^52gMn(m+)

See Fig. 29.

Fig. 29

Thick target yields calculated from the recommended cross sections for the ⁵²Cr(p,n)^52gMn(m+) and ⁵²Cr(d,2n)^52gMn(m+) reactions

Production of ⁵⁵Co (T _1/2 = 17.53 h)

Applications: ⁵⁵Co is a typical example of a positron emitter of sufficient half-life to follow kinetic processes that function over a longer timescale. This radionuclide has been used to target the epidermal growth factor (EGFR) by means of labelled DOTA-conjugated Affibody. Exhibits lower liver and heart uptake for metal-chelate peptide complexes, with improved performance when compared with ⁶⁸Ga. Also used as a Ca²⁺ analogue in imaging studies of Alzheimer disease, and shows promise in achieving improved imaging of cancer diseases.

⁵⁵Co (17.53 h): β⁺ (76%), and E_γ (keV) (P_γ(%)): 931.1 (75), 1316.6 (7.1).

⁵⁸Ni(p,α)⁵⁵Co, ⁵⁴Fe(d,n)⁵⁵Co and ⁵⁶Fe(p,2n)⁵⁵Co production routes have been evaluated.

⁵⁸Ni(p,α)⁵⁵Co

The seventeen experimental datasets available in the literature are shown in Fig. 30 [36, 45, 59, 74,75,76,77,78,79,80,81,82,83,84,85,86,87] together with the TENDL calculations. One dataset was rejected (Haasbroek et al. [76], values too high), while the remaining sixteen datasets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 31 together with the Padé fit (L = 10, N = 352, χ² = 1.97) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 30

Seventeen experimental datasets for the ⁵⁸Ni(p,α)⁵⁵Co reaction available in the literature [36, 45, 59, 74,75,76,77,78,79,80,81,82,83,84,85,86,87], and TENDL calculations

Fig. 31

Sixteen selected experimental datasets for the ⁵⁸Ni(p,α)⁵⁵Co reaction [36, 45, 59, 74, 75, 77,78,79,80,81,82,83,84,85,86,87] with the Padé fit (L = 10, N = 352, χ² = 1.97, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵⁴Fe(d,n)⁵⁵Co

The ten experimental datasets available in the literature are shown in Fig. 32 [88,89,90,91,92,93,94,95,96,97] together with the TENDL calculations. One dataset was rejected (Clark et al. [89], values too high), while the remaining nine datasets were used in the statistical fitting procedure (although some very discrepant points around 10 MeV from Hermanne [94] and the highest three points from Zhenlan [91] were also discarded). The selected data and their experimental uncertainties are shown in Fig. 33 together with the Padé fit (L = 13, N = 170, χ² = 2.14) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 32

Ten experimental datasets for the ⁵⁴Fe(d,n)⁵⁵Co reaction available in the literature [88,89,90,91,92,93,94,95,96,97], and TENDL calculations

Fig. 33

Nine selected experimental datasets for the ⁵⁴Fe(d,n)⁵⁵Co reaction [88, 90,91,92,93,94,95,96,97] with the Padé fit (L = 13, N = 170, χ² = 2.14, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁵⁶Fe(p,2n)⁵⁵Co

The fifteen experimental datasets available in the literature are shown in Fig. 34 [36, 59, 82, 98,99,100,101,102,103,104,105,106,107,108,109] together with the TENDL calculations. Four datasets were rejected (Michel et al. [82], Cohen and Newman [98], Williams and Fulmer [99], and Ditrói et al. [107], all show discrepant values), and the remaining eleven sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 35 together with the Padé fit (L = 8, N = 101, χ² = 2.74) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 34

Fifteen experimental datasets for the ⁵⁶Fe(p,2n)⁵⁵Co reaction available in the literature [36, 59, 82, 98,99,100,101,102,103,104,105,106,107,108,109], and TENDL calculations

Fig. 35

Eleven selected experimental datasets for the ⁵⁶Fe(p,2n)⁵⁵Co reaction [36, 59, 100,101,102,103,104,105,106, 108, 109] with the Padé fit (L = 8, N = 101, χ² = 2.74, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁵⁵Co

See Fig. 36.

Fig. 36

Thick target yields calculated from the recommended cross sections for the ⁵⁸Ni(p,α)⁵⁵Co, ⁵⁴Fe(d,n)⁵⁵Co and ⁵⁶Fe(p,2n)⁵⁵Co reactions

Production of ⁶¹Cu (T _½ = 3.339 h)

Applications: Copper radionuclides form stable complexes with several chelators that can be conjugated to a wide variety of organic molecules for both imaging (⁶¹Cu, ⁶²Cu, ⁶⁴Cu) and radiotherapy (⁶⁴Cu, ⁶⁷Ci). Relatively longer-lived ⁶¹Cu (T_½ = 3.339 h, 61% β⁺, 39% EC) possesses very good imaging properties that can be used for blood flow studies in a similar manner to ⁵¹Cr. Also has been applied to blood pool imaging (DOTA-human serum albumin) and the study of hypoxia in tumours (coupled to ATSM)—useful for following kinetics processes of the order of a few hours.

⁶¹Cu (3.339 h): β⁺ (61%), and E_γ (keV) (P_γ(%)): 282.956 (12.2), 656.008 (10.8), 1185.234 (3.7).

Evaluations have been made of the ⁶¹Ni(p,n)⁶¹Cu, ⁶⁰Ni(d,n)⁶¹Cu and ⁶⁴Zn(p,α)⁶¹Cu direct production routes.

⁶¹Ni(p,n)⁶¹Cu

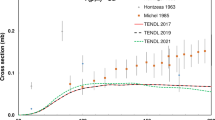
The seventeen experimental datasets available in the literature are shown in Fig. 37 [45, 56, 59, 64, 78, 79, 84, 87, 110,111,112,113,114,115,116,117] together with the TENDL calculations. Ref. [112] contains two datasets, labelled (a) and (b). Five datasets were rejected (Blosser and Handley [56], Tanaka and Furukawa [64], Barrandon et al. [59], Michel et al. [78], and Al-Saleh et al. [84], all of these datasets exhibit maximum values that are too high), and the remaining twelve sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 38 together with the Padé fit (L = 12, N = 192, χ² = 2.81) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 37

Seventeen experimental datasets for the ⁶¹Ni(p,n)⁶¹Cu reaction available in the literature [45, 56, 59, 64, 78, 79, 84, 87, 110,111,112,113,114,115,116,117], and TENDL calculations

Fig. 38

Twelve selected experimental datasets for the ⁶¹Ni(p,n)⁶¹Cu reaction [45, 79, 87, 110,111,112,113,114,115,116,117] with the Padé fit (L = 12, N = 192, χ² = 2.81, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶⁰Ni(d,n)⁶¹Cu

The five experimental datasets available in the literature are shown in Fig. 39 [90, 118,119,120,121] together with the TENDL calculations. All datasets were used in the statistical fitting procedure (Cogneau et al. [118] data were normalised, and data above 6-MeV particle beam energy discarded as inconsistent with model calculations). All of the data and their experimental uncertainties are shown in Fig. 40 together with the Padé fit (L = 16, N = 29, χ² = 1.16) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). This reaction is the main contributor to the formation of ⁶¹Cu on natural Ni by deuterons, adopted as a suitable beam monitor (see Ref. [30], Sect. 3.I).

Fig. 39

Five experimental datasets for the ⁶⁰Ni(d,n)⁶¹Cu reaction available in the literature [90, 118,119,120,121], and TENDL calculations

Fig. 40

Five experimental datasets for the ⁶⁰Ni(d,n)⁶¹Cu reaction [90, 118,119,120,121] with the Padé fit (L = 16, N = 29, χ² = 1.16, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶⁴Zn(p,α)⁶¹Cu

The seven experimental datasets available in the literature are shown in Fig. 41 [36, 59, 122,123,124,125,126] together with the TENDL calculations. One dataset was rejected (Barrandon et al. [59], discrepant behaviour near maximum), and the remaining six sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 42 together with the Padé (L = 12, N = 72, χ² = 0.88) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 41

Seven experimental datasets for the ⁶⁴Zn(p,α)⁶¹Cu reaction available in the literature [36, 59, 122,123,124,125,126], and TENDL calculations

Fig. 42

Six selected experimental datasets [36, 122,123,124,125,126] for the ⁶⁴Zn(p,α)⁶¹Cu reaction with the Padé fit (L = 12, N = 72, χ² = 0.88, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁶¹Cu

See Fig. 43.

Fig. 43

Thick target yields calculated from the recommended cross sections for the ⁶¹Ni(p,n)⁶¹Cu, ⁶⁰Ni(d,n)⁶¹Cu and ⁶⁴Zn(p,α)⁶¹Cu reactions

Production of ⁶²Cu (T _1/2 = 9.67 min) and longer-lived ⁶²Zn parent (T _1/2 = 9.193 h)

Applications: As stated earlier, copper isotopes form stable complexes with several chelators that can be conjugated to a wide variety of organic molecules for both imaging (⁶¹Cu, ⁶²Cu, ⁶⁴Cu) and therapy (⁶⁴Cu, ⁶⁷Ci). Short-lived ⁶²Cu has been proposed for the labelling of PTSM (pyruvaldehyde bis) to undertake myocardial and brain blood flow studies.

⁶²Cu (9.67 min): β⁺ (97.83%), and E_γ (keV) (P_γ(%)): 875.66 (0.147), 1172.97 (0.342).

⁶²Zn (9.193 h): β⁺ (8.2%), and E_γ (keV) (P_γ(%)): 548.35 (15.3), 596.56 (26).

Evaluations have been made of the ⁶³Cu(p,2n)⁶²Zn, ⁶³Cu(d,3n)⁶²Zn and ^natNi(α,xn)⁶²Zn indirect, and ⁶²Ni(p,n)⁶²Cu and ⁶²Ni(d,2n)⁶²Cu direct production routes.

⁶³Cu(p,2n)⁶²Zn

Twenty-four experimental datasets available in the literature are shown in Fig. 44 [36, 82, 98, 99, 127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146] together with the TENDL calculations. Seven datasets were rejected (Ghoshal [127], Williams and Fulmer [99], Greene and Lebowitz [128], Greenwood and Smither [130], Aleksandrov et al. [132], Levkovskij [36], and Tárkányi et al. [142], all disagree significantly with the other datasets), and the remaining seventeen sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 45 together with the Padé fit (L = 16, N = 213, χ² = 1.89) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). As the only reaction known to contribute to the formation of ⁶²Zn on ^natCu for protons below 30 MeV, the fitted data have been adopted as a beam monitor in this energy region (see Ref. [30], Sect. 2.6).

Fig. 44

Twenty-four experimental datasets for the ⁶³Cu(p,2n)⁶²Zn reaction available in the literature [36, 82, 98, 99, 127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146], and TENDL calculations

Fig. 45

Seventeen selected experimental datasets for the ⁶³Cu(p,2n)⁶²Zn reaction [82, 98, 129, 131, 133,134,135,136,137,138,139,140,141, 143,144,145,146] with the Padé fit (L = 16, N = 213, χ² = 1.89, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶³Cu(d,3n)⁶²Zn

While a known dataset by Bartell et al. [147] is not represented in Fig. 46 because the values are totally discrepant even after arbitrary normalisation, eight other experimental datasets available in the literature are shown [73, 95, 148,149,150,151,152,153] together with the TENDL calculations. The data by Fulmer and Williams [148] were subsequently rejected because they disagree significantly with the other datasets (attributed to the normalisation of inadequately defined low-intensity decay data). All of the remaining seven datasets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 47 together with the Padé fit (L = 12, N = 82, χ² = 1.89) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). As the only reaction known to contribute to the formation of ⁶²Zn on ^natCu for deuterons below 35 MeV, the fitted data have been adopted as a beam monitor in this energy region (see Ref. [30], Section III E).

Fig. 46

Eight experimental datasets for the ⁶³Cu(d,3n)⁶²Zn reaction available in the literature [73, 95, 148,149,150,151,152,153], and TENDL calculations

Fig. 47

Seven selected experimental datasets for the ⁶³Cu(d,3n)⁶²Zn reaction [73, 95, 149,150,151,152,153] with the Padé fit (L = 12, N = 82, χ² = 1.89, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

^natNi(α,xn)⁶²Zn

The nine experimental datasets available in the literature are shown in Fig. 48 [36, 127, 154,155,156,157,158,159,160] together with the TENDL calculations. Three datasets were rejected (Neirinckx [155] (energy shift near threshold), Singh et al. [159] (discrepant values at energies below 35 MeV), and Yadav et al. [160] (value too low)), and the remaining six sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 49 together with the Padé fit (L = 21, N = 45, χ² = 1.72) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 48

Nine experimental datasets for the ^natNi(α,xn)⁶²Zn reaction available in the literature [36, 127, 154,155,156,157,158,159,160], and TENDL calculations

Fig. 49

Six selected experimental datasets for the ^natNi(α,xn)⁶²Zn reaction [36, 127, 154, 156,157,158] with the Padé fit (L = 10, N = 45, χ² = 1.74, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶²Ni(p,n)⁶²Cu

The seven experimental datasets available in the literature are shown in Fig. 50 [36, 45, 66, 110, 161,162,163] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 51 together with the Padé fit (L = 12, N = 77, χ² = 1.33) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 50

Seven experimental datasets for the ⁶²Ni(p,n)⁶²Cu reaction available in the literature [36, 45, 66, 110, 161,162,163], and TENDL calculations

Fig. 51

Seven experimental datasets [36, 45, 66, 110, 161,162,163] for the ⁶²Ni(p,n)⁶²Cu reaction with the Padé fit (L = 12, N = 77, χ² = 1.33, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶²Ni(d,2n)⁶²Cu

The single dataset available in the literature is shown in Fig. 52 [118] together with the TENDL calculations. This dataset was used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 53 together with the Padé fit (L = 5, N = 16, χ² = 0.83) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 52

Experimental dataset for the ⁶²Ni(d,2n)⁶²Cu reaction available in the literature [118], and TENDL calculations

Fig. 53

Experimental dataset for the ⁶²Ni(d,2n)⁶²Cu reaction [118] with the Padé fit (L = 5, N = 16, χ² = 0.83, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁶²Cu, and ⁶²Zn parent

See Figs. 54 and 55.

Fig. 54

Thick target yields calculated from the recommended cross sections for the ⁶²Ni(p,n)⁶²Cu and ⁶²Ni(d,2n)⁶²Cu reactions

Fig. 55

Thick target yields calculated from the recommended cross sections for the ⁶³Cu(p,2n)⁶²Zn, ⁶³Cu(d,3n)⁶²Zn and ^natNi(α,xn)⁶²Zn reactions

Production of ⁶⁶Ga (T _½ = 9.49 h)

Applications: Both ⁶⁶Ga and ⁶⁸Ga are positron-emitting radionuclides that can be used in PET imaging. Longer-lived ⁶⁶Ga has been coupled to monoclonal antibodies (e.g., for tumour angiogenesis studies) and to nanoparticles. This radionuclide has also been proposed in hadron therapy as an in situ marker for the incorporation of Zn in tumours. Obvious disadvantages are the rather high radiation burden and inferior imaging properties caused by the many gamma rays that accompany decay.

⁶⁶Ga (9.49 h): β⁺ (57%), and E_γ (keV) (P_γ(%)): 833.5324 (5.9), 1039.220 (37.0).

Evaluations have been made of the ⁶⁶Zn(p,n)⁶⁶Ga and ⁶³Cu(α,n)⁶⁶Ga direct production routes.

⁶⁶Zn(p,n)⁶⁶Ga

The twenty experimental datasets available in the literature are shown in Fig. 56 [36, 56, 59, 124, 125, 164,165,166,167,168,169,170,171,172,173,174,175,176,177] together with the TENDL-2015 and TENDL-2017 calculations. Hermanne [173] contains two datasets labelled (a) and (b).Twelve datasets were rejected (Little and Lagunas-Solar [167] (values too low), Nortier et al. [171] (energy shift), Blosser and Handley [56] (only one data point that can not be checked), Howe [165] (energy shift), Kopecký [168] (values too low), Asad et al. [125] (values too low), Szelecsényi et al. [172] (preliminary results), Hermanne [173] set b (discrepant data points), Barrandon et al. [59] (values too low), Al-Saleh et al. [177] (values too low), Uddin et al. [124] (values too low), and Blaser et al. [164] (discrepant data points)), while the remaining eight sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 57 together with the Padé (L = 13, N = 188, χ² = 1.87) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 56

Twenty experimental datasets) for the ⁶⁶Zn(p,n)⁶⁶Ga reaction available in the literature [36, 56, 59, 124, 125, 164,165,166,167,168,169,170,171,172,173,174,175,176,177], and TENDL calculations. Ref. [173] contains two datasets labelled (a) and (b)

Fig. 57

Eight selected experimental datasets for the ⁶⁶Zn(p,n)⁶⁶Ga reaction [36, 166, 169, 170, 173,174,175,176] with the Padé fit (L = 13, N = 188, χ² = 1.87, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶³Cu(α,n)⁶⁶Ga

The twenty-three experimental datasets available in the literature are shown in Fig. 58 [36, 54, 81, 166, 178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196] together with the TENDL calculations. Seven datasets were rejected (Porges [178] (values too low), Bonesso et al. [188] (values too low), Zhukova et al. [182] (values too low), Singh et al. [190] (values too low), Rizvi et al. [184] (values too low), Porile and Morrison [179] (values too low), and Nassiff and Nassiff [183] (discrepant data points)), and the remaining sixteen sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 59 together with the Padé (L = 13, N = 252, χ² = 1.34) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). This reaction is also used to monitor α-particle beams (see Ref. [30], Section V D).

Fig. 58

Twenty-three experimental datasets for the ⁶³Cu(α,n)⁶⁶Ga reaction available in the literature [36, 54, 81, 166, 178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196], and TENDL calculations

Fig. 59

Sixteen selected experimental datasets for the ⁶³Cu(α,n)⁶⁶Ga reaction [36, 54, 81, 166, 180, 181, 185,186,187, 189, 191,192,193,194,195,196] with the Padé fit (L = 13, N = 252, χ² = 1.34, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁶⁶Ga

See Fig. 60.

Fig. 60

Thick target yields calculated from the recommended cross sections for the ⁶⁶Zn(p,n)⁶⁶Ga and ⁶³Cu(α,n)⁶⁶Ga reactions

Production of ⁶⁸Ga (T _1/2 = 67.71 min) and long-lived ⁶⁸Ge parent (T _1/2 = 270.95 d)

Applications: Rather short-lived ⁶⁸Ga became the first widespread generator-produced positron emitter, thereby competing somewhat with ¹⁸F for preferred adoption in PET imaging. First introduced for the imaging of neuroendocrine tumours (⁶⁸Ga-labelled DOTA-TOC), more recent significant success has been achieved in the form of very efficient imaging agents for prostate cancer diagnosis and staging (⁶⁸Ga-DOTA-PSMA and derivatives).

⁶⁸Ga (67.71 min): β⁺ (88.91%), and E_γ (keV) (P_γ(%)): 1077.34 (3.22).

⁶⁸Ge (270.95 d): detected by means of radiation from daughter ⁶⁸Ga.

Evaluations have been undertaken of the ⁶⁸Zn(p,n)⁶⁸Ga and ⁶⁵Cu(α,n)⁶⁸Ga direct routes and ^natGa(p,x)⁶⁸Ge and ⁶⁹Ga(p,2n)⁶⁸Ge generator production.

⁶⁸Zn(p,n)⁶⁸Ga

The eighteen experimental datasets available in the literature are shown in Fig. 61 [36, 41, 56, 59, 111, 162, 164,165,166, 169, 170, 173, 177, 195, 197,198,199,200] together with the TENDL calculations. Five datasets were rejected (Hermanne et al. [170] (energy shift), Blosser and Handley [56] (value too high), McGee et al. [41] (value too low), Hermanne [173] (energy shift), and Barrandon et al. [59] (values too low)), and the remaining thirteen sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 62 together with the Padé (L = 20, N = 282, χ² = 1.97) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 61

Eighteen experimental datasets for the ⁶⁸Zn(p,n)⁶⁸Ga reaction available in the literature [36, 41, 56, 59, 111, 162, 164,165,166, 169, 170, 173, 177, 195, 197,198,199,200], and TENDL calculations

Fig. 62

Thirteen selected experimental datasets for the ⁶⁸Zn(p,n)⁶⁸Ga reaction [36, 111, 162, 164,165,166, 169, 177, 195, 197,198,199,200] with the Padé fit (L = 20, N = 282, χ² = 1.97, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶⁵Cu(α,n)⁶⁸Ga

The fourteen experimental datasets available in the literature are shown in Fig. 63 [36, 54, 166, 178,179,180, 184, 186, 188, 190, 195, 196, 201, 202] together with the TENDL calculations. Four datasets were rejected (Porile and Morrison [179] (energy shift), Rizvi et al. [184] (energy shift), Bonesso et al. [188] (values too high), and Porges [178] (values too low)), and the remaining ten sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 64 together with the Padé (L = 10, N = 92, χ² = 1.21) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 63

Fourteen experimental datasets for the ⁶⁵Cu(α,n)⁶⁸Ga reaction available in the literature [36, 54, 166, 178,179,180, 184, 186, 188, 190, 195, 196, 201, 202], and TENDL calculations

Fig. 64

Ten selected experimental datasets for the ⁶⁵Cu(α,n)⁶⁸Ga reaction [36, 54, 166, 180, 186, 190, 195, 196, 201, 202] with the Padé fit (L = 10, N = 92, χ² = 1.21, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

^natGa(p,xn)⁶⁸Ge

The six experimental datasets available in the literature are shown in Fig. 65 [36, 48, 98, 203, 204] together with the TENDL calculations. Hermanne et al. [48] contains two datasets labelled (a) and (b). One dataset was rejected (Cohen and Newman [98], single data point too low), and the remaining five sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 66 together with the Padé (L = 11, N = 101, χ² = 1.42) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 65

Six experimental datasets for the ^natGa(p,xn)⁶⁸Ge reaction available in the literature [36, 48, 98, 203, 204], and TENDL calculations. Hermanne et al. [48] contains two sets of data labelled (a) and (b)

Fig. 66

Five selected experimental datasets for the ^natGa(p,xn)⁶⁸Ge reaction [36, 48, 203, 204] with the Padé fit (L = 11, N = 101, χ² = 1.42, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁶⁹Ga(p,2n)⁶⁸Ge

The four experimental datasets available in the literature are shown in Fig. 67 [36, 48, 203, 204] together with the TENDL calculations. All sets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 68 together with the Padé (L = 8, N = 53, χ² = 1.56) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 67

Four experimental datasets for the ⁶⁹Ga(p,2n)⁶⁸Ge reaction available in the literature [36, 48, 203, 204], and TENDL calculations

Fig. 68

Four experimental datasets for the ⁶⁹Ga(p,2n)⁶⁸Ge reaction [36, 48, 203, 204] with the Padé fit (L = 8, N = 53, χ² = 1.56, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for ⁶⁸Ga, and long-lived ⁶⁸Ge parent for generator

See Figs. 69 and 70.

Fig. 69

Thick target yields calculated from the recommended cross sections for the ⁶⁸Zn(p,n)⁶⁸Ga and ⁶⁵Cu(α,n)⁶⁸Ga direct reactions

Fig. 70

Thick target yields calculated from the recommended cross sections for the ^natGa(p,xn)⁶⁸Ge and ⁶⁹Ga(p,2n)⁶⁸Ge reactions to produce long-lived parent for ⁶⁸Ga generator

Production of ⁷²As (T _1/2 = 26.0 h) and longer-lived ⁷²Se parent (T _1/2 = 8.40 d)

Applications: ⁷²As is a long-lived positron-emitting radionuclide suitable for imaging the bio-distribution of monoclonal antibodies with long biological half-lives that are promising in PET oncological research. Chemical properties offer the possibility of covalent bonding to thiol groups.

⁷²As (26.0 h): β⁺ (87.8%), and E_γ (keV) (P_γ(%)): 629.92 (8.07), 833.99 (81).

⁷²Se (8.40 d): detected by means of radiation emitted by daughter ⁷²As.

Evaluations have been undertaken of the ⁷⁵As(p,4n)⁷²Se and ^natBr(p,x)⁷²Se routes for parent production, and the ^natGe(p,xn)⁷²As and ^natGe(d,xn)⁷²As direct production routes.

⁷⁵As(p,4n)⁷²Se

The two experimental datasets available in the literature for the energy domain considered are shown in Fig. 71 [205, 206] together with the TENDL calculations. Both datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 72 together with the Padé fit (L = 8, N = 33, χ² = 1.30) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 71

Two experimental datasets for the ⁷⁵As(p,4n)⁷²Se reaction available in the literature [205, 206], and TENDL calculations

Fig. 72

Two experimental datasets for the ⁷⁵As(p,4n)⁷²Se reaction [205, 206] with the Padé fit (L = 8, N = 33, χ² = 1.30, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

^natBr(p,x)⁷²Se

The two experimental datasets available in the literature are shown in Fig. 73 [207, 208] together with the TENDL calculations. Both sets of measurements by Fassbender et al. [207] and de Villiers et al. [208] originate from the same experimental study, and should be identical. Therefore, the data of de Villers et al. [208] were set aside, while only the other dataset was used in the statistical fitting procedure. These selected data and their experimental uncertainties are shown in Fig. 74 together with the Padé fit (L = 10, N = 14, χ² = 0.35) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). The contributions of the similar (p,2pxn) reactions on the two stable isotopes of Br can be clearly distinguished (⁷⁹Br: 50.69%; ⁸¹Br: 49.31%).

Fig. 73

Two experimental datasets for the ^natBr(p,x)⁷²Se reaction available in the literature [207, 208], and TENDL calculations

Fig. 74

One selected experimental dataset for the ^natBr(p,x)⁷²Se reaction [207] with the Padé fit (L = 10, N = 14, χ² = 0.35, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

^natGe(p,xn)⁷²As

The four experimental datasets available in the literature are shown in Fig. 75 [36, 209,210,211] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 76 together with the Padé (L = 18, N = 123, χ² = 1.97) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). Contributions of similar (p,xn) reactions with increasing thresholds can be clearly distinguished for the higher abundance ⁷²Ge,⁷⁴Ge and ⁷⁶Ge.

Fig. 75

Four experimental datasets for the ^natGe(p,xn)⁷²As reaction available in the literature [36, 209,210,211], and TENDL calculations

Fig. 76

Four experimental datasets for the ^natGe(p,xn)⁷²As reaction [36, 209,210,211] with the Padé fit (L = 18, N = 123, χ² = 1.97, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

^natGe(d,xn)⁷²As

The single experimental dataset available in the literature is shown in Fig. 77 [212] together with the TENDL calculations. All data points and their experimental uncertainties are shown in Fig. 78 together with the Padé fit (L = 10, N = 25, χ² = 1.13) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). The contribitions of the ⁷²Ge(d,2n) and ⁷⁴Ge(d,4n) reactions on high natural abundance Ge isotopes can be seen in both figures.

Fig. 77

One experimental dataset for the ^natGe(d,xn)⁷²As reaction available in the literature [212], and TENDL calculations

Fig. 78

One experimental dataset for the ^natGe(d,xn)⁷²As reaction [212] with the Padé fit (L = 10, N = 25, χ² = 1.13, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁷²As, and ⁷²Se parent

See Figs. 79 and 80.

Fig. 79

Thick target yields calculated from the recommended cross sections for the ^natGe(p,xn)⁷²As and ^natGe(d,xn)⁷²As reactions

Fig. 80

Thick target yields calculated from the recommended cross sections for the ⁷⁵As(p,4n)⁷²Se and ^natBr(p,x)⁷²Se reactions

Production of ⁷³Se (T _1/2 = 7.15 h)

Applications: ⁷³Se (T_½ = 7.15 h; EC = 34.6%, β⁺ = 65.4%; E_β+(max) = 1.65 MeV) is an interesting β⁺-emitting analogue of sulphur suitable for the imaging of enzymatic systems or sulphur-containing amino acids.

⁷³Se(7.15 h): β⁺ (65.4%), and E_γ (keV) (P_γ(%)): 67.07 (70), 361.2 (97.0).

Evaluations have been made of the ⁷⁵As(p,3n)⁷³Se and ⁷²Ge(α,3n)⁷³Se direct production routes.

⁷⁵As(p,3n)⁷³Se

The four experimental datasets available in the literature are shown in Fig. 81 [36, 206, 213, 214] together with the TENDL calculations. One dataset was rejected (Mushtaq et al. [206] (values too low near maximum)), and the remaining three sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 82 together with the Padé (L = 9, N = 64, χ² = 1.52) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 81

Four experimental datasets for the ⁷⁵As(p,3n)⁷³Se reaction available in the literature [36, 206, 213, 214], and TENDL calculations

Fig. 82

Three selected experimental datasets for the ⁷⁵As(p,3n)⁷³Se reaction [36, 213, 214] with the Padé fit (L = 9, N = 64, χ² = 1.52, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁷²Ge(α,3n)⁷³Se

The two experimental datasets available in the literature are shown in Fig. 83 [36, 215] together with the TENDL calculations. Both datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 84 together with the Padé fit (L = 8, N = 27, χ² = 3.81) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 83

Two experimental datasets for the ⁷²Ge(α,3n)⁷³Se reaction available in the literature [36, 215], and TENDL calculations

Fig. 84

Two experimental datasets for the ⁷²Ge(α,3n)⁷³Se reaction [36, 215] with the Padé fit (L = 8, N = 27, χ² = 3.81, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁷³Se

See Fig. 85.

Fig. 85

Thick target yields calculated from the recommended cross sections for the ⁷⁵As(p,3n)⁷³Se and ⁷²Ge(α,3n)⁷³Se reactions

Production of ⁷⁶Br (T _1/2 = 16.2 h)

Applications: Longer-lived positron-emitting radiohalogens were some of the first radionuclides studied to follow processes with kinetics inappropriate for ¹⁸F application. ⁷⁶Br was used in several studies to label monoclonal antibodies, although the large number of accompanying gamma rays that result in a relatively high radiation burden and poor imaging properties has seen a subsequent decline of interest in this radionuclide.

⁷⁶Br(16.2 h): β⁺ (55%) and E_γ (keV) (P_γ(%)): 559.09 (74), 657.02 (15.9), 1853.67 (14.7).

Evaluations have been made of the ⁷⁶Se(p,n)⁷⁶Br, ⁷⁷Se(p,2n)⁷⁶Br and ⁷⁵As(α,3n)⁷⁶Br production routes.

⁷⁶Se(p,n)⁷⁶Br

The five experimental datasets available in the literature are shown in Fig. 86 [36, 216,217,218,219] together with the TENDL calculations. Two datasets were rejected (Kovács et al. [218] (values too low near maximum), and Hassan et al. [219] (discrepant data near maximum)), and the remaining three sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 87 together with the Padé fit (L = 8, N = 39, χ² = 1.05) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 86

Five experimental datasets for the ⁷⁶Se(p,n)⁷⁶Br reaction available in the literature [36, 216,217,218,219], and TENDL calculations

Fig. 87

Three selected experimental datasets for the ⁷⁶Se(p,n)⁷⁶Br reaction [36, 216, 217] with the Padé fit (L = 8, N = 39, χ² = 1.05, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁷⁷Se(p,2n)⁷⁶Br

The four experimental datasets available in the literature are shown in Fig. 88 [36, 219,220,221] together with the TENDL calculations. Two datasets were rejected (Janssen et al. [220] (values too low), and Hassan et al. [219] (values too high)), and the remaining two sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 89 together with the Padé fit (L = 9, N = 52, χ² = 1.34) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 88

Four experimental datasets for the ⁷⁷Se(p,2n)⁷⁶Br reaction available in the literature [36, 219,220,221], and TENDL calculations

Fig. 89

Two selected experimental datasets for the ⁷⁷Se(p,2n)⁷⁶Br reaction [36, 221] with the Padé fit (L = 9, N = 52, χ² = 1.34, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁷⁵As(α,3n)⁷⁶Br

The five experimental datasets available in the literature are shown in Fig. 90 [216, 217, 222,223,224] together with the TENDL calculations. All datasets were used for the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 91 together with the Padé fit (L = 10, N = 70, χ² = 2.43) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale). An additional dataset published after the evaluation cut-off date was also included in the fit (Breunig et al. [224]) and is shown in Fig. 90.

Fig. 90

Five experimental datasets for the ⁷⁵As(α,3n)⁷⁶Br reaction available in the literature [216, 217, 222,223,224], and TENDL calculations

Fig. 91

Five experimental datasets for the ⁷⁵As(α,3n)⁷⁶Br reaction [216, 217, 222,223,224] with the Padé fit (L = 10, N = 70, χ² = 2.43, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for ⁷⁶Br

See Fig. 92.

Fig. 92

Thick target yields calculated from the recommended cross sections for the ⁷⁶Se(p,n)⁷⁶Br, ⁷⁷Se(p,2n)⁷⁶Br and ⁷⁵As(α,3n)⁷⁶Br reactions

Production of ⁸²Sr parent (T _1/2 = 25.35 d) of short-lived ⁸²Rb (T _1/2 = 1.2575 min)

Applications: Generator-produced ⁸²Rb is widely used in myocardial perfusion imaging, particularly in the USA. This isotope undergoes rapid uptake by myocardiocytes, and therefore is a valuable tool for identifying myocardial ischemia by means of PET. Such a short half-life allows one to perform both stress and rest perfusion studies within 30 min.

⁸²Rb (1.2575 min): β⁺ (95.43%), and E_γ (keV) (P_γ(%)): 776.52 (15.08).

⁸²Sr (25.35 d): detected by means of radiation emitted by daughter ⁸²Rb.

Evaluations have been undertaken of the ^natRb(p,xn)⁸²Sr and ⁸⁵Rb(p,4n)⁸²Sr parent production routes.

^natRb(p,xn)⁸²Sr

The seven experimental datasets available in the literature are shown in Fig. 93 [138, 225,226,227,228,229,230] together with the TENDL calculations. Two datasets were rejected (Horiguchi et al. [225] (values too high), and Deptula et al. [226] (values too high)), and the remaining five sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 94 together with the Padé fit (L = 13, N = 49, χ² = 1.15) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 93

Seven experimental datasets for the ^natRb(p,xn)⁸²Sr reaction available in the literature [138, 225,226,227,228,229,230], and TENDL calculations

Fig. 94

Five selected experimental datasets for the ^natRb(p,xn)⁸²Sr reaction [138, 227,228,229,230] with the Padé fit (L = 13, N = 49, χ² = 1.15, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸⁵Rb(p,4n)⁸²Sr

The five experimental datasets available in the literature are shown in Fig. 95 [138, 225, 227, 229, 230] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 96 together with the Padé fit (L = 9, N = 49, χ² = 1.60) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 95

Five experimental datasets for the ⁸⁵Rb(p,4n)⁸²Sr reaction available in the literature [138, 225, 227, 229, 230], and TENDL calculations

Fig. 96

Five experimental datasets for the ⁸⁵Rb(p,4n)⁸²Sr reaction [138, 225, 227, 229, 230] with the Padé fit (L = 9, N = 49, χ² = 1.60, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for ⁸²Sr parent of short-lived ⁸²Rb

See Fig. 97.

Fig. 97

Thick target yields calculated from the recommended cross sections for the ^natRb(p,xn)⁸²Sr and ⁸⁵Rb(p,4n)⁸²Sr reactions to produce long-lived parent for short-lived ⁸²Rb

Production of ^82mRb (T_½ = 6.472 h)

Applications: Longer-lived ^82mRb isomeric state could possibly act as a substitute for generator-produced ⁸²Rb in PET cardiology centres that operate a cyclotron. However, this isomer suffers from a relatively high radiation burden that arises from the longer half-life and gamma-ray emissions.

^82mRb (6.472 h): β⁺ (21.2%), and E_γ (keV) (P_γ(%)): 554.35 (62.4), 619.11 (37.98), 698.37 (26.3), 776.52 (84.39), 827.83 (21.0), 1044.08 (32.07), 1317.43 (23.7), 1474.88 (15.5).

Evaluations have been undertaken of the ⁸²Kr(p,n)^82mRb and ⁸²Kr(d,2n)^82mRb reactions.

⁸²Kr(p,n)^82mRb

The four experimental datasets available in the literature are shown in Fig. 98 [231, 232] (each reference contains two datasets labelled (a) and (b)), together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 99 together with the Padé fit (L = 9, N = 33, χ² = 1.13) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 98

Four experimental datasets for the ⁸²Kr(p,n)^82mRb reaction available in the literature [231, 232] (each reference contains two datasets labelled (a) and (b)), and TENDL calculations

Fig. 99

Four experimental datasets for the ⁸²Kr(p,n)^82mRb reaction [231, 232] with the Padé fit (L = 9, N = 33, χ² = 1.13, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸²Kr(d,2n)^82mRb

A single experimental dataset available in the literature is shown in Fig. 100 [233] together with the TENDL calculations. This one dataset was used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 101 together with the Padé fit (L = 5, N = 14, χ² = 2.27) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 100

One experimental dataset for the ⁸²Kr(d,2n)^82mRb reaction available in the literature [233], and TENDL calculations

Fig. 101

One experimental dataset for the ⁸²Kr(d,2n)^82mRb reaction [233] with the Padé fit (L = 5, N = 14, χ² = 2.27, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ^82mRb

See Fig. 102.

Fig. 102

Thick target yields calculated from the recommended cross sections for the ⁸²Kr(p,n)^82mRb and ⁸²Kr(d,2n)^82mRb reactions

Production of ⁸⁶Y (T _1/2 = 14.74 h)

Applications: Extensive studies of ⁸⁶Y have been performed as a positron emitter (31.9%) with 14.74 h half-life that can adopted as a theranostic pair with clinically-established therapeutic beta-emitting ⁹⁰Y. The role of ⁸⁶Y is to monitor the localised therapeutic dose distribution in the body for dosimetry calculations. Has also been studied for prostate cancer imaging, and used to label monoclonal antibodies in EGFR targeting. However, interest in this radionuclide has declined because of the high radiation burden and resultant poor imaging properties.

⁸⁶Y (14.74 h): β⁺ (31.9%), and E_γ (keV) (P_γ(%)): 627.72 (32.6), 1076.63 (82.5), 1153.05 (30.5).

Evaluations have been made of the ⁸⁶Sr(p,n)⁸⁶Y, ⁸⁸Sr(p,3n)⁸⁶Y and ⁸⁵Rb(α,3n)⁸⁶Y production routes.

⁸⁶Sr(p,n)⁸⁶Y

The four experimental datasets available in the literature are shown in Fig. 103 [36, 82, 234, 235] together with the TENDL calculations. One dataset was rejected (Rösch et al. [235] (scattered data, and values too high near maximum)), while the three remaining sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 104 together with the Padé fit (L = 9, N = 28, χ² = 0.615) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 103

Four experimental datasets for the ⁸⁶Sr(p,n)⁸⁶Y reaction available in the literature [36, 82, 234, 235], and TENDL calculations

Fig. 104

Three selected experimental datasets for the ⁸⁶Sr(p,n)⁸⁶Y reaction [36, 82, 234] with the Padé fit (L = 9, N = 28, χ² = 0.615, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸⁸Sr(p,3n)⁸⁶Y

The two experimental datasets available in the literature are shown in Fig. 105 [36, 236] together with the TENDL calculations. Both datasets were used in the statistical fitting procedure. These data and their experimental uncertainties are shown in Fig. 106 together with the Padé fit (L = 8, N = 15, χ² = 1.27) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 105

Two experimental datasets for the ⁸⁸Sr(p,3n)⁸⁶Y reaction available in the literature [36, 236], and TENDL calculations

Fig. 106

Two experimental datasets for the ⁸⁸Sr(p,3n)⁸⁶Y reaction [36, 236] with the Padé fit (L = 8, N = 15, χ² = 1.27, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸⁵Rb(α,3n)⁸⁶Y

Five experimental datasets available in the literature are shown in Fig. 107 [36, 237,238,239,240] together with the TENDL calculations. Three datasets were rejected (Guin et al. [239], Iwata [237], and Agarwal et al. [240] (values refer to direct ground state production only, and are not cumulative). The data points of Demeyer et al. [238] below 45 MeV are discrepant, and were also deleted. Thus, the remaining data points for only two datasets were used in the statistical fitting procedure [36, 238]. These selected data and their experimental uncertainties are shown in Fig. 108 together with the Padé fit (L = 8, N = 32, χ² = 0.91) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 107

Five experimental datasets for the ⁸⁵Rb(α,3n)⁸⁶Y reaction available in the literature [36, 237,238,239,240], and TENDL calculations

Fig. 108

Two selected experimental datasets for the ⁸⁵Rb(α,3n)⁸⁶Y reaction [36, 238] with the Padé fit (L = 8, N = 32, χ² = 0.91, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁸⁶Y

See Fig. 109.

Fig. 109

Thick target yields calculated from the recommended cross sections for the ⁸⁶Sr(p,n)⁸⁶Y, ⁸⁸Sr(p,3n)⁸⁶Y and ⁸⁵Rb(α,3n)⁸⁶Y reactions

Production of ⁸⁹Zr (T _1/2 = 78.41 h)

Applications: Long-lived positron-emitting ⁸⁹Zr has been extensively studied with respect to following the in vivo behaviour of therapeutic monoclonal antibodies (mAbs) and other biomolecules with slow biokinetics. One significant disadvantage is the limited number of suitable ⁸⁹Zr chelating agents and difficulties related to their development.

⁸⁹Zr (78.41 h): β⁺ (22.74%), and E_γ (keV) (P_γ(%)): 909.15 (99.04).

Evaluations have been made of the ⁸⁹Y(p,n)⁸⁹Zr and ⁸⁹Y(d,2n)⁸⁹Zr production routes.

⁸⁹Y(p,n)⁸⁹Zr

The sixteen experimental datasets available in the literature are shown in Fig. 110 [36, 56, 82, 110, 234, 241,242,243,244,245,246,247,248,249,250,251] together with the TENDL calculations. Five datasets were rejected (Birattari et al. [244] (energy shift), Blosser and Handley [56] (value too high), Satheesh et al. [250] (energy shift), Delaunay-Olkowsky et al. [234] (value too low), and Saha et al. [242] (values too high)), and the remaining eleven datasets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 111 together with the Padé fit (L = 11, N = 316, χ² = 3.74) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 110

Sixteen experimental datasets for the ⁸⁹Y(p,n)⁸⁹Zr reaction available in the literature [36, 56, 82, 110, 234, 241,242,243,244,245,246,247,248,249,250,251], and TENDL calculations

Fig. 111

Eleven selected experimental datasets for the ⁸⁹Y(p,n)⁸⁹Zr reaction [36, 82, 110, 241, 243, 245,246,247,248,249, 251] with the Padé fit (L = 11, N = 316, χ² = 3.74, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸⁹Y(d,2n)⁸⁹Zr

The seven experimental datasets available in the literature are shown in Fig. 112 [252,253,254,255,256,257,258] together with the TENDL calculations. Two datasets were rejected (La Gamma and Nassiff [253] (values too low), and Degering et al. [255] (energy shift)), and the remaining five sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 113 together with the Padé fit (L = 9, N = 64, χ² = 2.95) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 112

Seven experimental datasets for the ⁸⁹Y(d,2n)⁸⁹Zr reaction available in the literature [252,253,254,255,256,257,258], and TENDL calculations

Fig. 113

Five selected experimental datasets for the ⁸⁹Y(d,2n)⁸⁹Zr reaction [252, 254, 256,257,258] with the Padé fit (L = 9, N = 64, χ² = 2.95, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁸⁹Zr

See Fig. 114.

Fig. 114

Thick target yields calculated from the recommended cross sections for the ⁸⁹Y(p,n)⁸⁹Zr and ⁸⁹Y(d,2n)⁸⁹Zr reactions

Production of ⁹⁰Nb (T _1/2 = 14.60 h)

Applications: As a non-conventional positron emitter, ⁹⁰Nb with a half-life of 14.60 h can be used to visualise and quantify processes with medium and slow kinetics, such as tumour accumulation of antibodies and antibody fragments, or polymers and other nanoparticles. Exhibits promise in immuno-PET, although a search for appropriate chelators is desirable. Also emits several high-energy gamma rays that increase the radiation burden.

⁹⁰Nb (14.60 h): β⁺ (51.2%), and E_γ (keV) (P_γ(%)): 132.716 (4.13), 141.178 (66.8), 1129.224 (92.7).

Evaluations have been undertaken of the ⁹³Nb(p,x)⁹⁰Nb and ⁸⁹Y(α,3n)⁹⁰Nb production.

⁹³Nb(p,x)⁹⁰Nb

The six experimental datasets available in the literature are shown in Fig. 115 [82, 249, 259,260,261,262] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 116 together with the Padé fit (L = 9, N = 94, χ² = 3.18) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 115

Six experimental datasets for the ⁹³Nb(p,x)⁹⁰Nb reaction available in the literature [82, 249, 259,260,261,262], and TENDL calculations

Fig. 116

Six experimental datasets for the ⁹³Nb(p,x)⁹⁰Nb reaction [82, 249, 259,260,261,262] with the Padé fit (L = 9, N = 94, χ² = 3.18, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁸⁹Y(α,3n)⁹⁰Nb

The six experimental datasets available in the literature are shown in Fig. 117 [36, 263,264,265,266,267] together with the TENDL calculations. Four datasets were rejected (Singh et al. [266], Chaubey and Rizvi [265], Mukherjee et al. [264], and Smend et al. [263], all systematically lower values), while the remaining two sets were used in the statistical fitting procedure. The selected data and their experimental uncertainties are shown in Fig. 118 together with the Padé fit (L = 16, N = 33, χ² = 1.29) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 117

Six experimental datasets for the ⁸⁹Y(α,3n)⁹⁰Nb reaction available in the literature [36, 263,264,265,266,267], and TENDL calculations

Fig. 118

Two selected experimental datasets for the ⁸⁹Y(α,3n)⁹⁰Nb reaction [36, 267] with the Padé fit (L = 16, N = 33, χ² = 1.29, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ⁹⁰Nb

See Fig. 119.

Fig. 119

Thick target yields calculated from the recommended cross sections for the ⁹³Nb(p,x)⁹⁰Nb and ⁸⁹Y(α,3n)⁹⁰Nb reactions

Production of ^94mTc (T _1/2 = 52.0 min)

Applications: Gamma-ray emitting ^99mTc is the most widespread medical radionuclide for diagnosis, whereas ^94mTc with a half-life of 52.0 min. is a positron emitter with a positron branch of 70.2% and E_β+(max) of 2.44 MeV. Therefore, there has been interest in ^94mTc as a PET analogue to ^99mTc since they both undergo the same chemistry. Obvious disadvantages of ^94mTc are the rather short half-life of 52.0 min., with many accompanying gamma rays and the inability to prepare the pure isomer without also generating significant amounts of ground state ^94gTc.

^94mTc (52.0 min): β⁺ (70.2%), and E_γ (keV) (P_γ(%)): 871.05 (94.2), 1522.1 (4.5), 1868.68 (5.7).

Evaluations have been made of the ⁹²Mo(α,x)^94mTc and ⁹⁴Mo(p,n)^94mTc production routes.

⁹²Mo(α,x)^94mTc

The four experimental datasets available in the literature are shown in Fig. 120 [36, 268,269,270] together with the TENDL calculations. Three datasets were rejected (Graf and Münzel [268], Denzler et al. [269], and Ditrói et al. [270], all contradictory sets of data), while the remaining single set of Levkovskij [36] was used in the statistical fitting procedure (and also accepted as a standard for the monitoring of α beams). The selected data and their experimental uncertainties are shown in Fig. 121 together with the Padé fit (L = 12, N = 28, χ² = 1.33) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 120

Four experimental datasets for the ⁹²Mo(α,x)^94mTc reaction available in the literature [36, 268,269,270], and TENDL calculations

Fig. 121

One selected experimental dataset for the ⁹²Mo(α,x)^94mTc reaction [36] with the Padé fit (L = 12, N = 28, χ² = 1.33, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

⁹⁴Mo(p,n)^94mTc

The seven experimental datasets available in the literature are shown in Fig. 122 [36, 142, 271,272,273,274,275] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. These data and their experimental uncertainties are shown in Fig. 123 together with the Padé fit (L = 9, N = 57, χ² = 1.21) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 122

Seven experimental datasets for the ⁹⁴Mo(p,n)^94mTc reaction available in the literature [36, 142, 271,272,273,274,275], and TENDL calculations

Fig. 123

Seven experimental datasets for the ⁹⁴Mo(p,n)^94mTc reaction [36, 142, 271,272,273,274,275] with the Padé fit (L = 9, N = 57, χ² = 1.21, solid line) and estimated total uncertainties in percentages, including 4% systematic uncertainty (dashed line, right-hand scale)

Thick target yields for production of ^94mTc

See Fig. 124.

Fig. 124

Thick target yields calculated from the recommended cross sections for the ⁹²Mo(α,x)^94mTc and ⁹⁴Mo(p,n)^94mTc reactions

Production of ^110mIn (T _1/2 = 69.1 min) and longer-lived ¹¹⁰Sn parent (T _1/2 = 4.154 h)

Applications: ^110mIn is a positron-emitting analogue for established SPECT ¹¹¹In. Potential to provide more quantitative diagnostic information as well as in vivo quantification of the uptake kinetics of radiopharmaceuticals (e.g., applied along with ¹¹¹In-labelled DTPA-D-Phe1-octeotride for neuroendocrine tumours).

^110mIn can be produced directly and via parent ¹¹⁰Sn.

^110mIn (69.1 min): β⁺ (61.3%), and E_γ (keV) (P_γ(%)): 2129.40 (2.15), 2211.33 (1.74), 2317.41 (1.285).

¹¹⁰Sn (4.154 h): E_γ (keV) (P_γ(%)): 280.459 (97.06).

Evaluations have been made of the ^natIn(p,xn)¹¹⁰Sn, ¹⁰⁸Cd(α,2n)¹¹⁰Sn, ¹¹⁰Cd(p,n)^110mIn, ¹¹⁰Cd(d,2n)^110mIn and ¹⁰⁷Ag(α,n)^110mIn production routes.

^natIn(p,xn)¹¹⁰Sn

The four experimental datasets available in the literature are shown in Fig. 125 [276,277,278,279] together with the TENDL calculations. All datasets were used in the statistical fitting procedure. The data and their experimental uncertainties are shown in Fig. 126 together with the Padé fit (L = 17, N = 112, χ² = 1.50) and estimated uncertainty in percentages, including 4% systematic uncertainty (right-hand scale).

Fig. 125

Four experimental datasets for the ^natIn(p,xn)¹¹⁰Sn reaction available in the literature [276,277,278,279], and TENDL calculations

Fig. 126