Computational modelling of the separation of molten polymer blends by a centrifugal technique

Abstract

Computational modelling of a centrifugal technique for separating binary mixtures of thermoplastic polymers in the molten state is presented. The technique may be useful for the recycling of polymeric materials. The study investigates the physical process of component separation due to the centrifugal force in a batch process, showing the potential of using a dispersed model for describing the complex mechanism underlying the technique. Given the long time scales of change of the flow field, the polymer melts are modelled as inelastic, shear-thinning materials. The centrifugal force drives the component with the higher density to the outer region of an annular cross section occupied by the melt inside a rotating containment. The model system PET/LDPE is investigated in detail. The simulations allow to predict the process time needed for the separation. The simulations are the basis for studying a continuous process in a rotating tube.

Introduction

The ever more increasing use of polymeric materials in daily life and in industries has led to large quantities of polymeric waste, which are to date recycled at a small rate only. Thermoplastic wastes, however, may be molten made available for recycling. The majority of those materials are immiscible in the molten state, and components with different bulk densities may be separated using a centrifugal technique. Ronkay and Dobrovszky [1] showed in their proof-of-concept experiments that this kind of a technique can be used for the separation of components in binary polymer melt blends. They used a batch technique, with a test rig consisting of a rotating can driven by an electric motor. The tested materials were polyethylene terephthalate (PET) and low-density polyethylene (LDPE), which are polymers that are immiscible in the molten state. The polymer blends were prepared in a mixer and at a sufficiently high temperature. When both the LDPE and PET granules were entirely molten, separation of the components was detected. In another study, Dobrovszky [2] investigated the influence of temperature and rotation time on the separation of PET and high-density polyethylene (HDPE) melts and proved the feasibility of the technique. Tsori and Leibler [3] reported that even two miscible polymers can be separated when using sufficiently high rotational speed. They showed a calculated distribution of phases along the radial direction in the rotating containment. With increasing rotational speed, the gradient of the concentration increases, and beyond a certain rotational speed the distribution shows a sharp interface.

Numerical simulations can show the feasibility of multiphase materials separation techniques and make them realizable for industrial applications. Several modelling methods exist to describe a separation process. Weiwei et al. [4] simulated the separation of oil and water under gravitational force using the Volume-of-Fluid method (hereafter abbreviated VoF), mixture and Eulerian models. The VoF method tracks the interface between two (or more) phases, providing good separation and differentiation of the phases. The mixture and Eulerian models, on the other hand, treat the phases as interpenetrating and generally do not resolve the interfaces. Therefore, they require thorough modelling of the phase interaction. The resulting field distributions are not as well resolved as with the VoF method, but, as a compensation, these models allow to use a coarser computational grid, making the computation more affordable. Wardle and Weller [5] developed a solver to model an extraction process, such as taking place in an annular centrifugal contactor. In such liquid-liquid extraction process, the domain includes both phase-segregated and dispersed flow regimes. Therefore, an Eulerian model with per-phase momentum equations was combined with an additional interface capturing capability. In that work, constant diameters for the droplets of each phase were used, indicating the necessity of an extension of the solver with variable droplet size. The authors demonstrated the capability of the model to capture a liquid-liquid extraction and predict the mass-transfer efficiency in such a device. Similar development was made by De Santis et al. [6] to describe a similar process. In addition, a reduced population balance approach was implemented in order to determine the accurate droplet size distribution in the dispersed flow regimes. Another classical example of separation using a centrifugal technique is the hydro-cyclone, where solid particles are separated from a liquid phase. In some applications, hydro-cyclones are used even for liquid-liquid separation. The most intuitive approach for simulating solid-liquid separation is the Eulerian-Lagrangian coupling, where the path of particles is traced with a Lagrangian approach. Narasimha et al. [7] reviewed different multiphase modelling approaches for the flow in a hydro-cyclone, with main focus on the Euler-Lagrangian approach and the mixture model. The Euler-Lagrangian based models are able to visualize the distribution of particles with different diameters in the domain by resolving the particle trajectories. The mixture model, on the other hand, considers the particles as a dispersed phase, and, with different amendments of phase interaction, wall lift forces, turbulence models etc., it can predict the solids transportation in such processes. The motivation of use of a mixture model is the significantly lower computation time. Exploiting this benefit, Kuang et al. [8] also dealt with the comparability of the two approaches and developed a mathematical model for a dense medium cyclone. The modelling included two steps – a VoF model only for the liquid and air phases, and a mixture model involving all the phases present, where particles of different sizes are represented as different phases. Multiphase mixture models are not restricted to classical industrial applications. Haribabu et al. [9] used the mixture model to examine the filtration process of a whey protein. Milk is another example of a dispersed mixture, where water and oil represent the continuous and the dispersed phases, respectively. In that investigation, the material was modelled as a suspension of hard spheres. Accordingly, a constant diameter for the oil droplets was chosen, and it was found that this kind of approach is able to predict well the permeate fluxes of the dispersed phase.

It can be seen that there exist a number of models to describe multiphase flow and separation processes. In our investigation we focus on a fluid flow related description of the problem. In this, the mixture model using one momentum equation was chosen because of its simplicity and computational speed. Since the real time of a few thousand seconds of the process investigated would have to be covered by the analysis, the computational time is of major importance. After the validation of the VoF model, it can serve as a virtual test, saving time and resources during the further development of the process. The obtained results and plots can also visualize quantities and the progress of separation which cannot readily be measured in a rotating domain. In this way, combining experimental data and numerical analysis, the physics of the technique will be better understood.

The paper is structured as follows: the next section presents the experimental method used and materials investigated. "Mathematical model and methods" formulates the problem and details the mathematical model used. In "Results and discussion", the simulation results are shown, quantifying the separation results. The paper ends by the conclusions and suggestions for further work in "Conclusions and future work".

Experimental method and materials

The numerical modelling of the separation process was inspired by experiments of the Department of Polymer Engineering at Budapest University of Technology and Economics. The experiments were implemented in a prototype polymer melt separator (Fig. 1a). The polymer mixture was created using two different methods [2]. In the first method, a dry mixture of granules was prepared and melted in the separation device. In the second method, the polymer components were compounded externally and then loaded into the separation device in a molten state. The molten polymer mixture was rotated and, in case of suitable parameters, the phases could be separated successfully due to the centrifugal force. The outer region of such sample consists of the heavier phase, in this specific example PET (white colour in Fig. 1b). Further inside, the lighter polymer phase LDPE (darker colour) is seen. The central region of the volume is filled by air, which indicates that the cylinder was not filled entirely with polymer, and the air, as the lightest phase, gathered in the centre. This experiment is the subject of the current numerical study, where the phase separation takes place due to the centrifugal force, starting from the initial, homogeneous state.

Fig. 1

a Assembly of the polymer separator (reprinted from [2], with permission from Elsevier) and (b) annular shape of separated polymers as a separation result (reprinted from [1], with permission from Elsevier)

The non-Newtonian behaviour of the polymer melts, with their dynamic viscosities varying with the shear rate in the flow, plays an important role in the flow behaviour. Many polymer melts behave as shear-thinning fluids, that is, their viscosity $\eta \left(\dot{\gamma }\right)$ decreases with increasing shear rate $\dot{\gamma }$. In the current investigation, the Carreau-Yasuda rheological model was used to represent this non-Newtonian behaviour. The simulations describe the fluids as inelastic, generalized Newtonian, and represent the viscosity using that model. Figure 2 displays viscosity data from shear rheometry together with their representation by the Carreau-Yasuda model for the investigated materials (LDPE and PET). The numerical values of the parameters in Eq. (1) are listed in Table 1 for the two polymers at the temperature of 280°C. The values of the parameter ${\eta }_{\infty }$ obtained from the curve fit are actually small negative numbers ≤ O(-3 Pa s), which physically make no sense. Therefore, the values were replaced by zeros.

Fig. 2

Dynamic viscosity of LDPE and PET as a function of the shear rate at 280°C from shear rheometry and by the Carreau-Yasuda fit

Table 1 Parameters of the Carreau-Yasuda model and density of the investigated polymers at 280 °C

$$\eta \left(\dot{\gamma }\right)={\eta }_{\infty }+\left({\eta }_{0}-{\eta }_{\infty }\right){\left[1+{\left(\lambda \dot{\gamma }\right)}^{a}\right]}^{\left(n-1\right)/a}$$

(1)

Mathematical model and methods

Formulation of the problem, description of the separation process

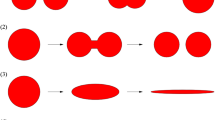
In the current investigation we study the process of separation of the components of a molten binary polymer mixture using a batch technique. In the realisation of such a process, the polymer components are pre-treated to produce a homogeneous mixture, the mixture is filled into a closed, cylindrical volume and rotated with a certain rotational speed. In this case, the homogeneous mixture exhibits a uniform composition in the entire domain. However, if the mixture is observed below a certain length scale, and the components are immiscible, the components can be distinguished. As a result of the rotational motion, a centrifugal force acts on the components of the polymer mixture. Due to the different densities, the centrifugal force is different for the different components, causing a relative motion which makes the heavier component migrate to the outer region of the domain, while the lighter phase moves to the inner region. The rate of separation depends on the speed of the relative motion between the components. In the polymer mixture studied, the PET is the heavier component, which is dispersed in the lighter LDPE. When the centrifugal force is imposed, the PET moves to the outer region of the domain. At the beginning, the relative motion is slow, because the individual PET portions are small, so that their total interfacial area is large, leading to a large drag force (Fig. 3a). With ongoing time, the PET droplets coalesce, forming bigger drops, thus reducing the overall drag force. Consequently, the velocity of the PET increases (Fig. 3b). The coalescence process continues, until a layer is formed at the circumference of the containment (Fig. 3c). The thickness of that layer grows, until the full separation of the components is achieved (Fig. 3d). The aim of the present study is to develop a multiphase dispersed model, which is able to capture the fluid mechanics of the separation process, using a reasonable mesh size suitable for the description of a technical application. The mixture component distributions in Fig. 3, used here for illustration of the process, were computed using the VoF method. Such results will be a reference for the verification of the mixture model.

Fig. 3

Schematic of the separation process

Governing equations of the mixture model

The motion of the polymer melt is governed by the balance equations of fluid mechanics, i.e. the continuity and the momentum equations, together with the constitutive rheological equation for the flowing material. In the present investigation of a binary mixture of polymer melts, the so-called algebraic slip mixture model, or briefly the mixture model, is used for describing the motion of the components. It is an alternative formulation of the Eulerian model mentioned earlier, derived by averaging the continuity and momentum equations for n mixture components. The volume fraction of the dispersed phase is calculated solving the resulting continuity equation, where a correction flux based on the interphase velocities is present. Only one momentum transport equation is solved, which is formulated in terms of weighted physical quantities and material properties. A detailed description of the mixture model is due to Manninen [10]. Primarily this paper was used to implement the model for the present purposes.

In the following, the model equations and correlations are discussed. The continuity equation is given as

$$\frac{\partial {\rho }_{m}}{\partial t}+\nabla \cdot ({\rho }_{m}{{\varvec{U}}}_{m})=0$$

(2)

where ${\rho }_{m}$ and ${{\varvec{U}}}_{m}$ are the mixture density and mixture velocity, respectively, given as

$${\rho }_{m}=\sum_{k=1}^{n}{\alpha }_{k}{\rho }_{k}$$

(3)

$${{\varvec{U}}}_{m}=\frac{1}{{\rho }_{m}}\sum_{k=1}^{n}{\alpha }_{k}{\rho }_{k}{{\varvec{U}}}_{k}$$

(4)

In these definitions, ${\alpha }_{k}$ and ${\rho }_{k}$ are the volume fraction and the density of the individual phase $k$, respectively. The momentum equations read

$$\frac{\partial ({\rho }_{m}{{\varvec{U}}}_{m})}{\partial t}+\nabla \cdot \left({\rho }_{m}{{\varvec{U}}}_{m}{{\varvec{U}}}_{m}\right)=-\nabla p+\nabla \cdot {{\varvec{\tau}}}_{m}+{\rho }_{m}({\varvec{\omega}}\times{\varvec{\omega}}\times {\varvec{r}})-\nabla \cdot {\sum }_{k}{\alpha }_{k}{\rho }_{k}{{\varvec{U}}}_{dr}{{\varvec{U}}}_{dr}$$

(5)

where $p,{\varvec{\omega}}, {\varvec{r}}$ and ${{\varvec{U}}}_{dr}$ are the pressure, the angular velocity, the position vector and the drift velocity, respectively. ${{\varvec{\tau}}}_{m}$ is the weighted mean viscous stress tensor, ${\rho }_{m} ({\varvec{\omega}}\times{\varvec{\omega}}\times {\varvec{r}})$ is the volume-specific centrifugal force, while the term $\nabla \cdot {\sum }_{k}{\alpha }_{k}{\rho }_{k}{{\varvec{U}}}_{dr}{{\varvec{U}}}_{dr}$ represents the momentum diffusion due to the relative motion between the components. Turbulent stress, stress due to surface tension, as well as gravity and body forces are not important for the present simulations and therefore neglected.

Simulating a process from the real application with capturing of the interface of all dispersed droplets, that is, using VoF or separated model, in the entire domain is not possible for reasons of computational costs. Therefore, the mixture model is used. Although the interface can be modelled optionally even with the mixture model, in this study this extension is not investigated. Several dispersed models exist, and most of them use a drag force based on the diameter of the dispersed phase for modelling the interaction between the components due to the relative motion. In this way, the diameter of the dispersed phase plays an important role and influences the rate of separation significantly.

In the further derivations, a binary mixture will be described, and the subscripts $1$ and $2$ will be used for the continuous and dispersed phases, respectively. For solving the momentum equation, the drift velocity ${{\varvec{U}}}_{dr}$ has to be determined. The drift velocity is interpreted for the dispersed phase $2$ and defined as the difference between the velocity of that phase and the mixture velocity, i.e.

$${{\varvec{U}}}_{dr}={{\varvec{U}}}_{2}-{{\varvec{U}}}_{m}$$

(6)

The drift velocity is a consequence of forces acting on the components. In the present case, it is the centrifugal force. That force, and therefore the momentum of the dispersed phase, is balanced by the drag force. A presentation of the balance equation in different situations can be found in [10]. In our case we assume that the dispersed phase exhibits a constant spherical shape during the motion, and it has interaction only with the continuous medium, that is, an interaction between the droplets of the dispersed phase is not accounted for. The drag coefficient ${C}_{D}$ can be calculated using the Schiller-Naumann model, which was developed for Reynolds numbers of the relative particle motion below 1000. At higher Reynolds numbers, the constant value of $0.44$ is used. The drag model therefore reads

$$\begin{aligned}{C}_{D}&=\frac{24}{{Re}_{p}}\left(1+0.15 {{Re}_{p}}^{0.687}\right) &\;\mathrm{if} \;{Re}_{p}<1000 \\{C}_{D}&=0.44\;& \mathrm{if} \;{Re}_{p}>1000\end{aligned}$$

(7)

where ${Re}_{p}$ is the Reynolds number of particle motion relative to the continuous phase and can be calculated as

$${Re}_{p}=\frac{{d}_{p} {\rho }_{1}\left|{{\varvec{U}}}_{sl}\right| }{{\eta }_{1}}$$

(8)

In this equation, ${d}_{p}$ is the particle (or droplet) diameter of the dispersed phase, $\left|{{\varvec{U}}}_{sl}\right|$ is the absolute value of the slip velocity and ${\rho }_{1}$ and ${\eta }_{1}$ are the density and the dynamic viscosity of the continuous phase. The slip velocity is another notable quantity in the mixture model. It is the difference between the dispersed and the continuous phase velocities

$${{\varvec{U}}}_{sl}={{\varvec{U}}}_{2}-{{\varvec{U}}}_{1}$$

(9)

Since the individual component velocities are not known in the mixture model, the force balance equation cannot be formulated. Making several simplifications, using the above defined drag model and exposing the spherical droplets to a Stokes flow, the slip velocity can be determined explicitly as it is elaborated in [10]. The equation reads

$${{\varvec{U}}}_{sl}=\frac{{d}_{p}^{2}}{18 {\eta }_{1}}({\rho }_{2}-{\rho }_{m})\frac{{u}_{centr}^{2}}{r}{{\varvec{e}}}_{{\varvec{r}}}$$

(10)

where ${u}_{centr}^{2}/r$ is the centrifugal acceleration.

Assuming only one dispersed phase, the drift velocity can be calculated as following.

$${{\varvec{U}}}_{dr}=\left(1-{c}_{2}\right) {{\varvec{U}}}_{sl}$$

(11)

where the mass fraction ${c}_{2}$ is related to the volume fraction ${\alpha }_{2}$ as per

$${c}_{2}={\alpha }_{2} {\rho }_{2}/{\rho }_{m}$$

(12)

Equation (5) can now be solved, and ${U}_{m}$ can be substituted in the continuity equation for the dispersed phase, which reads

$$\frac{\partial {\alpha }_{2} {\rho }_{2}}{\partial t}+\nabla \cdot \left({\alpha }_{2}{\rho }_{2}{{\varvec{U}}}_{m}\right)=-\nabla \cdot \left({\alpha }_{2}{\rho }_{2}{{\varvec{U}}}_{dr}\right)$$

(13)

In the presently analysed flow, mass sources or sinks do not occur, since there is no mass transfer between the mixture components. As it can be seen using the known mixture and drift velocities, the volume fraction field of the dispersed phase can be calculated.

Case setup of the dispersed model, boundary and initial conditions

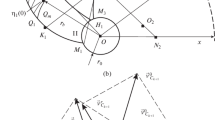
The present study investigates a 2D axisymmetric flow, which represents an infinitely long, closed, rotating cylinder domain (Fig. 4). We assume that the domain is initially filled with a molten uniform mixture of two polymeric components. In the real process a mixture of spherical granules initially filled into the containment, voids filled with air exist between the granules. For the present simulations, the volume fraction of the air is set to 39 %, which refers to a typical value for a gas-solid system. In such a gas-liquid system, the air as the lightest phase migrates to the inner region in a short time period as compared to the entire process time, meaning that the domain may be initialized with a developed air core in the centre. Outside the air core, the two polymer components are located. In preliminary computational analyses it was found that the air has no dynamic influence on the liquid phase. The flow in the air core is therefore excluded from the simulations, analysing only the two molten polymer components LDPE and PET, by setting a slip-wall boundary condition at the gas-liquid interface. Two compositions of the molten polymer mixture, 50/50 wt% PET/LDPE and 40/60 wt% PET/LDPE, were examined. The domain is initialized accordingly, for 50/50 wt% PET/LDPE this yields 39.4 vol% PET and 60.6 vol% LDPE, while, for 40/60 wt% PET/LDPE, we obtain 30.2 vol% PET and 69.8 vol% LDPE. Based on the volume fractions, the volumes of fully separated and neat zones can be calculated. These volumes serve also for monitoring the variation of the average volume fraction (Fig. 4), so that, in the state of full separation of the polymer components, the outer region will be occupied entirely by PET, while the middle region is occupied by LDPE. The inner region is dedicated for the air core.

Fig. 4

Domain and regions of the investigated flow

Heat transfer across the domain boundaries is not accounted for. Therefore, the temperature of the polymeric system remains constant, and the energy equation is not solved in the simulations. The rotation of the entire domain at the angular speed $\omega$ is implemented with the single reference frame with the rotational speed of 2000 rpm. Therefore, the motion of the phases is obtained relative to the rotation. Because of the low phase velocities in the relative frame, the flow is expected to be laminar. A turbulence model was therefore not included. The rotating wall is included to the reference frame, so that it exhibits a velocity of solid-body rotation $R \omega$, with the radius $R=0.05 m$. Due to the no-slip condition, a shear-driven flow is developed in the polymer melt in time, which converges to solid-body rotation of the melt, exhibiting the absolute velocity $r \omega$, which increases linearly with the distance $r$ from the axis of rotation. The side walls have free slip condition, so that the fields computed in the domain represent the flow in a cylinder which is infinitely long in the axial direction. Due to the simplicity of the domain, a structured mesh with 190 computational cells was created. This allows well-aligned fluxes for an accurate calculation of the volume fraction distributions. The transport equation for the component volume fraction is integrated in time using an explicit scheme. The CFL number was 0.5. For the spatial discretization of the transport equation, the upwind scheme was used, which provided a stable numerical solution.

Results and discussion

In the present section, the results from the computational study are shown and discussed. The goal of the study is to simulate the separation process reported in [1, 2]. For this purpose, appropriate parameter settings for the computations are determined. As a parameter, the diameter of the disperse-phase particles migrating through the continuous phase plays a key role. Although this diameter seems to be a known parameter, since it can be measured on microscopic images of the homogeneous mixture before the separation, particle coalescence causes it to vary during the separation process, so that a value from the initial state of the mixture cannot be used for the computations. Instead, the volume fraction distribution obtained from computations using the VoF method is used as a reference to determine an appropriate equivalent particle diameter. The window of experimental separation times between 5 and 20 minutes, reported in [1, 2] and predicted by the simulations, was the criterion for determining the particle diameter. Using this diameter, the mixture model was used as an efficient alternative to the VoF method. The results demonstrate the capabilities and limitations of the mixture model to represent a separation process.

Evolution of the separation process with the VoF model

In this section, the development and interaction of the components in the 50/50 wt % PET/LDPE mixture are summarized. In the simulations using the VoF method, the droplets of the dispersed component have initial diameters from 500 to 3000 μm. This state represents the dry mixture of granules, which is shaken and molten in the domain to form a quasi-uniform mixed polymer system. Another pre-treatment technique is the use of a compounder. With this method, the dispersed-phase diameter may differ from the investigated size range and may be orders of magnitude finer. Such fine dispersion requires a corresponding resolution for application of the VoF method. However, this study focuses on the visualization of a separation mechanism and a methodology for a possible validation of a dispersed model using reasonable computational time. For the verification of the accuracy of the VoF method, a grid sensitivity analysis was carried out, simulating the same process with different resolutions in the regions of the polymer mixture (Fig. 5, bottom). The base mesh size for this study was 60 μm (~50,000 cells), which is a sufficiently fine resolution for capturing the mechanisms of droplet interaction, including coalescence, break-up of droplets and wake entrainment. In this study, it was found that the neglect of the dynamic interaction with the air core does not influence the separation rate, so that the interface between the polymer mixture and the air may be treated as a free slip boundary. This allows to use longer time steps and a sharper interface reconstruction scheme in the VoF method. From the transient variation of the volume fraction distribution, the procedure of the separation for the component pairing studied was visualized. In the present case, the dispersed phase PET has the lower viscosity, which influences significantly the shape of the droplets and the migration process. After coalescence of the dispersed, small fractions, the resulting bigger droplets migrate towards the outer region. Because of the low viscosity, the big drops elongate, and, in the wake region, filaments are formed, which detach and break up into small droplets. On average, the radial velocity of the small droplets is much lower than for the larger drops. Potentially, the small drops coalesce again with others. After migration of much of the dispersed phase to the outer region, the probability of coalescence decreases, thus reducing the separation rate. It can be seen in Fig. 5 that, in the outer region, the heavier component PET is pure, while, in the middle region, dispersed droplets remain. The process time required for a successful separation therefore depends on the required purity of the lighter component achieved at a certain time.

Fig. 5

(Top) Evolution of the component distribution computed with the VoF method. (Bottom) Evolution of the volume-mean (average) volume fraction in the middle and outer regions, obtained with different mesh sizes

Comparison of VoF and mixture model for 50/50 wt% PET/LDPE

With the aim to establish a parameter setting for use with the mixture model, simulations were carried out with that model, taking the results from the VoF method as a reference. The volume fraction distribution was evaluated in the middle and outer regions introduced in Fig. 4 of "Case setup of the dispersed model, boundary and initial conditions", and the aim was to achieve the same evolutions from the two approaches. The discretized computational domain consists of 190 cells, as shown in Fig. 4.

As primary results for the flow field, the velocity and pressure fields in the fluid domain are shown in Fig. 6. As mentioned in "Case setup of the dispersed model, boundary and initial conditions", the frame motion in the simulations is activated from the beginning of the analysis, since, with the present high-viscosity fluids, the velocity field develops very rapidly, converging to solid-body rotation within a few seconds after start of the motion. The analytically obtained angular velocity component for solid-body rotation is $v\left(r\right)=\omega r$. The angular velocity distribution does not change through the analysis and it does not dependent on the phase fraction distribution. The linear profile of the angular velocity, which corresponds to solid-body rotation, is accurately reproduced by the simulation (Fig. 6a).

Fig. 6

Radial profiles of (a) the angular velocity, (b) the pressure in the initial state, and (c) the pressure a long time after start, the pressure profiles together with the LDPE volume fraction

The component pressures are taken to be equal in the mixture model, i.e. capillary effects from the curved phase boundaries are not accounted for. Analytically, the pressure is obtained as

$$p\left(r\right)-{p}_{in}=\underset{{r}_{in}}{\overset{r}{\int }}\frac{dp}{dr}dr={\omega }^{2}\underset{{r}_{in}}{\overset{r}{\int }}{\rho }_{m}rdr ,$$

(14)

where the radial position of the inner polymer surface ${r}_{in}\cong 0.031 m$ in our case, and $r$ is the variable radial position. The mixture density ${\rho }_{m}\left(t,r\right)$ as a function of time and the radial position in the field is obtained as a solution of the problem (2) – (5). Therefore, in order to determine the radial pressure profile, the integral in (14) must be evaluated numerically as per

$${p}_{i}={p}_{i-1}+{\omega }^{2}\frac{\Delta r}{2}\left({\rho }_{m,i}{r}_{i}+{\rho }_{m,i-1}{r}_{i-1}\right)$$

(15)

In special cases, like the initial state and the steady state after a long process time, the density distribution in the field is known, so that the computational data may be compared to analytical results. In the initial state, the dispersed phase is distributed evenly in the field, giving the constant value ${\rho }_{m}={\rho }_{m,0}$. In this case, the pressure profile (Fig. 6b) becomes

$${\left.p\left(r\right)-{p}_{in}\right|}_{t=0}={\omega }^{2}{\rho }_{m,0}\frac{\left({r}^{2}-{r}_{in}^{2}\right)}{2}$$

(16)

Furthermore, at steady state, when the phases are separated, the phase fraction distribution and ${\rho }_{m}\left(r\right)$ exhibit the shape of a step function. The pressure gradient consequently is obtained as $dp/dr={\rho }_{1}{\omega }^{2}r$ in the middle region and as $dp/dr={\rho }_{2}{\omega }^{2}r$ at the outer region. At the interface between the phases, the pressure profile is continuous, but exhibits a bend, due to a step in the pressure gradient. In our case, the comparison is shown in Fig. 6c for a state close to full component separation, using the computed phase fraction distribution represented by the dashed line and evaluating the pressure profile by Eq. (15).

Figure 7 shows the volume fraction distributions at six instants of time during the separation process as obtained by simulations using the VoF method and the mixture model for a 50/50 wt% PET/LDPE mixture. The particle diameter set in the mixture model was 1.5 mm. The criterion for the proper mean particle diameter in the dispersed model is that the evolutions of the volume-mean volume fractions in the middle and outer regions collapse with the data from the VoF method. The best results were produced with particle diameters in the range 1.5-2 mm.

Fig. 7

Component volume fraction distribution as a function of time in the separation process as computed with (left) the VoF method and (right) with the mixture model (d = 1.5 mm) for 50/50 wt% PET/LDPE

It is important to repeat that the dispersed-phase diameter is not necessarily a real physical measure for the dispersed-phase particle size occupying a certain volume in the domain or in a cell. It is rather used as a parameter for modelling the drag force, and it can be even bigger than the cell size. Commonly, the computational mesh of the dispersed model should be large compared to the particle size, meaning that the dispersed phase may be uniformly dispersed in the mixture. On the other hand, the computational grid also has to be fine enough to resolve the flow field properly. These are two contradictory requirements. Moreover, in our specific case, the initial secondary phase can grow during the process, forming a continuous phase from the dispersed phase at the same time. Because of using bigger dispersed droplets already at the initial state, there are some local regions where the dispersed phase does not appear dispersed in the selected computational grid. In other words the phase fraction distribution is not the same for the VoF method and the mixture model at the initial state (Fig. 7, t = 0 s). The sensitivity of the computational results to such inequalities in the initial volume fraction field was checked, and the difference in the evolutions between the more realistic field from the VoF computations and an ideally dispersed initial state was within 4-5 %. This shows that the key information of the initial condition is rather the volume fractions of the mixture components. This shows the capability of the mixture model to represent polymer mixtures without knowing the exact distribution of the dispersed particles.

Figure 8 shows the evolution of the average volume fractions in the middle and outer region as computed using the VoF method and the mixture model, the latter with two different particle sizes. It can be seen that, with the VoF method, the average volume fraction of PET in the outer region increases steeply at the beginning of the process. This can be explained with the initial state, where the relatively big PET droplets migrate easily to the outer region. Also, simulations with this method predict noticeable jumps time after time. This indicates that bigger drops travel through the considered region. In contrast, the dispersed model yields an averaged description for the separation process with a smooth function, as expected. At the beginning of the process, depending on the dispersed-phase diameter, the increase of the average volume fractions of the components is nearly linear in time. After a certain time, the profiles flatten. Re-arranging the equation

Fig. 8

Volume-mean volume fraction evolution of the phases in the middle region (a) and in the outer region (b) for 50/50 wt% PET/LDPE

$${{\varvec{U}}}_{dr}=\left(1-{c}_{2}\right)\frac{{d}_{p}^{2}}{18{\eta }_{1}}({\rho }_{2}-{\rho }_{m})\frac{{u}_{centr}^{2}}{r}{{\varvec{e}}}_{{\varvec{r}}}$$

(17)

into

$${{\varvec{U}}}_{dr}\propto C(1-{\alpha }_{PET})\left(1-{c}_{PET}\right)$$

(18)

it can be seen that, by filling a control volume with the dispersed phase, the drift velocity ${U}_{dr}$ decreases, thus slowing down the separation process. This explains the continuous decrease of the slope of the volume fraction evolutions. With both computational approaches, the pure separated fractions are achieved slowly. The time elapsed for a volume fraction increase of a few percent can be even several ten minutes. Instead of defining a certain purity criterion for successful separation, the process was monitored until 1 hour after start. Also, it is worth mentioning that a few percent of error can be attributed to the cell volume-based monitoring. The phase fraction is computed in the cell center, and derivation of the spatial profile from the constant values in the cells or by linear interpolation between the cells leads to inaccuracies.

This problem concerns more the monitoring with the mixture model, where the computational cell sizes are bigger.

The achieved agreement between the two computational approaches predicting the evolution of the mixture component fractions in the melt in time is satisfactory. For a description of the real process with the selected polymer mixture, the mixture model is used, setting the particle diameter of the dispersed phase to 1.5 mm, although results from this method deviate from the data obtained with the VoF method at the beginning of the process. Overall, the mixture model characterizes the reference development observed with the VoF method realistically, yielding a good prediction of the separation time. This case was visualized in Fig. 7.

Comparison of VoF and mixture model for 40/60 wt% PET/LDPE

The same comparative study was carried out for a mixture with 40/60 wt% PET/LDPE to investigate the sensitivity of the evolution of the mixture component volume fractions to the initial mixture composition. The mechanism of separation seen in Fig. 9 is the same as with the 50/50 wt% mixture. The evolution of the component volume fractions in time predicted by the mixture model, however, differs more strongly from the VoF data when using particle diameters of 1.5 and 2 mm, as seen in Fig. 10. The reason may be that, with the smaller PET volume fraction, the distance between the dispersed PET droplets increases. This reduces the probability of interaction, so that there is less frequent coalescence of dispersed droplets, and, therefore, the overall mean droplet size smaller. This fact leads to the important conclusion that a mean particle diameter appropriate for the mixture model depends not only on process parameters like rotational speed and material properties of the mixture components, but also on the initial volume fraction of the dispersed phase in the mixture. This must be observed when determining the parameter settings for use with the mixture model.

Fig. 9

Component volume fraction distribution as a function of time in the separation process as computed with (left) the VoF method and (right) with the mixture model (d = 1.5 mm) for 40/60 wt% PET/LDPE

Fig. 10

Volume-mean volume fraction evolution of the phases in the middle region (a) and in the outer region (b) for 40/60 wt% PET/LDPE

Extension of the mixture model using bidisperse particle ensembles

The above results show that the default mixture model, using a certain particle diameter to represent the dispersed phase, provides a satisfactory description of the separation process. However, it cannot capture the details of the separation process evolution in time. In the present case, the variation of an equivalent diameter of the dispersed phase portions in time is fairly dynamic, involving coalescence of the dispersed portions, and therefore depends on details of the material behaviour. This causes discrepancies between the results obtained with the VoF method and the mixture model. Therefore, an extension of the mixture model is needed. A possible approach for a universally applicable setting of particle parameters would be the use of a polydisperse particle ensemble. To illustrate the beneficial impact of such a setup, the dispersed PET phase was composed from two size classes. The selection of proper diameters and their composition was based on the results from the VoF method. Inspection of the average volume fraction evolution (the black lines in Figs. 8 and 10) shows that, in the present process, the separation process may be characterized with two stages in time. At the beginning (until ~400-500 s after start), the separation is dominated by the migration of bigger droplets, resulting in a steep increase of the components in the respective regions. After that, the rate of separation decreases and remains more or less stable until the end of the process, indicating the decrease of the relative phase velocity. The evolution of the component separation process therefore cannot be represented with a monodispersed particle ensemble characterised by one single particle diameter. The two-stage process rather suggests the use of a bi-disperse particle ensemble.

In an attempt to develop this more advanced mixture model, the 50/50 wt% PET/LDPE mixture is discussed first. The appropriate droplet diameter representing the initial process stage is obtained from the contour evolutions in the first 300 s in the VoF data. Although the diameter and the shape of the dispersed droplets vary remarkably from almost perfectly spherical to elongated filaments in the field, some average diameter for sphere particle may be determined. Accordingly, 3 mm was selected for the bigger dispersed phase diameter. As the volume fraction of this dispersed phase, 75 % (in absolute composition 75 % of 39.4 vol% of PET) turned out appropriate, which refers to the value read from Fig. 8 at ~400 s. The volumes of the regions in the field are given by the total volume of the respective phase, e.g. the outer region volume represents the volume percentage of PET from the mixture in the initial state. This means that, at ~400 s, 75 % of the PET fraction is separated, and we assume that the separation is dominated by the bigger, coalesced droplets until that time. With the same consideration, the parameters of the second dispersed phase are determined. This yields 0.75 mm particle diameter and the volume fraction of 25 % of the second particle fraction in the ensemble.

In Fig. 11, the evolutions of the PET and LDPE separation as obtained with the VoF model and with the mixture model using the named bidisperse particle ensemble are shown. Figure 12 presents the profiles of the component volume fractions in time, showing that the separation evolution predicted by this mixture model approximates the VoF data very well. At the beginning of the process, the mixture is dominated by the 3 mm particles, while, after approximately 600 s, when the majority of the dispersed phase with 3 mm diameter has migrated to the outer region, the migration of the smaller particles dominates the rest of the domain and determines the separation rate. This setup also resulted in a smoother distribution and transition along the radial direction (Fig. 11). This is a first step towards a polydisperse particle population of the dispersed phase for future work, which may be accompanied by a transport equation governing the evolution of the size classes, including coalescence and break-up models.

Fig. 11

Component volume fraction distribution as a function of time in the separation process as computed with (left) the VoF method and (right) with the bidispersed mixture model (d = 0.75 & 3 mm) for 50/50 wt% PET/LDPE

Fig. 12

Volume-mean volume fraction evolution of the components (a) in the middle region and (b) in the outer region for 50/50 wt% PET/LDPE using the bidispersed mixture model

The same analysis was carried out for the second polymer mixture with 40/60 wt% PET/LDPE. The approach of the selection of particle ensemble was the same as for the 50/50 wt% mixture composition. In this case, in the initial stage, the rate of separation is smaller than with the mixture containing more PET. Therefore 2.5 mm was set for the bigger particle diameter. The steep increase also ended earlier than with the other mixture, resulting in a volume fraction of 65 % for this first dispersed phase. In the remaining process time (after ~400 s), the dominant droplet diameter was observed to be similar as for the 50/50 wt% PET/LDPE mixture, that is 0.75 mm. The volume fraction of the second dispersed phase was set to 35 %. Figure 13 shows the volume fraction distributions computed by the two approaches. Compared to the monodisperse cases in Fig. 9, the improvement is well observable, especially at the initial stage (t ≤ 300 and 600 s), where the development in the extended mixture model follows very closely the data from the VoF simulations. The average volume fraction evolution in the designated regions plotted in Fig. 14 verifies the good conformance seen in Fig. 13. Although the mixture model underestimates the separation result with ~5 % in the outer region, the overall agreement with the data from the VoF method is excellent. The deviation may even be slightly reduced by a slight increase of the diameter for the larger particle diameter.

Fig. 13

Component volume fraction distribution as a function of time in the separation process as computed with (left) the VoF method and (right) with the bidispersed mixture model (d = 0.75 & 2.5 mm) for 40/60 wt% PET/LDPE

Fig. 14

Volume-mean volume fraction evolution of the components (a) in the middle region and (b) in the outer region for 40/60 wt% PET/LDPE using the bidispersed mixture model

The improvement by representing the separation process using polydispersed particle ensembles as compared to monodisperse particles is evident. The excellent results also show that, using the distribution from the VoF method for setting the particle diameters, is the right method. This means that, extending the mixture model, the particle diameters represent a physical property of the system and the drag model used in the mixture model to describe the phase motion is well-founded in our case. It is also worth noting that adding another dispersed phase did not increase the computational time noticeably.

Influence of rotational speed on the process time

The numerical method developed allows process parameters to be varied in order to predict their influences on the process result. One parameter influencing the centrifugal force is the diameter of the rotating containment, which, however, is kept constant at the value of d_c = 0.1 m in this study. Another essential process parameter of any centrifugal technique is the rotational speed. In the present section, the influence of the rotational speed on the process time is studied. The centrifugal force as a force driving the phase motion increases with the second power of the rotational speed. Taking this into account it may seem that the rotational speed should be increased as much as possible. However, considering the drag force on the particles, which depends on their velocity relative to the continuous phase and counteracts the centrifugal force, the rotational speed should not be increased too far. Besides that, there are also mechanical restrictions from the containment against raising the rotational speed. Therefore, finding an optimal rotational speed for a certain polymer melt mixture is not self-evident. For the evaluation it is necessary to define the process time when the separation is considered to be successful. In the present study we measure this time to the instant when the mean volume fraction of the heavier phase has reached 90 % in the outer region. Simulations were carried out using the bidispersed mixture model for the two polymer mixture compositions, varying the rotational speed between 1000 and 4000 rpm. For this study, it was assumed that the disperse phase formation process does not vary with the rotational speed. Therefore, no new VoF simulations were carried out to determine the phase distribution. The resulting process times are listed in Table 2 below, and the values are depicted in Fig. 15 as functions of the rotational speed for the two polymer mixtures. The data show that the process time decreases with increasing rotational speed. The mixture, which is more dilute in the migrating component PET, exhibits the longer separation times, since drop coalescence is less pronounced there, so that the migrating PET portions remain smaller and therefore take longer to move to the outer region. According to the curve fitting of the data, the process time scales as ${t}_{p} \propto { \omega }^{-1.91}$ for the 50/50 wt.%, and as ${t}_{p} \propto { \omega }^{-1.965}$ for the 40/60 wt.% mixture. The process time depends on the rotational speed more strongly for the mixture, which is more dilute in PET. The reason may be the weaker mutual hindrance of the migration of the PET portions in the more dilute case. Knowing the process time for one rotational speed for a given polymer mixture, the scaling laws allow the related time to be determined for other rotational speeds also. The coefficients in front of the powers of $\omega$ in the equations for the process time depend on the material properties viscosity and density, as well as on the dispersed-phase particle size, the volume fraction of the phases, and on the geometry of the rotating containment.

Table 2 Predicted process time as a function of rotational speed for the two investigated polymer mixtures

Fig. 15

Process time to 90% PET in the outer region as a function of rotational speed for 50/50 wt% PET/LDPE (red) and 40/60 wt% PET/LDPE (blue). The fit curve equations yield the process time in seconds with the rotational speed ω inserted in rpm

Conclusions and future work

A computational study investigates a centrifugal process to separate a binary mixture of molten polymers for recycling purposes. The polymeric mixture components studied are PET and LDPE, which are immiscible in the molten state. Filling the polymer mixture into a containment and rotating it, the technique applies a centrifugal force to the polymer mixture to separate the components according to their densities. The technique was experimentally studied in [1, 2]. The simulations with Computational Fluid Dynamics (CFD) were carried out using the software Ansys FLUENT. The polymer mixture was treated as a two-phase fluid with one continuous and one dispersed phase. This binary mixture was modelled using the VoF method with high resolution and high computational costs, to create a reference data set, and with the well-established mixture or algebraic slip model for the production runs. The mixture model is a simple approach for simulating multiphase flow and yields results in a short time, since it allows for coarse spatial resolution of the computational domain. In the modelling of the dynamic interaction of the phases, the diameter of the dispersed-phase particles plays an important role. In a first approach of the present study, a monodisperse particle ensemble was selected for modelling the drag force on the migrating disperse-phase particles. The particle diameter was used as a parameter so as to represent the component separation evolution in time predicted with the VoF method. Since in the real process the particle diameter varies in time, the parameter value determined plays the role of a factor best suited for the simulations. Extending this approach to a bidisperse particle system, with two different size classes, improves the representation of the VoF results significantly, indicating that a polydisperse particle ensemble may be best suited for these simulations, since it best represents the physical situation.

The results achieved show that the process time for polymer component separation found in the experiments of [1, 2] is well reproduced by the simulations. Computations with varying rotational speed show that the separation is reached in a shorter time with the higher rotational speed, as expected. The process time ${t}_{p}$ scales with the rotational speed $\omega$ approximately as ${t}_{p} \propto { \omega }^{-1.9}$, with a stronger dependency of ${t}_{p}$ on $\omega$ for the mixture which is more dilute in the migrating component due to weaker mutual hindrance of the dispersed component portions.

Future studies may involve polydisperse particle ensembles for the dispersed phase to best represent the physical properties of the polymer mixture. The particle sizes to be involved may be functions of the component volume fraction. A population balance model would represent the evolution of the particle size due to coalescence and breakup of the particles. For this purpose, the dispersed phase particle size spectrum in the initial homogeneous mixture will be set as an input property. For practical reasons, experimental results usually present the end state of the separation process. Intermediate states in the course of the separation are not easily accessible from publications in the literature. The time evolution of the separation computed is therefore difficult to validate.

The present study investigates a batch separation technique, where a quantity of the polymer mixture is separated and solidified in a given containment. An alternative technique is to continuously feed the polymer mixture to a rotating tube, where it is separated and the mixture components are withdrawn from different outlets. In such a device, a pressure-driven axial flow, exhibiting axial velocities varying with the radial coordinate in the tube cross sections, transports the mixture through the tube. This kind of continuous process will be studied in future computational simulations.